Smart-Sensors to Estimate Insulation Health in Induction Motors via Analysis of Stray Flux
Abstract
:1. Introduction
2. Materials and Methods
2.1. Discrete Wavelet Transform (DWT)
2.2. Wavelet Entropy
2.3. Stray Flux Analysis
2.4. Artificial Neural Network
2.5. Smart-Sensor
2.5.1. Primary Sensors
2.5.2. DAS and LCD
2.6. HSP Unit
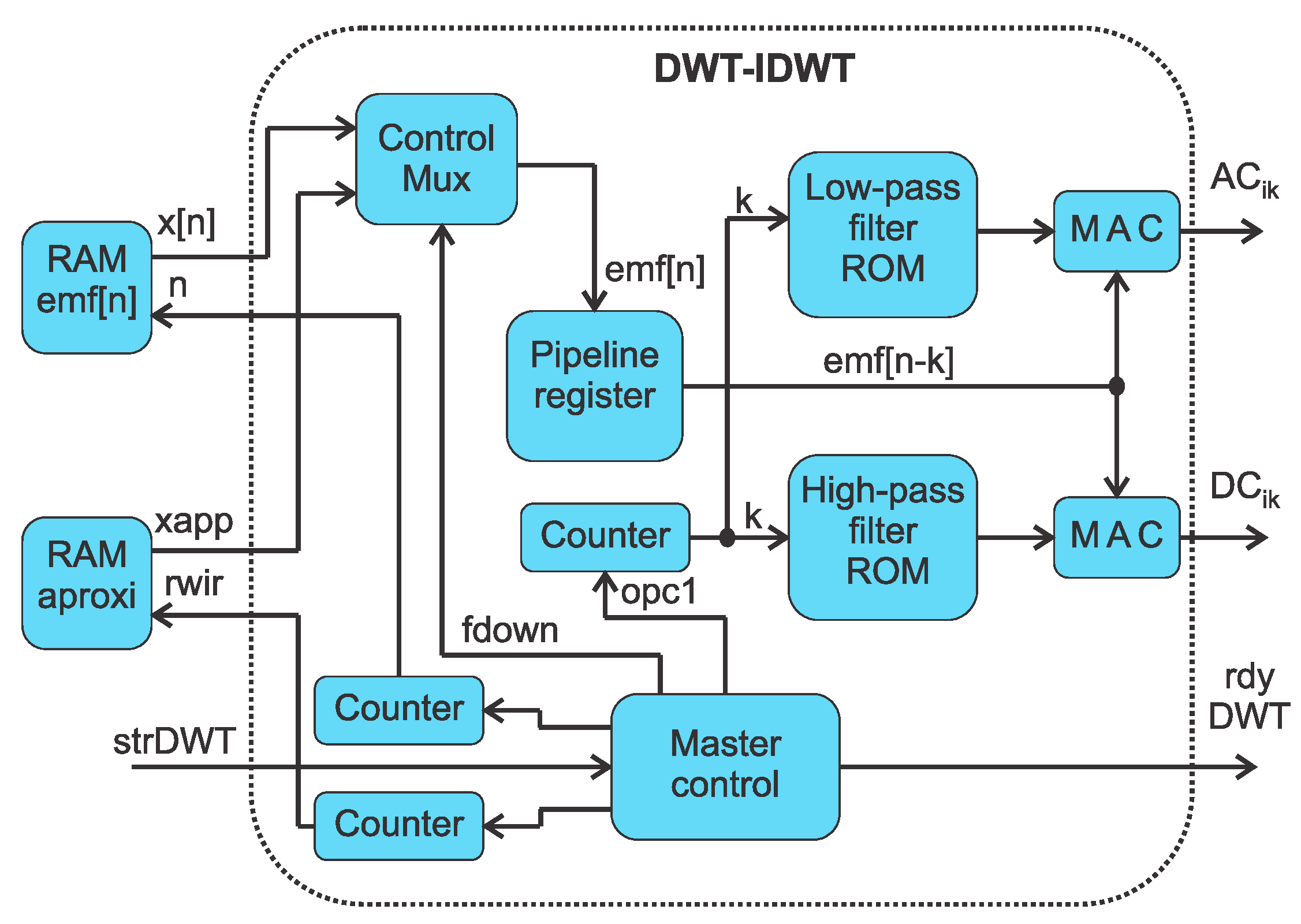
2.6.1. DWT–IDWT Digital Structure
2.6.2. Wavelet Entropy Digital Structure
2.6.3. FFNN Digital Structure
3. Results
Experimental Set-Up
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al Badawi, F.S.; AlMuhaini, M. Reliability modelling and assessment of electric motor driven systems in hydrocarbon industries. IET Electr. Power Appl. 2015, 9, 605–611. [Google Scholar] [CrossRef]
- Trejo-Hernandez, M.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.; Rodriguez-Donate, C.; Dominguez-Gonzalez, A.; Herrera-Ruiz, G. FPGA-based fused smart-sensor for tool-wear area quantitative estimation in CNC machine inserts. Sensors 2010, 10, 3373–3388. [Google Scholar] [CrossRef] [PubMed]
- Cabal-Yepez, E.; Garcia-Ramirez, A.G.; Romero-Troncoso, R.J.; Garcia-Perez, A.; Osornio-Rios, R.A. Reconfigurable monitoring system for time-frequency analysis on industrial equipment through STFT and DWT. IEEE Trans. Ind. Inform. 2013, 9, 760–771. [Google Scholar] [CrossRef]
- Granados-Lieberman, D.; Romero-Troncoso, R.; Cabal-Yepez, E.; Osornio-Rios, R.; Franco-Gasca, L. A real-time smart sensor for high-resolution frequency estimation in power systems. Sensors 2009, 9, 7412–7429. [Google Scholar] [CrossRef]
- Cabal-Yepez, E.; Fernandez-Jaramillo, A.A.; Romero-Troncoso, R.J.; Garcia-Perez, A.; Osornio-Rios, R.A. Smart sensor for electrical machine monitoring through statistical analysis. In Proceedings of the 2012 XXth International Conference on Electrical Machines, 2–5 September 2012. [Google Scholar]
- Garcia-Ramirez, A.G.; Osornio-Rios, R.A.; Granados-Lieberman, D.; Garcia-Perez, A.; Romero-Troncoso, R.J. Smart sensor for online detection of multiple-combined faults in VSD-fed induction motors. Sensors 2012, 12, 11989–12005. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A survey of condition monitoring and protection methods for medium-voltage induction motors. IEEE Trans. Ind. Appl. 2011, 1, 34–46. [Google Scholar] [CrossRef]
- Bonnett, A.H.; Yung, C. Increased efficiency versus increased reliability. IEEE Ind. Appl. Mag. 2008, 14, 29–36. [Google Scholar] [CrossRef]
- Motor Reliability Working Group. Report of large motor reliability survey of industrial and commercial installations, Part I. IEEE Trans. Ind. Appl. 1985, 1, 865–872. [Google Scholar]
- Thorsen, O.V.; Dalva, M. A survey of faults on induction motors in offshore oil industry, petrochemical industry, gas terminals, and oil refineries. IEEE Trans. Ind. Appl. 1995, 31, 1186–1196. [Google Scholar] [CrossRef]
- Capolino, G.A.; Antonino-Daviu, J.A.; Riera-Guasp, M. Modern diagnostics techniques for electrical machines, power electronics, and drives. IEEE Trans. Ind. Electron. 2015, 62, 1738–1745. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Li, J. Diagnosis of inter-turn short circuit of synchronous generator rotor winding based on volterra kernel identification. Energies 2018, 11, 2524. [Google Scholar] [CrossRef]
- Malekpour, M.; Phung, B.T.; Ambikairajah, E. Online technique for insulation assessment of induction motor stator windings under different load conditions. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 349–358. [Google Scholar] [CrossRef]
- Cabanas, M.F.; Norniella, J.G.; Melero, M.G.; Rojas, C.H.; Cano, J.M.; Pedrayes, F.; Orcajo, G.A. Detection of stator winding insulation failures: Online and offline tests. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013. [Google Scholar]
- Siddique, A.; Yadava, G.S.; Singh, B. A review of stator fault monitoring techniques of induction motors. IEEE Trans. Energy Conver. 2005, 20, 106–114. [Google Scholar] [CrossRef]
- Brown, A.; David, E.; Essalihi, M. Insulation resistance measurements for machine insulation. In Proceedings of the 2011 Electrical Insulation Conference (EIC), Annapolis, MD, USA, 5–8 June 2011. [Google Scholar]
- Stone, G.C. Recent important changes in IEEE motor and generator winding insulation diagnostic testing standards. IEEE Trans. Ind. Appl. 2005, 41, 91–100. [Google Scholar] [CrossRef]
- Yang, J.; Lee, S.B.; Yoo, J.; Lee, S.; Oh, Y.; Choi, C.A. Stator winding insulation condition monitoring technique for inverter-fed machines. IEEE Trans. Power Electron. 2007, 22, 2026–2033. [Google Scholar] [CrossRef]
- Lee, S.B.; Yang, J.; Younsi, K.; Bharadwaj, R.M. An online ground wall and phase-to-phase insulation quality assessment technique for AC-machine stator windings. IEEE Trans. Ind. Appl. 2006, 42, 946–957. [Google Scholar]
- Seshadrinath, J.; Singh, B.; Panigrahi, B.K. Vibration analysis based interturn fault diagnosis in induction machines. IEEE Trans. Ind. Inf. 2014, 10, 340–350. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, T.C.; Naikan, V.N. Induction motor inter turn fault detection using infrared thermographic analysis. Infrared Phys. Tech. 2016, 77, 277–282. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, Z. Diagnosis of the three-phase induction motor using thermal imaging. Infrared Phys. Tech. 2017, 81, 7–16. [Google Scholar] [CrossRef]
- Stone, G.C. A perspective on online partial discharge monitoring for assessment of the condition of rotating machine stator winding insulation. IEEE Electr. Insul. Mag. 2012, 28, 8–13. [Google Scholar] [CrossRef]
- Wolkiewicz, M.; Tarchała, G.; Orłowska-Kowalska, T.; Kowalski, C.T. Online stator interturn short circuits monitoring in the DFOC induction-motor drive. IEEE Trans. Ind. Electron. 2016, 63, 2517–2528. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Kappatou, J.C. The zero-sequence current as a generalized diagnostic mean in Δ-connected three-phase induction motors. IEEE Trans. Energy Conver. 2014, 29, 138–148. [Google Scholar] [CrossRef]
- Cash, M.A.; Habetler, T.G.; Kliman, G.B. Insulation failure prediction in AC machines using line-neutral voltages. IEEE Trans. Ind. Appl. 1998, 34, 1234–1239. [Google Scholar] [CrossRef]
- Lee, S.B.; Tallam, R.M.; Habetler, T.G. A robust, online turn-fault detection technique for induction machines based on monitoring the sequence component impedance matrix. IEEE Trans. Power Electron. 2003, 18, 865–872. [Google Scholar]
- Dasgupta, A.; Nath, S.; Das, A. Transmission line fault classification and location using wavelet entropy and neural network. Electric Power Compon. Syst. 2012, 40, 1676–1689. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods. 2001, 105, 65–75. [Google Scholar] [CrossRef]
- İşler, Y.; Kuntalp, M. Combining classical HRV indices with wavelet entropy measures improves to performance in diagnosing congestive heart failure. Comput. Biol. Med. 2007, 37, 1502–1510. [Google Scholar] [CrossRef]
- Guojun, L.; Yong, W.; Le, L.; Shaofeng, G.; Haiqing, N.; Xuemei, W. Suppressing white noise in PD signal based on wavelet entropy and improved threshold function. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017. [Google Scholar]
- Antonino-Daviu, J.A.; Riera-Guasp, M.; Folch, J.R.; Palomares, M.P. Validation of a new method for the diagnosis of rotor bar failures via wavelet transform in industrial induction machines. IEEE Trans. Ind. Appl. 2006, 42, 990–996. [Google Scholar] [CrossRef] [Green Version]
- Antonino-Daviu, J.A.; Jover, P.; Riera, M.; Arkkio, A.; Roger-Folch, J. DWT analysis of numerical and experimental data for the diagnosis of dynamic eccentricities in induction motors. Mech. Syst. Signal Proc. 2007, 21, 2575–2589. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Pérez-Cruz, J.A. General approach for the transient detection of slip-dependent fault components based on the discrete wavelet transform. IEEE Transa. Ind. Electron. 2008, 55, 4167–4180. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.A.; Riera-Guasp, M.; Pineda-Sánchez, M.; Pons-Llinares, J.; Puche-Panadero, R.; Pérez-Cruz, J. Feature extraction for the prognosis of electromechanical faults in electrical machines through the DWT. Int. J. Comput. Intell. Syst. 2009, 2, 158–167. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Rosso, O.A.; Başar, E.; Schürmann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Blanco, S.; Figliola, A.; Quiroga, R.Q.; Rosso, O.A.; Serrano, E. Time-frequency analysis of electroencephalogram series. Wavelet packets and information cost function. Phys. Rev. E. 1998, 57. [Google Scholar] [CrossRef]
- Ramirez-Nunez, J.A.; Antonino-Daviu, J.A.; Climente-Alarcón, V.; Quijano-López, A.; Razik, H.; Osornio-Rios, R.A.; Romero-Troncoso, R.D. Evaluation of the detectability of electromechanical faults in induction motors via transient analysis of the stray flux. Trans. Ind. Appl. 2018, 54, 4324–4332. [Google Scholar] [CrossRef]
- Iglesias-Martínez, M.E.; Antonino-Daviu, J.A.; Fernández de Córdoba, P.; Conejero, J.A. Rotor Fault Detection in Induction Motors Based on Time-Frequency Analysis Using the Bispectrum and the Autocovariance of Stray Flux Signals. Energies 2019, 12, 597. [Google Scholar] [CrossRef]
- Frosini, L.; Harlişca, C.; Szabó, L. Induction machine bearing fault detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Dehghan, H.; Haghjoo, F.; Cruz, S.M. A Flux-Based Differential Technique for Turn-to-Turn Fault Detection and Defective Region Identification in Line-Connected and Inverter-Fed Induction Motors. IEEE Trans. Energy Conver. 2018, 33, 1876–1885. [Google Scholar] [CrossRef]
- Romary, R.; Roger, D.; Brudny, J.F. Analytical computation of an AC machine external magnetic field. Euro. Phys. J.-Appl. Phys. 2009, 47. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Garcia-Perez, A.; Osornio-Rios, R.A.; Romero-Troncoso, R.D. Empirical mode decomposition and neural networks on FPGA for fault diagnosis in induction motors. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef]
- Rairán-Antolines, J.D. Reconstruction of periodic signals using neural networks. Tecnura 2014, 18, 34–46. [Google Scholar]
- Mitchell, J.N. Computer multiplication and division using binary logarithms. IRE Trans. Electron. Comput. 1962, 4, 512–517. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; de la Fraga, L.G.; Rangel-Magdaleno, J. Engineering applications of FPGAs; Springer: New York, NY, USA, 2016. [Google Scholar]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Trejo-Hernandez, M.; Romero-Troncoso, R.d.J.; Antonino-Daviu, J.A. Smart-Sensors to Estimate Insulation Health in Induction Motors via Analysis of Stray Flux. Energies 2019, 12, 1658. https://doi.org/10.3390/en12091658
Zamudio-Ramirez I, Osornio-Rios RA, Trejo-Hernandez M, Romero-Troncoso RdJ, Antonino-Daviu JA. Smart-Sensors to Estimate Insulation Health in Induction Motors via Analysis of Stray Flux. Energies. 2019; 12(9):1658. https://doi.org/10.3390/en12091658
Chicago/Turabian StyleZamudio-Ramirez, Israel, Roque Alfredo Osornio-Rios, Miguel Trejo-Hernandez, Rene de Jesus Romero-Troncoso, and Jose Alfonso Antonino-Daviu. 2019. "Smart-Sensors to Estimate Insulation Health in Induction Motors via Analysis of Stray Flux" Energies 12, no. 9: 1658. https://doi.org/10.3390/en12091658






