Comparative Analysis of Different Methodologies Used to Estimate the Ground Thermal Conductivity in Low Enthalpy Geothermal Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Global Description of the Area under Study
2.2. Thermal Conductivity Characterization
2.2.1. KD2 Pro Measurements
- kT = Global thermal conductivity of the whole borehole column.
- k1 = Thermal conductivity of the geological formation of layer 1.
- k2 = Thermal conductivity of the geological formation of layer 2.
- k3 = Thermal conductivity of the geological formation of layer 3.
- k4 = Thermal conductivity of the geological formation of layer 4.
- T1 = Thickness of layer 1 expressed as a percentage of the total well thickness.
- T2 = Thickness of layer 2 expressed as a percentage of the total well thickness.
- T3 = Thickness of layer 3 expressed as a percentage of the total well thickness.
- T4 = Thickness of layer 4 expressed as a percentage of the total well thickness.
2.2.2. Geophysics
- k = thermal conductivity (W/mK)
- x = electrical resistivity (Ω·m)
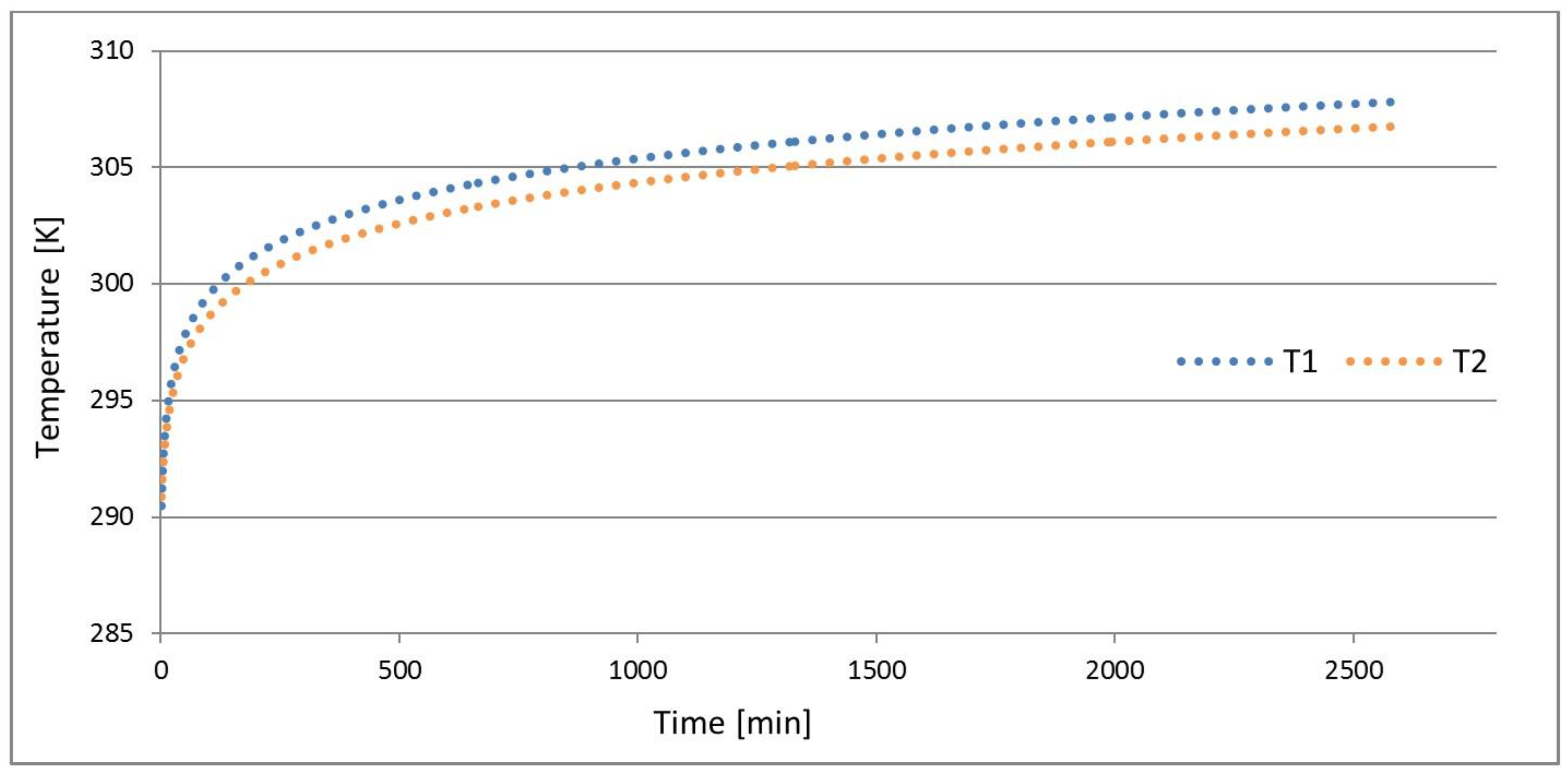
2.2.3. Thermal Response Test
- -
- Circuit filling and establishment of the appropriate working pressure.
- -
- Activation of the circulating TRT pump and starting of the first heating stage (3 kW).
- -
- General system operation during a certain period of time.
- -
- Downloading and data management from the Kamstrup register.
- -
- Calculation of the global thermal conductivity parameter.
- r = borehole radius (m)
- ke = estimated thermal conductivity (W/mK)
- cv = volumetric thermal capacity (J/m3/K)
- Q = heat flux (kW/min)
- b = slope (min)
- H = borehole length (m)
3. Results and Discussion
3.1. Previous Methods Results
3.2. TRT Results
3.3. General Comparison
- Thermal conductivities obtained by the alternative techniques are in strong agreement with the TRT result. The seismic prospecting method provides the most similar value, with a difference of only 0.024 W/mK with respect to the TRT value.
- The use of electrical resistivity tomography also allows to obtain thermal conductivity values close to the TRT result. In this case, the difference between both methods is 0.316 W/mK.
- The least accurate method is the use of the thermal conductivity map obtained by in situ KD2 Pro measurements. Despite having the least accuracy of all the procedures considered here, the difference with respect to the TRT is 0.358 W/mK.
- By evaluating the mentioned differences in terms of percentage, the errors of each alternative methodology in comparison with the TRT are 15.48% for the thermal conductivity map, 1.04% for seismic prospecting, and 13.66% when applying electrical resistivity tomography.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ally, M.R.; Munk, J.D.; Baxter, V.D.; Gehl, A.C. Exergy analysis of a two-stage ground source heat pump with a vertical bore for residential space conditioning under simulated occupancy. Appl. Energy 2015, 155, 502–514. [Google Scholar] [CrossRef]
- Han, C.; Yu, X.B. Performance of a residential ground source heat pump system in sedimentary rock formation. Appl. Energy 2016, 164, 89–98. [Google Scholar] [CrossRef]
- Pasquier, P. Interpretation of the first hours of a thermal response test using the time derivative of the temperature. Appl. Energy 2018, 213, 56–75. [Google Scholar] [CrossRef]
- Henk, J.L. Witte, Error analysis of thermal response tests. Appl. Energy 2013, 109, 302–311. [Google Scholar]
- Pasquier, P.; Zarrella, A.; Marcotte, D. A multi-objetive optimization strategy to reduce correlation and uncertainty for thermal response test analysis. Geothermics 2019, 79, 176–187. [Google Scholar] [CrossRef]
- Bandos, T.V.; Montero, Á.; Fernández de Córdoba, P.; Urchueguía, J.F. Improving parameter estimates obtained from termal response tests: Effect of ambient air temperature variations. Geothermics 2011, 40, 136–143. [Google Scholar] [CrossRef]
- Choi, W.; Ooka, R. Interpretation of disturbed data in thermal response tests using the infinite line source model and numerical parameter estimation method. Appl. Energy 2015, 148, 476–488. [Google Scholar] [CrossRef]
- ASHRAE. Geothermal energy. In ASHRAE Handbook Heating, Ventilating, and Air-Conditioning Applications; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2007; pp. 32.1–32.30. [Google Scholar]
- Gehlin, S.; Hellström, G. Comparison of four models for thermal response test evaluation. ASHRAE Trans. 2003, 109, 131–142. [Google Scholar]
- Spitler, J.D.; Gehlin, S.E. Thermal response testing for ground source heat pump systems: An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D. Minimum duration of in-situ tests on vertical boreholes. ASHRAE Trans. 2003, 109, 475–486. [Google Scholar]
- Bozzoli, F.; Pagliarini, G.; Rainieri, S.; Schiavi, L. Short-time thermal response test based on a 3-D numerical model. J. Phys. Conf. Ser. 2012, 395, 012–056. [Google Scholar] [CrossRef]
- Bujok, P.; Grycz, D.; Klempa, M.; Kunz, A.; Porzer, M.; Pytlik, A.; Rozehnal, Z.; Vojčinák, P. Assessment of the influence of shortening the duration of TRT (thermal response test) on the precision of measured values. Energy 2014, 64, 120–129. [Google Scholar] [CrossRef]
- Poulsen, S.; Alberdi-Pagola, M. Interpretation of ongoing thermal response tests of vertical (BHE) borehole heat exchangers with predictive uncertainty based stopping criterion. Energy 2015, 88, 157–167. [Google Scholar] [CrossRef]
- Choi, W.; Kikumoto, H.; Choudhary, R.; Ooka, R. Bayesian inference for thermal response test parameter estimation and uncertainty assessment. Appl. Energy 2018, 209, 306–321. [Google Scholar] [CrossRef]
- Witte, H.J.L.; van Gelder, G.J.; Spitler, J.D. In Situ Measurement of Ground Thermal Conductivity: The Dutch Perspective. ASHRAE Trans. 2002, 108, 859–867. [Google Scholar]
- Freifeld, B.M.; Finsterle, S.; Onstott, T.C.; Toole, P.; Pratt, L.M. Ground surface temperature reconstructions: Using in situ estimates for thermal conductivity acquired with a fiber optic distributed thermal perturbation sensor. Geophys. Res. Lett. 2008, 35, L14309. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Said, S.A.; Mokheimer, E.M.; Habib, M.A.; Badr, H.M.; Al-Shayea, N.A. First in situ determination of the ground thermal conductivity for borehole heat exchanger applications in Saudi Arabia. Renew. Energy 2009, 34, 2218–2223. [Google Scholar] [CrossRef]
- Geological and Mining Institute of Spain (IGME). Geological National Mapping (MAGNA); IGME: Madrid, Spain, 2018. [Google Scholar]
- Chamorro, C.R.; García-Cuesta, J.L.; Mondéjar, M.E.; Linares, M.M. An estimation of the enhanced geothermal systems potential for the Iberian Peninsula. Renew. Energy 2014, 66, 1–14. [Google Scholar] [CrossRef]
- Blázquez, C.S.; Martín, A.F.; Nieto, I.M.; García, P.C.; Pérez, L.S.S.; Aguilera, D.G. Thermal conductivity map of the Avila region (Spain) based onthermal conductivity measurements of different rock and soil samples. Geothermics 2017, 65, 60–71. [Google Scholar] [CrossRef]
- Blázquez, C.S.; Martín, A.F.; García, P.C.; González-Aguilera, D. Thermal conductivity characterization of three geological formations by the implementation of geophysical methods. Geothermics 2018, 72, 101–111. [Google Scholar] [CrossRef]
- Nieto, I.M.; Martín, A.F.; Blázquez, C.S.; Aguilera, D.G.; García, P.C.; Vasco, E.F.; García, J.C. Use of 3D electrical resistivity tomography to improve the design of low enthalpy geothermal systems. Geothermics 2019, 79, 1–13. [Google Scholar] [CrossRef]
- Raymond, J.; Therrien, R.; Gosselin, L. Borehole temperature evolution during thermal response tests. Geothermics 2011, 40, 69–78. [Google Scholar] [CrossRef]
- Andersson, O.; Gehlin, S. State of the Art: Sweden, Quality Management in Design, Construction and Operation of Borehole Systems. Available online: http://media.geoenergicentrum.se/2018/06/Andersson_Gehlin_2018_State-of-the-Art-report-Sweden-for-IEA-ECES-Annex-27.pdf (accessed on 20 April 2019).
- Gustafsson, A.-M.; Westerlund, L.; Hellström, G. CFD-modelling of natural convection in a groundwater-filled borehole heat exchanger. Appl. Therm. Eng. 2010, 30, 683–691. [Google Scholar] [CrossRef]
- UNE-EN ISO 172628:2017. Geotechnical Investigation and Testing. Geothermal Testing. Determination of Thermal Conductivity of Soil and Rock Using a Borehole Heat Exchanger; International Organization for Standardizatio: Geneva, Switzerland, 2017. [Google Scholar]
- Bates, D.R.; Estermann, I. Advances in Atomic and Molecular Physics; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Ingersoll, L.R.; Plass, H.J. Theory of the ground pipe heat source for the heat pump. Heat. Pip. Air Cond. 1948, 119–122. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Decagon Devices; KD2 Pro; Decagon Devices: Pullman, WA, USA, 2016.
- W-GeoSoft; Geophysical Software; W-GeoSoft: Bioley-Orjulaz, Switzerland, 1988.
- Geotomo Software; Geotomo Software: Penang, Malaysia, 2019.
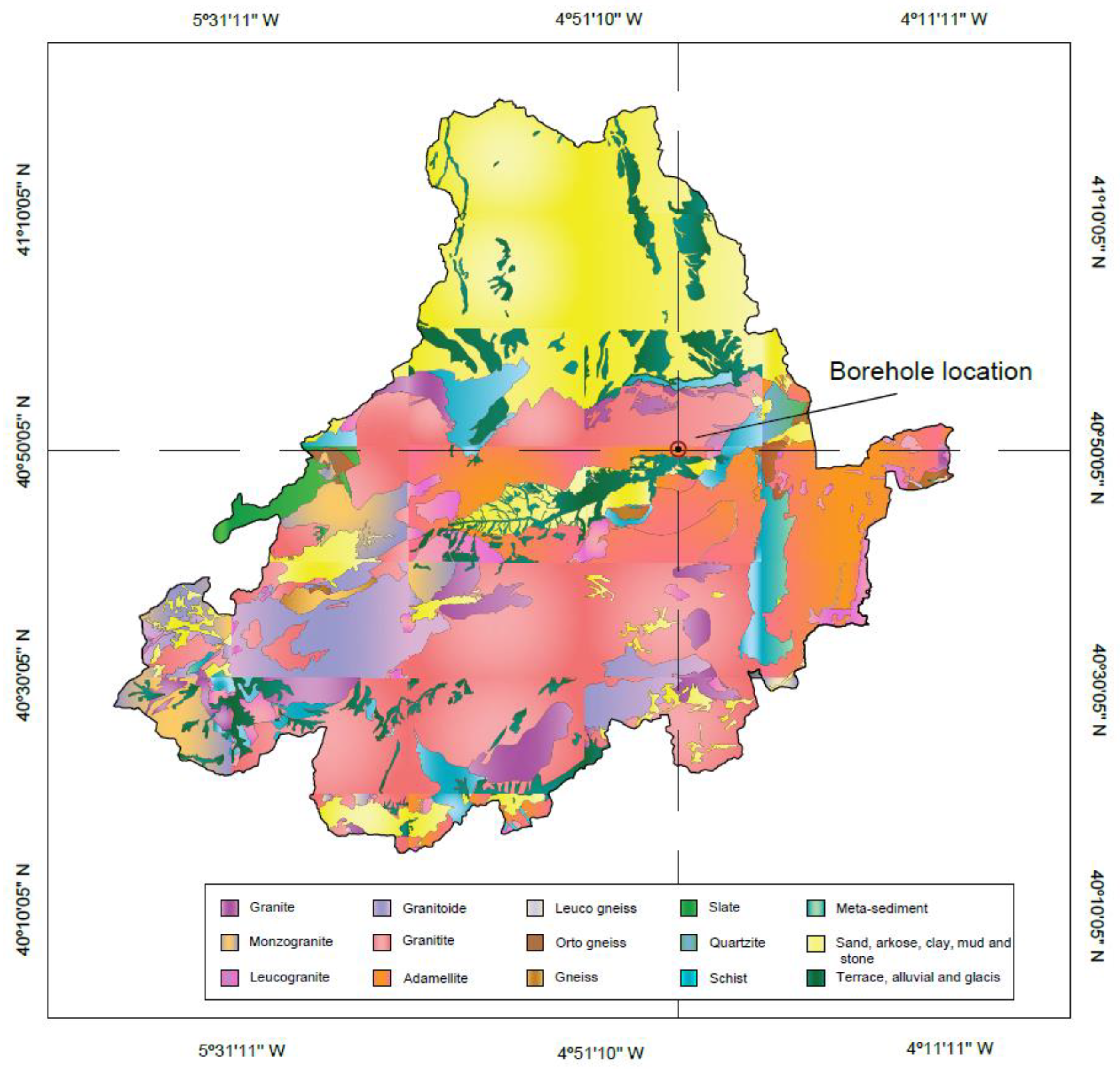


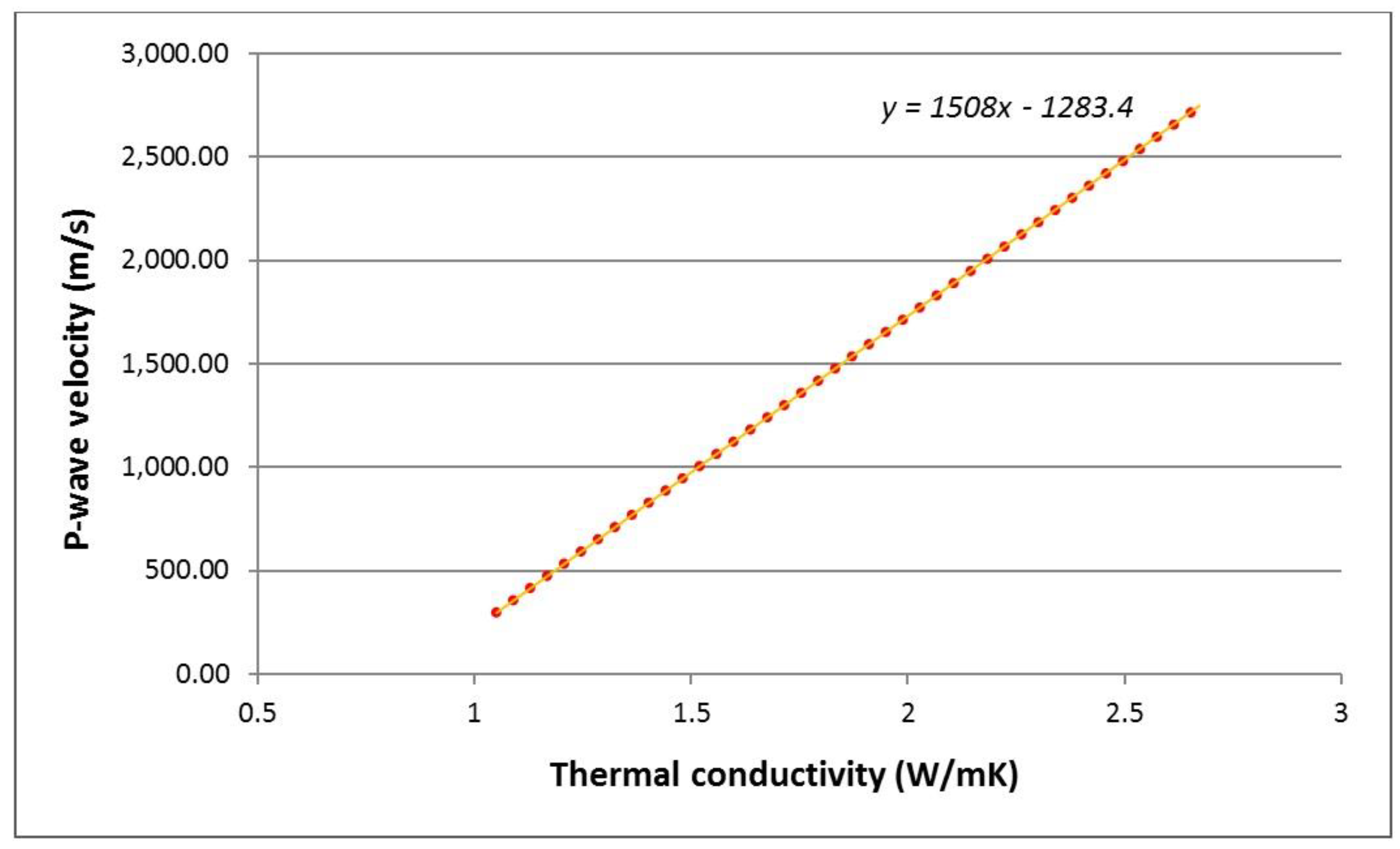
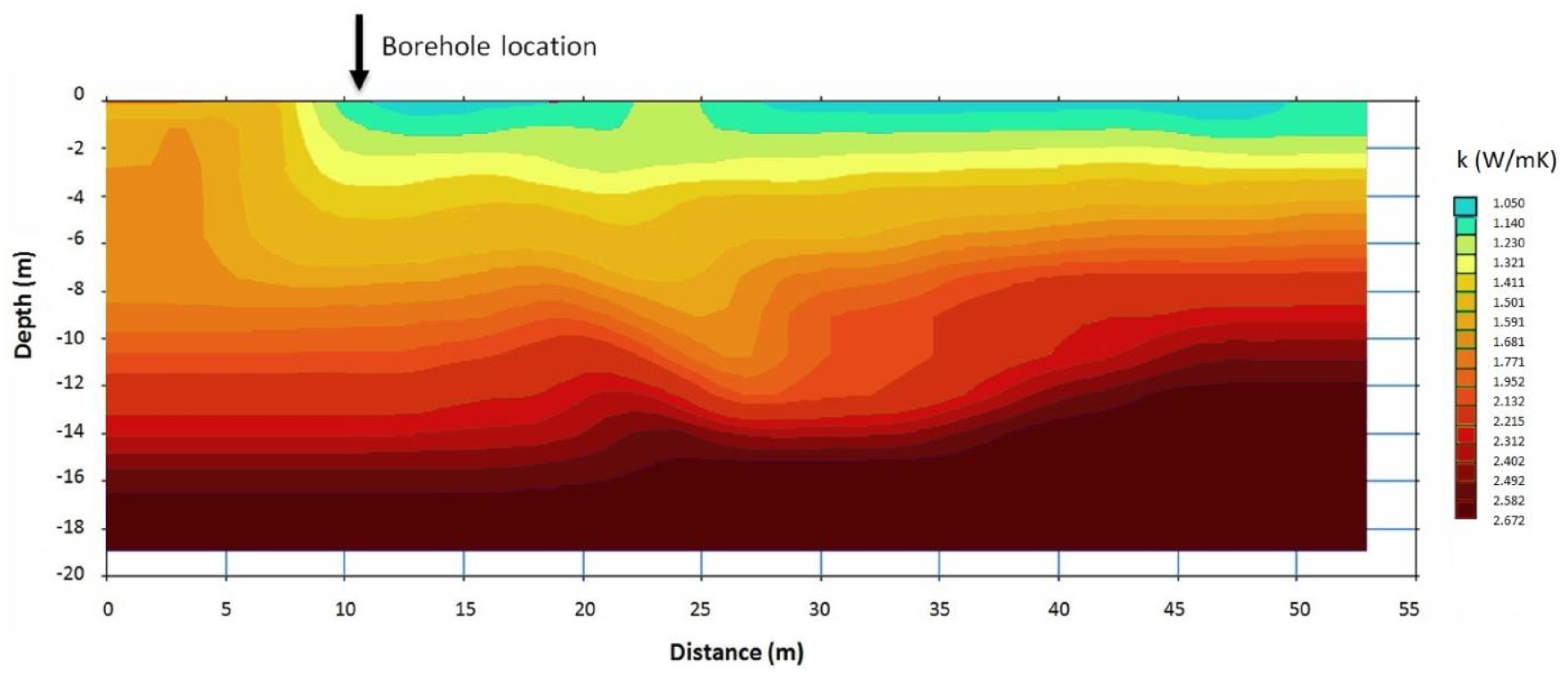
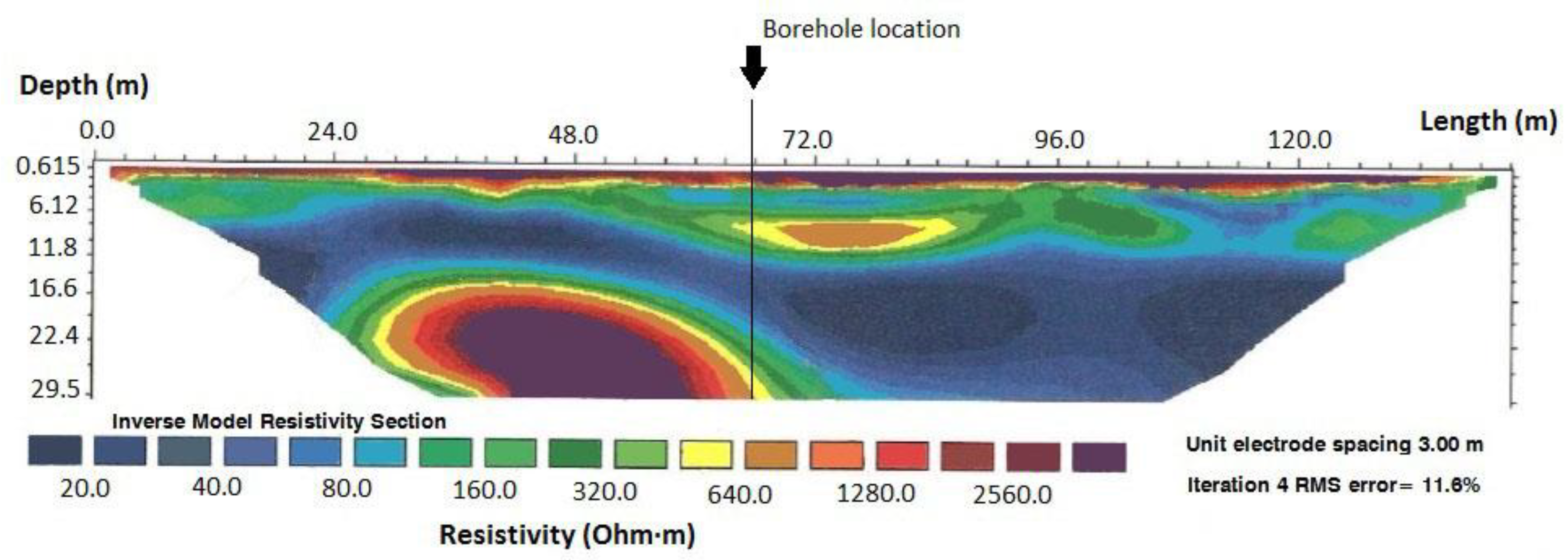



| Borehole Position | |
|---|---|
| Latitude | 40°39′2,45 N |
| Longitude | 4°40′44,84 O |
| Geological Composition | Thickness (m) | Thermal Conductivity (W/mK) * | |
|---|---|---|---|
| Layer 1 | Anthropogenic fills | 10 | 1.502 |
| Layer 2 | Sandstones and clayey conglomerate | 7.5 | 1.882 |
| Layer 3 | Sandstones and conglomerate | 20 | 2.041 |
| Layer 4 | Altered adamellite | 5.5 | 2.565 |
| Geological Formation | Thermal Conductivity * (W/mK) | |
|---|---|---|
| Minimum value | Anthropogenic fills | 1.105 |
| Maximum value | Altered adamellite | 2.672 |
| Thickness (m) | Thermal Conductivity (W/mK) | |
|---|---|---|
| Layer 1 | 1.2 | 1.140 |
| Layer 2 | 1.1 | 1.230 |
| Layer 3 | 1.3 | 1.321 |
| Layer 4 | 1.35 | 1.411 |
| Layer 5 | 2 | 1.501 |
| Layer 6 | 0.8 | 1.591 |
| Layer 7 | 0.9 | 1.681 |
| Layer 8 | 0.9 | 1.771 |
| Layer 9 | 1 | 1.952 |
| Layer 10 | 0.9 | 2.132 |
| Layer 11 | 1.4 | 2.215 |
| Layer 12 | 0.9 | 2.312 |
| Layer 13 | 0.7 | 2.402 |
| Layer 14 | 0.8 | 2.492 |
| Layer 15 | 0.9 | 2.582 |
| Layer 16 * | 26.85 | 2.672 |
| Thickness (m) | Electrical Resistivity (Ohm·m) | Thermal Conductivity (W/mK) | |
|---|---|---|---|
| Layer 1 | 1 | 1280 | 1.943 |
| Layer 2 | 4.12 | 100 | 1.498 |
| Layer 3 | 6.88 | 450 | 1.574 |
| Layer 4 | 10 | 55 | 1.494 |
| Layer 5 | 7.5 | 360 | 1.550 |
| Layer 6 * | 13.5 | 2500 | 2.988 |
| Methodology | Thermal Conductivity (W/mK) |
|---|---|
| KD2 Pro | 1.955 |
| Seismic prospecting | 2.337 |
| Electrical resistivity | 1.997 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sáez Blázquez, C.; Martín Nieto, I.; Farfán Martín, A.; González-Aguilera, D.; Carrasco García, P. Comparative Analysis of Different Methodologies Used to Estimate the Ground Thermal Conductivity in Low Enthalpy Geothermal Systems. Energies 2019, 12, 1672. https://doi.org/10.3390/en12091672
Sáez Blázquez C, Martín Nieto I, Farfán Martín A, González-Aguilera D, Carrasco García P. Comparative Analysis of Different Methodologies Used to Estimate the Ground Thermal Conductivity in Low Enthalpy Geothermal Systems. Energies. 2019; 12(9):1672. https://doi.org/10.3390/en12091672
Chicago/Turabian StyleSáez Blázquez, Cristina, Ignacio Martín Nieto, Arturo Farfán Martín, Diego González-Aguilera, and Pedro Carrasco García. 2019. "Comparative Analysis of Different Methodologies Used to Estimate the Ground Thermal Conductivity in Low Enthalpy Geothermal Systems" Energies 12, no. 9: 1672. https://doi.org/10.3390/en12091672
APA StyleSáez Blázquez, C., Martín Nieto, I., Farfán Martín, A., González-Aguilera, D., & Carrasco García, P. (2019). Comparative Analysis of Different Methodologies Used to Estimate the Ground Thermal Conductivity in Low Enthalpy Geothermal Systems. Energies, 12(9), 1672. https://doi.org/10.3390/en12091672









