The Study of Flow Characteristics During the Decomposition Process in Hydrate-Bearing Porous Media Using Magnetic Resonance Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Apparatus and Materials
2.2. Absolute Permeability Measurement
- (1)
- The MRI cell was filled with glass beads to simulate the porous media and form a hydrate in the sample tube.
- (2)
- After the hydrate formation, the VNMRJ software 4.0 (Palo Alto, CA, USA) was run in the image acquisition computer, shimming, tuning, and then the imaging sequence was set, the relevant parameters were set, and the appropriate slice was selected to start scanning.
- (3)
- A decomposition ratio was selected during the decomposition process, and the water injected into the pump was cooled to 1 °C by a water bath, rather than a heat flow injection into the MRI cell. The outlet pressure and flow rate were controlled by a back-pressure valve. This stopped the decomposition of the undecomposed hydrate, and the entering of cold water also displaced the free gas generated by the decomposition, so that the amount of the hydrate did not change.
- (4)
- A differential pressure sensor was used to record the pressure difference at the inlet and outlet of the MRI cell, and the flow of liquid into the MRI cell was recorded with a pump.
- (5)
- The tubing was disassembled and the MRI cell was cleaned.
2.3. Relative Permeability Measurement Method
- (1)
- The glass beads were inserted into the MRI cell to simulate the porous media, and the hydrate was formed in the MRI cell by referring to the experimental procedure in last section.
- (2)
- After the hydrate formation was completed, the VNMRJ software in the image acquisition computer was used to shim and tune. Then the spin echo multi-section scanning (SEMS) imaging sequence was set, the relevant parameters were set, and the appropriate slice was selected to get ready for scanning.
- (3)
- After the system was debugged, and the injection pump flow rate was set, a heat flow was injected into the MRI cell to decompose the hydrate in the MRI cell. In the meantime, the flow of the decomposed water was measured using a nuclear magnetic resonance imaging system. When a certain percentage of decomposition was reached, the injection of the heat flow was stopped, and the temperature and pressure conditions of the MRI cell were controlled to stop the decomposition of the hydrate in the porous media.
- (4)
- The CH4 was injected at a constant rate to drive out the free water in the hydrated porous media while the MRI imaging system was used to determine the saturation change and velocity distribution during the process of gas driving water.
- (5)
- Water was injected at a constant rate to drive the CH4 in the hydrate bearing porous media, while the saturation change and velocity distribution during the water driving gas process were measured using an MRI imaging system.
- (6)
- The relative permeability of the gas and water phases of the hydrate bearing porous media of such decomposition degree was calculated using the experimental data obtained.
- (7)
- The relative permeability of the two phases in the hydrate bearing porous media at different decomposition degrees were obtained by repeating the above steps.
2.4. Flow Measurement Method in Hydrate Decomposition Process
- (1)
- The glass beads were inserted into the MRI cell to simulate the porous media, and the hydrate was formed in the MRI cell referring to the experimental procedure in Section 2.2.
- (2)
- After the hydrate was formed, the VNMRJ software in the image collection computer was used for shimming and tuning. Then the SEMS imaging sequence was set, with the relevant parameters set. The appropriate slice was selected to get ready for scanning.
- (3)
- The injection pump flow rate was set. A heat flow was injected into the MRI cell to decompose the hydrate in the MRI cell. At the same time, the flow of the decomposed water was measured using a nuclear MRI system.
- (4)
- The pipeline was dissembled and the MRI cell was cleaned. Different hydrates were generated, and different heat flow injection rates were set. Then flow changes in the decomposition process of gas and liquid hydrate at different injection rates were obtained by repeating the above steps.
3. Results and Discussion
3.1. Permeability of Decomposition Process in Hydrate-Bearing Porous Media
3.1.1. Analysis of Absolute Permeability
3.1.2. Analysis of Relative Permeability
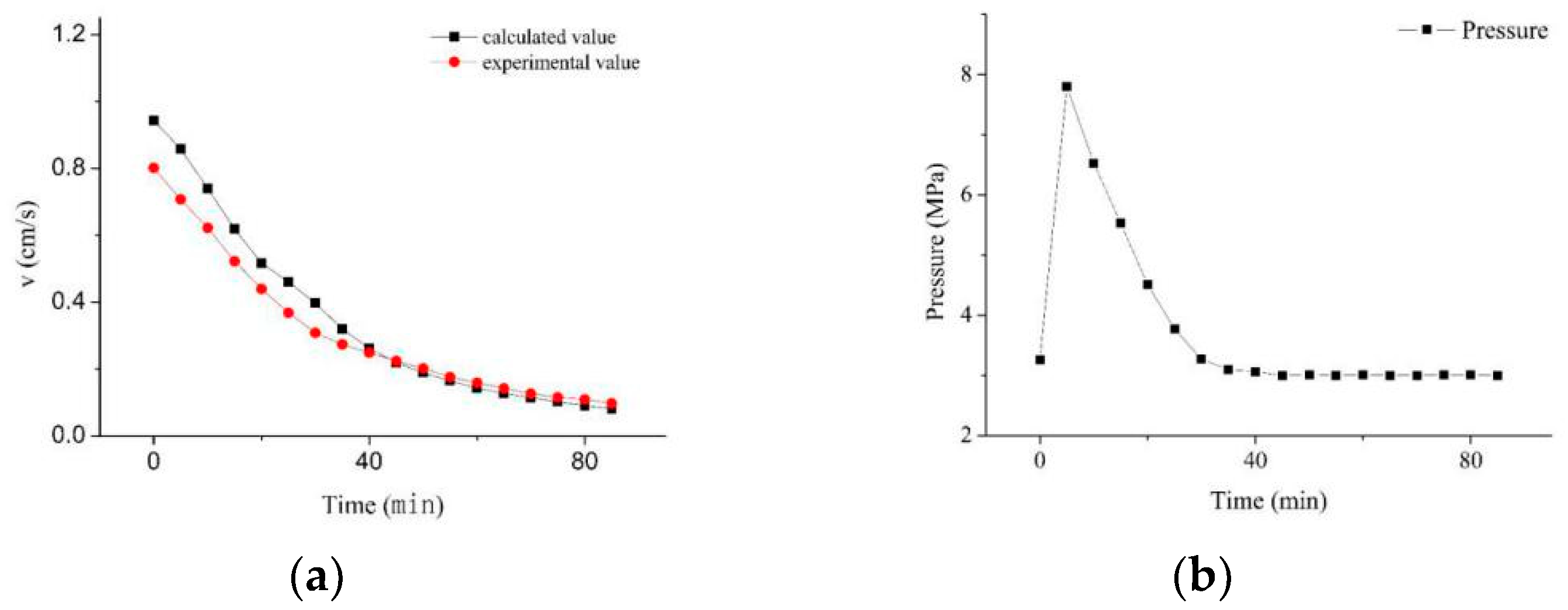
3.2. Analysis of Flow Rate during the Decomposition in Hydrate-Bearing Porous Media
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Collett, T.; Bahk, J.J.; Baker, R.; Boswell, R.; Divins, D.; Frye, M.; Goldberg, D.; Husebo, J.; Koh, C.; Malone, M.; et al. Methane hydrates in nature-current knowledge and challenges. J. Chem. Eng. Data 2015, 60, 319–329. [Google Scholar] [CrossRef]
- Sloan, E.D. Clathrate Hydrates of Natural Gases, 2nd ed.; Marcel Decker Inc.: New York, NY, USA, 1998; pp. 66–79. [Google Scholar]
- MacDonald, G.J. Role of methane clathrates in past and future climates. Clim. Chang. 1990, 16, 247. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sandler, S.I. Global Distribution of Methane Hydrate in Ocean Sediment. Energy Fuels 2005, 19, 459–470. [Google Scholar] [CrossRef]
- Koh, C.A. Towards fundamental understanding of natural gas hydrates. Chem. Soc. Rev. 2002, 31, 157. [Google Scholar] [CrossRef] [PubMed]
- Belosludov, V.R.; Lavrentiev, M.Y.; Dyadin, Y.A. Dynamic and thermodynamic properties of clathrate hydrates. J. Incl. Phenom. Mol. Recognit. Chem. 1990, 8, 59–69. [Google Scholar] [CrossRef]
- Li, G.; Moridis, G.J.; Zhang, K.; Li, X.S. Evaluation of gas production potential from marine gas hydrate deposits in Shenhu Area of South China Sea. Energy Fuels 2010, 24, 6018–6033. [Google Scholar] [CrossRef]
- Li, B.; Li, X.S.; Li, G.; Jia, J.L.; Feng, J.C. Measurements of water permeability in unconsolidated porous media with methane hydrate formation. Energies 2013, 6, 3622–3636. [Google Scholar] [CrossRef]
- Seol, Y.; Kneafsey, T.J. X-ray computed-tomography observations of water flow through anisotropic methane hydrate-bearing sand. J. Petrol. Sci. Eng. 2009, 66, 121–132. [Google Scholar] [CrossRef]
- Seol, Y.; Kneafsey, T.J. Methane hydrate induced permeability modification for multiphase flow in unsaturated porous media. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Konno, Y.; Yoneda, J.; Egawa, K.; Ito, T.; Jin, Y.; Kida, M.; Suzuki, K.; Fujii, T.; Nagao, J. Permeability of sediment cores from methane hydrate deposit in the Eastern Nankai Trough. Mar. Pet. Geol. 2015, 66, 487–495. [Google Scholar] [CrossRef]
- Priest, J.A.; Druce, M.; Roberts, J.; Schultheiss, P.; Nakatsuka, Y.; Suzuki, K. PCATS Triaxial: A new geotechnical apparatus for characterizing pressure cores from the Nankai Trough, Japan. Mar. Pet. Geol. 2015, 66, 460–470. [Google Scholar] [CrossRef]
- Oyama, H.; Konno, Y.; Masuda, Y.; Narita, H. Dependence of depressurization-induced dissociation of methane hydrate bearing laboratory cores on heat transfer. Energy Fuels 2009, 23, 4995–5002. [Google Scholar] [CrossRef]
- Konno, Y.; Oyama, H.; Nagao, J.; Naiki, M.; Jiro, N. Sustainable gas production from methane hydrate reservoirs by the cyclic depressurization method. Energy Convers. Manag. 2016, 108, 439–445. [Google Scholar] [CrossRef]
- Klapp, S.A.; Bohrmann, G.; Kuhs, W.F.; Murshed, M.M.; Pape, T.; Klein, H.; Techmer, K.S.; Heeschen, K.U.; Abegg, F. Microstructures of structure I and II gas hydrates from the Gulf of Mexico. Mar. Petrol. Geol. 2010, 27, 116–125. [Google Scholar] [CrossRef]
- Yang, M.; Song, Y.; Zhao, Y.; Liu, Y.; Jiang, L.; Li, Q. MRI measurements of CO2 hydrate dissociation rate in a porous medium. Magn. Reson. Imaging 2011, 29, 1007–1013. [Google Scholar] [CrossRef]
- Wu, Y.; Tahmasebi, P.; Lin, C.; Zahid, M.A.; Dong, C.; Golab, A.N.; Ren, L. A comprehensive study on geometric, topological and fractal characterizations of pore systems in low-permeability reservoirs based on SEM, MICP, NMR, and X-ray CT experiments. Mar. Petrol. Geol. 2019, 103, 12–28. [Google Scholar] [CrossRef]
- Baumann, T.; Petsch, R.; Niessner, R. Direct 3-D measurement of the flow velocity in porous media using magnetic resonance tomography. Environ. Sci. Technol. 2000, 34, 4242–4248. [Google Scholar] [CrossRef]
- Ikuo, O.; Shuichiro, H.; Kuniyasu, O. MRI velocity measurements of water flow in porous media containing a stagnant immiscible liquid. Meas. Sci. Technol. 2001, 12, 1465. [Google Scholar]
- Minagawa, H.; Nishikawa, Y.; Ikeda, I.; Sakamoto, Y.; Miyazaki, K.; Takahara, N.; Komai, T.; Narita, H. Relation between permeability and pore-size distribution of methane-hydrate-bearing sediments. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. [Google Scholar]
- Mantle, M.D.; Sederman, A.J.; Gladden, L.F. Single- and two-phase flow in fixed-bed reactors: MRI flow visualisation and lattice-Boltzmann simulations. Chem. Eng. Sci. 2001, 56, 523–529. [Google Scholar] [CrossRef]
- Mantle, M.D.; Sederman, A.J.; Gladden, L.F.; Raymahasay, S.; Winterbottom, J.M.; Stitt, E.H. Dynamic MRI visualization of two-phase flow in a ceramic monolith. AICHE J. 2004, 48, 909–912. [Google Scholar] [CrossRef]
- Martin, B.; Chandrasekhar, R. Method for measuring local hydraulic permeability using magnetic resonance imaging. Phys. Rev. E 2001, 63, 6. [Google Scholar]
- Martin, B.; Chandrasekhar, R. Direct measurement of porous media local hydrodynamical permeability using gas MRI. Magn. Reson. Imaging 2001, 19, 379–383. [Google Scholar]
- Thomas, B.; Charles, J.W. Visualization of colloid transport through heterogeneous porous media using magnetic resonance imaging. Colloids Surf. A 2005, 265, 2–10. [Google Scholar]
- Yuen, E.H.L.; Sederman, A.J.; Sani, F.; Alexander, P.; Gladden, L.F. Correlations between local conversion and hydrodynamics in a 3-D fixed-bed esterifieation Proeess: An MRI and lattice-Boltzmann study. Chem. Eng. Sci. 2003, 58, 613–619. [Google Scholar] [CrossRef]
- Davies, S.; Hardwick, A.; Spowage, K.; Packer, K.J. Fluid velocity imaging of reservoir core samples. Magn. Reson. Imaging 1994, 12, 265–268. [Google Scholar] [CrossRef]
- Merrill, M.; Jin, Z. Veloeity measurements in natural porous rocks. Magn. Reson. Imaging 1994, 12, 345–348. [Google Scholar] [CrossRef]
- Deurer, M.; Vogeler, L.; Khrapitehev, A.; Scotter, D. Imaging of water-flow in porous media by magnetic resonance imaging microscopy. J. Environ. Qual. 2002, 31, 487–493. [Google Scholar] [CrossRef]
- Erslanda, G.; Husebø, J.; Graue, A.; Baldwin, B.A.; Howardc, J.; Stevens, J. Measuring gas hydrate formation and exchange with CO2 in Bentheim sandstone using MRI tomography. Chem. Eng. J. 2010, 158, 25–31. [Google Scholar] [CrossRef]
- Zhang, X.; Tahmasebi, P. Micromechanical evaluation of rock and fluid interactions. Int. J. Greenh. Gas Control 2018, 76, 266–277. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S. A pore-scale mathematical modeling of fluid-particle interactions: Thermo-hydro-mechanical coupling. Int. J. Greenh. Gas Control 2019, 83, 245–255. [Google Scholar] [CrossRef]
- Fagbemi, S.; Tahmasebi, P.; Piri, M. Interaction Between Fluid and Porous Media with Complex Geometries: A Direct Pore—Scale Study. Water Resour. Res. 2018, 54, 6336–6356. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, L.; Xue, K.; Lam, W.; Li, Y.; Song, Y. In situ observation of gas hydrates growth hosted in porous media. Chem. Phys. Lett. 2014, 612, 124–128. [Google Scholar] [CrossRef]
- Kumar, A.; Maini, B.; Bishnoi, P.R.; Clarke, M.; Zatsepina, O.; Srinivasan, S. Experimental determination of permeability in the presence of hydrates and its effect on the dissociation characteristics of gas hydrates in porous media. J. Pet. Sci. Eng. 2010, 70, 114–122. [Google Scholar] [CrossRef]
- Honarpour, M.; Mahmood, S.M. Relative-permeability measurements: An overview. J. Pet. Technol. 1988, 40, 963–966. [Google Scholar] [CrossRef]
- Johnson, E.F.; Bossler, D.P.; Naumann, V.O. Calculation of relative permeability from displacement experiments. AIME 1959, 216, 370–372. [Google Scholar]
- Li, H.; Yang, D.; Arhuoma, M. Relative permeability estimation from displacement experiments using EnKF method. In Proceedings of the CPS/SPE International Oil and Gas Conference and Exhibition, Beijing, China, 8–10 June 2010. [Google Scholar]
- Eydinov, D.; Gao, G.; Li, G.; Reynolds, A.C. Simultaneous estimation of relative permeability and porosity/permeability fields by history matching production data. J. Pet. Technol. 2009, 48, 13–25. [Google Scholar] [CrossRef]
- Chardaire-Riviere, C.; Chavent, G.; Jaffre, J.; Liu, J.; Bourbiaux, B. Simultaneous estimation of relative permeability and capillary pressure. SPE Form. Eval. 1992, 7, 283–289. [Google Scholar] [CrossRef]
- Emmanuil, G.S.; Moritz, B. Hydromechanics Theory and Fundamentals; Wiley-VCH: Weinheim, Germany; John Wiley distributor: Chichester, UK, 2011; pp. 296–330. [Google Scholar]
- Nariman, M.; Sheng, D.; Yongkoo, S.; Jaewon, J. Impact of hydrate saturation on water permeability in hydrate-bearing sediments. J. Pet. Sci. Eng. 2019, 174, 696–703. [Google Scholar]
- Seol, Y.; Myshakin, E. Experimental and numerical observations of hydrate reformation during depressurization in a core-scale reactor. Energy Fuels 2011, 25, 1099–1110. [Google Scholar] [CrossRef]



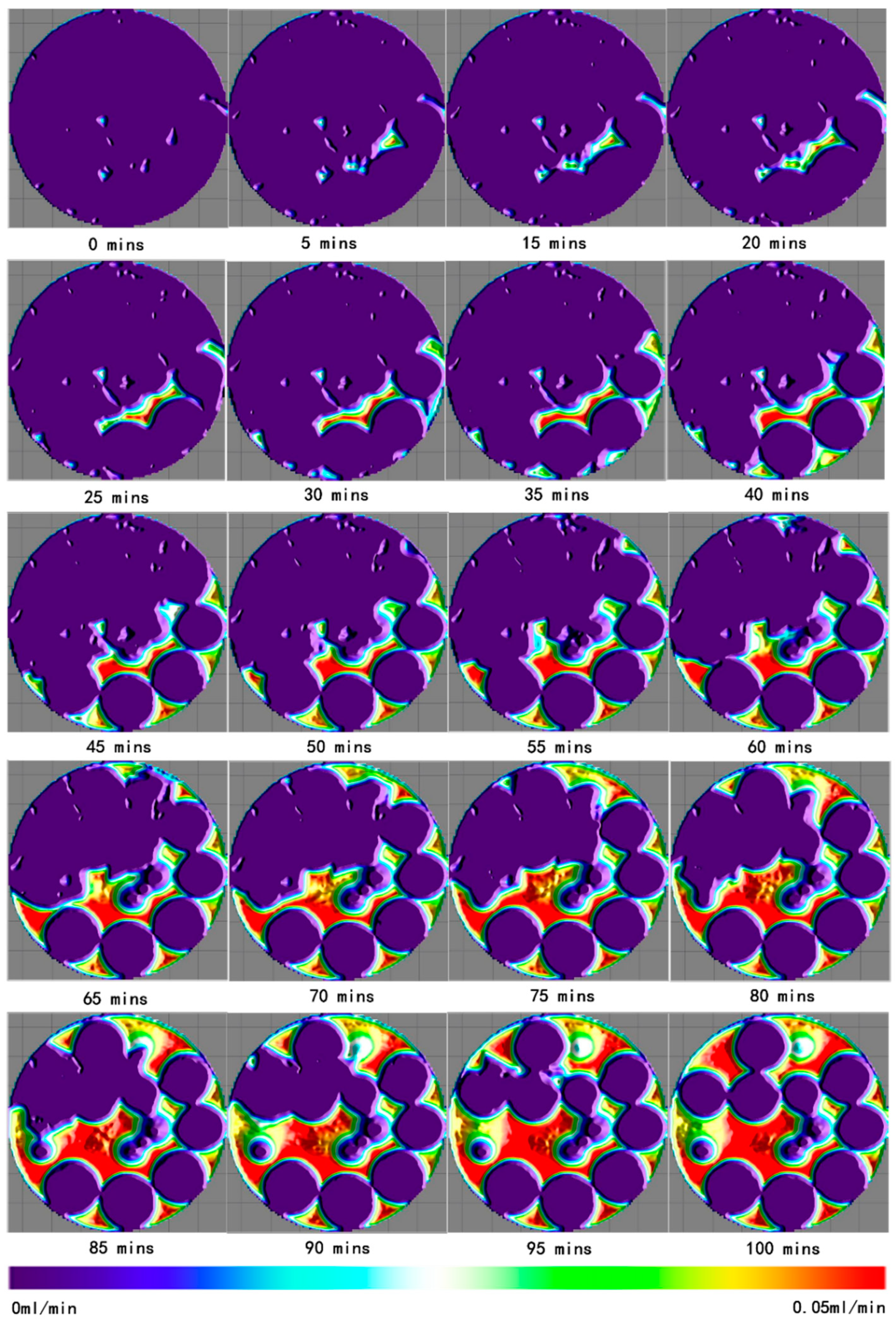
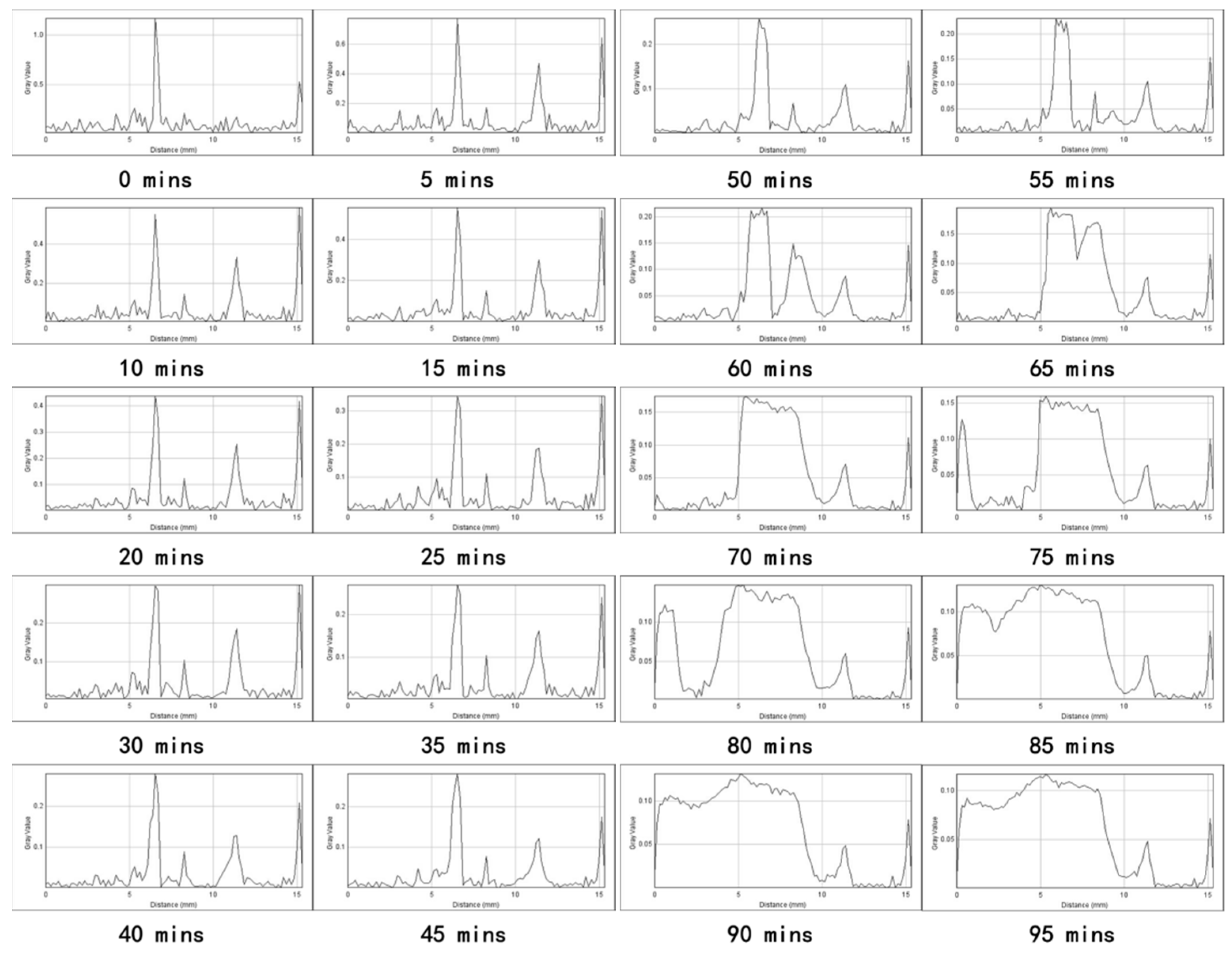
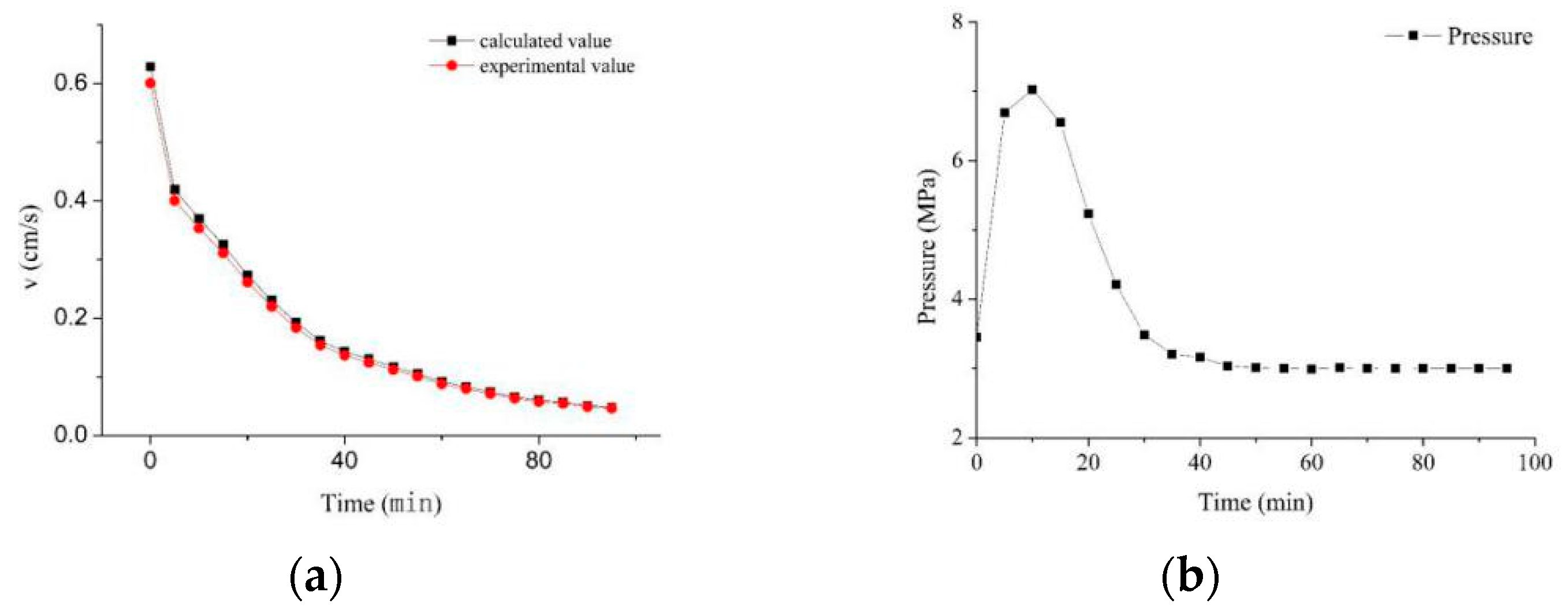

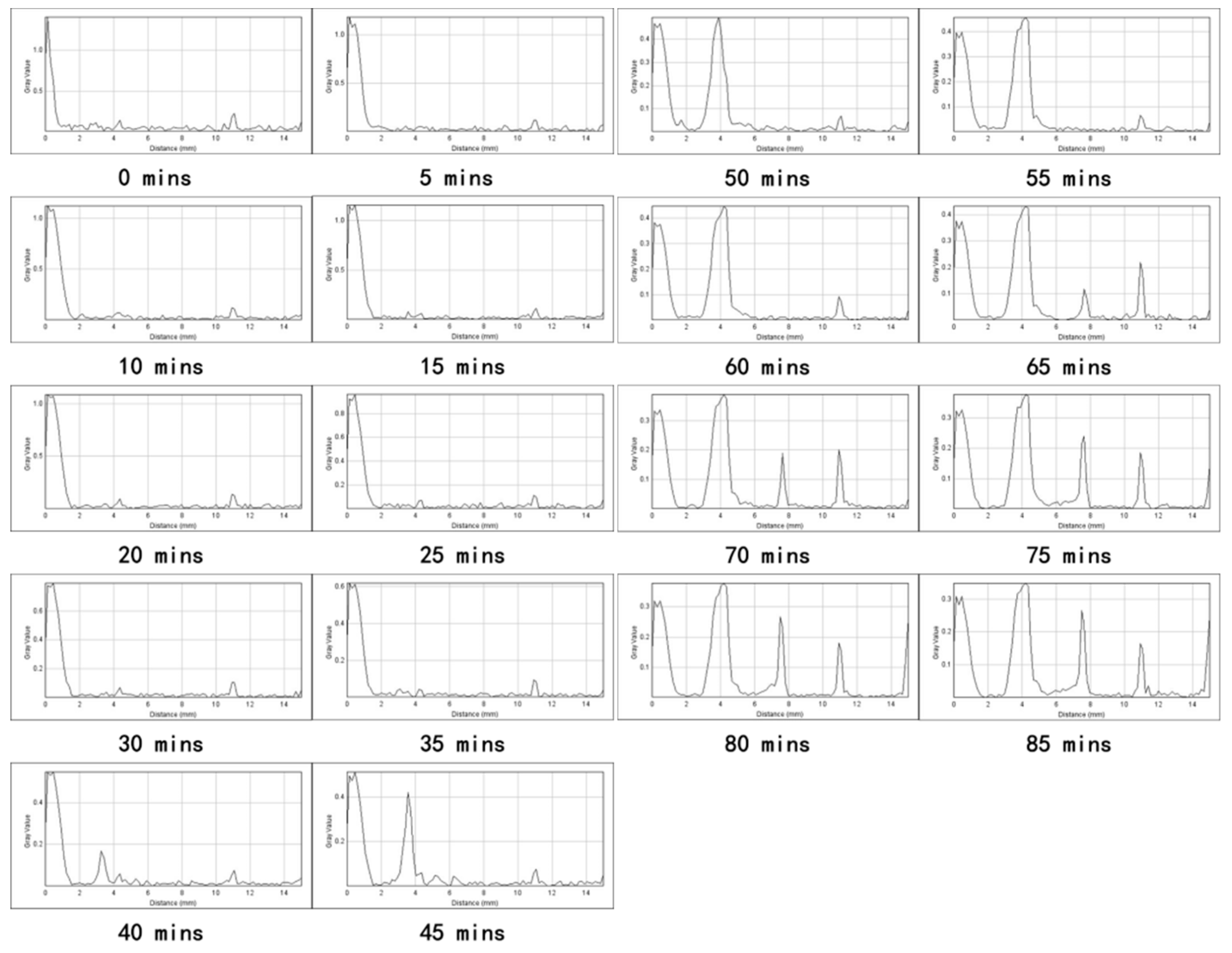
| Decomposition Rate | Porosity | Absolute Permeability |
|---|---|---|
| µm2 | ||
| 100.0% | 0.030 | 10.9 |
| 88.5% | 0.045 | 46.8 |
| 78.9% | 0.082 | 80.7 |
| 70.0% | 0.117 | 91.2 |
| 54.1% | 0.179 | 97.2 |
| 34.9% | 0.254 | 99.8 |
| 15.1% | 0.331 | 101.3 |
| 0.0% | 0.390 | 102.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, K.; Yang, L.; Zhao, J.; Li, Y.; Song, Y.; Yao, S. The Study of Flow Characteristics During the Decomposition Process in Hydrate-Bearing Porous Media Using Magnetic Resonance Imaging. Energies 2019, 12, 1736. https://doi.org/10.3390/en12091736
Xue K, Yang L, Zhao J, Li Y, Song Y, Yao S. The Study of Flow Characteristics During the Decomposition Process in Hydrate-Bearing Porous Media Using Magnetic Resonance Imaging. Energies. 2019; 12(9):1736. https://doi.org/10.3390/en12091736
Chicago/Turabian StyleXue, Kaihua, Lei Yang, Jiafei Zhao, Yanghui Li, Yongchen Song, and Shan Yao. 2019. "The Study of Flow Characteristics During the Decomposition Process in Hydrate-Bearing Porous Media Using Magnetic Resonance Imaging" Energies 12, no. 9: 1736. https://doi.org/10.3390/en12091736
APA StyleXue, K., Yang, L., Zhao, J., Li, Y., Song, Y., & Yao, S. (2019). The Study of Flow Characteristics During the Decomposition Process in Hydrate-Bearing Porous Media Using Magnetic Resonance Imaging. Energies, 12(9), 1736. https://doi.org/10.3390/en12091736






