High Efficiency Solar Power Generation with Improved Discontinuous Pulse Width Modulation (DPWM) Overmodulation Algorithms
Abstract
1. Introduction
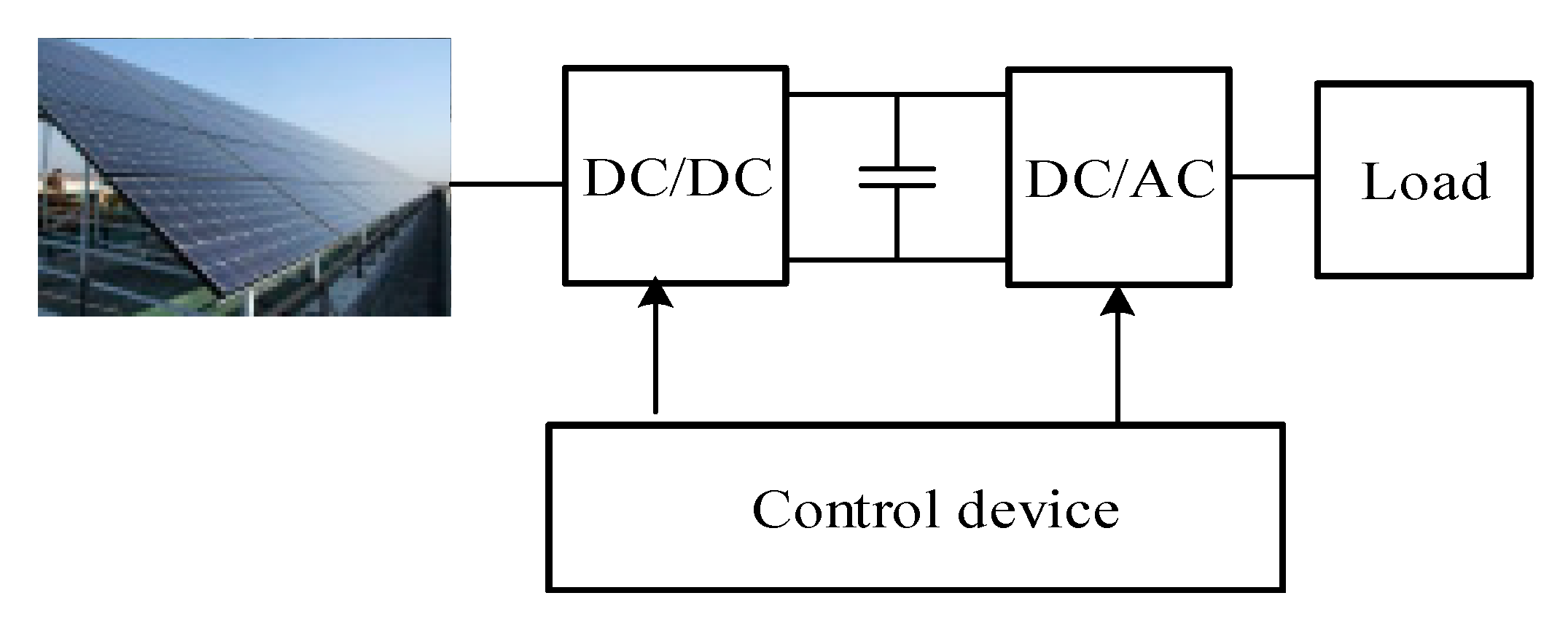
2. Equivalent Circuit of a PV Power System
2.1. Perturbation and Observation (P&O) MPPT Algorithm
2.2. A Boost DC-DC Converter and the Equivalent Circuit
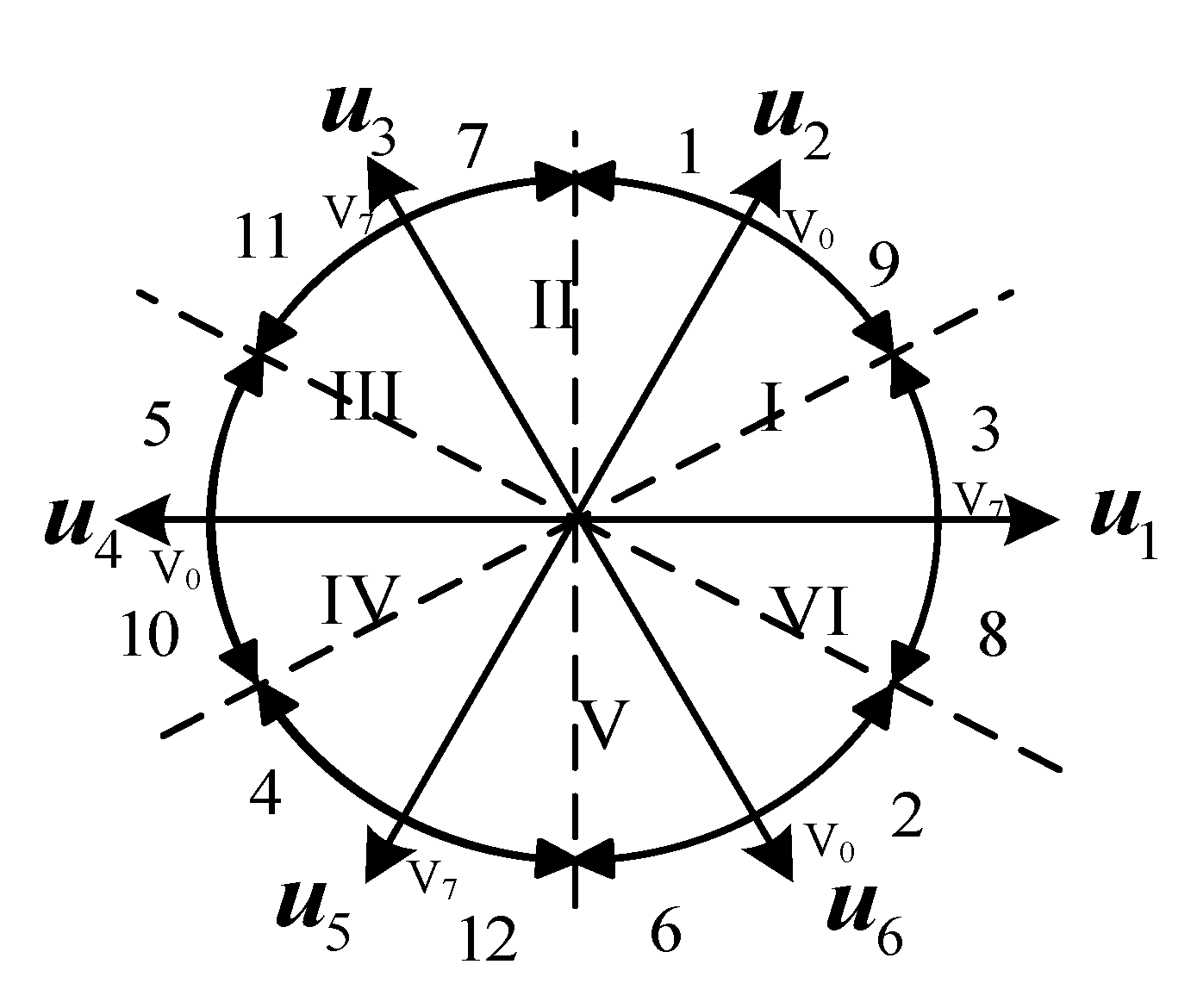
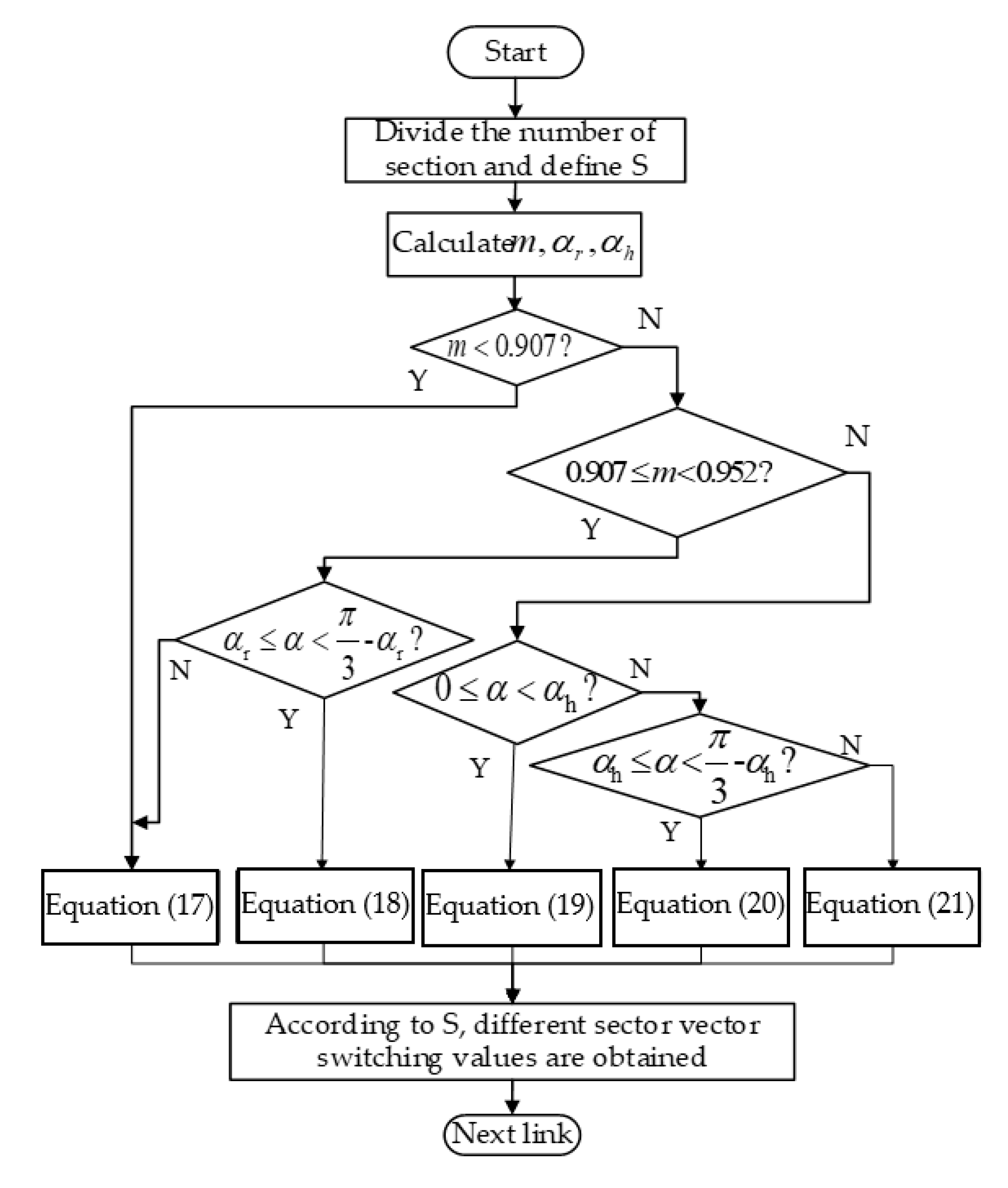
2.3. Division of the Overmodulation Area
2.4. Full Modulation Region Voltage Vector
3. DPWM Overmodulation Algorithm
4. Simulation and Experimental Validation of the Proposed Scheme
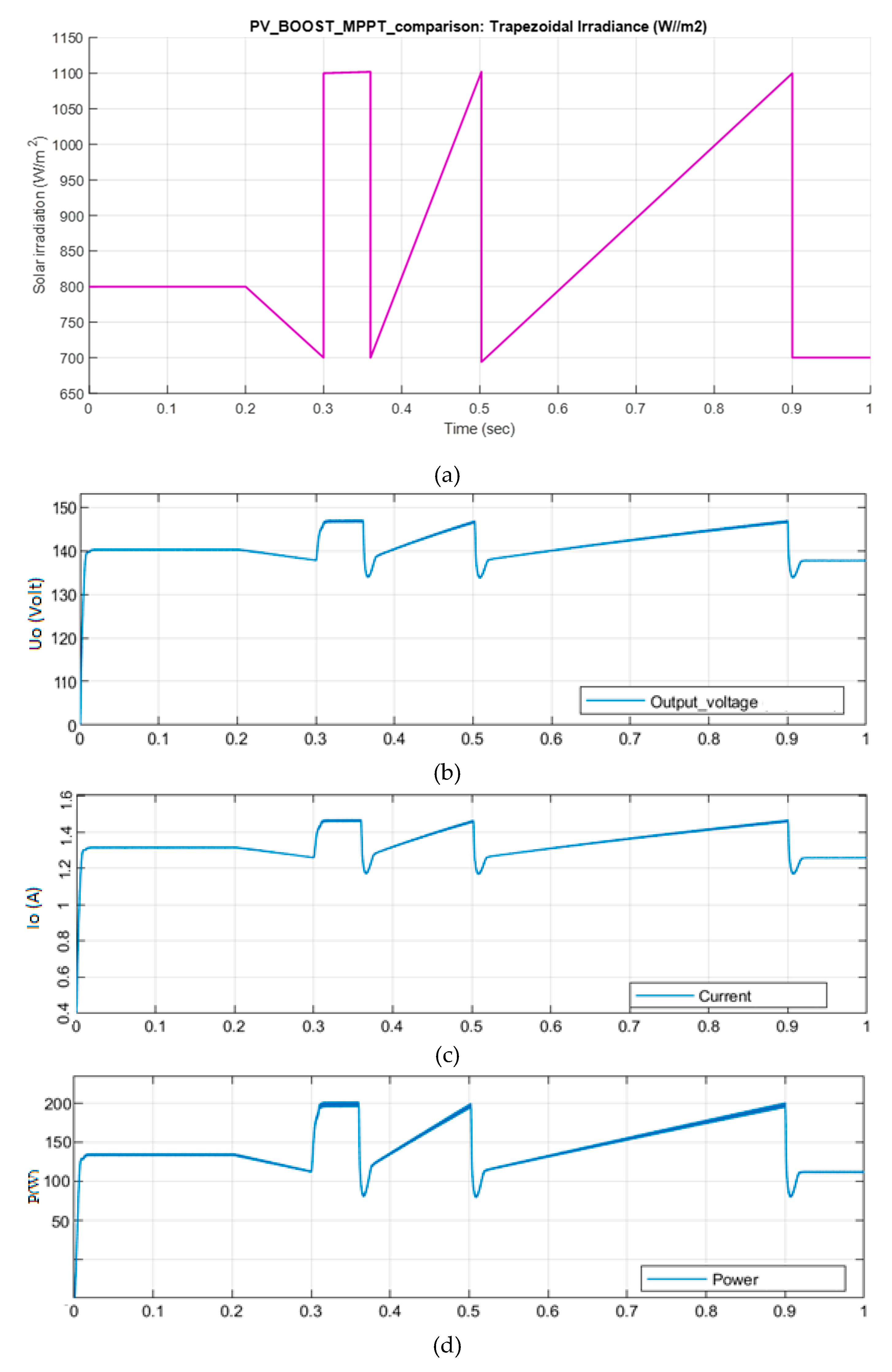
4.1. Simulation Results of Different Varied Solar Irradiations
4.2. DC/AC under the DPWM scheme
5. Conclusions
- (i)
- A P&O MPPT algorithm is applied to a boost DC/DC converter so as to effectively harvest solar energy and transform to DC electricity;
- (ii)
- A novel control technology is proposed, combining discontinuous pulse width modulation (DPWM) and overmodulation technology to better utilize the DC-link voltage.
- (iii)
- It has been shown by measurements that through implementing this algorithm, the switching losses in the power electronic devices are reduced.
- (iv)
- The test results have confirmed that the DPWM overmodulation algorithm can effectively reduce harmonic distortion of the three-phase output voltage and current. It has also improved the conversion efficiency of photovoltaic systems.
- (v)
- The proposed technology is simple to implement in practical PV inverters as there are no alterations to existing hardware design. It may also be applied to other grid-tie inverters to improve their performance.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Angle between the output voltage vector and the horizontal axis | |
| Angle between the intersection of the output voltage vector and the hexagon boundary, and the vertex of hexagon | |
| Control angle to determine how long the output voltage vector stays at the vertex of hexagon | |
| Current ripple factor of the inductor | |
| Voltage ripple factor of the inductor | |
| , | Capacitance of the input capacitor in DC/DC converter |
| , | Capacitance of the output capacitor in DC/DC converter |
| Duty ratio of DC/DC converter | |
| Switching frequency of a DC/DC converter | |
| , , | Inverter output currents |
| Equivalent output current at maximum power point | |
| L | Filter inductance |
| Symmetrical load inductance | |
| Inductance of a DC/DC converter | |
| m | Modulation coefficient |
| N | Sector |
| Maximum power of a PV module | |
| R | Filter inductance |
| RL | Symmetrical load resistance |
| Equivalent resistance at maximum power point | |
| Load resistance of the DC/DC converter | |
| S | Sector number |
| ,, | Action time of adjacent fundamental voltage vectors and zero vector |
| Switching period | |
| Basic voltage space vectors | |
| , | Two components of the output voltage vector in the coordinates |
| DC-link voltage | |
| Amplitude of the phase voltage | |
| Maximum phase voltage in linear modulation area | |
| Output voltage | |
| Equivalent output voltage at maximum power point | |
| Load voltage of the DC/DC converter | |
| Turn-on time | |
| Turn-off time | |
| Switching frequency of power devices | |
| Forward current of IGBT | |
| Amplitude of the sinusoidal current |
References
- Bukhari, S.A.A.S.; Cao, W.P.; Soomro, T.A.; Guanhao, D. Future of microgrids with distributed generation and electric vehicles. In Development and Integration of Microgrids; Cao, W.P., Yang, J., Eds.; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Aly, M.; Ahmed, E.M.; Shoyama, M. Modulation Method for Improving Reliability of Multilevel T-type Inverter in PV Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Gosumbonggot, J.; Fujita, G. Global Maximum Power Point Tracking under Shading Condition and Hotspot Detection Algorithms for Photovoltaic Systems. Energies 2019, 12, 225. [Google Scholar] [CrossRef]
- Baimel, D.; Tapuchi, S.; Levron, Y.; Belikov, J. Improved Fractional Open Circuit Voltage MPPT Methods for PV Systems. Electronics 2019, 8, 321. [Google Scholar] [CrossRef]
- Afzal Awan, M.M.; Mahmood, T. A Novel Ten Check Maximum Power Point Tracking Algorithm for a Standalone Solar Photovoltaic System. Electronics 2018, 7, 327. [Google Scholar] [CrossRef]
- Boobalan, S.; Dhanasekaran, R. Hybrid topology of asymmetric cascaded multilevel inverter with renewable energy sources. In Proceedings of the 2014 International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 8–10 May 2014; pp. 1046–1051. [Google Scholar]
- Ali, W.H.; Cofie, P.; Fuller, J.H.; Lokesh, S.; Kolawole, E.S. Performance and efficiency simulation study of a smart-grid connected photovoltaic system. Energy Power Eng. 2017, 9, 71. [Google Scholar] [CrossRef][Green Version]
- Djokic, S.; Langella, R.; Meyer, J.; Stiegler, R.; Testa, A.; Xu, X. On evaluation of power electronic devices efficiency for nonsinusoidal voltage supply and different operating power. IEEE Trans. Instrum. Meas. 2017, 66, 2216–2224. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Zhao, W.; Tao, L. Review of high efficiency photovoltaic inverter. Chin. J. Power Sources 2016, 4, 931–934. [Google Scholar]
- Wilkinson, S.; Gilligan, C. PV Inverter Service Plans & Extended Warranties Report—2013; HIS Technology: London, UK, 2013. [Google Scholar]
- Suresh, K.; Prasad, M.V. Performance and evaluation of new multilevel inverter topology. Int. J. Adv. Eng. Technol. 2012, 2, 485–494. [Google Scholar]
- Zhu, X. Three level and efficiency of photovoltaic Inverter. Electr. Age 2016, 8, 46–47. [Google Scholar]
- Griva, G.; Oleschuk, V. Synchronous operation of dual-inverter-based photovoltaic system with low DC-voltages. In Proceedings of the 2010 International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Park, Y.; Sul, S.K.; Hong, K.N. Overmodulation strategy for current control in photovoltaic inverter. IEEE Trans. Ind. Appl. 2016, 1, 322–331. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Gu, X.; Xia, C. Synchronized space-vector PWM for three-level VSI with lower harmonic distortion and switching frequency. IEEE Trans. Power Electron. 2016, 31, 6428–6441. [Google Scholar] [CrossRef]
- Beig, A.; Kanukollu, S.; Hosani, K.; Dekka, A. Space-vector-based synchronized three-level discontinuous PWM for medium-voltage high-power VSI. IEEE Trans. Ind. Electron. 2014, 61, 3891–3901. [Google Scholar] [CrossRef]
- Mathew, J.; Mathew, K.; Azeez, N.B.; Rajeevan, P.P.; Gopakumar, K. A hybrid multilevel inverter system based on dodecagonal space vectors for medium voltage IM drives. IEEE Trans. Power Electron. 2013, 28, 3723–3732. [Google Scholar] [CrossRef]
- Carrasco, G.; Silva, C.A. Space vector PWM method for five-phase two-level VSI with minimum harmonic injection in the overmodulation region. IEEE Trans. Ind. Electron. 2013, 5, 2042–2053. [Google Scholar] [CrossRef]
- Holmes, D.; Lipo, T. Pulse Width Modulation for Power Converters: Principles and Practice; Wiley IEEE Press: Piscataway, NJ, USA, 2003. [Google Scholar]
- Elmelegi, A.; Aly, M.; Ahmed, E.M. Developing Phase-Shift PWM-Based Distributed MPPT Technique for Photovoltaic Systems. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 492–497. [Google Scholar]
- Faranda, R.; Sonia, L. Energy comparison of MPPT techniques for PV Systems. WSEAS Trans. Power Syst. 2008, 3, 446–455. [Google Scholar]
- Espi, J.M.; Castello, J. A Novel Fast MPPT Strategy for High Efficiency PV Battery Chargers. Energies 2019, 12, 1152. [Google Scholar] [CrossRef]
- Tan, B.; Ke, X.; Tang, D.; Yin, S. Improved Perturb and Observation Method Based on Support Vector Regression. Energies 2019, 12, 1151. [Google Scholar] [CrossRef]
- Narendiran, S. Grid tie inverter and mppt—A review. In Proceedings of the IEEE 2013 International Conference on Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design; John, Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Razman, A.; Tan, C.W. Design of boost converter based on maximum power point resistance for photovoltaic applications. Sol. Energy 2018, 160, 322–335. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of Perturb and Observe Maximum Power Point Tracking Method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Wu, X.; Liu, W.; Ruan, Y.; Zhang, L. SVPWM over-modulation algorithm and its application in two-level Inverter. Electr. Mach. Control 2015, 1, 76–81. [Google Scholar]
- Wu, D.; Xia, X.; Zhang, Z.; Li, C. A SVPWM overmodulation method based on three-phase bridge arm coordinates. Trans. China Electrotech. Soc. 2015, 1, 150–158. [Google Scholar]
- Zhou, X.W.; Liu, W.G.; Lang, B.H. Study on generalized discontinuous PWM algorithm and harmonic. Small Spec. Electr. Mach. 2007, 11, 5–7. [Google Scholar]
- Jia, L.; Li, H.M.; Liang, J. Research on switching losses of an inverter under discontinuous PWM strategies. Mech. Electr. Eng. Mag. 2006, 1, 51–53. [Google Scholar]
- Liang, W.H.; Du, X.T.; You, L.R. Realization of expend linear modulation area and overmodulation algorithm in SVPWM. Power Electron. 2013, 5, 10–12. [Google Scholar]
- Fan, S.L.; Zhao, J.A. Novel overmodulation method based on optimized SPWM. Power Electron. 2013, 6, 26–28. [Google Scholar]
- Mao, P.; Xie, S.J.; Xu, Z.G. Switching transients model and loss analysis of IGBT module. Proc. Chin. Soc. Electr. Eng. 2010, 15, 40–47. [Google Scholar]








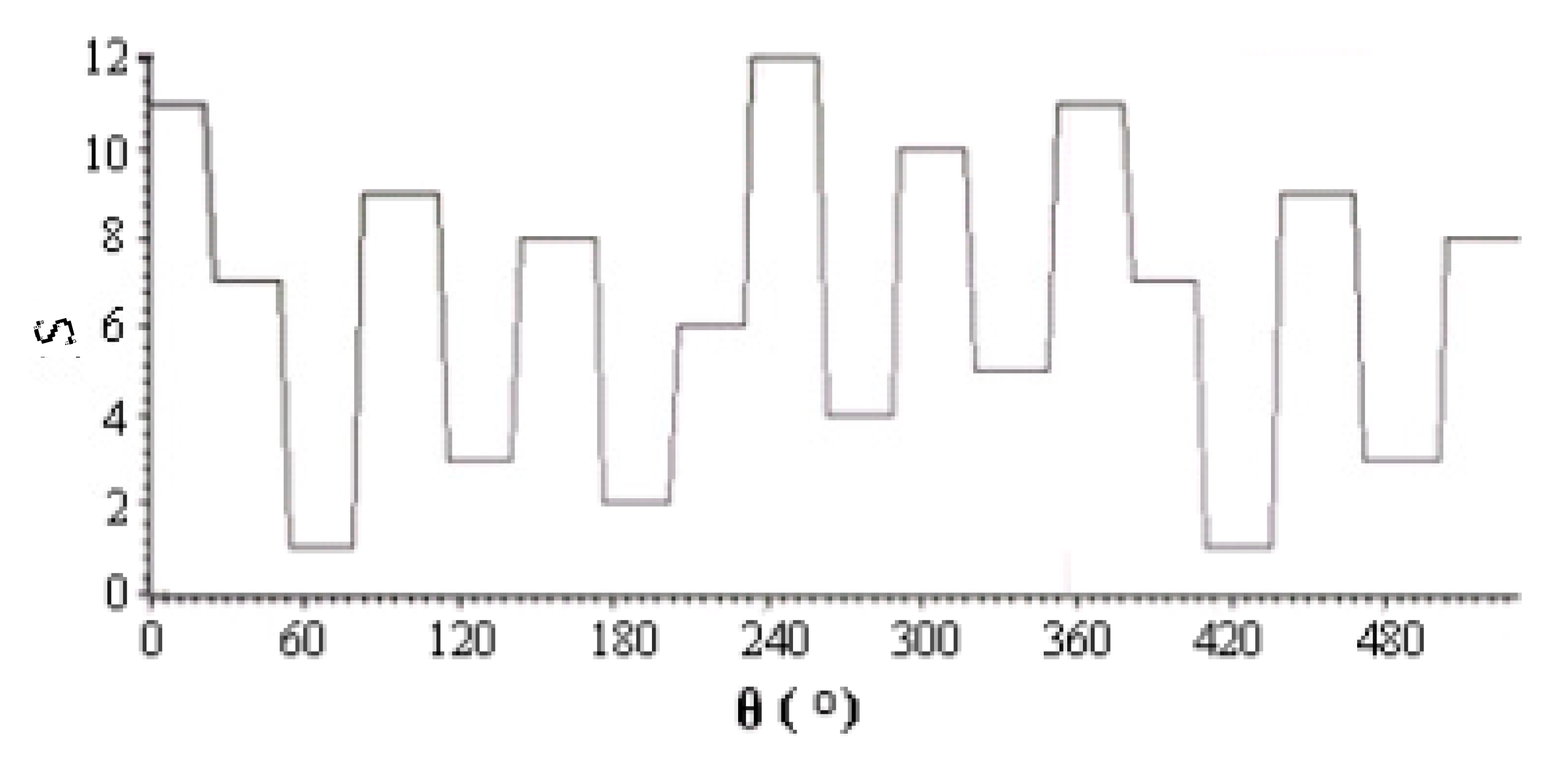


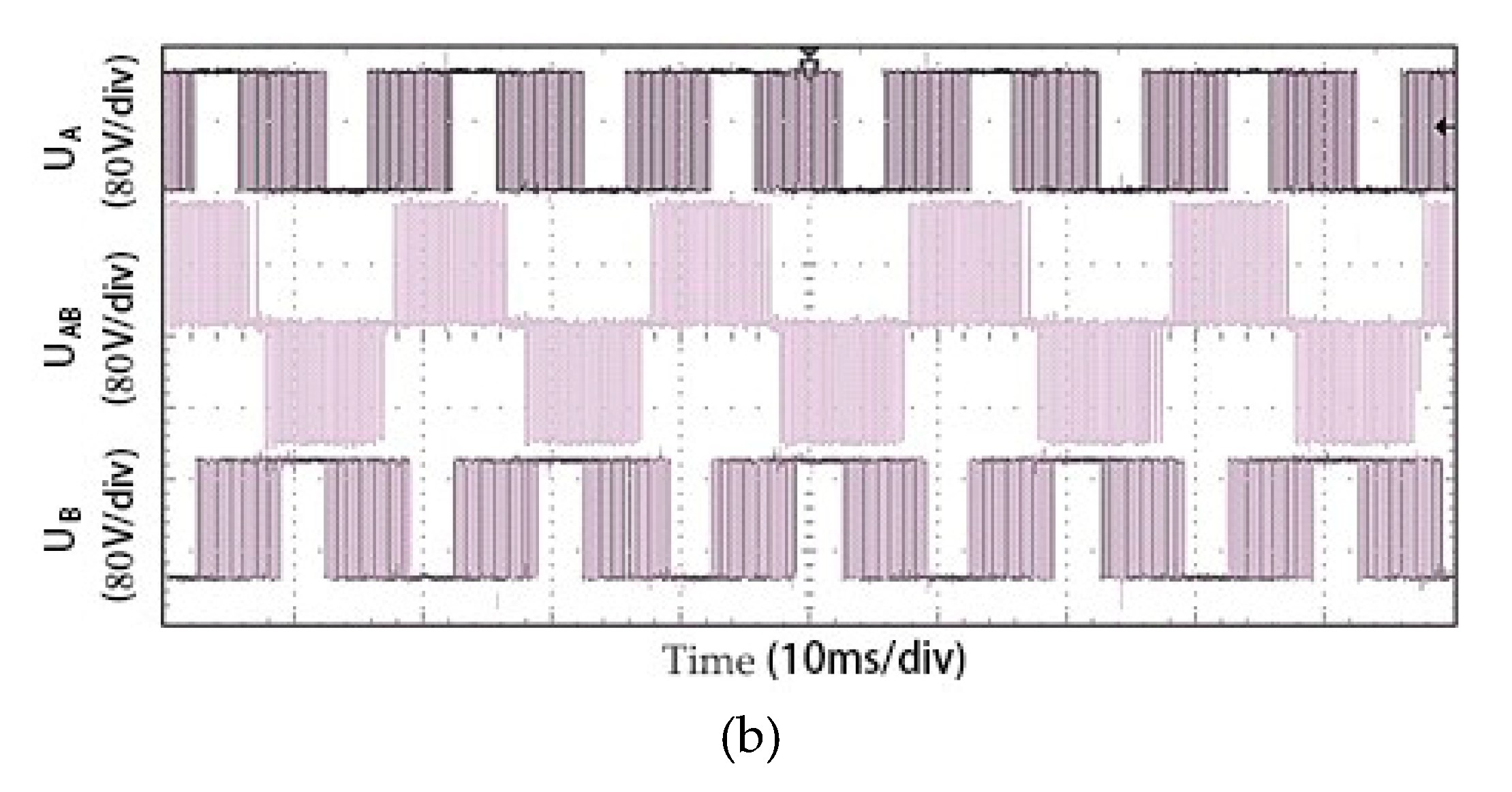

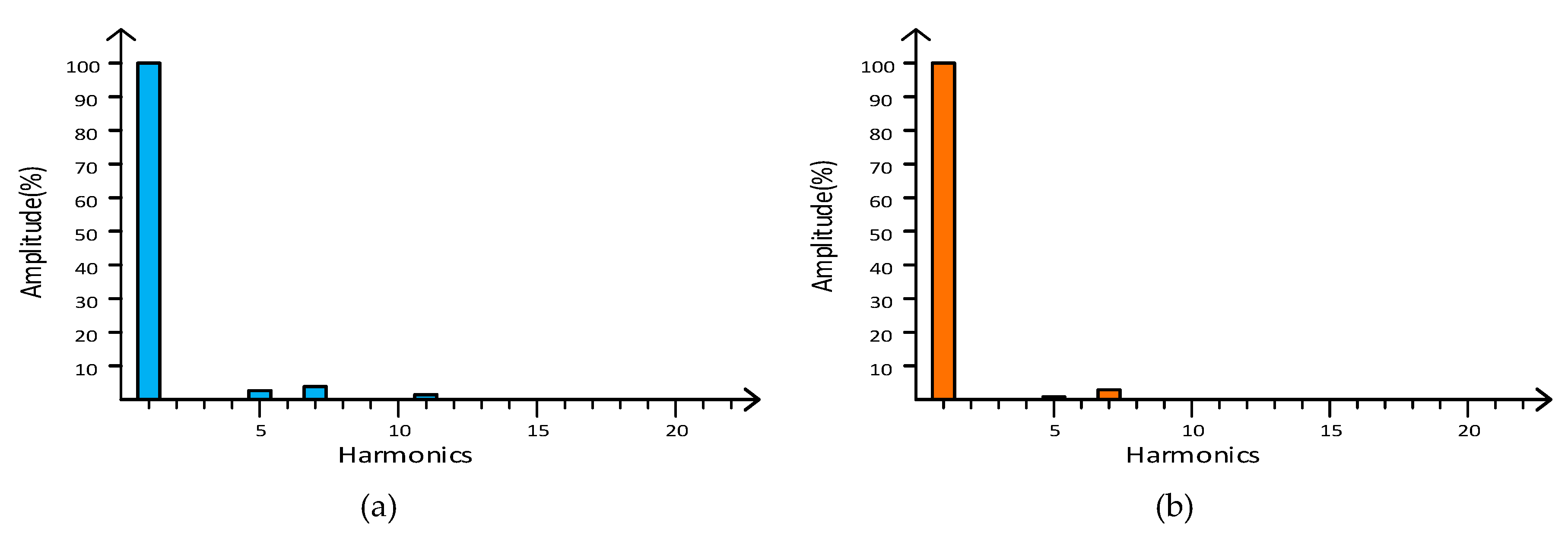
| No. | Scenario | Example Route | Action |
|---|---|---|---|
| 1 | A → B | Increase voltage | |
| 2 | D → C | Decrease voltage | |
| 3 | C → D | Decrease voltage | |
| 4 | B → A | Increase voltage |
| S | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Sector N | II | VI | I | IV | III | V |
| Action condition | Sector N | S for the 30° | Sector |
|---|---|---|---|
| I | 3 (True) | 9 (False) | |
| IV | 10 (True) | 4 (False) | |
| II | 1 (True) | 7 (False) | |
| V | 6 (True) | 12 (False) | |
| III | 11 (True) | 5 (False) | |
| VI | 2 (True) | 8 (False) |
| Open-Circuit Voltage (V) | Short-Circuit Current (A) | Max Voltage (V) | Max Current (A) | Max Power (W) |
|---|---|---|---|---|
| 45.2 | 5.36 | 37.1 | 5.11 | 190 |
| Harmonics | SVPWM | DPWM |
|---|---|---|
| 5th | 3.55% | 0.93% |
| 7th | 4.84% | 3.68% |
| 11th | 1.61% | 0 |
| THD | 6.58% | 4.40% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, H.; Chen, X.; Bukhari, A.A.S.; Cao, W.; Chai, L.; Li, B. High Efficiency Solar Power Generation with Improved Discontinuous Pulse Width Modulation (DPWM) Overmodulation Algorithms. Energies 2019, 12, 1765. https://doi.org/10.3390/en12091765
Li L, Wang H, Chen X, Bukhari AAS, Cao W, Chai L, Li B. High Efficiency Solar Power Generation with Improved Discontinuous Pulse Width Modulation (DPWM) Overmodulation Algorithms. Energies. 2019; 12(9):1765. https://doi.org/10.3390/en12091765
Chicago/Turabian StyleLi, Lan, Hao Wang, Xiangping Chen, Abid Ali Shah Bukhari, Wenping Cao, Lun Chai, and Bing Li. 2019. "High Efficiency Solar Power Generation with Improved Discontinuous Pulse Width Modulation (DPWM) Overmodulation Algorithms" Energies 12, no. 9: 1765. https://doi.org/10.3390/en12091765
APA StyleLi, L., Wang, H., Chen, X., Bukhari, A. A. S., Cao, W., Chai, L., & Li, B. (2019). High Efficiency Solar Power Generation with Improved Discontinuous Pulse Width Modulation (DPWM) Overmodulation Algorithms. Energies, 12(9), 1765. https://doi.org/10.3390/en12091765






