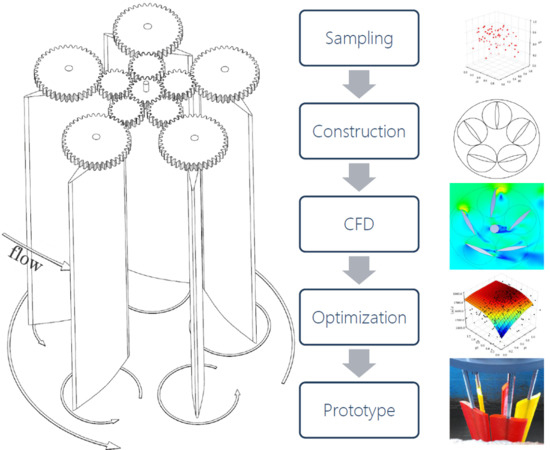
Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD
Abstract
1. Introduction
2. The Kirsten–Boeing Turbine
3. Validation of the Simulation Environment
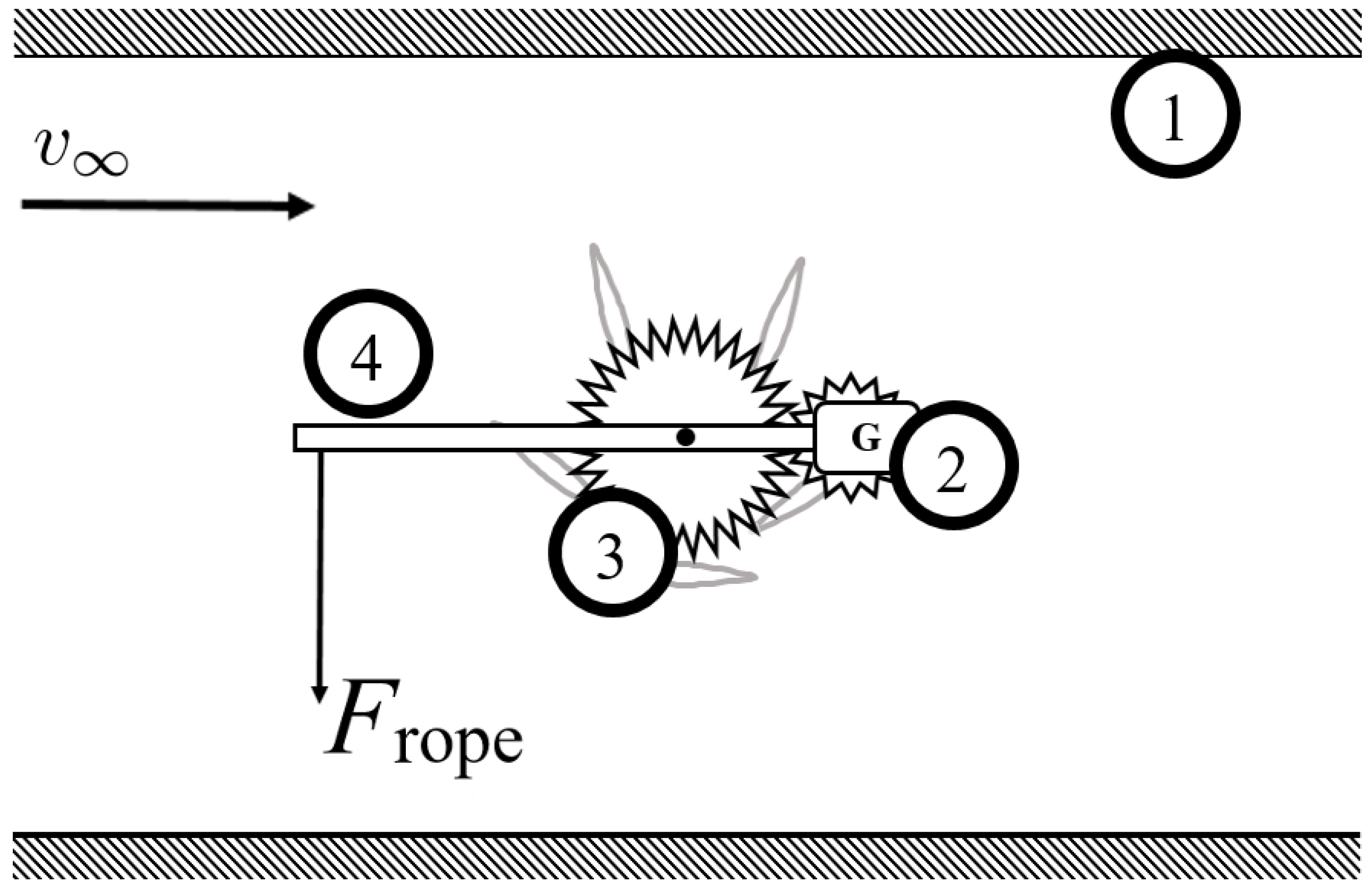
3.1. Experimental Environment and Measuring Equipment
3.2. Structure of the Simulation
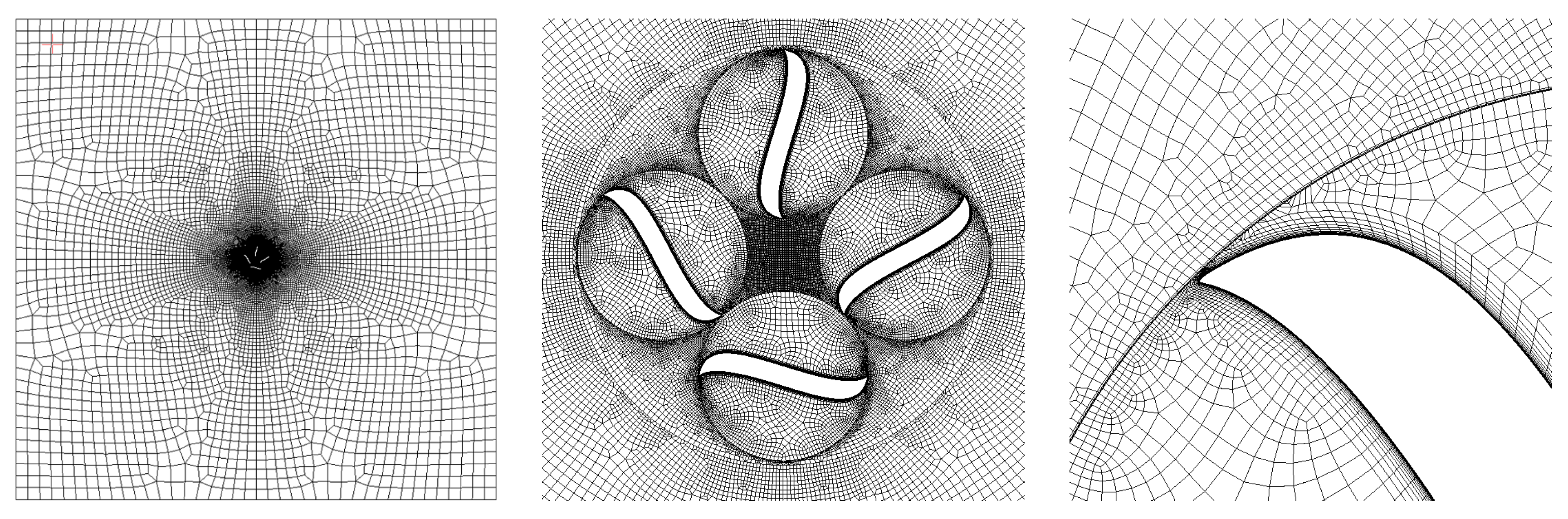
3.3. Mesh Independent Solution
3.4. Setup–Mesh Movement
3.5. Setup—Domain Properties
3.6. Setup—Performance and Efficiency
3.7. Results of the Simulation
4. Study of the Basic Design Parameters
- The optimum number of blades
- Improved blade geometry
- Influence of the blade width
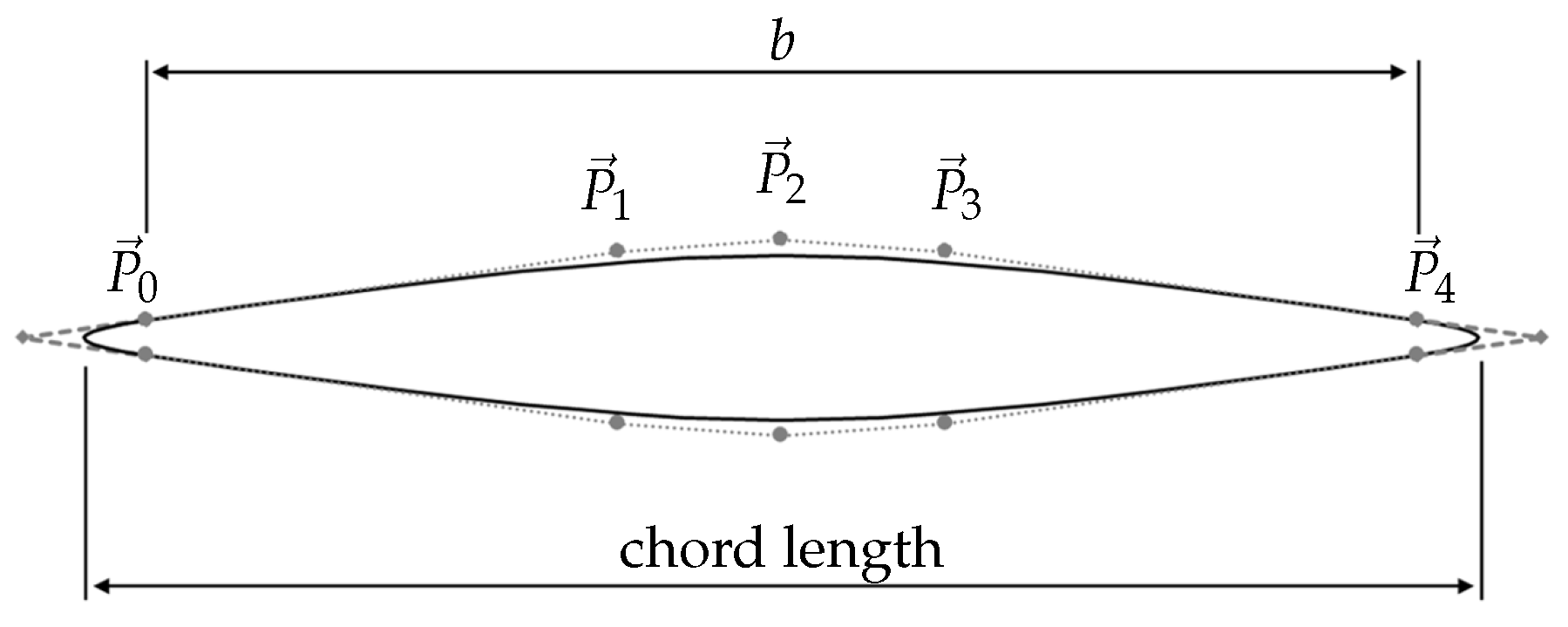
4.1. Parametric Geometry Creation
4.2. Setup—Parameter Study
4.3. Optimal Number of Blades
4.4. Optimization of the Blade Profile
4.5. Influence of the Blade Width
5. Metamodel Based Optimization of The Blade Shape
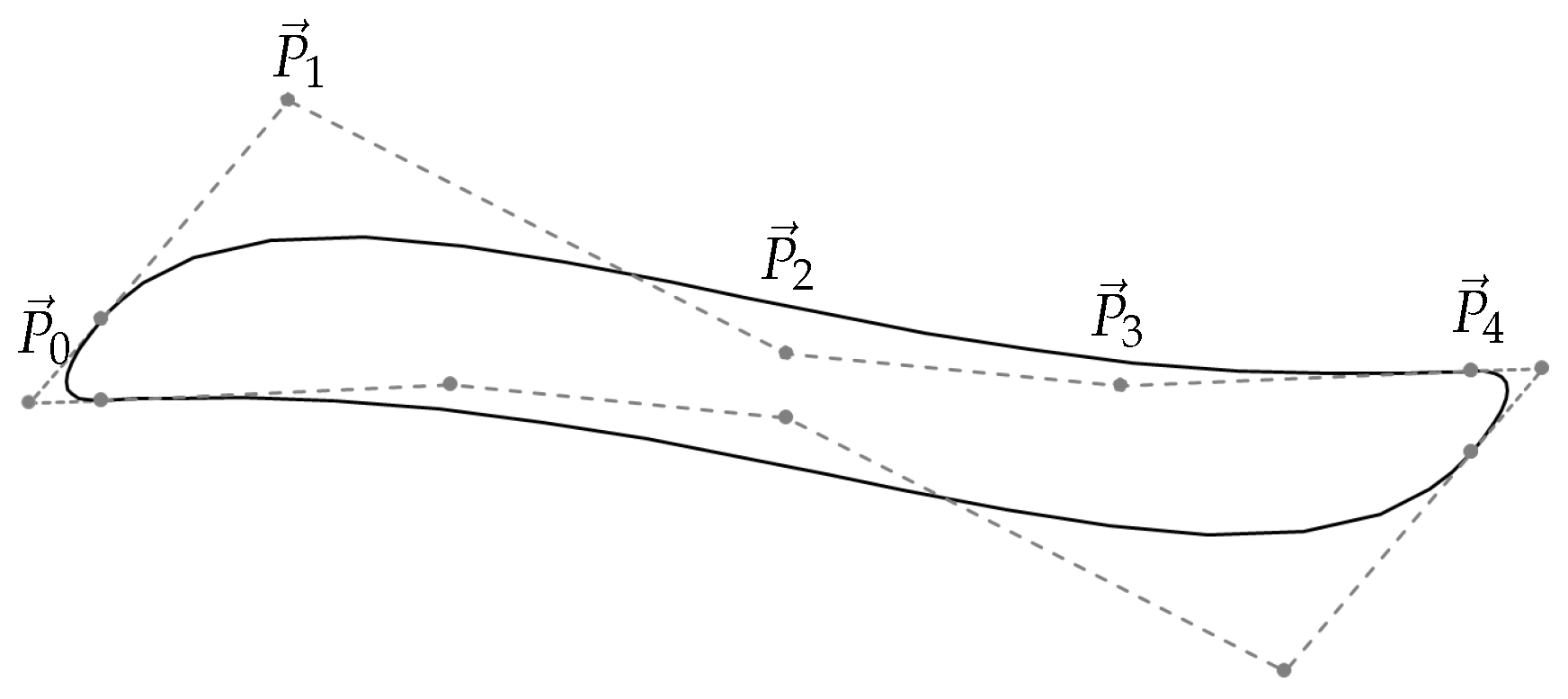
5.1. Geometry Creation
5.2. Meshing and Solver
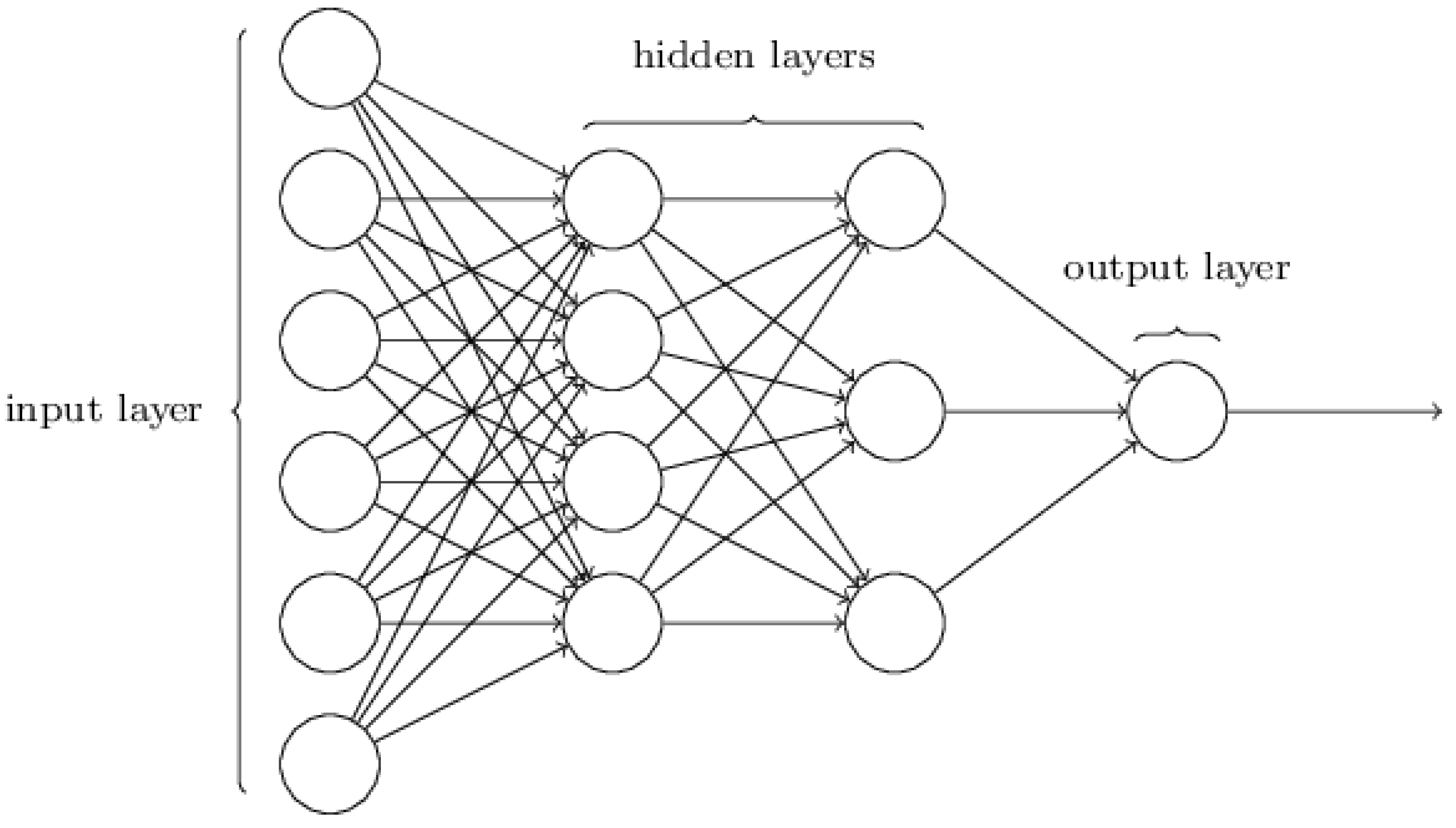
5.3. Multilayer Perceptron with Tensorflow
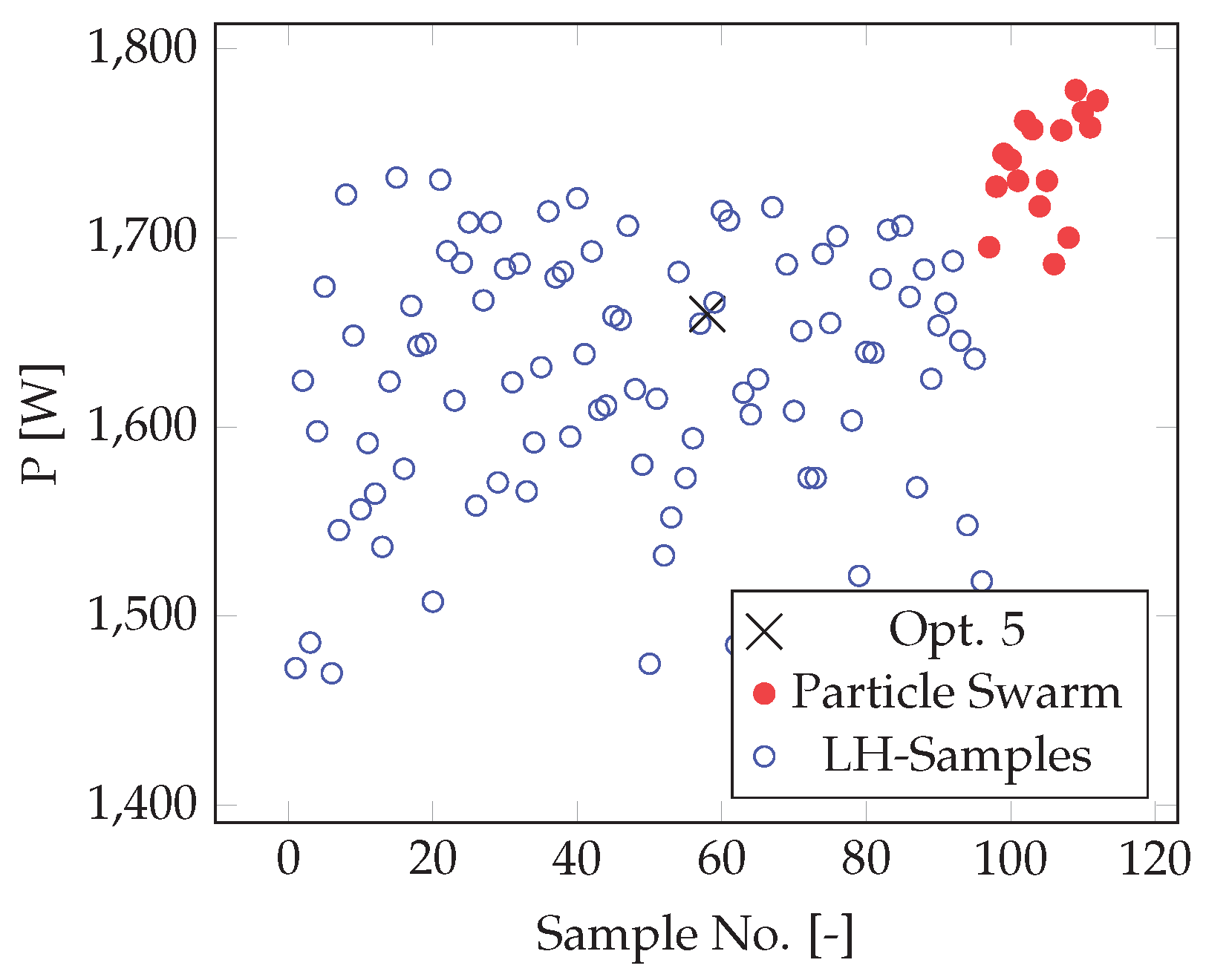
5.4. Particle Swarm Optimization
6. Design of the Four Bladed Prototype
6.1. Sampling
6.2. Meshing and Solver
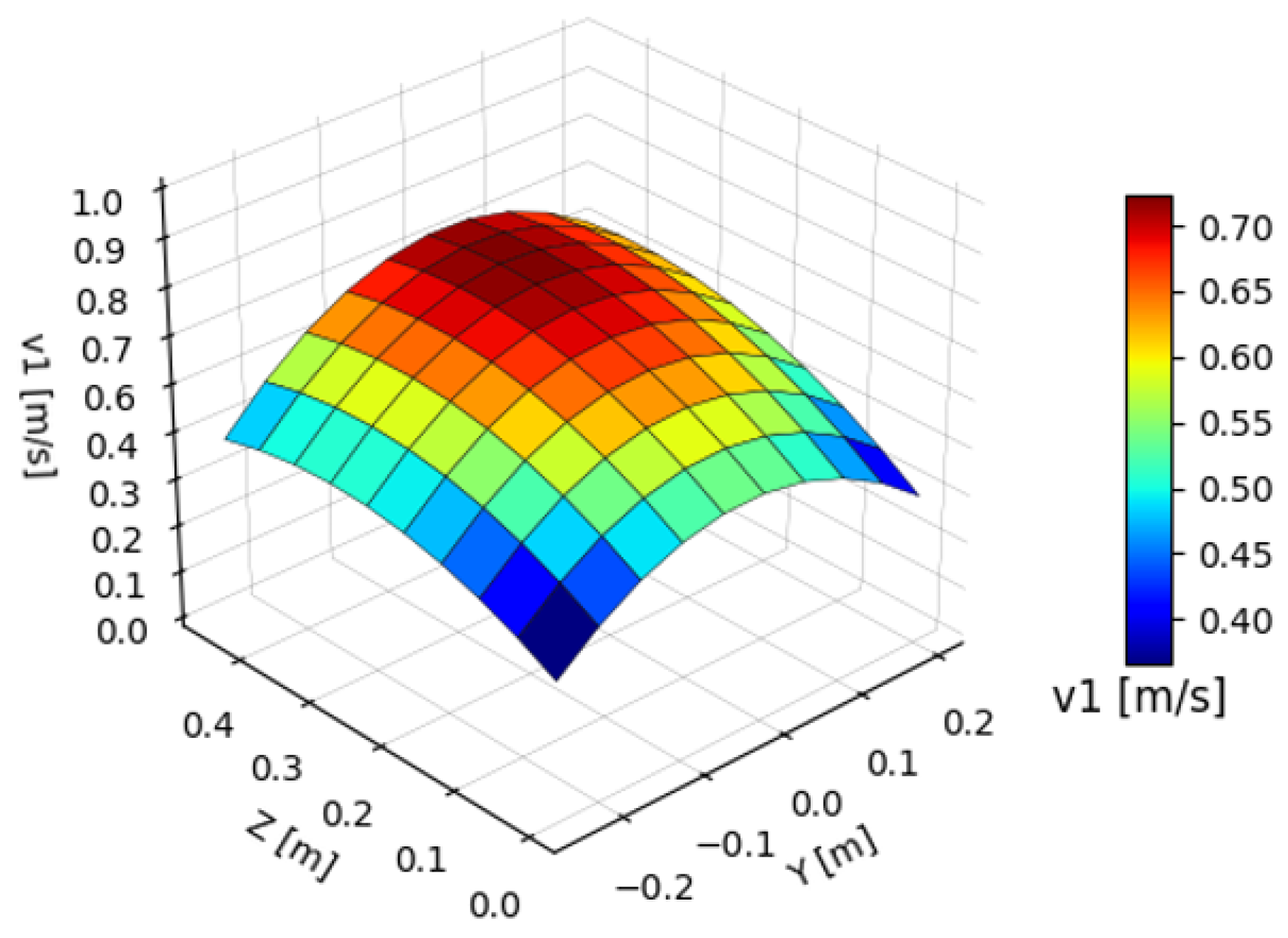
6.3. Results of the Optimization
7. Conclusions
Author Contributions
Funding

Conflicts of Interest
Appendix A

References
- Sachse, H. Kirsten-Boeing Propeller; Technical Report; National Advisory Committee for Aeronautics: Washington, DC, USA, 1926.
- Voith. Schaufelrad mit beweglichen Schaufeln. Available online: https://patents.google.com/patent/DE500340C/zh (accessed on 13 March 2019).
- Miller, R.H. Energietechnik und Kraftmaschinen 6, Techniklexikon; Rowohlt Taschenbuch-Verlag: Hamburg, Germany, 1972. [Google Scholar]
- Gasch, R.; Twele, J.; Bade, P.; Conrad, W.; Heilmann, C.; Kaiser, K.; Kortenkamp, R.; Kühn, M.; Langreder, W.; Liersch, J.; et al. Auslegung von Windturbinen nach Betz und Schmitz; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2005. [Google Scholar]
- Jensen, J.; Wieland, J.; Schmidt, J.; Metzger, J.; Stiller, H.L. BMWi-Projekt StEwaKorad; Technical Report; Lehrstuhl für Hydromechanik, Binnen- und Küstenwasserbau: Siegen, Germany, 2016. [Google Scholar]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. 2D CFD Modeling of H-Darrieus Wind Turbines Using a Transition Turbulence Model. Energy Procedia 2014, 45, 131–140. [Google Scholar] [CrossRef]
- Bezier, P. Numerical Control; Mathematics and Applications; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1972. [Google Scholar]
- Box, G.; Draper, N. Empirical Model-building and Response Surfaces; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- LeDell, E. Mulitlayer Perceptron. Available online: https://github.com/ledell/sldm4-h2o/blob/master/sldm4-deeplearning-h2o.Rmd (accessed on 13 March 2019).
- Nielsen, M. How the Backpropagation Algorithm Works. Available online: http://neuralnetworksanddeeplearning.com/chap2.html (accessed on 13 March 2019).
- Google. An Open-Source Machine Learning Framework for Everyone. Available online: https://www.tensorflow.org (accessed on 13 March 2019).
- Chrisman, L. LATIN-hypercube vs. Monte-Carlo-Sampling. Available online: http://www.lumina.com/blog/latin-hypercube-vs.-monte-carlo-sampling (accessed on 13 March 2019).
- Nair, V.; Hinton, G. Rectified Linear Units Improve Restricted Boltzmann Machines; Technical Report; ICML: Toronto, ON, Canada, 2010. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Most, T.; Will, J. Sensitivity Analysis using the Metamodel of Optimal Prognosis; Technical Report; Dynardo: Weimar, Germany, 2011. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Available online: https://ieeexplore.ieee.org/document/488968 (accessed on 13 March 2019).
- Schneider, H. Profil: Charakteristische Geometrische Größen. Available online: http://wiki.rc-network.de/index.php/Profil:_Charakteristische_geometrische_Gr%C3%B6%C3%9Fen (accessed on 13 March 2019).
- Bayeul-lainé, A.C.; Bois, G. Unsteady simulation of flow in micro vertical axis wind turbine. In Proceedings of the 21st International Symposium on Transport Phenomena, Kaohsiung City, Taiwan, 2–5 November 2010. [Google Scholar]

 |  |
| (a) | (b) |






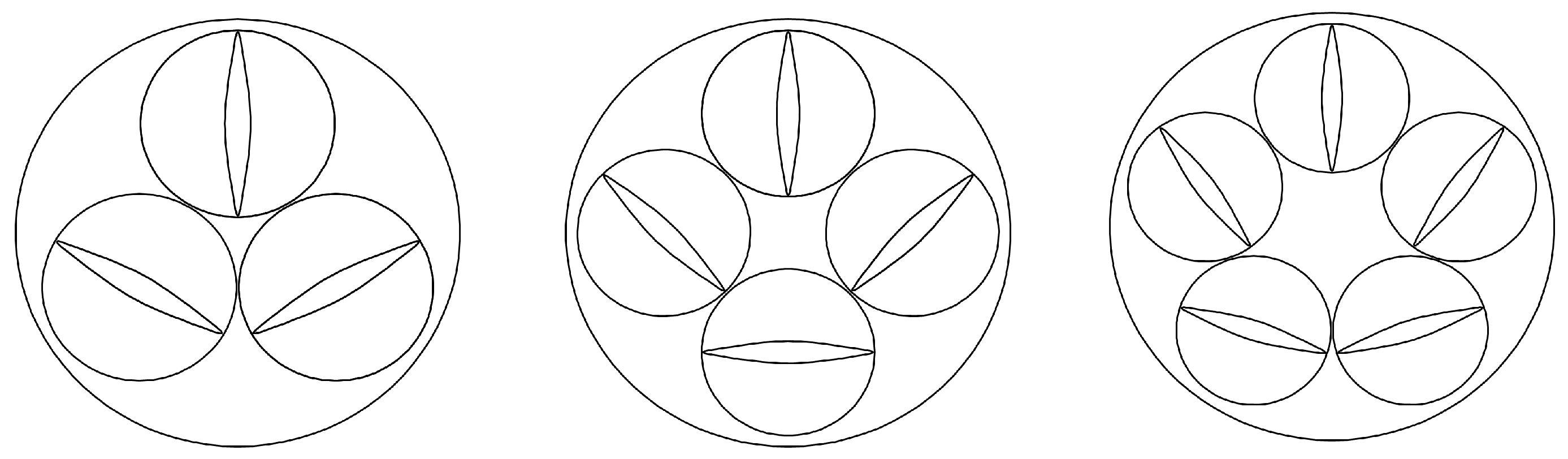














| i | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| free | 0 | free | |||
| free | free | free | free | free |
| i | 0 | 1 | 2 |
|---|---|---|---|
| × | |||
| × |
| No. | Profile | max. Power [W] | Relative to Reference (4) |
|---|---|---|---|
| 1 | 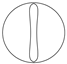 | 74.8 | 1.17 |
| 2 |  | 74.4 | 1.16 |
| 3 |  | 69.3 | 1.08 |
| 4 |  | 64.1 | 1.00 |
| 5 |  | 44.6 | 0.70 |
| 6 |  | 43.3 | 0.68 |
| 7 | 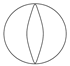 | 26.0 | 0.41 |
| No. | Profile | max Power [W] | Relative to Reference |
|---|---|---|---|
| 1 |  | 8.13 | 1.00 |
| 2 | 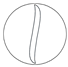 | 12.01 | 1.48 |
| 3 | 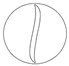 | 12.25 | 1.51 |
| No. | Profile | max Power [W] | Relative to Reference |
|---|---|---|---|
| 1 |  | 10.22 | 1.00 |
| 2 |  | 13.59 | 1.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Küppers, J.-P.; Metzger, J.; Jensen, J.; Reinicke, T. Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD. Energies 2019, 12, 1777. https://doi.org/10.3390/en12091777
Küppers J-P, Metzger J, Jensen J, Reinicke T. Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD. Energies. 2019; 12(9):1777. https://doi.org/10.3390/en12091777
Chicago/Turabian StyleKüppers, Jan-Philipp, Jens Metzger, Jürgen Jensen, and Tamara Reinicke. 2019. "Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD" Energies 12, no. 9: 1777. https://doi.org/10.3390/en12091777
APA StyleKüppers, J.-P., Metzger, J., Jensen, J., & Reinicke, T. (2019). Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD. Energies, 12(9), 1777. https://doi.org/10.3390/en12091777