A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation
Abstract
1. Introduction
Paper Organization
2. State-of-the-Art and Novel Contributions
2.1. State-of-the-Art
- The use of combinatorial ensemble techniques is shown to significantly improve the accuracy of RES-based DG forecasting in addition to guaranteeing a more reliable and/or robust prediction;
- An ensemble of simple probabilistic/statistical techniques is shown to produce better and more robust DG forecasting than individual complex models;
- KDE has been recently employed to “activate” input sets for probabilistic price forecasting models, showing great success in improving the accuracy. This was only found to be tested on price forecasting, and no studies were found using this methodology for DG forecasting [5].
2.2. Novel Contributions
- The objective was to develop an algorithm suitable for predicting DG from RESs. The specific focus of this study was on solar PV; however, the proposed approach is generalizable;
- Only historical, publicly available data (e.g., meteorological forecasts) and the corresponding local output (i.e., recorded power generation) were given as inputs (i.e., no knowledge of any physical model was known and no dependence on private/proprietary data were needed);
- The algorithm can run despite inconsistency or loss of data points. Using KDE, the most suitable inputs are “activated” from the historical dataset.
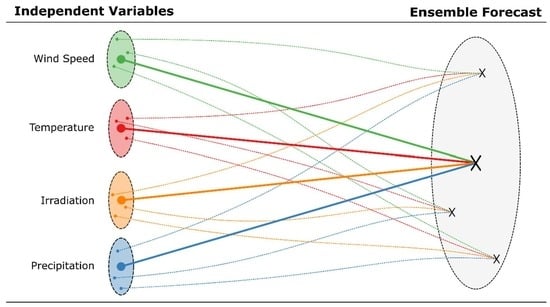
3. Proposed Methodology
4. Case Study and Validation
4.1. PV Installation in Portugal
4.2. Numerical Irradiance-Based Forecast
4.3. Seasonal Test Weeks
- During the summer, the maximum power output prediction based on Equation (15) was greater than the recorded value. This is what one would expect, and the operating efficiency and/or reliability of the installation would seldom reach the maximum theoretical power output;
- During the winter, the prediction based only on solar irradiation failed to predict any value of output power (one can see that the predicted values were zeros throughout the winter and also by looking at the plot of the winter week). This is due to the fact that the meteorological forecasts provided by GFS are averaged over large temporal and spatial resolutions. As such, the forecasted irradiance would dissipate during winter weather conditions.
4.4. Implementation and Validation
5. Results and Discussion
5.1. Results of the Proposed Ensemble Algorithm
- The proposed ensemble algorithm successfully managed to forecast the wind power output, relying only on the historical GFS meteorological data, for all four tests weeks of all seasons;
- The power production in cases when the deterministic model based on irradiance was inadequate (i.e., winter season) was successfully predicted;
- Despite only being provided averaged data, the confidence intervals successfully managed to cover high-frequency fluctuations during most days;
- The confidence interval grows and shrinks in response to such fluctuations even within the same day (e.g., Summer week, day 5);
- The forecasted mostly underestimated the power output than. This is favorable to overestimation particularly from the point of view of operators of DG installations.
5.2. Comparison and Validation
- According to all error criteria used, the proposed method outperformed the irradiance-based prediction for all seasons. It outperformed the ANN in all seasons except winter;
- Both the ANN and the proposed method managed to provide a reasonably accurate prediction of the output power in the winter, where a numerical irradiance-based model completely fails;
- Despite the ANN being capable of providing a better average error for the winter, the capability of the proposed method to capture high-frequency fluctuations in its confidence intervals provides an advantage over the ANN;
- The proposed method was extraordinarily fast in terms of computational time, being 32 times faster than the ANN while outperforming the ANN in the majority of situations.
5.3. Prospects for Future Work
- The effect of using additional meteorological variables (e.g., absolute and relative atmospheric pressure) should be investigated in terms of the forecast accuracy and computational burden;
- Optimal tuning of the bandwidth coefficients should be studied. This can be performed in a pre-processing stage (e.g., with correlation analysis) or using a reinforcement learning-based design in which the values are self-tuned every time the code is run. In the latter, using an optimization method to determine the optimal values may be an option for a hybrid structure;
- Due to the fact of its high computational efficiency and its reliance only on publicly available historical weather forecasts, the proposed method seems to have great potential to be applied to forecast RES-based DG. As such, follow-up work should test the proposed method on other RES technologies such as wind power.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Annual Data






References
- Kotsalos, K.; Miranda, I.; Silva, N.; Leite, H. A Horizon Optimization Control Framework for the Coordinated Operation of Multiple Distributed Energy Resources in Low Voltage Distribution Networks. Energies 2019, 12, 1182. [Google Scholar] [CrossRef]
- Dev, S.; Alskaif, T.; Hossari, M.; Godina, R.; Louwen, A.; Van Sark, W. Solar Irradiance Forecasting Using Triple Exponential Smoothing. In 2018 International Conference on Smart Energy Systems and Technologies, SEST 2018-Proceedings; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Gough, M.; Lotfi, M.; Castro, R.; Madhlopa, A.; Khan, A.; Catalão, J.P.S. Urban Wind Resource Assessment: A Case Study on Cape Town. Energies 2019, 12, 1479. [Google Scholar] [CrossRef]
- Formica, T.J.; Khan, H.A.; Pecht, M.G. The Effect of Inverter Failures on the Return on Investment of Solar Photovoltaic Systems. IEEE Access 2017, 5, 21336–21343. [Google Scholar] [CrossRef]
- Monteiro, C.; Ramirez-Rosado, I.J.; Fernandez-Jimenez, L.A.; Ribeiro, M. New Probabilistic Price Forecasting Models: Application to the Iberian Electricity Market. Int. J. Electr. Power Energy Syst. 2018, 103, 483–496. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent Advances in Electricity Price Forecasting: A Review of Probabilistic Forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Palmer, T. The ECMWF Ensemble Prediction System: Looking Back (More than) 25 Years and Projecting Forward 25 Years. Q. J. R. Meteorol. Soc. 2018. [CrossRef]
- Su, D.; Batzelis, E.; Pal, B. Machine Learning Algorithms in Forecasting of Photovoltaic Power Generation. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019. [Google Scholar] [CrossRef]
- Bracale, A.; Carpinelli, G.; De Falco, P. Developing and Comparing Different Strategies for Combining Probabilistic Photovoltaic Power Forecasts in an Ensemble Method. Energies 2019, 12, 11. [Google Scholar] [CrossRef]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A Review and Discussion of Decomposition-Based Hybrid Models for Wind Energy Forecasting Applications. Appl. Energy. 2019, 235, 939–953. [Google Scholar] [CrossRef]
- Bracale, A.; Carpinelli, G.; De Falco, P. A Probabilistic Competitive Ensemble Method for Short-Term Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2017, 8, 551–560. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Tree-Based Ensemble Methods for Predicting PV Power Generation and Their Comparison with Support Vector Regression. Energy 2018, 164, 465–474. [Google Scholar] [CrossRef]
- Thorey, J.; Chaussin, C.; Mallet, V. Ensemble Forecast of Photovoltaic Power with Online CRPS Learning. Int. J. Forecast. 2018, 34, 762–773. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Liu, L.; Zhan, M.; Bai, Y. A Recursive Ensemble Model for Forecasting the Power Output of Photovoltaic Systems. Sol. Energy 2019, 189, 291–298. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Li, J.; Lee, K.Y.; Gooi, H.B. An Ensemble Framework For Day-Ahead Forecast of PV Output in Smart Grids. IEEE Trans. Ind. Inform. 2018, 15, 4624–4634. [Google Scholar] [CrossRef]
- Pan, C.; Tan, J. Day-Ahead Hourly Forecasting of Solar Generation Based on Cluster Analysis and Ensemble Model. IEEE Access 2019, 7, 112921–112930. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar Power Generation Forecasting Using Ensemble Approach Based on Deep Learning and Statistical Methods. Appl. Comput. Inform. 2019. [CrossRef]
- Osório, G.J.; Matias, J.C.O.; Catalão, J.P.S. Electricity Prices Forecasting by a Hybrid Evolutionary-Adaptive Methodology. Energy Convers. Manag. 2014, 80, 363–373. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hybrid Wavelet-PSO-ANFIS Approach for Short-Term Electricity Prices Forecasting. IEEE Trans. Power Syst. 2011, 26, 137–144. [Google Scholar] [CrossRef]
- Osório, G.; Lotfi, M.; Shafie-khah, M.; Campos, V.; Catalão, J.; Osório, G.J.; Lotfi, M.; Shafie-khah, M.; Campos, V.M.A.; Catalão, J.P.S. Hybrid Forecasting Model for Short-Term Electricity Market Prices with Renewable Integration. Sustainability 2018, 11, 57. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. To Combine or Not to Combine? Recent Trends in Electricity Price Forecasting. In HSC Research Report; Hugo Steinhaus Center, Wroclaw University of Technology: Wrocław, Poland, 2016. [Google Scholar]
- Global Forecast System (GFS) | National Centers for Environmental Information (NCEI) formerly known as National Climatic Data Center (NCDC). Available online: https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs (accessed on 14 December 2019).
- The Mathworks Inc. Statistics and Machine Learning Toolbox User’s Guide R2019; The Mathworks Inc.: Natick, MA, USA, 2019. [Google Scholar]










| Parameter | Value | Units |
|---|---|---|
| Number of Panels (300 kWp each) | 53 | - |
| Panel Area (each) | 1.713 | m2 |
| Total Installed Capacity | 18 | kWp |
| Inverter Capacity | 20 | kW |
| Nominal DC Voltage | 600 | V |
| Overall Efficiency | 20 | % |
| Historical Variable | Data Source | Spatial Resolution | Temporal Resolution | Units |
|---|---|---|---|---|
| Wind Speed | Meteorological Forecast | 22 km | 3 h | m/s |
| Temperature | Meteorological Forecast | 22 km | 3 h | °C |
| Solar Irradiance | Meteorological Forecast | 22 km | 3 h | W/m2 |
| Precipitation | Meteorological Forecast | 22 km | 3 h | mm |
| Humidity | Meteorological Forecast | 22 km | 3 h | % |
| Inverter AC Power (Output) | Real Measurement | - | ~5 min | kW |
| Bandwidth Coefficient | Value |
|---|---|
| (hour of the day) | 0.4 |
| (day of the year) | 1.0 |
| (wind speed forecast) | 0.8 |
| (temperature forecast) | 0.5 |
| (solar irradiance forecast) | 0.1 |
| (precipitation forecast) | 0.8 |
| (humidity forecast) | 0.5 |
| Criterion | Method | Winter | Spring | Summer | Autumn |
|---|---|---|---|---|---|
| MAE (kW) | Irradiance Forecast | 34.6 | 15.7 | 17.4 | 15.3 |
| Neural Network | 10.7 | 15.5 | 8.4 | 7.9 | |
| Proposed Method | 12.6 | 14.0 | 3.6 | 7.7 | |
| RMSD (kW) | Irradiance Forecast | 3.062 | 2.138 | 2.508 | 1.857 |
| Neural Network | 0.949 | 2.114 | 1.203 | 0.951 | |
| Proposed Method | 1.115 | 1.914 | 0.523 | 0.928 | |
| NRMSD (%) | Irradiance Forecast | 34.6 | 15.7 | 17.4 | 15.3 |
| Neural Network | 10.7 | 15.5 | 8.4 | 7.9 | |
| Proposed Method | 12.6 | 14.0 | 3.6 | 7.7 |
| Computational Time to Forecast all Four Weeks (Average of 10,000 runs) | |
|---|---|
| Neural Network | 1.46 s |
| Proposed Method | 0.045 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lotfi, M.; Javadi, M.; Osório, G.J.; Monteiro, C.; Catalão, J.P.S. A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies 2020, 13, 216. https://doi.org/10.3390/en13010216
Lotfi M, Javadi M, Osório GJ, Monteiro C, Catalão JPS. A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies. 2020; 13(1):216. https://doi.org/10.3390/en13010216
Chicago/Turabian StyleLotfi, Mohamed, Mohammad Javadi, Gerardo J. Osório, Cláudio Monteiro, and João P. S. Catalão. 2020. "A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation" Energies 13, no. 1: 216. https://doi.org/10.3390/en13010216
APA StyleLotfi, M., Javadi, M., Osório, G. J., Monteiro, C., & Catalão, J. P. S. (2020). A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies, 13(1), 216. https://doi.org/10.3390/en13010216