Data-Driven Fault Localization in Distribution Systems with Distributed Energy Resources
Abstract
:1. Introduction
- (1)
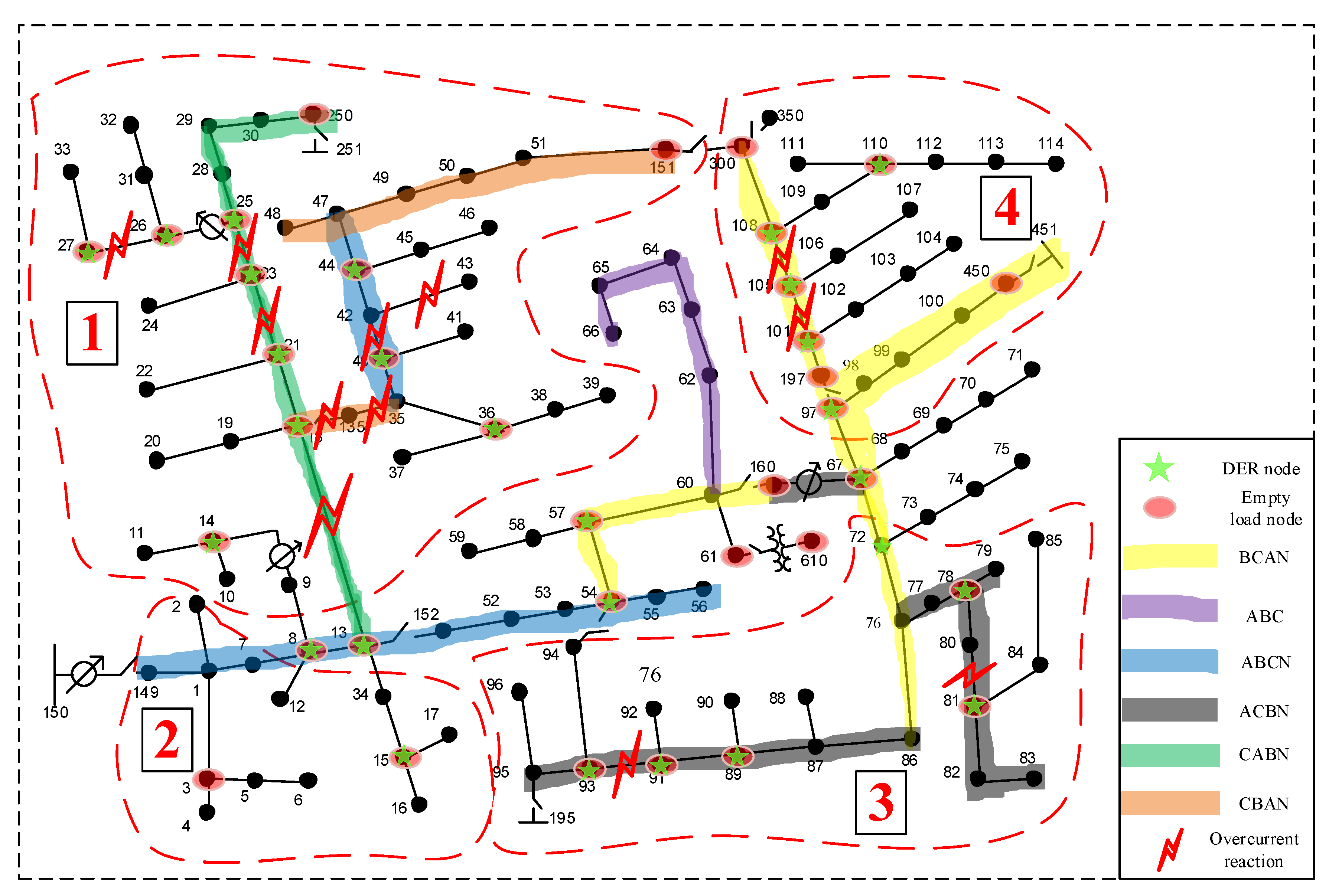
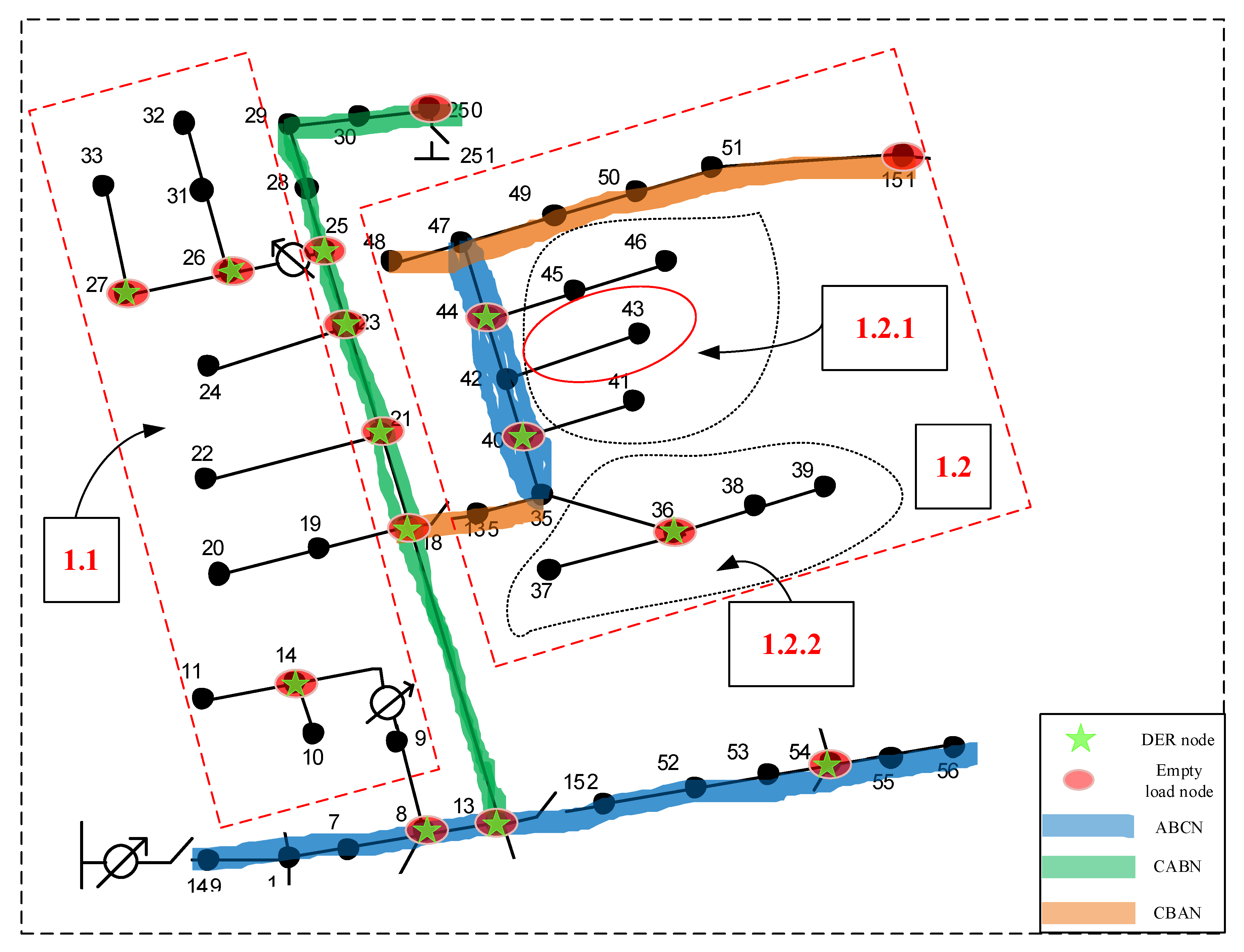
- To conduct fault localization based upon fault detection in different subregions, one needs to regionalize the system in an appropriate manner. This paper provides a general criterion for system regionalization based upon the division of the network tree to facilitate the hierarchical search of the fault location.
- (2)
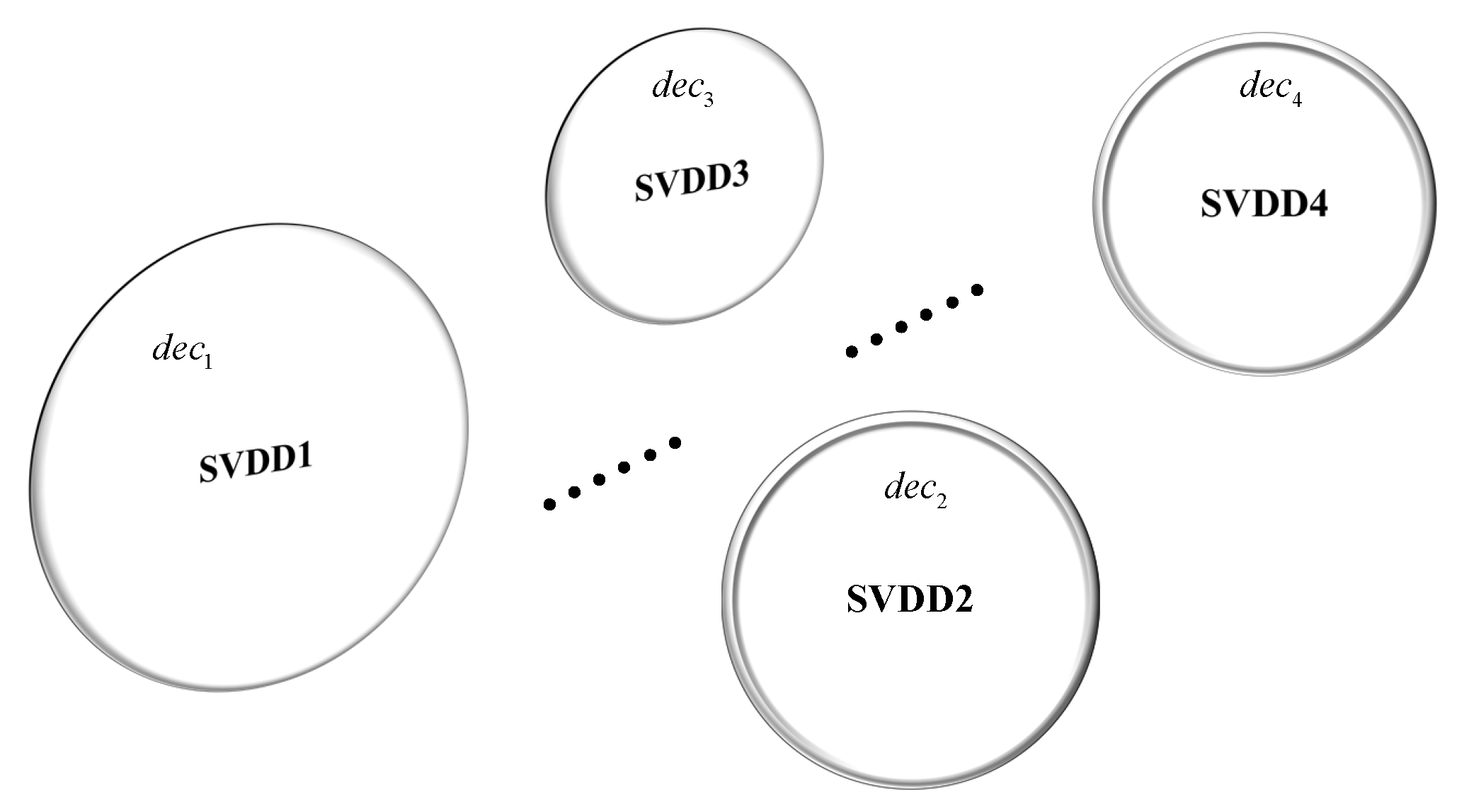
- Rather than hard decisions, we soften them by properly combining SVDD and kernel density estimator (KDE) to obtain quantified confidence levels of decisions, i.e., the p-values. The confidence level will guide one to localize the faulty node with desirable resolution.
- (3)
- Experimental simulations conducted under the IEEE-123 node test feeder show that the data-driven fault localization strategy proposed in this paper significantly outperforms the conventional fault localization methods based upon relay operations.
2. Methodology
2.1. Problem Formulation
2.2. Support Vector Data Description
2.3. Kernel Density Estimation
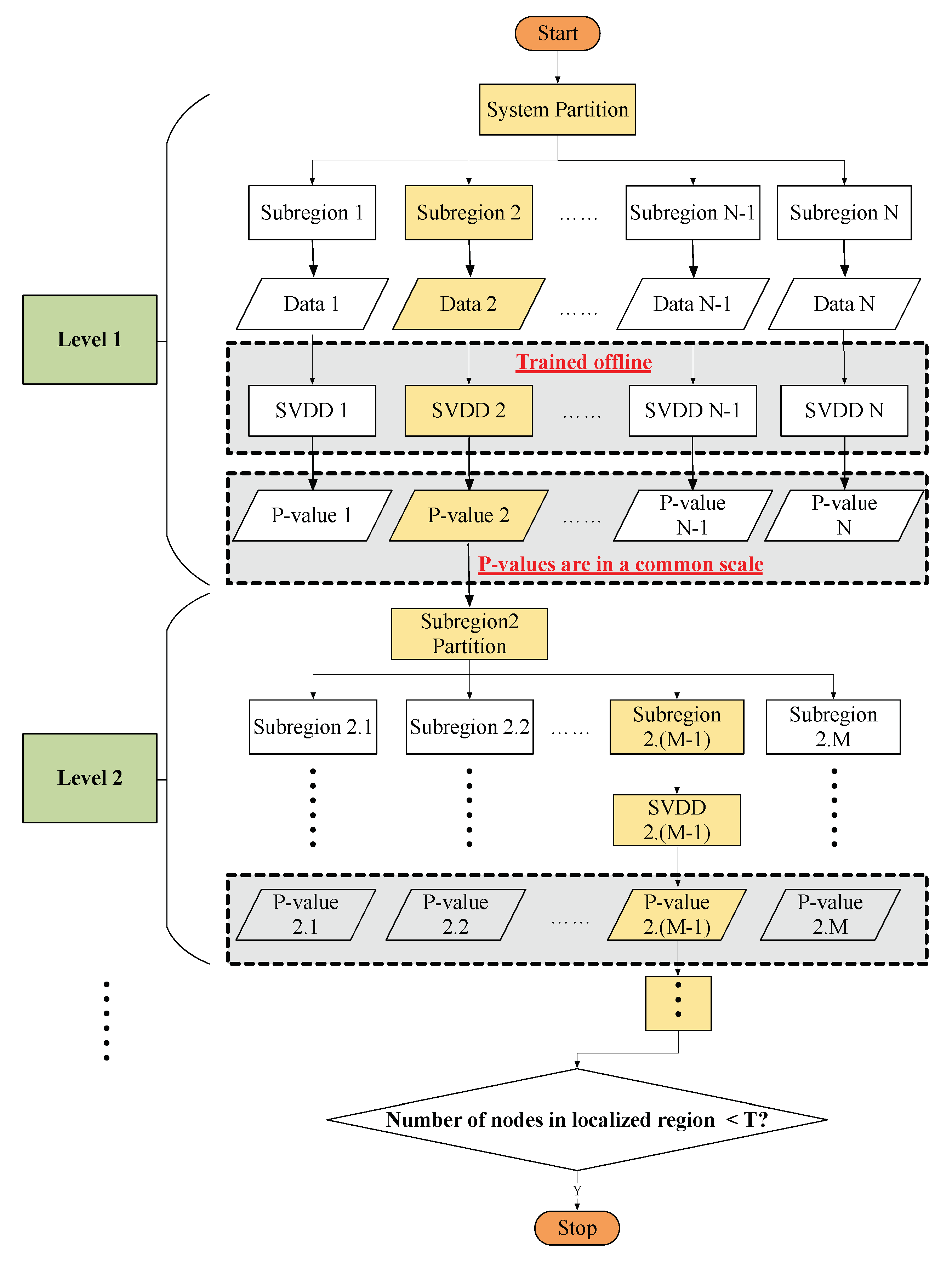
3. The Data-Driven Fault Localization Strategy
3.1. Criterion for Distribution Systems Partition
- (1)
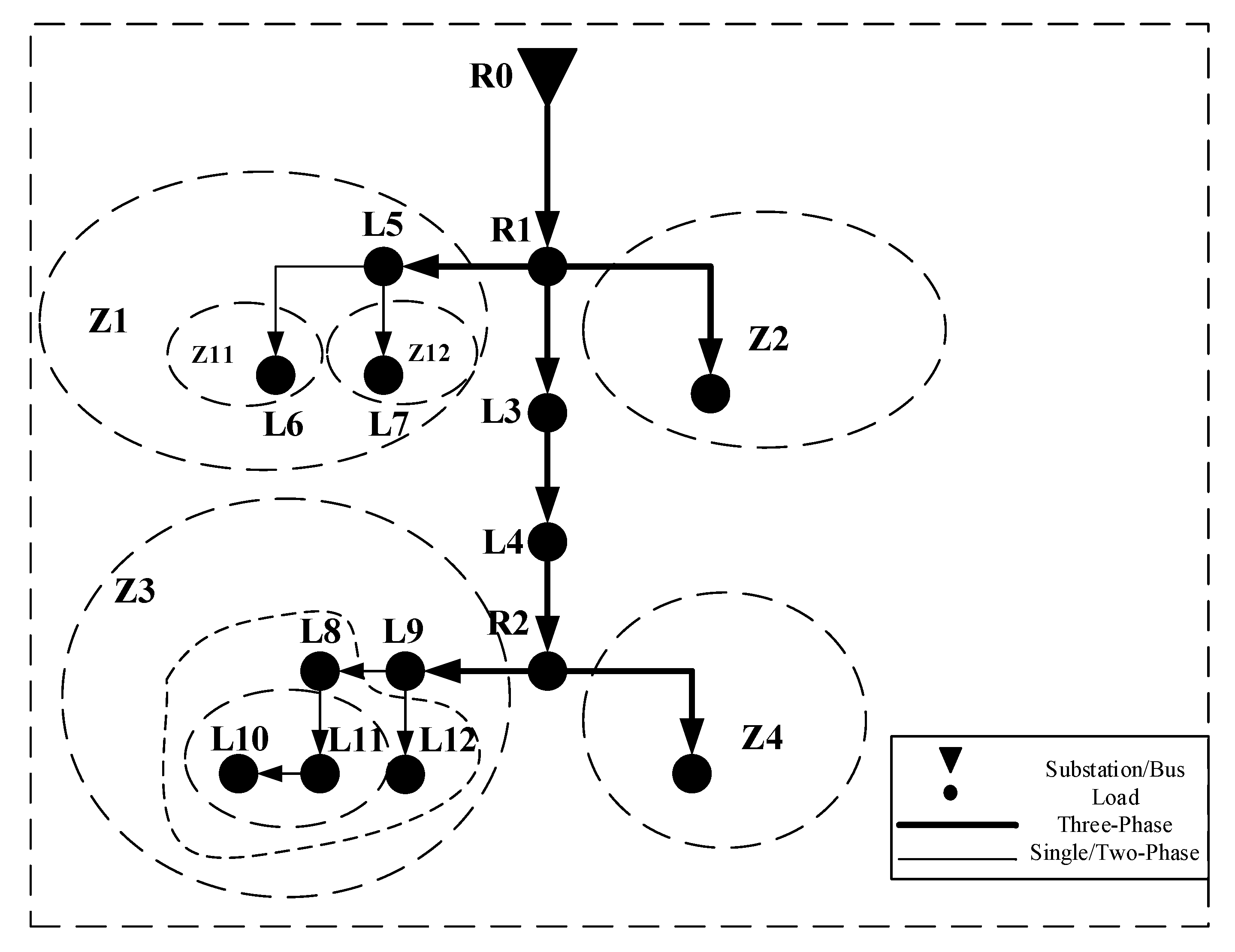
- Represent a distribution system in terms of a tree graph, denoted as , with L denoting the collection of user nodes , and E representing the set of directed edges in the rooted tree . Identify and classify the branches into three categories: three-phase branches, two-phase branches and single-phase branches.
- (2)
- In general, for a typical radial distribution system, there is usually a clear three-phase trunk wiring. Starting from the root node R in rooted tree G, select one of the paths consisting of three-phase nodes as the trunk of the entire system and go to step (3); If there is no trunk in the rooted tree G, go to step (5).
- (3)
- Along the selected trunk of the system, if an internal node in the trunk, , has at least two children nodes, set the internal node as root node of the subtree , and its subordinate nodes belong to subregion , where k is the index of the subtree/subregion.
- (4)
- In each subtree/subregion, continue to repeat step (2) and find following subtrees/subregions at the lower level of the hierarchy.
- (5)
- In subtree without a trunk, if all subordinate nodes have a degree (except leaf node), partition all nodes into two halves; If not, starting from the root node , continue to repeat the partitioning procedure in the descendant node of until the number of descendant nodes in the lower level subregion is smaller than a predefined lower bound which is set according to the minimum protection area for this system.
3.2. The Details of the Proposed Data-Driven Strategy
4. Simulations
4.1. Simulation Setup and Data Organization
4.2. Fault Localization via Traditional Relay Operations
4.3. Fault Localization via the Proposed Data-Driven Strategy
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saha, M.M.; Izykowski, J.J.; Rosolowski, E. Fault Location on Power Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Minniti, S.; Haque, N.; Nguyen, P.; Pemen, G. Local markets for flexibility trading: Key stages and enablers. Energies 2018, 11, 3074. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Duan, D.; Yang, Q.; Cheng, X.; Yang, L.; Cui, S. One-Class Classifier Based Fault Detection in Distribution Systems with Distributed Energy Resources. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 932–936. [Google Scholar]
- Häger, M.; Sollerkvist, F.; Bollen, M. The impact of distributed energy resources on distribution-system protection. In Proceedings of the Nordic Distribution and Asset Management Conference (Nordac), Stockholm, Sweden, 20–21 August 2006. [Google Scholar]
- Jiang, Z.; Sahasrabudhe, V.; Mohamed, A.; Grebel, H.; Rojas-Cessa, R. Greedy Algorithm for Minimizing the Cost of Routing Power on a Digital Microgrid. Energies 2019, 12, 3076. [Google Scholar] [CrossRef] [Green Version]
- Bollen, M.; Rönnberg, S. Hosting capacity of the power grid for renewable electricity production and new large consumption equipment. Energies 2017, 10, 1325. [Google Scholar] [CrossRef] [Green Version]
- Shafiullah, M.; Abido, M.A. A review on distribution grid fault location techniques. Electr. Power Compon. Syst. 2017, 45, 807–824. [Google Scholar] [CrossRef]
- Bretas, A.S.; Salim, R.H. A new fault location technique for distribution feeders with distributed generation. WSEAS Trans. Power Syst. 2006, 1, 894. [Google Scholar]
- Brahma, S.M. Fault location in power distribution system with penetration of distributed generation. IEEE Trans. Power Deliv. 2011, 26, 1545–1553. [Google Scholar] [CrossRef]
- Alwash, S.F.; Ramachandaramurthy, V.K.; Mithulananthan, N. Fault-location scheme for power distribution system with distributed generation. IEEE Trans. Power Deliv. 2015, 30, 1187–1195. [Google Scholar] [CrossRef] [Green Version]
- Mao, Z.T.Y. A fault location and realization method for overhead high voltage power transmission. Procedia Eng. 2011, 15, 964–968. [Google Scholar]
- Lin, S.; He, Z.; Li, X.; Qian, Q. Travelling wave time–frequency characteristic-based fault location method for transmission lines. IET Gener. Transm. Distrib. 2012, 6, 764–772. [Google Scholar] [CrossRef]
- Ding, J.; Li, L.; Zheng, Y.; Zhao, C.; Chen, H.; Wang, X. Distributed travelling-wave-based fault location without time synchronisation and wave velocity error. IET Gener. Transm. Distrib. 2017, 11, 2085–2093. [Google Scholar] [CrossRef]
- Majidi, M.; Etezadi-Amoli, M. A new fault location technique in smart distribution networks using synchronized/nonsynchronized measurements. IEEE Trans. Power Deliv. 2017, 33, 1358–1368. [Google Scholar] [CrossRef]
- Al-shaher, M.A.; Sabry, M.M.; Saleh, A.S. Fault location in multi-ring distribution network using artificial neural network. Electr. Power Syst. Res. 2003, 64, 87–92. [Google Scholar] [CrossRef]
- Javadian, S.; Nasrabadi, A.; Haghifam, M.R.; Rezvantalab, J. Determining fault’s type and accurate location in distribution systems with DG using MLP neural networks. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 284–289. [Google Scholar]
- Gururajapathy, S.; Mokhlis, H.; Illias, H. Fault location and detection techniques in power distribution systems with distributed generation: A review. Renew. Sustain. Energy Rev. 2017, 74, 949–958. [Google Scholar] [CrossRef]
- Gururajapathy, S.S. Fault Location in Distribution Systems Using Mathematical Analysis and Support Vector Machine. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 2017. [Google Scholar]
- Zheng, X.; Geng, X.; Xie, L.; Duan, D.; Yang, L.; Cui, S. A svm-based setting of protection relays in distribution systems. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 Feburary 2018; pp. 1–6. [Google Scholar]
- Khan, S.S.; Madden, M.G. One-class classification: Taxonomy of study and review of techniques. Knowl. Eng. Rev. 2014, 29, 345–374. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Fu, W.; Wang, K.; Xue, X.; Hu, W.; Shan, Y. Fault diagnosis for rolling bearing based on semi-supervised clustering and support vector data description with adaptive parameter optimization and improved decision strategy. Appl. Sci. 2019, 9, 1676. [Google Scholar] [CrossRef] [Green Version]
- Jung, D.; Ng, K.Y.; Frisk, E.; Krysander, M. Combining model-based diagnosis and data-driven anomaly classifiers for fault isolation. Control Eng. Pract. 2018, 80, 146–156. [Google Scholar] [CrossRef]
- Cui, J. Faults classification of power electronic circuits based on a support vector data description method. Metrol. Meas. Syst. 2015, 22, 205–220. [Google Scholar] [CrossRef]
- Castelo de Oliveira, T.E.; Bollen, M.; Ribeiro, P.F.; de Carvalho, P.; Zambroni, A.C.; Bonatto, B.D. The concept of dynamic hosting capacity for distributed energy resources: Analytics and practical considerations. Energies 2019, 12, 2576. [Google Scholar] [CrossRef] [Green Version]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef] [Green Version]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Li, Q.; Racine, J.S. Nonparametric Econometrics: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: Abingdon, UK, 2018. [Google Scholar]
- Jones, C.; Marron, J.S.; Sheather, S.J. Progress in data-based bandwidth selection for kernel density estimation. Comput. Stat. 1996, 11, 337–381. [Google Scholar]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef] [Green Version]
- Kersting, W.H. Radial distribution test feeders. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 908–912. [Google Scholar]
- Chassin, D.P.; Schneider, K.; Gerkensmeyer, C. GridLAB-D: An open-source power systems modeling and simulation environment. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–5. [Google Scholar]
- Blackburn, J.L.; Domin, T.J. Protective Relaying: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- So, C.; Li, K. Time coordination method for power system protection by evolutionary algorithm. IEEE Trans. Ind. Appl. 2000, 36, 1235–1240. [Google Scholar] [CrossRef]

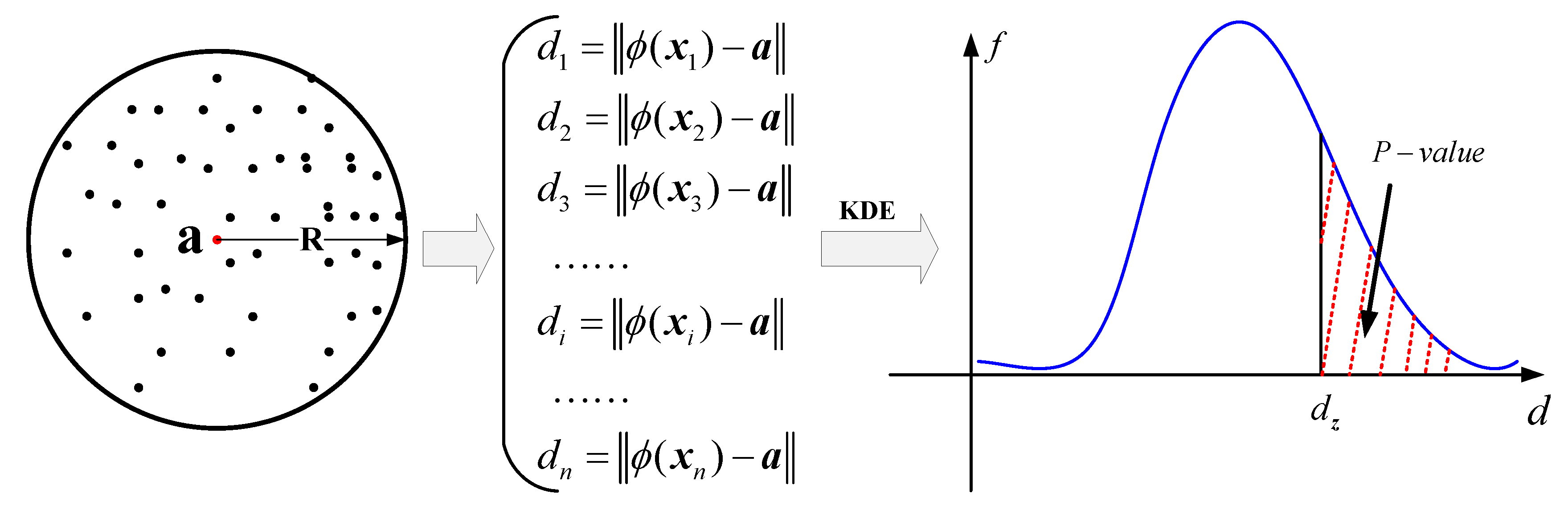



| Fault Line | 5–6 | 42–44 | 42–43 | 53–54 | 67–68 | 81–82 | 105–106 |
|---|---|---|---|---|---|---|---|
| Tripped Line | 1–3 3–5 5–6 21–23 23–25 26–27 80–81 91–93 101–105 105–108 | 21–23 23–25 26–27 35–40 40–42 42–44 80–81 91–93 101–105 105–108 135–35 | 13–18 21–23 23–25 26–27 35–40 40–42 42–43 80–81 91–93 101–105 105–108 135–35 | 21–23 23–25 26–27 80–81 87–89 91–93 101–105 105–108 | 21–23 23–25 26–27 80–81 87–89 91–93 101–105 105–108 | 21–23 23–25 26–27 72–76 76–77 76–86 77–78 80–81 87–89 91–93 101–105 105–108 | 21–23 23–25 26–27 67–97 80–81 91–93 101–105 105–106 105–108 197–101 |
| p-Value | Fault Line | 5–6 (sr:2) | 42–44 (sr:1) | 42–43 (sr:1) | 53–54 (Trunk) | 67–68 (Trunk) | 81–82 (sr:3) | 105–106 (sr:4) |
|---|---|---|---|---|---|---|---|---|
| Subregion | ||||||||
| subregion 1 | 8.96 × | 6.97 × | 3.35 × | 1.19 × | 7.13 × | 1.83 × | 3.15 × | |
| subregion 2 | 3.98 × | 8.90 × | 5.95 × | 6.16 × | 3.24 | 1.36 | 5.91 | |
| subregion 3 | 5.32 | 6.04 | 4.04 | 3.16 | 1.45 | 3.11 | 9.19 | |
| subregion 4 | 3.54 | 5.94 | 6.58 | 1.70 | 4.44 | 3.41 | 4.58 | |
| trunk | 2.42 | 3.35 | 7.38 | 4.82 | 4.82 | 4.82 | 1.84 | |
| p-Value | Subregion | Subregion 1.1 | Subregion 1.2 | Trunk Subregion |
|---|---|---|---|---|
| Fault Line | ||||
| 42–43 (subregion 1) | 0.4849 | 4.29 | 3.77 | |
| p-Value | Subregion | Subregion 1.2.1 | Subregion 1.2.2 |
|---|---|---|---|
| Fault Line | |||
| 42–43 (subregion 1) | 6.98 | 0.5196 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Duan, D.; Yang, Q.; Hong, X.; Cheng, X.; Yang, L.; Cui, S. Data-Driven Fault Localization in Distribution Systems with Distributed Energy Resources. Energies 2020, 13, 275. https://doi.org/10.3390/en13010275
Lin Z, Duan D, Yang Q, Hong X, Cheng X, Yang L, Cui S. Data-Driven Fault Localization in Distribution Systems with Distributed Energy Resources. Energies. 2020; 13(1):275. https://doi.org/10.3390/en13010275
Chicago/Turabian StyleLin, Zhidi, Dongliang Duan, Qi Yang, Xuemin Hong, Xiang Cheng, Liuqing Yang, and Shuguang Cui. 2020. "Data-Driven Fault Localization in Distribution Systems with Distributed Energy Resources" Energies 13, no. 1: 275. https://doi.org/10.3390/en13010275





