Assessment of Early Stopping through Statistical Health Prognostic Models for Empirical RUL Estimation in Wind Turbine Main Bearing Failure Monitoring
Abstract
:1. Introduction
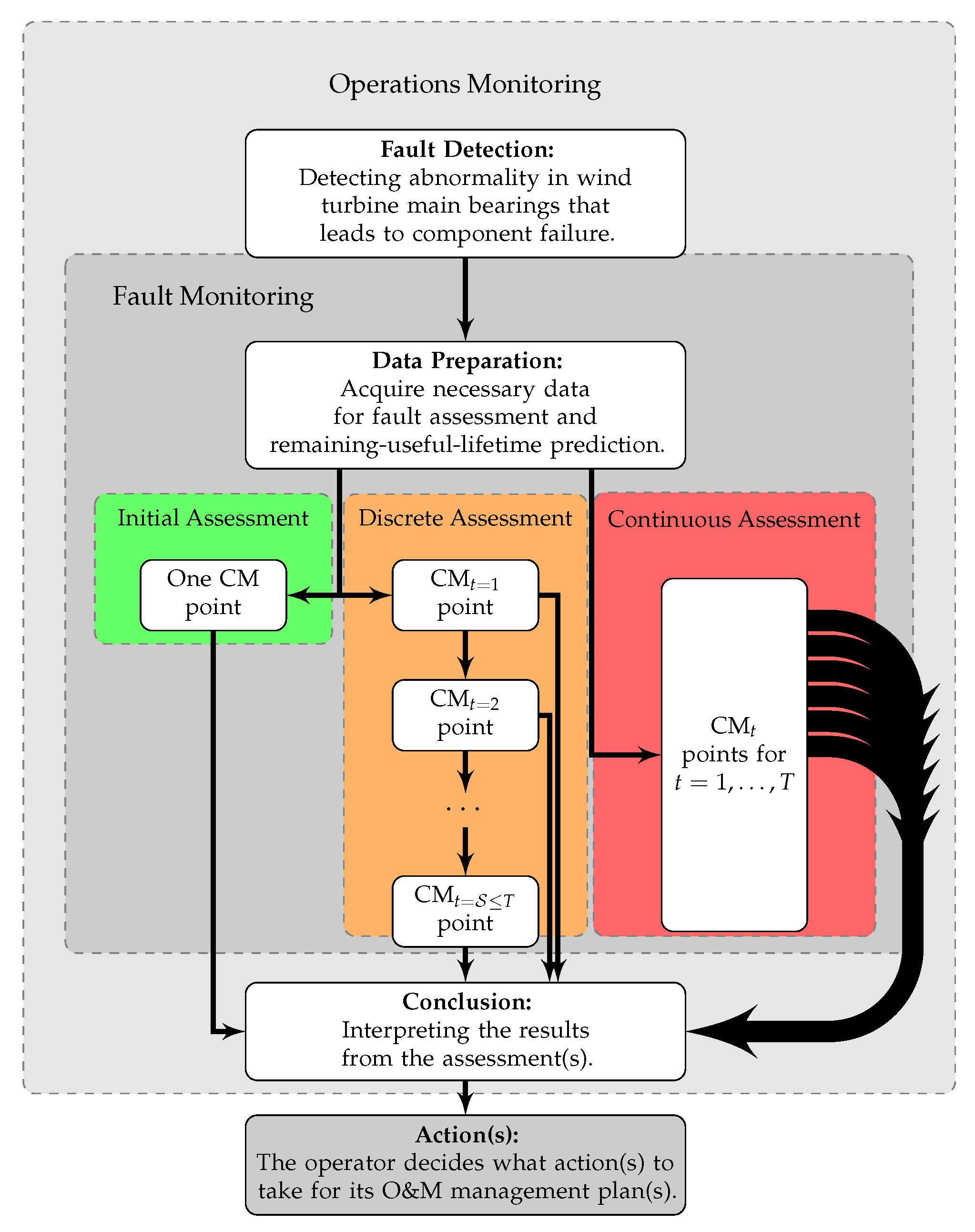
2. Methodology
2.1. Data and Notation
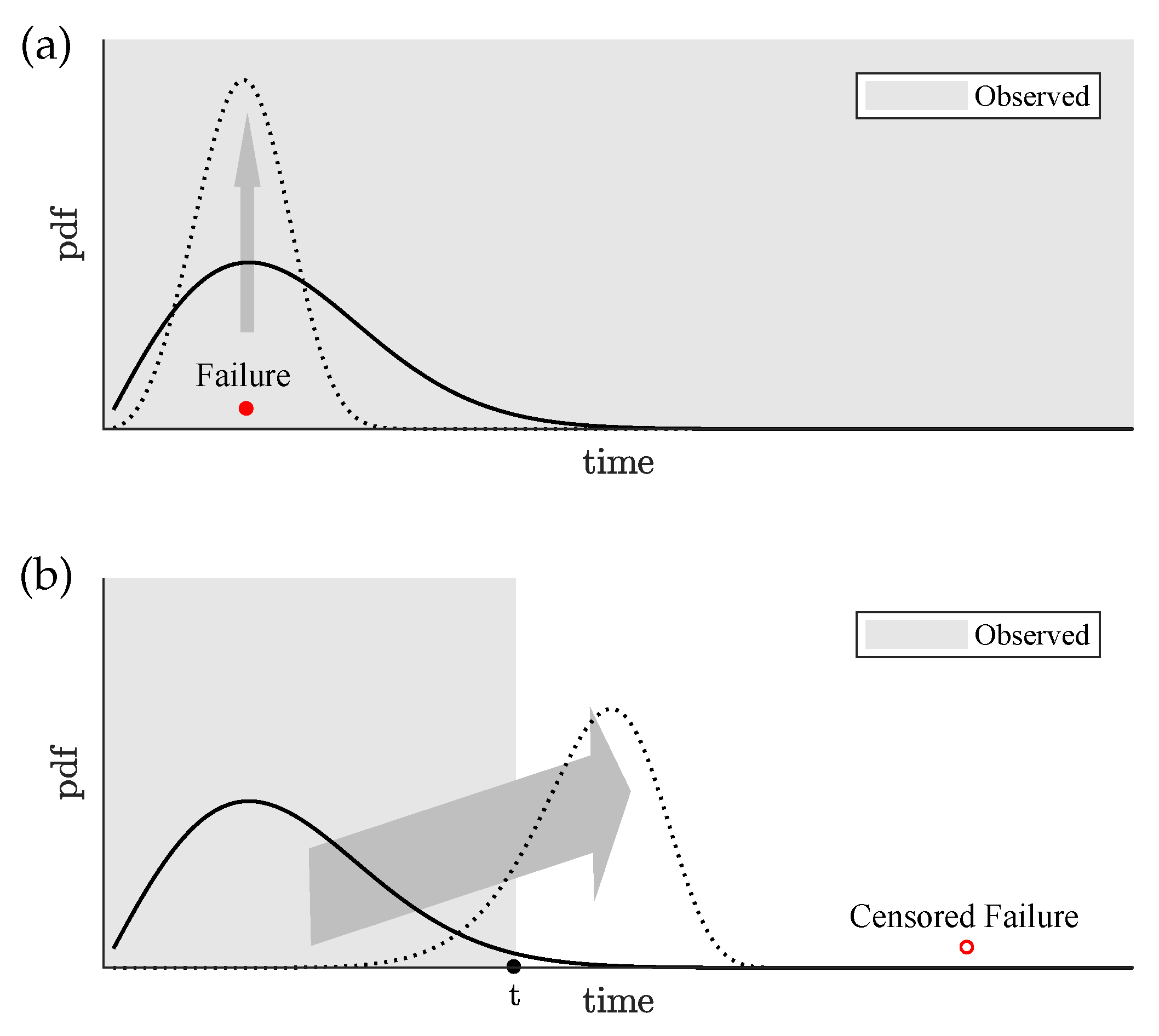
2.2. Empirical Remaining-Useful-Lifetime Estimation
2.2.1. Initial Assessment
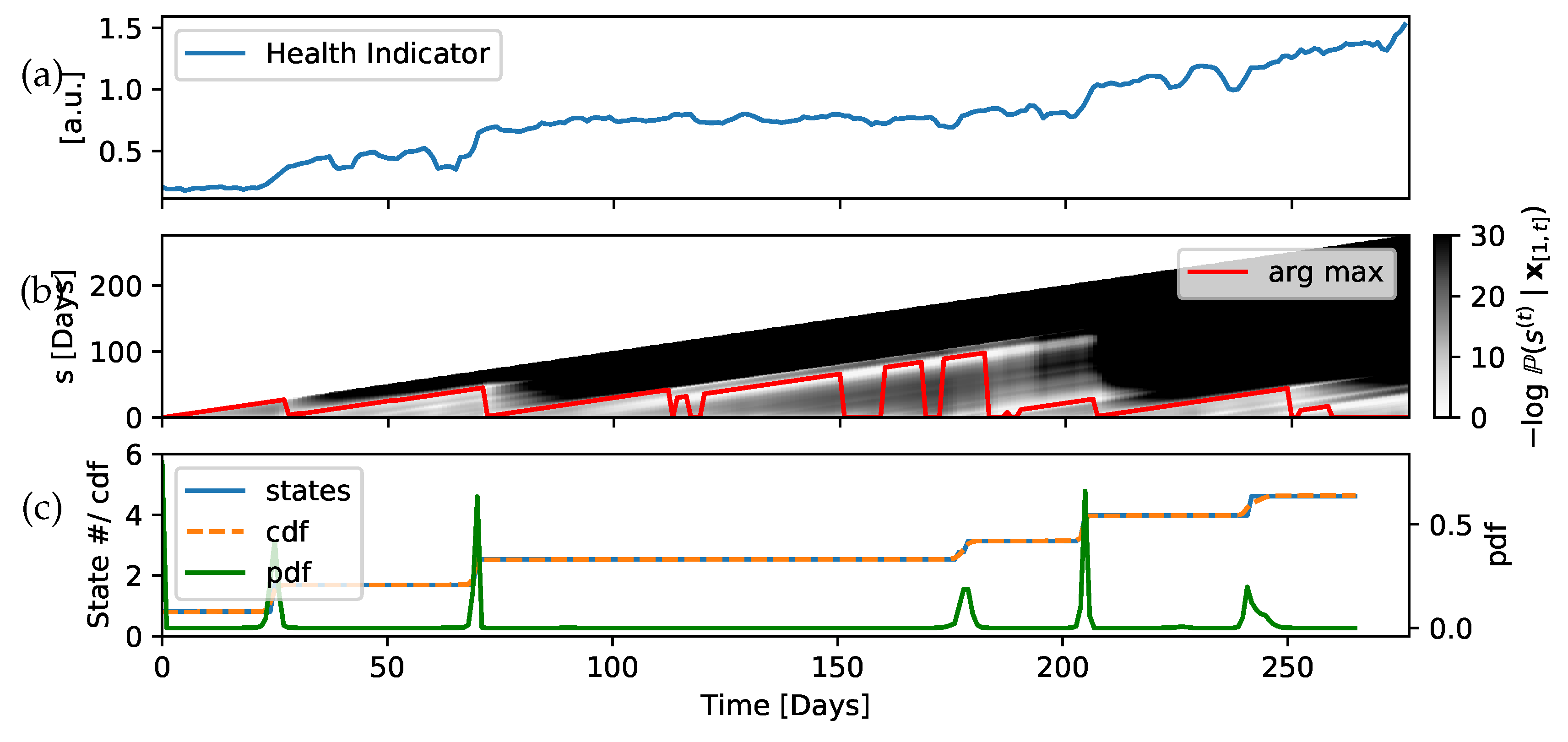
2.2.2. State Abstraction and Discrete Assessment
2.2.3. Continuous Assessment: RUL Recurrent Neural Network
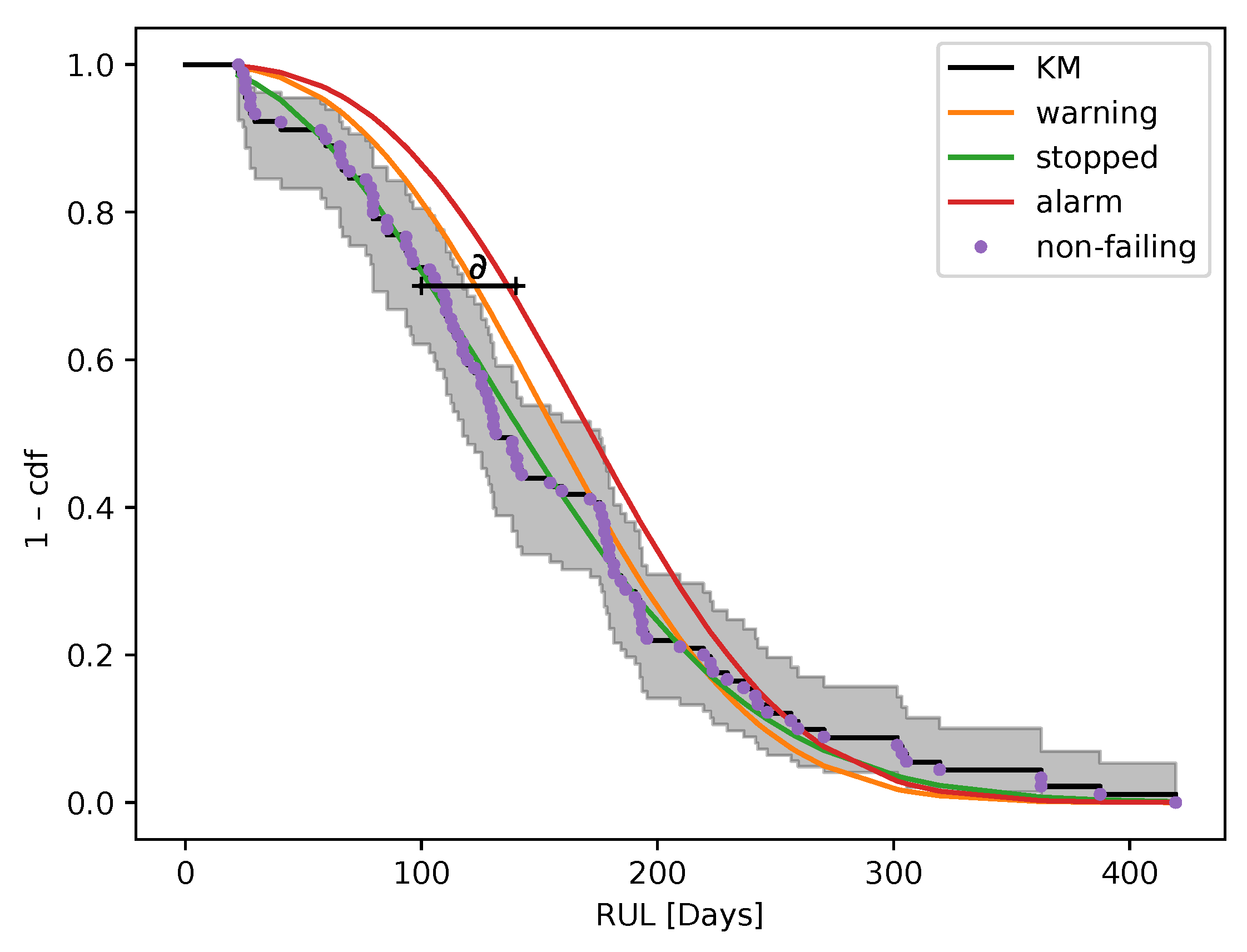
3. Assessment of Early Stopping—A Bearing Failure Study
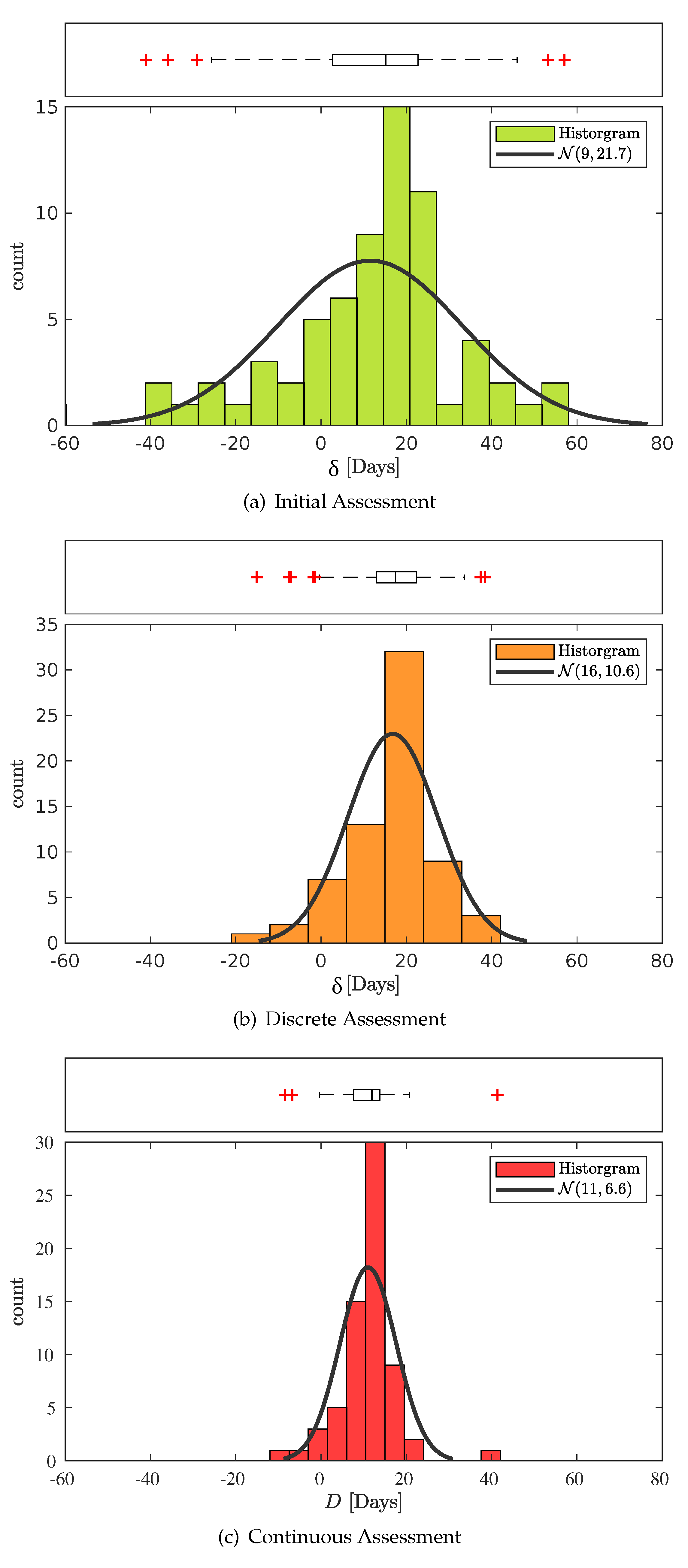
3.1. Initial Assessment
3.2. Discrete Assessment
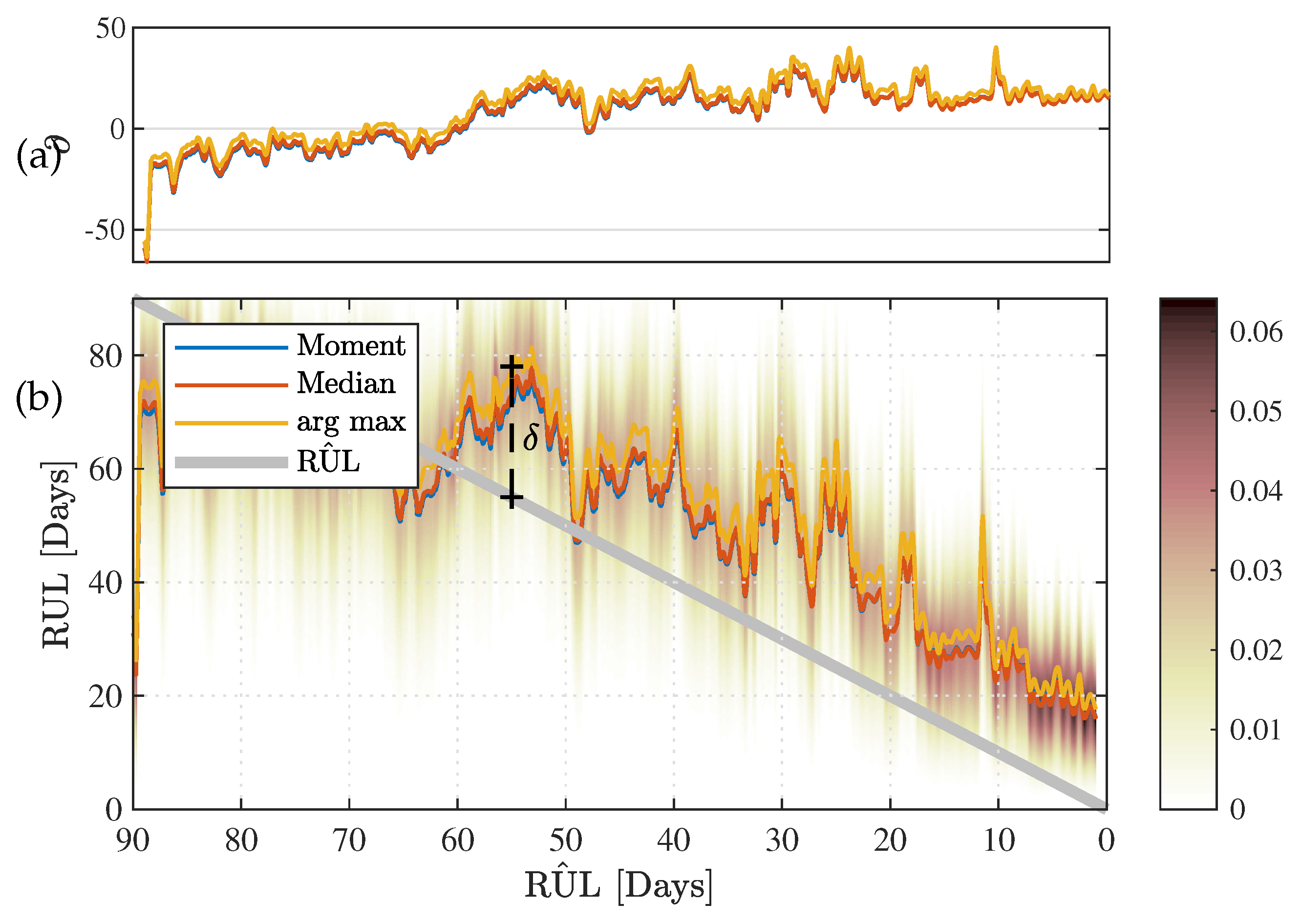
3.3. Continuous Assessment
4. Discussion
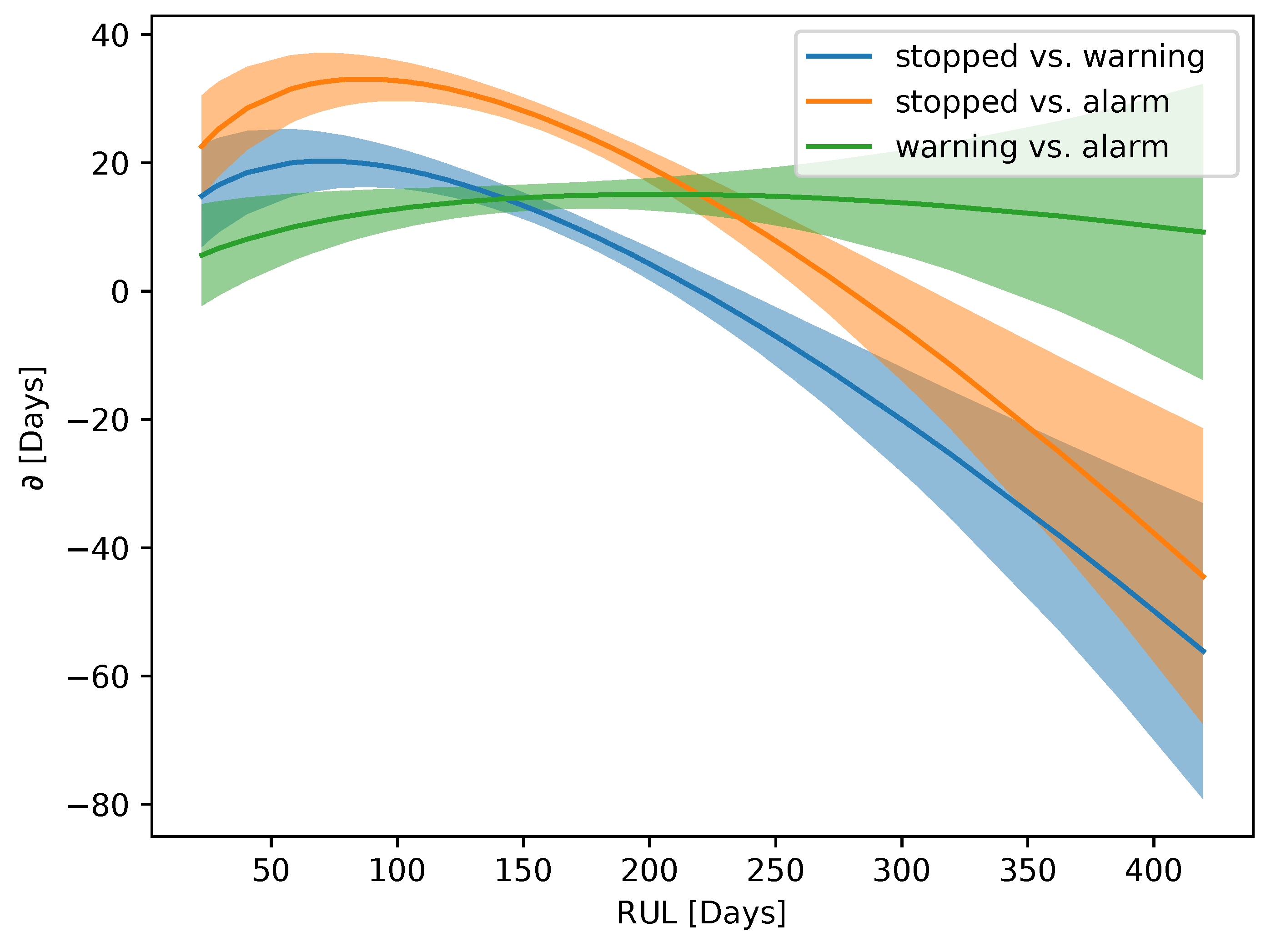
4.1. Discrepancy Between Assessments
4.2. The Naïve O&M Assumption
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| cdf | cumulative distribution function |
| CM | Condition Monitoring |
| KM | Kaplan-Meier |
| NN | Neural Network |
| O&M | Operation and Maintenance |
| probability density function | |
| RNN | Recurrent Neural Network |
| RUL | Remaining-Useful-Lifetime |
| SCADA | Supervisory Control and Data Acquisition |
Nomenclature
| a | scalar |
| vector | |
| matrix | |
| sample vector | |
| samples on the interval a to b | |
| set of all possible events | |
| event | |
| subset of | |
| RUL | random variable for the remaining-useful-lifetime |
| real remaining-useful-lifetime | |
| hazard function | |
| H | cumulative hazard function |
| censoring variable | |
| likelihood function | |
| hyper-parameter for conditional prior and sample model | |
| independent conditional prior | |
| probability distribution over the current state | |
| sample model | |
| mismatch between RUL and | |
| D | average mismatch |
References
- Petersen, K.R.; Madsen, E.S.; Bilberg, A. Offshore Wind Power at Rough Sea: The need for new Maintenance Models. In Proceedings of the 20th EurOMA Conference, Dublin, Ireland, 9–12 June 2013. [Google Scholar]
- Nielsen, J.; Sørensen, J. On risk-based operation and maintenance of offshore wind turbine components. Reliab. Eng. Syst. Saf. 2011, 96, 218–229. [Google Scholar] [CrossRef]
- Blanco, M.I. The economics of wind energy. Renew. Sustain. Energy Rev. 2009, 13, 1372–1382. [Google Scholar] [CrossRef]
- Van Bussel, G.J.W.; Zaaijer, M.B. Reliability, Availability and Maintenance Aspects of Large-Scale Offshore Wind Farms, a Concepts Study. In Proceedings of the MAREC 2001 Marine Renewable Energies Conference, Newcastle, UK, 27 March 2001; Volume 113, pp. 119–126. [Google Scholar]
- Wilkinson, M.; Spinato, F.; Knowles, M. Towards the Zero Maintenance Wind Turbine. In Proceedings of the 41st International Universities Power Engineering Conference (UPEC ’06), Newcastle, UK, 6–8 Septemeber 2006; Volume 1, pp. 74–78. [Google Scholar] [CrossRef]
- Kim, N.; An, D.; Choi, J. Prognostics and Health Management of Engineering Systems: An Introduction; Springer: Berlin, Germany, 2016. [Google Scholar]
- Sheppard, J.W.; Kaufman, M.A.; Wilmer, T.J. IEEE Standards for Prognostics and Health Management. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 34–41. [Google Scholar] [CrossRef] [Green Version]
- Walford, C.A. Wind Turbine Reliability: Understanding and Minimizing Wind Turbine Operation and Maintenance Costs; Technical Report SAND2006-1100; Sandia National Laboratories: Albuquerque, NM, USA, 2006. Available online: https://energy.sandia.gov/wp-content/gallery/uploads/SAND-2006-1100.pdf (accessed on 12 December 2019).
- Herp, J.; Pedersen, N.L.; Nadimi, E.S. A Novel Probabilistic Long-Term Fault Prediction Framework Beyond SCADA Data—With Applications in Main Bearing Failure. J. Phys. Conf. Ser. 2019, 1222, 012043. [Google Scholar] [CrossRef] [Green Version]
- Trappey, A.J.C.; Trappey, C.V.; Ma, L.; Chang, J.C. Integrating Real-Time Monitoring and Asset Health Prediction for Power Transformer Intelligent Maintenance and Decision Support. In Engineering Asset Management—Systems, Professional Practices and Certification; Tse, P.W., Mathew, J., Wong, K., Lam, R., Ko, C., Eds.; Springer: Cham, Switzerland, 2015; pp. 533–543. [Google Scholar]
- You, G.W.; Park, S.; Oh, D. Diagnosis of Electric Vehicle Batteries Using Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2017, 64, 4885–4893. [Google Scholar] [CrossRef]
- Herp, J.; Ramezani, M.H.; Bach-Andersen, M.; Pedersen, N.L.; Nadimi, E.S. Bayesian state prediction of wind turbine bearing failure. Renew. Energy 2018, 116, 164–172. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Zhou, Z.; Zio, E.; Wang, W. An adaptive method for health trend prediction of rotating bearings. Dig. Signal Process. 2014, 35, 117–123. [Google Scholar] [CrossRef]
- Si, X.S. An Adaptive Prognostic Approach via Nonlinear Degradation Modeling: Application to Battery Data. IEEE Trans. Ind. Electron. 2015, 62, 5082–5096. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Katzman, J.; Shaham, U.; Bates, J.; Cloninger, A.; Jiang, T.; Kluger, Y. DeepSurv: Personalized Treatment Recommender System Using A Cox Proportional Hazards Deep Neural Network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]
- Si, X.; Zhang, Z.; Hu, C. Data-Driven Remaining Useful Life Prognosis Techniques: Stochastic Models, Methods and Applications; Springer Series in Reliability Engineering; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Ranganath, R.; Tang, L.; Charlin, L.; Blei, D.M. Deep Exponential Families. arXiv 2014, arXiv:1411.2581. [Google Scholar]
- Ranganath, R.; Perotte, A.; Elhadad, N.; Blei, D. Deep Survival Analysis. arXiv 2016, arXiv:1608.02158. [Google Scholar]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar] [CrossRef]
- Mazhar, M.; Kara, S.; Kaebernick, H. Remaining life estimation of used components in consumer products: Life cycle data analysis by Weibull and artificial neural networks. J. Op. Manag. 2007, 25, 1184–1193. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, C.; Wang, J.; Li, G. Reliability Assessment of CNC Machining Center Based on Weibull Neural Network. Math. Probl. Eng. 2015, 2015, 8. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, K.; Atan, O.; Farahat, A.K.; Zhang, C.; Ristovski, K.; Gupta, C. Two Birds with One Network: Unifying Failure Event Prediction and Time-to-failure Modeling. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1308–1317. [Google Scholar]
- Bach-Andersen, M.; Rømer-Odgaard, B.; Winther, O. Flexible non-linear predictive models for large-scale wind turbine diagnostics. Wind Energy 2016, 20, 753–764. [Google Scholar] [CrossRef]
- Kleinbaum, D.; Klein, M. Survival Analysis: A Self-Learning Text, 3rd ed.; Statistics for Biology and Health; Springer: New York, NY, USA, 2011. [Google Scholar]
- Patti, S.; Biganzoli, E.; Boracchi, P. Review of the Maximum Likelihood Functions for Right Censored Data. A New Elementary Derivation. In COBRA Preprint Series; bepress: Berkeley, CA, USA, 2007. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric Estimation from Incomplete Observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Herp, J.; Ramezani, M.H. State transition of wind turbines based on empirical inference on model residuals. In Proceedings of the 2015 Conference on Research in Adaptive and Convergent Systems, RACS 2015, Prague, Czech Republic, 9–12 October 2015; pp. 32–37. [Google Scholar] [CrossRef]
- Herp, J.; Ramezani, M.H.; Nadimi, E. Dependency in State Transitions of Wind Turbines-Inference on model Residuals for State Abstractions. IEEE Trans. Ind. Electron. 2017. [Google Scholar] [CrossRef]
- Prescott Adams, R.; MacKay, D.J.C. Bayesian Online Changepoint Detection. arXiv 2007, arXiv:0710.3742. [Google Scholar]
- Fisher, R.A. On the Mathematical Foundations of Theoretical Statistics. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1922, 222, 309–368. [Google Scholar] [CrossRef] [Green Version]
- Hipp, C. Sufficient Statistics and Exponential Families. Ann. Stat. 1974, 2, 1283–1292. [Google Scholar] [CrossRef]
- Fisher, R.A. Applications of “Student’s” distribution. Metron 1925, 5, 90–104. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2006; Available online: http://www.deeplearningbook.org (accessed on 12 December 2019).



| Event | Start Time | Stop Time | ||||||
|---|---|---|---|---|---|---|---|---|
| 12 October 2014, 09:59:01 | 13 October 2014, 10:12:43 | |||||||
| 12 October 2014, 15:39:06 | 13 October 2014, 10:22:43 | |||||||
| ⋮ | ⋮ | ⋮ | ||||||
| 19 October 2014, 02:22:00 | 19 October 2014, 13:00:00 | |||||||
| 19 October 2014, 02:42:59 | 19 October 2014, 13:00:00 | |||||||
| ⇓ | ||||||||
| Events | ||||||||
| Sample | ⋯ | ⋯ | ||||||
| 0 | 0 | ⋯ | 0 | 1 | 0 | ⋯ | 1 | |
| 0 | 0 | ⋯ | 0 | 1 | 0 | ⋯ | 1 | |
| t | 0 | 0 | ⋯ | 0 | 1 | 1 | ⋯ | 0 |
| 0 | 0 | ⋯ | 0 | 0 | 1 | ⋯ | 0 | |
| 1 | 0 | ⋯ | 0 | 0 | 1 | ⋯ | 1 | |
| ⇓ | ||||||||
 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herp, J.; Pedersen, N.L.; Nadimi, E.S. Assessment of Early Stopping through Statistical Health Prognostic Models for Empirical RUL Estimation in Wind Turbine Main Bearing Failure Monitoring. Energies 2020, 13, 83. https://doi.org/10.3390/en13010083
Herp J, Pedersen NL, Nadimi ES. Assessment of Early Stopping through Statistical Health Prognostic Models for Empirical RUL Estimation in Wind Turbine Main Bearing Failure Monitoring. Energies. 2020; 13(1):83. https://doi.org/10.3390/en13010083
Chicago/Turabian StyleHerp, Jürgen, Niels L. Pedersen, and Esmaeil S. Nadimi. 2020. "Assessment of Early Stopping through Statistical Health Prognostic Models for Empirical RUL Estimation in Wind Turbine Main Bearing Failure Monitoring" Energies 13, no. 1: 83. https://doi.org/10.3390/en13010083
APA StyleHerp, J., Pedersen, N. L., & Nadimi, E. S. (2020). Assessment of Early Stopping through Statistical Health Prognostic Models for Empirical RUL Estimation in Wind Turbine Main Bearing Failure Monitoring. Energies, 13(1), 83. https://doi.org/10.3390/en13010083






