Comparison of Length Scale Parameterization Methodologies
Abstract
:1. Introduction
1.1. MOST with Three-Dimensional High Frequency Data
1.2. Richardson Method
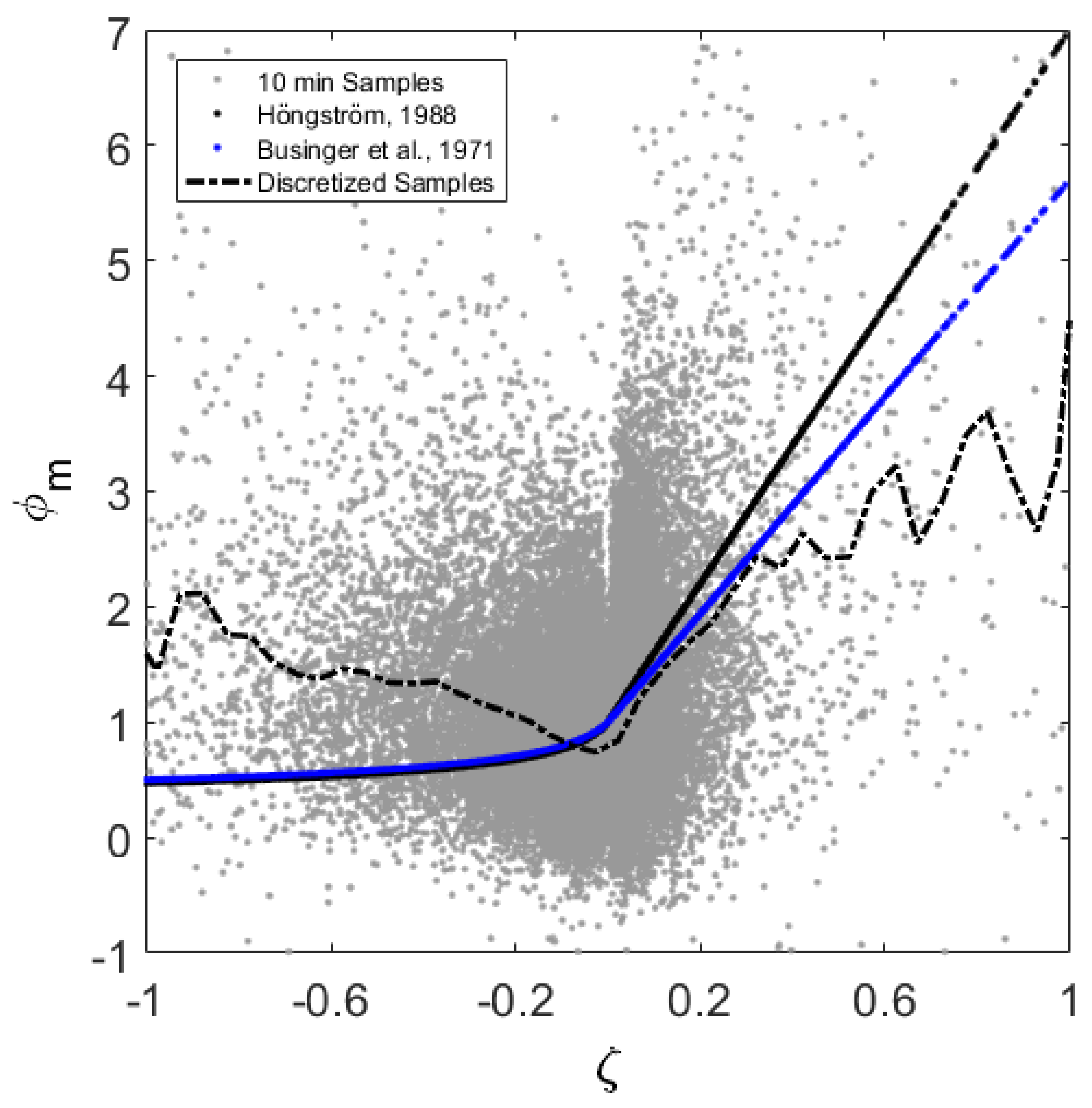
1.2.1. Flux-Profile Relations
1.2.2. Wind Shear Method
2. Experimental Setup
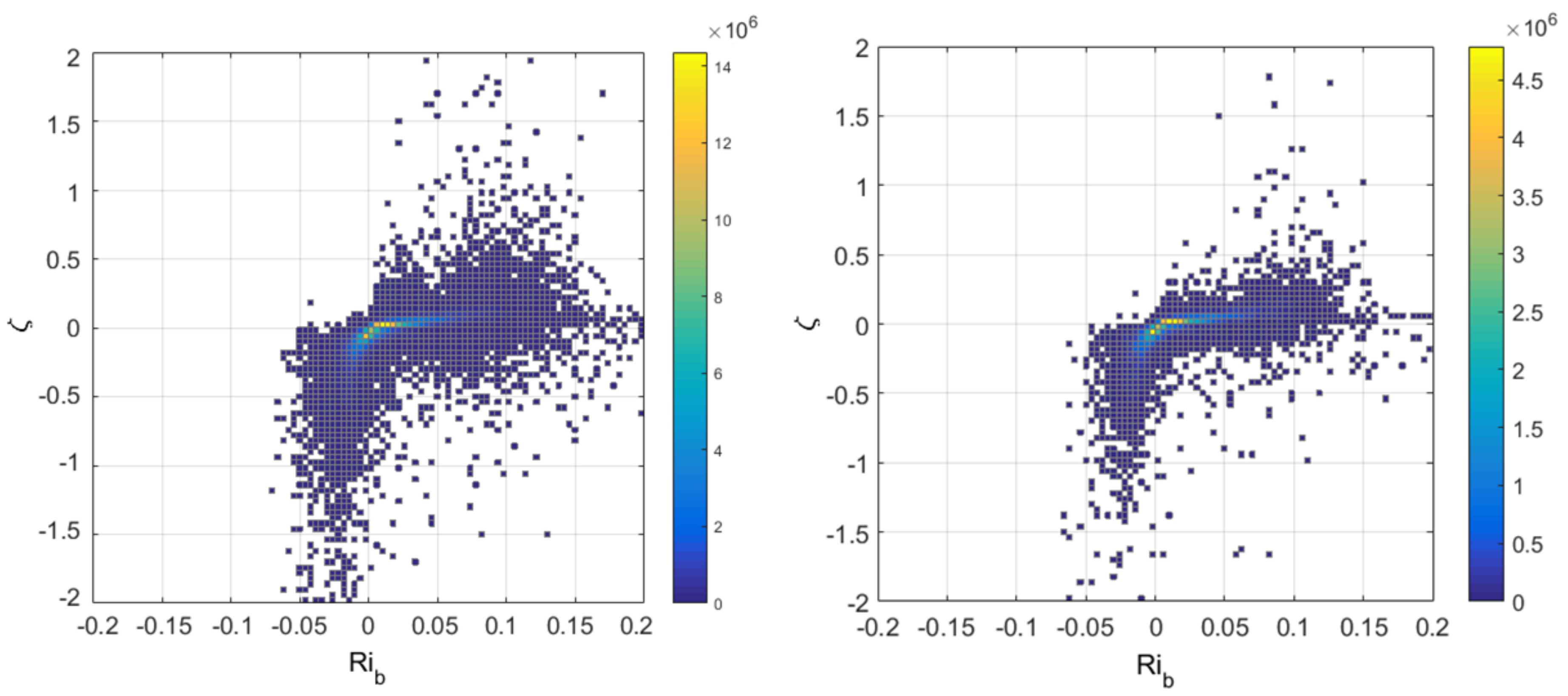
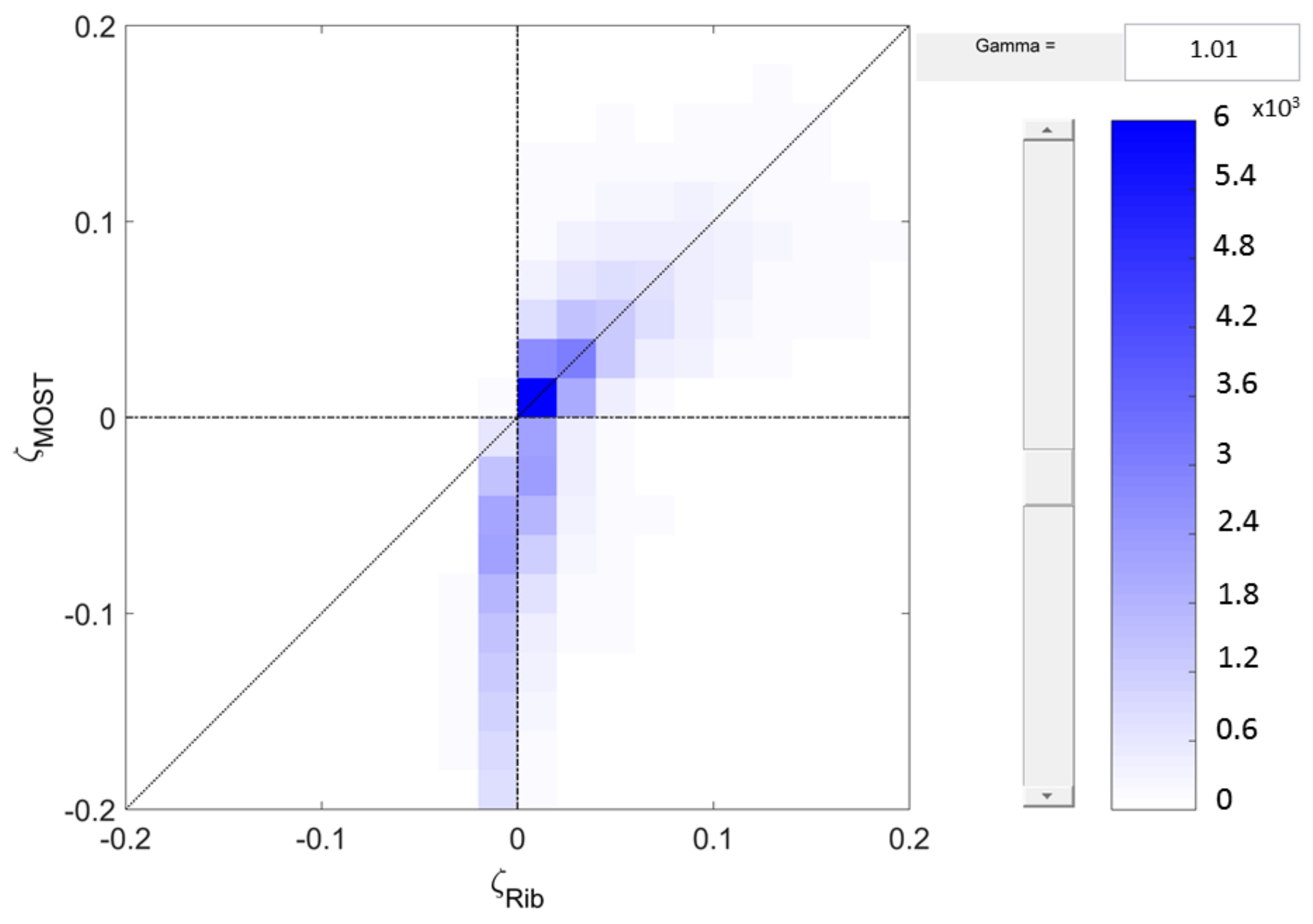
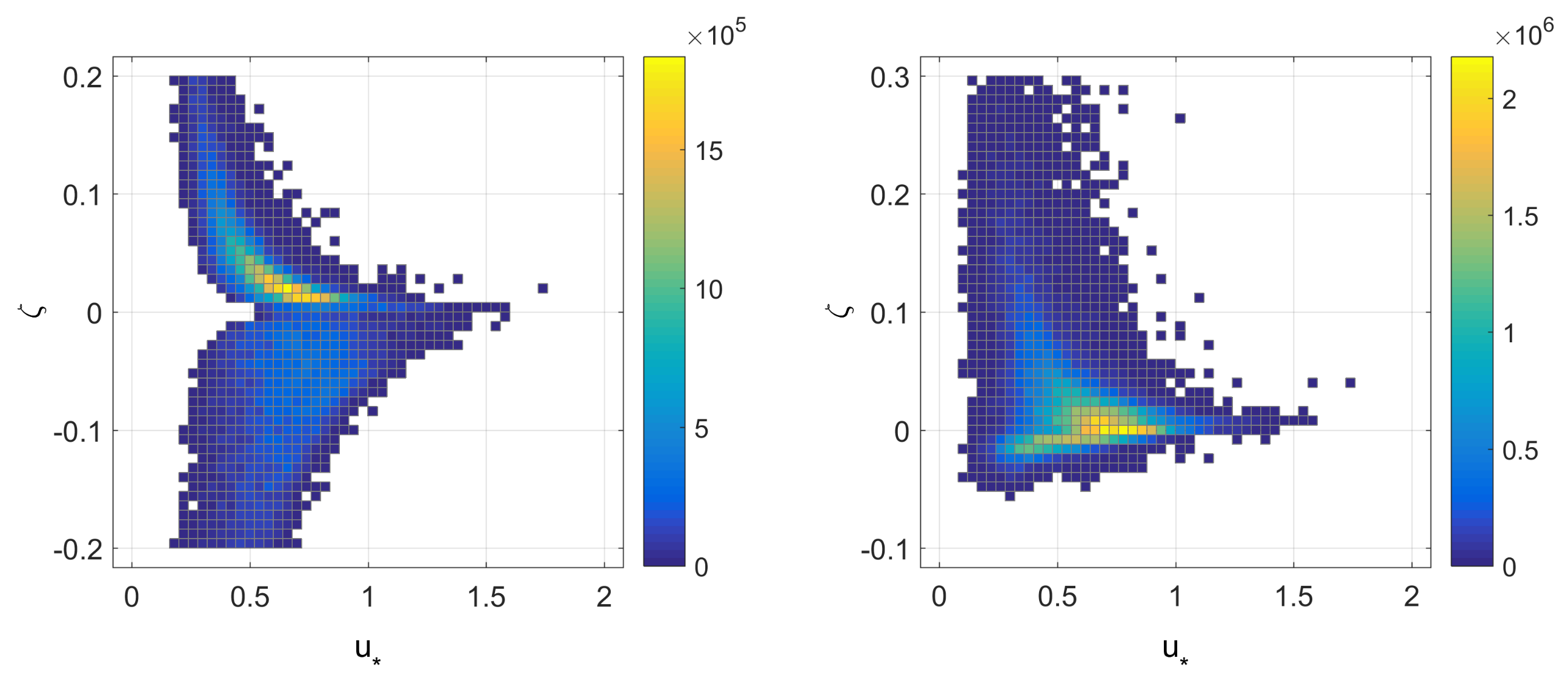
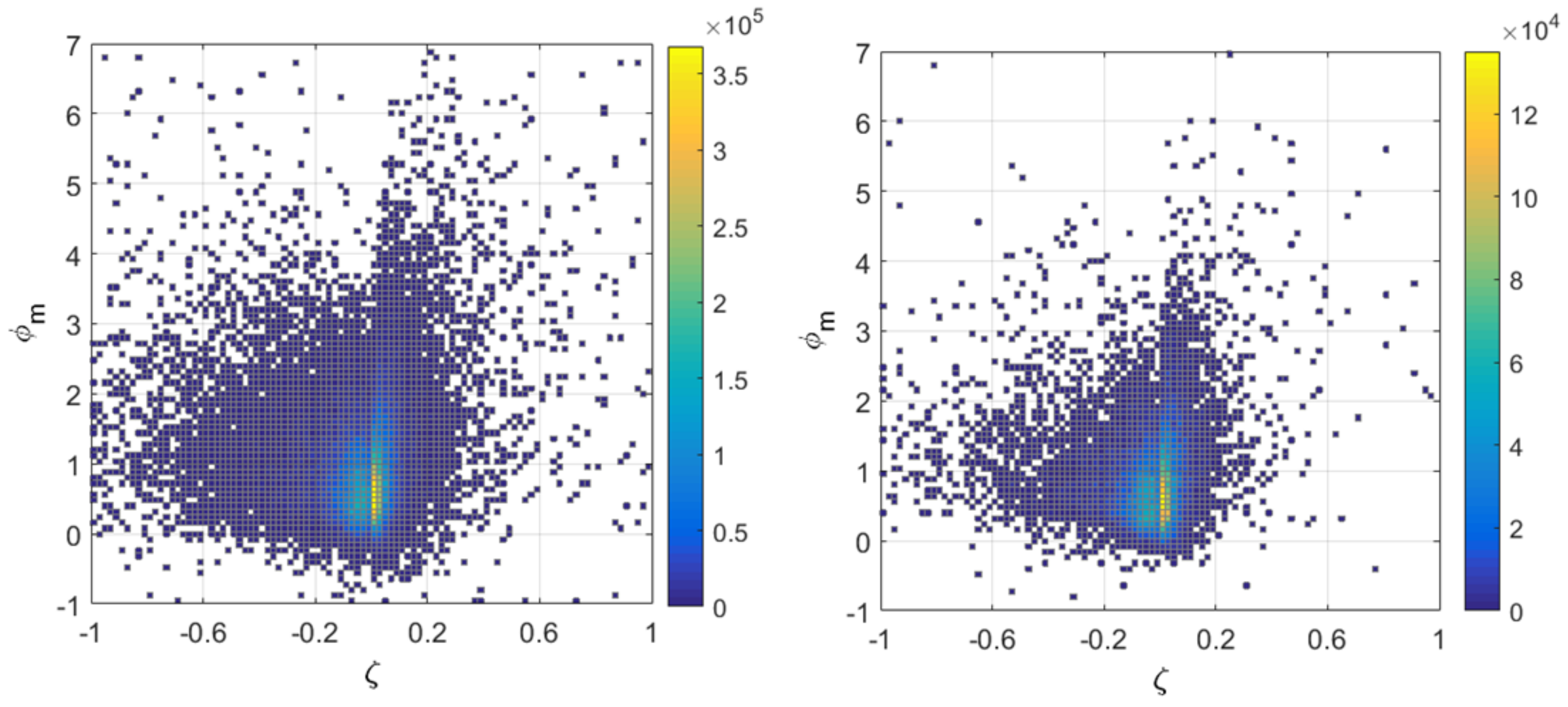
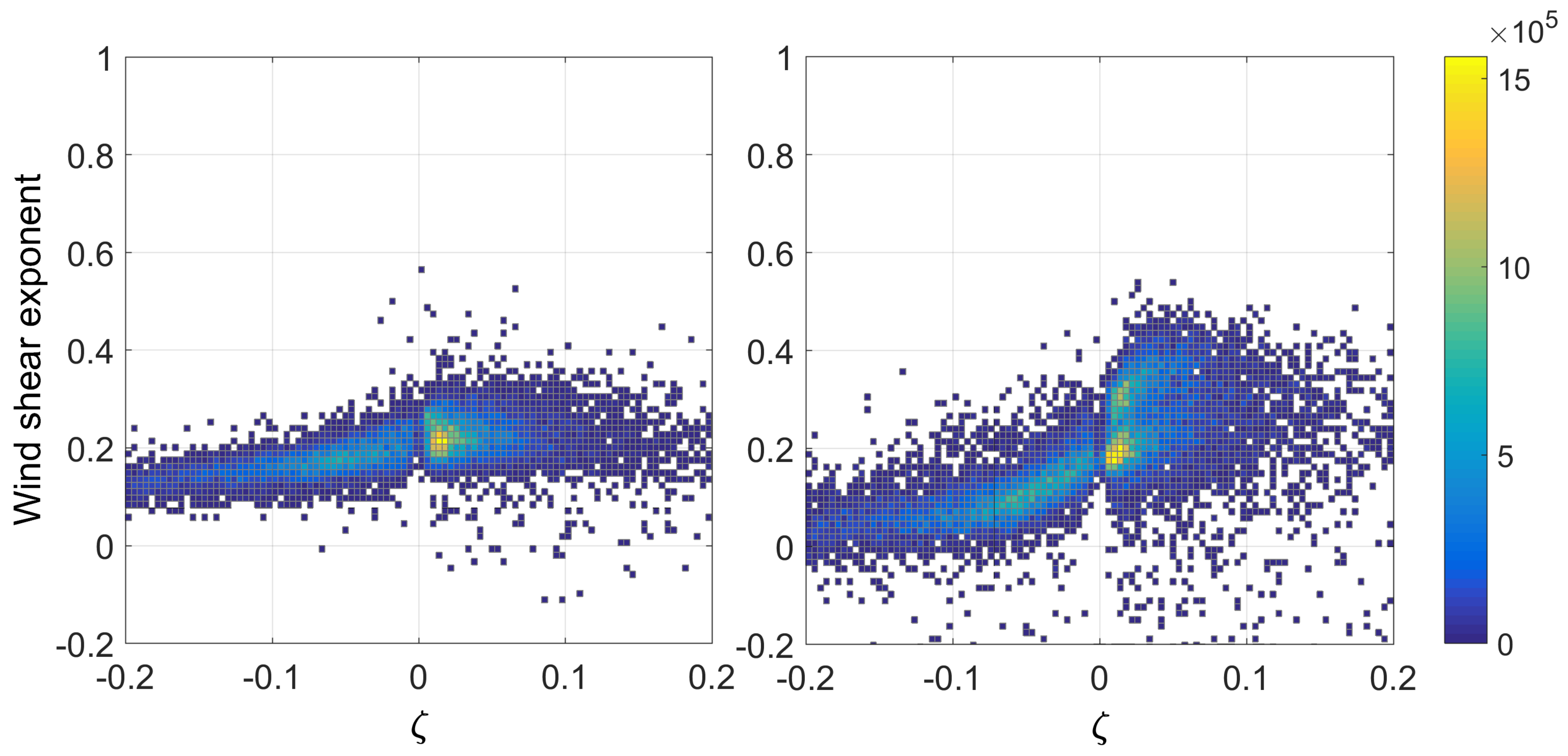
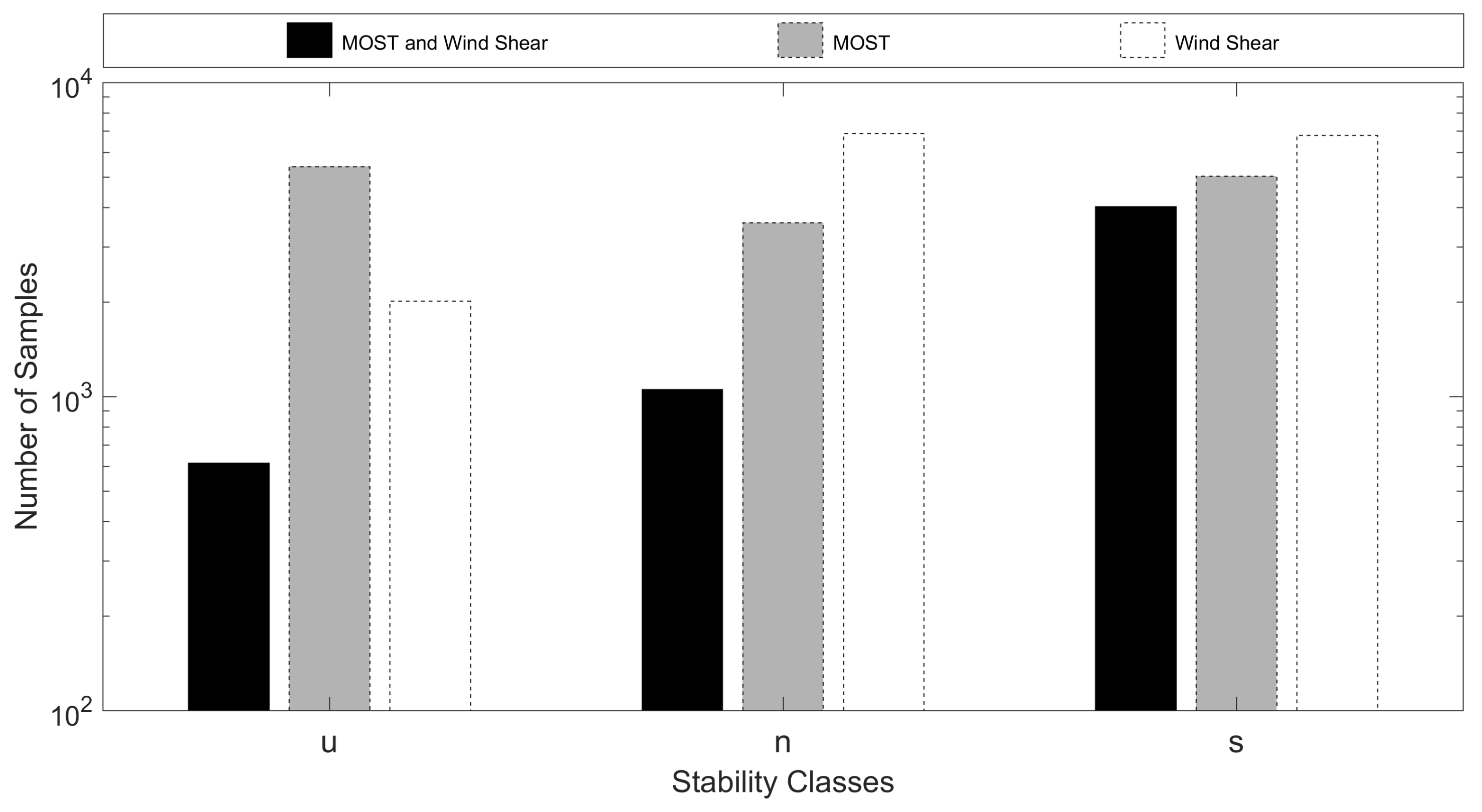
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, G.I. Statistical theory of turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1935, 151, 421–444. [Google Scholar] [CrossRef] [Green Version]
- Halstead, M. A stability-term in the wind-gradient equation. Eos Trans. Am. Geophys. Union 1943, 24, 204–208. [Google Scholar] [CrossRef]
- Holzman, B. The influence of stability on evaporation. Ann. N. Y. Acad. Sci. 1943, 44, 13–18. [Google Scholar] [CrossRef]
- Monin, A.; Obukhov, A. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, e187. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. The critical Richardson number and limits of applicability of local similarity theory in the stable boundary layer. Bound.-Layer Meteorol. 2013, 147, 51–82. [Google Scholar] [CrossRef] [Green Version]
- Sorbjan, Z.; Grachev, A.A. An evaluation of the flux–gradient relationship in the stable boundary layer. Bound.-Layer Meteorol. 2010, 135, 385–405. [Google Scholar] [CrossRef]
- Högström, U. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer; Springer: New York, NY, USA, 1988; pp. 55–78. [Google Scholar]
- Yang, K.; Tamai, N.; Koike, T. Analytical solution of surface layer similarity equations. J. Appl. Meteorol. 2001, 40, 1647–1653. [Google Scholar] [CrossRef]
- Dellwik, E.; Jensen, N.O. Flux–profile relationships over a fetch limited beech forest. Bound.-Layer Meteorol. 2005, 115, 179. [Google Scholar] [CrossRef]
- Grachev, A.; Fairall, C.; Bradley, E. Convective profile constants revisited. Bound.-Layer Meteorol. 2000, 94, 495–515. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. SHEBA flux–profile relationships in the stable atmospheric boundary layer. Bound.-Layer Meteorol. 2007, 124, 315–333. [Google Scholar] [CrossRef]
- Byun, D.W. On the analytical solutions of flux-profile relationships for the atmospheric surface layer. J. Appl. Meteorol. 1990, 29, 652–657. [Google Scholar] [CrossRef]
- Arya, S. Parametric relations for the atmospheric boundary layer. Bound.-Layer Meteorol. 1984, 30, 57–73. [Google Scholar] [CrossRef]
- Foken, T.; Skeib, G. Profile measurements in the atmospheric near-surface layer and the use of suitable universal functions for the determination of the turbulent energy exchange. Bound.-Layer Meteorol. 1983, 25, 55–62. [Google Scholar] [CrossRef]
- Golder, D. Relations among stability parameters in the surface layer. Bound.-Layer Meteorol. 1972, 3, 47–58. [Google Scholar] [CrossRef]
- Dyer, A.; Hicks, B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.; De Bruin, H. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound.-Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Dias, N.; Gonçalves, J.; Freire, L.; Hasegawa, T.; Malheiros, A. Obtaining potential virtual temperature profiles, entrainment fluxes, and spectra from mini unmanned aerial vehicle data. Bound.-Layer Meteorol. 2012, 145, 93–111. [Google Scholar] [CrossRef]
- Liu, H.; Peters, G.; Foken, T. New equations for sonic temperature variance and buoyancy heat flux with an omnidirectional sonic anemometer. Bound.-Layer Meteorol. 2001, 100, 459–468. [Google Scholar] [CrossRef]
- Kaimal, J.; Gaynor, J. Another look at sonic thermometry. Bound.-Layer Meteorol. 1991, 56, 401–410. [Google Scholar] [CrossRef]
- Essa, K.S. Estimation of Monin–Obukhov length using Richardson and bulk Richardson number. In Proceedings of the Second Conference on Nuclear and Particle Physics (NUPPAC-99), Cairo, Egypt, 13–17 November 2000; Volume 711. [Google Scholar]
- Zoumakis, N.; Kelessis, A. On the theoretical relationship between the Monin–Obukhov stability parameter and the bulk Richardson number. Il Nuovo Cimento C 1993, 16, 1–7. [Google Scholar] [CrossRef]
- Peña, A.; Gryning, S.E.; Hasager, C.B. Measurements and Modelling of the Wind Speed Profile in the Marine Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2008, 129, 479–495. [Google Scholar] [CrossRef]
- Peña, A.; Hahmann, A.N. Atmospheric stability and turbulence fluxes at Horns Rev—An intercomparison of sonic, bulk and WRF model data. Wind Energy 2012, 15, 717–731. [Google Scholar] [CrossRef]
- DeMarrais, G.A. Wind-speed profiles at Brookhaven National Laboratory. J. Meteorol. 1959, 16, 181–190. [Google Scholar] [CrossRef] [Green Version]
- Heald, R.; Mahrt, L. The dependence of boundary-layer shear on diurnal variation of stability. J. Appl. Meteorol. 1981, 20, 859–867. [Google Scholar] [CrossRef] [Green Version]
- Sutton, O. The problem of diffusion in the lower atmosphere. Q. J. R. Meteorol. Soc. 1947, 73, 257–281. [Google Scholar] [CrossRef]
- Touma, J.S. Dependence of the wind profile power law on stability for various locations. J. Air Pollut. Control Assoc. 1977, 27, 863–866. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: New York, NY, USA, 2012; Volume 13. [Google Scholar]
- Gryning, S.E.; Batchvarova, E.; Brümmer, B.; Jørgensen, H.; Larsen, S. On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer. Bound.-Layer Meteorol. 2007, 124, 251–268. [Google Scholar] [CrossRef]
- Burns, S.; Horst, T.; Jacobsen, L.; Blanken, P.; Monson, R. Using sonic anemometer temperature to measure sensible heat flux in strong winds. Atmos. Meas. Tech. 2012, 5, 2095–2111. [Google Scholar] [CrossRef] [Green Version]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Deardorff, J.W. Dependence of air-sea transfer coefficients on bulk stability. J. Geophys. Res. 1968, 73, 2549–2557. [Google Scholar] [CrossRef]
- Grachev, A.; Fairall, C. Dependence of the Monin–Obukhov stability parameter on the bulk Richardson number over the ocean. J. Appl. Meteorol. 1997, 36, 406–414. [Google Scholar] [CrossRef]
- Holtslag, M.; Bierbooms, W.; Van Bussel, G. Estimating atmospheric stability from observations and correcting wind shear models accordingly. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 555, p. 012052. [Google Scholar]
- Panofsky, H.; Blackadar, A.; McVehil, G. The diabatic wind profile. Q. J. R. Meteorol. Soc. 1960, 86, 390–398. [Google Scholar] [CrossRef]
- Irwin, J.S. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Essa, K.S.; Embaby, M.; Etman, S.M. A notional variation of the wind profile power-law exponent as a function of surface roughness and stability. In Proceedings of the 4th Conference on Nuclear and Particle Physics, Guildford, UK, 29–30 March 2004. [Google Scholar]
- Van den Berg, G. Wind turbine power and sound in relation to atmospheric stability. Wind Energy 2008, 11, 151–169. [Google Scholar] [CrossRef]
- Walter, K.; Weiss, C.C.; Swift, A.H.; Chapman, J.; Kelley, N.D. Speed and direction shear in the stable nocturnal boundary layer. J. Sol. Energy Eng. 2009, 131, 011013. [Google Scholar] [CrossRef]
- Wharton, S.; Lundquist, J.K. Assessing atmospheric stability and its impacts on rotor-disk wind characteristics at an onshore wind farm. Wind Energy 2012, 15, 525–546. [Google Scholar] [CrossRef]


| Height | Channel | Sensor | Unit |
|---|---|---|---|
| 101.0 m | Thies First, Class Adv. Anemometer | m/s | |
| 99.0 m | |||
| 76.0 m | |||
| 30.0 m | |||
| 52.0 m | , , | Gill WindMaster 3D Anemometer | m/s, C |
| 10.0 m | , , | ||
| 98.0 m | Thies First, Class Wind Vane | ||
| 74.0 m | |||
| 28.0 m | |||
| 90.0 m | Galtec KPC 1.S/6-ME | %, C | |
| 35.0 m | |||
| 3.0 m | |||
| 90.0 m | Thies 3.1157.10.000 Pressure | hPa | |
| 2.0 m | |||
| 2 m | - | Ammonit Meteo40 Data Logger | - |
| Pasquill Class | Name | Shear Exponent Range | Shear Exponent Value |
|---|---|---|---|
| A–C | (Very-Slightly) Unstable | m ≤ 0.1 | 0.07–0.1 |
| D | (Near) Neutral | 0.1 < m ≤ 0.2 | 0.15 |
| E | Slightly Stable | 0.2 < m ≤ 0.4 | 0.35 |
| F | (Moderately-very) Stable | 0.4 ≤ m | 0.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuna, F.; Bingöl, F. Comparison of Length Scale Parameterization Methodologies. Energies 2020, 13, 89. https://doi.org/10.3390/en13010089
Tuna F, Bingöl F. Comparison of Length Scale Parameterization Methodologies. Energies. 2020; 13(1):89. https://doi.org/10.3390/en13010089
Chicago/Turabian StyleTuna, Faruk, and Ferhat Bingöl. 2020. "Comparison of Length Scale Parameterization Methodologies" Energies 13, no. 1: 89. https://doi.org/10.3390/en13010089
APA StyleTuna, F., & Bingöl, F. (2020). Comparison of Length Scale Parameterization Methodologies. Energies, 13(1), 89. https://doi.org/10.3390/en13010089





