Thermal Transport in Nonlinear Unsteady Colloidal Model by Considering the Carbon Nanomaterials Length and Radius
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Formulation
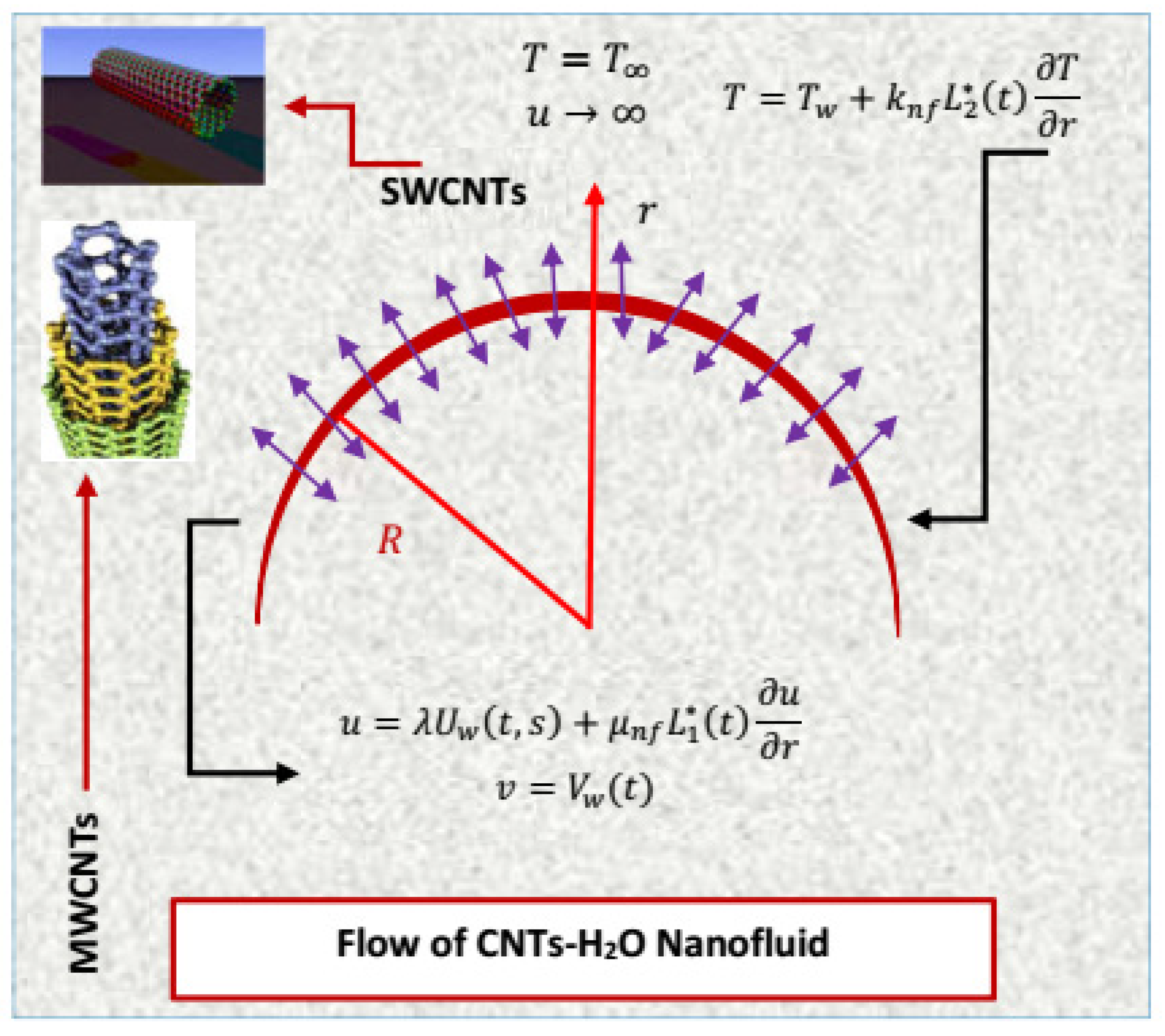
2.1.1. Statement and Geometry of the Model
2.1.2. Governing Model and Similarity Transformations
2.1.3. Effective Nanofluid Models
2.1.4. Nondimensional Nanofluid Model
2.1.5. Significant Quantities from Engineering Aspects
2.2. Mathematical Analysis
3. Physical Interpretation of the Results
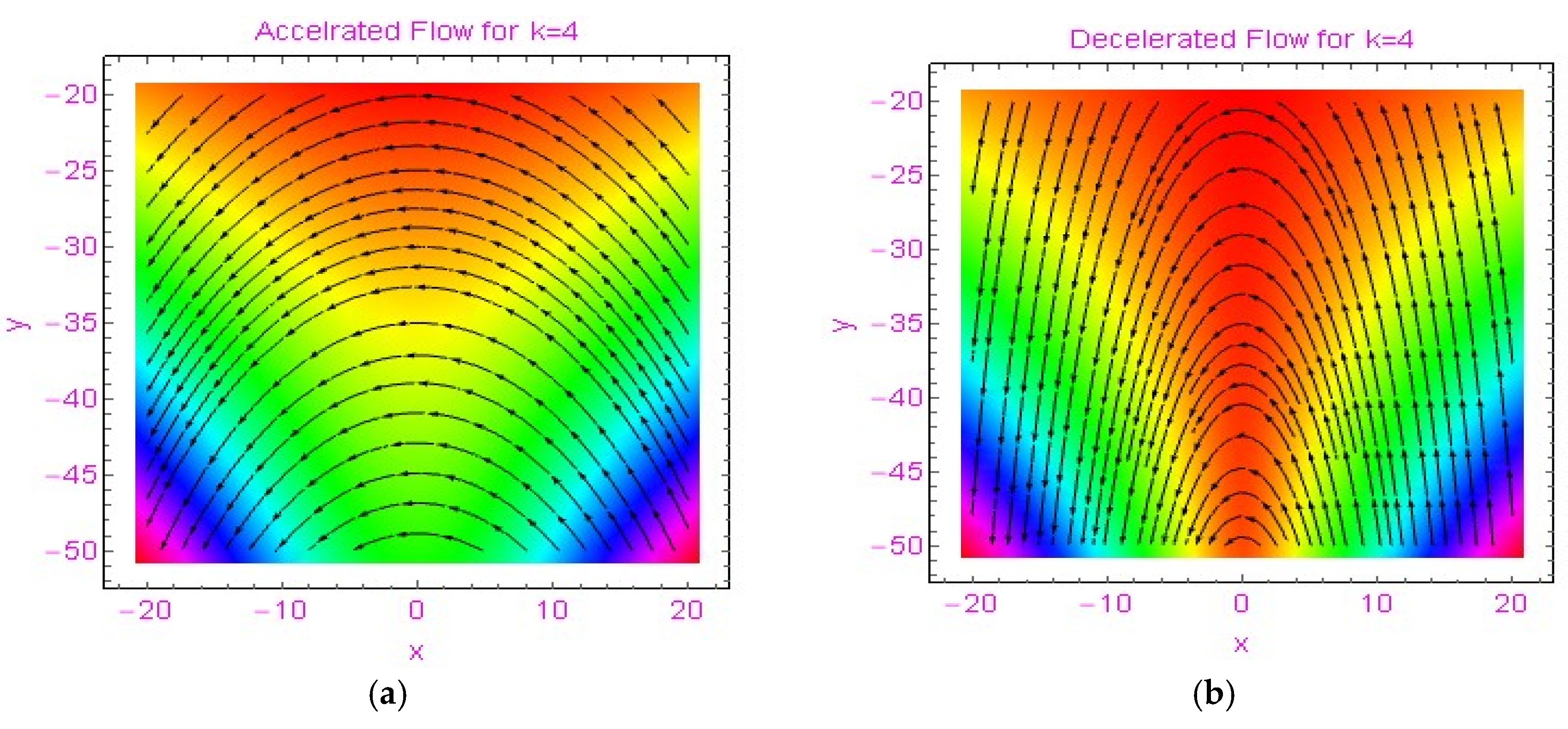
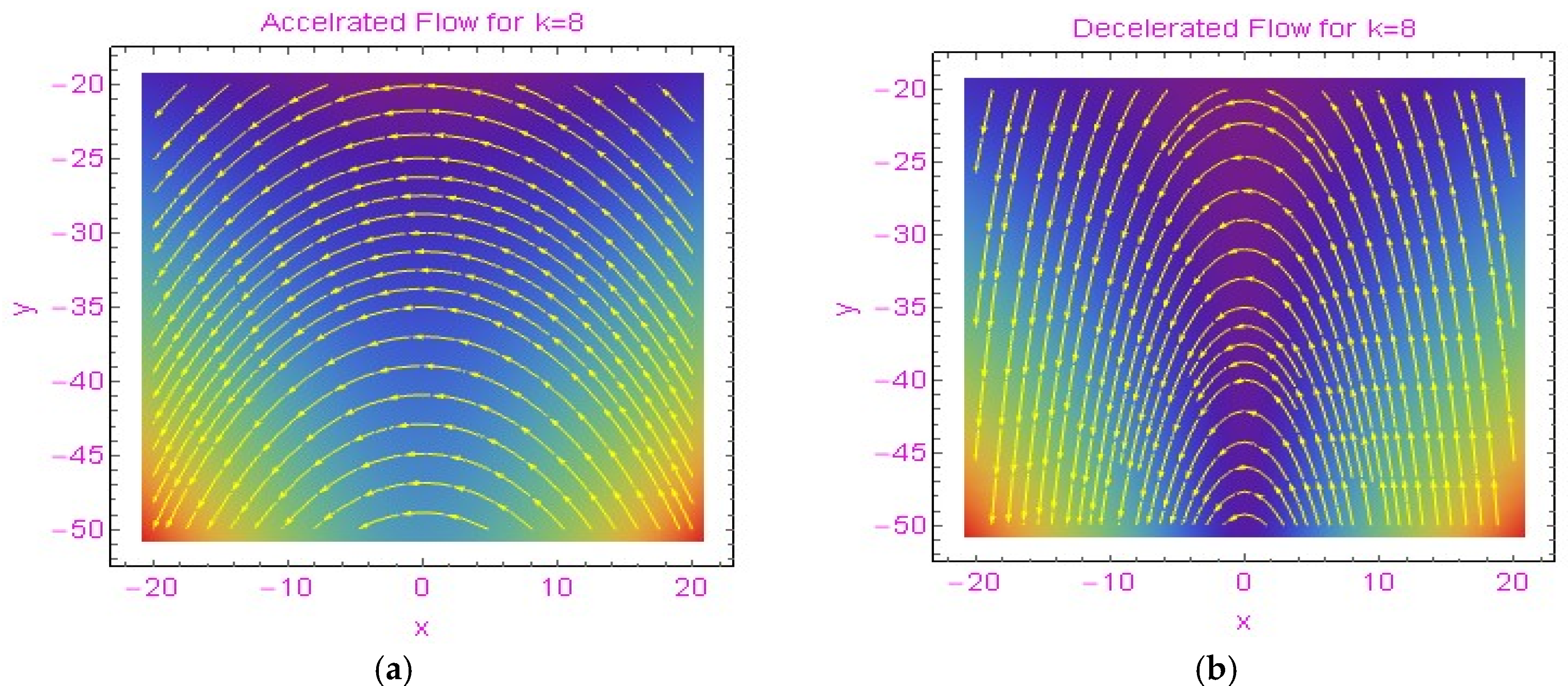
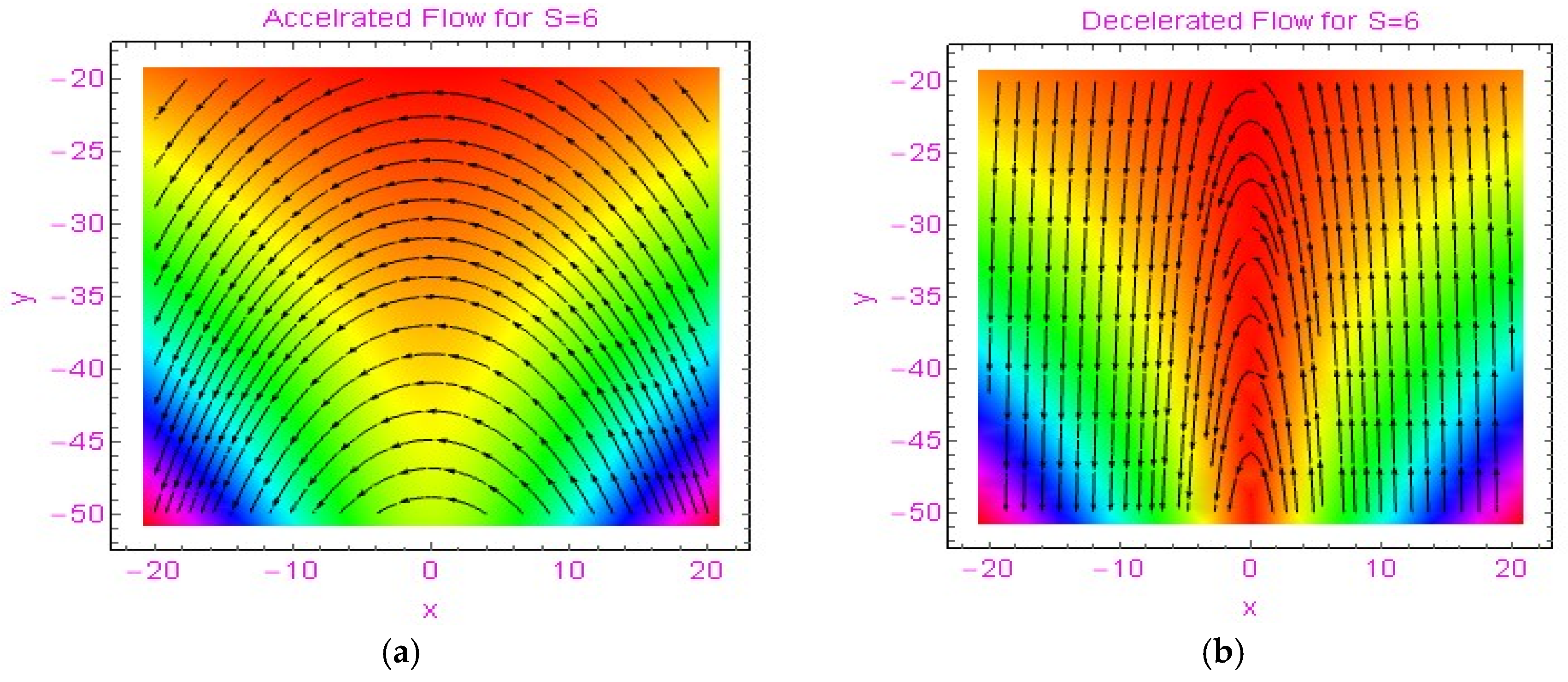
3.1. The Velocity Distribution
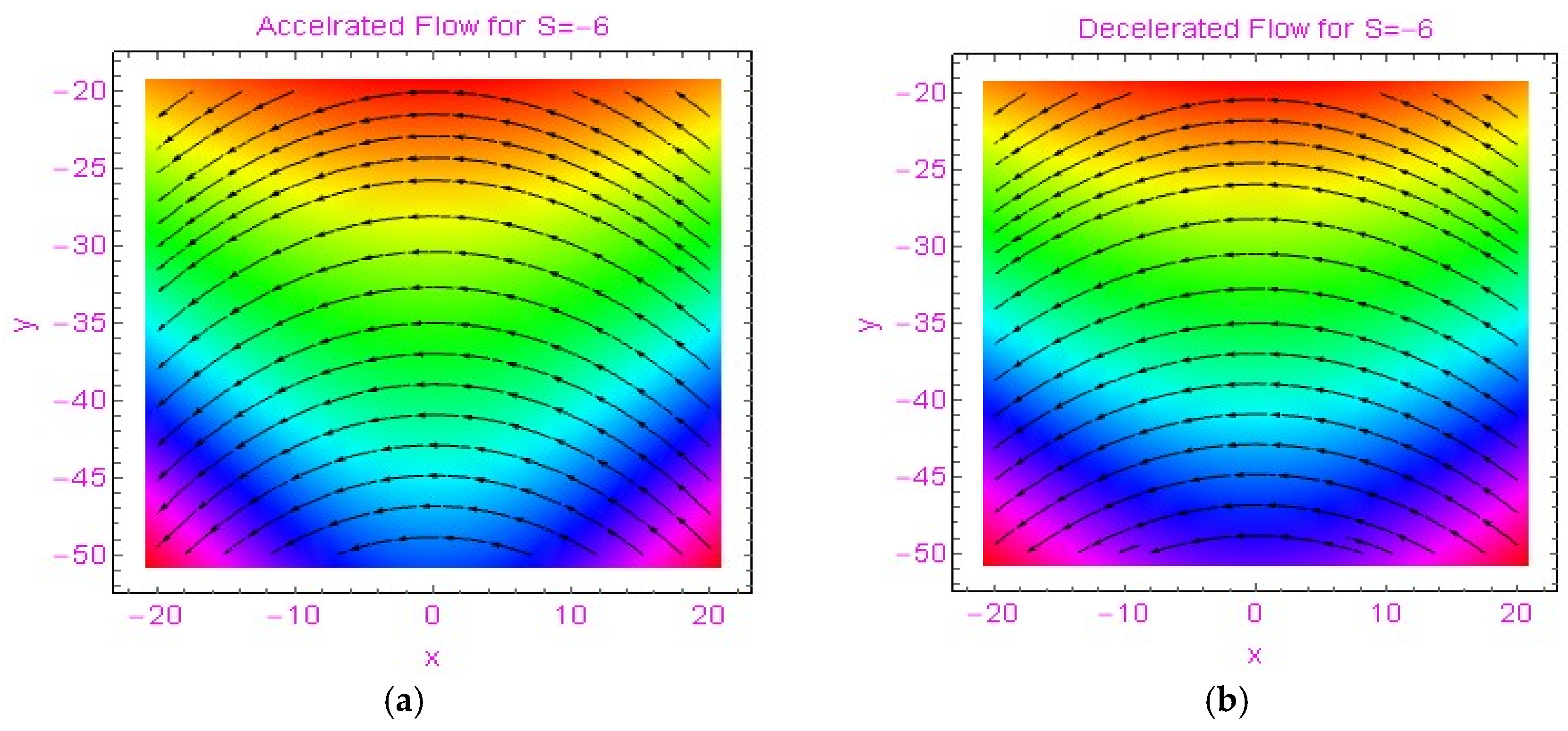
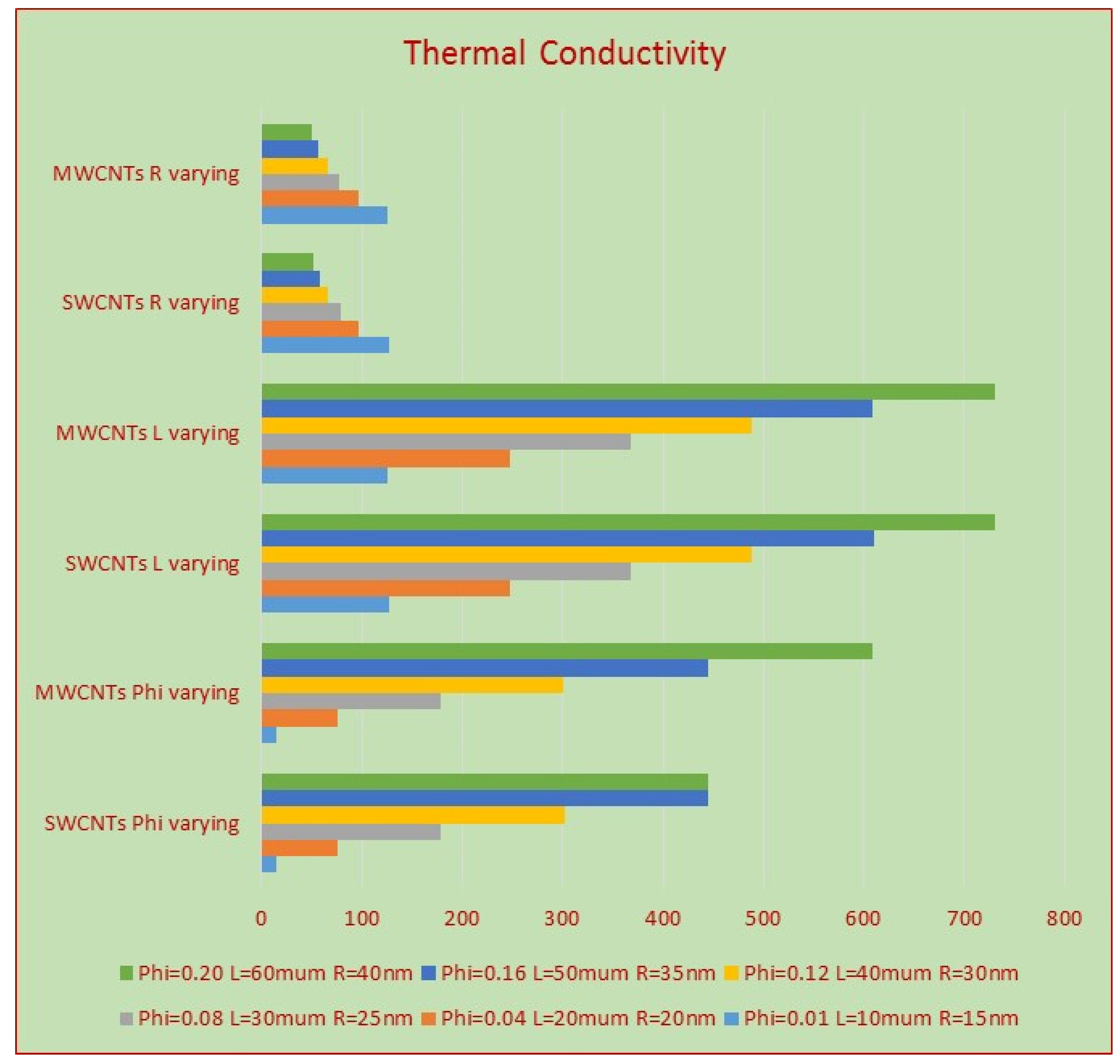
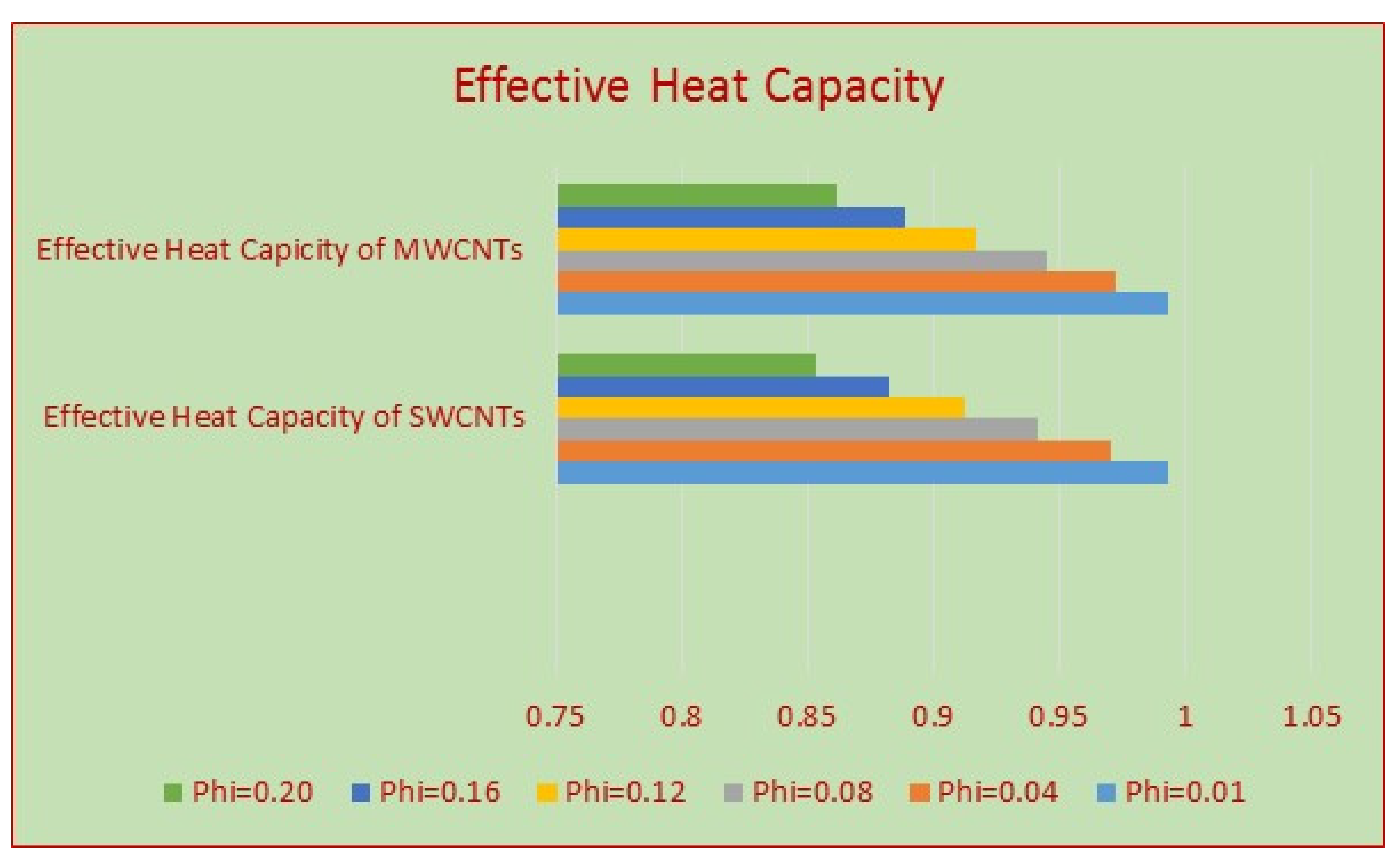
3.2. Streamlines and Thermophysical Characteristics
3.3. Local Heat Transfer Rate and Skin Friction
4. Conclusions
- The stretching of the surface provides more flowing area, due to which the nanofluid particles scattered at the surface and, consequently, the velocity of the nanofluids declines over the surface.
- The nanofluids flow abruptly over a shrinking surface and asymptotically vanish apart from the surface.
- The greater heat transfer rate at the surface is perceived for the suction and stretching/shrinking parameters.
- The decreasing trends in the shear stresses over the curved surface are examined for larger curvature, whereas they increase for the stretching/shrinking and suction parameters.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| L | length of carbon nanotubes |
| d | diameter of carbon nanotubes |
| CNT | carbon nanotubes |
| CuO | copper oxide |
| SWCNTs | single walled carbon nanotubes |
| MWCNTs | multi walls carbon nanotubes |
| ODEs | ordinary differential equations |
| RK | Runge–Kutta scheme |
References
- Maxwell, J.C.A. Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1881. [Google Scholar]
- Choi, S. Enhancing Thermal Conductivity of Fluids with Nanoparticles in Developments and Applications of Non-Newtonians Flows. ASME 1995, 66, 99–105. [Google Scholar]
- Hamilton, H.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer konstanten von heterogenen substanzen, I—Dielektrizitatskonstanten und leitfahigkeiten der mischkorper aus isotropen substanzen. Ann. Phys. Leipz. 1935, 24, 636–679. [Google Scholar] [CrossRef]
- Wasp, E.J.; Kenny, J.P.; Gandhi, R.L. Solid–liquid flow slurry pipeline transportation. Trans Tech. Publ. 1977, 4. Available online: https://books.google.com.pk/books/about/Solid_liquid_flow_slurry_pipeline_transp.html?id=zO1SAAAAMAAJ&redir_esc=y. (accessed on 10 May 2020).
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanopart. Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in micro-heat sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Li, C.H.; Peterson, G.P. Experimental investigation of temperature and volume fraction variations on the effective thermal conductivity of nanoparticle suspensions (nanofluids). J. Appl. Phys. 2006, 99, 084314. [Google Scholar] [CrossRef]
- Patel, H.E.; Sundararajan, T.; Das, S.K. An experimental investigation into the thermal conductivity enhancement in oxide and metallic nanofluids. J. Nanopart. Res. 2010, 12, 1015–1031. [Google Scholar] [CrossRef]
- Godson, R.L.; Mohan, L.B.; Wongwises, D.S. Experimental investigation on the thermal conductivity and viscosity of silver—Deionized water nanofluid. Exp. Heat Transf. 2010, 23, 317–332. [Google Scholar] [CrossRef]
- Corcione, M. Rayleigh–Bénard convection heat transfer in nanoparticle suspensions. Int. J. Heat Fluid Flow 2011, 32, 65–77. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Li, Z.; Shamlooei, M. Nanofluid MHD natural convection through a porous complex shaped cavity considering thermal radiation. Phys. Lett. A 2018, 382, 1615–1632. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zia, Q.M.Z.; Ellahi, R. Influence of Induced Magnetic Field on Free Convection of Nanofluid Considering Koo-Kleinstreuer-Li (KKL) Correlation. Appl. Sci. 2016, 6, 324. [Google Scholar] [CrossRef] [Green Version]
- Khan, U.; Adnan, A.N.; Mohyud-Din, S.T. 3D Squeezed Flow of γAl2O3-H2O and γAl2O3-C2H6O2 Nanofluids: A Numerical Study. Int. J. Hydrogen Energy 2017, 42, 24620–24633. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan, K.U.; Mohyud-Din, S.T. Influence of an Effective Prandtl number Model on Squeezed Flow of γAl2O3-H2O and γAl2O3-C2H6O2 Nanofluids. J. Mol. Liq. 2017, 238, 447–454. [Google Scholar] [CrossRef]
- Adnan, A.M.; Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Analytical and Numerical Investigation of Thermal Radiation effects on Flow of viscous Incompressible fluid with Stretchable Convergent/divergent Channels. J. Mol. Liq. 2016, 224, 768–775. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Yamada, E.; Ota, T. Effective Thermal conductivity of dispersed materials. Heat Mass Transf. 1980, 13, 27–37. [Google Scholar] [CrossRef]
- Xue, Q.Z. Model for Thermal conductivity of carbon nanotubes-based composites. Phys. Condens. Matter 2005, 17, 1655–1660. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, A.U.; Hussain, S.T. Model based study of SWCNT and MWCNT thermal conductivities effect on the heat transfer due to the oscillating wall conditions. Int. J. Hydrogen Energy 2017, 42, 28945–28957. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan, K.U.; Mohyud-Din, S.T. Influence of Thermal Radiation and viscous dissipation on squeezed flow of water between two Riga plates saturated with carbon nanotubes. Colloids Surf. A 2017, 522, 389–398. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Heat transfer effects on carbon nanotubes suspended nanofluid flow in a channel with non-parallel walls under the effect of velocity slip boundary condition: A numerical study. Neural Comput. Appl. 2017, 28, 37–46. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Hussain, S.; Khan, U.; Mohyud-Din, S.T.; Darus, M. Thermal Analysis of Nanofluid Flow over a Curved Stretching Surface Suspended by Carbon Nanotubes with Internal Heat Generation. Appl. Sci. 2018, 8, 395. [Google Scholar] [CrossRef] [Green Version]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Dual solutions for nanofluid flow past a curved surface with nonlinear radiation, Soret and Dufour effects. J. Phys. 2018, 1000, 012152. [Google Scholar] [CrossRef] [Green Version]
- Saleh, S.H.M.; Arifin, N.M.; Nazar, R.; Pop, I. Unsteady Micropolar Fluid over a Permeable Curved Stretching Shrinking Surface. Math. Probl. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Wang, C.Y. The three-dimensional flow due to a stretching flat surface. Phys. Fluids 1984, 27, 1915–1917. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid flow due to a stretching cylinder. Phys. Fluids 1988, 31, 466–468. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Nadeem, U.S.; Adnan, K.U. Stability analysis of Cu-H2O nanofluid over a curved stretching/shrinking sheet: Existence of dual solutions. Can. J. Phys. 2018, 97, 911–922. [Google Scholar] [CrossRef]
- Ahmed, N.; Khan, A.U.; Mohyud-Din, S.T. Unsteady Radiative Flow of Chemically reacting Fluid over a Convectively Heated Stretchable Surface with Cross-Diffusion Gradients. Int. J. Therm. Sci. 2017, 121, 182–191. [Google Scholar] [CrossRef]





| Properties | ||||
|---|---|---|---|---|
| SWCNTs | 2600 | 425 | 6600 | -------- |
| MWCNTs | 1600 | 796 | 3000 | -------- |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohyud-Din, S.T.; Adnan; Abdeljawad, T.; Khan, U.; Ahmed, N.; Khan, I. Thermal Transport in Nonlinear Unsteady Colloidal Model by Considering the Carbon Nanomaterials Length and Radius. Energies 2020, 13, 2448. https://doi.org/10.3390/en13102448
Mohyud-Din ST, Adnan, Abdeljawad T, Khan U, Ahmed N, Khan I. Thermal Transport in Nonlinear Unsteady Colloidal Model by Considering the Carbon Nanomaterials Length and Radius. Energies. 2020; 13(10):2448. https://doi.org/10.3390/en13102448
Chicago/Turabian StyleMohyud-Din, Syed Tauseef, Adnan, T. Abdeljawad, Umar Khan, Naveed Ahmed, and Ilyas Khan. 2020. "Thermal Transport in Nonlinear Unsteady Colloidal Model by Considering the Carbon Nanomaterials Length and Radius" Energies 13, no. 10: 2448. https://doi.org/10.3390/en13102448
APA StyleMohyud-Din, S. T., Adnan, Abdeljawad, T., Khan, U., Ahmed, N., & Khan, I. (2020). Thermal Transport in Nonlinear Unsteady Colloidal Model by Considering the Carbon Nanomaterials Length and Radius. Energies, 13(10), 2448. https://doi.org/10.3390/en13102448





