Multiobjective Approach for Medium- and Low-Voltage Planning of Power Distribution Systems Considering Renewable Energy and Robustness
Abstract
:1. Introduction
2. Scenario Generation Methodology
3. Robust Planning Indices
4. Problem Formulation
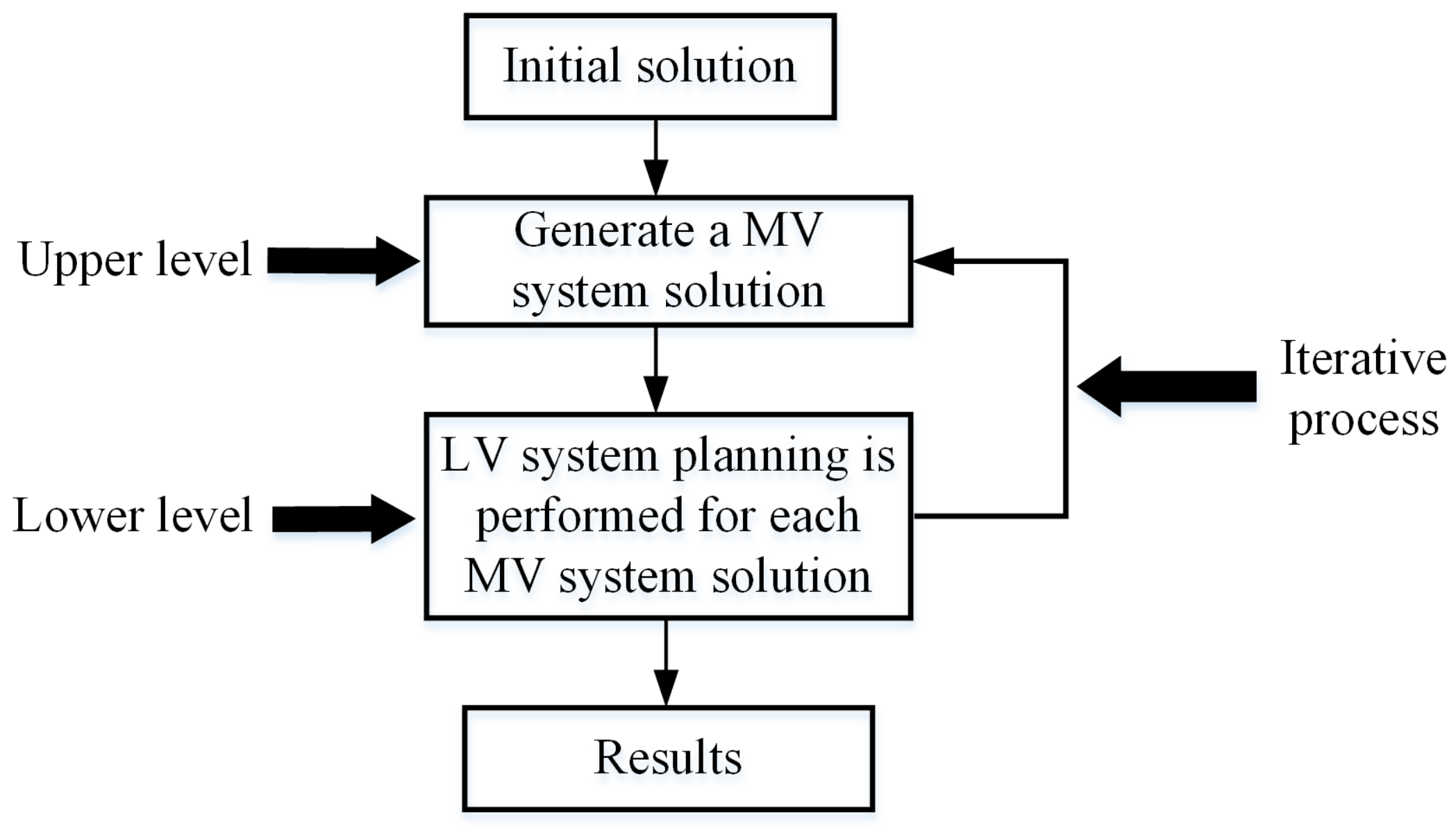
5. Solution Technique
5.1. Codification
5.2. Initial Solution
| Algorithm 1: Initial solution of the MV/LV system. |
|
5.3. Decomposition Search Applied to the MV/LV Planning
| Algorithm 2: MV/LV system planning methodology. |
|
5.4. Heuristic for Meshed Networks
| Algorithm 3: Heuristic for meshed networks. |
|
5.5. Solution Evaluation
6. Tests and Results
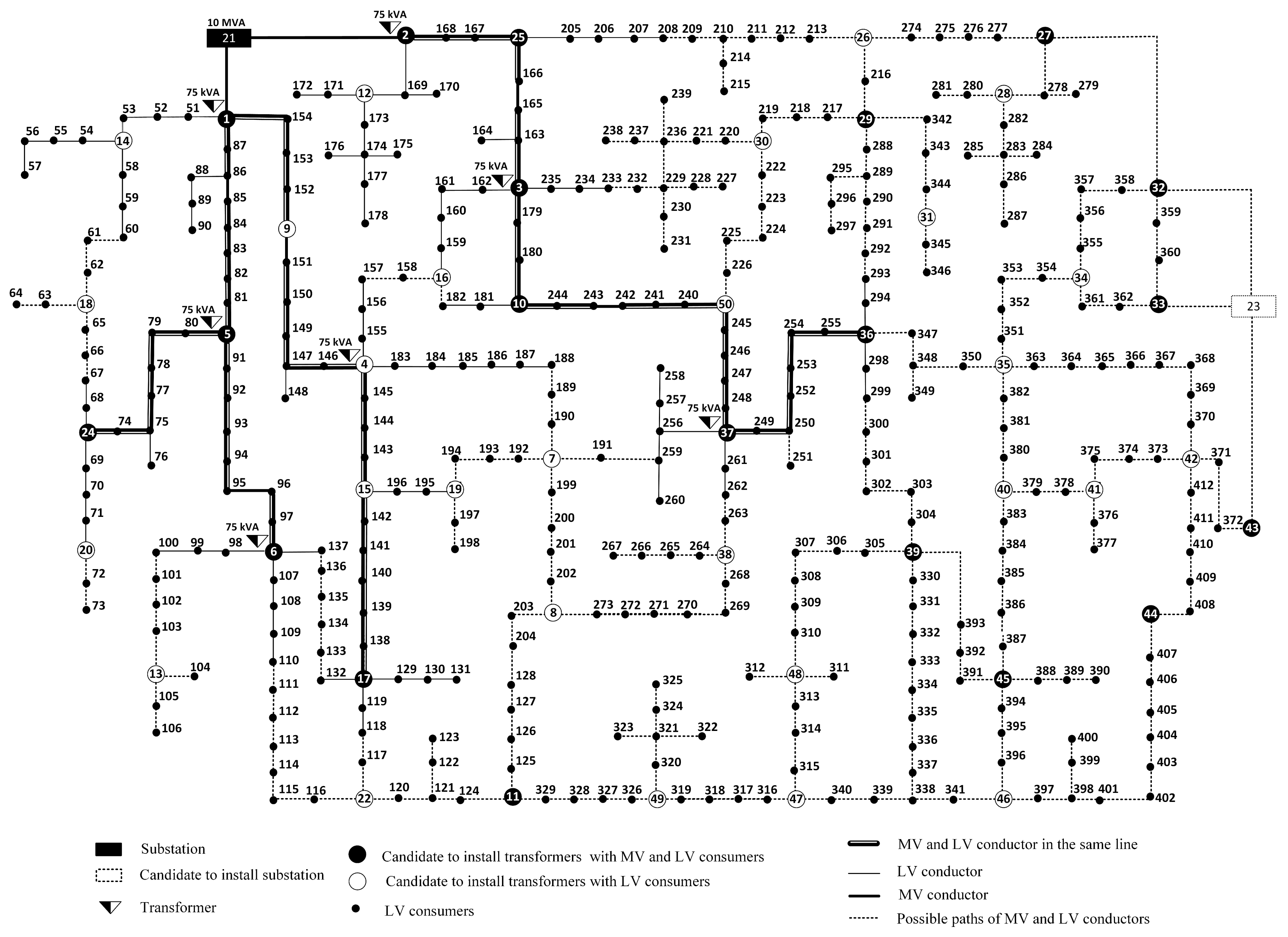
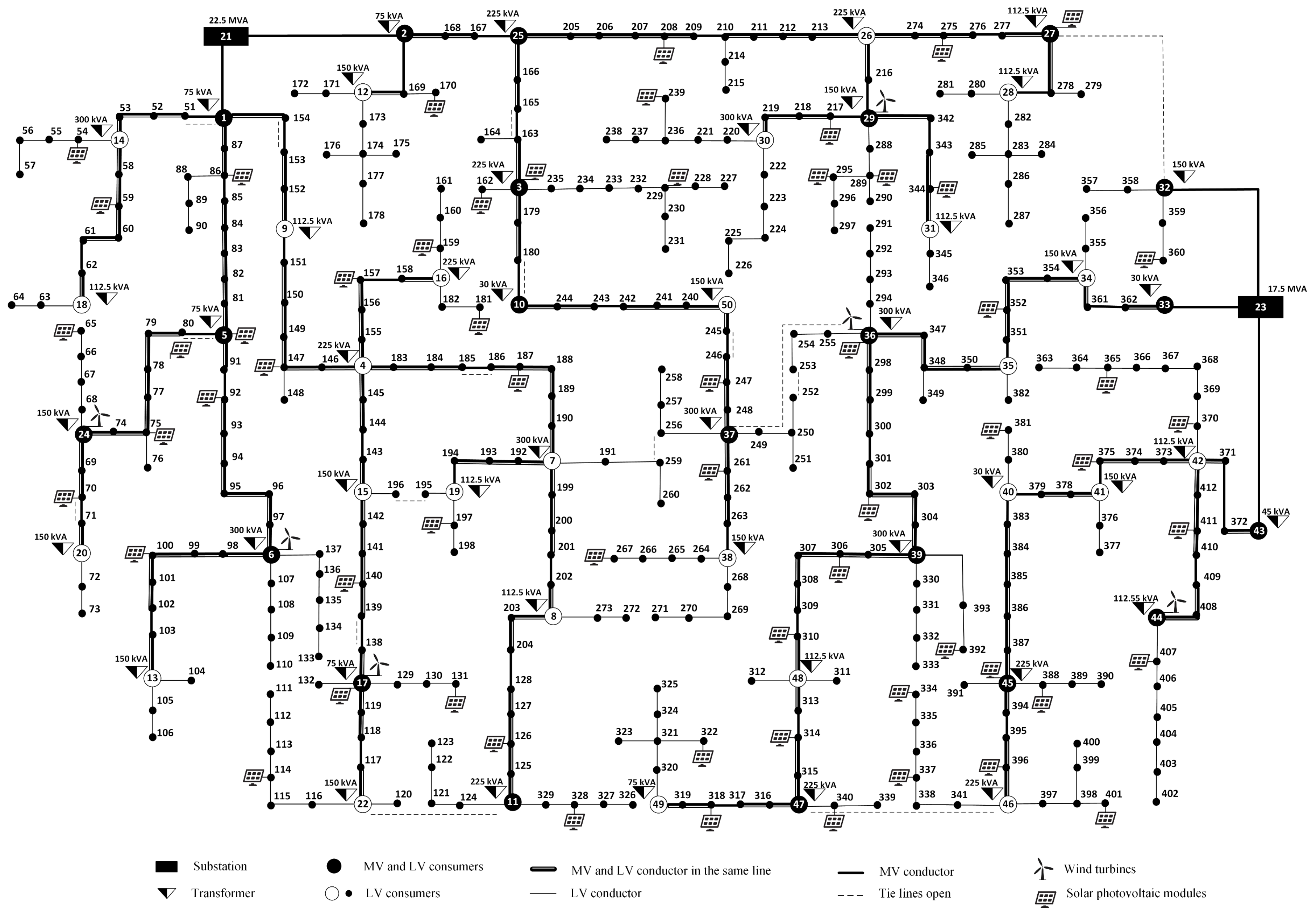
6.1. System Data
6.2. Numerical Results
6.2.1. MV/LV Planning: Fixed Weight Factor
6.2.2. MV/LV Planning: Variable Weight Factor
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Sets | |
| , | set of conductor types of the MV and LV systems, respectively |
| set of renewable generation units | |
| , | set of existing and future lines of MV and LV systems, respectively |
| set of existing and future lines of the MV/LV system | |
| , | set of nodes of MV and LV systems, respectively |
| set of nodes of existing or proposed substations and transformers, respectively | |
| set of operating scenarios | |
| set of system phases a, b, and c | |
| set of substation and distribution transformer types, respectively | |
| set of transformer tap positions | |
| Parameters | |
| a | tap variation of distribution transformer |
| cost to change cables , where m is an MV cable and n is an LV cable, for cables , where p is an MV cable and q is an LV cable, in branch ($) | |
| cost of losses in scenario w, in year t ($/MWh) | |
| cost of substation and transformer k installed at bus i, respectively | |
| maximum financial resource for planning | |
| maximum current through line (A) | |
| annual interest rate (%) | |
| losses of iron and copper in substation k, respectively (MW) | |
| losses of iron and copper in transformer k, respectively (MW) | |
| number of years of the planning horizon | |
| active and reactive power demand at bus i in scenario w, in year t, respectively (MW, MVAr) | |
| maximum active power generation from DG at bus i (MW) | |
| maximum loading of substation and transformer k installed at bus i, respectively (MVA) | |
| duration of each operation block b in year t (h) | |
| duration of each operation scenario w in year t (h) | |
| power factor | |
| , | minimum and maximum voltage limits at bus i, respectively |
| nominal voltage at bus i | |
| robust index weight associated with the DG in operating scenario w in year t | |
| robust index weight associated with the voltages of MV and LV systems in operating scenario w, in year t, respectively | |
| robust index weight associated with the current through cables installed in MV and LV systems in operating scenario w, in year t, respectively | |
| robust index weight associated with substations and distribution transformers in operating scenario w, in year t, respectively | |
| impedance of distribution transformer k installed at bus i (%) | |
| discretisation interval of transformer tap | |
| weight factor associated with the objective function | |
| Variables | |
| , | binary decision variable that defines the operation of MV and LV cables of type k in branch , respectively |
| financial resource for planning | |
| current in phase f, through line in scenario w, in year t (A) | |
| , | currents at the MV and LV levels, in transformer i in scenario w, in year t, respectively (A) |
| magnetizing current of the MV/LV distribution transformer at node i in scenario w, in year t (A) | |
| power losses in the cables of MV and LV systems in year t, respectively (MW) | |
| power losses at substations and transformers in year t, respectively (MW) | |
| , | active and reactive power injections at bus i in scenario w, in year t, respectively (MW, MVAr) |
| , | active and reactive power generated at bus i in scenario w, in year t, respectively (MW, MVAr) |
| power demanded by substation i in scenario w, in year t (MVA) | |
| power demanded by transformer i in scenario w, in year t (MVA) | |
| , | power consumption in substation and transformer i in scenario w, in year t, respectively (MVA) |
| , | binary decision variable for the installation of substations and distribution transformer of type k at bus i, respectively |
| , | power supplied by substation and transformer i in operation scenario w, in year t, respectively (MVA) |
| V | voltage in the node |
| , | voltage magnitude in phase f, at nodes i and j in scenario w, in year t, respectively (V) |
| , | input voltage magnitude of the MV system and output of the LV system in transformer i in scenario w, in year t, respectively (V) |
| nodal phase angle |
Appendix A
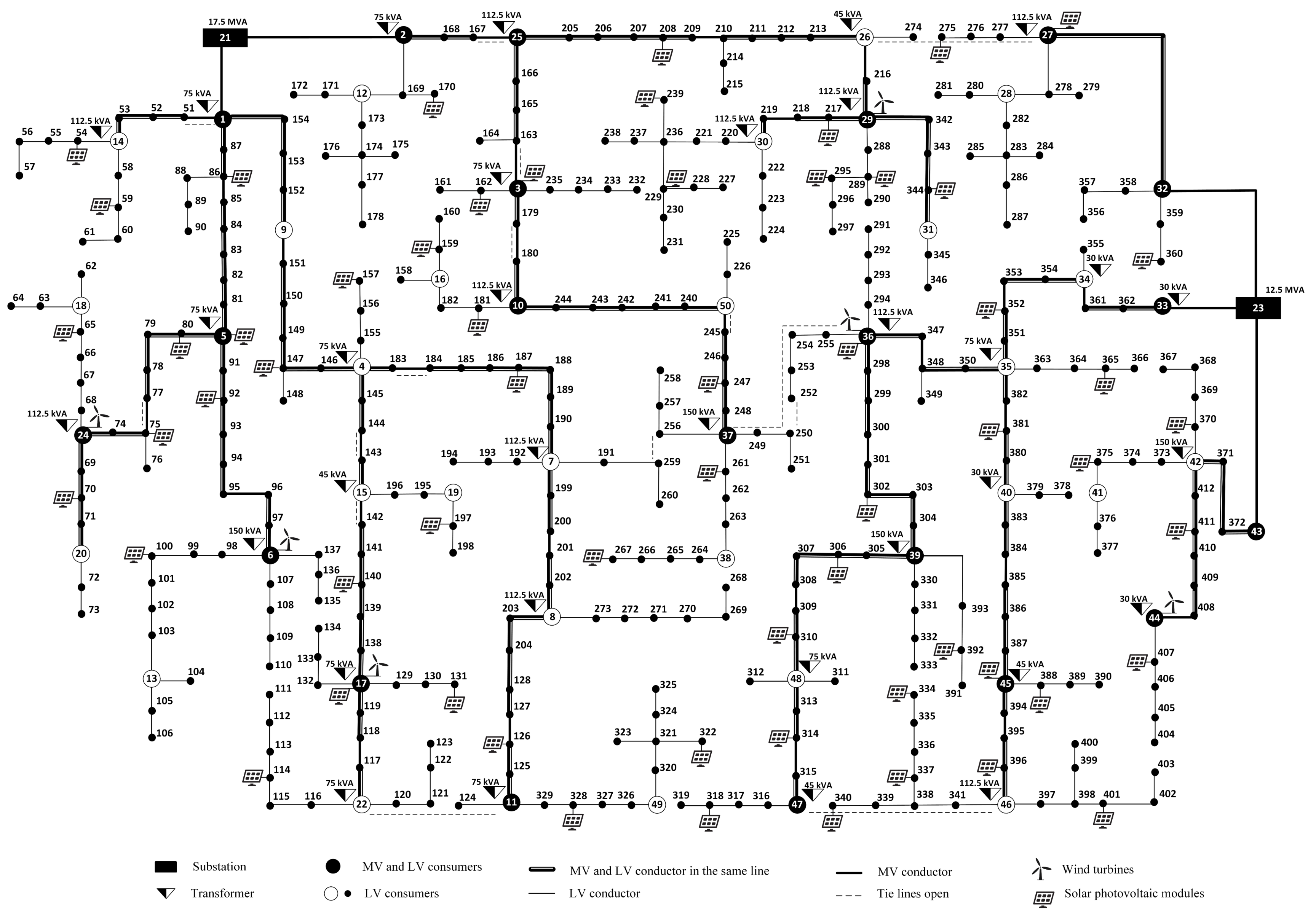
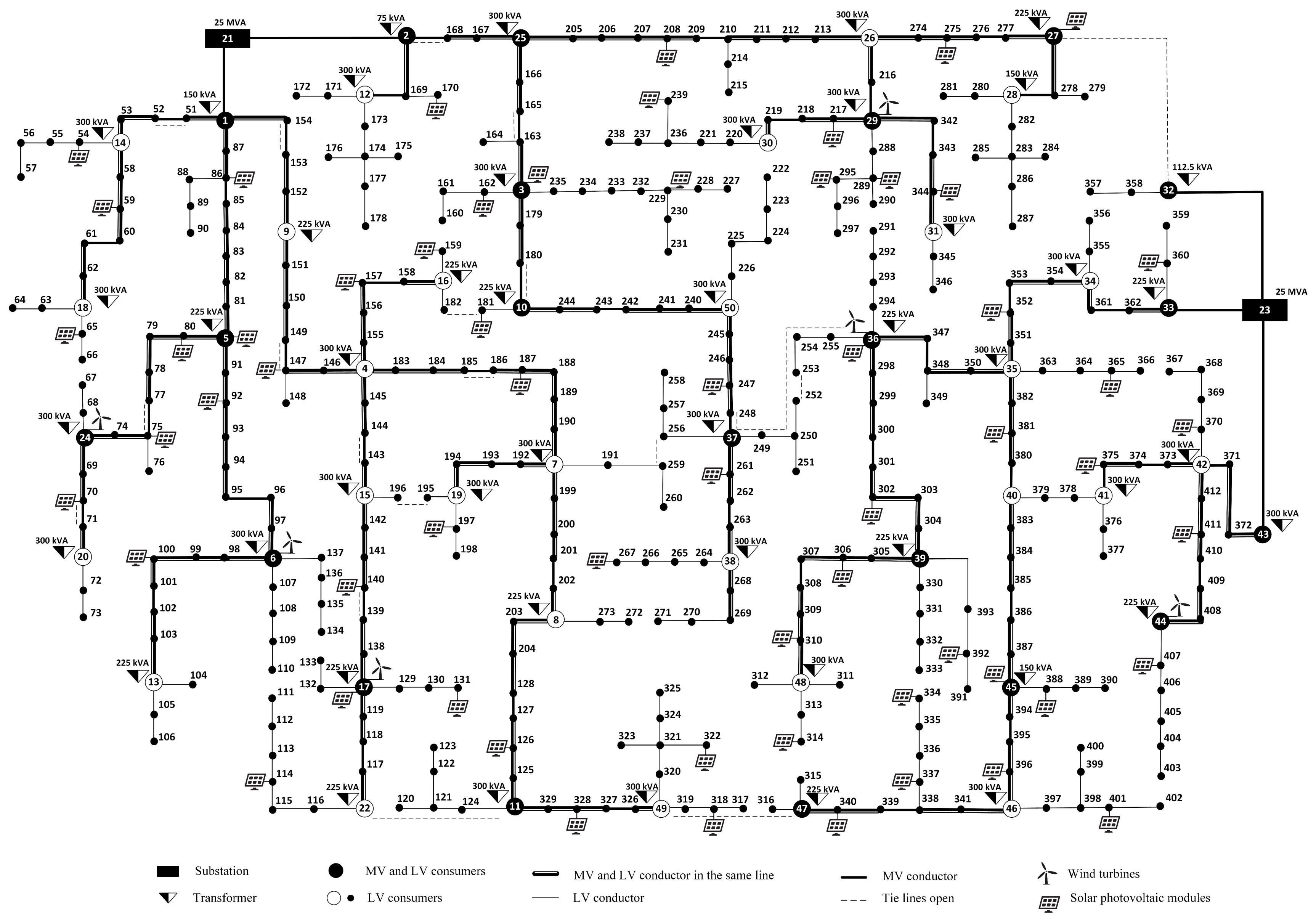
References
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- El-Khattam, W.; Bhattacharya, K.; Hegazy, Y.; Salama, M.M.A. Optimal investment planning for distributed generation in a competitive electricity market. IEEE Trans. Power Syst. 2004, 19, 1674–1684. [Google Scholar] [CrossRef]
- Singh, R.K.; Goswami, S.K. Optimum allocation of distributed generations based on nodal pricing for profit, loss reduction, and voltage improvement including voltage rise issue. Int. J. Electr. Power Energy Syst. 2010, 32, 637–644. [Google Scholar] [CrossRef]
- Muñoz-Delgado, G.; Contreras, J.; Arroyo, J.M. Multistage Generation and Network Expansion Planning in Distribution Systems Considering Uncertainty and Reliability. IEEE Trans. Power Syst. 2016, 31, 3715–3728. [Google Scholar] [CrossRef]
- Montoya-Bueno, S.; Muñoz, J.I.; Contreras, J. A Stochastic Investment Model for Renewable Generation in Distribution Systems. IEEE Trans. Sustain. Energy 2015, 6, 1466–1474. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Gözel, T.; Hocaoglu, M.H. An analytical method for the sizing and siting of distributed generators in radial systems. Electr. Power Syst. Res. 2009, 79, 912–918. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R.C. Analytical Expressions for DG Allocation in Primary Distribution Networks. IEEE Trans. Energy Convers. 2010, 25, 814–820. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghoshal, S.; Ghosh, S. Optimal sizing and placement of distributed generation in a network system. Int. J. Electr. Power Energy Syst. 2010, 32, 849–856. [Google Scholar] [CrossRef]
- El-Zonkoly, A.M. Optimal placement of multi-distributed generation units including different load models using particle swarm optimisation. IET Gener. Transm. Distrib. 2011, 5, 760–771. [Google Scholar] [CrossRef]
- Borges, C.L.T.; Falcão, D.M. Optimal distributed generation allocation for reliability, losses, and voltage improvement. Int. J. Electr. Power Energy Syst. 2006, 28, 413–420. [Google Scholar] [CrossRef]
- Celli, G.; Ghiani, E.; Mocci, S.; Pilo, F. A multiobjective evolutionary algorithm for the sizing and siting of distributed generation. IEEE Trans. Power Syst. 2005, 20, 750–757. [Google Scholar] [CrossRef]
- Hedayati, H.; Nabaviniaki, S.A.; Akbarimajd, A. A Method for Placement of DG Units in Distribution Networks. IEEE Trans. Power Deliv. 2008, 23, 1620–1628. [Google Scholar] [CrossRef]
- Rau, N.S.; Wan, Y.-H. Optimum location of resources in distributed planning. IEEE Trans. Power Syst. 1994, 9, 2014–2020. [Google Scholar] [CrossRef]
- El-Khattam, W.; Hegazy, Y.G.; Salama, M.M.A. An integrated distributed generation optimization model for distribution system planning. IEEE Trans. Power Syst. 2005, 20, 1158–1165. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Z.Y.; Meng, K.; Yang, H.; Lai, M.; Wong, K.P. Multi-objective distributed wind generation planning in an unbalanced distribution system. CSEE J. Power Energy Syst. 2017, 3, 186–195. [Google Scholar] [CrossRef]
- Naderi, E.; Seifi, H.; Sepasian, M.S. A Dynamic Approach for Distribution System Planning Considering Distributed Generation. IEEE Trans. Power Deliv. 2012, 27, 1313–1322. [Google Scholar] [CrossRef]
- Khalesi, N.; Rezaei, N.; Haghifam, M. DG allocation with application of dynamic programming for loss reduction and reliability improvement. Int. J. Electr. Power Energy Syst. 2011, 33, 288–295. [Google Scholar] [CrossRef]
- Banerjee, B.; Islam, S.M. Reliability based optimum location of distributed generation. Int. J. Electr. Power Energy Syst. 2011, 33, 1470–1478. [Google Scholar] [CrossRef]
- Falaghi, H.; Singh, C.; Haghifam, M.; Ramezani, M. DG integrated multistage distribution system expansion planning. Int. J. Electr. Power Energy Syst. 2011, 33, 1489–1497. [Google Scholar] [CrossRef]
- Singh, D.; Singh, D.; Verma, K.S. Multiobjective Optimization for DG Planning with Load Models. IEEE Trans. Power Syst. 2009, 24, 427–436. [Google Scholar] [CrossRef]
- Placement of distributed generators and reclosers for distribution network security and reliability. Int. J. Electr. Power Energy Syst. 2005, 27, 398–408. [CrossRef]
- Keane, A.; O’Malley, M. Optimal allocation of embedded generation on distribution networks. IEEE Trans. Power Syst. 2005, 20, 1640–1646. [Google Scholar] [CrossRef]
- Alkaabi, S.S.; Zeineldin, H.H.; Khadkikar, V. Adaptive planning approach for customer DG installations in smart distribution networks. IET Renew. Power Gener. 2018, 12, 81–89. [Google Scholar] [CrossRef]
- Billinton, R.; Karki, R. Maintaining supply reliability of small isolated power systems using renewable energy. IEE Proc. Gener. Transm. Distrib. 2001, 148, 530–534. [Google Scholar] [CrossRef]
- Rupolo, D.; Pereira Junior, B.R.; Contreras, J.; Mantovani, J.R.S. Medium- and low-voltage planning of radial electric power distribution systems considering reliability. IET Gener. Transm. Distrib. 2017, 11, 2212–2221. [Google Scholar] [CrossRef]
- Yosef, M.; Sayed, M.M.; Youssef, H.K.M. Allocation and sizing of distribution transformers and feeders for optimal planning of MV/LV distribution networks using optimal integrated biogeography based optimization method. Electr. Power Syst. Res. 2015, 128, 100–112. [Google Scholar] [CrossRef]
- Paiva, P.C.; Khodr, H.M.; Dominguez-Navarro, J.A.; Yusta, J.M.; Urdaneta, A.J. Integral planning of primary-secondary distribution systems using mixed integer linear programming. IEEE Trans. Power Syst. 2005, 20, 1134–1143. [Google Scholar] [CrossRef]
- Fletcher, R.H.; Strunz, K. Optimal Distribution System Horizon Planning; Part I: Formulation. IEEE Trans. Power Syst. 2007, 22, 791–799. [Google Scholar] [CrossRef]
- Fletcher, R.H.; Strunz, K. Optimal Distribution System Horizon Planning; Part II: Application. IEEE Trans. Power Syst. 2007, 22, 862–870. [Google Scholar] [CrossRef]
- Amjady, N.; Attarha, A.; Dehghan, S.; Conejo, A.J. Adaptive Robust Expansion Planning for a Distribution Network with DERs. IEEE Trans. Power Syst. 2018, 33, 1698–1715. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.Y. Probability-Weighted Robust Optimization for Distributed Generation Planning in Microgrids. IEEE Trans. Power Syst. 2018, 33, 7042–7051. [Google Scholar] [CrossRef]
- Zare, A.; Chung, C.Y.; Zhan, J.; Faried, S.O. A Distributionally Robust Chance-Constrained MILP Model for Multistage Distribution System Planning with Uncertain Renewables and Loads. IEEE Trans. Power Syst. 2018, 33, 5248–5262. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. Robust Design of Microgrids with Reconfigurable Topology Under Severe Uncertainty. IEEE Trans. Sustain. Energy 2018, 9, 559–569. [Google Scholar] [CrossRef]
- Taylor, J.A. Convex Optimization of Power Systems; Cambridge University Press: Cambridge, UK, 2015; Volume 1. [Google Scholar]
- Delbem, A.C.B.; de Carvalho, A.; Policastro, C.A.; Pinto, A.K.O.; Honda, K.; Garcia, A.C. Node-Depth Encoding for Evolutionary Algorithms Applied to Network Design. In Genetic and Evolutionary Computation– GECCO 2004; Deb, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 678–687. [Google Scholar]
- Mladenovic, N.; Hansen, P. Variable Neighborhood Search; Kluwer Academic Publishers: Berlin, Germany, 2003; Volume 1, pp. 145–184. [Google Scholar]
- Cheng, C.S.; Shirmohammadi, D. A three-phase power flow method for real-time distribution system analysis. IEEE Trans. Power Syst. 1995, 10, 671–679. [Google Scholar] [CrossRef]
- MV/LV Test System. Available online: https://drive.google.com/open?id=1Tba34jHNUk1S7MY4EFaHBsM1sli9lJ9j (accessed on 16 October 2019).


| Block | Fd | Fws | Fsi | (h) |
|---|---|---|---|---|
| 1 | 0.802 | 0.459 | 0.147 | 350 |
| 0.681 | 0.210 | 0.000 | ||
| 2 | 0.569 | 0.446 | 0.476 | 2650 |
| 0.480 | 0.209 | 0.012 | ||
| 3 | 0.416 | 0.456 | 0.430 | 3900 |
| 0.365 | 0.190 | 0.012 | ||
| 4 | 0.319 | 0.471 | 0.041 | 1860 |
| 0.282 | 0.164 | 0.000 |
| Case I | Case II | Case III | |
|---|---|---|---|
| CS($) | 1500.00 | 1950.00 | 1500.00 |
| CT ($) | 67.68 | 133.53 | 60.08 |
| CF ($) | 424.61 | 498.53 | 374.93 |
| CL ($) | 117.39 | 120.58 | 83.99 |
| RPI | 143.68 | 957.70 | 68.13 |
| T (s) | 2.63 | 2.94 | 10.28 |
| Case IV | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (C) | (B) | (A) | |||||||
| CS ($) | 2700.00 | 2700.00 | 2550.00 | 2100.00 | 1800.00 | 1650.00 | 1500.00 | 1500.00 | 1500.00 |
| CT ($) | 188.06 | 179.68 | 163.67 | 139.94 | 119.28 | 91.78 | 83.94 | 72.49 | 64.42 |
| CF ($) | 767.46 | 724.38 | 711.12 | 586.18 | 468.44 | 437.70 | 421.76 | 401.33 | 408.11 |
| CL ($) | 115.75 | 115.13 | 108.89 | 99.47 | 104.21 | 98.65 | 91.11 | 92.40 | 90.41 |
| RPI | 1461.87 | 1455.99 | 1381.92 | 993.54 | 707.97 | 490.28 | 198.30 | 124.63 | 99.14 |
| T (s) | 9.78 | 10.32 | 9.29 | 10.56 | 11.9 | 12.6 | 8.81 | 9.39 | 9.84 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rupolo, D.; Pereira Junior, B.R.; Contreras, J.; Mantovani, J.R.S. Multiobjective Approach for Medium- and Low-Voltage Planning of Power Distribution Systems Considering Renewable Energy and Robustness. Energies 2020, 13, 2517. https://doi.org/10.3390/en13102517
Rupolo D, Pereira Junior BR, Contreras J, Mantovani JRS. Multiobjective Approach for Medium- and Low-Voltage Planning of Power Distribution Systems Considering Renewable Energy and Robustness. Energies. 2020; 13(10):2517. https://doi.org/10.3390/en13102517
Chicago/Turabian StyleRupolo, Diogo, Benvindo Rodrigues Pereira Junior, Javier Contreras, and José Roberto Sanches Mantovani. 2020. "Multiobjective Approach for Medium- and Low-Voltage Planning of Power Distribution Systems Considering Renewable Energy and Robustness" Energies 13, no. 10: 2517. https://doi.org/10.3390/en13102517
APA StyleRupolo, D., Pereira Junior, B. R., Contreras, J., & Mantovani, J. R. S. (2020). Multiobjective Approach for Medium- and Low-Voltage Planning of Power Distribution Systems Considering Renewable Energy and Robustness. Energies, 13(10), 2517. https://doi.org/10.3390/en13102517






