Abstract
In recent years, the Oil & Gas industry has been subjected to a progressive electrification process aiming to comply with global environmental requirements on CO2 emissions reduction. High-power electric motors fed by Variable Frequency Drives (VFDs) have replaced gas turbines as drivers for gas compression applications. In Liquefied Natural Gas (LNG) plants, unexpected downturns could be experienced in case of high torsional vibrations of power generations units. These torsional vibrations derive from the interaction among turbine-generator (TG) units and VFDs and are known as Sub-Synchronous Torsional Interactions (SSTIs). SSTIs can lead to instability when the overall electromechanical system lacks sufficient damping. In this scenario, electrical damping assessment is fundamental in order to ensure stability and reliable operation of an LNG plant. Negative electrical damping is strictly related to the negative incremental resistance behavior of the power converters and it is influenced by the converter’s control system. In this paper, a real case study based on Thyristor Variable Frequency Drives (TVFDs) is considered. Ad hoc dynamic models of the power converters and of the TG unit are developed and combined in order to provide an accurate estimation of the electrical damping. It is demonstrated that the electrical damping is affected by variations of the main control system parameters and how the use of a simplified model instead of an ad hoc model can impact the stability evaluation.
1. Introduction
The energy industry is today accelerating the transition to a low-carbon future to meet global environmental requirements. In this context, a more efficient operation of Oil & Gas plants is essential, and this cannot overlook a structured electrification process. With specific reference to the midstream segment, large electric motors fed by Variable Frequency Drives (VFDs) are thus more and more adopted in lieu of heavy-duty Gas Turbines (GTs) as drivers for gas compression applications, typically powered by local electrical grids. In this scenario, considering the power size of Liquefied Natural Gas (LNG) plants, Thyristor Variable Frequency Drives (TVFDs) are often adopted [1]. A preliminary study about the interactions among Turbine-Generator (TG) units and TVFDs in island-operated grids is presented in [2]. The aim is to identify proper plant operations without unexpected downturns due to excessive torsional vibrations of the power generation units. The torsional vibrations, derived from TG and TVFD interactions, are known as Sub-Synchronous Torsional Interactions (SSTIs) [3,4]. In LNG plants, the SSTI phenomena represent a challenge for the power system stability and could overcome the admissible fatigue life limits of TG shaft-lines.
Limited literature has been published about SSTI phenomena in LNG plants [5,6,7,8]. Differently, numerous studies can be found on SSTI for High Voltage Direct Current (HVDC) applications [9,10,11,12,13]. In this context, SSTI is categorized as the evolution of the Sub-Synchronous Resonance (SSR) phenomenon [14,15,16,17,18]. In [19,20,21], the plant torsional stability in the presence of SSR phenomena is assessed by means of eigenvalues and eigenvectors. Oscillatory stability is verified if all the torsional modes have positive damping.
In [3,22], it is demonstrated how power converters can modify the damping of TG units modes. The analysis is provided in the case of a stiff network, but it has to be highlighted that LNG plants are typically island-operated grids where large TVFDs are fed by a few TG units. In [23], a similar analysis is provided for an island-operated grid.
VFDs can operate in various frequency regions as electrical circuits with negative resistance. Depending on the control system, this operation can be verified in the region corresponding to the TG sub-synchronous frequencies. Negative resistance implies negative electrical damping, but the electrical damping contributes to the overall damping of the combined electromechanical system. If negative electrical damping is measured around the TG torsional natural frequencies (TNFs), instability can be verified [3,24].
Commonly in the LNG industry, accurate models of the power converters are generally not included in the overall plant stability analysis. The power conversion stage is taken into account through an average model where only the passive components of the circuits are considered, as in [13,25]. On the contrary, independent of the specific application, small-signal analysis allows us to achieve dynamic models of the power system for fair stability assessment in the case of weak grids [26,27]. In this paper, an ad-hoc state-space dynamic model of a combined electromechanical system is developed. A TG shaft-line lumped parameter model is obtained using the modal analysis theory described in [28,29] in order to identify the Torsional Natural Frequencies (TNFs) and the mechanical damping relative to these frequencies. Small-signal analysis is used to determine a detailed dynamic state-space model of the TVFD and of the electrical generator with the aim to provide an accurate evaluation of the electrical damping of an LNG plant. The dynamic state-space model of the TVFD reproduces exactly the real operation of the power conversion stage in the time domain and the power electronics devices commutation.
Comparing the dynamic state-space model with a simplified average mode, it is possible to demonstrate that the use of a simplified model of the TVFD leads to underrate the current oscillations due to the SSTI phenomena and, as a consequence, it could impact the stability assessment.
The rest of the paper is organized as follows: in Section 2 the considered case study is presented; in Section 3 the sub-synchronous torsional interaction phenomena are discussed; Section 4 deals with the dynamic state-space model of the TVFD, while Section 5 deals with the TG unit model; the combined electromechanical model is shown in Section 6, the electrical damping assessment and some stability considerations are presented in the same section; finally Section 7 concludes the paper with some remarks.
2. Case Study
VFDs for LNG applications can be based on thyristors or IGBTs. In the case of very high power plants, the power conversion stage is generally based on thyristors. Starting from a real industrial LNG plant, the considered case study is presented in Figure 1. Looking at the LNG plant, a gas turbine generator unit is connected to the Point of Common Coupling (PCC). The PCC is connected to a synchronous Motor (M) and to a lumped load. The synchronous motor is supplied by a TVFD. M is connected to a compression train and it acts as starter and helper motor, allowing the start-up of the entire train and providing additional power when required by the gas process. The compression train is composed of two Centrifugal Compressor (CCs) and a GT as in [1]. The TVFD shown in Figure 1 is composed of two Line-Commutated-Converters (LCCs). The LCCs are based on 6-pulse H-Bridges. The first stage of each LCC is a line-commutated-rectifier (LCR) operating at the grid frequency fn. The second stage of each LCC is a Load-Commutated-Inverter (LCI) whose fundamental frequency is the motor frequency fm. In the considered power stage, the firing angle of each LCR is controlled by a current control loop; differently it is assumed that the firing angles of the LCIs are constant. The main parameters of the TG unit and of the TVFD are reported in Table 1.
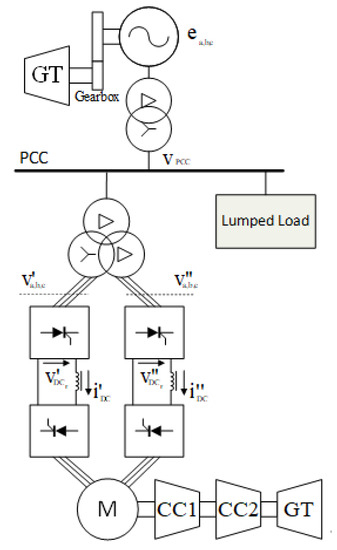
Figure 1.
Liquefied Natural Gas (LNG) plant configuration.

Table 1.
TG and TVFD parameters.
3. Sub-Synchronous Torsional Interaction Phenomena
TG units connected to a stiff electrical grid are typically unaffected by transient events acting on the grid (e.g., load steps or large motor start-up). Differently, in island-operated grids, an electrical disturbance might have enough energy to propagate through the grid, becoming a mechanical excitation for the turbine-generator shaft [4,5].
Figure 2 shows a simplified representation of the SSTI onset where current disturbances Δi are transformed into air gap torque disturbances ΔTAGT for the electrical TG. In the case of transient events, such as load variation or motor start-up, other disturbances (denoted as ΔTT) occur and their interaction with the air gap torque disturbances ΔTAGT creates the overall torque disturbances ΔT. Torque disturbances imply torsional speed oscillations Δω of the TG units. Finally, torsional oscillations provide voltage oscillations in the grid denoted as ΔvPCC. The VFD connected between the PCC of the grid and the Motor (M) transforms the voltage variations (at its input) in current variations Δi (at its output). The loop resulting from the described phenomena can be stable when the torsional vibrations on the TG unit naturally damp following the transient event. The loop can be unstable when such vibrations keep increasing over time with insufficient or negative damping [9,11].
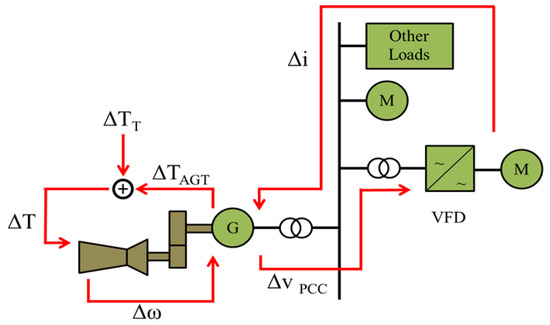
Figure 2.
Sub-Synchronous Torsional Interaction (SSTI) Phenomena Onset.
The overall damping of each TG unit supplying an island-operated grid is the sum of the shaft-line inherent mechanical damping plus the electrical damping resulting from the above-mentioned electro-mechanical loop [24]. Denoted as , the electrical damping at a certain Torsional Natural Frequency (TNF) fn, depends on the air gap torque oscillation at the same TNF () and the corresponding speed oscillation ():
The mechanical damping is passive, and it depends on the sole characteristic of the turbine-generator shaft line [28]. The mechanical damping is a positive number at all frequencies [28,29]. Differently, the electrical damping can be positive or negative and, in the last condition, it decreases the overall damping. Negative electrical damping is due to the negative incremental resistance behavior of the power converter’s impedance and it is influenced by the converter’s control structure [3]. Instability is achieved when the amplitude of the electrical damping is negative and its value is greater than the mechanical damping value. According to the Nyquist criterion, the closed-loop system shown in Figure 2 is asymptotically stable only in the case where the overall damping is positive.
4. Model and Control of the Thyristor Variable Frequency Drive
In this section, the small-signal dynamic model of the TVFD is provided. Figure 3 presents only the first power conversion stage of the overall TVFD, supplied by a step-up transformer with two secondary windings. The overall TVFD is composed of two branches whose DC-links are connected through a mutual inductance . In each branch, there is an LCR. The LCRs are assumed to be equal, and the DC-links can be modeled considering their resistance and inductance connected in series and taking into account the mutual coupling. The power conversion stage shown in Figure 3 operates on the whole as a 12-pulse rectifier. The voltages and denote the DC-link output voltages and the input voltages of the LCIs which represent the second power conversion stage of the overall TVFD (Figure 1).
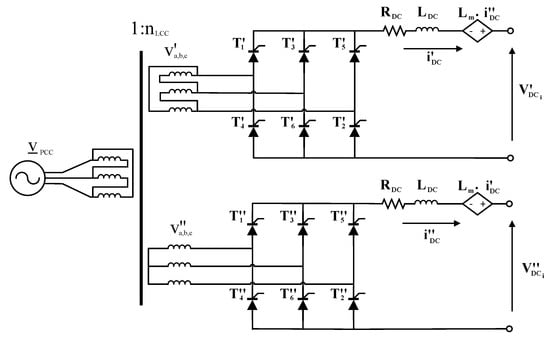
Figure 3.
First power conversion stage of the overall thyristor variable frequency drive (TVFD).
The control system of the first power conversion stage of the overall TFVD is represented in Figure 4. The overall power provided by the system is regulated by controlling the current by means of two PI controllers, one for each LCR. The PI controllers determine the firing angles of the LCRs denoted as α’ for the first LCR and α’’ for the second LCR. Besides, two Phase-Locked Loops (PLLs) have to guarantee the synchronization with the grid voltages [30,31]. As a consequence, the firing angles provided to the LCRs are the sum of α’ and α’’ plus αerr′ and αerr′′ which represent the contribution of the PLLs. It has to be highlighted that the same PLL operations are affected by the grid voltage fluctuations which are caused by the grid current variations. Besides, as described in the previous section, it is assumed that the second power conversion stage, which consists of two LCIs, operates with constant firing angles.
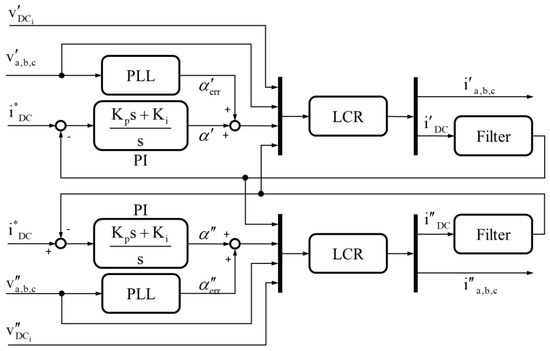
Figure 4.
Control system of the TVFD first power conversion stage.
4.1. Small-Signal Model of the AC/DC Power Conversion Stage
In [32], the small-signal model of a 6-pulse H-Bridge rectifier is presented. The same approach is extended to develop the small-signal model of the AC/DC power conversion stage of the TVFD.
As described before, the AC/DC power conversion stage consists of two LCRs which operate overall as a 12-pulse rectifier. Considering, for example, the commutation among the couples of thyristors , and , for the first LCR and the couples , and , for the second LCR, the operation of the 12-pulse rectifier can be divided into five stages. Considering the magnetic coupling between the first and the second LCR, the equivalent circuit for each stage is shown in Figure 5. The same analysis could be applied to all the other thyristors couples in the case of commutation to describe the complete operation of the 12-pulse rectifier in a period of the supplying voltage.
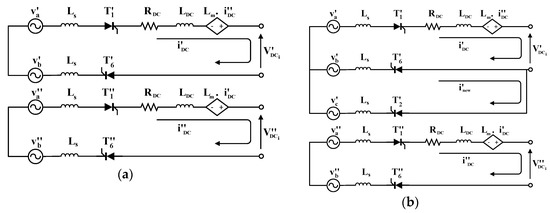
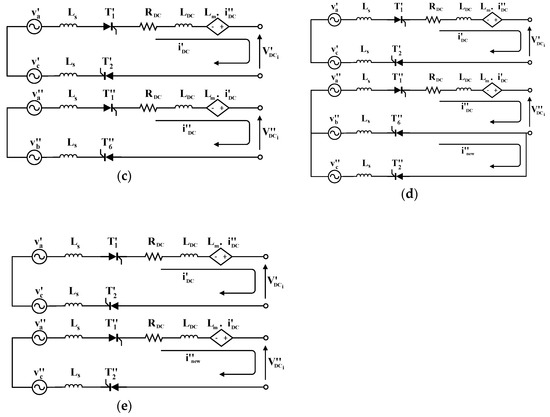
Figure 5.
12-pulse rectifier equivalent circuit: (a) before commutation; (b) commutation in the first LCR; (c) after commutation in the first LCR; (d) commutation in the second LCR; (e) completed commutation.
On the basis of the Kirchhoff laws and according to Figure 5a, when thyristors and of each LCR are in conduction mode,
with
where the vector of the DC-link currents is indicated as ; , , and are, respectively, the resistance and inductance of the DC-links and the mutual inductance; is the equivalent grid inductance which is a comprehensive form of the transformer inductance; and denote the LCIs-side DC-link currents and DC-link voltage vector, respectively; is the vector of the LCR-side voltages in a d-q reference frame:
Denoting as the Park transformation matrix, which allows us to transform the input voltages and in ,
where is the Park angle.
Equation (3) is valid in the time range (Figure 5a), where t0 denotes the initial time instant, and is the turn-on time of thyristor of the first LCR.
When thyristor of the first LCR is turned on (Figure 5b), it is possible to define the vector :
with
Equation (6) describes the converter operation during the second stage of Figure 5b and it is valid in the time range . At the instant is completely turned off.
Equation (8) is valid in the third stage of the operation and in particular in the time range where is the turn-on time of thyristor of the second LCR.
Successively, in the fourth stage, the equations describing the operation of the circuit (Figure 5d) are:
with
Equation (10) describes the AC/DC power conversion stage in the time range where is completely turned off at the instant indicated as .
Finally, when the thyristor of the second LCR is completely turned off (Figure 5e), the vector can be defined and it results
Equation (12) describes the AC/DC power conversion stage operation in the time range where t1 denotes the end of the fifth stage.
In conclusion, it is possible to calculate:
with
From Equations (3), (6), (8), (10) and (12), it is possible to define and as a function of the initial conditions and of the external inputs:
Since and are non-linear, small-signal linearization can be applied around the steady-state operating point. For example, Equation (18) can be rewritten, and the currents can be expressed in order to point out the dependency on the firing angles’ small perturbations Δα’ and Δα’’. This results in
with .
It is known that π/3 is the period of the currents and ; hence, it is possible to generalize
Equation (20) can be converted as follows:
where the matrixes contained in Equation (21) are defined as follows:
In order to obtain a classic state-space representation, the small-signal perturbations of the currents and are set as outputs of the overall system. Hence,
where .
Including also the action of the PLLs in the small-signal linearized model, the closed-loop state-space model can be expressed by:
Hence, Figure 4 can be replaced by Figure 6 including the provided state-space dynamic model of the AC/DC power conversion stage in the overall control loop.
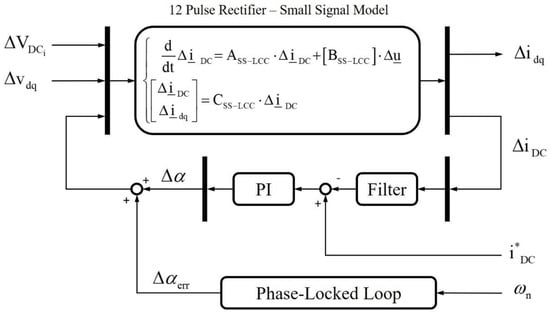
Figure 6.
Control system and TVFD first power conversion stage model based on small-signal linearization and state-space representation.
4.2. Model Validation of the AC/DC Power Conversion Stage
Considering the electrical parameters of the power conversion stage reported in Table 1, the small-signal model of the TVFD AC/DC power conversion stage is assessed and compared with a simplified model. Figure 7 shows the simplified equivalent circuit of the TVFD AC/DC power conversion stage, where the dynamic behavior of the converters and the commutation process is neglected. The circuit represents an average model of the AC/DC power conversion stage where only the DC-links of the LCRs are modeled and the 12-pulse rectifier is considered through the average voltage provided by the two LCRs denoted as V′DCr and V′′DCr.
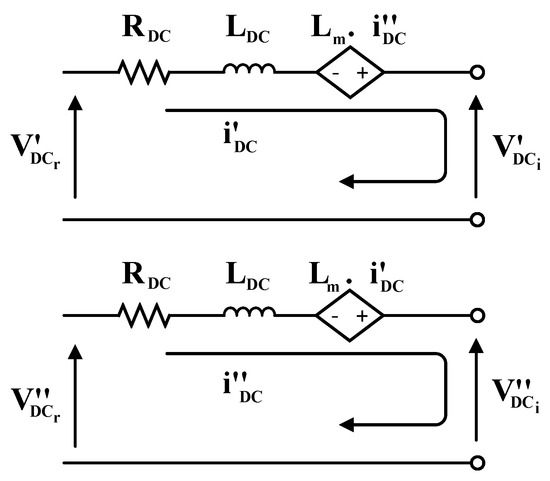
Figure 7.
Simplified equivalent circuit of the TVFD AC/DC power stage.
Starting from the simplified circuit shown in Figure 7, a state-space representation similar to Equation (25) can be obtained.
The small-signal dynamic model discussed in the previous section, the simplified average model and a simulation time-varying model based on PLECS (Piecewise Linear Electrical Circuit Simulation) software (4.3.2 version) have been compared. The PLECS simulation platform is used in the Simulink environment. The PLECS model reproduces exactly the real operation of the AC/DC power conversion stage in the time domain and the thyristors commutation on the basis of the power electronic devices datasheet implementation.
The current variations due to voltage variations have been analyzed since they are strictly related to the electrical damping estimation. Voltage variations (at frequencies defined as ) have been applied as inputs of the different models. The frequencies of interest are in the range (0–60 Hz) which includes the first TNF of the TG unit. The measurements of are fundamental in order to test the effectiveness of the proposed AC/DC power conversion model. As an example, Figure 8 reports the d-axis current variations (related to the primary side of the transformer) in the case of voltage variations set at 5 Hz and 10 Hz. It can be noticed that the current waveforms provided by the small-signal dynamic model, the simplified average model, and the simulation PLECS model are all in phase but the currents have different amplitudes. As expected, the PLECS current waveforms reproduce the real currents affected by the thyristors switching.
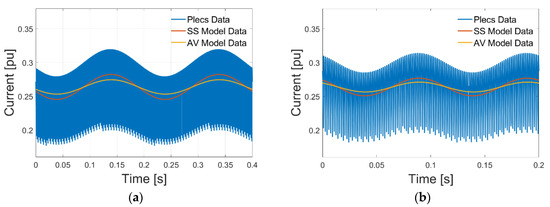
Figure 8.
due to voltage variations at: (a) 5 Hz; (b) 10 Hz.
The effects of the same voltage variations at 5 Hz and 10 Hz are considered in Figure 9, where the results are presented in the frequency domain. In reference to the same figure, Fast Fourier Transform (FFT) has been adopted to discern the different frequency components. It is possible to observe how the PLECS model and the small-signal dynamic model provide exactly the same current variations. Differently, the simplified average model underrates the amplitude of the current variations. This demonstrates that the small-signal dynamic model is preferable to the simplified average model in order to obtain a fair assessment of the impact of the SSTI phenomena.
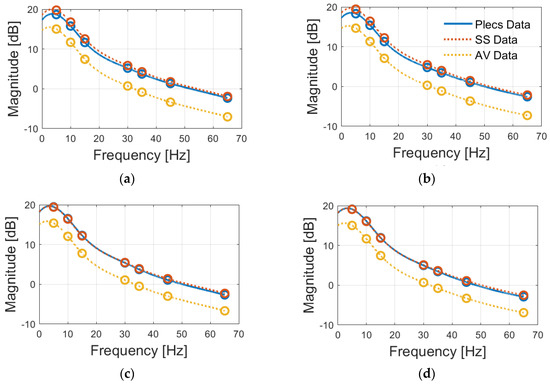
Figure 9.
System response: (a) SISO system between and ; (b) SISO system between and ; (c) SISO system between and ; (d) SISO system between and .
5. Model and Control of the Turbine-Generator Unit
Starting from the synchronous machine model presented in [2], a combined electromechanical model of the TG is developed in order to be compatible with the state-space representation of the TVFD presented in Section 4.1.
In the considered case study, the shaft-line mechanical behavior is described by a lumped model of the GT coupled to the synchronous generator through a mechanical gearbox. The synchronous generator air-gap torque can be calculated as a function of currents and fluxes in a d-q reference frame. The excitation circuit is controlled by an Automatic Voltage Regulator (AVR) as shown in Figure 10.
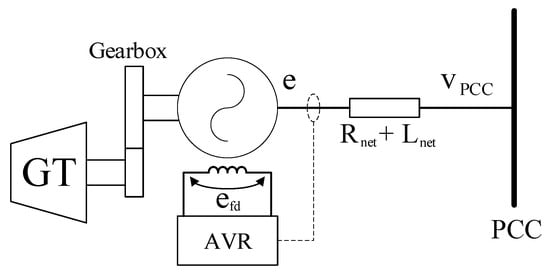
Figure 10.
Simplified model of the synchronous generator (SG).
5.1. Small-Signal Model of the Synchronous Generator
The shaft-line model has several degrees of freedom (DOFs), as discussed in [28,29]. In this paper a simplified approach is preferred and three DOFs are associated with the shaft-line: the first represents the whole GT, the second represents the gearbox, and the third represents the whole synchronous generator (Figure 11).
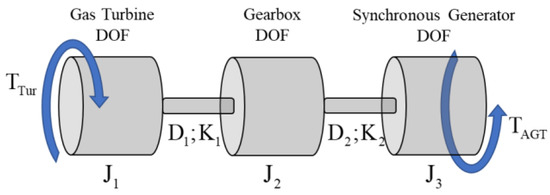
Figure 11.
Mechanical equivalent model of the turbo-generator (TG) shaft-line.
Newton’s second law allows us to obtain the motion differential equation of a multi-mass system:
with
where the vector is defined as the torsional mechanical model vector, is the three DOF rotor position vector, is the vector of the torques applied to the shaft-line (composed of the turbine torque and the generator torque ), J is the inertia diagonal matrix, K is the stiffness tri-diagonal matrix and D is the damping tri-diagonal matrix.
Considering a d-q reference frame rotating at the rotor frequency ωR, the d-q circuits of the synchronous generator are presented in Figure 12.
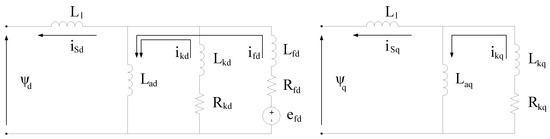
Figure 12.
d-q equivalent circuits of the synchronous generator.
The stator currents and and the flux linkages and can be defined as:
with
where ω is the stator voltage pulsation, and are the d-q axes grid voltages, Ψfd is the field winding flux linkage, Ψkd and Ψkq are the d-q axes amortisseur winding flux linkages, Rnet and Xnet are the respective resistance and the reactance of the step-up transformer connecting the generator to the PCC; Ra is the stator resistance; Rfd, Rkd and Rkq are the field and ammortisseur circuit resistances referring to the stator side; Lad and Laq are the d-q axes magnetizing inductances, L1 is the stator winding leakage inductance; Lfd, Lkd and Lkq are the field and damper circuit inductances referring to the stator side.
The air-gap torque TAGT can be calculated as:
In order to simplify the analysis, a new common reference frame R-I can be introduced. The synchronous machine d-q reference frame and the R-I reference frame are shown in Figure 13. Hence, the machine stator currents can be expressed in the new R-I common reference frame as:
where γ is defined as shown in Figure 13.
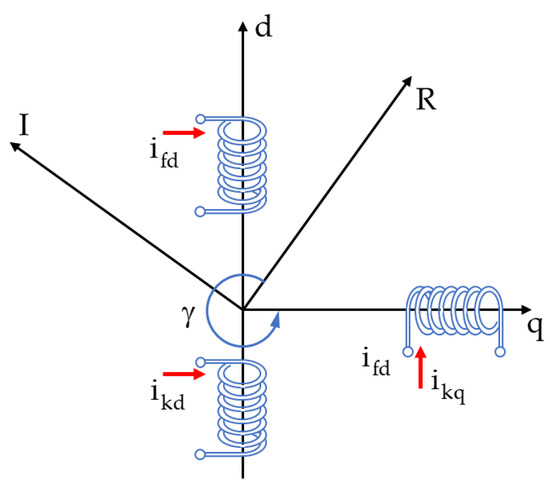
Figure 13.
d-q and R-I reference frames.
Denoting as the rotor angle, Equations (27)–(29) can be linearized around the initial conditions characterized by the initial rotor position , initial rotor fluxes and , initial current vector , initial voltage vector , and initial field voltage :
where the coefficients are derived in Appendix A.
The small-signal model of the circuit shown in Figure 10 is described by the following equation:
where is the rotor flux perturbation vector.
The derivative of depends on the field voltage that in Equation (32) is taken into account through the action of the AVR.
The model of the considered AVR is shown in Figure 14. As in [2], it is composed of a voltage transducer (whose proportional gain and time constant are Kr and Tr, respectively) and by a PI controller (whose proportional gain and integral time constant are and , respectively).
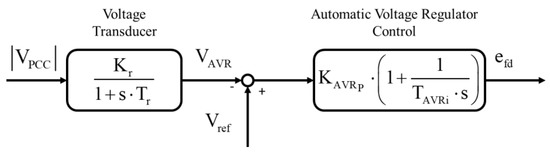
Figure 14.
Automatic voltage regulator (AVR) control.
The grid voltage magnitude variation can be expressed as
with
The derivative of the transducer voltage can be calculated as
The state-space electromechanical model of the TG can be obtained combining Equations (26), (32) and (34) and defining the space vector as :
In conclusion, the TG eigenvalue calculation is based on the matrix ASM eigenvalue determination. The real part of eigenvalues provides information of the overall damping including both the mechanical and the electrical contribution.
5.2. Model Validation of the Synchronous Generator
Independent of the causes, SSTIs lead to generator shaft torsional vibrations. The overall damping of the TG unit is given by the sum of the shaft-line inherent mechanical damping and the electrical damping. Considering Figure 10 and Figure 11, the torsional torque on the gas turbine is taken into account to evaluate the damping. Thanks to the modal analysis, the torsional natural frequencies of the shaft-line and the damping related to these frequencies can be identified.
In Table 2, the TG torsional mechanical model parameters are reported.

Table 2.
TG torsional mechanical model parameters.
With reference to the data of Table 1 and Table 2, the state-space electromechanical model of the TG has been assessed through a comparison with a simulation time-varying model based on PLECS software (4.3.2 version). Simulation results are related to rated conditions. The results provided by the time-varying model have been used in order to verify the accuracy of the small-signal model defined in Equation (35). In particular, the impulse response of the PLECS simulation model has been analyzed in the frequency domain to determine the damping related to each torsional frequency. The achieved information was compared with frequencies and damping obtained through the eigenvalue analysis of the matrix in the state-space model (Equation (35)).
Fourier transform-based approaches are not suitable for this frequency domain study since the torsional torque signals are typically affected by time-varying components. Differently, Prony analysis is widely used to test the power system’s transient behavior [33,34,35,36]. Prony analysis can accurately identify growing or decaying components of signals where there is no prior knowledge of the frequencies. Indeed, each signal y(t) can be defined as:
where is the magnitude, is the damping factor, is the pulsation, and is the phase angle.
The greatest advantage of Prony analysis is the ability to identify the damping factor of each mode since each exponential component in Equation (36) represents a unique mode of the original signal . As a consequence, transient harmonics can be identified accurately.
In Figure 15, the TG is excited by a torsional impulse with magnitude 1 pu and duration 10−4 s. The complete torque transient behavior calculated by the state-space TG model is shown in the upper side of Figure 15, while the comparison between the torque provided by the simulation PLECS model and the torque fitting using the Prony series are reported on the lower side of Figure 15 considering a time range (0–2) s.
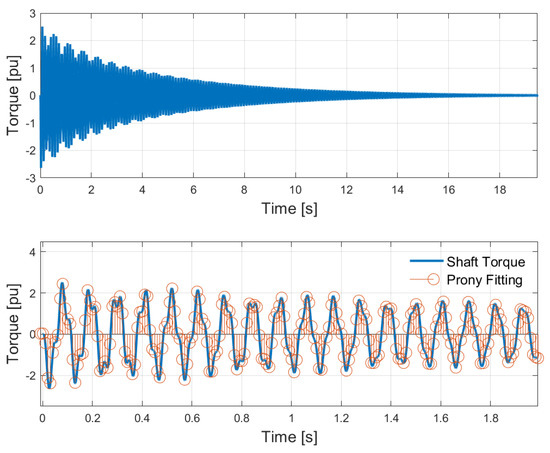
Figure 15.
Torque oscillation after a transient event: simulation PLECS model and Prony series fitted signals.
The torque waveform depends on the natural frequency and the damping factor of the first torsional mode. The post processing analysis, through Prony series, allows us to fit the real torque signal with an optimal approximation, as highlighted in Figure 15. The natural frequency and the damping factor estimated through Prony series are: , .
Considering the TG state-space model, the overall damping factor can be evaluated by the eigenvalues of the matrix , remembering that is the matrix which multiplies the state vector in Equation (35). Table 3 reports the eigenvalues corresponding to the oscillatory mode of the matrix. Focusing on the first torsional model, the natural frequency is equal to 9.2047 Hz while the damping factor is equal to 0.0035.

Table 3.
Eigenvalues of the TG state-space model.
Comparing the results provided by the state-space model and the simulation of the PLECS model processed through Prony series, it can be concluded that the frequency of the first torsional mode is estimated with an error less than 5%, while the overall damping factor is estimated with an error less than 3%. Hence, the accuracy of the proposed state-space electromechanical model is proved.
6. Damping Assessment and Stability Considerations
In the previous sections, both the state-space model of the TVFD and of the TG unit are represented in the following form:
where represents the variations of the state variables of the TVFD and of the TG unit, is the vector of the current perturbations, and is the vector of the voltage perturbations.
In order to achieve the overall electromechanical model of the LNG plant, all voltages and currents have been measured in a common reference frame. For this purpose, the reference frame R-I rotating at the synchronous generator speed (Figure 13) is used as a common reference frame.
Denoting as the current provided by the TG unit and as the AC current of the TVFD, the currents vectors can be defined as:
with
Considering the simplified scheme of the LNG plant shown in Figure 2, the overall state-space model can be obtained combining Equations (25) and (35):
with
Hence, the PCC node equation is:
Finally, the LNG plant model can be rearranged as:
with
6.1. Electrical Damping Assessment
The LNG plant eigenvalue calculations provide information about the stability of the overall power system. The LNG plant eigenvalue calculations are based on determination of the matrix eigenvalues. Each pair of complex eigenvalues corresponds to an oscillatory mode. The real part of the eigenvalues provides information of the overall damping including both the mechanical and the electrical damping. The imaginary component provides information about the oscillation frequency. Denoting as λi the i-th complex-conjugate pair of eigenvalues at a frequency ωi:
The oscillatory mode is stable if the real part σi of the eigenvalue is negative. This implies that the resulting TG shaft line oscillations damp naturally following a transient event in the grid. In particular, the decay rate of the oscillation amplitude depends on the frequency fi and the real part σi:
where ξ(fi) denotes the overall damping.
If ξ(fi) is negative, the oscillations at frequency keep increasing over time. As defined in [24], the overall damping can be divided into two contributions:
Denoting as ξm(fi) the mechanical contribution to the overall damping ξ(fi), the mechanical damping can be evaluated through the modal analysis as described in [28,29]. ξm(fi) is always positive; hence, the overall damping ξ(fi) can be negative only if the electrical damping contribution ξe(fi) is negative. The mechanical damping at frequency fi can be calculated by the coefficients D1 and D2 reported in Table 2. Differently, Equation (45) allows us to calculate the electrical damping ξe(fi) by subtraction.
In the considered case study, the electrical damping ξe(fi) and the eigenvalues of the matrix depend on the synchronous generator, the TVFD, and their control system. Considering the data reported in Table 1 and Table 2, the mechanical damping ξm(TNF1°) and ξm(TNF2°) related to the first and to the second TNFs can be derived (Table 4).

Table 4.
TG mechanical damping at the first and the second TNFs.
Looking at Equations (42) and (44), the overall damping ξ(TNFs) is assessed by the eigenvalues of the matrix , and the electrical damping ξe(TNFs) is calculated as a consequence.
6.2. Stability Evaluation
The parameter variation of the LCR’s current controller and of the PLL controllers influences the electric damping ξe(TNFs). Starting from the control parameters reported in Table 5, the current controller and PLL controller proportional gains have been varied successively.

Table 5.
Current controller and PLL controller parameters.
In Figure 16, the proportional gain of the LCR’s PI controllers is increased up to 0.7 pu while the integral time constant is kept constant. There is a decrease of the electrical damping ξe(TNF1°) related to the first TNF, which leads the LNG plant to instability in the case the proportional gain is greater than 0.1. The worst case is verified when Kp = 0.22 pu. In this condition, the electrical damping absolute value is the highest and, as a consequence, the overall damping ξ(TNF1°) is negative. For Kp < 0.1, the overall damping ξ(TNF1°) is positive and the system is stable.
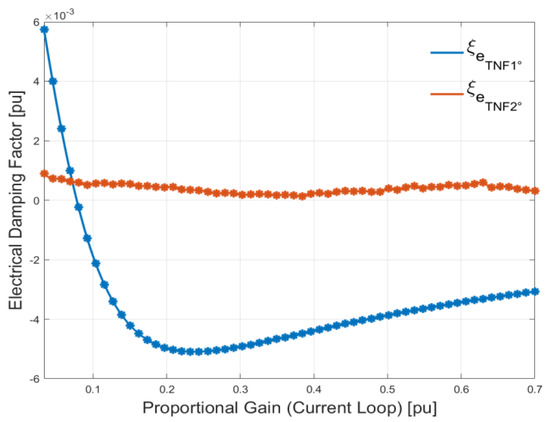
Figure 16.
Electrical damping as a function of the current controller parameter variation.
Considering the application of a torque impulse to the TG shaft at t = 0.5 s, the overall electro-mechanical system is perturbed. In Figure 17, two different conditions are analyzed: in the first case, Kp = 0.22, in the second case, Kp = 0.06. It can be observed that in the first case, the alternating component of the shaft torque increases progressively, while in the second case, the shaft torque decreases over time.
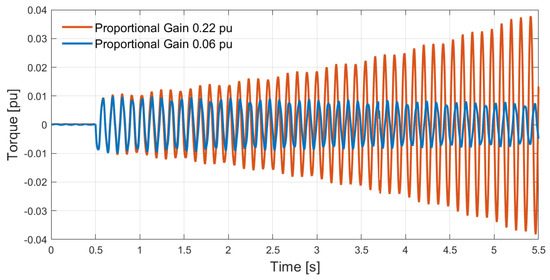
Figure 17.
Alternating component of the shaft torque after a perturbation phenomenon in case of current controller proportional gain variation.
Considering the reference frame shown in Figure 13, the TG model and the power conversion stage model described by Equations (35) and (25), respectively, can be rearranged as:
where the voltage variation is selected as input, and the current variations and are selected as output.
In Figure 18 and Figure 19, the Bode diagrams of the systems described in Equations (46) and (48) are shown.
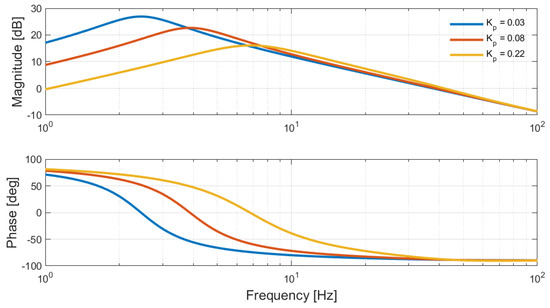
Figure 18.
Bode diagram of the power conversion stage model (Equation (47)) in case of different current controller proportional gain values.
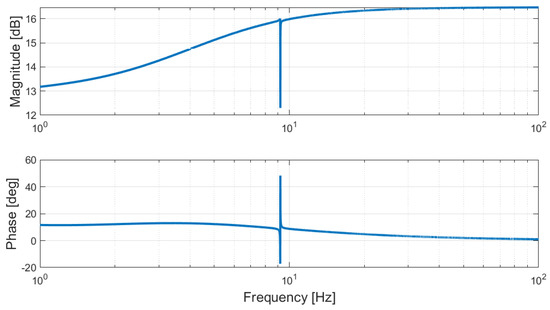
Figure 19.
Bode diagram of the TG model (Equation (46)).
Looking at Figure 18, it can be observed that, considering different values of Kp, the magnitudes are very similar in the frequencies range of interest. As a consequence, the variations of the currents drained by the power conversion stage at the PCC are not suggestive of instability conditions. Differently the Bode phase plots related to the first TNF are indicative of instability. In the case ξe(TNF1°) is positive or zero, the current variations exhibit around 90° of lag with respect to the voltage variation .
Considering the TG model (Equation (46)), it can be noticed that the variations of the currents injected in the PCC are around 10° with respect to voltage variation (Figure 19). Observing Figure 18 and Figure 19 and considering Kp = 0.03 pu, it can be concluded that the currents at the PCC related to the TG and to the power conversion stage have a phase shift greater than 90 degrees. In this condition, positive electrical damping is guaranteed. The phase shift between the currents decreases in the other cases, ξe(TNF1°) presents negative values, and the electro-mechanical system leads to instability conditions.
In conclusion, the study of the overall model defined in Equation (42) is necessary in order to provide proper stability assessment.
In Figure 20, the proportional gain of the PLL controller is varied while the PLL integral time constant is considered constant. In the case the proportional gain is greater than 17, there is a decrease of the electrical damping ξe(TNF1°) related to the first TNF, which leads the LNG plant to instability. This is confirmed by the results provided in Figure 21 when the proportion gain of the PLL controllers is assumed equal to 7 in the first case and equal to 30 in the second case. In the first case, ξe(TNF1°) is positive, and the torque oscillation damps naturally; in the second case, the torque oscillation increases over time, and the LNG plant is unstable.
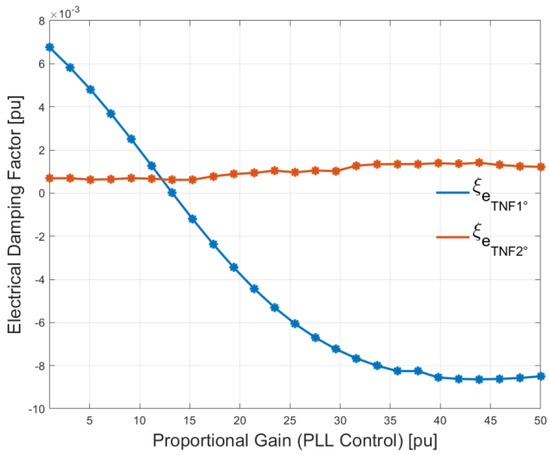
Figure 20.
Electrical damping as a function of the PLL controller parameter variation.
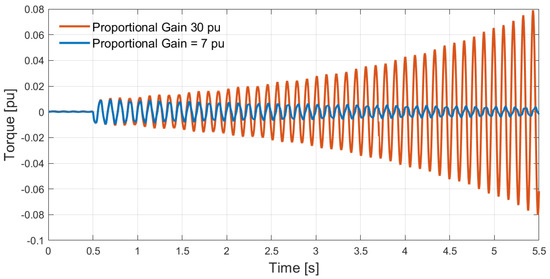
Figure 21.
Alternating component of the shaft torque after a perturbation phenomenon in case of PLL controller proportional gain variation.
7. Conclusions
Commonly for the LNG plants, stability analysis is developed, neglecting a detailed model of the power converters. In this paper, it is pointed out that stability evaluation provided in the case of a simplified model of the power conversion stage can be misleading. It can impact the effectiveness of the results and, as a consequence, the operation of the LNG plant. Small-signal analysis is used to determine a detailed dynamic state-space model of the TVFD and of the electrical generator with the aim to provide an accurate evaluation of the electrical damping of the LNG plant. It is proved that the use of simplified models can affect the estimation of the electrical disturbances due to the SSTI phenomena. The impact of the main control parameters variations on the electrical damping assessment is finally investigated.
Author Contributions
Formal analysis, L.B.; investigation, L.B.; data curation, D.S.; writing—original draft preparation, L.B., R.A.M., D.S. and F.M.; writing—review and editing, L.B., R.A.M., D.S. and F.M.; supervision, R.A.M.; project administration, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank Baker Hughes for providing data used in the development of this publication.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Assuming linear magnetic conditions, based on the small-signal linearization, it is possible to define
where is the initial rotor position, and are the initial rotor fluxes, is the initial current vector in the R-I frame, is the initial voltage vector, and is the initial field voltage.
Considering the relation between the common reference frame R-I and the individual synchronous machine reference frame defined in Equation (30), the variations of the currents and of the voltage can be expressed as:
Neglecting the constant terms and the variations with order higher than the first:
where defining the coefficients:
The matrix elements are:
Equation (A7) defines the small perturbations of the stator currents in the reference frame R-I to be included in the state-space model of the synchronous machine defined in Equation (35).
The matrixes that compose the turbo-generator model are derived from Equations (26)–(28) and (32) considering the small-signal representation in Equations (A1)–(A5).
The coefficients of Equation (35) can be defined as follows:
with
References
- Bongini, L.; Mastromauro, R.A. Sub-synchronous torsional interactions and start-up issues in Oil&Gas Plants: A real case study. In Proceedings of the 2019 AEIT International Annual Conference (AEIT), Florence, Italy, 18–20 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Svetti, F.; Rotondo, P.; Sgrò, D.; Meucci, F. Practical guideline for Oil&Gas design against sub-synchronous torsional interaction phenomena. In Proceedings of the Turbomachinery and Pump Symposia, Houston, TX, USA, 14–17 September 2015; pp. 1–13. [Google Scholar]
- Harnefors, L. Analysis of subsynchronous torsional interaction with power electronic converter. IEEE Trans. Power Syst. 2007, 22, 305–313. [Google Scholar] [CrossRef]
- Schramm, S.; Sihler, C.; Song-Manguelle, J.; Rotondo, P. Damping torsional interharmonic effects of large drives. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 484–490. [Google Scholar] [CrossRef]
- Sihler, C. Suppression of torsional vibrations in rotor shaft systems by a thyristor controlled device. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 1424–1430. [Google Scholar] [CrossRef]
- Sihler, C.; Schramm, S.; Song-Manguelle, J.; Rotondo, P.; del Puglia, P.S.; Larsen, E. Torsional mode damping for electrically driven gas compression trains in extended variable speed operation. In Proceedings of the 38th Turbomachinery Symposium, Houston, TX, USA, 14–17 September 2009; pp. 81–92. [Google Scholar]
- Sannino, A.; Liljestrand, L.; Rothman, B.; Nestli, T.; Kjall-Ohlsson, M.; Holsten, P. All-electric LNG liquefaction plants: Technical challenges and possible concept solutions. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 2407–2413. [Google Scholar] [CrossRef]
- Peyghami, S.; Azizi, A.; Mokhtari, H.; Blaabjerg, F. Active damping of torsional vibrations due to the sub-harmonic instability on a synchronous generator. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. 1–8. [Google Scholar]
- de Toledo, P.F.; Angquist, L.; Nee, H. Frequency-domain modelling of sub-synchronous torsional interaction of synchronous machines and a high voltage direct current transmission link with line-commutated converters. IET Gener. Transm. Distrib. 2010, 4, 418–431. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, R.; Li, R.; Yu, H.; Zhao, G. Subsynchronous Torsional interaction of wind farms with FSIG wind turbines connected to LCC-HVDC lines. Energies 2017, 10, 1435. [Google Scholar] [CrossRef]
- Choo, Y.C.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S.; Negnevitsky, M. Analysis of subsynchronous torsional interaction of HVDC system integrated hydro units with small generator-to-turbine inertia ratios. IEEE Trans. Power Syst. 2014, 29, 1064–1076. [Google Scholar] [CrossRef]
- Jiang-Hafner, Y.; Duchen, H.; Linden, K.; Hyttinen, M.; de Toledo, P.F.; Tulkiewicz, T.; Skytt, A.-K.; Bjorklund, H. Improvement of subsynchronous torsional damping using VSC HVDC. In Proceedings of the International Conference on Power System Technology, Kunming, China, 13–17 October 2002; pp. 998–1003. [Google Scholar] [CrossRef]
- Adrees, A.; Milanovic, J.V. Effects of uncertainties in shaft mechanical parameters on maximum torsional torques in meshed networks with HVDC lines. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 27 August 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Li, W.; Xiao, X.; Tao, S. Design and engineering practice of HVDC SSDC for suppressing sub-synchronous oscillations. In Proceedings of the2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Amin, M.; Molinas, M. Sub-synchronous oscillation mechanism and its suppression in MMC-based HVDC connected wind farms. IET Gener. Transm. Distrib. 2018, 12, 1021–1029. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M.; Lyu, J. Oscillatory phenomena between wind farms and HVDC systems: The impact of control. In Proceedings of the2015 IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12–15 July 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Adrees, A.; Milanović, J.V. Methodology for evaluation of risk of subsynchronous resonance in meshed compensated networks. IEEE Trans. Power Deliv. 2014, 29, 815–823. [Google Scholar] [CrossRef]
- Perera, N.; Midence, R.; Liyanage, V. Protection for sub synchronous torsional interaction conditions using an industrial sub-harmonic relay. In Proceedings of the2018 71st Annual Conference for Protective Relay Engineers (CPRE), College Station, TX, USA, 26–29 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Michi, L.; Giannuzzi, G.; Pisani, C.; Carlini, E.M.; Zaottini, R.; Puddu, R. Improving dynamic stability with HVDC systems: Italy-Montenegro interconnector case. In Proceedings of the 2019 AIET International Annual Conference, Florence, Italy, 18–20 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Rahman, M.A.; Ghosh, S.K. Stability of a power electronics based microgrid system. In Proceedings of the2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–5 September 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Michi, L.; Giannuzzi, G.; Pisani, C.; Carlini, E.M.; Zaottini, R. Improving dynamic stability in presence of static generation: Issues and potential countermeasures. In Proceedings of the 2019 AIET International Annual Conference, Florence, Italy, 18–20 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Hsu, Y.Y.; Wang, L. Modal control of HVDC system for the damping of subsynchronous oscillation. IEEE Proc. C. Gener. Transm. Distrib. 1989, 136, 78–86. [Google Scholar] [CrossRef]
- IEEE SSR Working Group. First benchmark model for computer simulation of subsynchronous resonance. IEEE Trans. Power Appar. Syst. 1977, 96, 1565–1572. [Google Scholar] [CrossRef]
- IEEE SSR Working Group. Proposed terms and definitions for subsynchronous oscillations. IEEE Trans. Power Syst. 1980, PAS-99, 506–511. [Google Scholar] [CrossRef]
- Jörg, P.; Tresch, A.; Bruha, M. A model based approach to optimize controls of a large LCI VSD for minimal grid-side sub-synchronous torsional interaction. In Proceedings of the PCIC Europe 2013, Istanbul, Turkey, 28–30 May 2013; pp. 1–7. [Google Scholar]
- Yang, H.; Yuan, X. Modeling and analyzing the effect of frequency variation on weak grid-connected VSC system stability in DC voltage control timescale. Energies 2019, 12, 4458. [Google Scholar] [CrossRef]
- Wang, S.; Wu, X.; Chen, G.; Xu, Y. Small-signal stability analysis of photovoltaic-hydro integrated systems on ultra-low frequency oscillation. Energies 2020, 13, 1012. [Google Scholar] [CrossRef]
- Lozano, R.; Brogliato, B.; Maschke, B.; Egeland, O. Dissipative Systems Analysis and Control—Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Chee-Mun, O. Dynamic Simulation of Electric Machinery Using Matlab/Simulink; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Best, R.E. Phase-Locked Loops: Design, Simulation and Applications; McGraw Hill: New York, NY, USA, 2007. [Google Scholar]
- Nagliero, A.; Mastromauro, R.A.; Liserre, M.; Dell’Aquila, A. Synchronization techniques for grid connected wind turbines. In Proceedings of the35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 4606–4613. [Google Scholar] [CrossRef]
- Yang, X.; Chen, C. HVDC Dynamic modelling for small signal analysis. IEE Proc. Gener. Transm. Distrib. 2004, 151. [Google Scholar] [CrossRef]
- Moo, C.S.; Chang, Y.N.; Mok, P.P. A digital measurement scheme for time-varying transient harmonics. IEEE Trans. Power Deliv. 1995, 10, 588–594. [Google Scholar] [CrossRef]
- Huang, S.J.; Huang, C.L.; Hsieh, C.T. Application of Gabor transform technique to supervise power system transient harmonics. IEE Proc. Gener. Transm. Distrib. 1996, 143, 461–466. [Google Scholar] [CrossRef]
- Hauer, J.F. Application of Prony analysis to the determination of modal content and equivalent models for measured power system response. IEEE Trans. Power Deliv. 1991, 6, 1062–1068. [Google Scholar] [CrossRef]
- Hildebrand, F.B. Introduction to Numerical Analysis; McGraw-Hill Book: New York, NY, USA, 1956. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).