1. Introduction
Currently, the interest in renewable energy sources (RESs) integration in power systems in many countries all over the world is fast rising due to the significant shortage and/or price increase of fossil fuel and the need to avoid the harmful effects of global climate change [
1,
2]. It is required that the universal temperature increase should be lower than 2 °C and the maximum temperature rise being limited to 1.5 °C in comparison to the preindustrial level [
3]. The use of renewable energy resources in world energy systems to realize these aims, and the reduction of global warming has been recognized. Recent developments in renewable energy technologies have availed various sustainable options. This has resulted in the ease of issuance of the Renewable Energy Law to incentivize government, industry or many cities around the globe to commence the inclusion of renewable energy programs in their domains to achieve sustainable development and environmental protection [
4]. Thus, the world’s renewable energy generations and their integration levels in conventional power grids are rising speedily [
5]. For example, to mention but a few, It is recorded that 25% of the energy required to meet electricity demand in Germany can now be obtained from renewable energy sources as against 5% about 20 years ago [
6]. In Australia, effort at increasing both wind and solar power penetration levels to achieve the 20% renewable energy target by 2020 proposed by the National Renewable Energy Target (RET) scheme is well underway [
7]. Additionally, in Turkey, the contribution of renewable energy generation was 6% in 2015 and the proportion of renewable energy generation is expected to grow to at least 30% in 2023 [
8]. Reference [
9] asserts that Saudi Arabia Vision 2030 aims to generate about 9.5 GW of power from renewable energy sources by 2023 and solar photovoltaic (PV) generation will constitute a major portion.
However, the role of solar energy sources being the third largest renewable power source in the world, (after wind energy and hydropower being the second and first largest renewable sources respectively), with photovoltaic (PV) technology is becoming one of the most promising energy sources in most countries. This is because the sun energy is largely accessible to everyone and it is a clean, abundant and sustainable energy source [
10]. Currently, medium and large-scale grid-connect PV systems are more dominant in the USA, China and Germany medium among other countries [
11]. PV technologies consist of photovoltaic cells, which convert incident solar radiation into DC energy [
12,
13]. Grid-connected solar photovoltaic generator (SPVG), as well as the other distributed renewable energy generations, can be used in modern power grids, for peak-shaving, strengthening local network and generation of power close to the consumers [
14]. Even though SPVG output tallies well with peak load demand, there is a need to understand the characteristics of some of the model controls (also applicable to other forms of dispersed generation), which in part make these generators’ capabilities intrinsically different from those of conventional generator. To ensure the operation of these resources in power grids does not jeopardize its stability, an extensive study is needed to evaluate its influence on the power system static or dynamic stability based on suitable controls with which the best installation site can be determined. Since large-scale RESs, for example, solar plants, which penetrate in the grid without enough reactive power compensation, or renewable energy generators (REGs) situated far from load centers or connected to the system weak zone can impact adversely on the system security and stability [
15,
16]. Additionally, the central station or distributed solar photovoltaic generator (SPVG) for example has a power electronic converter that supplies reactive power for grid voltage control at a specific power factor [
17,
18]. Besides, REG voltage control capability is less compared to the conventional synchronous generator’s and when the voltage control capability is less than the system requirement, the grid may become unstable. Thus, the impacts of grid-connected RES on system voltage stability should be well studied [
19,
20]. Voltage stability is defined as the ability of the power system to maintain steady acceptable voltages at all buses in the network under normal operating conditions or after being subjected to a disturbance [
21,
22,
23]. The level of voltage stability in the power system is mostly based on the strength of the network and the size of power transfer. Reference [
24] states that power system voltage can also be affected by load and reactive power compensation device features, voltage control devices and generator reactive power capability. Static voltage stability can be studied using modal analysis, the continuation method, the optimization method, etc.
Nonetheless, the power-voltage (P–V)-curves and voltage-reactive power (V–Q)-curves methods are commonly used [
25,
26,
27,
28,
29,
30]. The P–V-and V–Q-curves show the reaction of bus voltage with increasing real power transfer from source to sink or with the absorption or injection of reactive power from or into the same bus. Notwithstanding, the P–V- and V–Q-curve methods are deterministic methods but accurate. Reference [
31] used a P–V-curve to analyze the effect of a wind generator on the static voltage stability of the Zhanjiang power system using PSD-BPA Software. The study conducted in [
15] employs continuation power flow (CPF) in the DIgSILENT/PowerFactory environment to investigate the impact of a large wind farm on China power system voltage stability. Additionally, the authors of [
17] analyzed the impact of some control strategies of doubly-fed induction generator (DFIG) based wind power generation and solar photovoltaic generation on power system static voltage stability with the V–Q-curve using the Power Factory and compared the operational characteristics of the controlled DFIG based generators to the conventional synchronous generator and asserted that RESs gives reduced support for power system voltage. Furthermore, the study performed in [
27] utilizes the CPF based P–V-curves method in the power system toolbox (PSAT) environment to investigate the influence of REGs on power system voltage stability. Reference [
32] proposed two models for large SPVG integrated to the power system. Viz: (1) the constant power, P and constant reactive power, Q control and (2) constant P and constant voltage, V control. Additionally, it uses P–V-curves based on the proposed methods to evaluate the effect of SPVG on power system stability using PSAT Software.
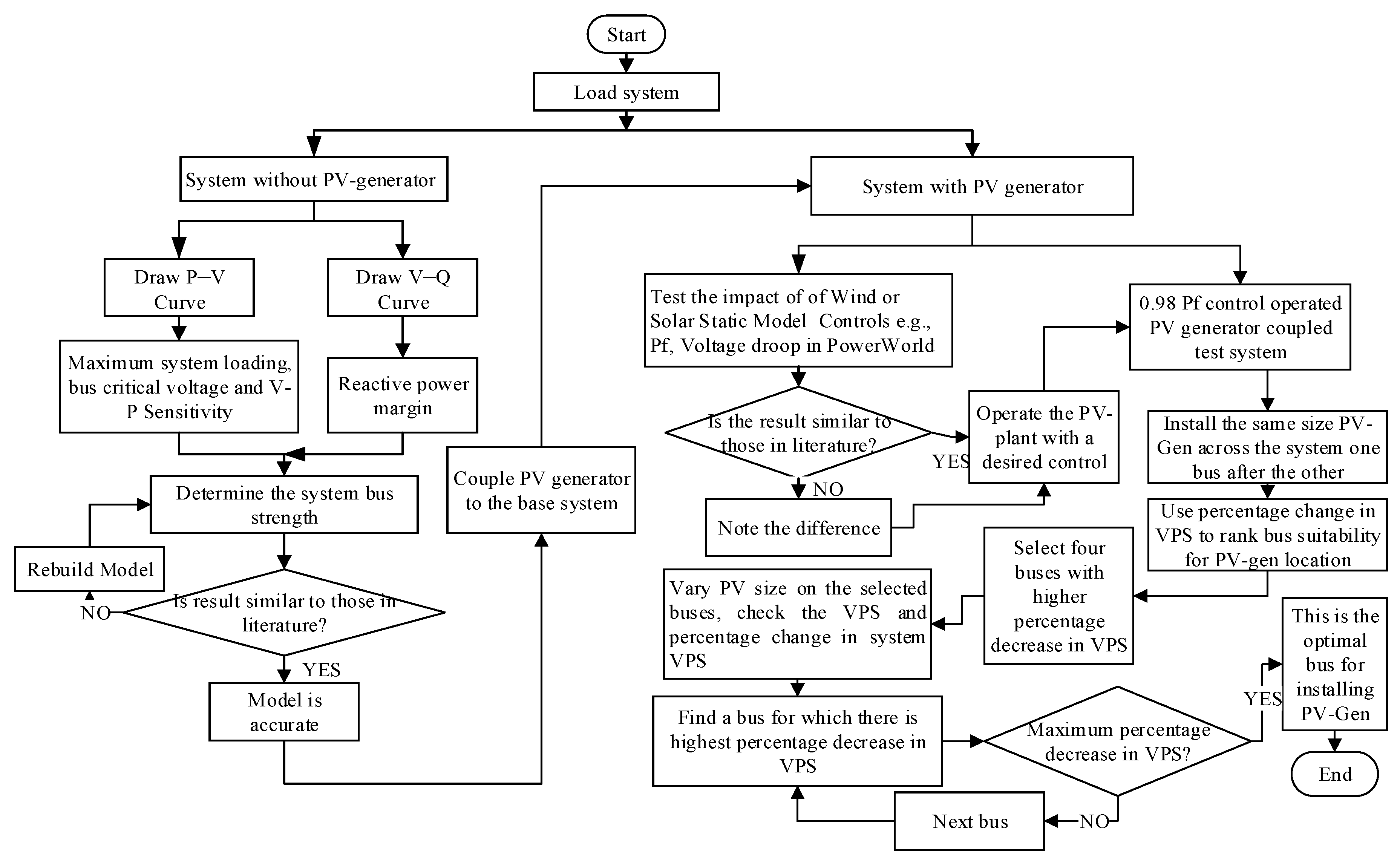
The presence of the power electronic converter system in photovoltaic plants (like other dispersed renewable generators) has made the control of both active and reactive power possible in the grid-connected PV generator to a certain degree. The reactive capability of distributed renewable generators can be varied within their control schemes. Voltage instability can arise due to the variable injection of renewable power generators (RPGs) in the power system. The simulation of different reactive power and/or voltage control values of these RPGs within an allowable operation standard to determine their influence in the power system stability is key for the determination of the best site for RPG installation, and its feasible penetrations provided that no any components of the power system are altered or no new compensator is used. Therefore, this paper reports the static voltage stability impact of solar photovoltaic generations on power networks using the PowerWorld simulator P–V- and V–Q-curves to investigate the renewable energy generator model performance suitability. The impact of varying power factor control and static voltage droop control of the photovoltaic plant on maximum generated power, threshold voltage profile and reactive power marginal loading has been examined. In addition, the concept of percentage change in voltage-power sensitivity (PCVPS) has been systematically utilized to determine the optimal location for solar photovoltaic generator on the power grid and the feasible solar photovoltaic generation penetrations have been defined for selected system buses. The following study scenarios are covered in this study:
Scenario 1: Determination of the system buses’ strengths without any PV generation installation to validate model accuracy.
Scenario2: PowerWorld-REG-model performance validation compared to other commonly used simulators model, e.g., Power factory, PSAT and PSS/E.
Scenario 3: Determination of the optimal site for solar PV placement.
1.1. Grid-Connected SPVG Structure
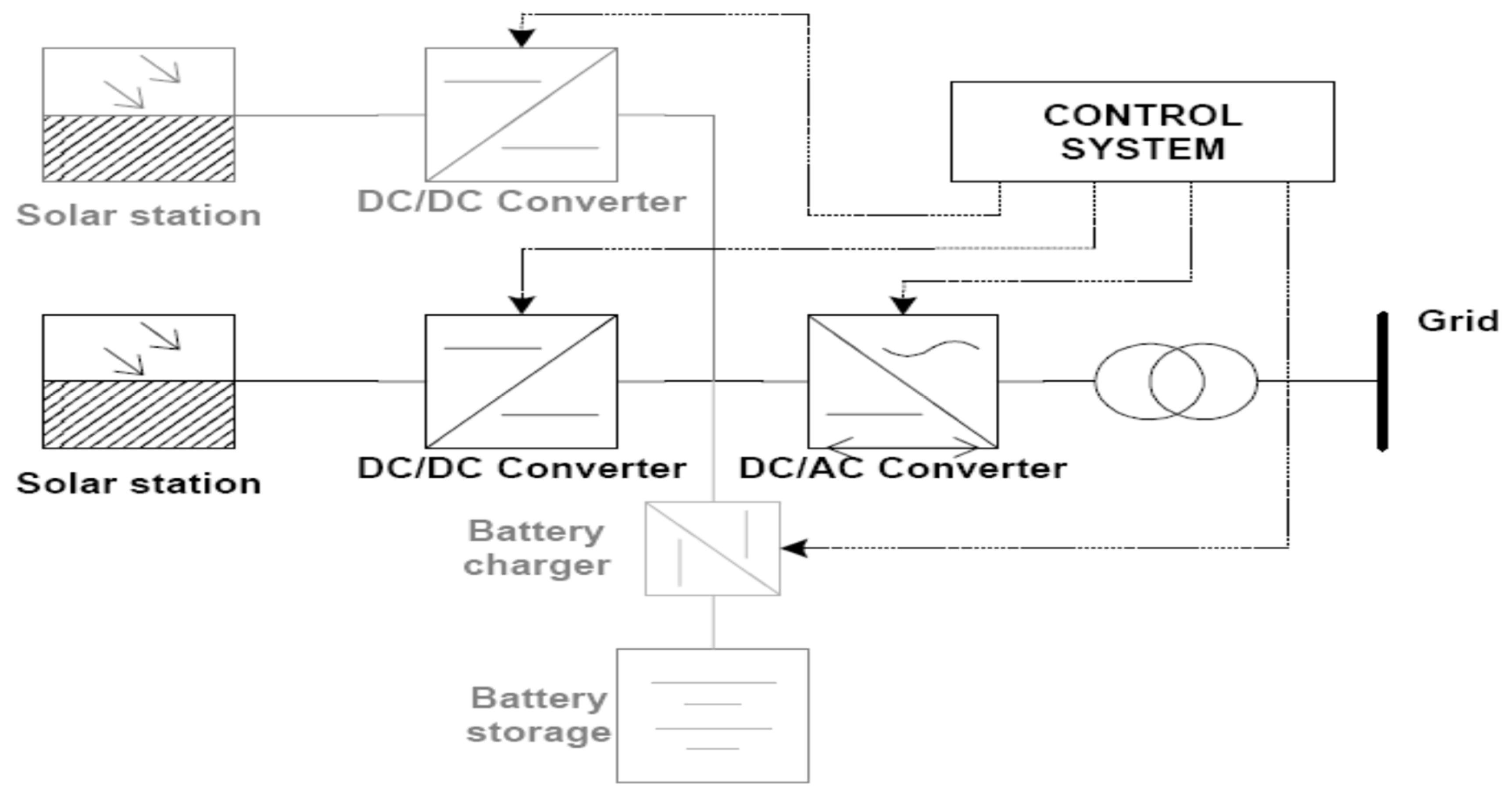
The deployment of grid-coupled SPVGs has recorded the fastest growth in the global energy industry sector, which occupies a key position in the international market [
33,
34]. Grid-connected solar photovoltaic generator (SPVG), shown in
Figure 1, normally has a photovoltaic (PV) array (module), the DC/DC converter and DC/AC inverter at the grid side and some controls and converters. A storage system is not always used in large grid-connected SPVG installations, except for start-up controls of some critical loads. However, in a few cases, a large storage has been incorporated into large-scale SPVG. The DC/AC inverter helps to condition an unregulated DC output power from the PV module to make it suitable for grid connection. The DC/DC converter functions as a maximum power point tracking (MPPT) system at the output of the array, which keeps the voltage to a pre-set value. For stability studies, the response of the MPPT is considered instantaneous due to a lack of moving parts. The rest of the SPVG (DC bus, inverter and grid-connection devices) are modeled like variable speed wind turbines. Since SPVGs are normally connected to the grid via converter, it can be modeled as Type 3 or Type 4 wind turbine generator (WTG) [
35,
36,
37,
38] according to the North-American Electricity Reliability Corporation’s (NERC’s) special report on standard models for variable generation. The power converter processes output power and acts as a buffer between the generator and the grid and regulates reactive power output and/or the voltage at the point of common coupling [
32,
39].
1.2. SPVG Load Flow Model
In power flow analysis, a simplified solar plant can be used. This model comprises of a single generator and a unit transformer with MVA ratings equal to N multiples of individual device ratings, where N denotes the number of converters in the plant. This is appropriate for a smaller solar plant having a point of interconnection (POI) at 34.5 kV or less. For a larger plant, a second transformer is required to step from the collector voltage to the sub-transmission or transmission voltage level. Due to the relatively small size of the solar plant, the impedance and charging of the collector system are ignored. The single equivalent of the solar plant is modeled as a conventional generator coupled to a 480 volt bus or 600 volt bus [
41]. The aggregator active power output (Pgen), minimum reactive power output (Qmin) and maximum reactive power output (Qmax) should tally with the solar plant capability. The reactive power capability is dependent on the number of converters available, and the need to meet interconnection requirements [
36].
4. Conclusions
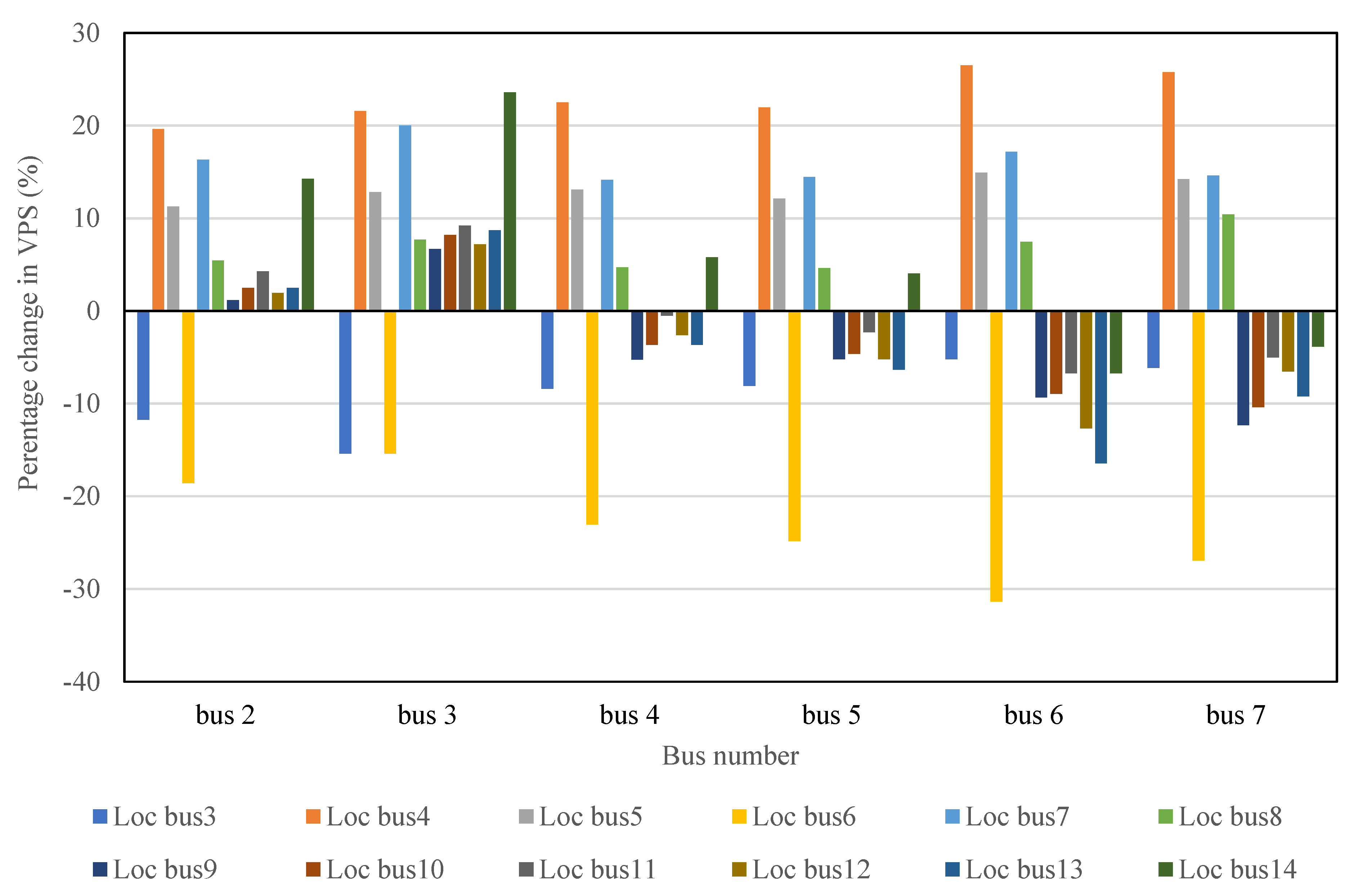
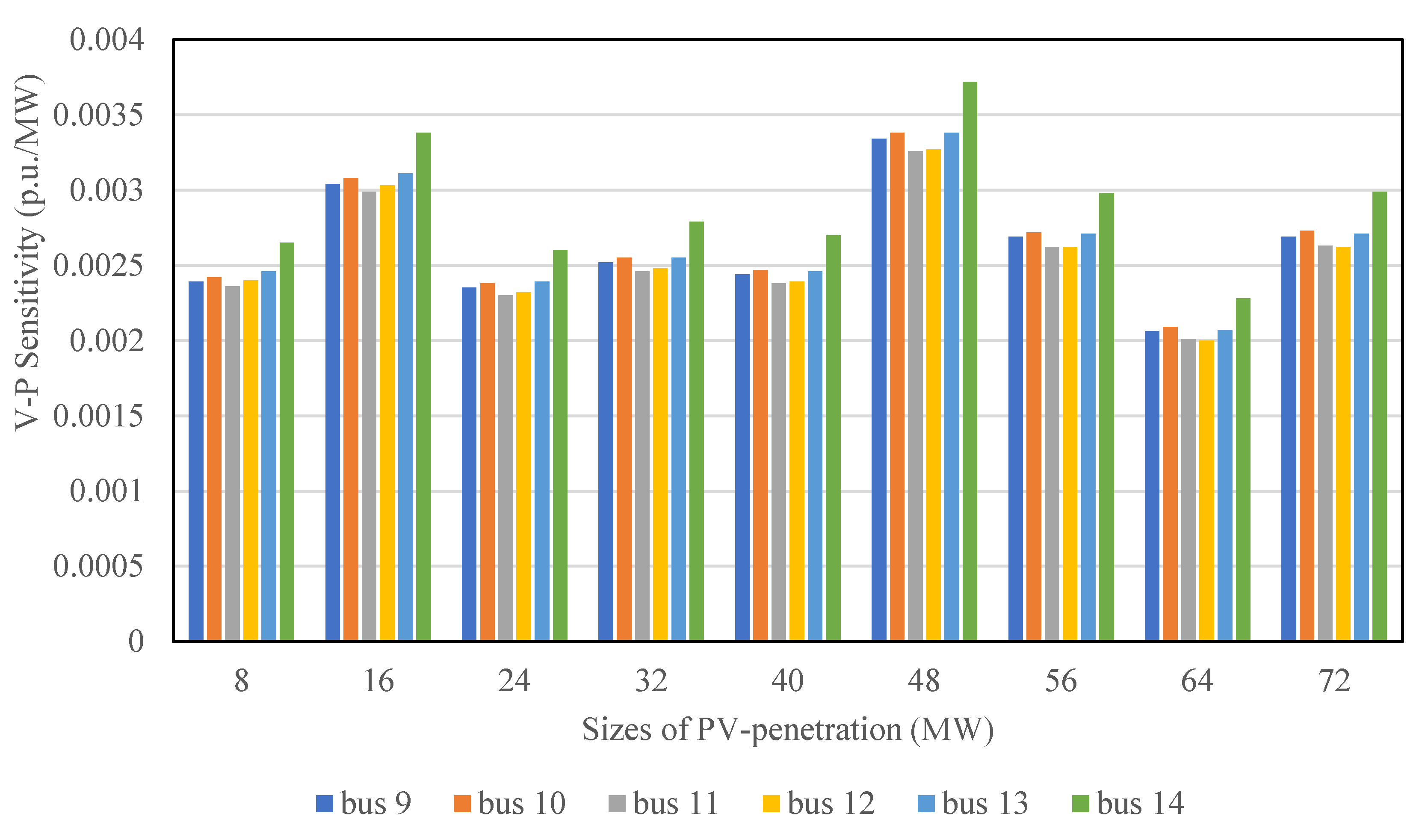
This study evaluated the influence of solar photovoltaic generation in power systems voltage stability based on variable power factor control, variable static voltage droop control, increasing penetrations, as well as the application of the concept of percentage change in voltage–power sensitivity to determine the best installation site for SPVG in the power system. The analysis was done for American standard IEEE-14 Bus Benchmark Network using the PowerWorld simulator. It was observed, from the variable power factor (pf) control impact on the active power margin, and reactive power margin, that there was a 5.4% (34.51 MW) rise of maximum power generated with a decreasing pf control value from unity to 0.96 but a 3.9% (24.9 MW) increase at the 0.94 pf control value and 5.1% (32.72 MW) increase at 0.9 pf while the reactive power marginal loading improved continuously and a total of a 49.2% (24.19 MVAr) increase was recorded at the 0.9 pf control value. It follows from above that the power system voltage stability threshold and power loadability margin were capable of rising and falling with a decreasing pf control value. Additionally, the variation of static voltage droop control values of RES at the interconnection point was found to have a negligible impact on reactive power loading at the interconnection points. In extension, the optimal installation site for SPVG operated at a fixed pf control value with variable penetrations was determined using PCVPSbased technique.
From the simulation results it could be concluded that in the steady-state analysis of the grid integrated power system the effects of pf control, voltage droop control should be considered by power grid engineers for effective system operation and, equally, the application of the percentage change in voltage–power sensitivity should be extended to real networks to determine the best positions for multiple installations of renewable energy resources. Future studies will be focused on the comparison of this concept with other optimization techniques.