Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Lithium-Ion Cobalt Battery with Applicability in HEVs/EVs—A Comparative Study
Abstract
:1. Introduction
2. Lithium-Ion Battery-Cell Modelling and Validation
- (1)
- BMS—definition, multitask safety functions, hardware and software components.
- (2)
- Battery selection criteria.
- (3)
- Battery parameters test.
- (4)
- Disturbances that affect battery functionality and the life span.
- (5)
- Measurement and estimation.
- (6)
- Cell modelling and validation test.
2.1. Battery Management System; Definition, Multitask and Safety Functions, Hardware and Software Components
- Estimation and monitoring the battery SOC/SOH.
- The currents balancing algorithm.
- FDDI estimation techniques.
2.2. Battery Selection Criteria
2.3. Battery Parameters Test
2.4. Disturbances that Affect the Battery Operation and the Life Span
2.5. Li-Ion Battery SOC—State of the Art of Measurement and Estimation Methods Reported in the Literature
- (1)
- Conventional direct measurement methods.
- (2)
- Adaptive filter algorithms.
- (3)
- Learning algorithms.
- (4)
- Non-linear observers.
- (5)
- Hybrid methods.
2.5.1. Conventional Direct Measurement Methods
- (1)
- Laboratory tests and chemistry dependent methods. In the literature are reported the main four cell modelling methods that are briefly presented in [10]. Among these we highlight the following:
- A laboratory method for determining SOC—even if it is not suitable for the field of HEV applications, it is still one of “the most accurate SOC measurement” methods [10]. This method consists of completely discharging the battery, recording the “discharged ampere-hours” and then determining the “remaining cell capacity available”.
- Chemistry-dependent methods for other chemistries—unsuitable for Li-ion batteries.
- Open-circuit voltage (OCV) method. This method uses “the stable electromotive force (EMF) of the open circuit” and the SOC relationship to “estimate the SOC value”, as is stated in [17]. In [10] are presented in detail some reasons why this method is inadequate for the dynamic estimation of the Li-ion battery SOC. Moreover, since its OCV = f (SOC) characteristic is almost flat for a considerably broad range of SOC values, it isn’t easy in this approach to estimate SOC more accurately [18].
- Terminal voltage measurement method. The terminal voltage of the Li-ion battery is “based on the voltage drops on the internal impedances when the battery is discharging. Thus the EMF of the battery is proportional to the terminal voltage” [18]. Moreover, since the “EMF of the battery is approximately linearly proportional to the battery SOC, the terminal voltage is also approximately linearly proportional to SOC” [18]. The “disadvantage of this approach is a large estimated error in the terminal voltage of the battery at the end of battery discharge; it is due to a sharp drop of the terminal voltage” [18].
- (2)
- Electro-chemical method. In this approach, it is “estimated the average amount of Li concentration in the positive or negative electrodes” using “partial differential equations“ [17]. These models may achieve an “accurate terminal voltage prediction”, but “it would be difficult to measure all the required physical parameters on a cell-by-cell basis in a high-volume consumer product” [8].
- (3)
- Impedance direct measurement method. In this approach, the “measurements provide knowledge of several parameters, the magnitudes of which may depend on the SOC of the battery” [18]. Since the “battery impedance parameters and their variations with SOC are not unique for all battery systems” it is required many impedance experiments to identify its parameters [18].
- (4)
- SOC Estimation spectroscopy method. This method uses the battery impedance and internal resistance “to describe the intrinsic electric characteristic under any current excitation, if temperature, SOC and SOH are fixed”, but “it is not suitable for use in HEVs/EVs” applications [17]. The reason you can find in the same reference [17]. According to [17], “it is tough to measure online electrical impedance spectroscopy over a wide range of AC frequencies at the different charge and discharge currents, especially when the SOC and impedance relationship is not stable, and the cost is expensive”. Also, is mentioned in the previous subsection that the internal resistance of the Li-ion battery is measured in direct current (DC) and requires the “value of the voltage and current at a small-time interval” [17]. Then, the battery SOC “may be indirectly inferred by measuring present battery cell impedance” [10] and the battery internal resistance correlated “with known impedances at various SOC levels” [8,18].
- (5)
- Ampere-hour counting method. Based on this method is calculated “the amount of charge that flows in and out of the battery” [10]. In this approach, the SOC is estimated directly in an open loop, so the SOC estimate is not accurate due to the current measurement errors. Instead, in a closed loop, the same method can estimate the SOC more accurate [8,10]. The SOC estimate accuracy degrades the accuracy significantly when the battery is not “fully discharged after a complete charging cycle”. Since in the most cases, the battery doesn’t perform a full charge followed by a full discharge, “a significant drift is difficult to avoid”, and thus, since “the signal drifts, the efficiency of coulomb counting decreases” [10]. Also, the Ampere-hour (Ah) counting method becomes “less effective when the battery self-discharges is subject to temperature changes” [10]. The “unknown initial value of battery SOC, capacity fading, self-discharge rate, and current sensor errors are the main sources of errors for Ah counting method” [17]. The presence of “an accurate measurement sensor and a predefined calibration point can overcome the method’s drawbacks” [17]. Additionally, the estimation error “can be maintained at a low value by defining a correction factor and a re-calibration point” [10]. It is worth mentioning that this method is more accurate compared to other SOC calculation methods [10,17]. The most significant advantage of the Ampere-hour counting method is its low power computation cost, and it is secure and reliable when the sensor current measurements are accurate, and a re-calibration point is accessible [10,17].
- (6)
- Model-based method. Since the “previous mentioned methods are not appropriate for online SOC estimation and to achieve an accurate online SOC estimate value, suitable battery models need to be developed” [17]. Among the most suitable models for online SOC estimation are the electrochemical and equivalent circuit models (ECMs) [10,11,17]. More details about ECMs models you can find in [3,4,7,8,9,10,11,12,17]. In closing, “an ideal ECM should be able to simulate the actual battery terminal voltage to any charging or discharging battery input current”, as is stated in [17].
2.5.2. Adaptive Filter Estimators
2.5.3. Learning Methods
2.5.4. Linear and Nonlinear Observers
2.5.5. Hybrid Methods
2.6. Li-Ion Battery Cell—Model Selection, Validation and Case Study
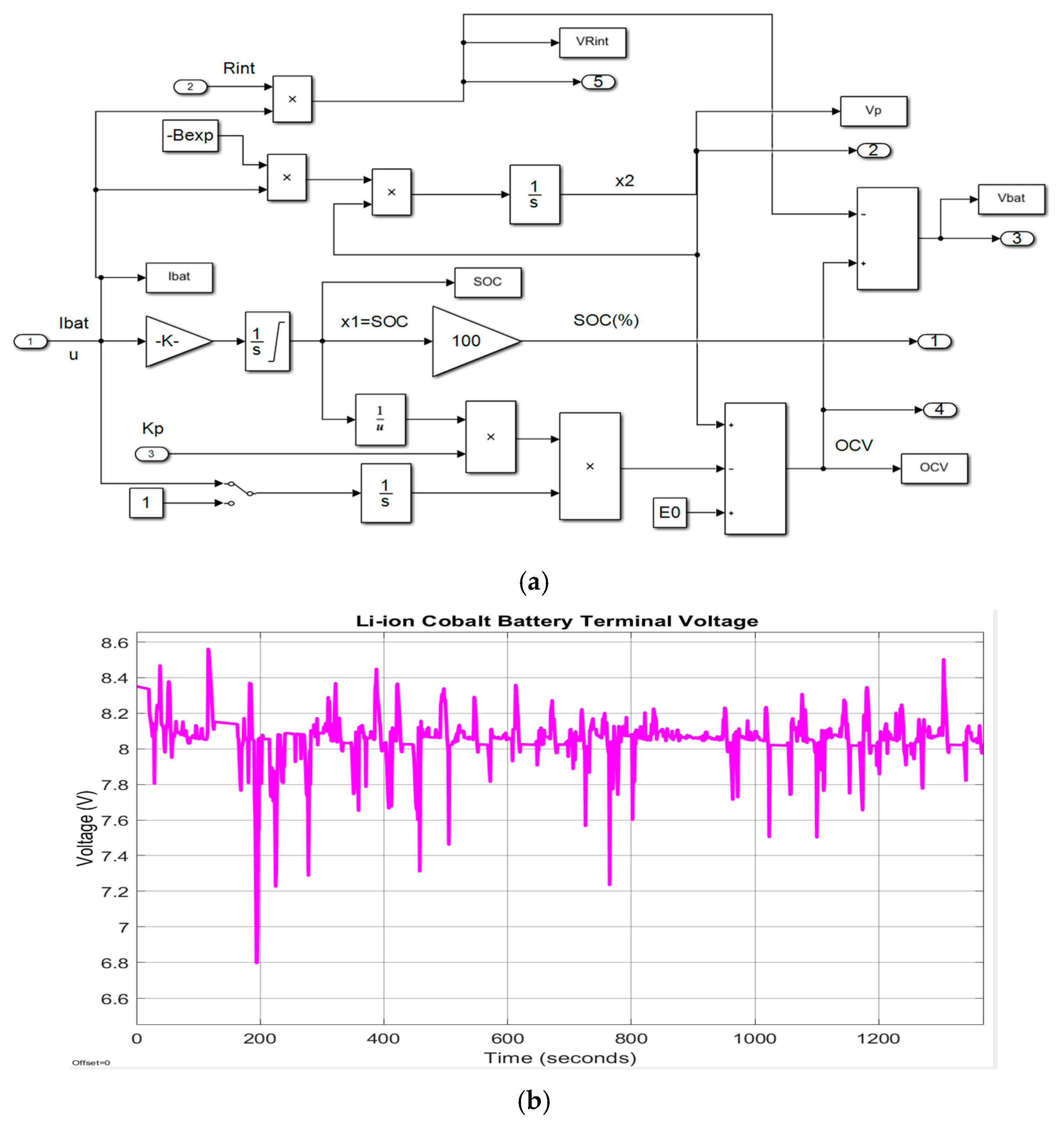
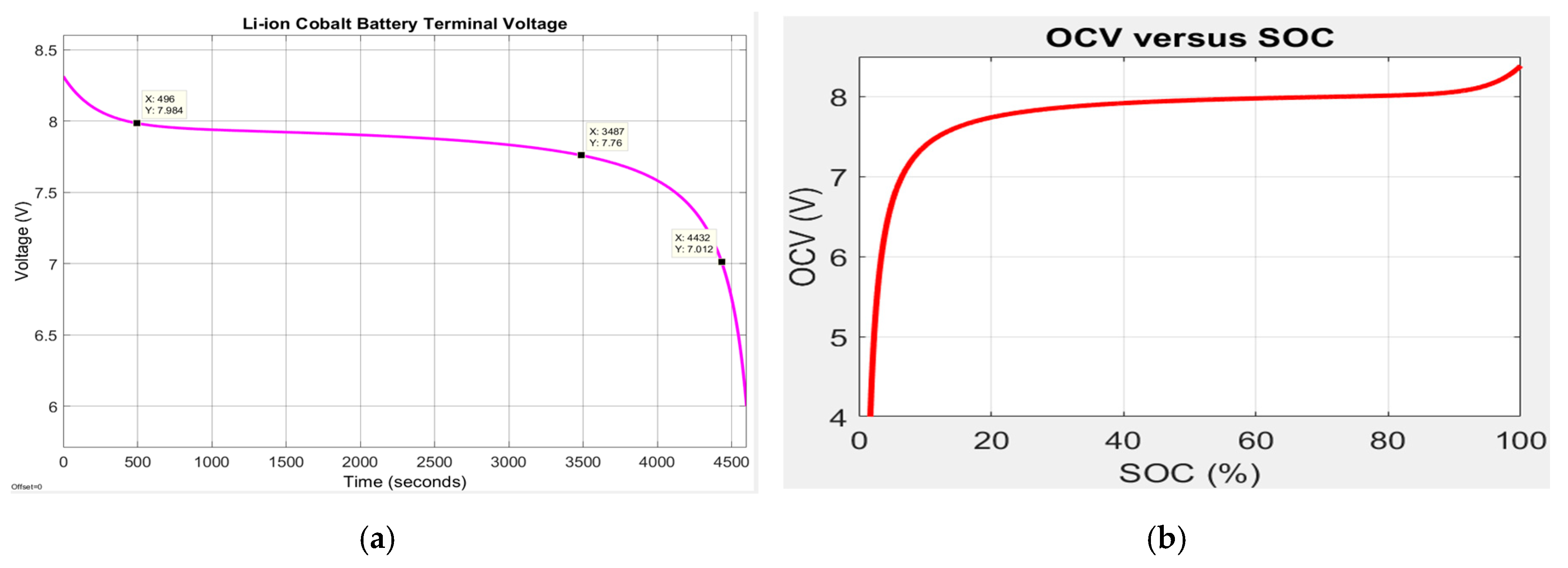
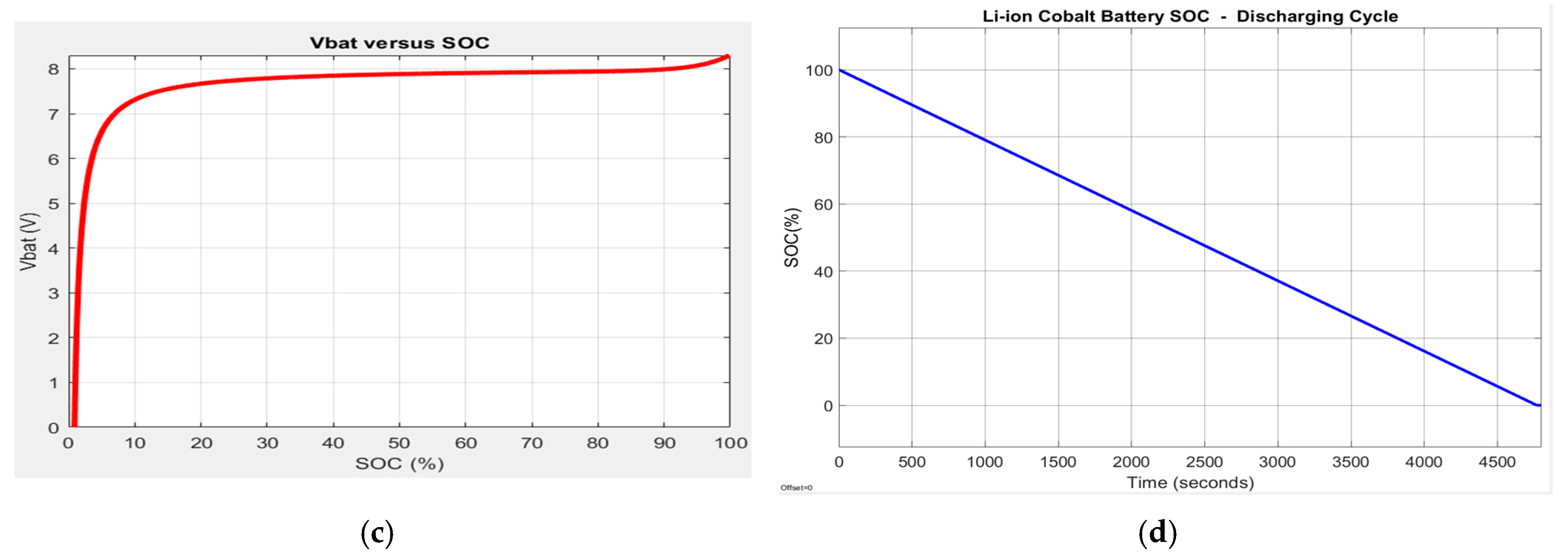
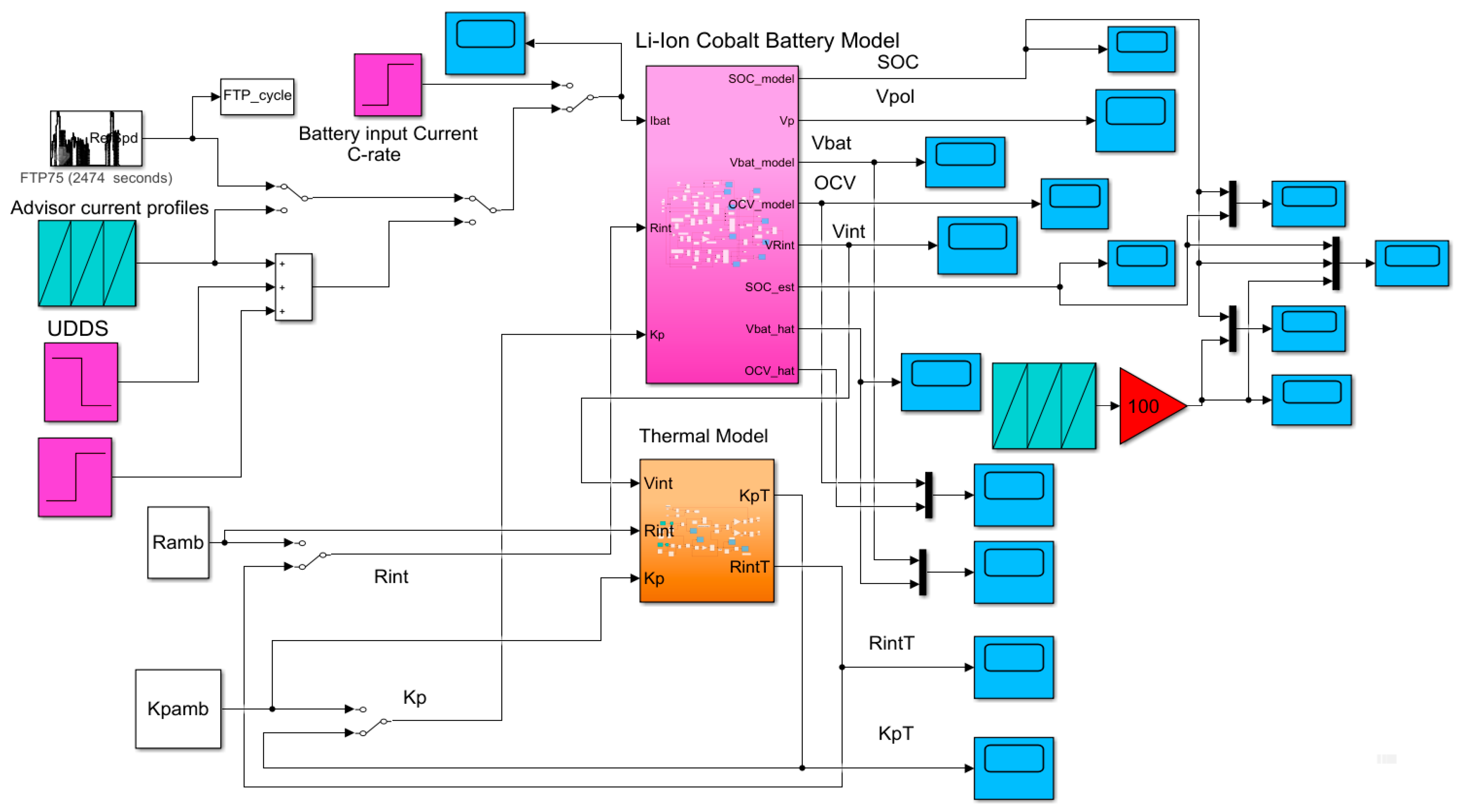
2.6.1. Li-Ion Cobalt MATLAB Simscape Model
2.6.2. Li-Ion Cobalt Model in Continuous Time State Space Representation
2.6.3. Li-Ion Model in Discrete Time State Space Representation
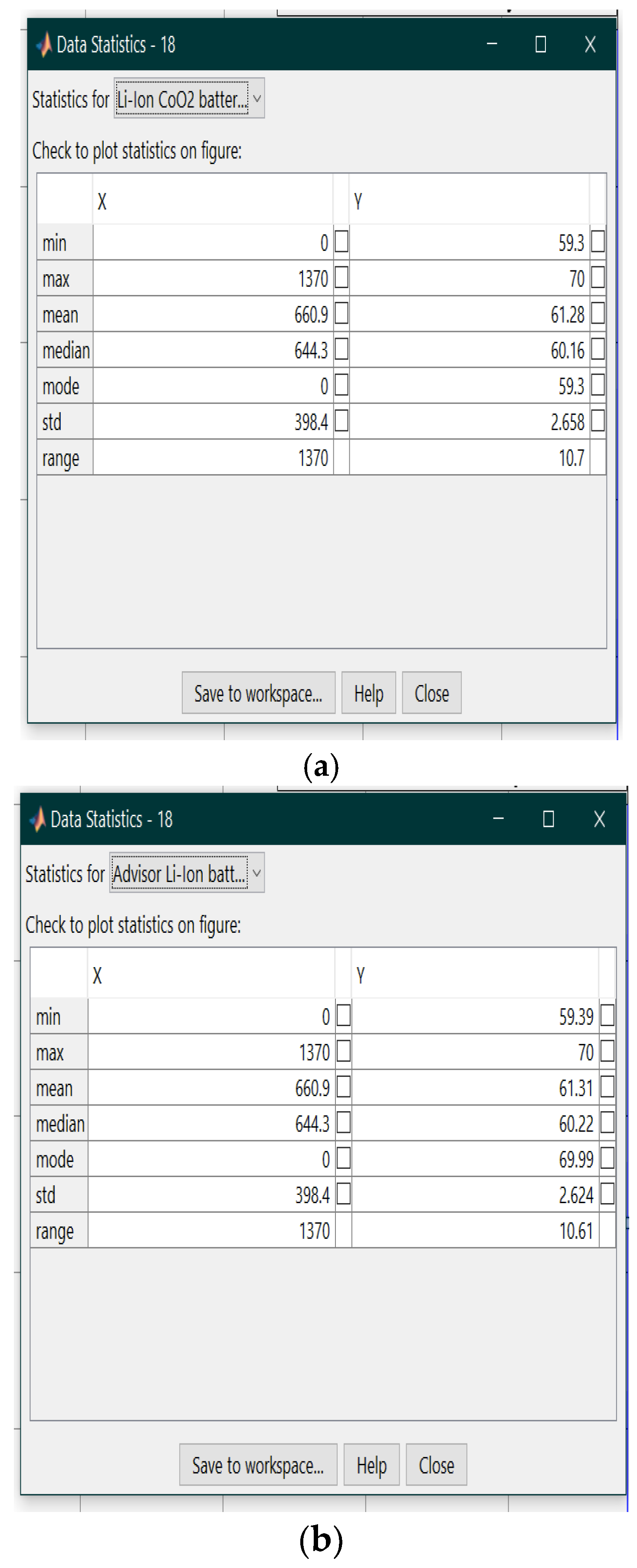
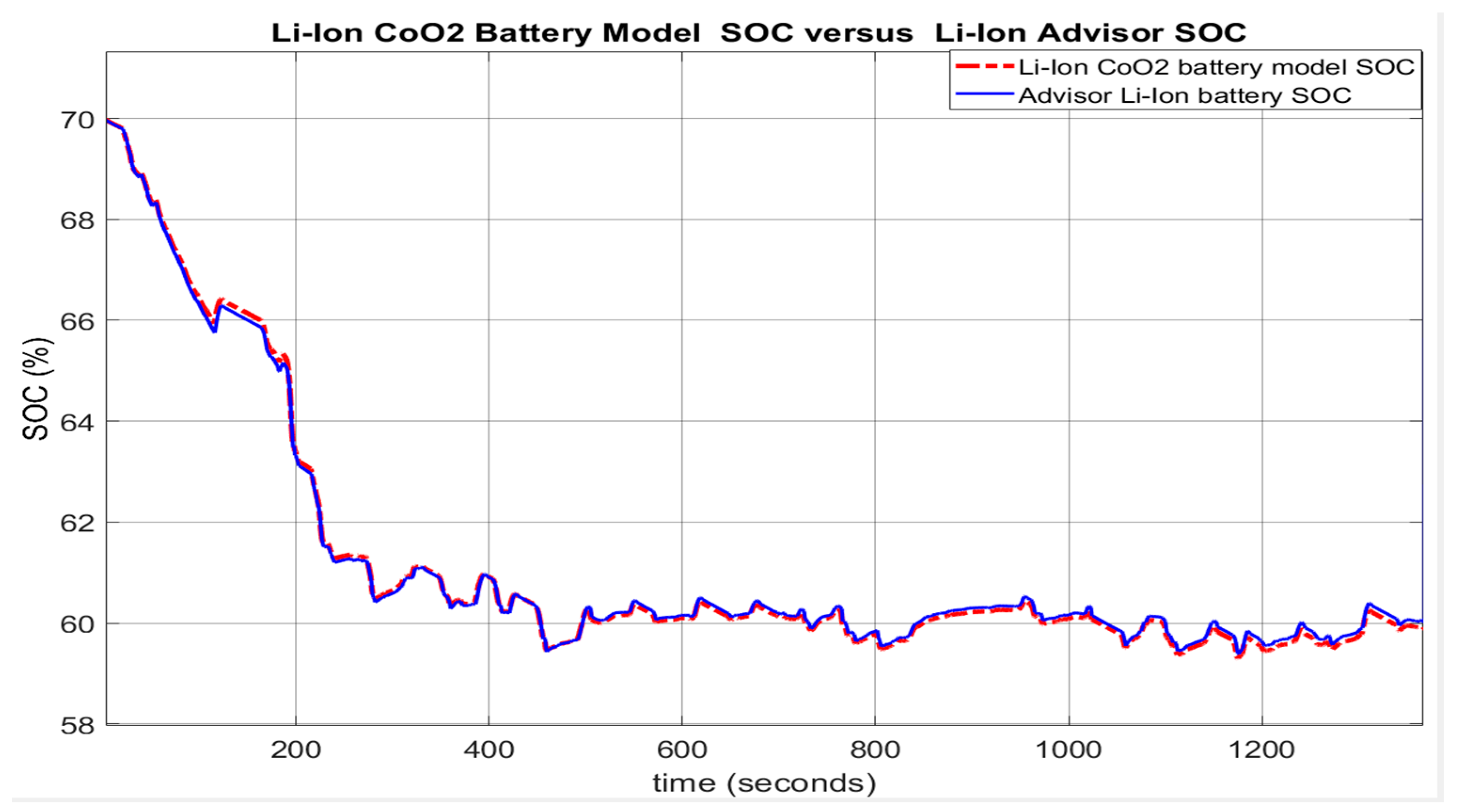
2.6.4. Model Validation on ADVISOR MATLAB Integrated Platform
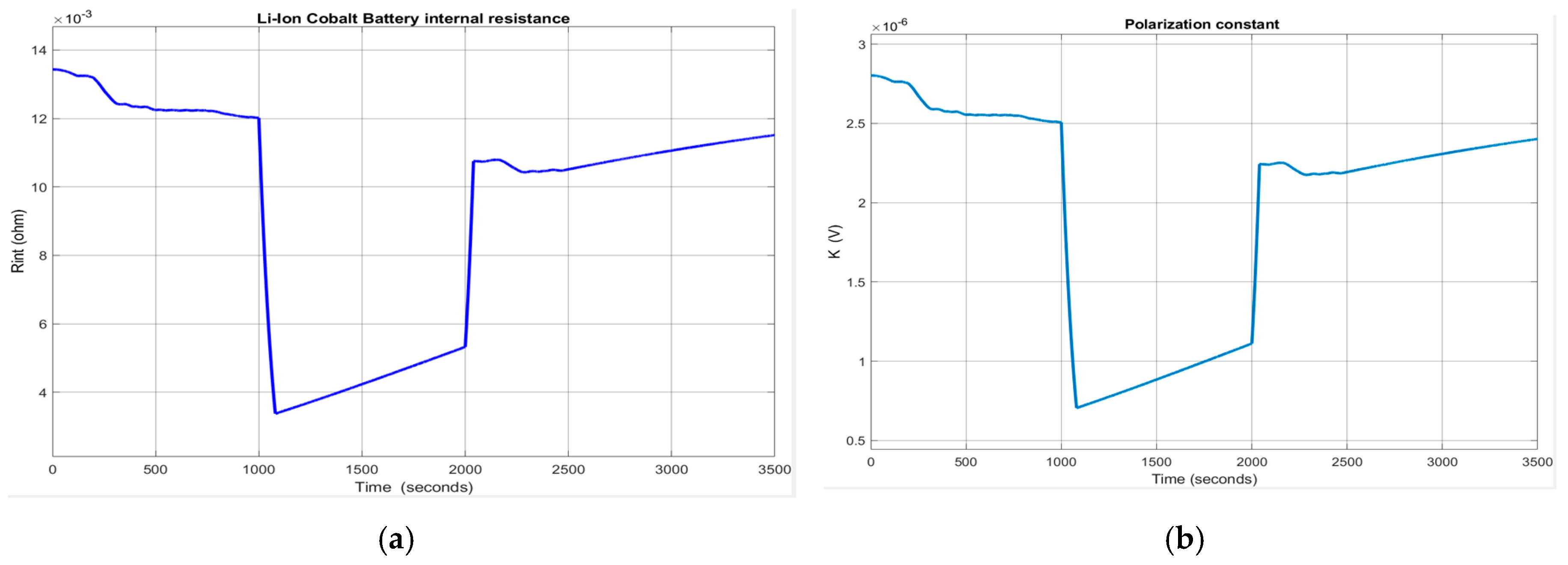
2.7. Li-Ion Cobalt Battery Thermal Model
3. Li-Ion Co Battery State of Charge Estimation Algorithms
3.1. Li-Ion Cobalt Battery-Adaptive Extended Kalman Filter SOC Estimator
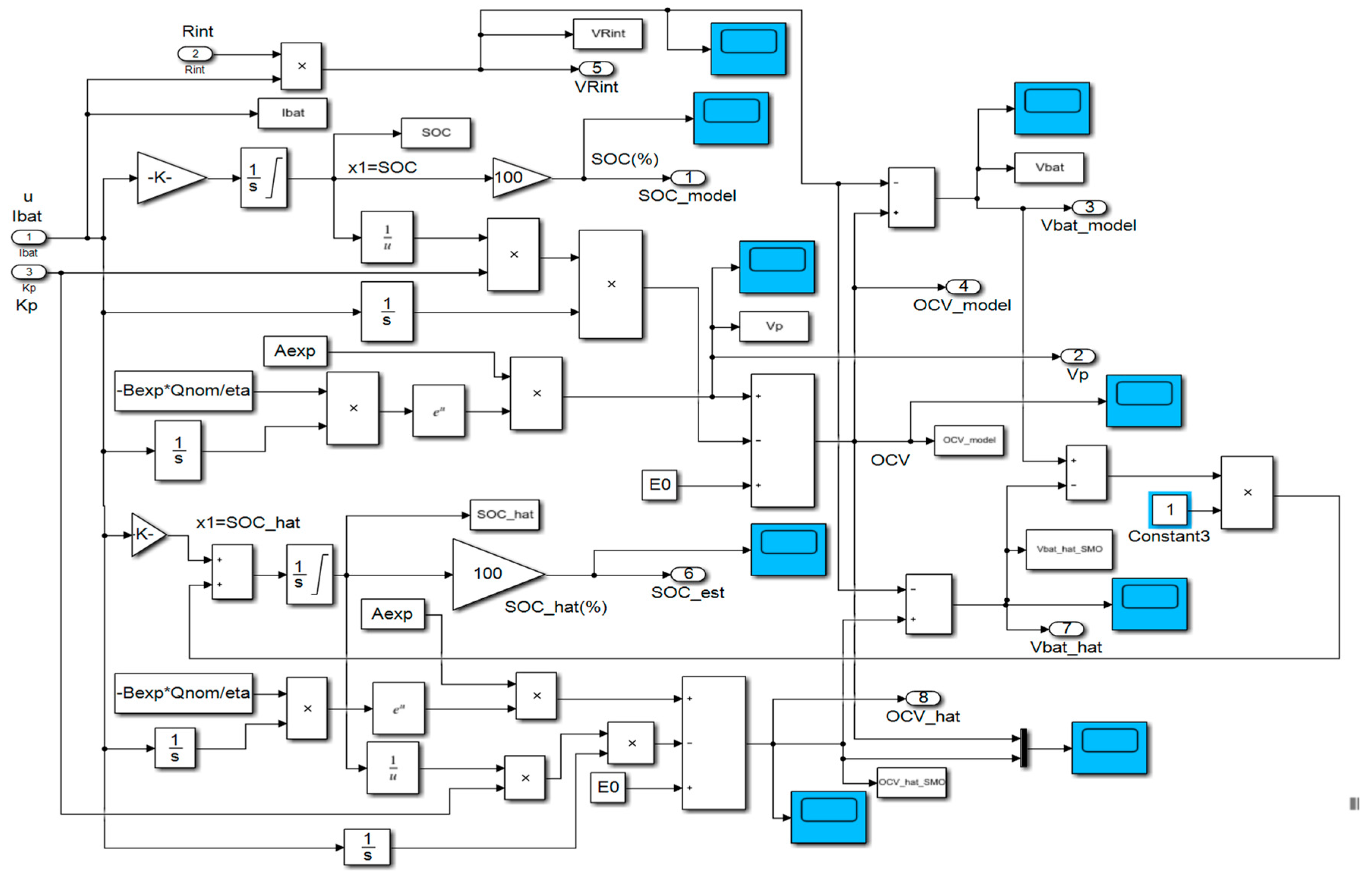
3.2. Li-Ion Cobalt Battery-Linear Observer SOC Estimator with Constant Gain
3.3. Real-Time MATLAB Simulation Results
- ○
- R1-scenario—changes in SOCini from 70% for UDDS and UDDS-EPA, 80%-FTP, driving cycles tests to:
- ○
- R11—for SOCini = 100%
- ○
- R12—for SOCini = 40%
- ○
- R2-scenario—changes in SOC initial value and in measurement sensor noise level
- ○
- R21—for SOCini = 100%, noise measurement level σ = 0.01(increased from 0.001)
- ○
- R22—for SOCini = 40%, noise measrement level, σ = 0.01(increased from 0.001)
- ○
- R3-scenario: changes in SOC initial value and in the value of the battery nominal capacity due to aging and/or temperature effects.
- ○
- R31—for SOCini = 100%, Qnom = 2.7 Ah (decresed from 5.4 Ah)
- ○
- R32—for SOCini = 40%, Qnom = 2.7 Ah (decresed from 5.4 Ah)
- ○
- R4-scenario: changes in SOC initial values and temperature effects on internal resistance Rint and on polarization constant K
- ○
- R41—for SOCini = 100%, Rint = Rint(T) changes from Rint = 0.01333 [Ω], K = K(T) changes from K = 0.0099892 [V]
- ○
- R42—for SOCini = 40%, Rint = Rint(T) changes from Rint = 0.01333 [Ω], K = K(T) changes from K = 0.0099892 [V]
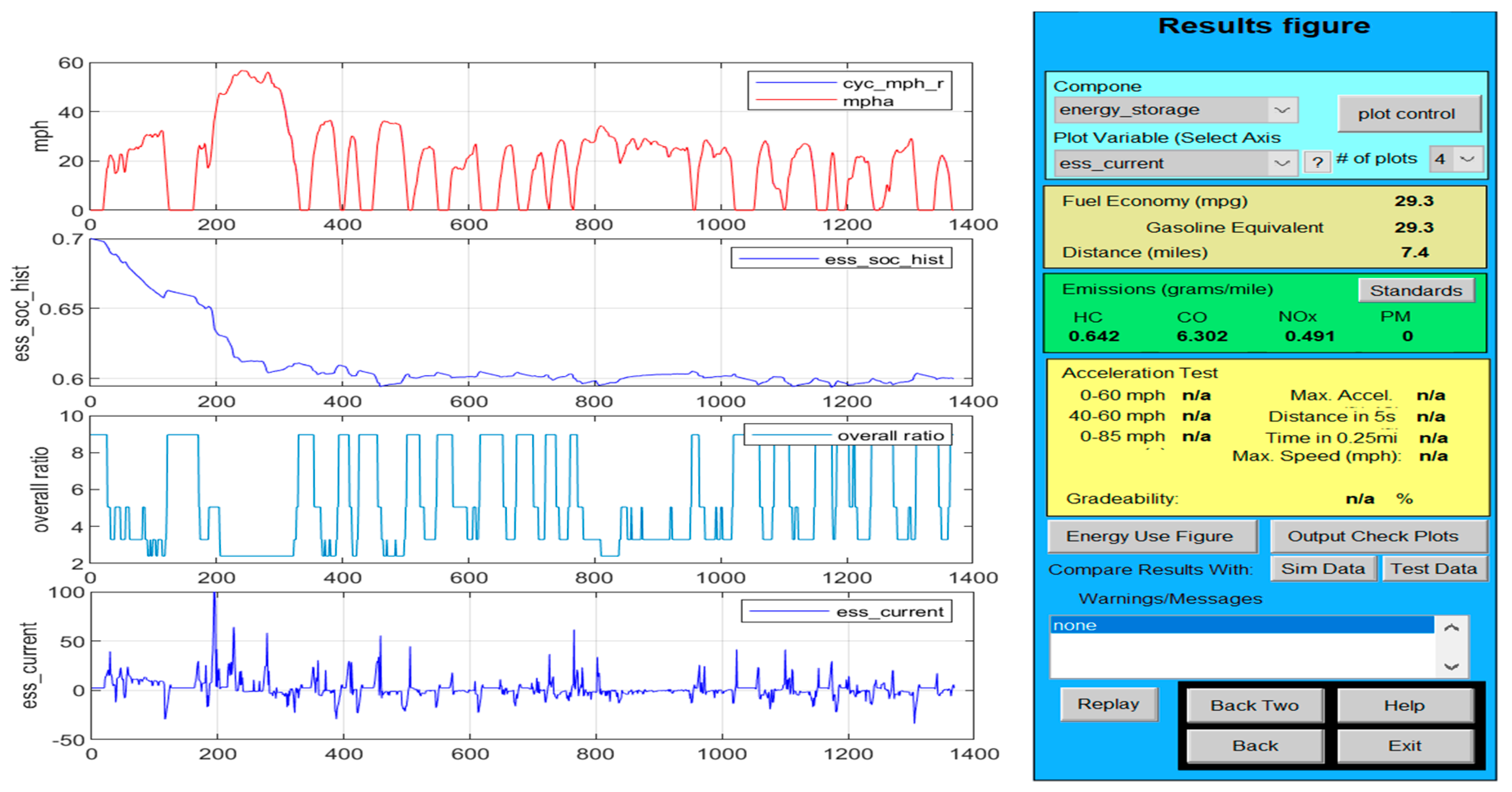
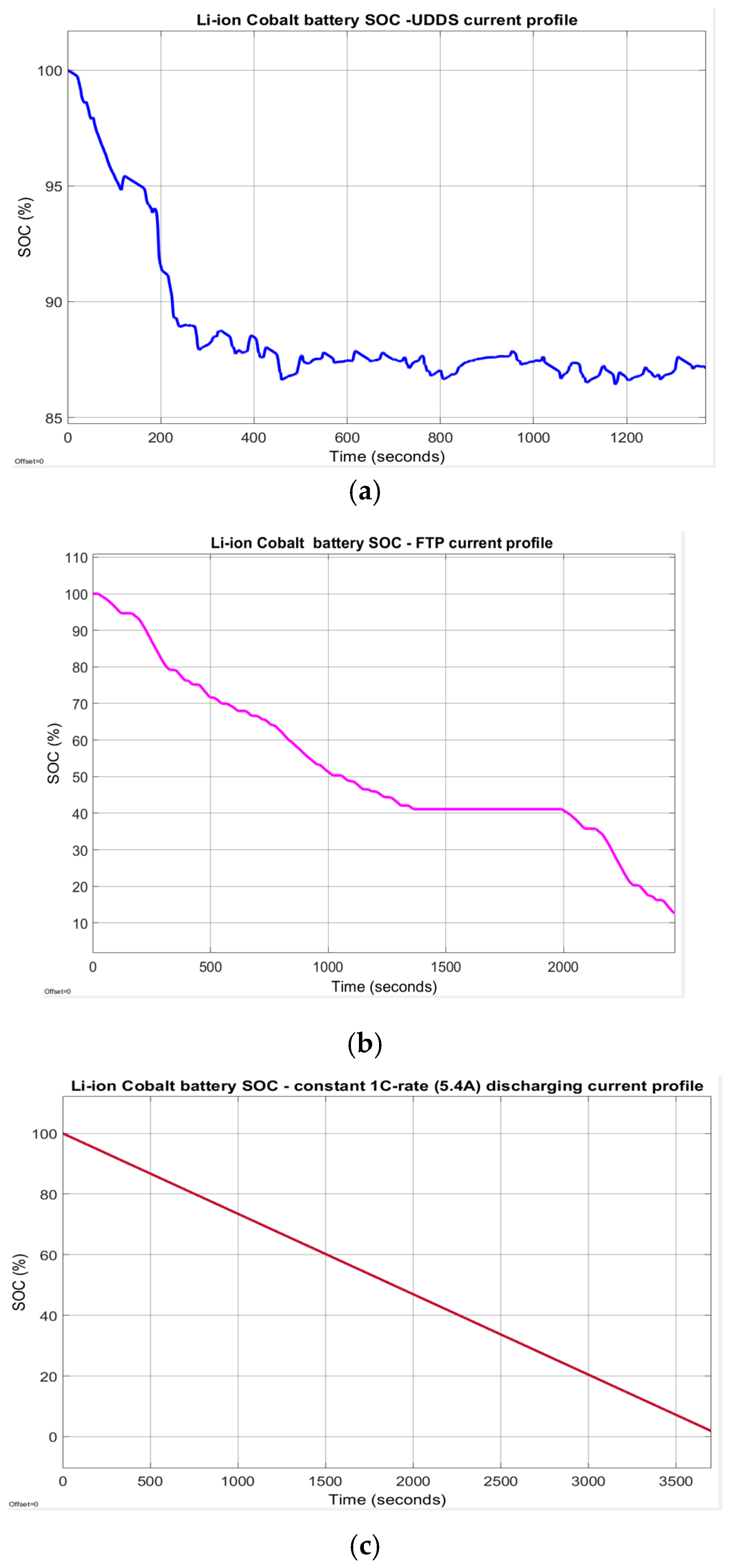
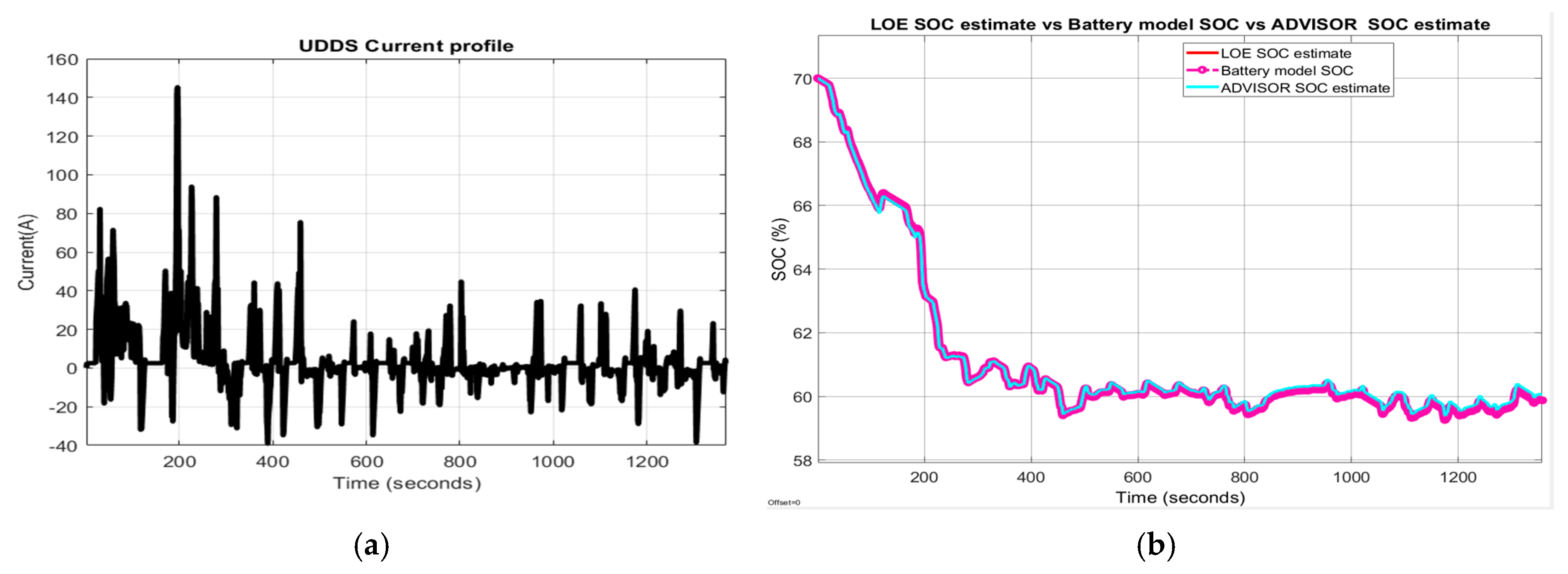
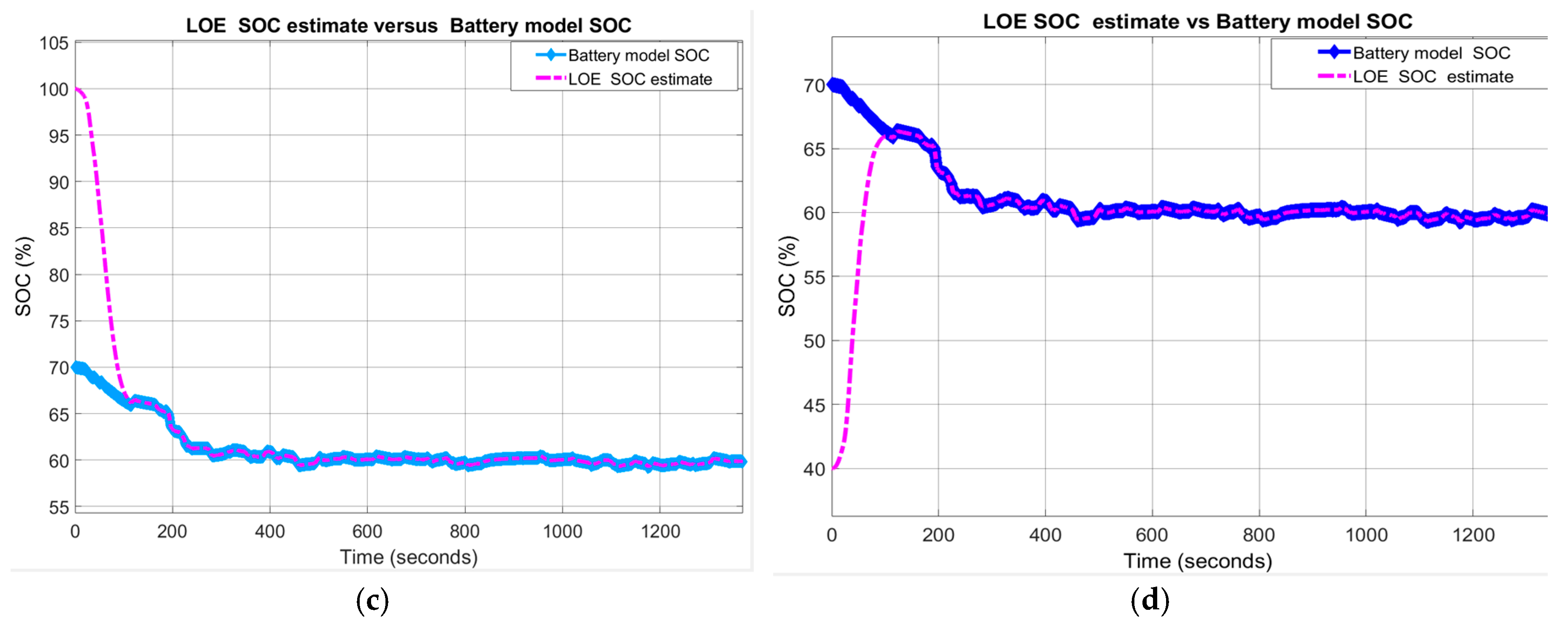
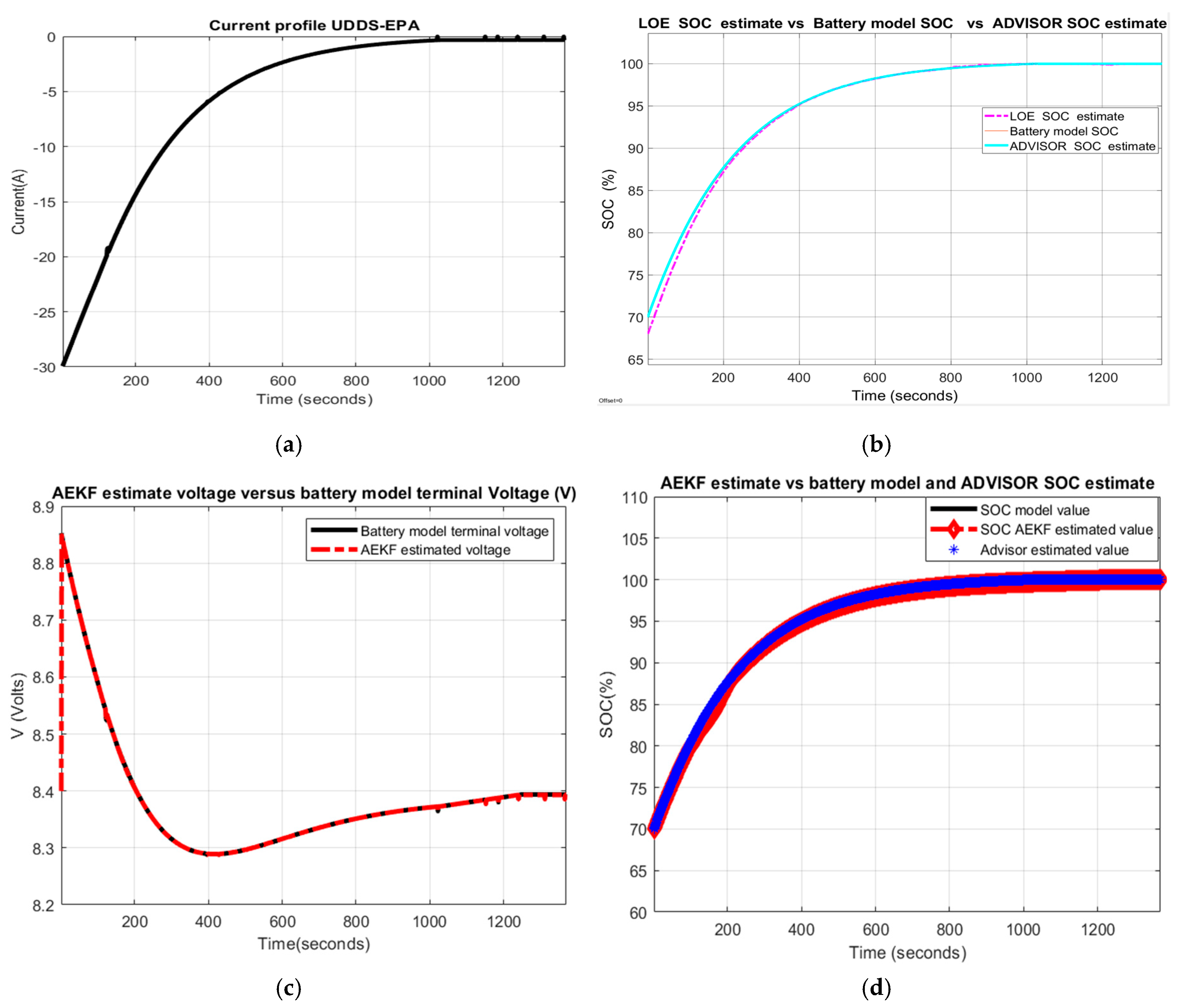
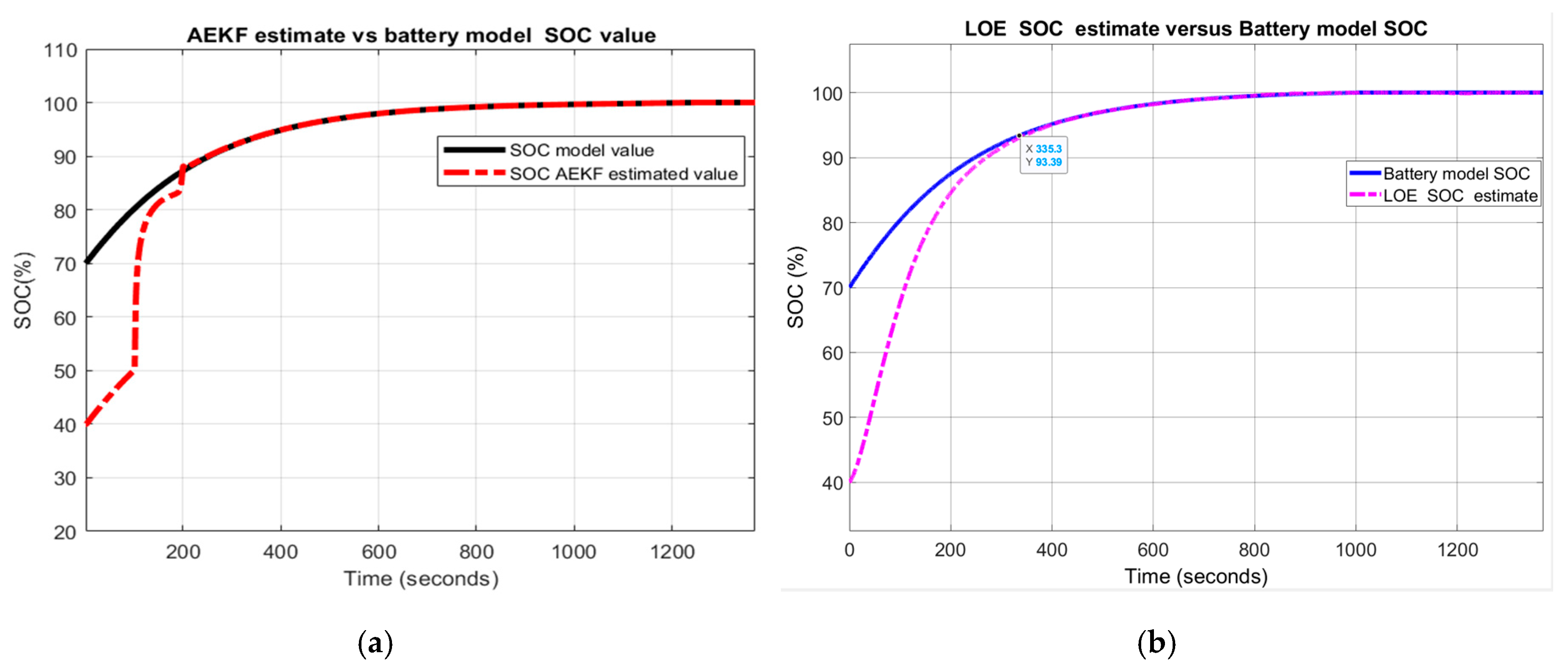
3.3.1. Test 1-UDDS Driving Cycle Profile
A. Li-ion Co generic model accuracy performance
- (a)
- UDDS driving cycle current profile for SOCini = 70%
- (b)
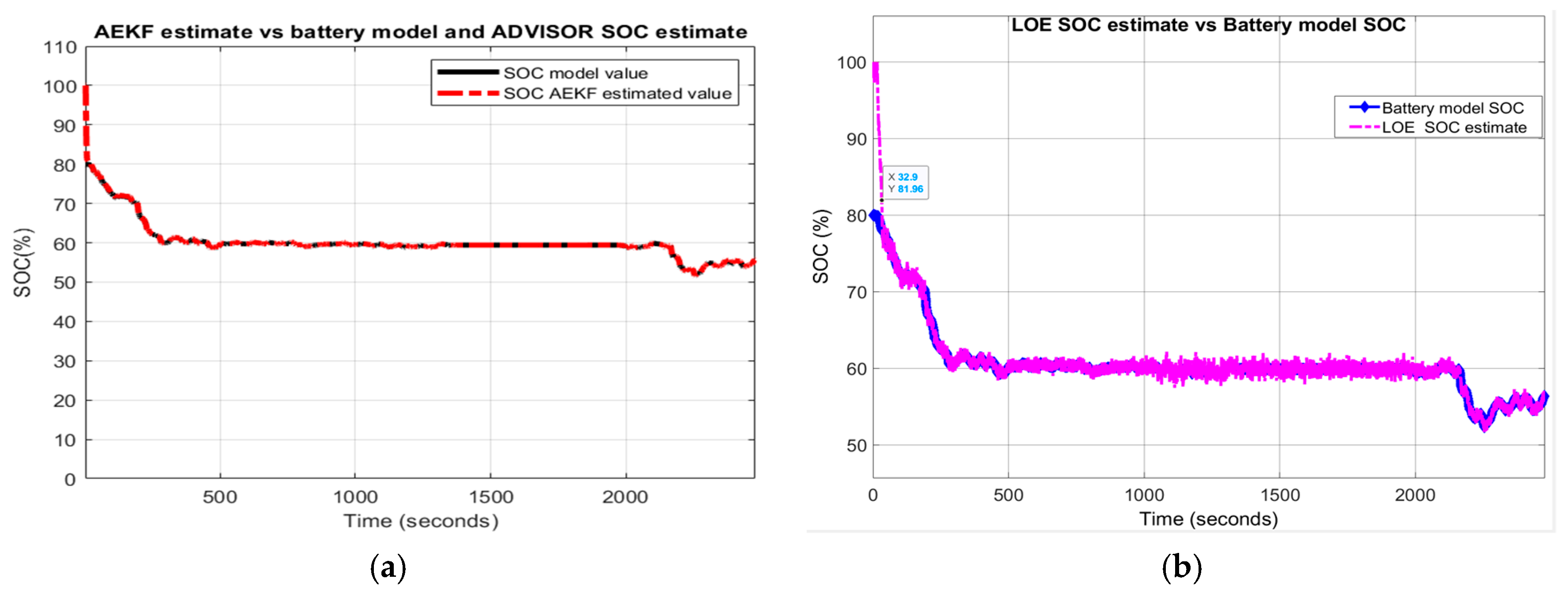
- LOE battery SOC estimate versus the battery model SOC and ADVISOR SOC estimate
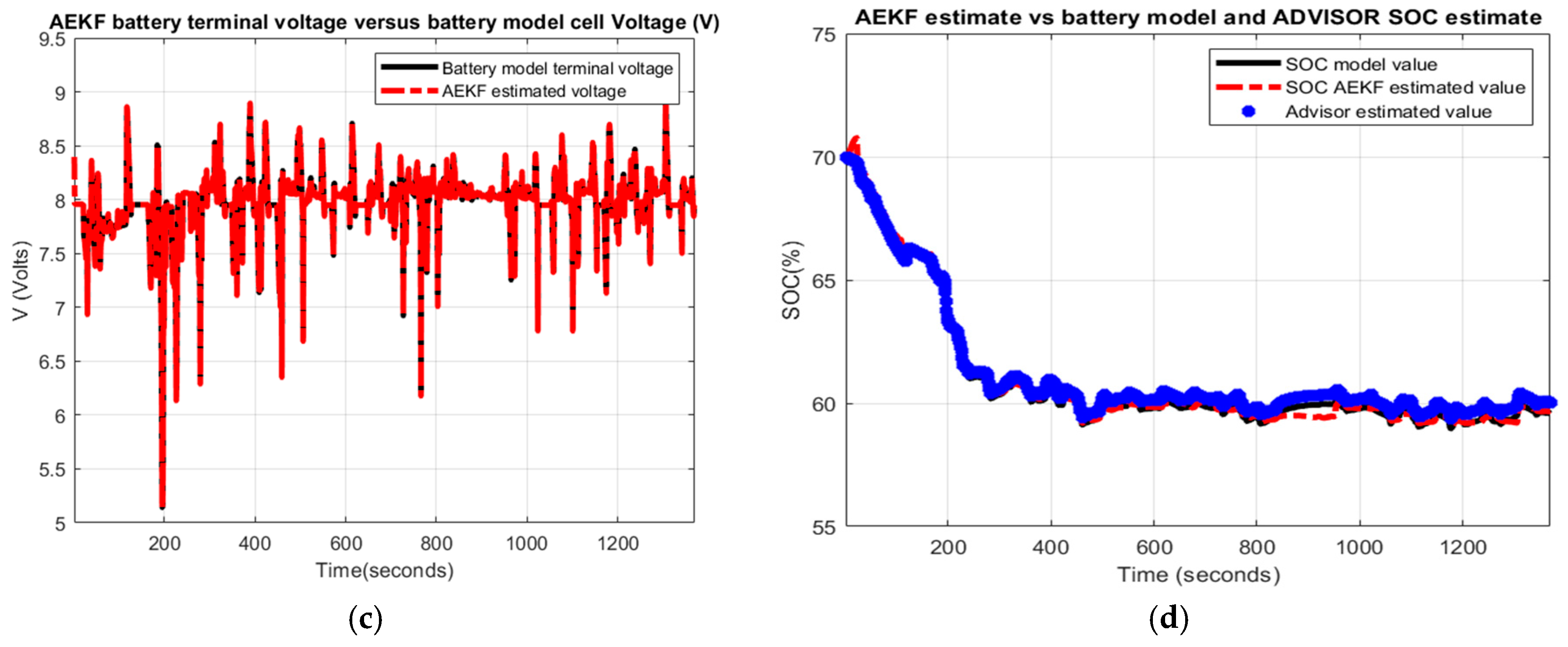
- (c)
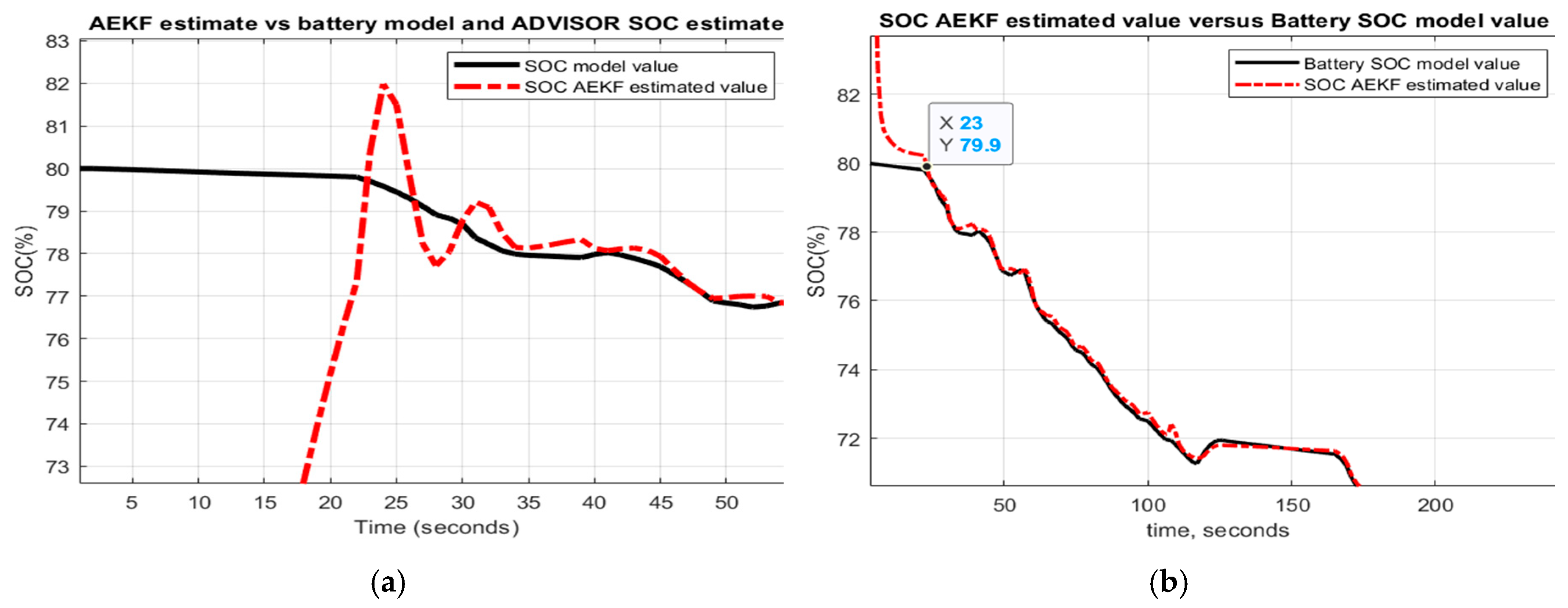
- AEKF battery terminal voltage estimate versus battery cell model terminal voltage
- (d)
- AEKF battery SOC estimate versus battery model SOC and AVISOR SOC estimate
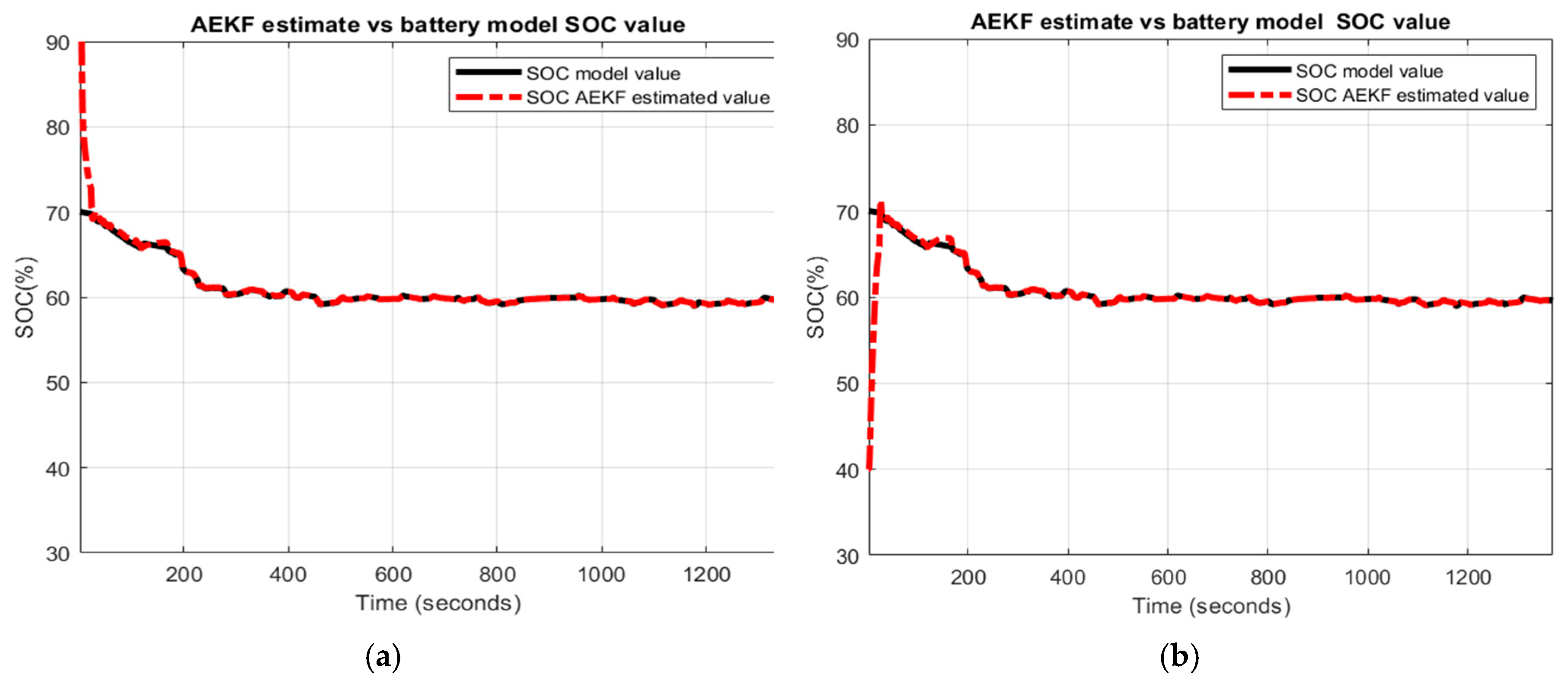
B. Robustness of AEKF and LOE SOC Estimators
- R1-scenario
- R2-scenario
- R3-scenario
- R4-scenario
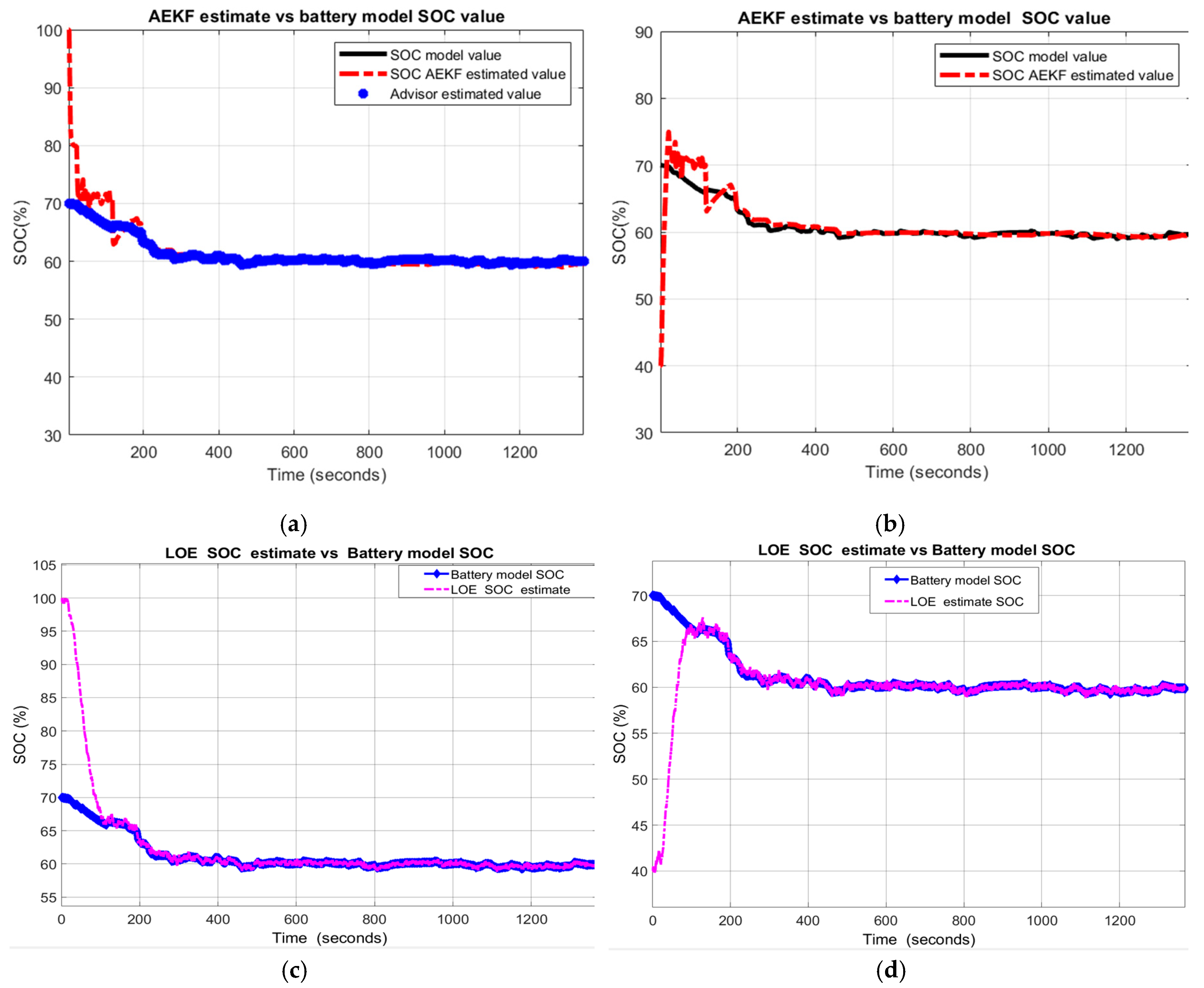
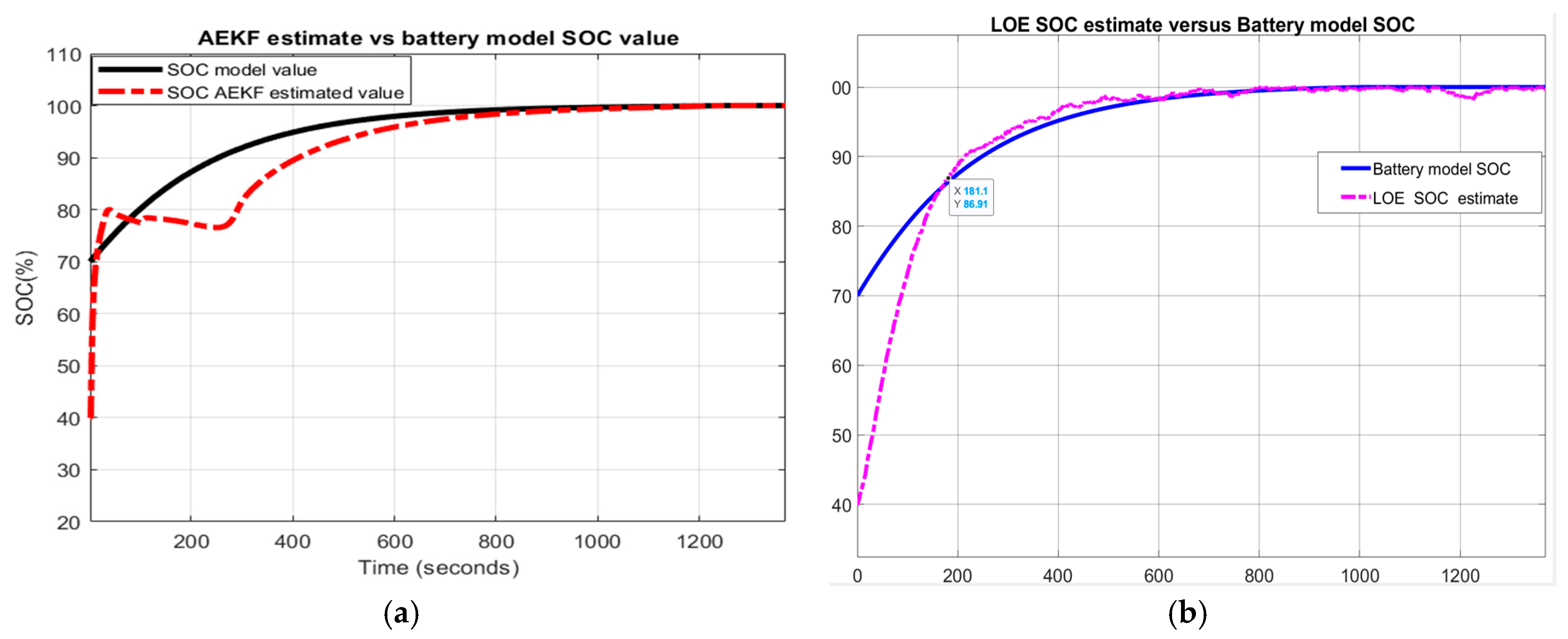
3.3.2. Test 2: UDDS-EPA Charging Current Profile
A. Cobalt Li-ion generic model accuracy and validation
- (a)
- UDDS-EPA driving cycle current profile
- (b)
- LOE SOC estimate versus battery model SOC and ADVISOR SOC estimate
- (c)
- AEKF battery terminal voltage
- (d)
- AEKF SOC estimate versus battery model SOC and ADVISOR SOC estimate
- (e)
- A great SOC accuracy of battery model versus ADVISOR SOC estimate is revealed in Figure 22b.
B. Robustness of AEKF SOC Estimator
- R1-scenario
- R2-scenario
- R3-scenario
- R4-scenario:
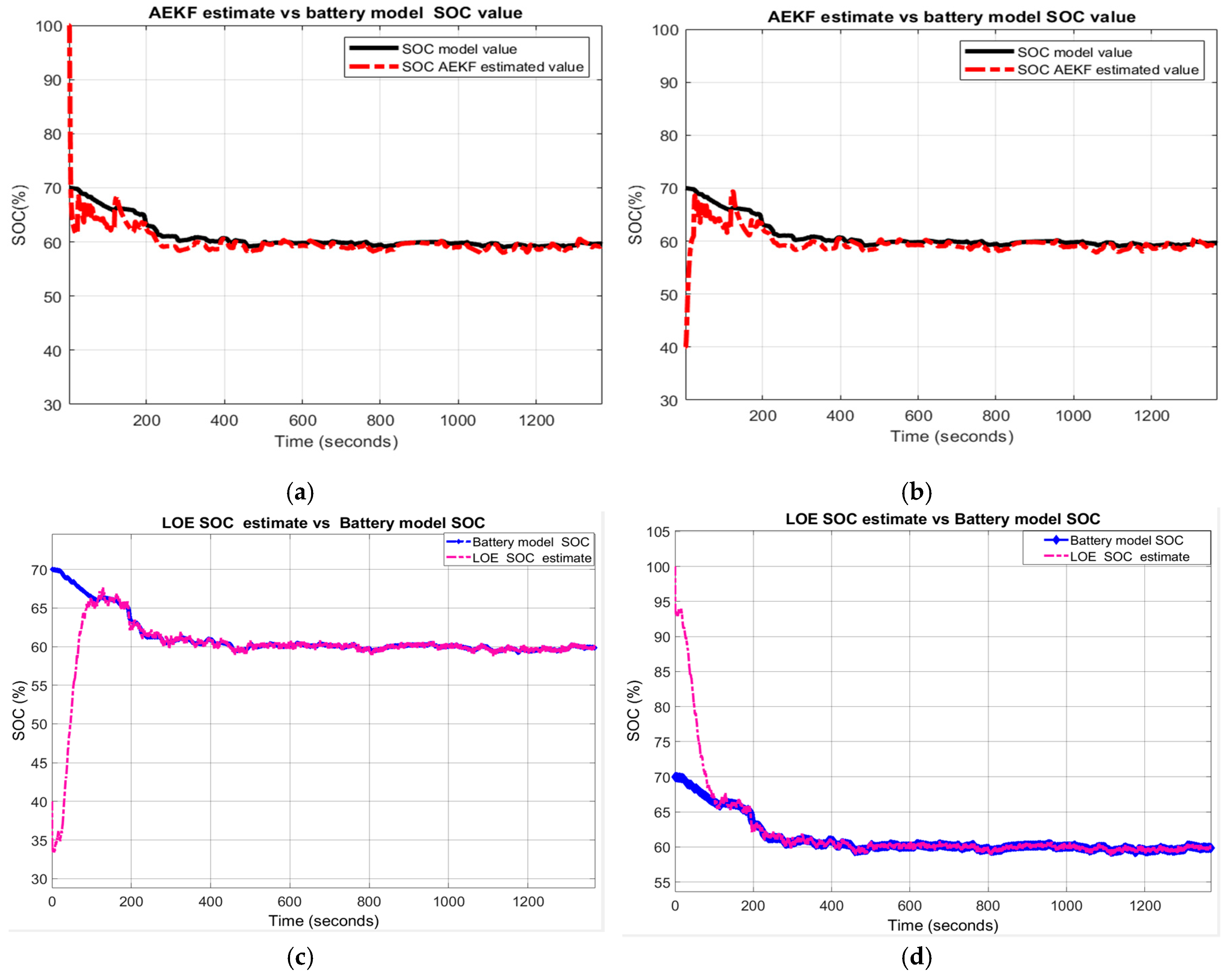
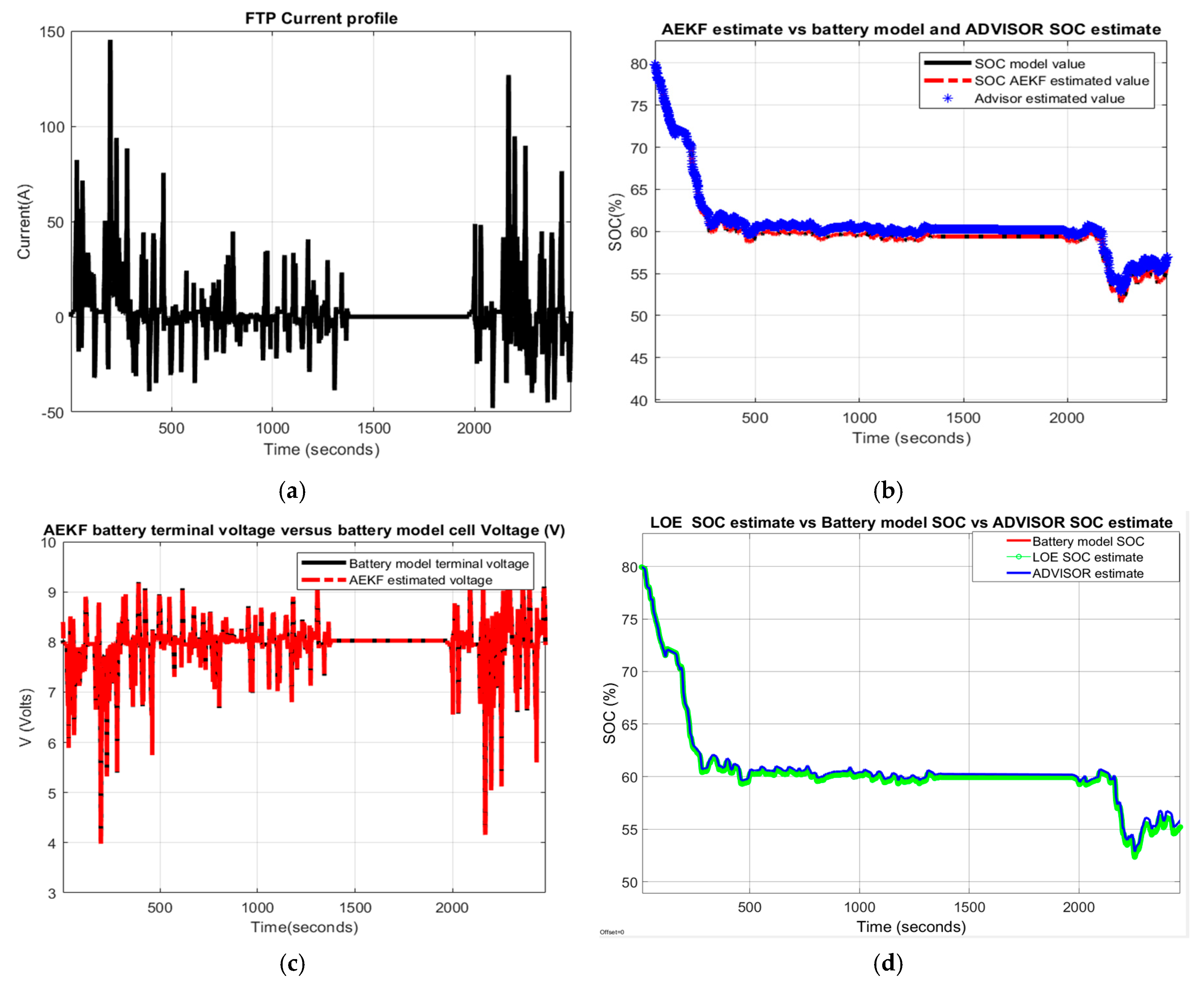
3.3.3. Test 3: FTP-ADVISOR Driving Cycle Current Profile
A. Battery model SOC accuracy and model validation
B. AEKF and LOE SOC estimators robustness
- R1-scenario
- R2-scenario
- R3-scenario
- R4-scenario
4. Discussions
4.1. SOC Estimators’ Convergence Speed
4.2. SOC Estimation Accuracy
4.3. SOC Estimator-Measurement Noise Filtration
4.4. SOC Estimators-Real Time Implementation
4.5. SOC Estimators-Statistical Errors Analysis
5. Conclusions
- Model selection—MATLAB Simscape Li-ion cobalt nonlinear model, simple, practical, accurate, easy to implement in real-time (Section 2.6.1)
- Model development in continuous time state-space representation (Section 2.6.2)
- Model development in discrete time state-space representation (Section 2.6.3)
- Model validation based on three different driving cycles tests, using ADVISOR 3.2 software tool (Section 2.6.4)
- Model implementation in MATLAB R 2019b Simulink environment (Simulink diagram from Figure 8 and Figure 9, Section 2.6.4)
- Thermal model design and Simulink implementation (Simulink diagram from Figure 12 Section 2.7)
- Adaptive Extended Kalman Filter SOC estimator with fading feature—Design and MATLAB implementation, Section 3.1)
- Linear observer SOC estimator-Design and Simulink implementation (Simulink model diagram from Figure 16, Section 3.2)
- MATLAB SOC simulations (Section 3.3)
- ○
- SOC initial value (“guess” value)
- ○
- SOC initial value and driving conditions
- ○
- SOC initial value, temperature effects on internal resistance and polarization constant, and driving conditions.
- ○
- SOC initial value, nominal value of battery capacity due to aging effects/temperature effects and driving conditions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Ni-Cad | nickel cadmium |
| Ni-MH | nickel metal hydride |
| Li-ion Co | lithium-ion cobalt |
| EV | electric vehicle |
| HEV | hybrid electric vehicle |
| BMS | battery management system |
| ADVISOR | advanced vehicle simulator |
| EPA | environmental protection agency |
| UDDS | urban dynamometer driving schedule |
| FTP-75 | Federal test procedure at 75 F |
| SMO | sliding mode observer |
| LOE | linear observer estimator |
| RMSE | root mean squared error |
| MSE | mean squared error |
| MAE | mean absolute error |
| OCV | open-circuit voltage |
| SOC | state of charge |
| SOE | state of energy |
| SOH | state of health |
| DOD | depth of discharge |
| NREL | National Renewable Energy Laboratory |
| UKF | unscented Kalman filter |
| AUKF | adaptive unscented Kalman filter |
Appendix A
Appendix A.1. Figures
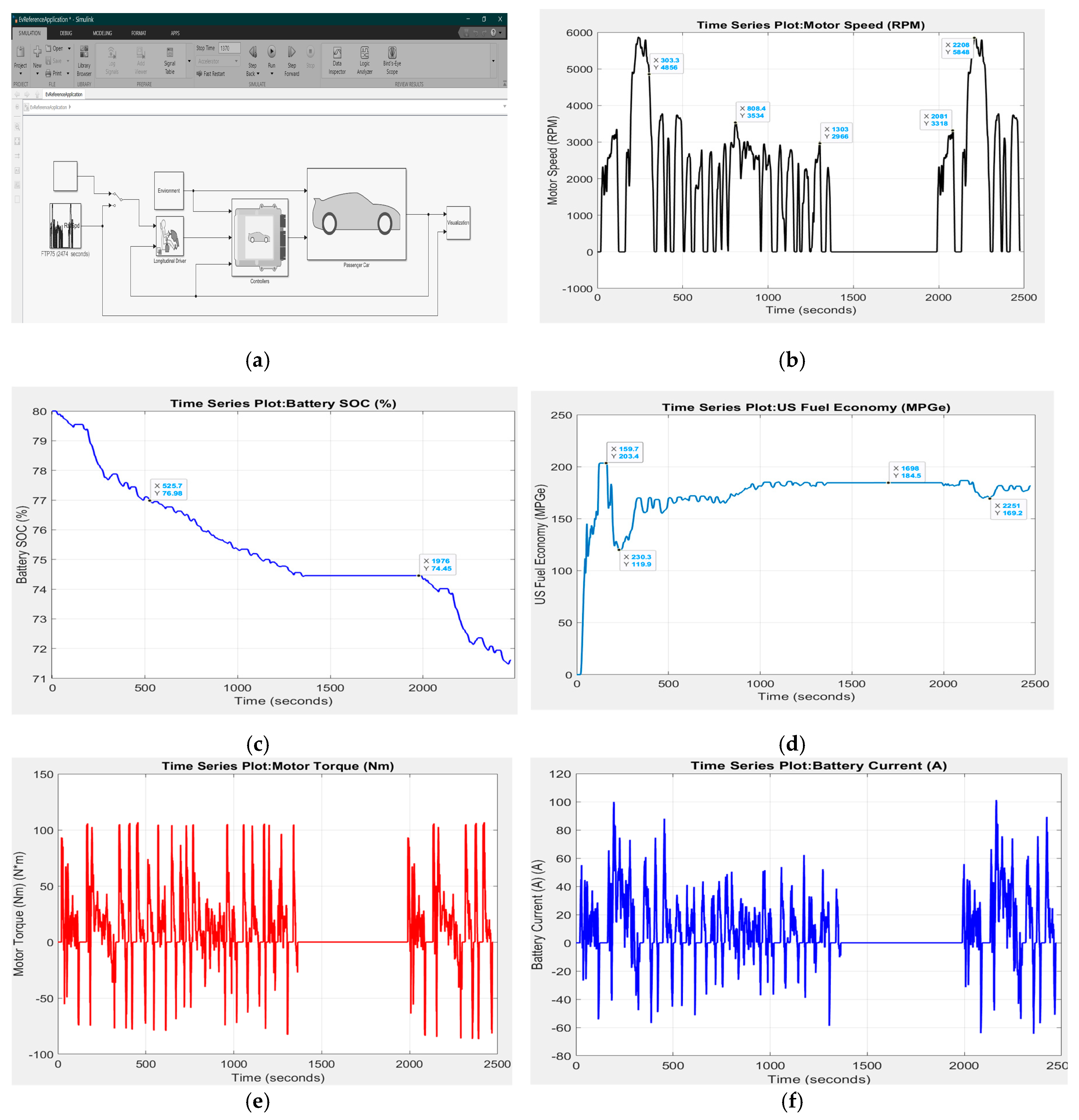
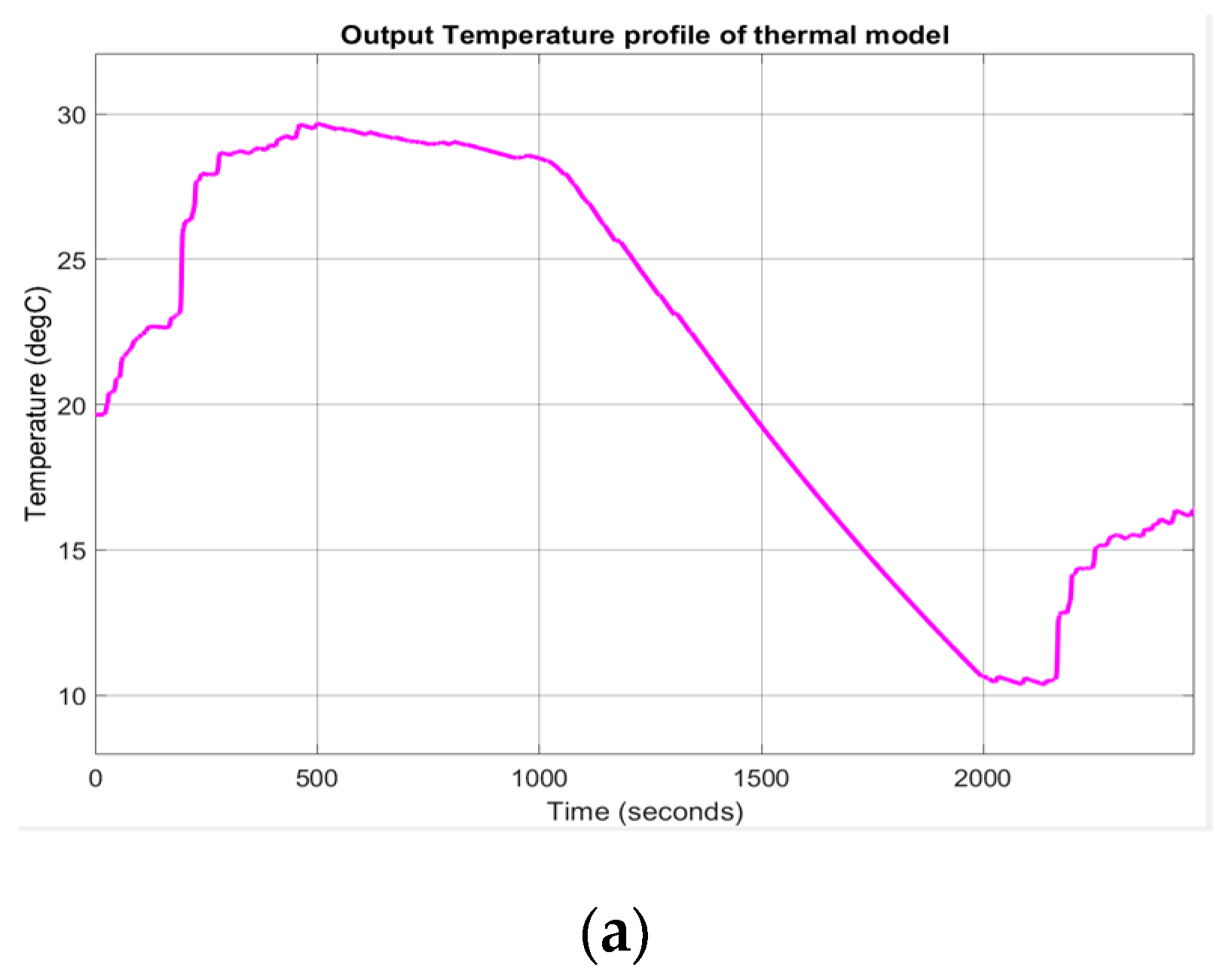
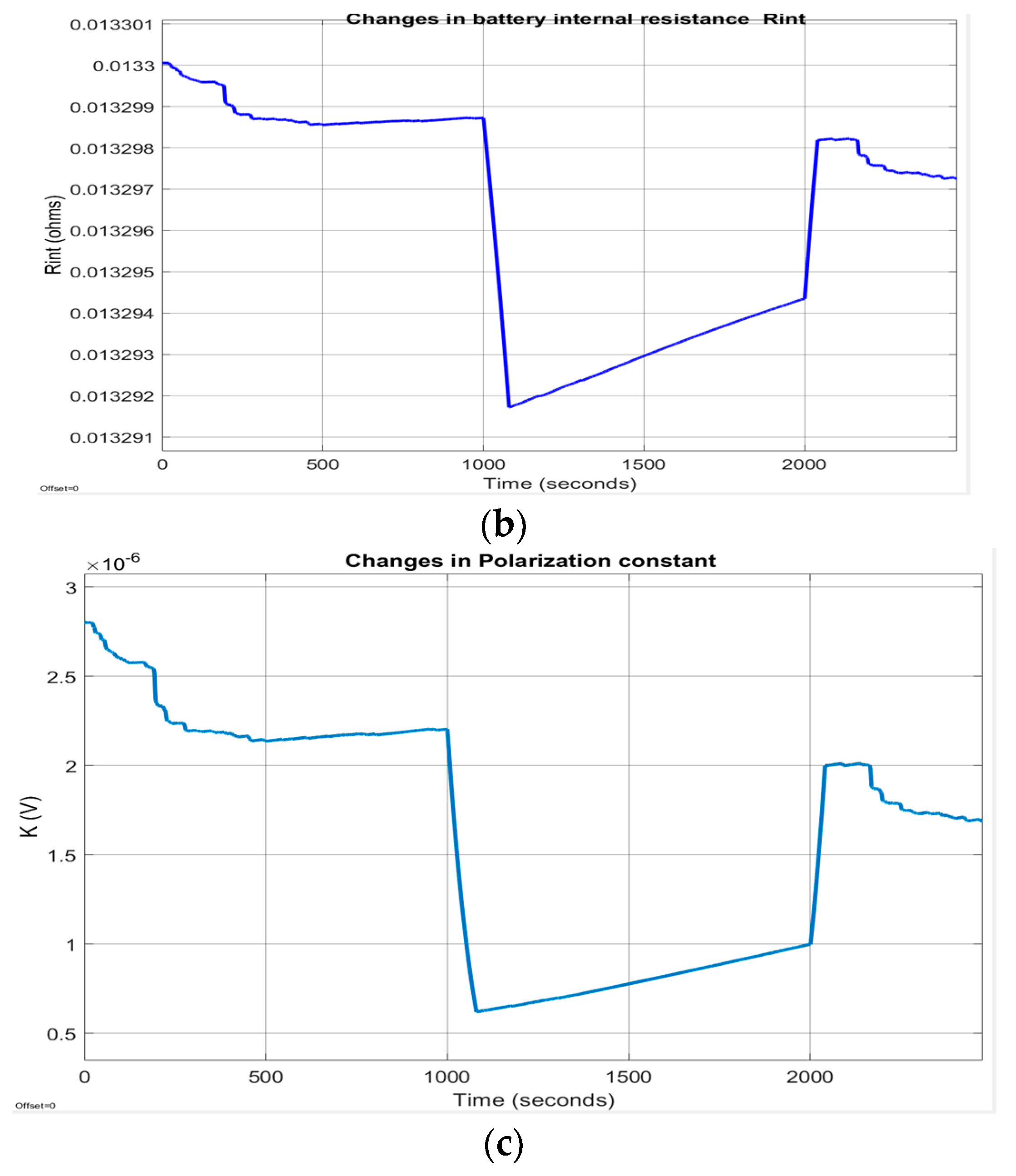
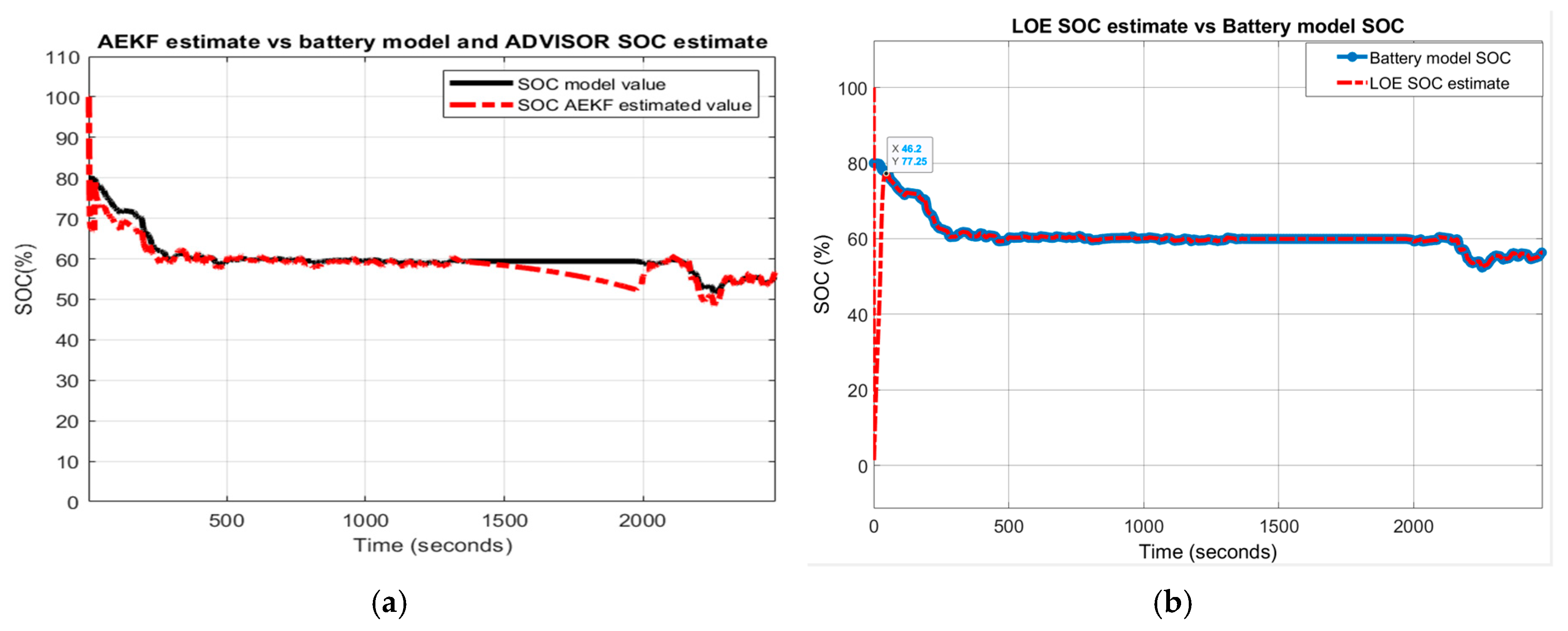
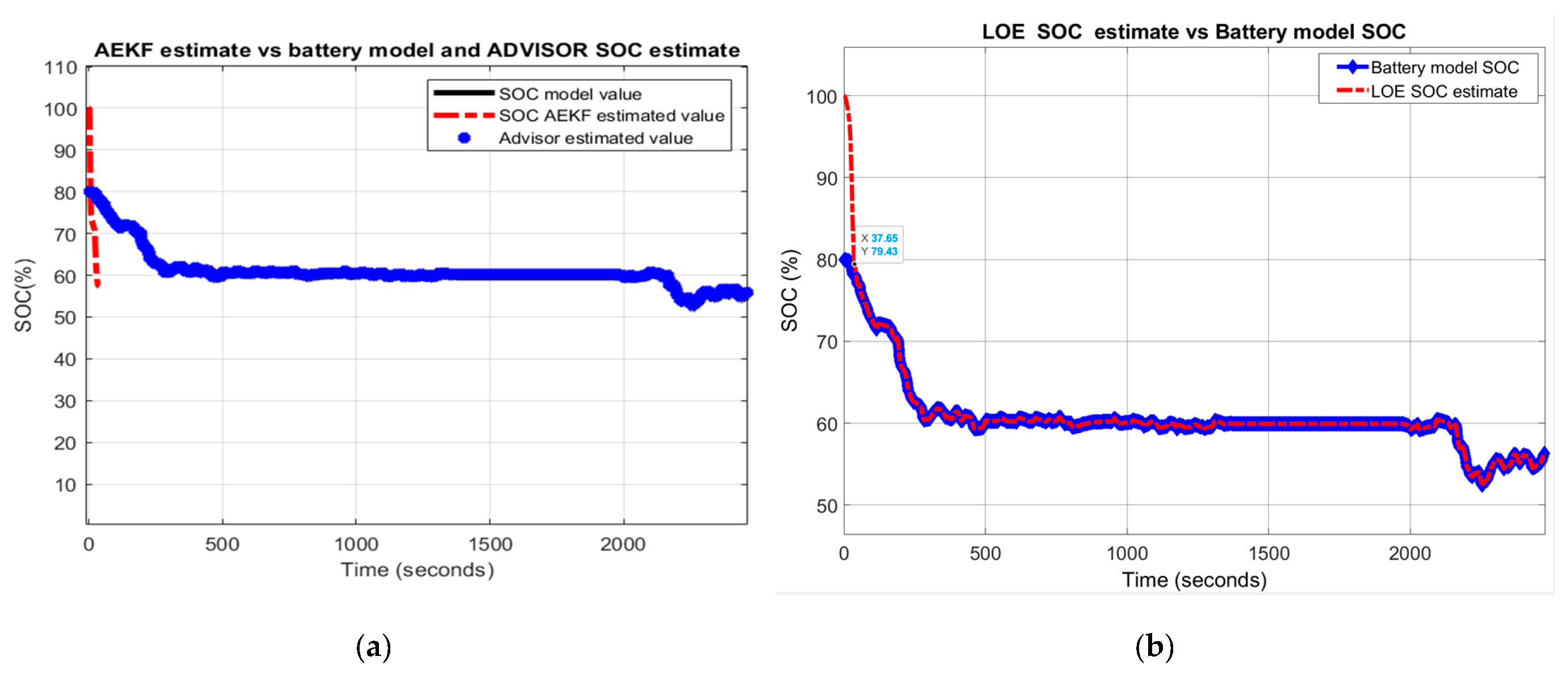
Appendix A.2. Tables
| Cycle Test | Accuracy | SOCest Initial Value (%) | Statistic Errors | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE AEKF | RMSE LOE | MSE AEKF | MSE LOE | MAE AEKF | MAE LOE | Std AEKF (%) | Std LOE (%) | |||
| UDDS-EPA | Battery model vs. ADVISOR | 70 | 0.2621 | 0.2630 | 0.0173 | 0.0180 | 0.0224 | 0.0285 | 7.22 | 4.29 |
| AEKF/LOE | 70 | 0.0325 | 0.0898 | 0.0000036 | 0.0004 | 0.0018 | 0.000459 | 2.6 | 7.35 | |
| R1-scenario | R12 | 0.2290 | 0.2031 | 0.0212 | 0.4126 | 0.0726 | 0.1896 | 18.8 | 11.14 | |
| R2-scenario | R22 | 0.2289 | 0.2013 | 0.2123 | 0.0405 | 0.0786 | 0.1879 | 18.8 | 11 | |
| R3-scenario | R32 | 0.2290 | 0.2311 | 0.0212 | 0.0534 | 0.0786 | 0.2251 | 18.87 | 7.4 | |
| R4-scenario | R42 | 0.2341 | 0.2041 | 0.0130 | 0.0416 | 0.0792 | 0.1913 | 19.55 | 11 | |
| Cycle Test | Accuracy | SOCest Initial Value (%) | Statistic Errors | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE AEKF | RMSE LOE | MSE AEKF | MSE LOE | MAE AEKF | MAE LOE | Std AEKF (%) | Std LOE (%) | |||
| FTP | Battery model vs. ADVISOR | 70 | 0.0819 | 0.0834 | 0.0028 | 0.0043 | 0.0264 | 0.0235 | 4 | 4.29 |
| AEKF/LOE | 70 | 0.0011 | 0.00063 | 0.00312 | 0.00006 | 0.008627 | 0.00067 | 4.3 | 2.82 | |
| R1-scenario | R12 | 0.2392 | 0.0.0913 | 0.4280 | 0.0083 | 0.0082 | 0.0488 | 4.1 | 10 | |
| R2-scenario | R22 | 0.0753 | 0.1004 | 0.00037 | 0.01 | 0.00169 | 0.0633 | 4.34 | 10.47 | |
| R3-scenario | R32 | 0.0793 | 0.2651 | 0.0006 | 0.0703 | 0.0220 | 0.1297 | 4.27 | 21.3 | |
| R4-scenario | R42 | 0.0683 | 0.0913 | 0.000198 | 0.0083 | 0.0071 | 0.0488 | 5.39 | 10.17 | |
References
- Moshirvaziri, A. Lithium-Ion Battery Modelling for Electric Vehicles and Regenerative Cell Testing Platform. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Electric Vehicle Integration into Modern Power Networks; Springer Science and Business Media LLC: Berlin, Germany, 2013; pp. 15–26.
- Xia, B.; Zheng, W.; Zhang, R.; Lao, Z.; Sun, Z. A Novel Observer for Lithium-Ion Battery State of Charge Estimation in Electric Vehicles Based on a Second-Order Equivalent Circuit Model. Energies 2017, 10, 1150. [Google Scholar] [CrossRef]
- Farag, M. Lithium-Ion Batteries, Modeling and State of Charge Estimation. Master’s Thesis, McMaster University of Hamilton, Hamilton, ON, Canada, 2013. [Google Scholar]
- Cui, X.; Shen, W.; Zhang, Y.; Cungang, H. A Novel Active Online State of Charge Based Balancing Approach for Lithium-Ion Battery Packs during Fast Charging Process in Electric Vehicles. Energies 2017, 10, 1766. [Google Scholar] [CrossRef] [Green Version]
- Lowe, M.; Tokuoka, S.; Trigg, T.; Gereffi, G. Li-Ion Batteries for Electric Vehicles. The US Chain. Research Report. Center on Globalization Governance and Competitiveness, 5 October 2010; pp. 1–68. Available online: https://unstats.un.org/unsd/trade/s_geneva2011/refdocs/RDs/Lithium-Ion%20Batteries%20(Gereffi%20-%20May%202010).pdf (accessed on 2 March 2018).
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Radu, S.M.; Tudoroiu, R.-E. Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study. Batteries 2018, 4, 19. [Google Scholar] [CrossRef] [Green Version]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Radu, S.M.; Tudoroiu, N. New Trends in Electrical Vehicle Powertrains. New Trends Electr. Veh. Powertrains 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Tudoroiu, N.; Radu, S.M.; Tudoroiu, R.-E. Improving Nonlinear State Estimation Techniques by Hybrid. Structures, 1st ed.; LAMBERT Academic Publishing: Saarbrucken, Germany, 2017; p. 56. ISBN 978-3-330-04418-0. [Google Scholar]
- Gonzalez, C. The Future of Electric Hybrid Aviation, Machine Design, Technologies-Batteries/Power Supplies, March 2016. Available online: http://www.machinedesign.com/batteriespower-supplies/future-electric-hybrid-aviation (accessed on 24 March 2018).
- Simon, J.J.; Uhlmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 28 July 1997; p. 3068. Available online: https://people.eecs.berkeley.edu/~pabbeel/cs287-fa09/readings/JulierUhlmann-UKF.pdf (accessed on 21 January 2018). [CrossRef]
- Xu, J.; Cao, B. Battery Management System for Electric Drive Vehicles – Modeling, State Estimation and Balancing. In New Applications of Electric Drives; IntechOpen: London, UK, 2015; pp. 87–113. [Google Scholar]
- Javier Muñoz Alvarez, J.M.; Sachenbacher, M.; Ostermeier, D.; Stadlbauer, H.J.; Hummitzsch, U.; Alexeev, A. Analysis of the State of the Art on BMS; Everlasting D6.1 Report; Lion Smart GmbH: Munchen, Germany, 2017. [Google Scholar]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef] [Green Version]
- Chang, W.-Y. The State of Charge Estimating Methods for Battery: A Review. ISRN Appl. Math. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.H.; Lee, J.M.; Cho, B.H. The state and parameter estimation of an Li-Ion battery using a new OCV-SOC concept. In Proceedings of the 2007 Power Electronics Specialists conference, Orlando, FL, USA, 17–21 June 2007; pp. 2799–2803. [Google Scholar]
- Chen, Z.; Fu, Y.; Mi, C.C. State of Charge Estimation of Lithium-Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filtering. IEEE Trans. Veh. Technol. 2012, 62, 1020–1030. [Google Scholar] [CrossRef]
- He, H.; Liu, Z.; Hua, Y. Adaptive Extended Kalman Filter Based Fault Detection and Isolation for a Lithium-Ion Battery Pack. Energy Procedia 2015, 75, 1950–1955. [Google Scholar] [CrossRef] [Green Version]
- Diab, Y.; Auger, F.; Schaeffer, E.; Wahbeh, M. Estimating Lithium-Ion Battery State of Charge and Parameters Using a Continuous-Discrete Extended Kalman Filter. Energies 2017, 10, 1075. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Xu, J.; Wang, X.; Mei, X. The Adaptive Fading Extended Kalman Filter SOC Estimation Method for Lithium-ion Batteries. Energy Procedia 2018, 145, 357–362. [Google Scholar] [CrossRef]
- Wang, D.; Bao, Y.; Shi, J. Online Lithium-Ion Battery Internal Resistance Measurement Application in State-of-Charge Estimation Using the Extended Kalman Filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef] [Green Version]
- Tremblay, O.; Dessaint, L.-A.; Dekkiche, A.-I. A Generic Battery Model. for the Dynamic Simulation of Hybrid. Electric Vehicles; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2007; pp. 284–289. [Google Scholar]
- Zhang, Y.; Xiong, R.; He, H.; Shen, W. Lithium-Ion Battery Pack State of Charge and State of Energy Estimation Algorithms Using a Hardware-in-the-Loop Validation. IEEE Trans. Power Electron. 2017, 32, 4421–4431. [Google Scholar] [CrossRef]
- Syed Mahdi, A. Battery Identification, Prediction and Modelling. Master’s Thesis, Colorado State University Fort Collins, Fort Collins, CO, USA, 2018. [Google Scholar]
- DiOrio, N.; Dobos, A.; Janzou, S.; Nelson, A.; Lundstrom, B. Technoeconomic Modeling of Battery Energy Storage in SAM; US NREL Technical Report; NREL/TP-6A20-64641. Contract No. DE-AC36-08GO28308; NREL: Denver, CO, USA, 2015. Available online: https://www.nrel.gov/docs/fy15osti/64641.pdf (accessed on 3 March 2020).
- Song, D.; Sun, C.; Wang, Q.; Jang, D. A Generic Battery Model and Its Parameter Identification. Energy Power Eng. 2018, 10, 10–27. [Google Scholar] [CrossRef] [Green Version]
- Johnson, V. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Wipke, K.B.; Cuddy, R.M. Using an Advanced Vehicle Simulator (ADVISOR) to Guide Hybrid Vehicle Propulsion System Development. Publisher: Golden, CO: National Renewable Energy Laboratory. August 1996. Research gate net. Available online: https://www.nrel.gov/docs/legosti/fy96/21615.pdf (accessed on 1 March 2020).
- Xing, Y.; Ma, E.W.M.; Tsui, K.-L.; Pecht, M.G. Battery Management Systems in Electric and Hybrid Vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Applications of Lithium-ion Batteries in Electric Drive Vehicles; Wiley: Singapore, 2015; p. 300. [Google Scholar]
- Lakkis, M.E.; Sename, O.; Corno, M.; Bresch, P.D. Combined battery SOC/SOH estimation using a nonlinear adaptive observer. European Control Conference 2015, Linz, Austria. In Proceedings of the European Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar] [CrossRef] [Green Version]
- Battery and Engineering Technologies. Battery Life and Death. Available online: http://www.mpoweruk.com/life.htm (accessed on 18 March 2018).
- Taesic, K. A Hybrid Battery Model Capable of Capturing Dynamic Circuit Characteristics and Nonlinear Capacity Effects. Master’s Thesis, University of Nebraska, Lincoln, NE, USA, July 2012. [Google Scholar]
- Siva, R.; Prasanna, M. Modeling, Simulation & Implementation of Li-Ion Battery Powered Electric and Plug-in Hybrid Vehicles. Master’s Thesis, University of Akron, Akron, OH, USA, August 2011. [Google Scholar]
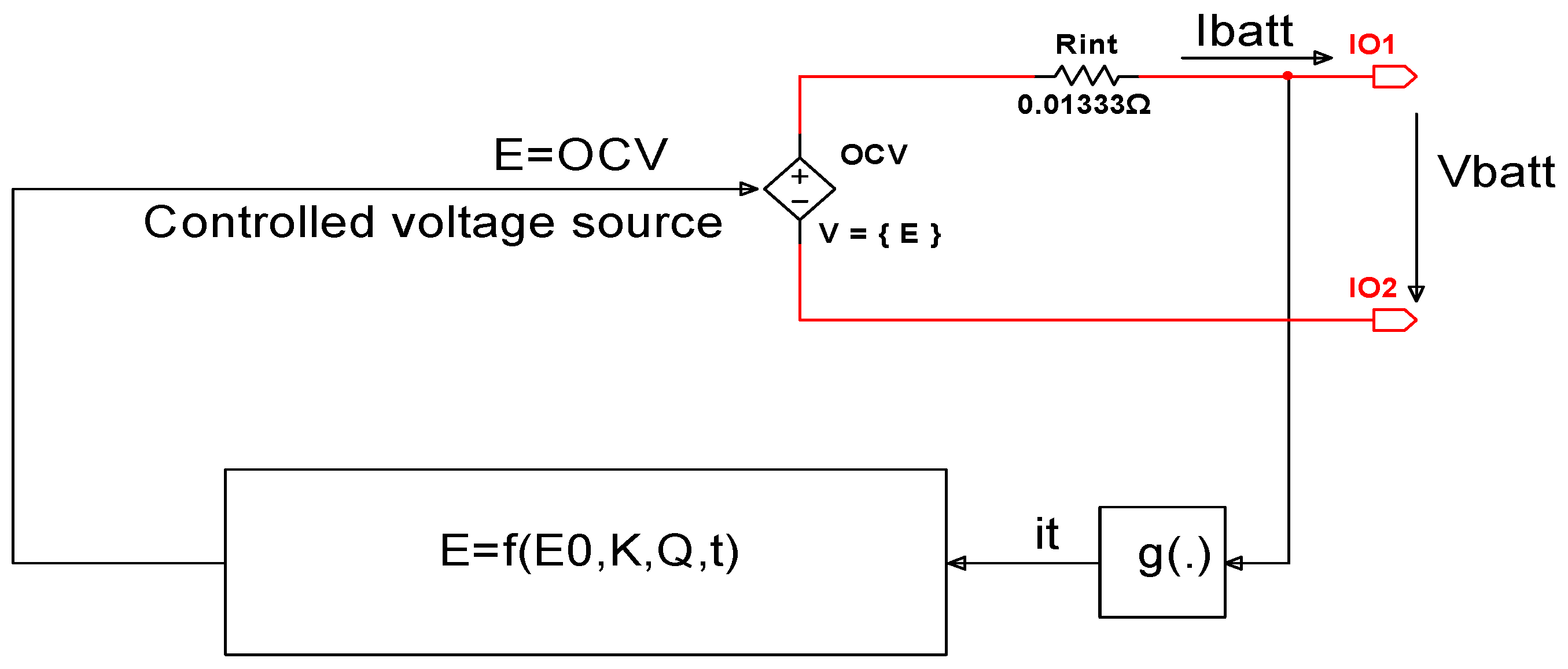
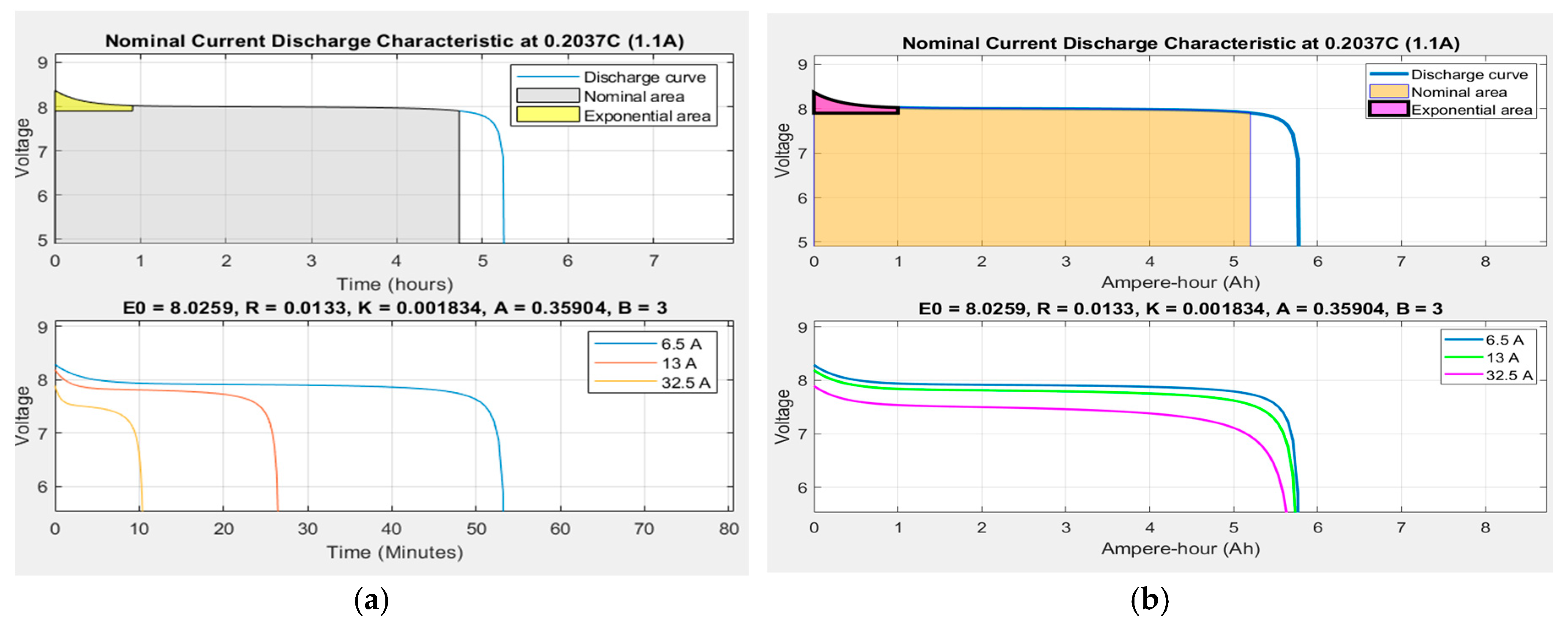
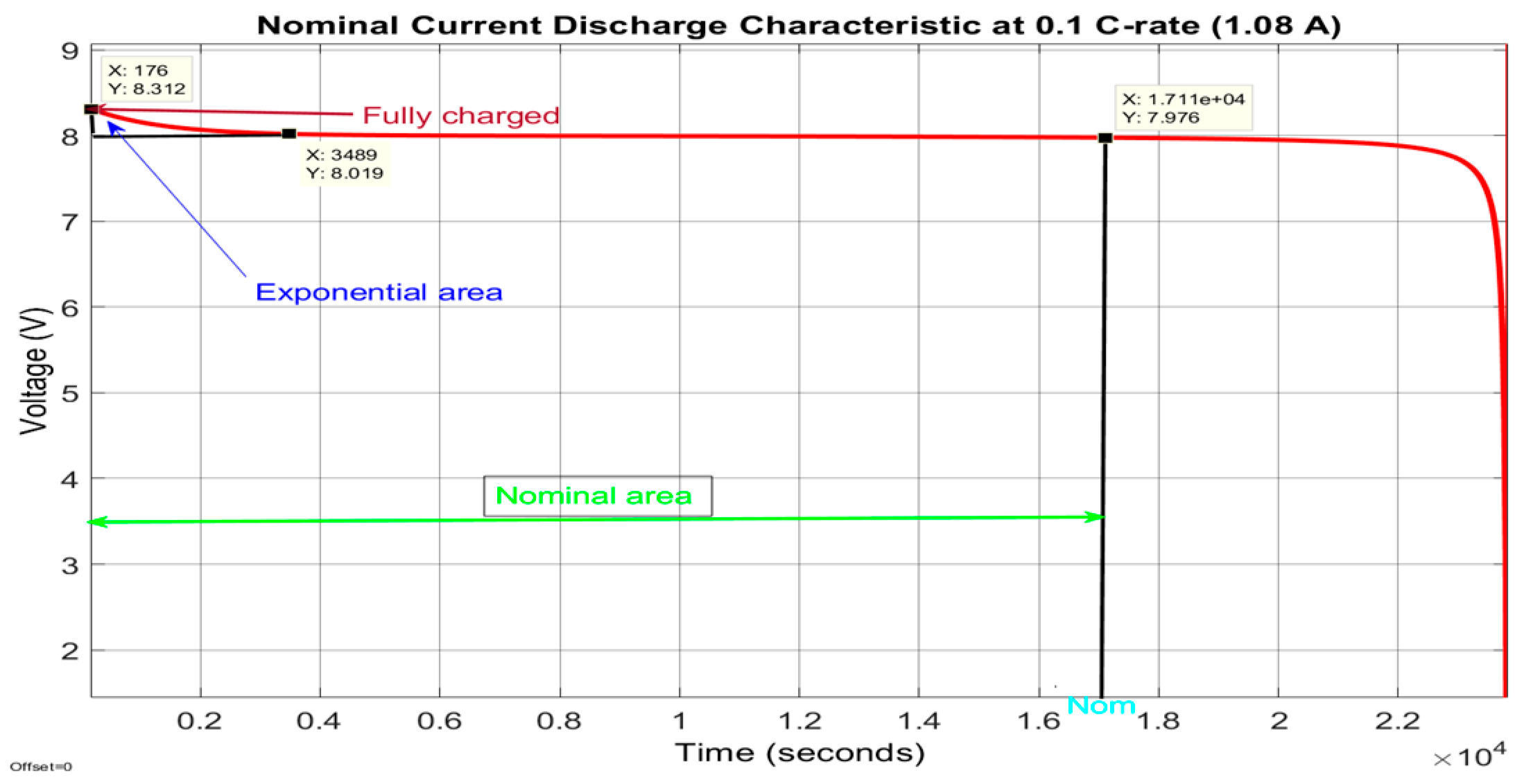
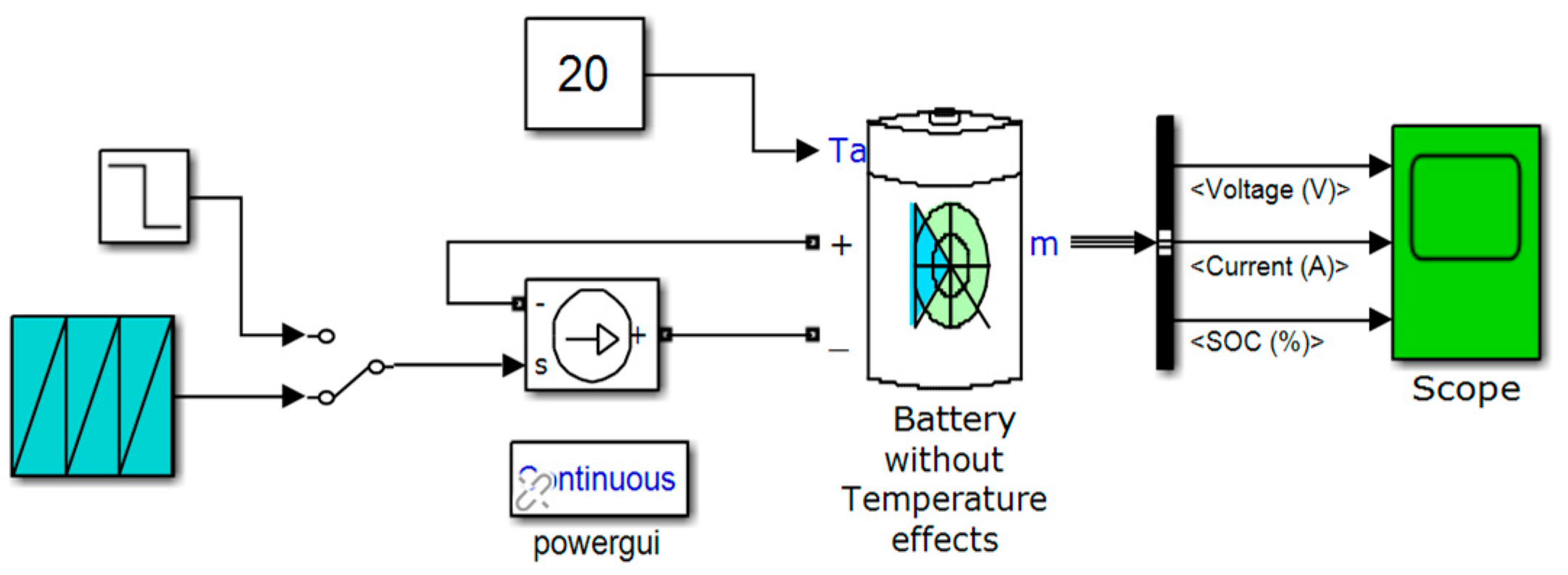








| Variable | Description | Unit | Value |
|---|---|---|---|
| E | No-load voltage (OCV) | V | - |
| E0 | Battery constant voltage | V | 8.0259 volts |
| K | Polarization voltage | V | 0.001834 volts |
| Qrated | Rated battery capacity | Ah | 5.4 Ampere-hours |
| Aexp | Exponential zone amplitude | V | 0.35904 volts |
| Bexp | Exponential zone time constant inverse | (Ah)−1 | 3/(Ah) = 3/(3600As) |
| Rint | Internal resistance of the battery | Ω | 0.0133 ohms |
| i(t) = Ibatt | Battery direct current (dc) input profile If i(t) ≥ 0 is discharging current If i(t) < 0 is charging current | A | UDDS, EPA UDDS, FTP, constant discharge/charge current |
| Vbatt | Battery terminal voltage | V | Vnom = 7.4 V |
| Actual battery charge | Ah | - | |
| SOC | Battery state of charge | unitless | 0–100% |
| OCV | Battery open circuit voltage (no-load voltage) | V | It is function of battery SOC |
| , | Coulombic efficiency coefficients for discharging and charging cycles | unitless | = 0.795 = 0.875 |
| Lithium-Ion Battery Cell | LiCoO2 |
|---|---|
| Rated capacity (Ah) | 5.4 |
| Maximum capacity (Ah) | 5.6 |
| Nominal voltage (V) | 7.4 |
| Cut-off voltage (V) | 5.25 |
| Fully charged voltage (V) | 8.307 |
| Nominal discharge current (A) | 1.1 |
| Exponential zone [Voltage (V) Capacity (Ah)] | [7.91] |
| Internal resistance (ohms) | 0.0133 |
| Capacity (Ah) at nominal voltage | 5.2 |
| Cycle Test | Accuracy | SOCest Initial Value (%) | Statistic Errors | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE AEKF | RMSE LOE | MSE AEKF | MSE LOE | MAE AEKF | MAE LOE | Std AEKF (%) | Std LOE (%) | |||
| UDDS | Battery model vs. ADVISOR | 70 | 0.4693 | 0.5500 | 0.2538 | 0.3026 | 0.0029 | 0.0658 | 2.66 | 1.37 |
| AEKF/LOE | 70 | 0.0325 | 0 | 0.0000036 | 0 | 0.0018 | 0 | 2.6 | 1.37 | |
| R1-scenario | R11 | 0.04225 | 0.1746 | 0.000384 | 0.0305 | 0.0131 | 0.1289 | 3.28 | 13.1 | |
| R12 | 0.0492 | 0.1551 | 0.0033 | 0.0240 | 0.0270 | 0.1057 | 4.47 | 10.1 | ||
| R2-scenario | R21 | 0.0463 | 0.2638 | 0.00044 | 0.0696 | 0.0145 | 0.2595 | 3.69 | 5.3 | |
| R22 | 0.0576 | 0.1573 | 0.0029 | 0.0247 | 0.0038 | 0.1088 | 4.03 | 10.14 | ||
| R3-scenario | R31 | 0.0471 | 0.1832 | 0.000504 | 0.0335 | 0.0168 | 0.1723 | 3.6 | 6.9 | |
| R32 | 0.0367 | 0.2811 | 0.000717 | 0.0790 | 0.0124 | 0.2655 | 2.97 | 8.5 | ||
| R4-scenario | R41 | 0.0459 | 0.2528 | 0.00041 | 0.0639 | 0.01329 | 0.2473 | 3.73 | 5.96 | |
| R42 | 0.0498 | 0.1636 | 0.0054 | 0.0267 | 0.0252 | 0.1195 | 4.89 | 9.82 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tudoroiu, N.; Zaheeruddin, M.; Tudoroiu, R.-E. Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Lithium-Ion Cobalt Battery with Applicability in HEVs/EVs—A Comparative Study. Energies 2020, 13, 2749. https://doi.org/10.3390/en13112749
Tudoroiu N, Zaheeruddin M, Tudoroiu R-E. Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Lithium-Ion Cobalt Battery with Applicability in HEVs/EVs—A Comparative Study. Energies. 2020; 13(11):2749. https://doi.org/10.3390/en13112749
Chicago/Turabian StyleTudoroiu, Nicolae, Mohammed Zaheeruddin, and Roxana-Elena Tudoroiu. 2020. "Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Lithium-Ion Cobalt Battery with Applicability in HEVs/EVs—A Comparative Study" Energies 13, no. 11: 2749. https://doi.org/10.3390/en13112749
APA StyleTudoroiu, N., Zaheeruddin, M., & Tudoroiu, R.-E. (2020). Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Lithium-Ion Cobalt Battery with Applicability in HEVs/EVs—A Comparative Study. Energies, 13(11), 2749. https://doi.org/10.3390/en13112749