A More Realistic Heat Pump Control Approach by Application of an Integrated Two-Part Control
Abstract
:1. Introduction
2. Control of a Heat Pump
2.1. Overview of Existing Control Approaches—The Control Principles
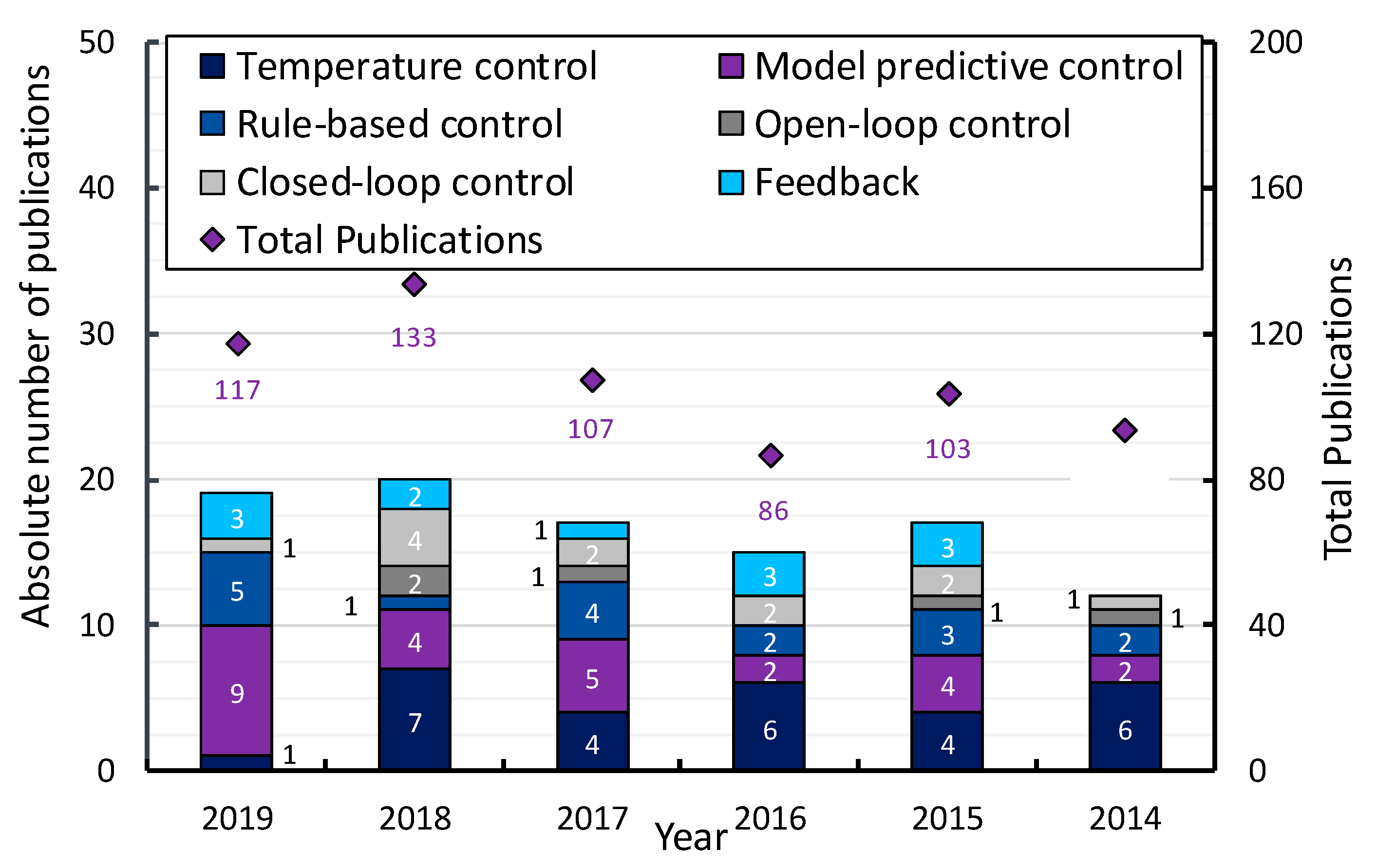
2.2. Focus and Control Approaches of HPC Publications—The Research Gap
2.3. The Integrated Two-Part Control
3. Methodology
3.1. Characteristics of the Building Energy System
3.2. Implementation of the Controlled System Module
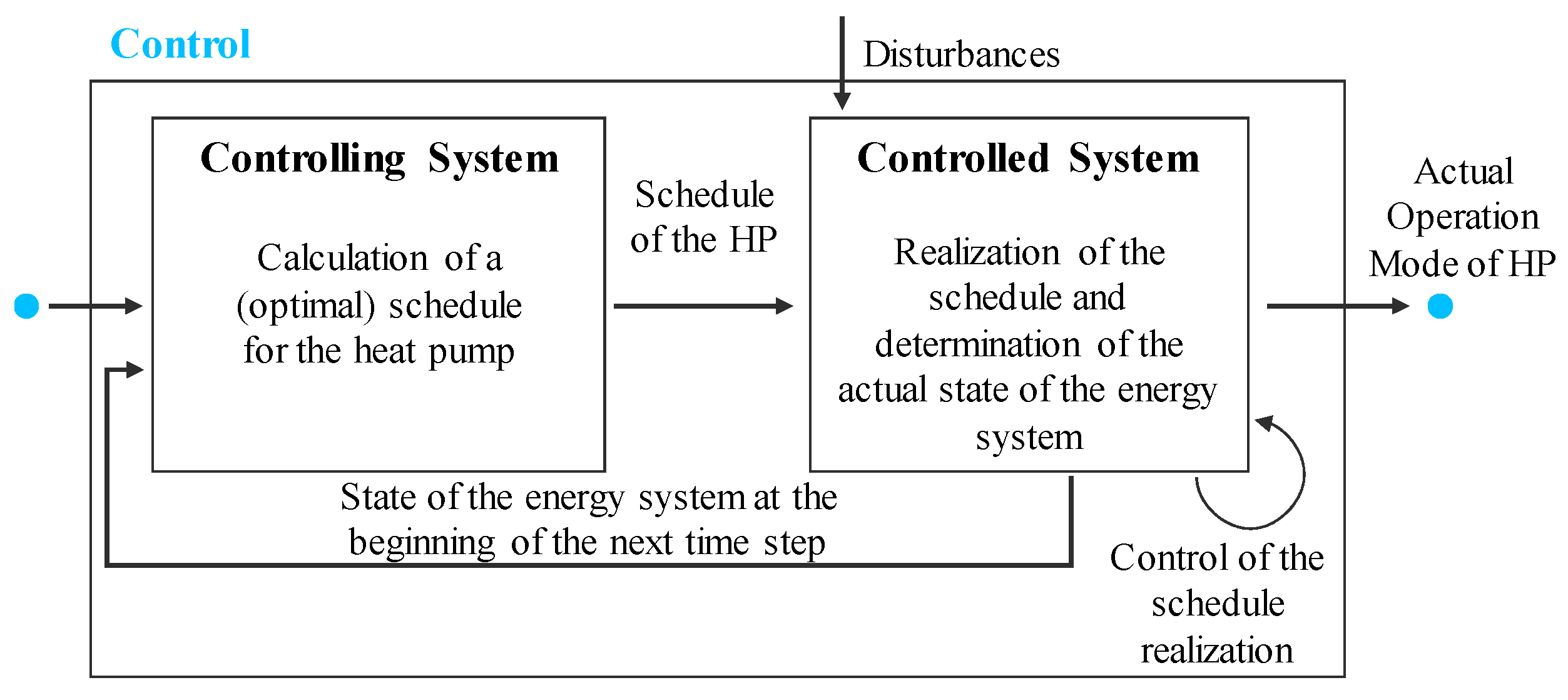
3.3. Implementation of the Controlling System Module
3.4. Implementation of the Integrated Two-Part Control
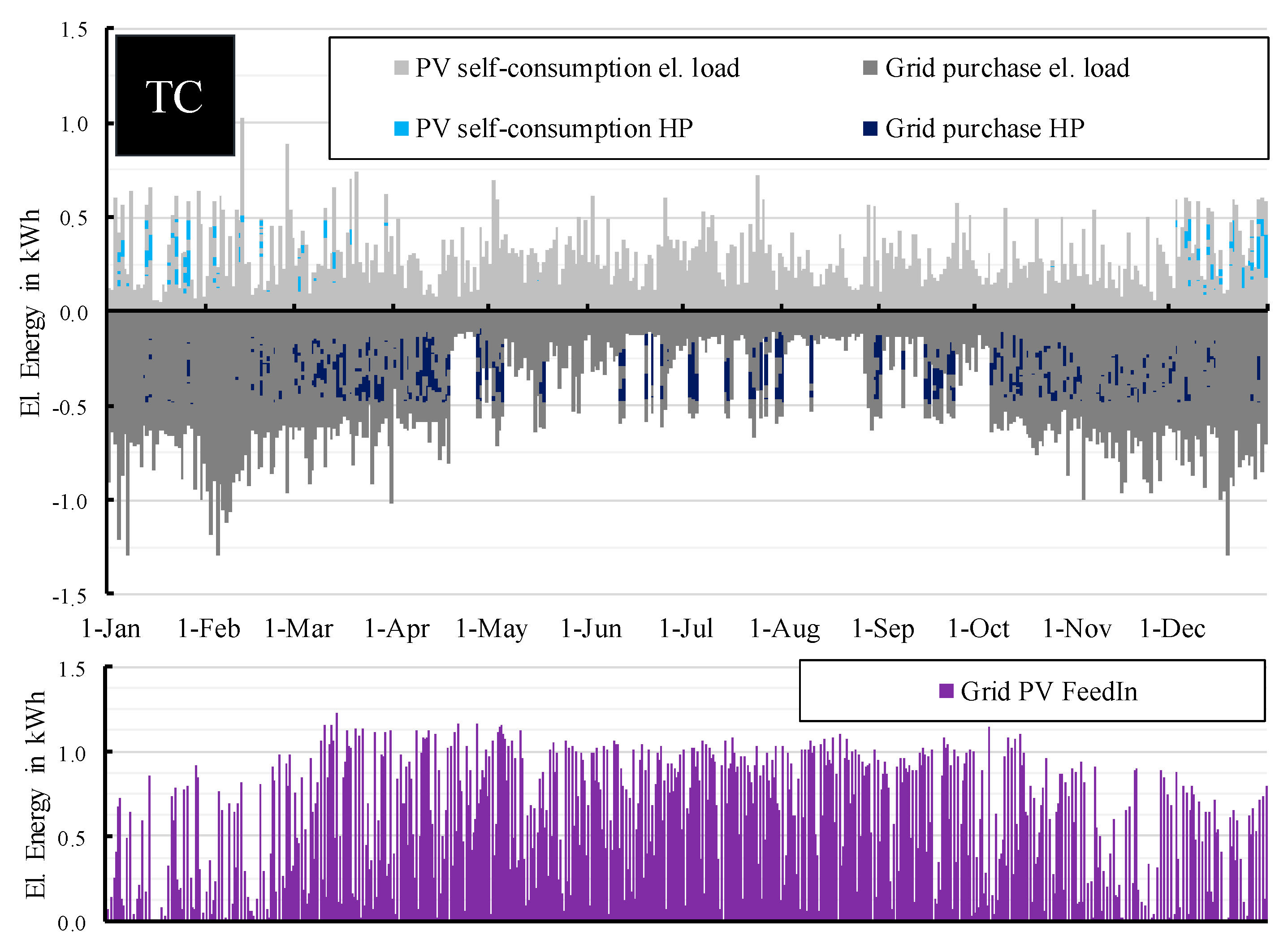
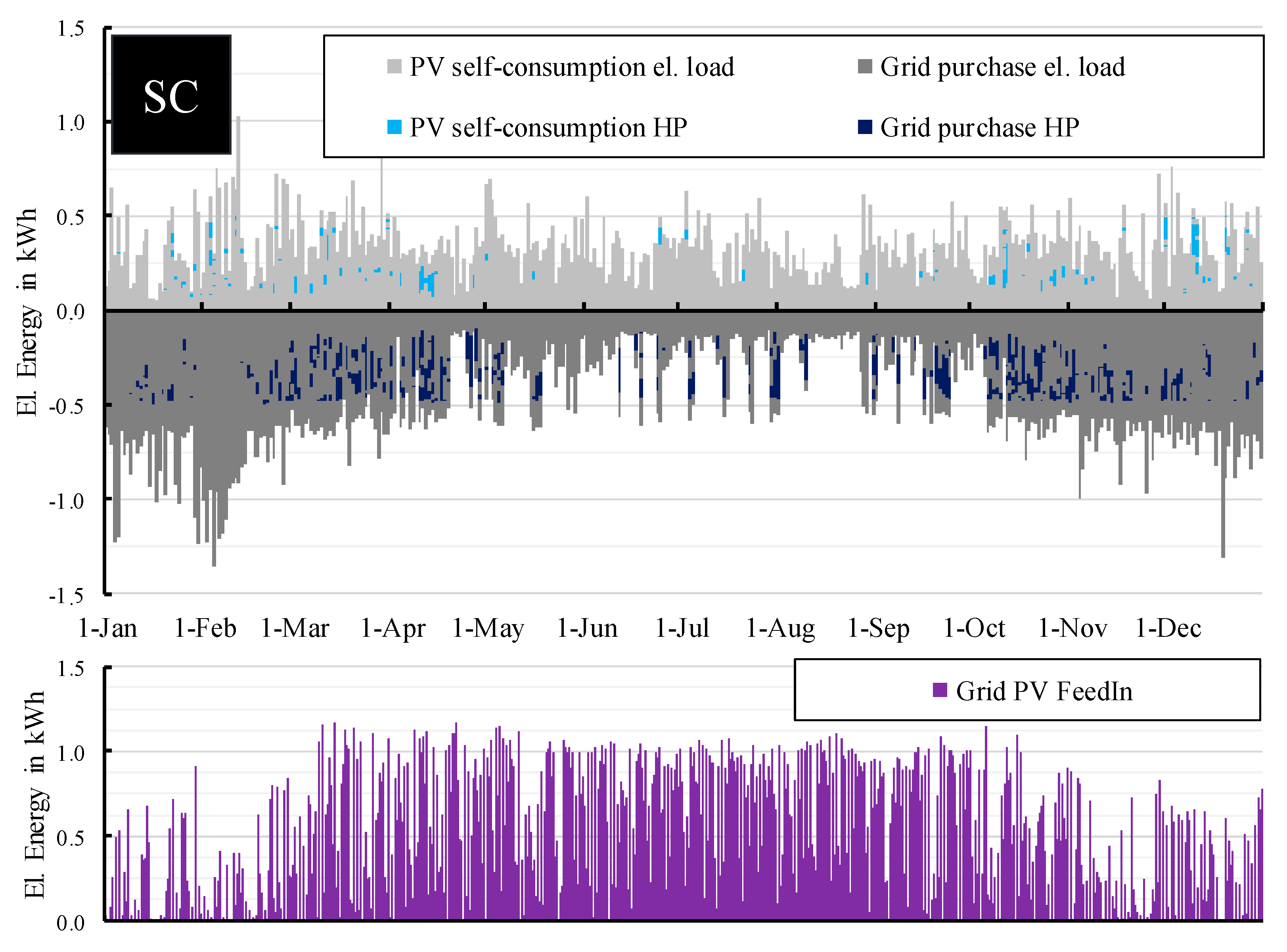
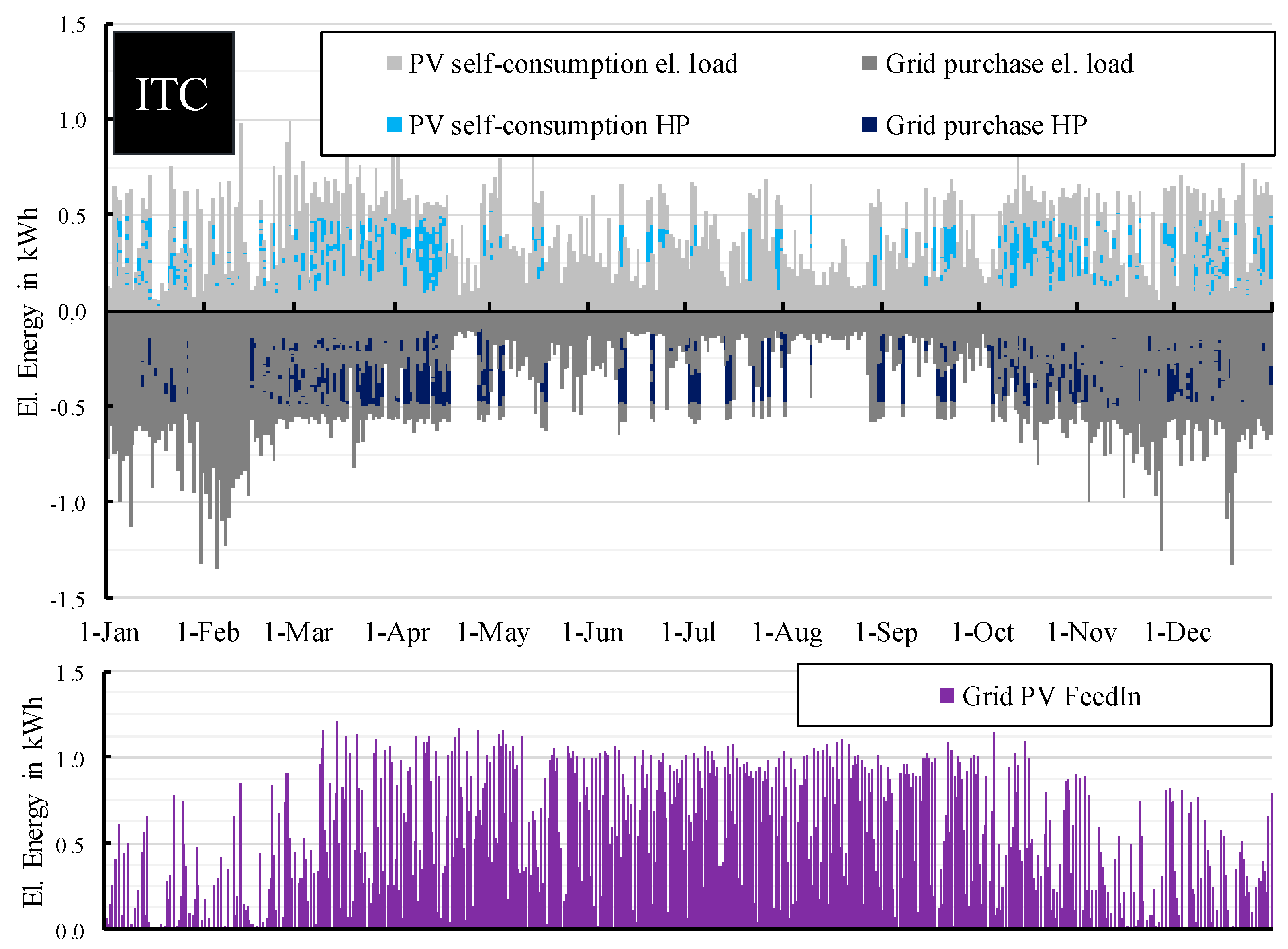
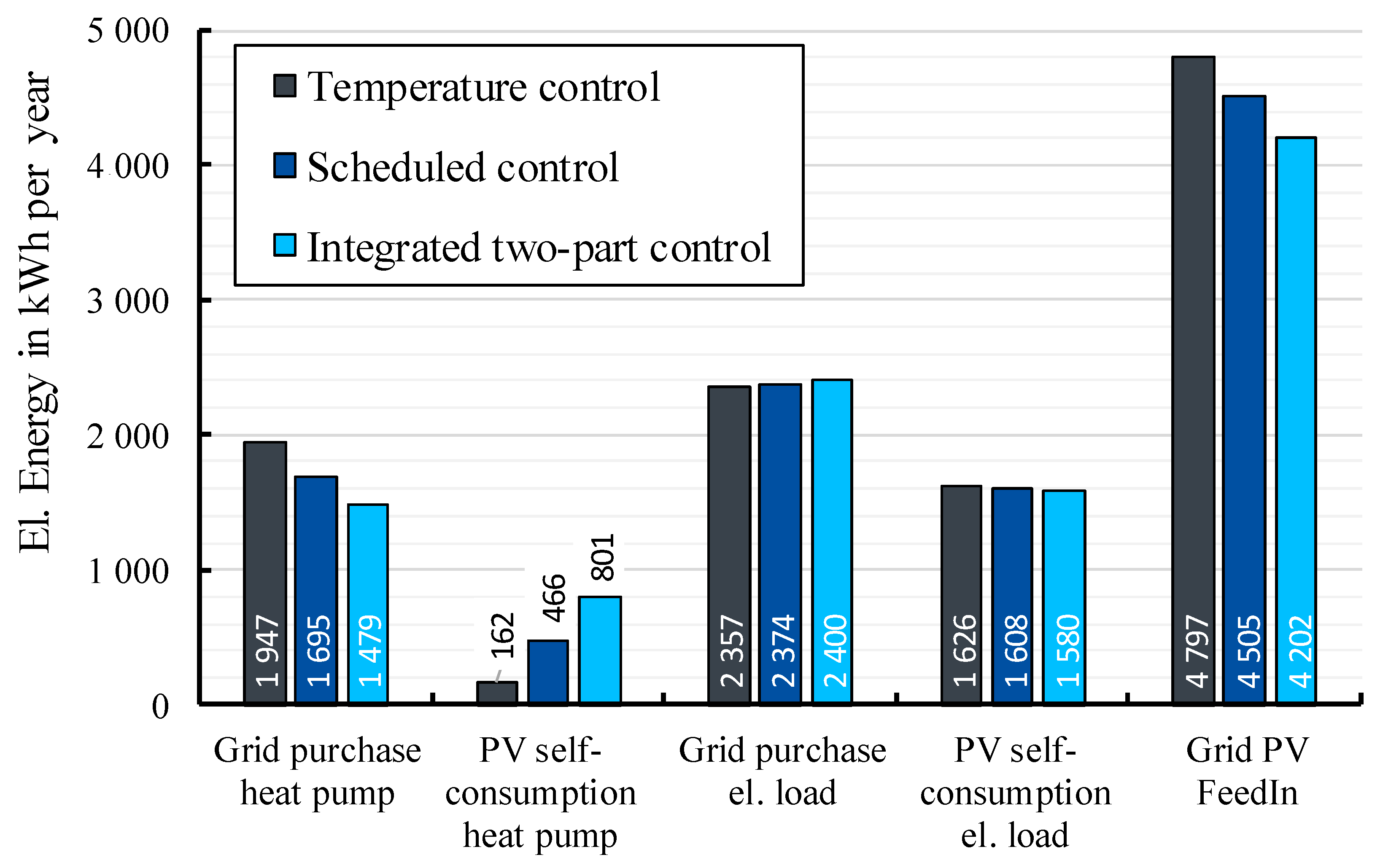
4. Comparison of the Control Approaches
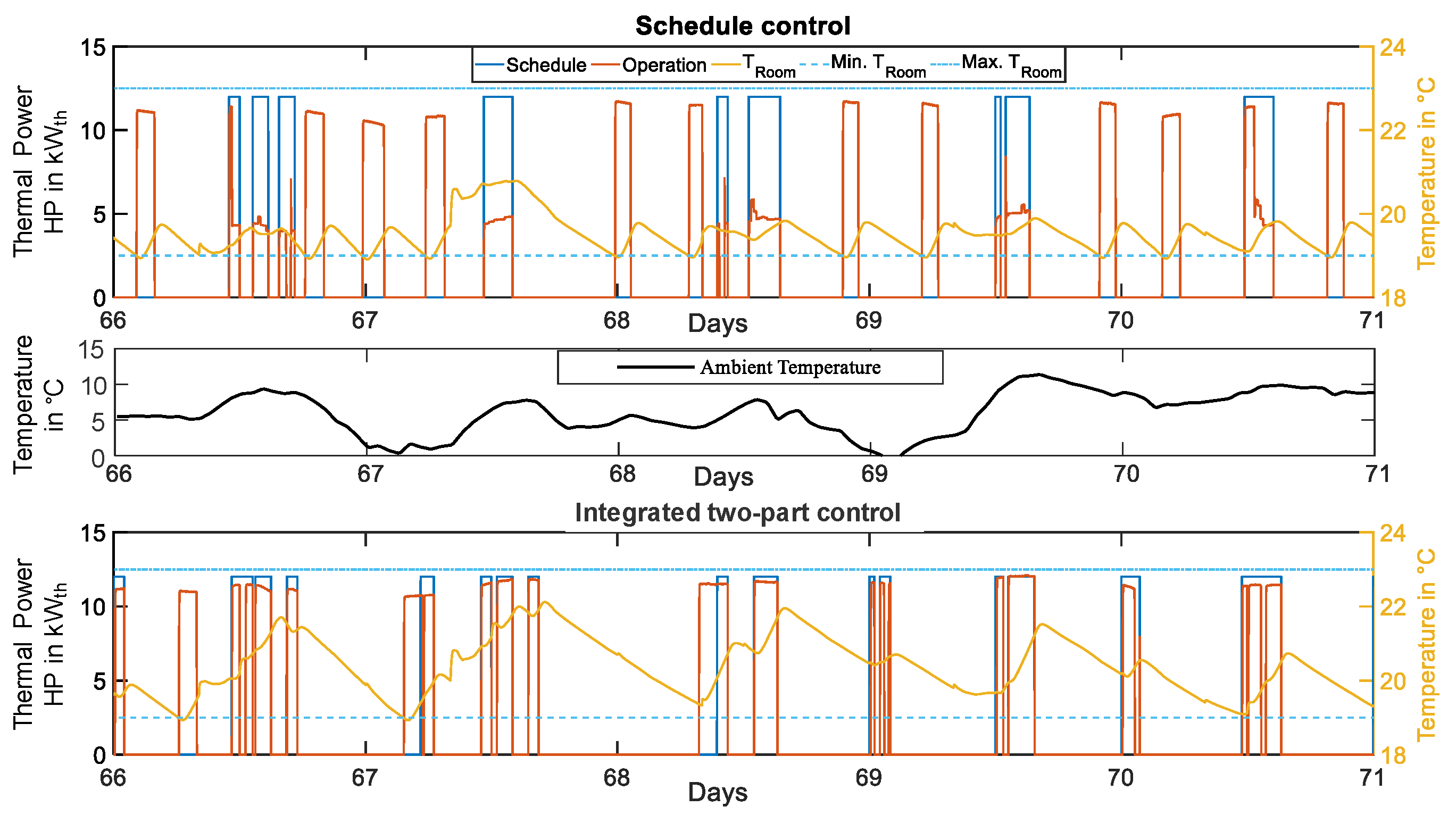
4.1. Implementation of the Controlling System Module
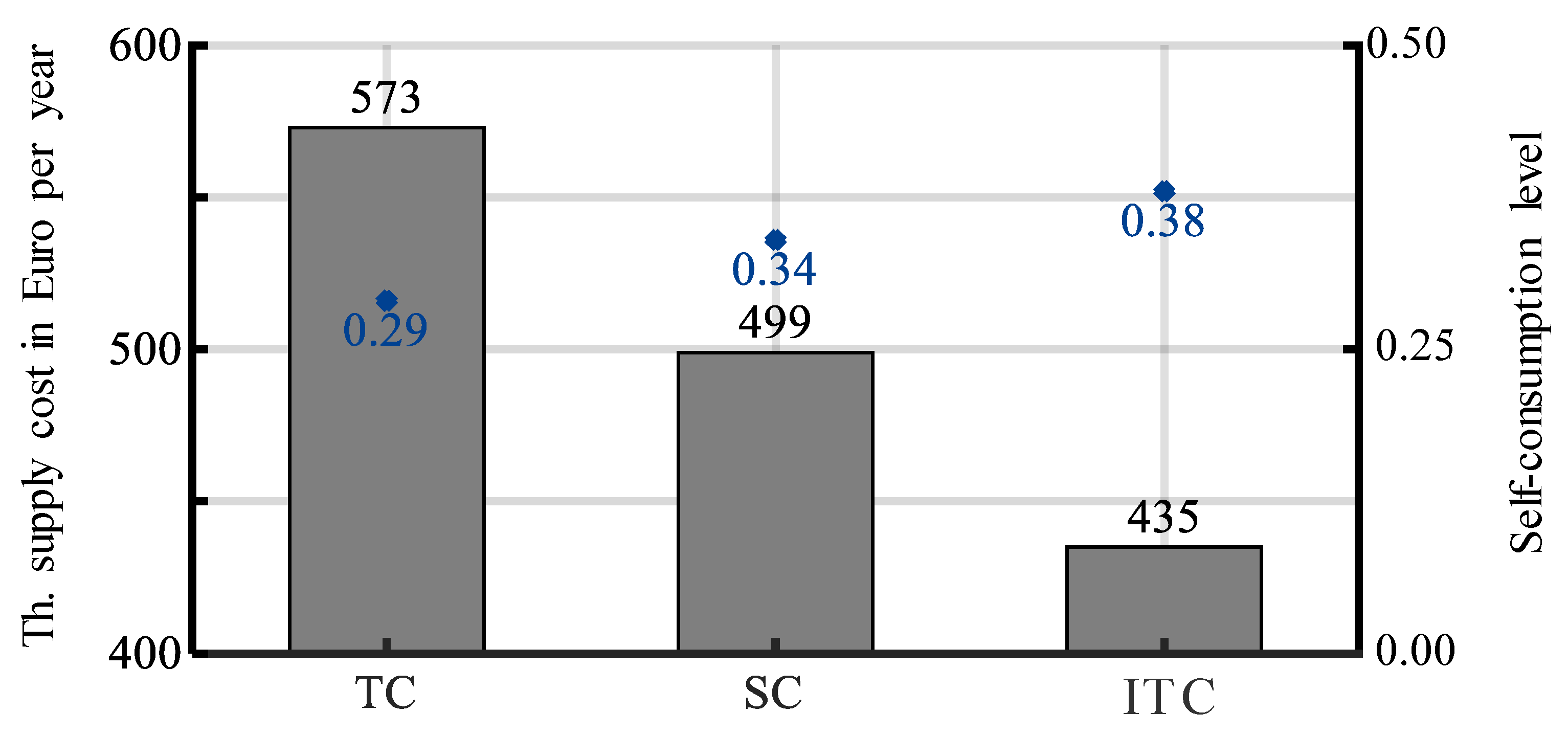
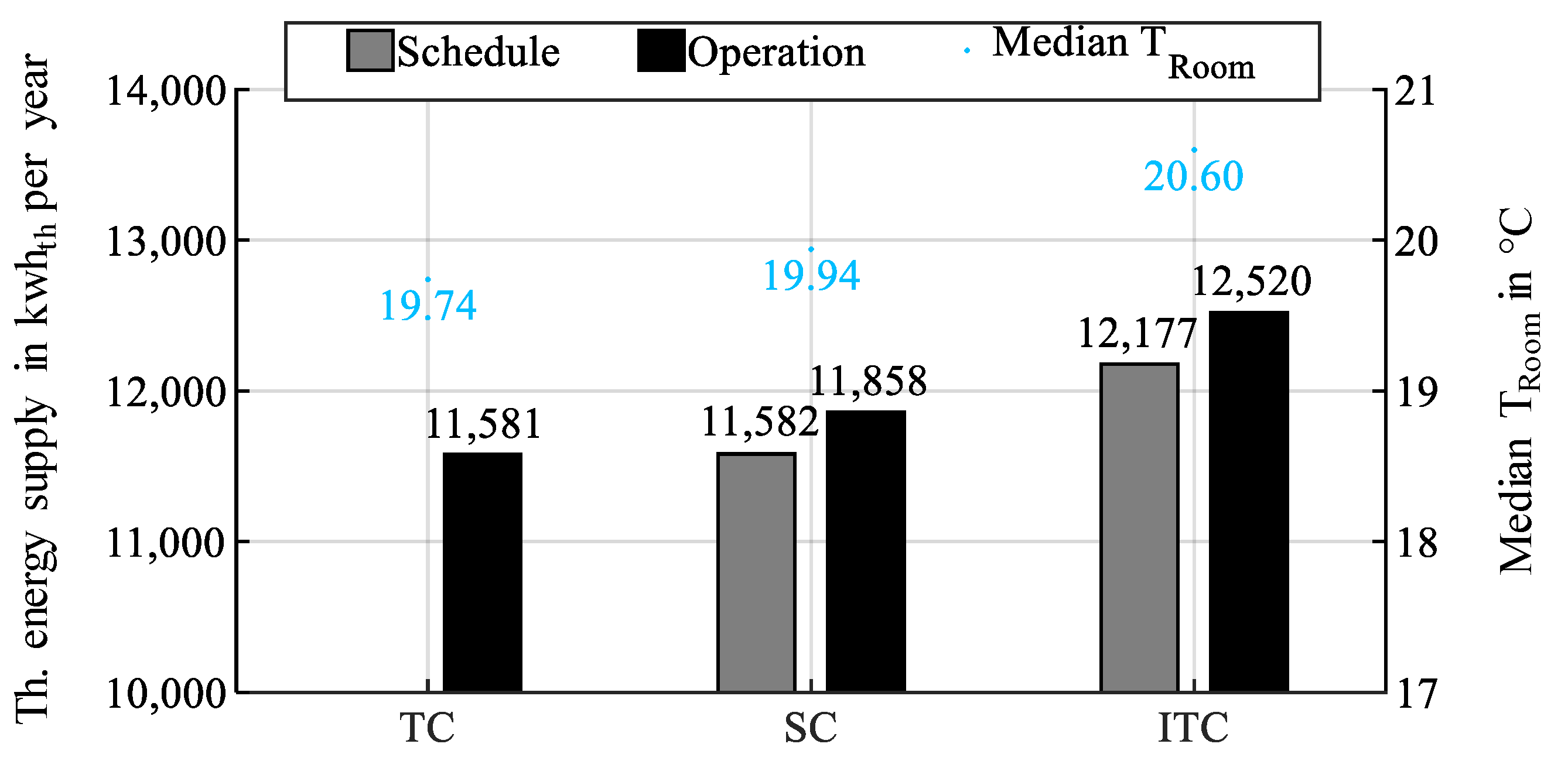
4.2. Economic Quality of the Schedules
5. Conclusions and Outlook
5.1. Conclusions
5.2. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Keywords |
|---|---|
| Performance/Efficiency | efficiency, efficient, performance |
| Technical Improvements | experimental, test, tested |
| Energetic Efficiency | energy save / saving, energy consumption, power consumption, energy loss |
| Cost savings | cost, price, economic |
| Flexibility | flexibility, flexible, DSM |
| Sustainability | renewable, sustainable, environmental |
| CO2-/greenhousegases | CO2, Carbon dioxide, carbon, greenhouse gas, ghg |
| Category | Keywords |
|---|---|
| Temperature control | thermostatically, temperature control |
| Model predictive control | model predictive, MPC |
| Rule control | rule controle, RBC |
| Open-loop control | open loop, OLC |
| Closed-loop control | closed loop, CLC |
| Feedback | feedback |
Appendix B
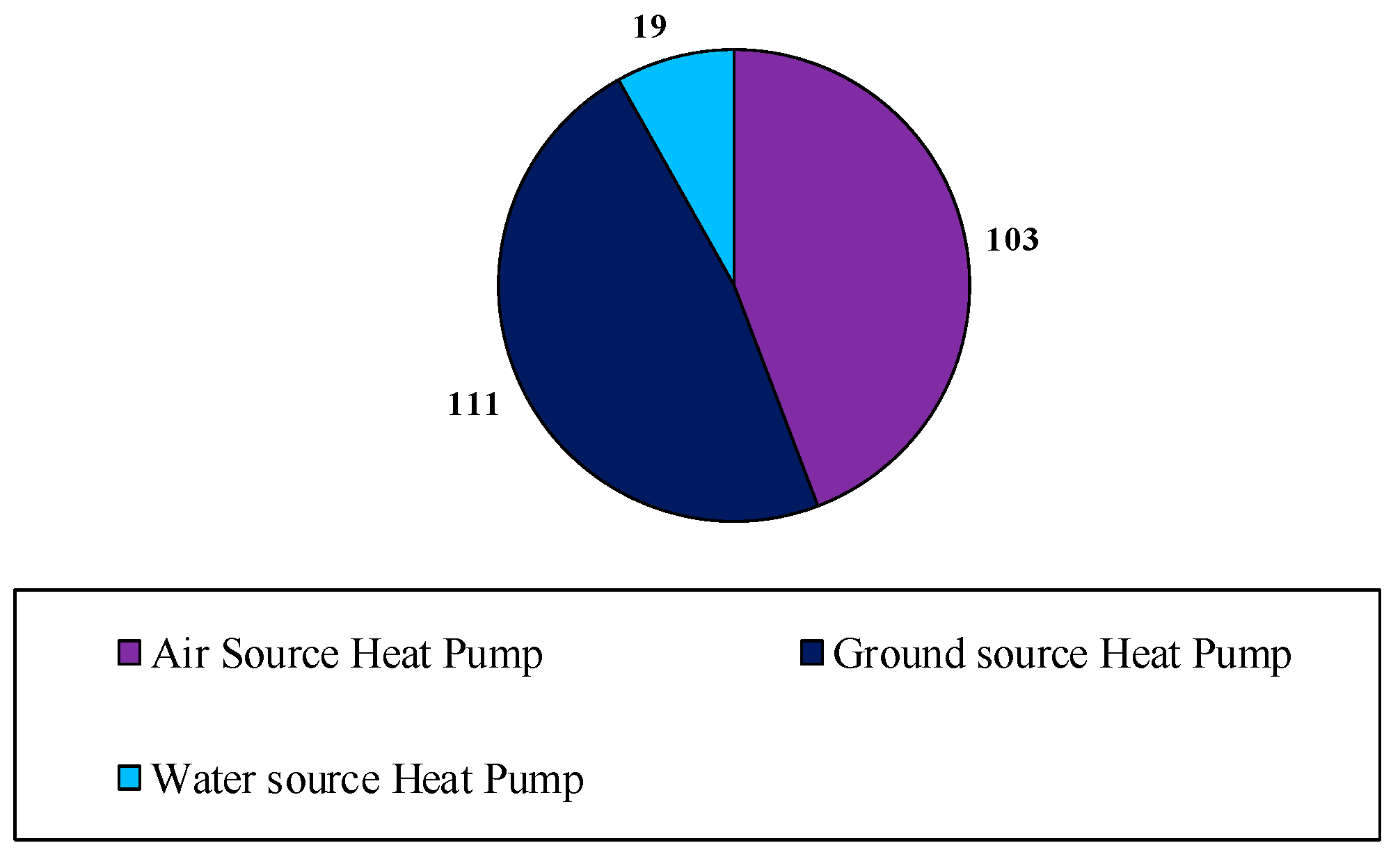
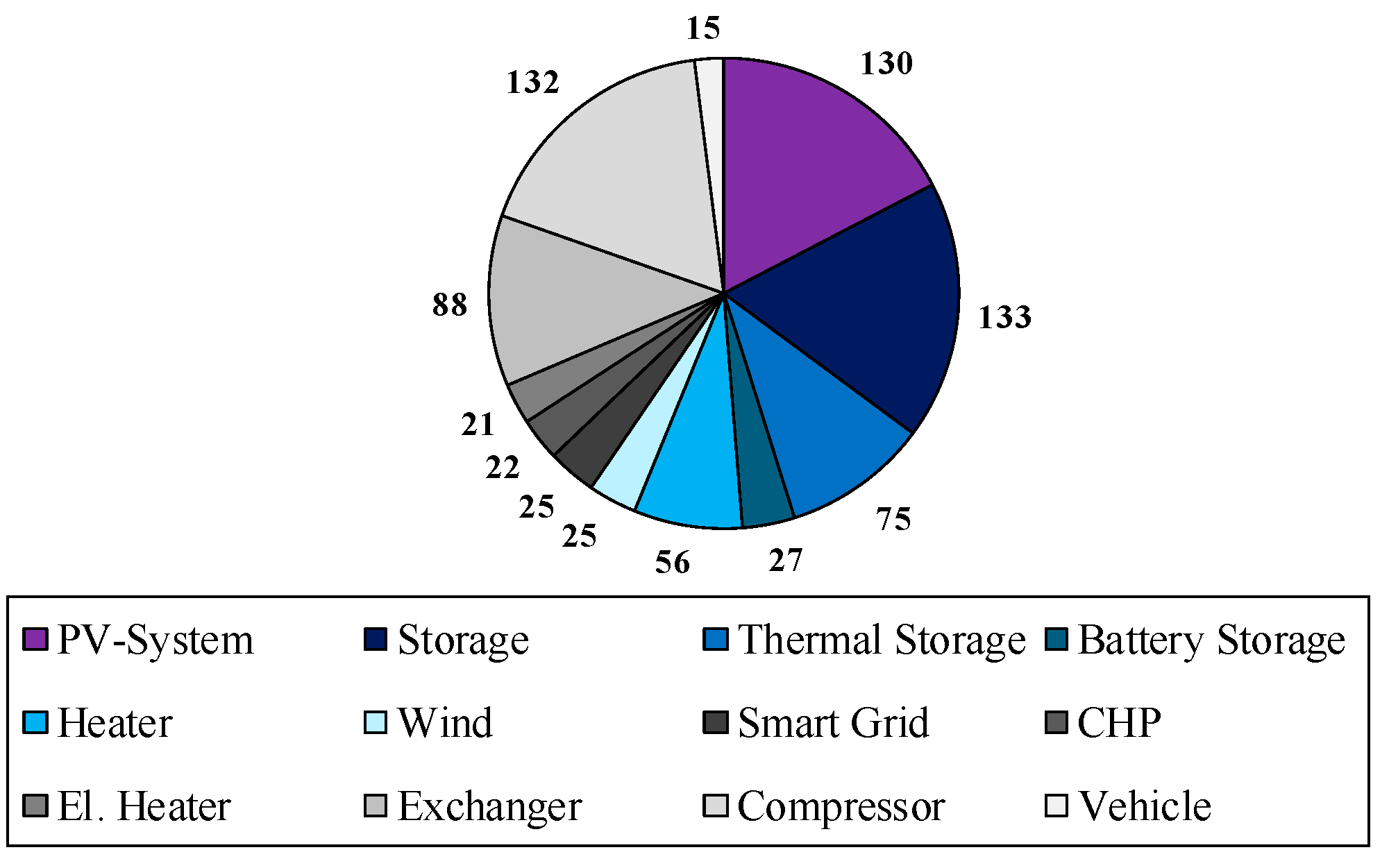
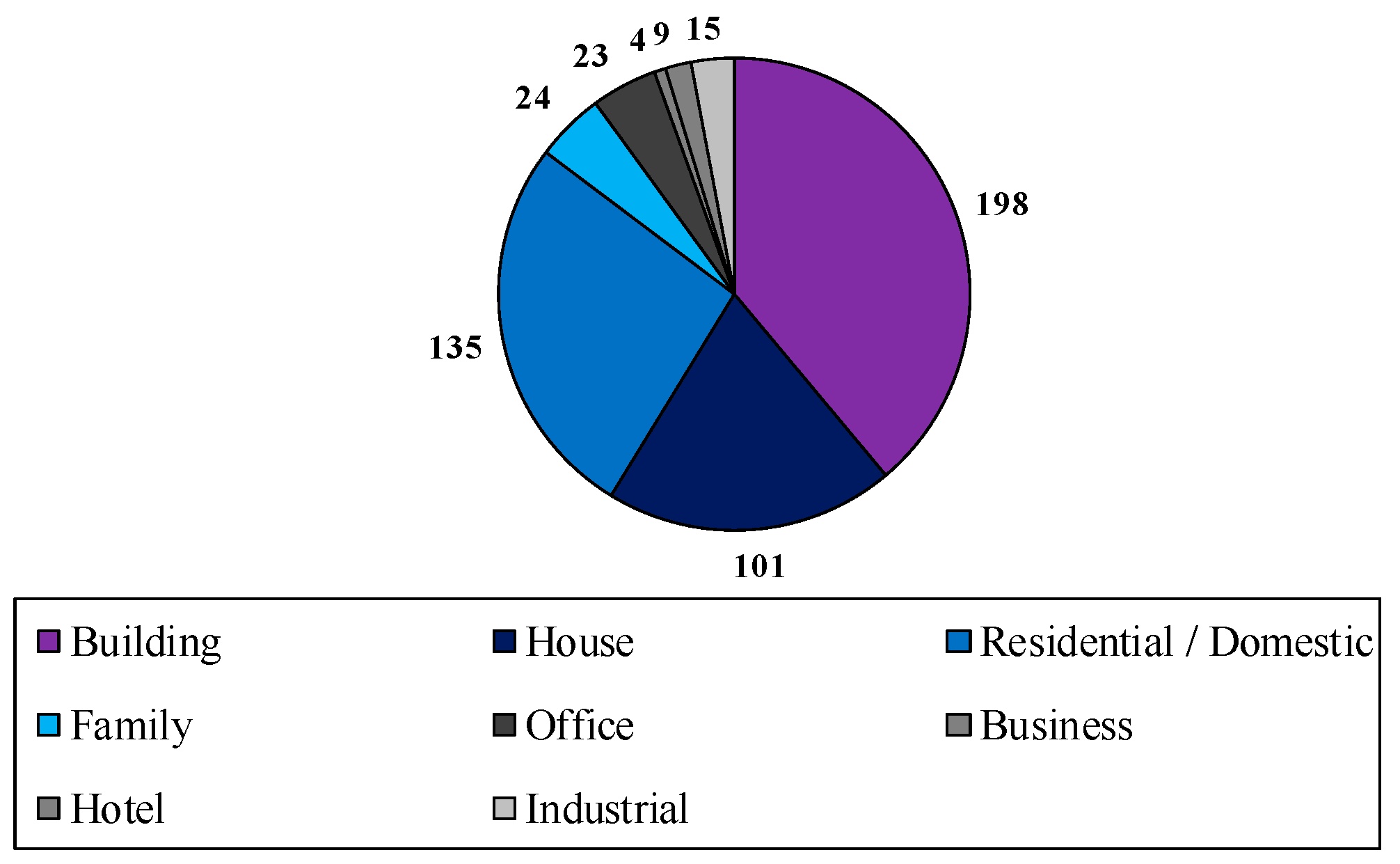
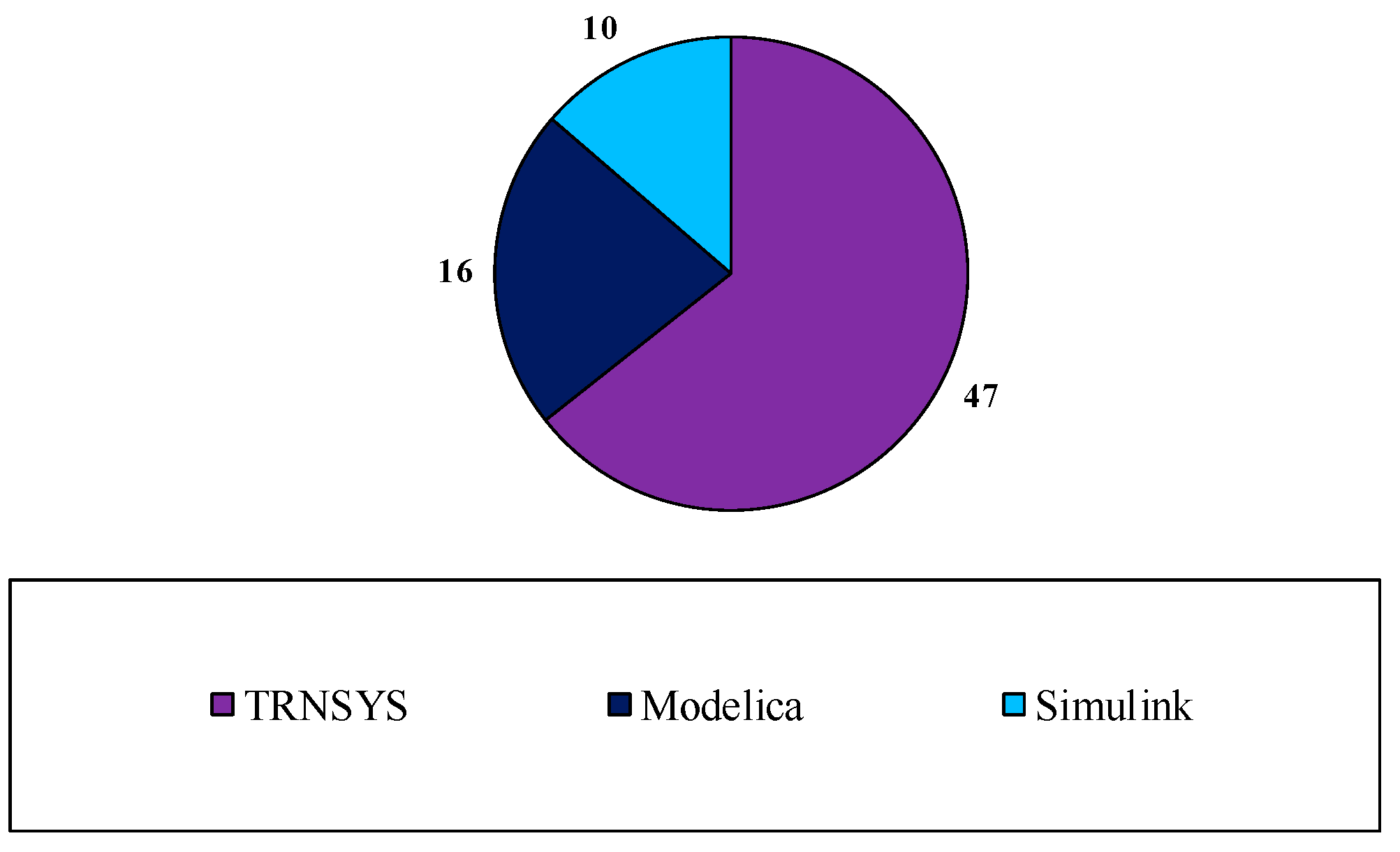
Appendix C
Appendix D
References
- Ziesing, H.J. Anwendungsbilanzen für Die Endenergiesektoren in Deutschland in Den JAHREN 2013 Bis 2017; Arbeitsgemeinschaft Energiebilanzen e.V.: Berlin, Germany, 2018. [Google Scholar]
- Bundesverband Wärmepumpe (BWP) e.V. Wärmepumpenabsatz 2019; Bundesverband Wärmepumpe (BWP) e.V.: Berlin, Germany, 2020. [Google Scholar]
- Fischer, D.; Madani, H. On heat pumps in smart grids: A review. Renew. Sust. Energy Rev. 2017, 70, 342–357. [Google Scholar] [CrossRef] [Green Version]
- German Commision for Electrical, Eltectronic and Information Technologies. International Electrotechnical Vocabulary—Part 351: Control Technology (IEC 60050-351:2013); DIN German Institute for Standardization: Berlin, Germany, 2014. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emai-Naeini, A. Feedback Control of Dynamic Systems, 7th ed.; Pearson: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; PTR Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Oldewurtel, F.; Parisio, A.; Jones, C.N.; Gyalistras, D.; Gwerder, M.; Stauch, V.; Lehmann, V.; Morari, M. Use of model predictive control and weather forecasts for energy efficient building climate control. Energy Build. 2012, 45, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Fischer, D.; Bernhardt, J.; Madani, H.; Wittwer, C. Comparison of control approaches for variable speed air source heat pumps considering time variable electricity prices and PV. Appl. Energy 2017, 204, 93–105. [Google Scholar] [CrossRef]
- Péan, T.Q.; Salom, J.; Costa-Castelló, R. Review of control strategies for improving the energy flexibility provided by heat pump systems in buildings. J. Process. Control 2019, 74, 35–49. [Google Scholar] [CrossRef]
- Sen, S.; Kothari, D.P. Optimal Thermal Generation Unit Commitment: A Review. Int. J. Elec. Power 1998, 20, 443–451. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Kamboj, V.K.; Shukla, V.K.; Singh, B.; Khurana, P. Unit commitment in electrical power system-a literature review. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012; pp. 275–280. [Google Scholar]
- Gillich, A.; Brodecki, L.; Hufendiek, K. Impacts of complementing goals besides emission targets on CO2 mitigation cost: A model-based analysis. Energy Strategy Rev. 2019, 26, 100395. [Google Scholar] [CrossRef]
- Sobieczky, F.; Lettner, C.; Natschläger, T.; Traxler, P. Adaptive heat pump and battery storage demand side energy management. E3S Web Conf. 2017, 22, 162. [Google Scholar] [CrossRef] [Green Version]
- Arabzadeh, V.; Alimohammadisagvand, B.; Jokisalo, J.; Siren, K. A novel cost-optimizing demand response control for a heat pump heated residential building. Build. Simul. 2018, 11, 533–547. [Google Scholar] [CrossRef]
- Carrion, M.; Arroyo, J.M. A Computationally Efficient Mixed-Integer Linear Formulation for the Thermal Unit Commitment Problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Fink, J.; van Leeuwen, R.P.; Hurink, J.L.; Smit, G.J.M. Linear programming control of a group of heat pumps. Energy Sustain. Soc. 2015, 5, 285. [Google Scholar] [CrossRef] [Green Version]
- Pau, M.; Cremer, J.L.; Ponci, F.; Monti, A. Day-Ahead Scheduling of Electric Heat Pumps for Peak Shaving in Distribution Grids. In Smart Cities, Green Technologies, and Intelligent Transport Systems; Donnellan, B., Klein, C., Helfert, M., Gusikhin, O., Pascoal, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 27–51. [Google Scholar]
- Toradmal, A.; Kemmler, T.; Thomas, B. Boosting the share of onsite PV-electricity utilization by optimized scheduling of a heat pump using buildings thermal inertia. Appl. Therm. Eng. 2018, 137, 248–258. [Google Scholar] [CrossRef]
- Widmann, C.; Lödige, D.; Toradmal, A.; Thomas, B. Enabling CHP units for electricity production on demand by smart management of the thermal energy storage. Appl. Therm. Eng. 2017, 114, 1487–1497. [Google Scholar] [CrossRef]
- Dengiz, T.; Jochem, P.; Fichtner, W. Demand response with heuristic control strategies for modulating heat pumps. Appl. Energy 2019, 238, 1346–1360. [Google Scholar] [CrossRef]
- Psimopoulos, E.; Bee, E.; Widén, J.; Bales, C. Techno-economic analysis of control algorithms for an exhaust air heat pump system for detached houses coupled to a photovoltaic system. Appl. Energy 2019, 249, 355–367. [Google Scholar] [CrossRef]
- Halvgaard, R.; Poulsen, N.K.; Madsen, H.; Jorgensen, J.B. Economic Model Predictive Control for building climate control in a Smart Grid. In 2012 IEEE PES Innovative Smart Grid Technologies (ISGT); IEEE: Washington, DC, USA, 2012; pp. 1–6. [Google Scholar]
- Crawley, D.B.; Hand, J.W.; Kummert, M.; Griffith, B.T. Contrasting the capabilities of building energy performance simulation programs. Build. Environ. 2008, 43, 661–673. [Google Scholar] [CrossRef] [Green Version]
- Harish, V.S.K.V.; Kumar, A. A review on modeling and simulation of building energy systems. Renew. Sustain. Energy Rev. 2016, 56, 1272–1292. [Google Scholar] [CrossRef]
- Weinand, J.M.; McKenna, R.; Fichtner, W. Developing a municipality typology for modelling decentralised energy systems. Util. Policy 2019, 57, 75–96. [Google Scholar] [CrossRef] [Green Version]
- Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA). EEG-Anlagenstammdaten: Veröffentlichung der Registerdaten; Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA): Bonn, Germany, 2019. [Google Scholar]
- Hafner, B.; Plettner, J.; Wemhöner, C.; Wenzel, W. CARNOT Blockset—Conventional and Renewable Energy Systems Optimization Toolbox; Solar-Institut Jülich: Jülich, Germany, 1999. [Google Scholar]



| Component | Property | Value | Unit |
|---|---|---|---|
| Household Load | Electrical Demand | 3995 | kWhel/year |
| Thermal Heat Demand | 11,581 | kWhth/year | |
| Photovoltaic System | Electrical Power | 6.8 | kWp |
| Electrical Energy | 6545 | kWhel/year | |
| Air Source Heat Pump | Electrical Power | 2.4 (A7/W35) | kWel |
| Thermal Power | 10.9 (A7/W35) | kWth | |
| COP | 4.5 (A7/W35) | – | |
| Electric Heater | Electrical Power | 5 | kWel |
| Thermal Energy Storage | Thermal Capacatiy | 48.9 | kWhth |
| Density | 2000 | kg/m3 | |
| Area | 220 | m2 | |
| Floor thickness | 0.08 | m2 | |
| Specific heat capacity | 1000 | J/kg/K | |
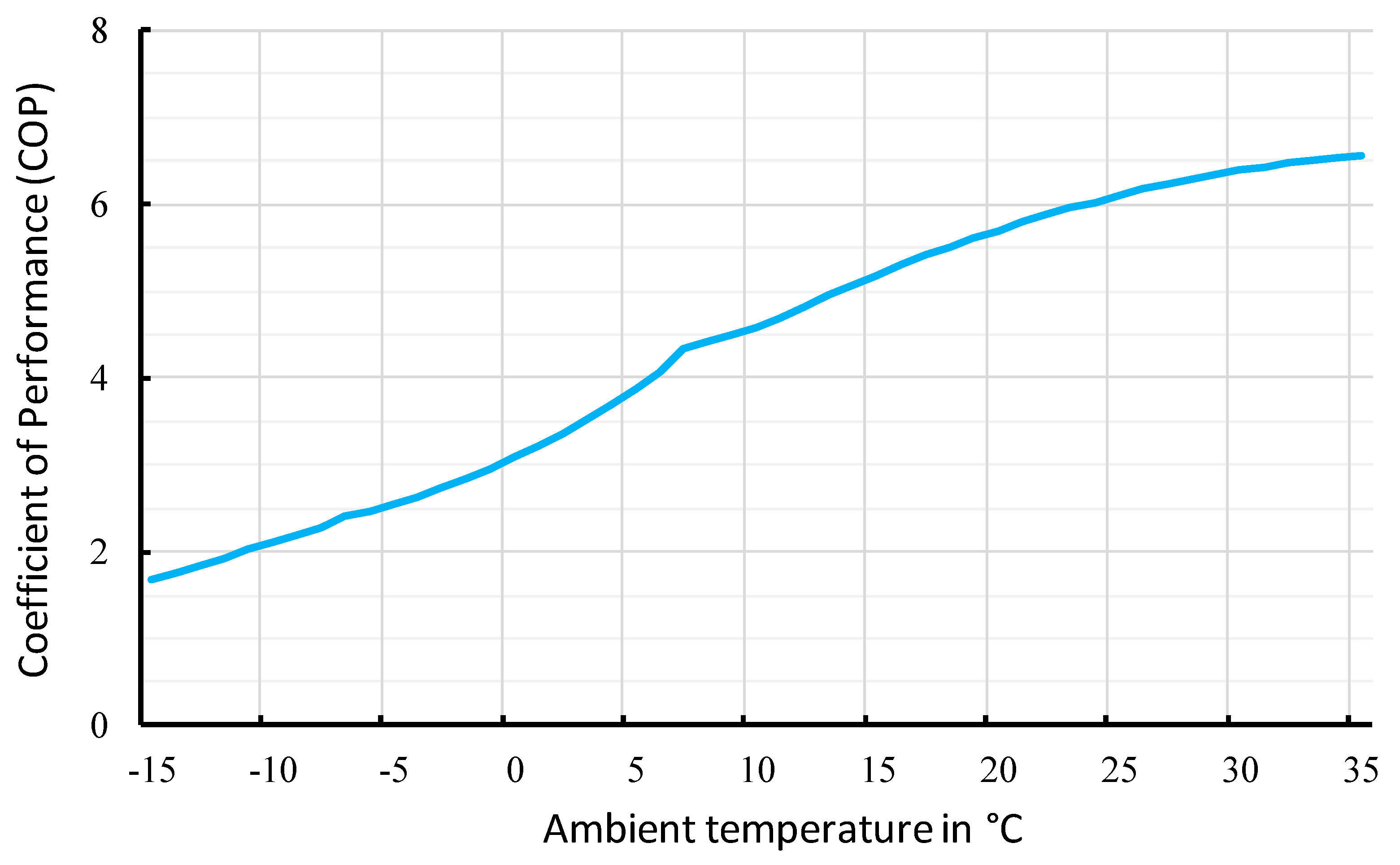
| Ambient Temperature | Min./Max. Value | −13/33 | °C |
| Coefficient of Performance (COP) | Min. Value | ||
| Max. Value | |||
| Power Grid | Purchase Price | 29.33 | €ct/kWhel |
| Feed-In Tariff | 12.60 | €ct/kWhel |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulz, M.; Kemmler, T.; Kumm, J.; Hufendiek, K.; Thomas, B. A More Realistic Heat Pump Control Approach by Application of an Integrated Two-Part Control. Energies 2020, 13, 2752. https://doi.org/10.3390/en13112752
Schulz M, Kemmler T, Kumm J, Hufendiek K, Thomas B. A More Realistic Heat Pump Control Approach by Application of an Integrated Two-Part Control. Energies. 2020; 13(11):2752. https://doi.org/10.3390/en13112752
Chicago/Turabian StyleSchulz, Maximilian, Thomas Kemmler, Julia Kumm, Kai Hufendiek, and Bernd Thomas. 2020. "A More Realistic Heat Pump Control Approach by Application of an Integrated Two-Part Control" Energies 13, no. 11: 2752. https://doi.org/10.3390/en13112752





