Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes
Abstract
1. Introduction
2. Modeling Formulation
2.1. Train Modeling
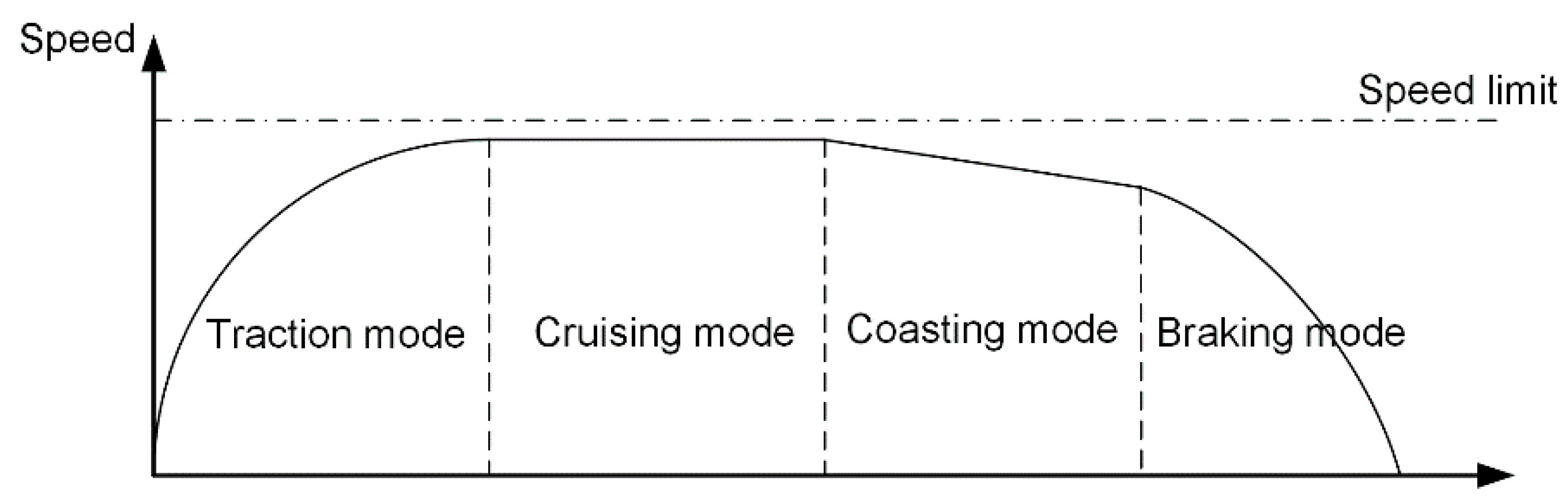
2.1.1. Train Kinematics
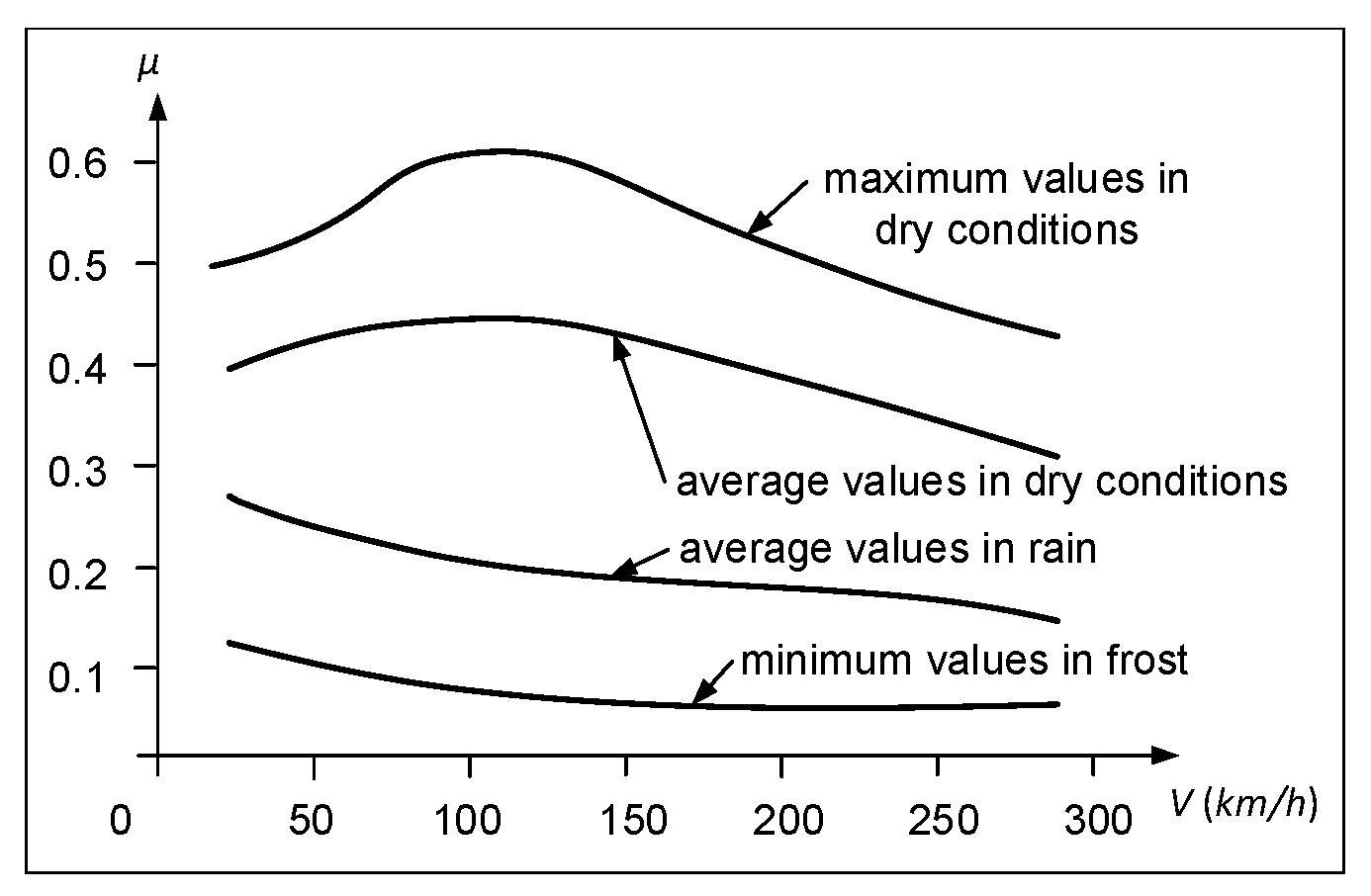
2.1.2. Driving Controls
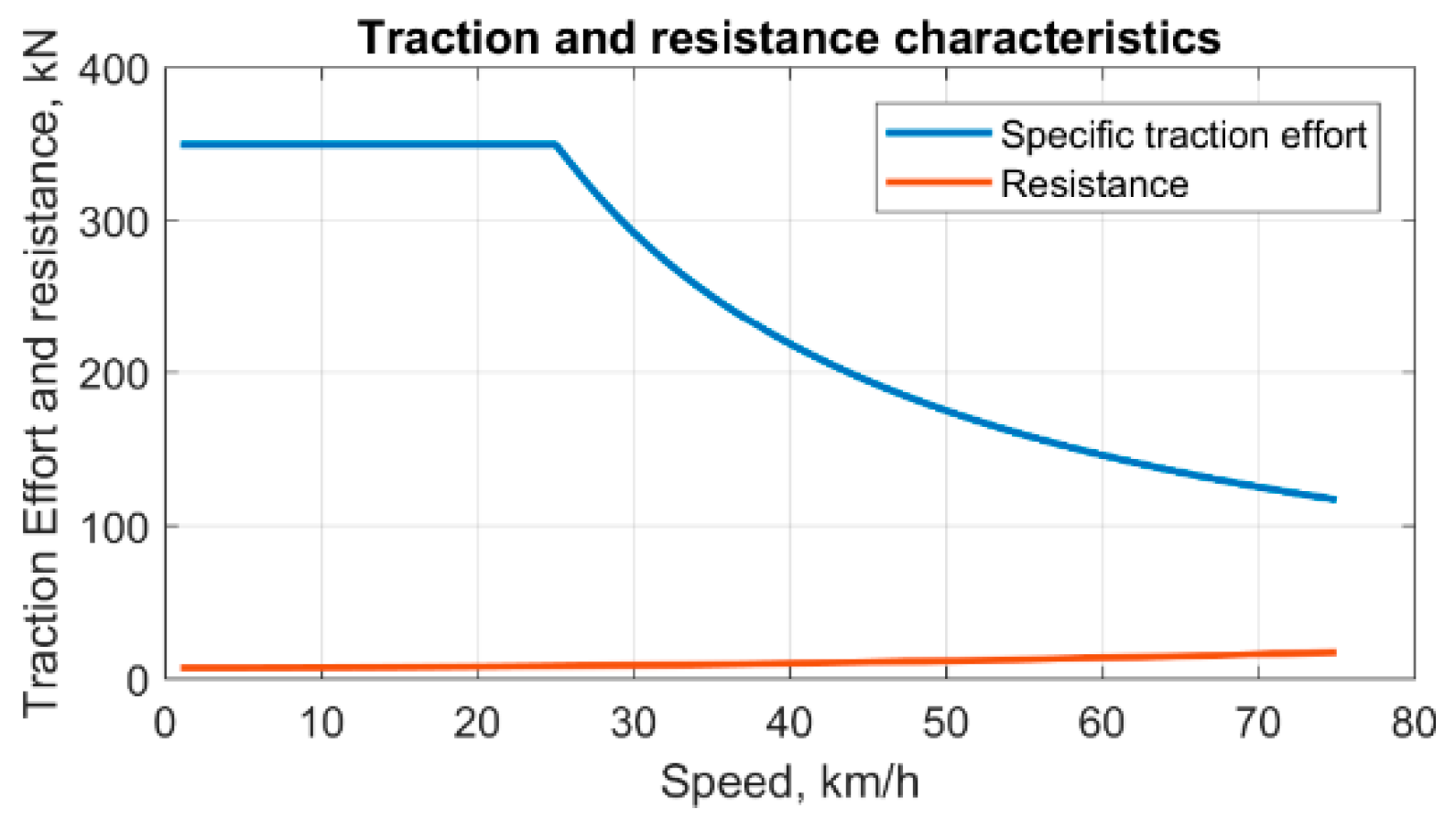
2.1.3. Train Power Demand
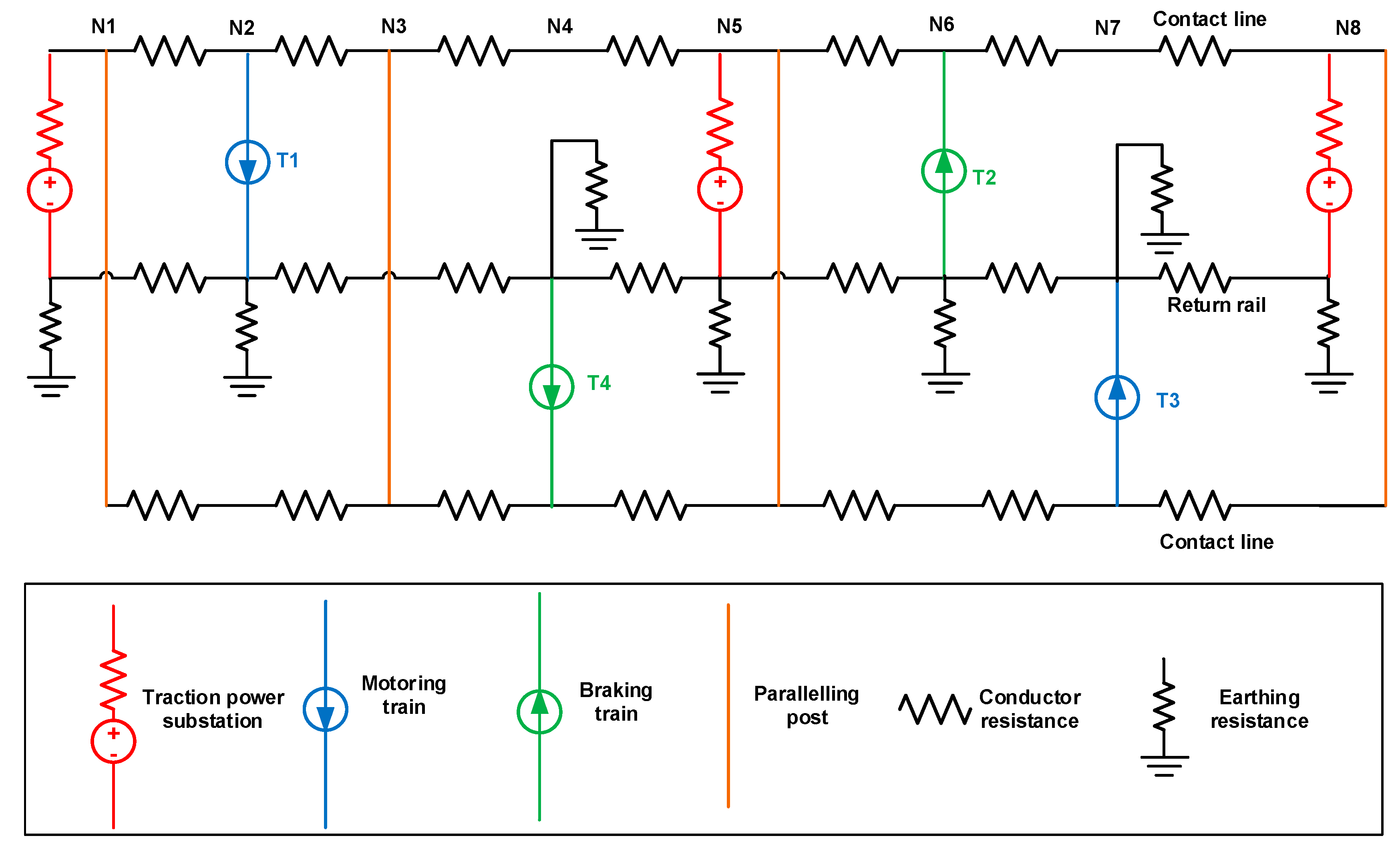
2.2. Traction Power Network Modeling
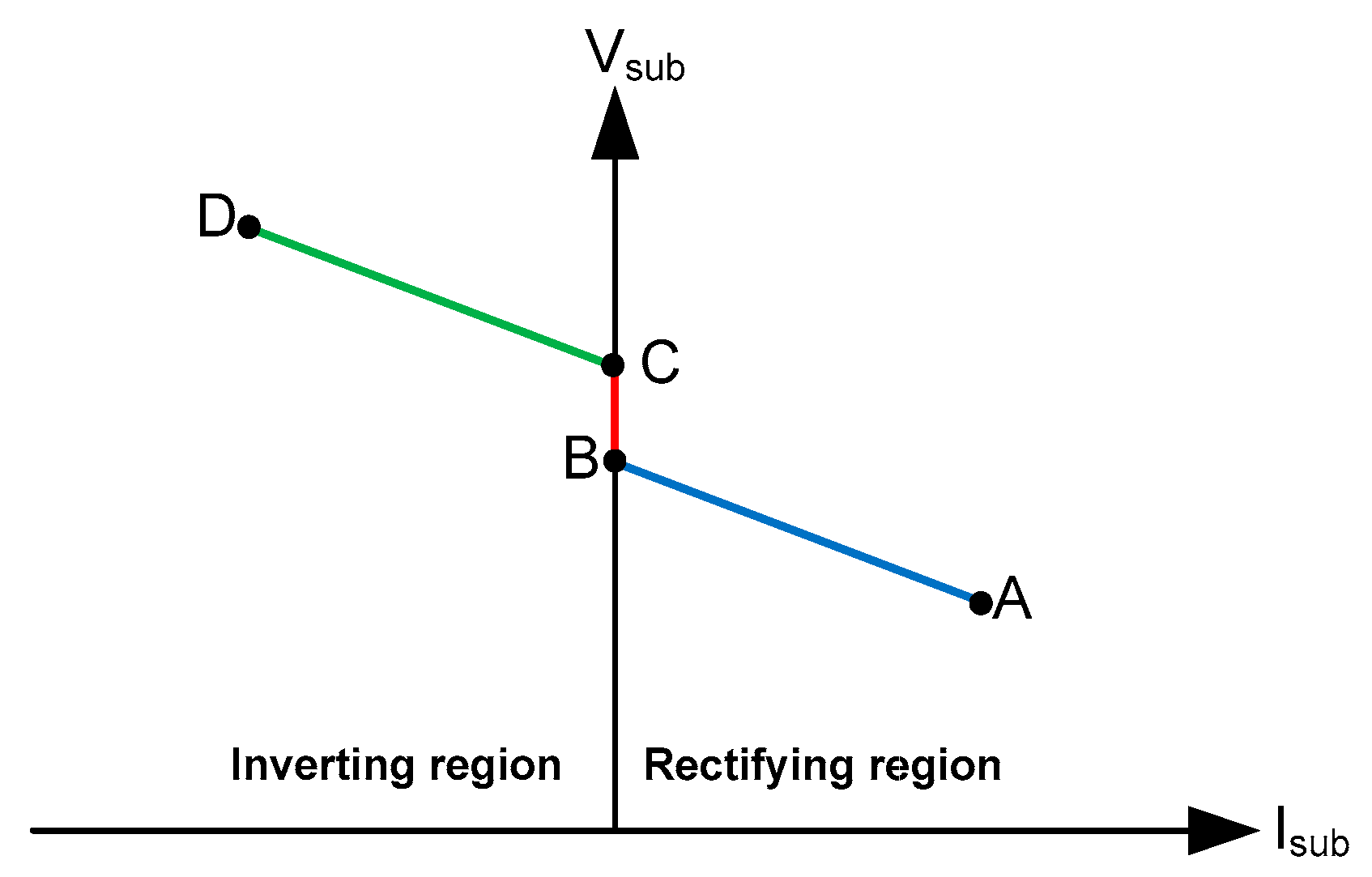
2.2.1. Traction Power Substation
2.2.2. Power Network Circuit
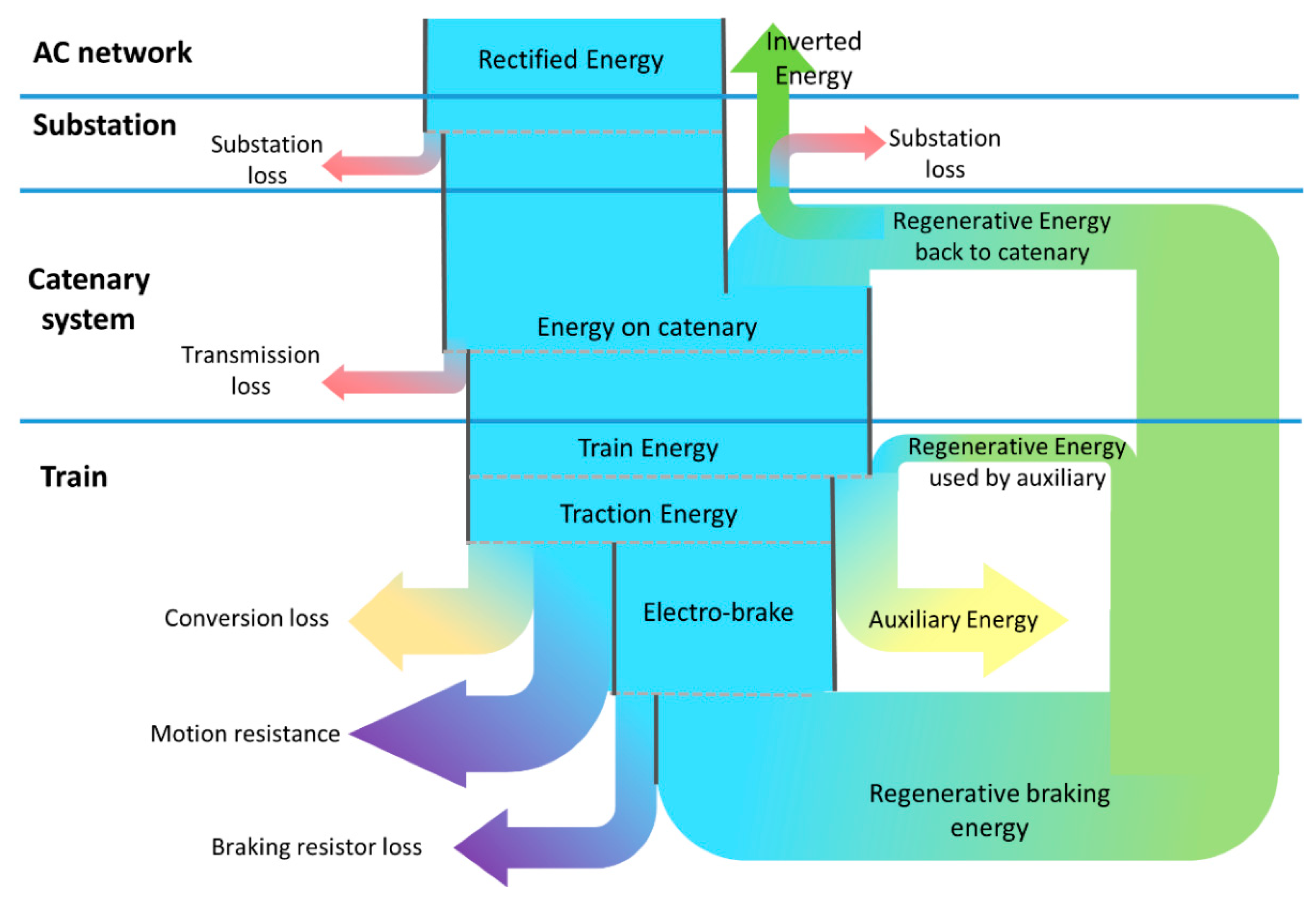
2.3. Energy Flow and Evaluation
3. Fault Identification
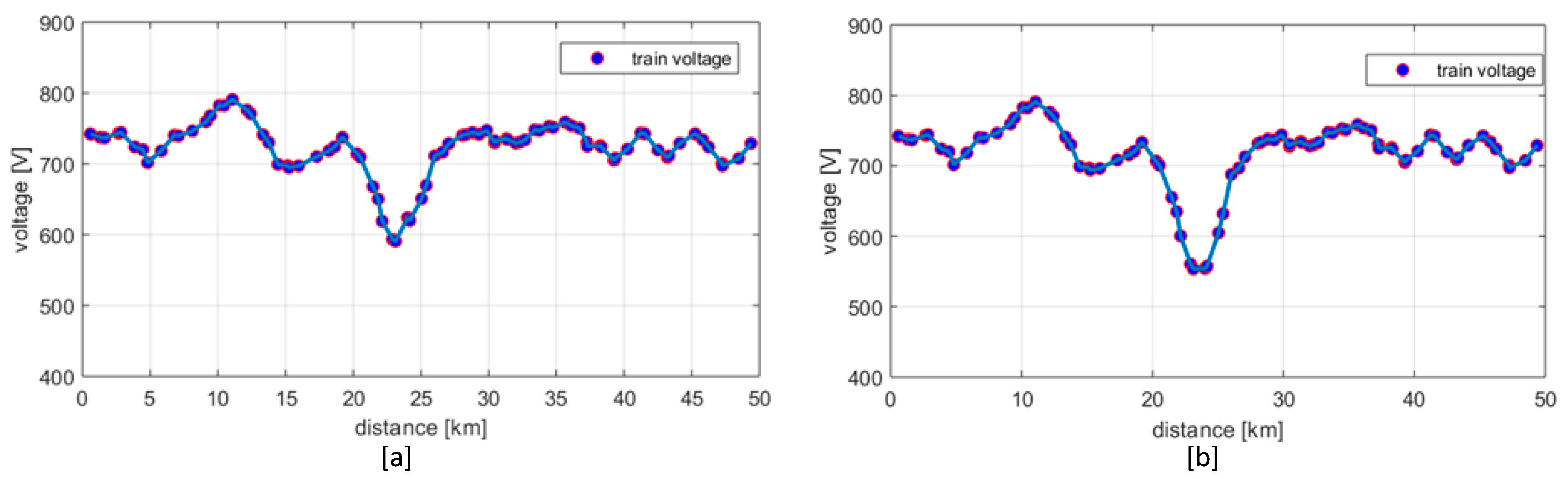
3.1. Under-Voltage Traction
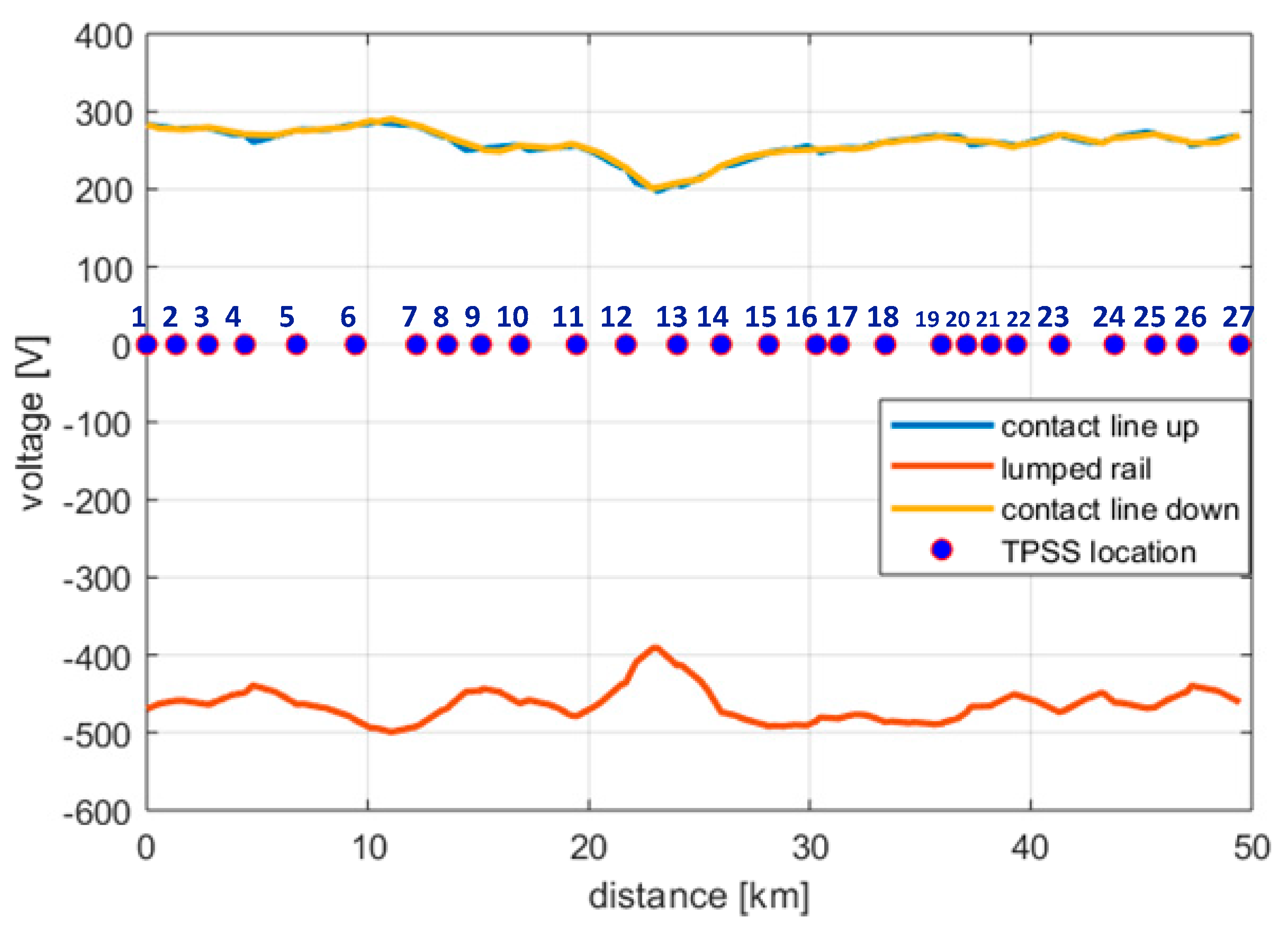
3.2. Rail Potential
3.3. TPSS Outage
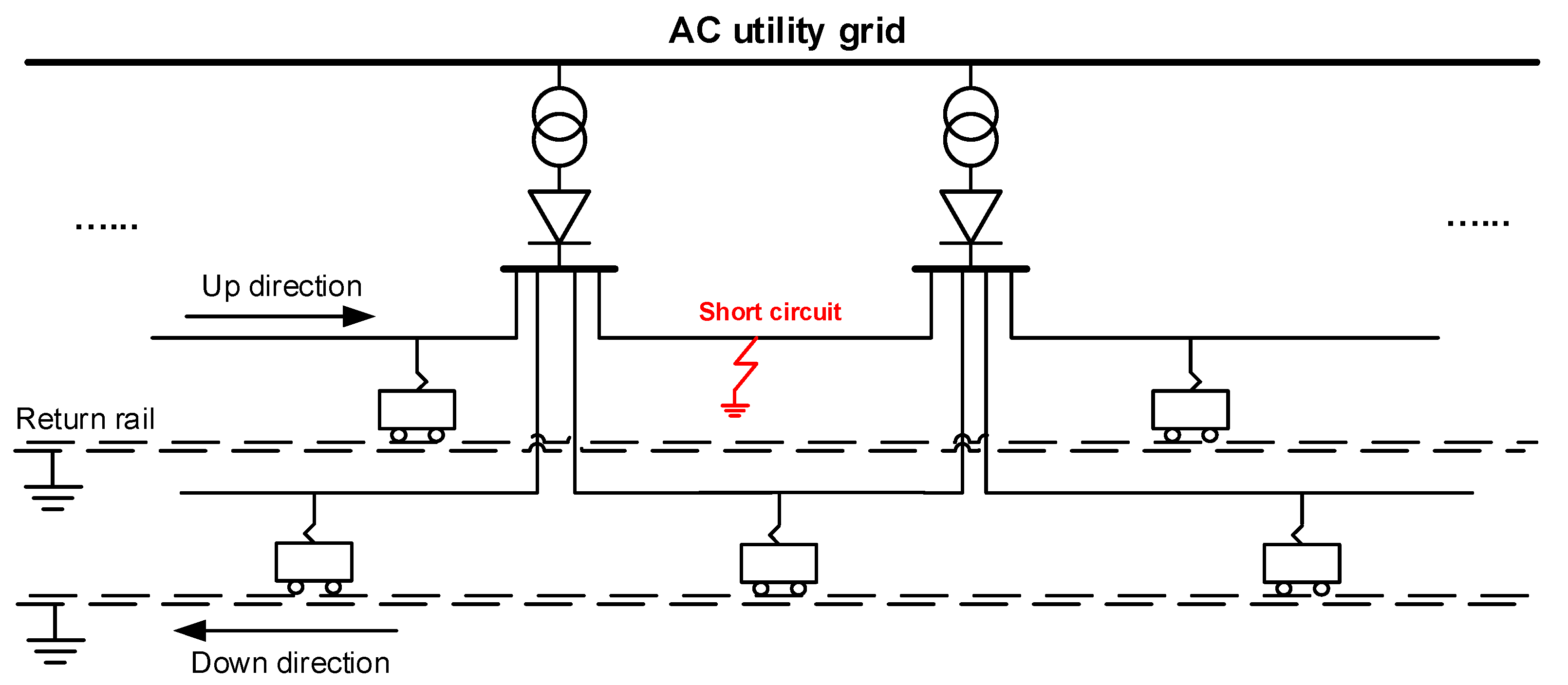
3.4. Short Circuit
4. Case Studies
4.1. Simulation Parameters
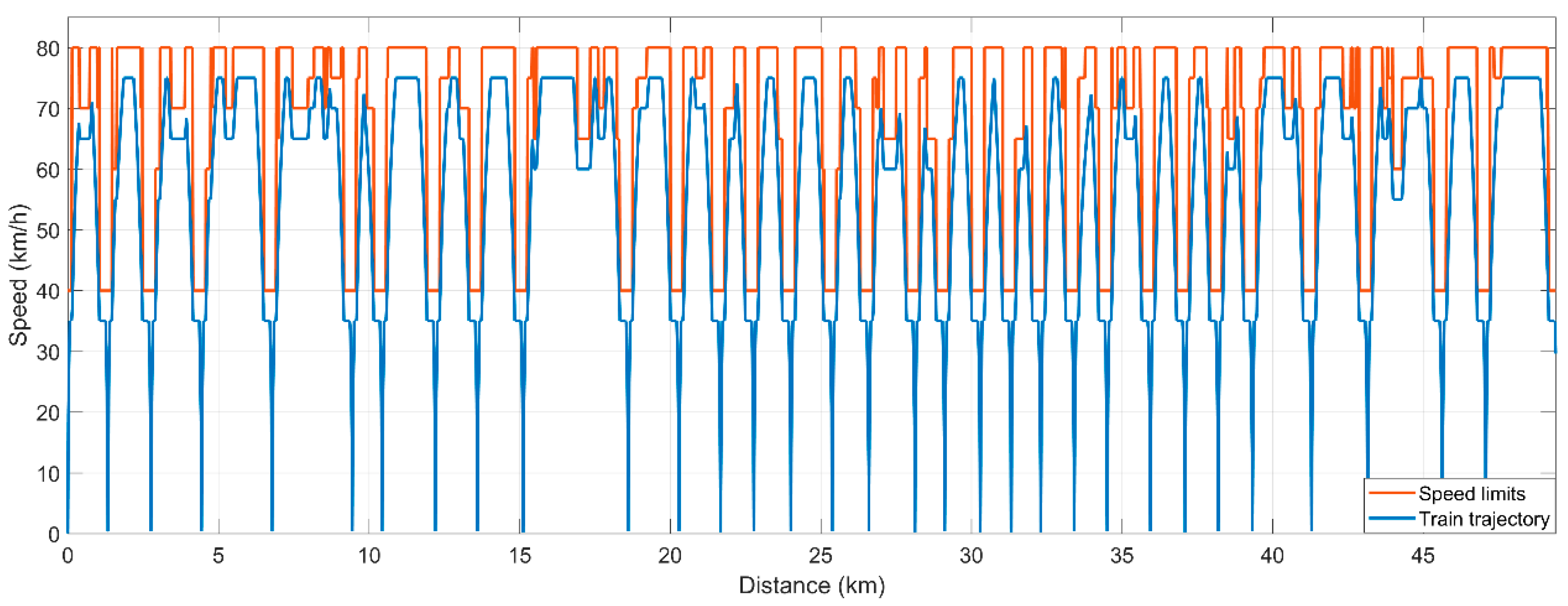
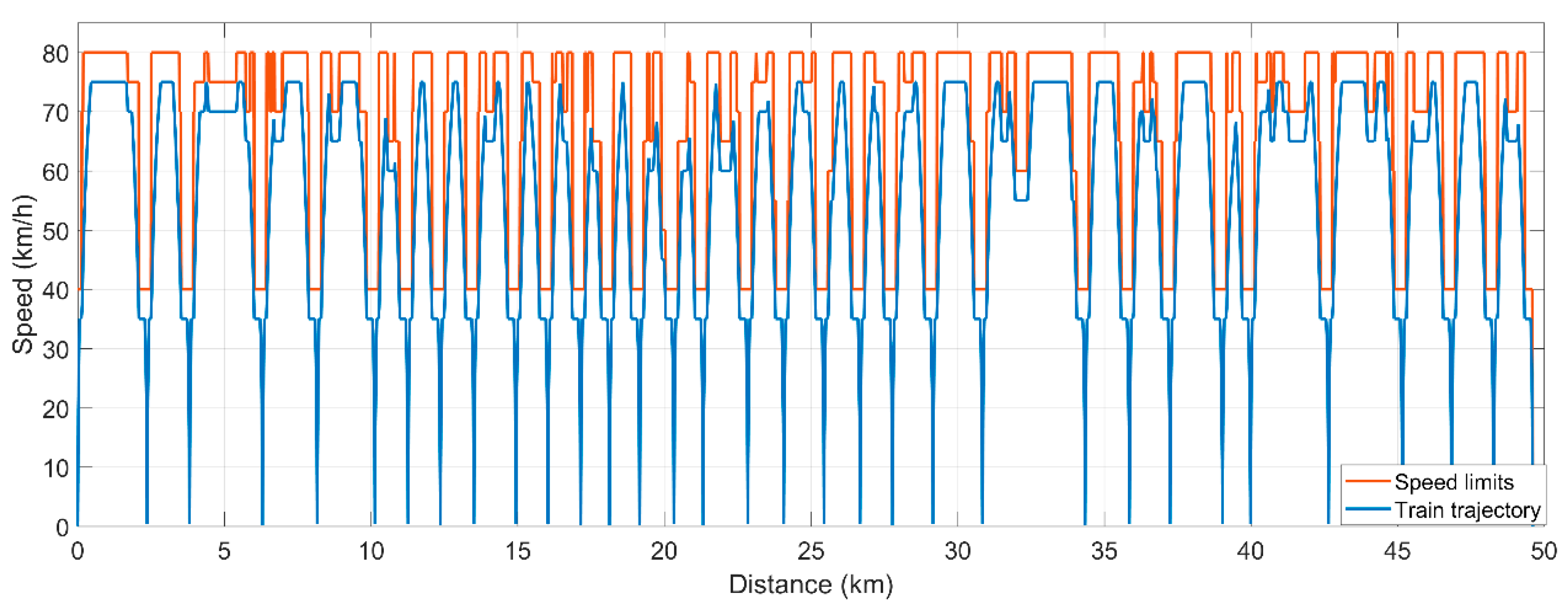
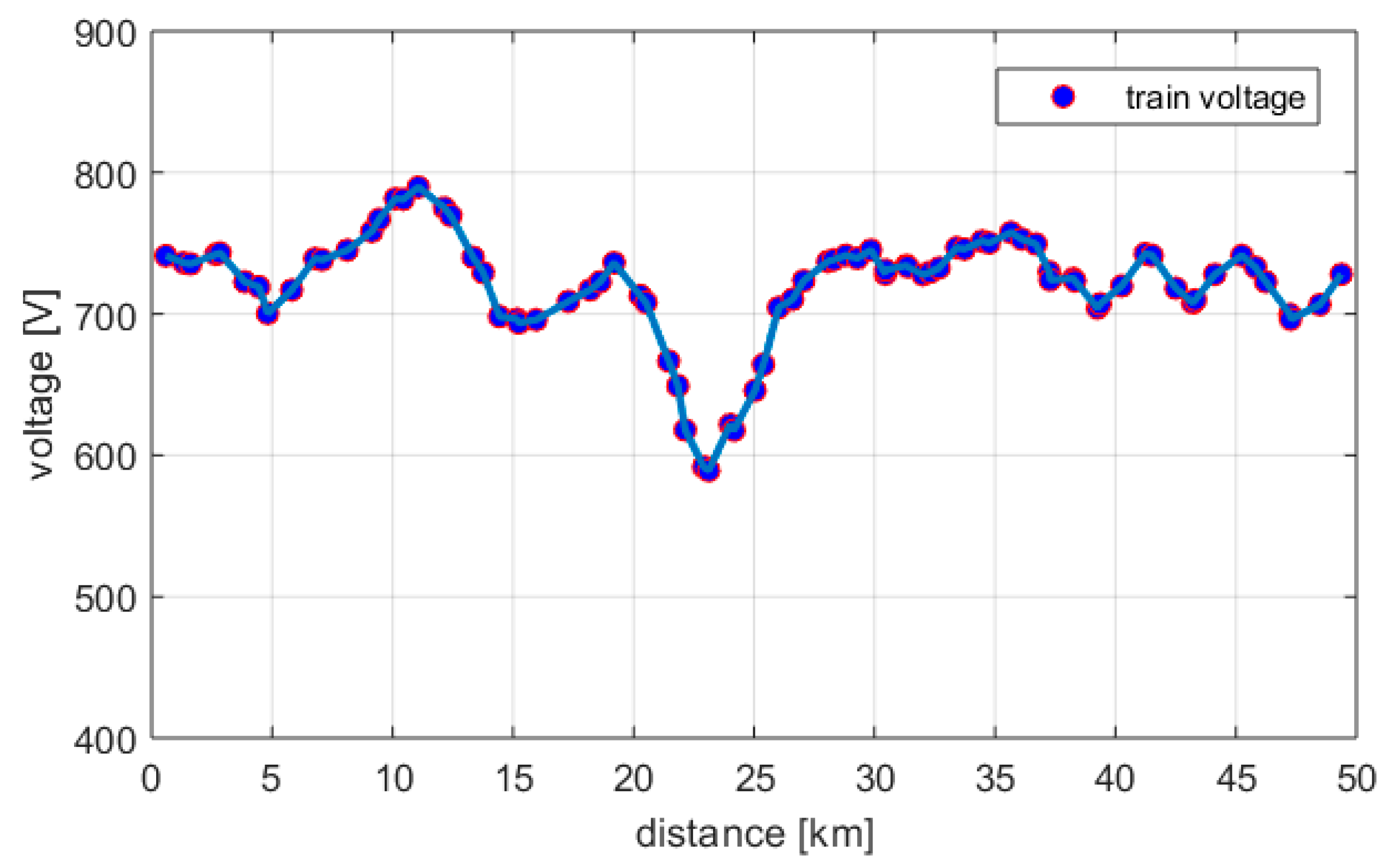
4.2. Train Motion Simulation Results
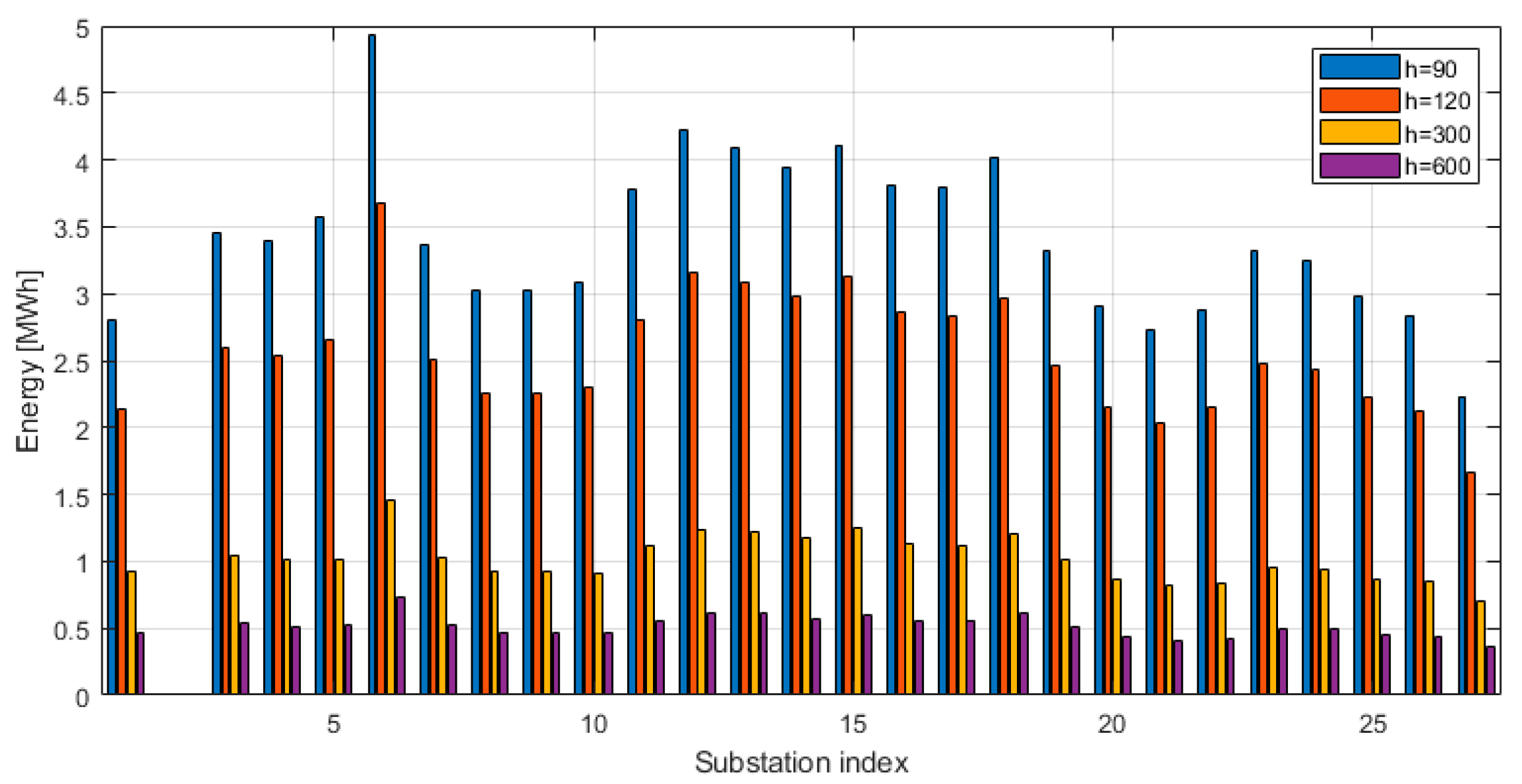
4.3. Energy Consumption with a Normal Operation
- When the auxiliary power is 0 kW, there is some energy inverted by substations. The inverted energy increases when the headway increases. When the headway is short, most regenerative braking energy is used by motoring trains in DC systems;
- When the auxiliary power is 480 kW, not much energy is inverted by substations. The inverted energy when the headway is 90, 100, and 120 s is zero, and the inverted energy increases a little when the headway is 300 and 600 s. This is because the train auxiliary uses a lot of regenerative braking energy;
- The time interval is 1 s in the simulation. When the headway is 90 s, there are 110 trains in the network. Therefore, there are 9900 train seconds in the simulation of each scenario. The time of under-voltage means the amount of time when the under-voltage traction mode occurs. When the auxiliary power is zero, the time of under-voltage is very low. However, when the auxiliary power is 480 kW, under-voltage happens 312 times during the operation. The time of under-voltage decreases when the headway increases;
- The regenerative energy efficiency is very high for all of the scenarios, and is between 99% and 100%. This denotes that nearly all of the electro-braking energy can be reused;
- The total system loss is the sum of the substation, feeder, and transmission loss. The loss accounts for around 10% of the total substation energy consumption.
- The total energy consumption of all TPSS decreases with the headway time;
- The maximum energy consumption occurs at TPSS-6 for the cases which are shown in red. This denotes that TPSS-6 could consume more energy than others for most cases. This is consistent with the fact that the rated tractive power of TPSS-6 is 3 MW × 2, which is higher than other the TPSS;
- The second highest energy consumption occurs at TPSS-12 for the cases;
- The energy consumption of each TPSS varies with different timetables. Some TPSS could consume a high amount of energy due to a particular timetable.
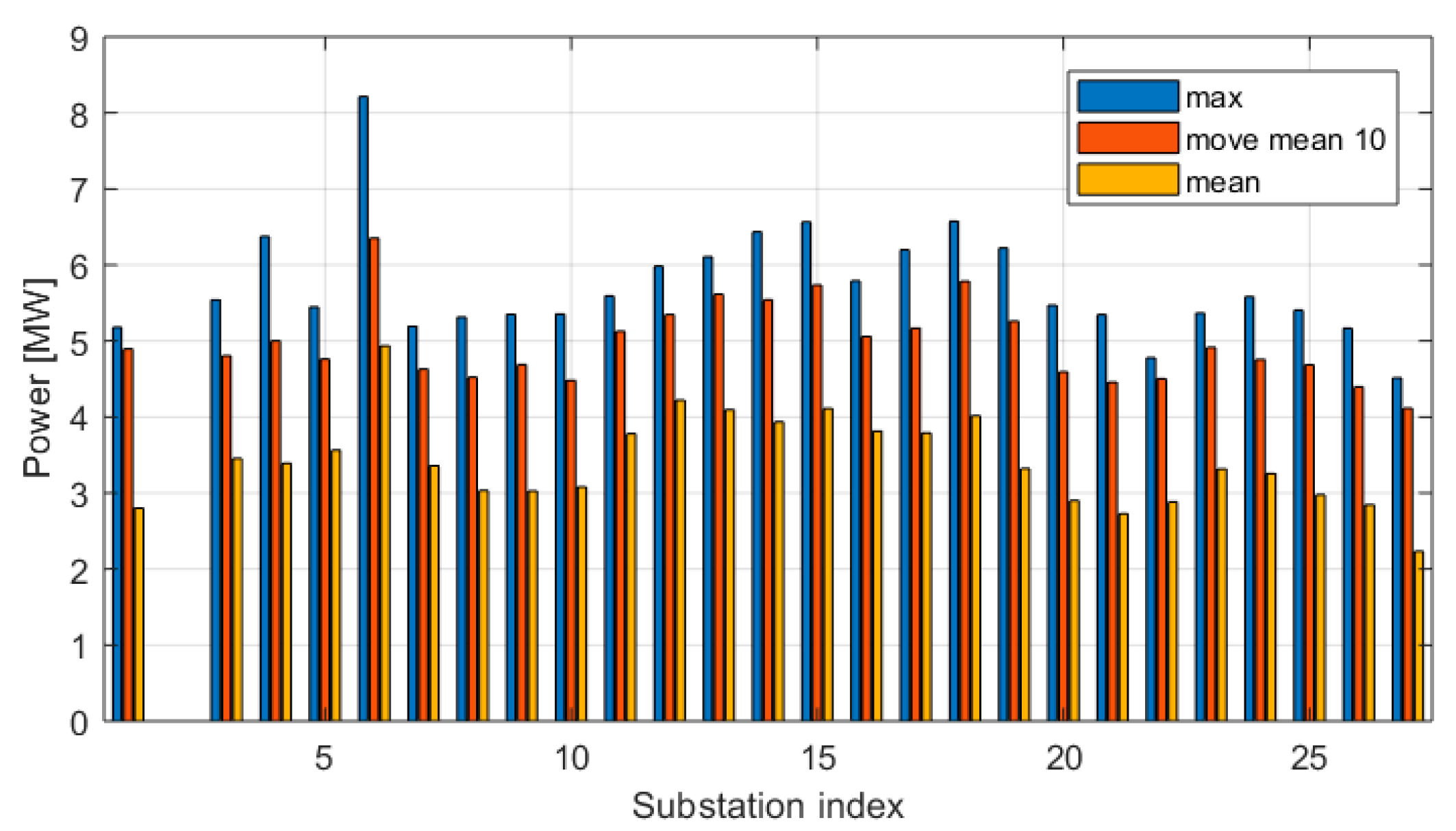
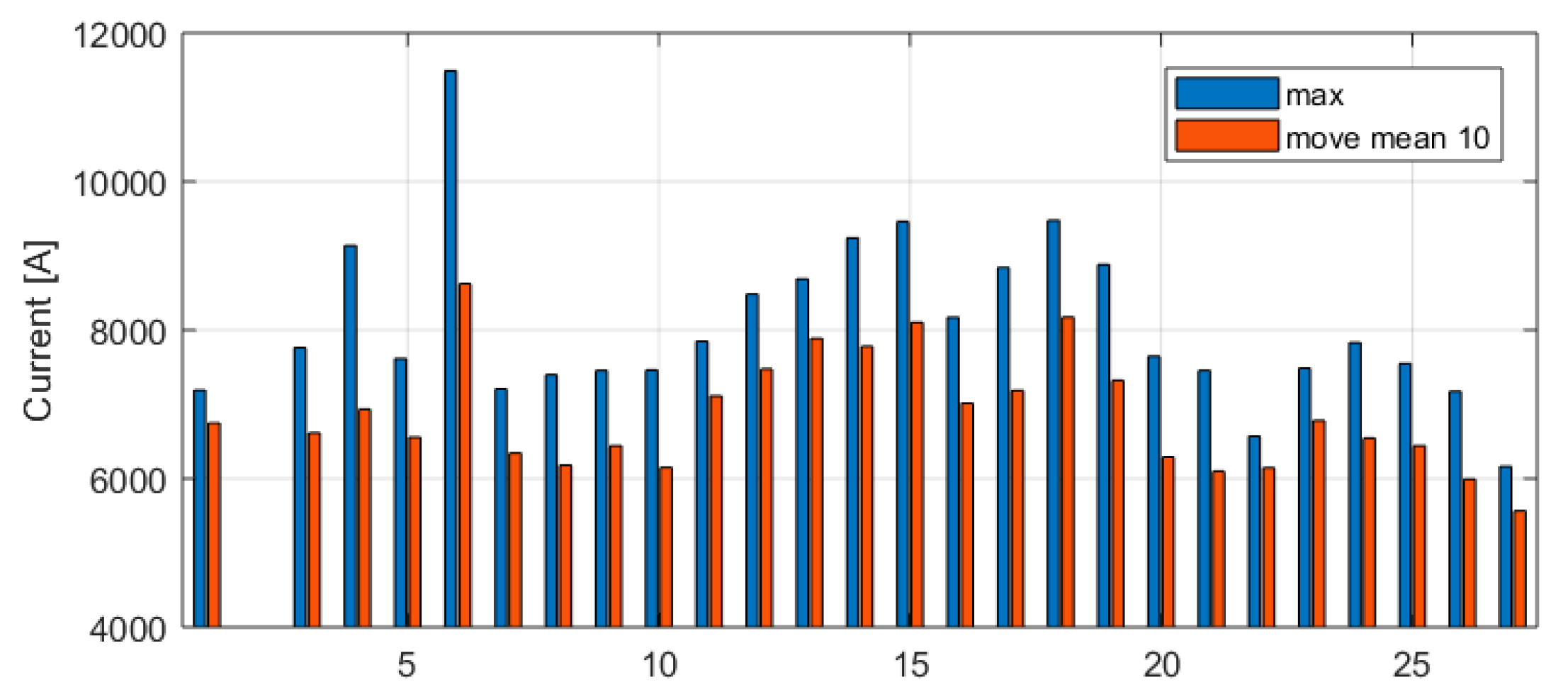
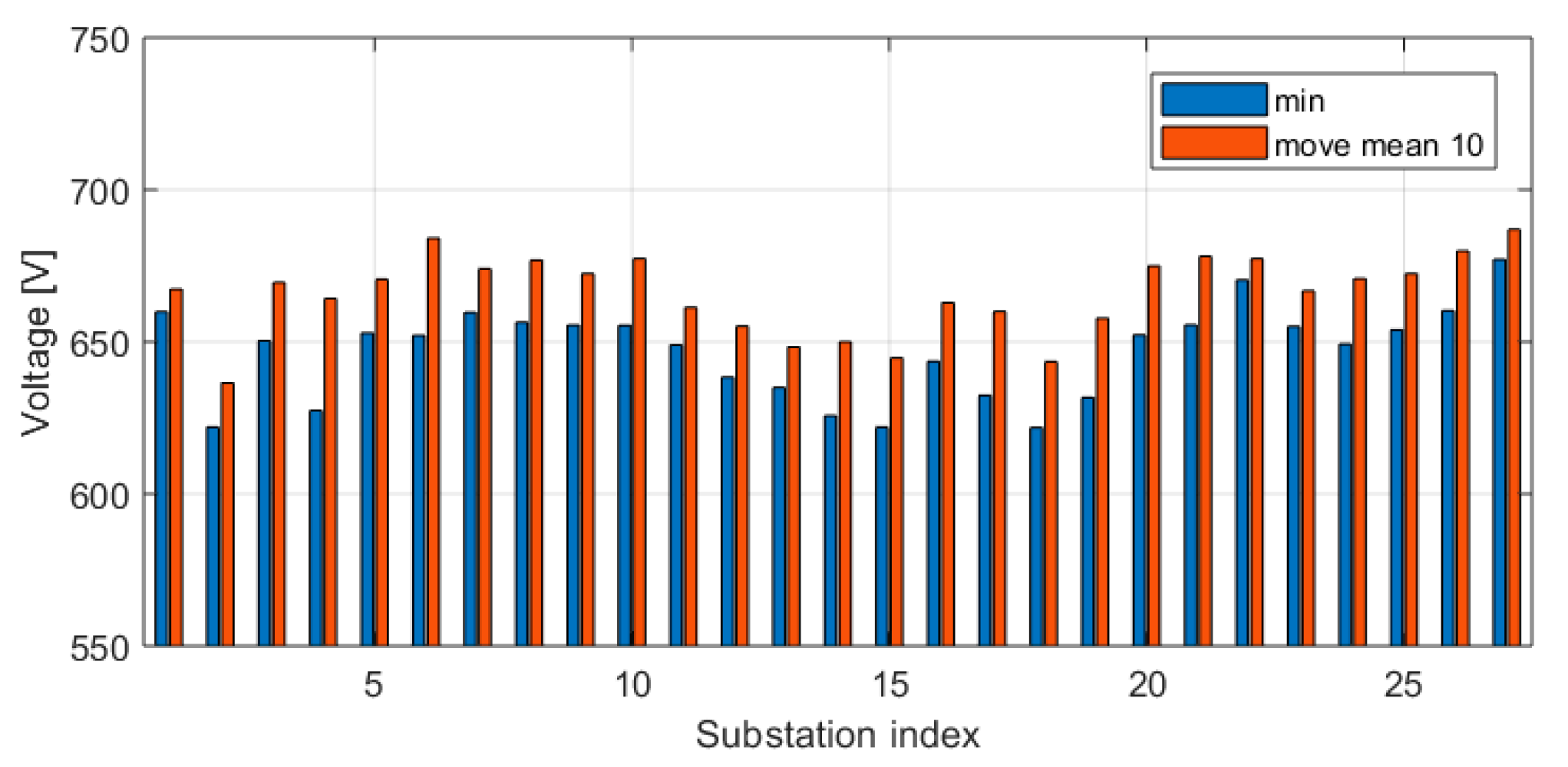
4.4. Study of Hotspots
4.5. Results with TPSS Switched off
4.5.1. Network Operation Results
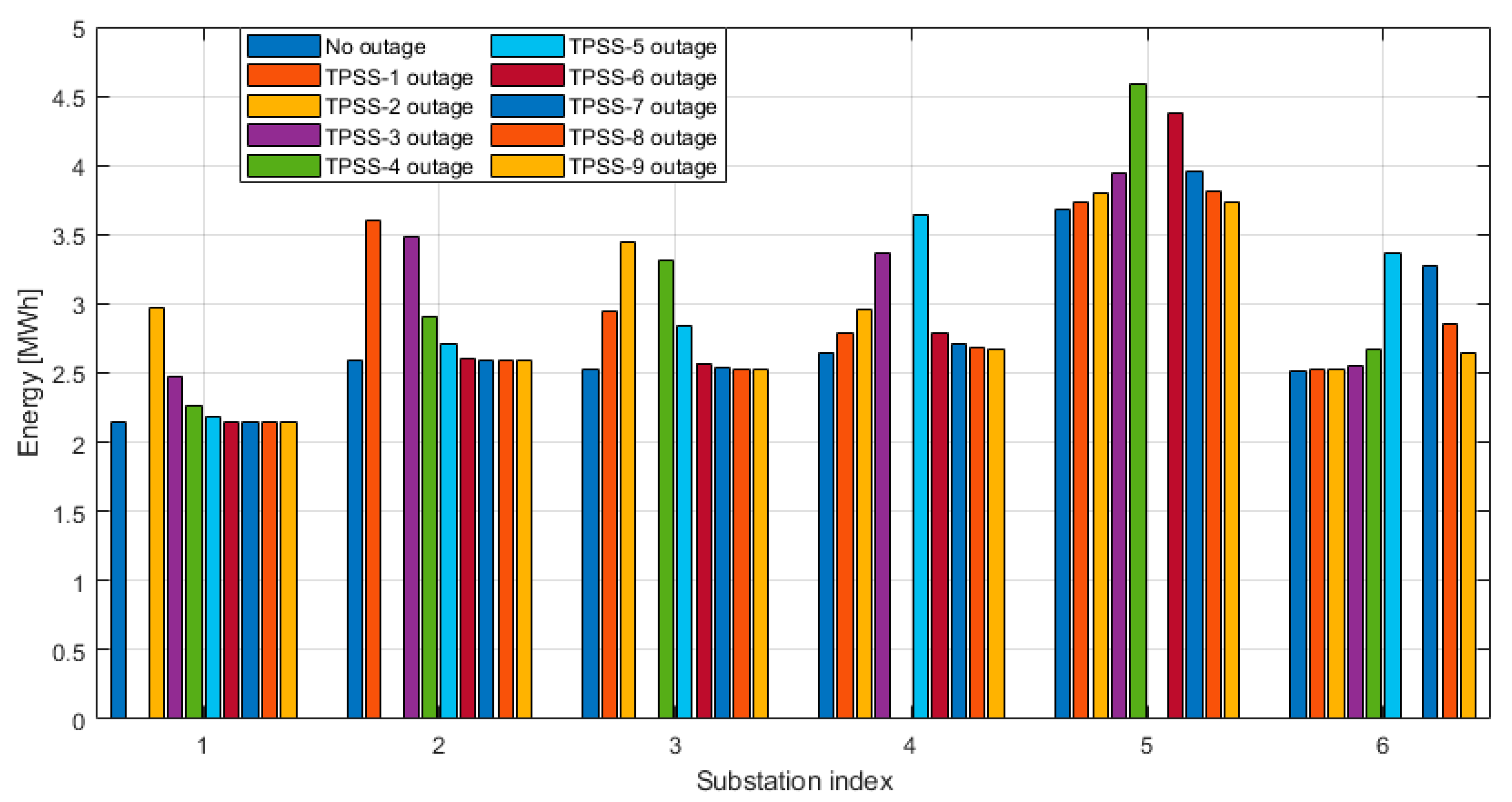
4.5.2. Energy Consumption
- If one of the TPSS is switched off, the energy consumption of this TPSS is zero. The energy consumption of TPSS around this faulty TPSS increases;
- The amount of energy consumption change of the working TPSS depends on the distance from the outage TPSS. The maximum variation occurs on the nearest working TPSS, which can represent up to 39% of the increase;
- The substation energy consumption is unlikely to be affected if there are more than three substations between this substation and the outage substation;
- If the fault TPSS supplied a very large amount of energy when it was on, the impact on the nearby TPSS will be more significant when this faulty TPSS is down.
4.6. Results with a Short Circuit
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chymera, M.Z.; Renfrew, A.C.; Barnes, M.; Holden, J. Modeling Electrified Transit Systems. IEEE Trans. Veh. Technol. 2010, 59, 2748–2756. [Google Scholar] [CrossRef]
- Chang, C.S.; Khambadkone, A.; Zhao, X. Modeling and simulation of DC transit system with VSI-fed induction motor driven train using PSB/MATLAB. In Proceedings of the 4th IEEE International Conference on Power Electronics and Drive Systems, Denpasar, Indonesia, 25 October 2001; Volume 2, pp. 881–885. [Google Scholar]
- Goodman, C.J.; Sin, L.K. DC railway power network solutions by diakoptics. In Proceedings of the IEEE/ASME Joint Railroad Conference, Chicago, IL, USA, 22–24 March 1994; pp. 103–110. [Google Scholar]
- Goodman, C.J. Modelling and simulation. In Proceedings of the 5th IET Professional Development Course on Railway Electrification Infrastructure and Systems (REIS 2011), London, UK, 6–9 June 2011; pp. 22–31. [Google Scholar]
- Cai, Y.; Irving, M.; Case, S. Modelling and numerical solution of multibranched DC rail traction power systems. IEE Proc. Electr. Power Appl. 1995, 142, 323. [Google Scholar] [CrossRef]
- Arboleya, P.; Mohamed, B.; El-Sayed, I. DC Railway Simulation Including Controllable Power Electronic and Energy Storage Devices. IEEE Trans. Power Syst. 2018, 33, 5319–5329. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, M.; Liu, Q. A Novel Power Flow Algorithm for Traction Power Supply Systems Based on the Thévenin Equivalent. Energies 2018, 11, 126. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, M.; Weston, P.; Hilmansen, S.; Zhao, N.; Roberts, C.; Chen, L. Energy evaluation of the power network of a DC railway system with regenerating trains. IET Electr. Syst. Transp. 2016, 6, 41–49. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A. A Review of the Energy Efficiency Improvement in DC Railway Systems. Energies 2019, 12, 1092. [Google Scholar] [CrossRef]
- Tian, Z.; Weston, P.; Zhao, N.; Hilmansen, S.; Roberts, C.; Chen, L. System energy optimisation strategies for metros with regeneration. Transp. Res. Part C Emerg. Technol. 2017, 75, 120–135. [Google Scholar] [CrossRef]
- Lin, S.; Huang, D.; Wang, A.; Huang, Y.; Zhao, L.; Luo, R.; Lu, G. Research on the Regeneration Braking Energy Feedback System of Urban Rail Transit. IEEE Trans. Veh. Technol. 2019, 68, 7329–7339. [Google Scholar] [CrossRef]
- Zhang, G.; Tian, Z.; Tricoli, P.; Hillmansen, S.; Liu, Z. A new hybrid simulation integrating transient-state and steady-state models for the analysis of reversible DC traction power systems. Int. J. Electr. Power Energy Syst. 2019, 109, 9–19. [Google Scholar] [CrossRef]
- Zhang, G.; Tian, Z.; Tricoli, P.; Hillmansen, S.; Wang, Y.; Liu, Z. Inverter Operating Characteristics Optimization for DC Traction Power Supply Systems. IEEE Trans. Veh. Technol. 2019, 68, 3400–3410. [Google Scholar] [CrossRef]
- Zhang, G.; Tian, Z.; Du, H.; Liu, Z. A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters. Energies 2018, 11, 1661. [Google Scholar] [CrossRef]
- Ye, J.-J.; Li, K.-P. Simulation optimization for train movement on a single-track railway. Chin. Phys. B 2013, 22, 050205. [Google Scholar] [CrossRef]
- Lu, S.; Hillmansen, S.; Ho, T.K.; Roberts, C. Single-Train Trajectory Optimization. IEEE Trans. Intell. Transp. Syst. 2013, 14, 743–750. [Google Scholar] [CrossRef]
- Lu, S.; Hilmansen, S.; Roberts, C. A Power-Management Strategy for Multiple-Unit Railroad Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 406–420. [Google Scholar] [CrossRef]
- Bocharnikov, Y.V.; Tobias, A.M.; Roberts, C. Reduction of train and net energy consumption using genetic algorithms for Trajectory Optimisation. In Proceedings of the IET Conference on Railway Traction Systems (RTS 2010), Birmingham, UK, 13–15 April 2010. [Google Scholar]
- Bocharnikov, Y.; Tobias, A.; Roberts, C.; Hillmansen, S.; Goodman, C. Optimal driving strategy for traction energy saving on DC suburban railways. IET Electr. Power Appl. 2007, 1, 675. [Google Scholar] [CrossRef]
- Chang, C.; Sim, M. Optimising train movements through coast control using genetic algorithms. IEE Proc. Electr. Power Appl. 1997, 144, 65. [Google Scholar] [CrossRef]
- Chang, C.S.; Chua, C.S.; Quek, H.B.; Xu, X.Y.; Ho, S.L. Development of train movement simulator for analysis and optimisation of railway signalling systems. In Proceedings of the 1998 International Conference on Developments in Mass Transit Systems, London, UK, 20–23 April 1998. [Google Scholar]
- Howlett, P. The Optimal Control of a Train. Ann. Oper. Res. 2000, 98, 65–87. [Google Scholar] [CrossRef]
- Howlett, P.G. Optimal strategies for the control of a train. Automacita 1996, 32, 519–532. [Google Scholar] [CrossRef]
- Zhao, N.; Chen, L.; Tian, Z.; Roberts, C.; Hilmansen, S.; Lv, J. Field test of train trajectory optimisation on a metro line. IET Intell. Transp. Syst. 2017, 11, 273–281. [Google Scholar] [CrossRef]
- Tian, Z.; Zhao, N.; Hillmansen, S.; Roberts, C.; Dowens, T.; Kerr, C. SmartDrive: Traction Energy Optimization and Applications in Rail Systems. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2764–2773. [Google Scholar] [CrossRef]
- Chen, S.; Ho, T.; Mao, B. Reliability evaluations of railway power supplies by fault-tree analysis. IET Electr. Power Appl. 2007, 1, 161. [Google Scholar] [CrossRef]
- Li, K.; Yang, Q.; Cui, Z.; Zhao, Y.; Lin, S. Reliability Evaluation of a Metro Traction Substation Based on the Monte Carlo Method. IEEE Access 2019, 7, 172974–172980. [Google Scholar] [CrossRef]
- Huh, J.-S.; Shin, H.-S.; Moon, W.-S.; Kang, B.-W.; Kim, J.C. Study on Voltage Unbalance Improvement Using SFCL in Power Feed Network With Electric Railway System. IEEE Trans. Appl. Supercond. 2013, 23, 3601004. [Google Scholar] [CrossRef]
- Huang, S.R.; Kuo, Y.L.; Chen, B.N.; Lu, K.C.; Huang, M.C. A short circuit current study for the power supply system of Taiwan railway. IEEE Trans. Power Deliv. 2001, 16, 492–497. [Google Scholar] [CrossRef]
- Huang, S.R.; Kuo, Y.L.; Chen, B.N.; Lu, K.C.; Huang, M.C. A short circuit current study for the power supply system of Taiwan railway. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 Jane 2000; pp. 1046–1052. [Google Scholar]
- Cho, G.-J.; Kim, C.-H.; Kim, M.-S.; Kim, D.-H.; Heo, S.-H.; Kim, H.-D.; Min, M.-H.; An, T.-P. A Novel Fault-Location Algorithm for AC Parallel Autotransformer Feeding System. IEEE Trans. Power Deliv. 2018, 34, 475–485. [Google Scholar] [CrossRef]
- Cho, G.; Kim, M.; Kim, D.; Kim, C. A Study on Modeling and Verification of the Percentage Differential Relay for the Protection of AC Electric Railway Feeding System. In Proceedings of the TENCON 2018—2018 IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 0752–0756. [Google Scholar]
- Wang, C.; Yin, X. Comprehensive Revisions on Fault-Location Algorithm Suitable for Dedicated Passenger Line of High-Speed Electrified Railway. IEEE Trans. Power Deliv. 2012, 27, 2415–2417. [Google Scholar] [CrossRef]
- Jin, J.; Allan, J.; Goodman, C.; Payne, K. Single pole-to-earth fault detection and location on a fourth-rail DC railway system. IEE Proc. Electr. Power Appl. 2004, 151, 498–504. [Google Scholar] [CrossRef]
- Park, J.-D. Ground Fault Detection and Location for Ungrounded DC Traction Power Systems. IEEE Trans. Veh. Technol. 2015, 64, 5667–5676. [Google Scholar] [CrossRef]
- Park, J.-D.; Candelaria, J. Fault Detection and Isolation in Low-Voltage DC-Bus Microgrid System. IEEE Trans. Power Deliv. 2013, 28, 779–787. [Google Scholar] [CrossRef]
- Hillmansen, S.; Roberts, C. Energy storage devices in hybrid railway vehicles: A kinematic analysis. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 135–143. [Google Scholar] [CrossRef]
- Loumiet, J.R.; Jungbauer, W.G. Train Accident Reconstruction and FELA and Railroad Litigation; Lawyers & Judges Pub Co: Tucson, AZ, USA, 2005; p. 767. [Google Scholar]
- Pozzobon, P. Transient and steady-state short-circuit currents in rectifiers for DC traction supply. IEEE Trans. Veh. Technol. 1998, 47, 1390–1404. [Google Scholar] [CrossRef]
- Finlayson, A.; Goodman, C.J.; White, R.D. Investigation into the computational techniques of power system modelling for a DC railway. Urban Transp. 2007 2006, 88. [Google Scholar] [CrossRef]
- BS-EN50388. Railway Applications-Power Supply and Rolling Stock-Technical Criteria; BSI: London, UK, 2012. [Google Scholar]
- BS-EN50163. Railway Applications-Supply Voltages of Traction Systems; BSI: London, UK, 2007. [Google Scholar]


| Movement Mode | uf | ub | Equations |
|---|---|---|---|
| Traction | 1 | 0 | |
| Cruising | 1 | 0 | |
| Coasting | 0 | 0 | |
| Braking | 0 | 1 |
| DC Railway Voltage Level (V) | Lowest Non-Permanent Voltage Vmin (V) | Rated Voltage Vn (V) | Highest Non-Permanent Voltage Vmax (V) |
|---|---|---|---|
| 600 | 400 | 600 | 800 |
| 750 | 500 | 750 | 1000 |
| 1500 | 1000 | 1500 | 1950 |
| Parameters | Value/Equation |
|---|---|
| Train mass with passengers, tonnes | 301 |
| Train formation | 3M3T |
| Train length, m | 148 |
| Rotary allowance | 0.08 |
| Train Resistance, N/tonne | 3.49 + 0.039 v + 0.00066 v2 (v: km/h) |
| Maximum traction and braking power, kW | 2518 |
| Maximum operation speed, km/h | 80 |
| Maximum traction effort, kN | 351 |
| Scenario Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Auxiliary Power (kW) | 0 | 0 | 0 | 0 | 0 | 480 | 480 | 480 | 480 | 480 |
| Headway (s) | 90 | 100 | 120 | 300 | 600 | 90 | 100 | 120 | 300 | 600 |
| Es (kWh) | 802 | 796 | 825 | 840 | 845 | 2221 | 2221 | 2214 | 2199 | 2191 |
| Erec (kWh) | 816 | 803 | 859 | 957 | 1066 | 2221 | 2221 | 2215 | 2209 | 2224 |
| Einv (kWh) | −14 | −8 | −34 | −117 | −222 | 0 | 0 | 0 | −10 | −34 |
| Esl (kWh) | 25 | 24 | 28 | 35 | 44 | 67 | 67 | 66 | 67 | 69 |
| Efl (kWh) | 16 | 13 | 17 | 12 | 10 | 84 | 73 | 67 | 33 | 21 |
| Etl (kWh) | 48 | 46 | 65 | 74 | 74 | 74 | 72 | 81 | 72 | 74 |
| Etr_demand (kWh) | 1507 | 1507 | 1507 | 1507 | 1507 | 1507 | 1507 | 1507 | 1507 | 1507 |
| Etr (kWh) | 1507 | 1507 | 1506 | 1507 | 1507 | 1476 | 1489 | 1479 | 1507 | 1507 |
| Eeb (kWh) | 796 | 796 | 796 | 796 | 796 | 796 | 796 | 796 | 796 | 796 |
| Ereg (kWh) | 794 | 795 | 791 | 788 | 790 | 796 | 796 | 796 | 796 | 796 |
| Eaux (kWh) | 0 | 0 | 0 | 0 | 0 | 1316 | 1316 | 1316 | 1316 | 1316 |
| ηreg | 100% | 100% | 99% | 99% | 99% | 100% | 100% | 100% | 100% | 100% |
| Time of under-voltage (s) | 0 | 0 | 8 | 0 | 0 | 312 | 192 | 250 | 3 | 0 |
| Time of train running (s) | 9900 | 9900 | 9900 | 9900 | 9900 | 9900 | 9900 | 9900 | 9900 | 9900 |
| TPSS Index | Positive Feeder Potential (V) | Negative Feeder Potential (V) | Output Voltage (V) | Current (A) | Power (kW) | |
|---|---|---|---|---|---|---|
| Normal operation | 10 | 722 | 3 | 720 | 3622 | 2760 |
| 11 | 728 | −9 | 737 | 2600 | 2012 | |
| 12 | 704 | 39 | 665 | 6909 | 4999 | |
| 13 | 690 | 66 | 624 | 9333 | 6490 | |
| 14 | 719 | 9 | 711 | 4159 | 3143 | |
| 15 | 730 | −12 | 742 | 2270 | 1765 | |
| 16 | 728 | −9 | 738 | 2527 | 1957 | |
| TPSS-13 switched off | 10 | 718 | 0 | 718 | 3701 | 2887 |
| 11 | 723 | −9 | 732 | 2864 | 2234 | |
| 12 | 696 | 45 | 651 | 7716 | 6019 | |
| 13 | 663 | 109 | 554 | 0 | 0 | |
| 14 | 708 | 21 | 687 | 5596 | 4365 | |
| 15 | 724 | −11 | 734 | 2747 | 2143 | |
| 16 | 724 | −11 | 735 | 2671 | 2083 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Zhao, N.; Hillmansen, S.; Su, S.; Wen, C. Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes. Energies 2020, 13, 2788. https://doi.org/10.3390/en13112788
Tian Z, Zhao N, Hillmansen S, Su S, Wen C. Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes. Energies. 2020; 13(11):2788. https://doi.org/10.3390/en13112788
Chicago/Turabian StyleTian, Zhongbei, Ning Zhao, Stuart Hillmansen, Shuai Su, and Chenglin Wen. 2020. "Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes" Energies 13, no. 11: 2788. https://doi.org/10.3390/en13112788
APA StyleTian, Z., Zhao, N., Hillmansen, S., Su, S., & Wen, C. (2020). Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes. Energies, 13(11), 2788. https://doi.org/10.3390/en13112788









