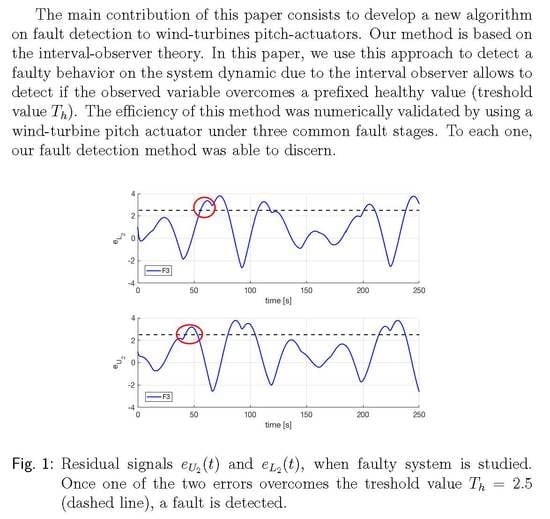
1. Introduction
Nowadays, wind turbines are essential machines to produce green energy from the natural air current. One way to increase this green energy is by increasing the wind-turbine blade dimensions. Hence, its price is increased too. Therefore, to ensure a good feasibility and long lifetime operation of the wind turbines blade-dynamics to effectively capture the wind, a fault detection system design for the pitch actuator systems of a wind turbine results in being virtually mandatory [
1,
2,
3,
4].
Recently, the benefit impact of wind turbines on earth and, in a near future, on Mars too is well accepted [
5,
6]. In wind turbine literature, an important topic is to improve its performance. In [
7], a study on misalignment of the wind turbine nacelle with respect to the wind direction is presented, and a study [
8] on the major driven force on the mooring line tension of offshore wind turbines. In [
9], the effect of age in the performance of wind turbine is investigated. The damage effects caused by the fatigue of the wind turbine components is an important issue to perform the behavior of wind turbines [
10]. In addition, improving the design can be an effective way to ameliorate the performance of the whole system [
11]. For example, the blade aerodynamic design of the wind turbine is studied in [
12]. Moreover, vibration control and fatigue reduction are studied to develop new strategies with the objective of increasing the performance and decreasing pitch actuator usage [
13,
14]. To fulfill this objective, stochastics models can be built to study fatigue loads [
15], or to predict drive-train vibrations [
16]. Furthermore, it is crucial to prevent system failures in order to ensure the performance. Innovative fault detection and diagnosis are essential to realize the required levels of reliability in recent wind turbines [
17,
18,
19]. To assure efficient operation on energy conversion of these wind systems, an efficient pitch actuator fault detection methodology is mandatory [
20]. Fault detection techniques can be classified into two major categories: model-based methods and signal processing-based methods. For model-based fault detection, the system model could be mathematical [
21]. Faults are detected based on the residual generated by state variable or model parameter estimation (see [
22] and a reference on it). For signal processing-based fault detection, mathematical or statistical operations are performed on the measurements (see, for example, [
23]).
Hence, the main objective of this paper is to present a recent algorithm to detect a fault in pitch actuators of wind rotary mechanisms. In the presence of pitch actuator faults, pitch systems may present changes on its behavior, affecting the pitching performance with the possibility of oscillation on the generator speed and making the turbine system unstable and unsafe [
24]. A fault on pitch actuator induces changes on dynamics, as high air content in oil, pump wear, or hydraulic leakage [
22]. In literature, there are many contributions on it. Some are based on data analysis [
25], others are based on the frequency response of the system actuator to a given input signal [
26], and so on [
27]. On the other hand, the use of interval observers has proved to be an excellent tool to measure uncertainties in dynamical systems [
28,
29,
30,
31]. Taking advantage of this, we use the main interval observer statement to postulate our fault detection method. Then, and by using a given training input signal, the performance of our approach is numerically validated. According to these numerical experiments, a pitch actuator fault is highlighted.
The rest of this paper is structured as follows.
Section 2 shows the theoretical frame on interval observers design and our general fault detection algorithm for any linear dynamic system. Then, in
Section 3, the application to wind turbine system is presented, along with the novel fault detection and fault classification algorithms. A set of numerical experiments support the main contribution of this paper. We use a wind turbine pitch actuator under three common faults. According to these numerical experiments, our approach is able to to discern the faulty stages from the healthy one. Finally, a brief conclusion and future work are discussed in
Section 4.
Notation 1. For a real matrix M or a vector, means that its components are positive, and means that its components are non-negative. Additionally, denotes that the set of real matrices have non-negative entries [28]. In consequence, denotes the set of real matrices having non-positive entries. 3. Interval Observer Statement Applied to Fault Detection in a Pitch-Actuator of a Wind-Turbine
We now present a fault detection algorithm applied to a wind turbine. To succeed, we first need to present the wind turbine mathematical model, and then adapt the general fault detection algorithm presented in
Section 2, in order to obtain a rule allowing for discerning if a fault on pitch actuator appears or not.
The pitch-actuator dynamic behavior, see
Figure 1, of a wind-turbine can be captured by using the next representation [
20,
37,
38]:
where
is the pitch angle related to its actuator,
is the reference command signal supplied by the control power management system, and
s represents the Laplace variable of a related signal in time-domain,
t. Additionally,
and
represent the natural frequency and the damping ration of the pitch actuator, respectively. On the other hand, in hydraulic pitch actuators, its degradation performance comes from different faulty operation cases, such as pump wear, hydraulic leakage, and high air oil content [
20,
37]. For a general report on fault detection in wind turbine, see [
1,
2], and Ref. [
3] presents a faulty scenario classification. In the present paper, we only consider the pitch actuator faults. Access to real wind turbine data sets is usually proprietary, and therefore they may not be openly accessible. To overcome this difficulty, in this work, numerical data were obtained from existing literature, presented in
Table 1 [
37,
38], where the nominal (H) and faulty (
,
and
) scenarios’ values of
and
in Equation (
9) under study in this work are defined.
System (
9) can be transformed into the state-space scheme as:
with
Here,
, and
such as
. To apply Proposition 1, and ensure stability, we need to define
L,
, and
for wind turbine system (
10). The next lemma collects it.
Lemma 1. The system (5) and (6), withdefine an interval observer (8) for the pitch actuator system (10) with and . The value of
is tuned to discriminate the pitch dynamic if a fault occurs (see
Table 1). Function
is designed to fulfill the hypothesis of Proposition 1, ensuring BIBO stability. Note that, if we define
in Equations (
5) and (
6), the residual signals (
13) vanish because both systems (
1), (
5), and (
6) consider the same matrices
A and
B, obtaining Luenberger observers.
Observe that the dynamic of the interval observer (
5) and (
6) is defined under the non-faulty scenario (H in
Table 1). Hence, the system matrices
A and
B in system (
10), and
L in Equation (
11), take values given by
and
; and then labeled as
,
and
, as follows:
Therefore, to detect a fault, we can go on analyzing the related residual signals:
where the variable
is selected because, besides representing the pitch system,
is the dynamical variable most sensitive to faults. We can now present an algorithm to design the fault detection system.
Next, we present some simulations to test our proposal fault detection method. First, the total time of simulation is set to 250 s, sufficiently enough to evaluate our fault detection design. Then, we program the system observers (
5) and (
6) and applied to the pitch actuator process (
9). This observer just uses the healthy parameters of the pitch actuator prototype. In our testing numerical experiments, we program the input prove signal as shown in
Figure 2; jointly, we have the response of the state variables for the healthy actuator. Here, we set
,
,
,
,
, and
for each test and then hereafter.
By following the FD-Algorithm stated in Algorithm 2, we need to define
from the nominal case H, as stated in
Table 1. We obtain
Figure 3, where both errors (
13) for this case are displayed. Then, we can define a threshold (third step of FD-Algorithm):
(this value can be obtained from
Figure 3 or evaluating a bound for
). Finally, we can use it to obtain a fault detection system (step 4 in Algorithm 2): faulty system (
10) is considered and residual signals
and
are evaluated. The obtained simulation results for each faulty scenario are shown in
Figure 4,
Figure 5 and
Figure 6. By using the stated excitation signal (or input signal), the occurrence of a fault is simple to realize: if
, then a fault has occurred.
Figure 4,
Figure 5 and
Figure 6 picture both errors (
13), proving that it is necessary to consider
and
in Equation (
13) to detect a fault because they do not detect a system fault at the same time. Thus, the designer has to evaluate (
13) and the first to overcome
detects a system fault.
| Algorithm 2: Wind turbine fault detection algorithm (FD-Algorithm) |
- Step 1
Consider the healthy parameters shown in Algorithm 1, and then define matrix L ( 11). - Step 2
Define a non-constant excitation signal . - Step 3
From the nominal plant (H), define a threshold as a bound to the system dynamic ( 13): - 3.1
Solve ( 10) for , and ( 12), along with ( 5) and ( 6). - 3.2
Define a threshold to the dynamic in ( 13).
- Step 4
Decision rule. - 4.1
Solve ( 10) for faulty A and B. - 4.2
Solve ( 5) and ( 6), with , and ( 12). - 4.3
If residual signals ( 13) are greater than the set threshold , then a fault is detected.
|
In
Figure 3, the positiveness of the residual signal can be shown. When the faulty system is considered, the Metzler condition can be lost, so the non-negativeness of
and
in Equation (
7) is not ensured. For instance, this can be noted in
Figure 4, where both errors take negative values.
On the other hand, an important experimental issue is to evaluate how fast our detection system responds.
Table 2 presents when the first fault is detected, for each case, and for both residual signals
and
:
where
is the total time of simulations.
Note that it takes less than a minute to detect a fault. In comparison to the technique stated, for instance in [
20], our approach may be considered as a fast response method for detecting a fault. Moreover, from
Figure 4 and
Figure 5 and
Table 2, a classification of a system fault can be stated, once the threshold value
is defined. In a general scenario, once
or
are greater than the stated value
, a fault is detected. However, how may we classify it as
,
or
? From
Table 2, a response to this question can be inferred using (
14). A classification algorithm is stated in Algorithm 3.
| Algorithm 3: Fault classification algorithm (FC-Algorithm) |
- Step 1
Nominal plant: determine . - Step 2
General plant: Evaluate the first value of t ( 14) such that or ( 13) verify: - 2.1
If for : then - 2.2
If for : then - 2.3
If for : then .
|
Finally, in real applications, even when we are actuating by using a known control signal to the pitch-actuator system of the wind turbine, there may exist a wind on the blades and then inducing of random dynamics on our structure. Hence, we repeat the previous simulations by adding a random signal to our control action as shown in
Figure 7. The obtained results are shown in
Figure 8,
Figure 9,
Figure 10 and
Figure 11. From these figures, we see that the same fault detection algorithm is still possible.
To test the proposed FD-Algorithm (Algorithm 2) and FC-Algorithm (Algorithm 3), a set of 500 numerical experiments with random input data are carried out. The accuracy of the algorithms is displayed in
Table 3, where the percentage of right fault classification is over detected ones.
Comparing the achievement of the proposed algorithm related to others in literature [
22,
25], our approach is robust to noisy data, which would be a serious problem, for instance, to the fault detection technique in [
25]. Thus, the image to process is obtained by reading a one-dimensional sensor in discrete-time domain. Moreover, our approach does not rely on accurate discrete-time modeling of the pitch system as the one stated in [
22], for which its performance depends on the discrete-time sampling too. On the other side, among the different approaches on monitoring the mechanical structures on a wind turbine, there is the stochastic method focused to predict, for instance, vibrations at the tower top of wind turbine and fatigue loads due to the wind [
15,
16]. This stochastic approach resulted robustly against changing conditions and was able to separate the response dynamics of the system response from the deterministic one.
4. Concluding Remarks and Future Work
In this work, pitch actuator faults were studied due to these systems having the highest failure rate in wind turbines. A fault in a pitch actuator may change the dynamics of the pitch system by varying the damping ratio and natural frequencies from their nominal values, thus affecting the whole performance of a costly wind turbine. Thus, a fast and stable fault detection algorithm is an important key to study.
By using the interval observer theory, an original algorithm on fault detection to wind-turbine pitch actuators was successfully realized. This algorithm is based on knowing the healthy parameters of the plant. Then, we assume that, even if a fault occurs, the values of these parameters are not far away from the healthy one. Thus, we can consider an interval observer for a healthy region. Under a general scenario, from the residual errors, we can determine if the system fits this region or not. Thus, a fault detection system is obtained. On the other hand, in this paper, we focus on detecting faults on wind turbine pitch actuators. Therefore, the fatigue load damage estimation, and other wind-turbine structures’ metric performances, are not studied here. The efficiency of this method was numerically validated by using a wind turbine pitch actuator under three common fault stages. For each one, our fault detection method was able to discern. Moreover, the time response of our approach fault detection method can be considered fast.
As in [
39], a Fourier theory can be used to study the principal harmonics of the residual signals. Comparing
Figure 3 and
Figure 8, where residual signals for healthy scenario are pictured, the behavior is almost the same. However, when a fault occurs, note that a a faulty system with a random component on the input signal presents more harmonics than the non-random one. Thus, as future work, a possible algorithm to detect a fault is to study the presence of harmonics in the residual signals by using the Fourier transform.