Steady-State Predictive Optimal Control of Integrated Building Energy Systems Using a Mixed Economic and Occupant Comfort Focused Objective Function
Abstract
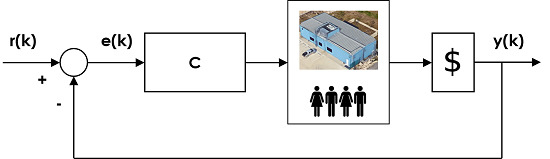
:1. Introduction
2. Background
3. Development of Economic Objective Function for Advanced Building Systems Control
3.1. Building Configuration
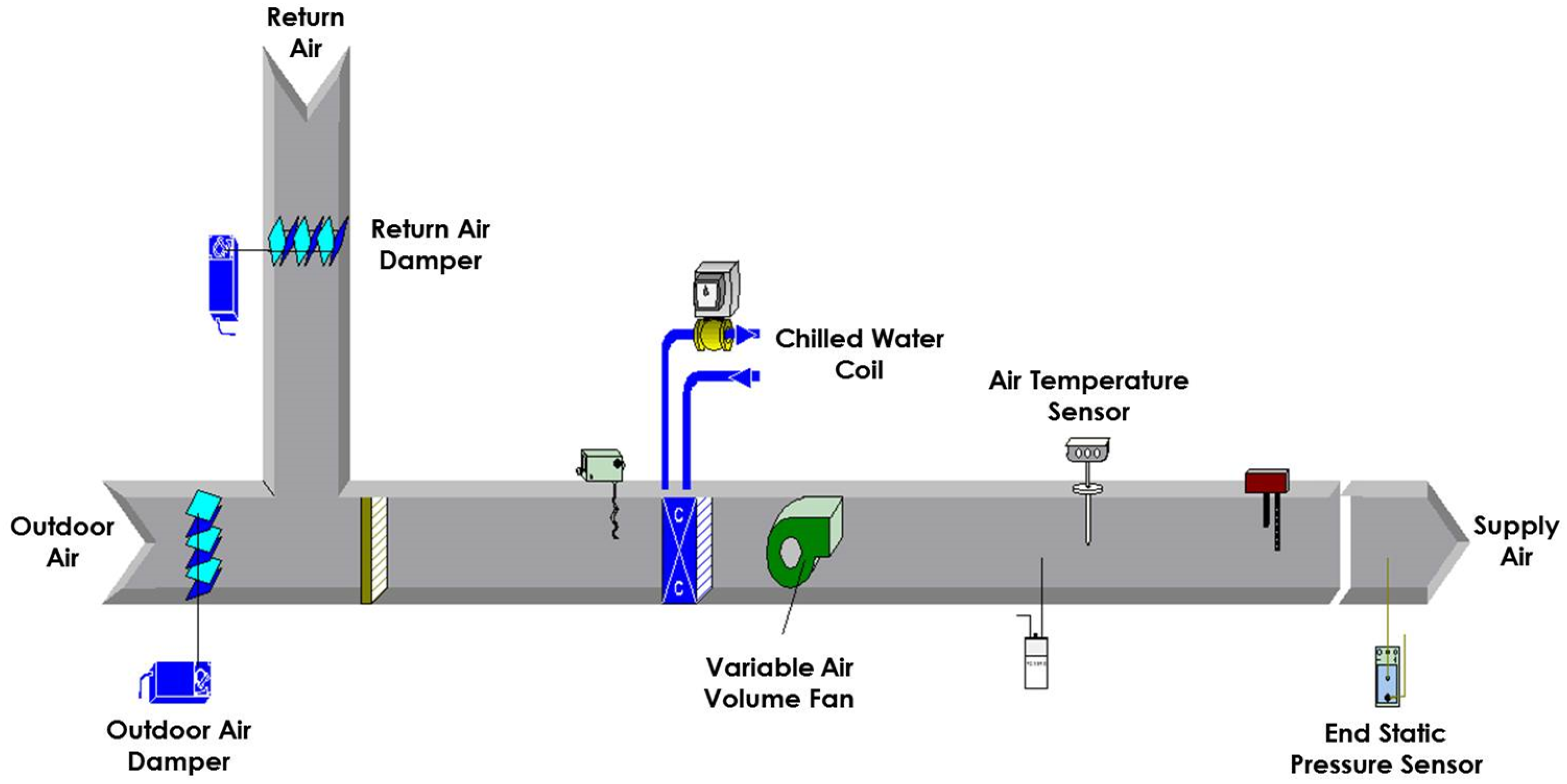
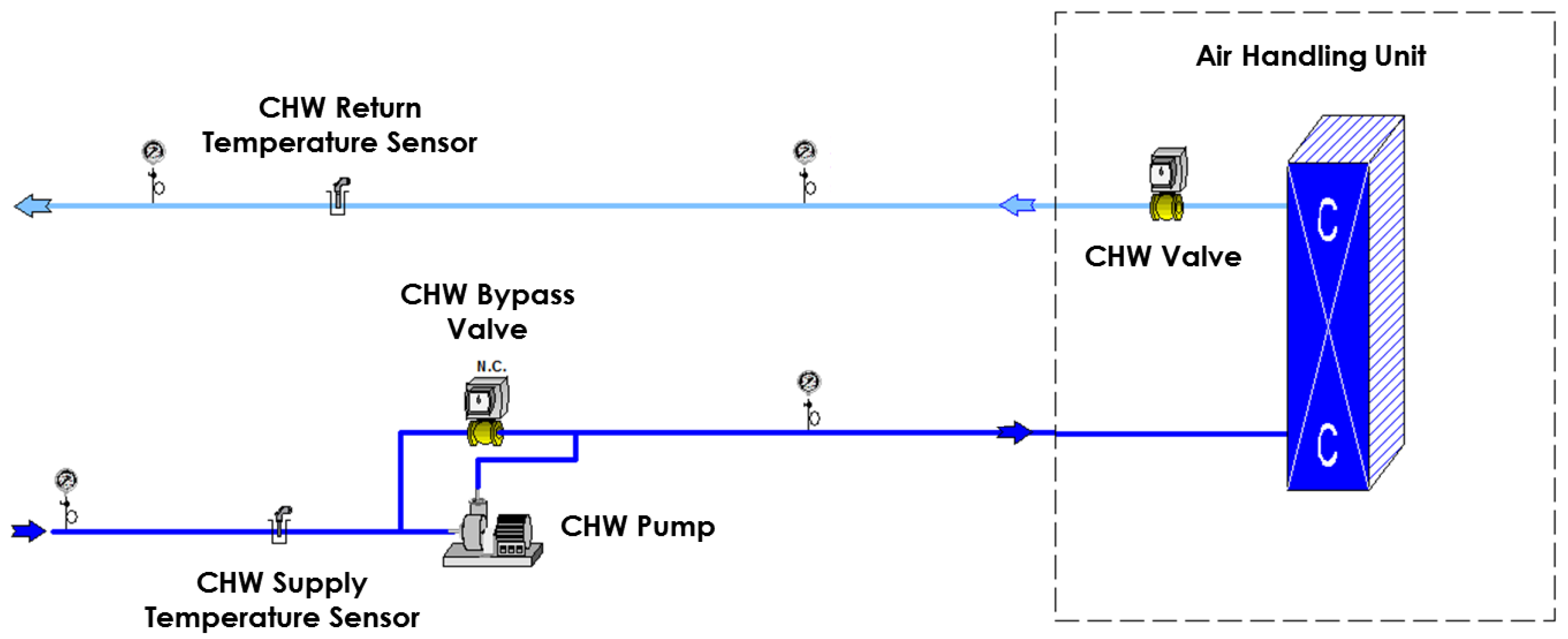
3.1.1. Rooftop Air Handling Units
3.1.2. Chilled Water Production
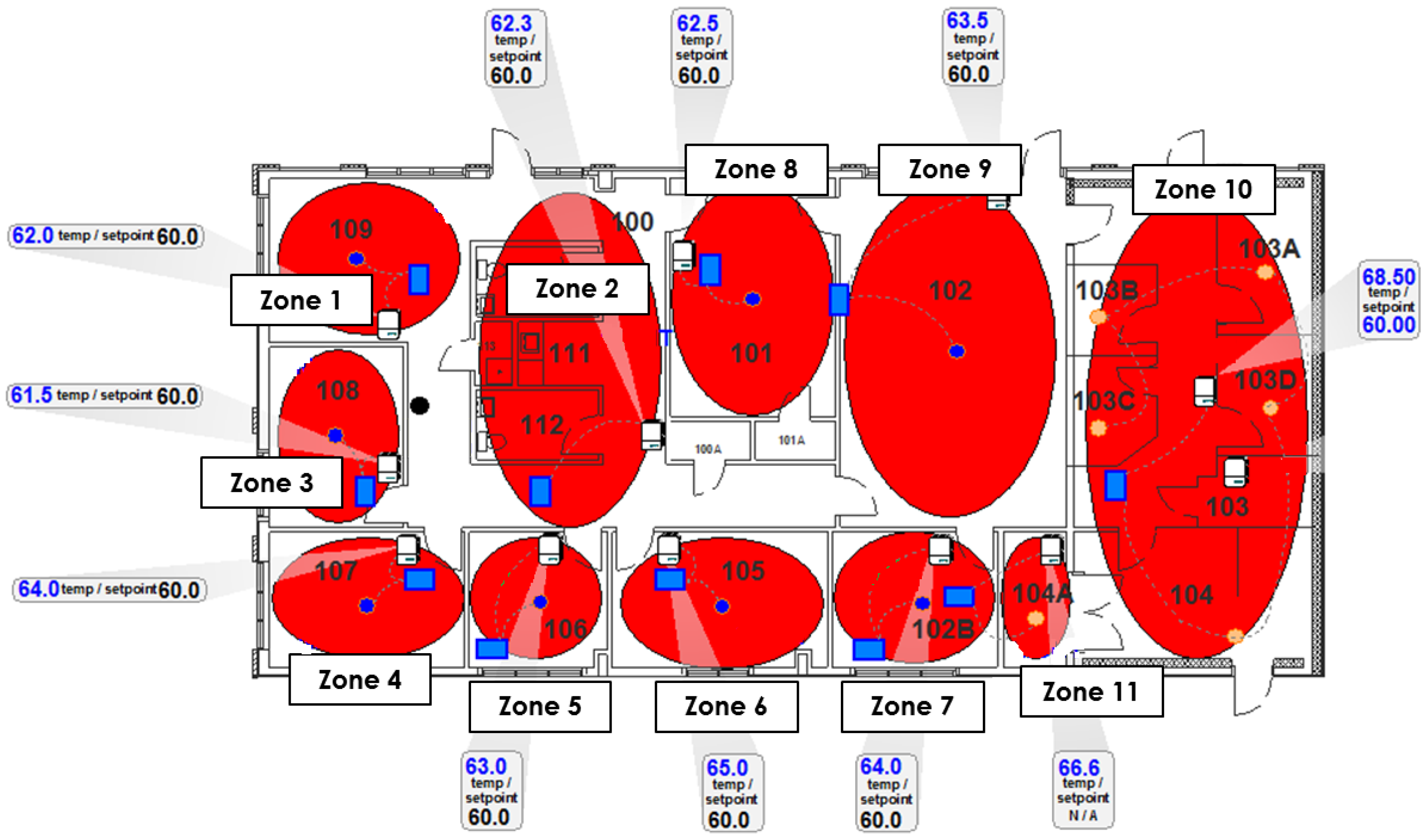
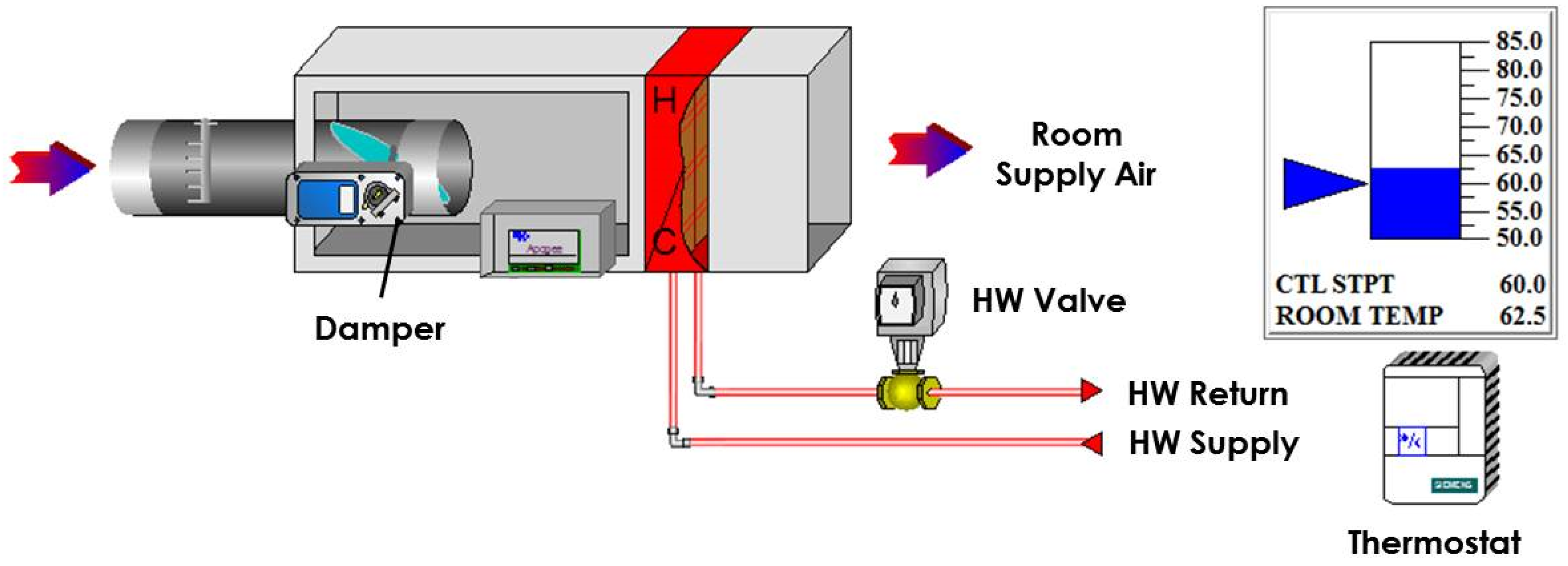
3.1.3. Conditioned Zones in Buildings
3.2. Economic Cost of Operating Equipment
3.2.1. AHU Fan Economic Objective Function Development
3.2.2. AHU Chilled Water Economic Objective Function Development
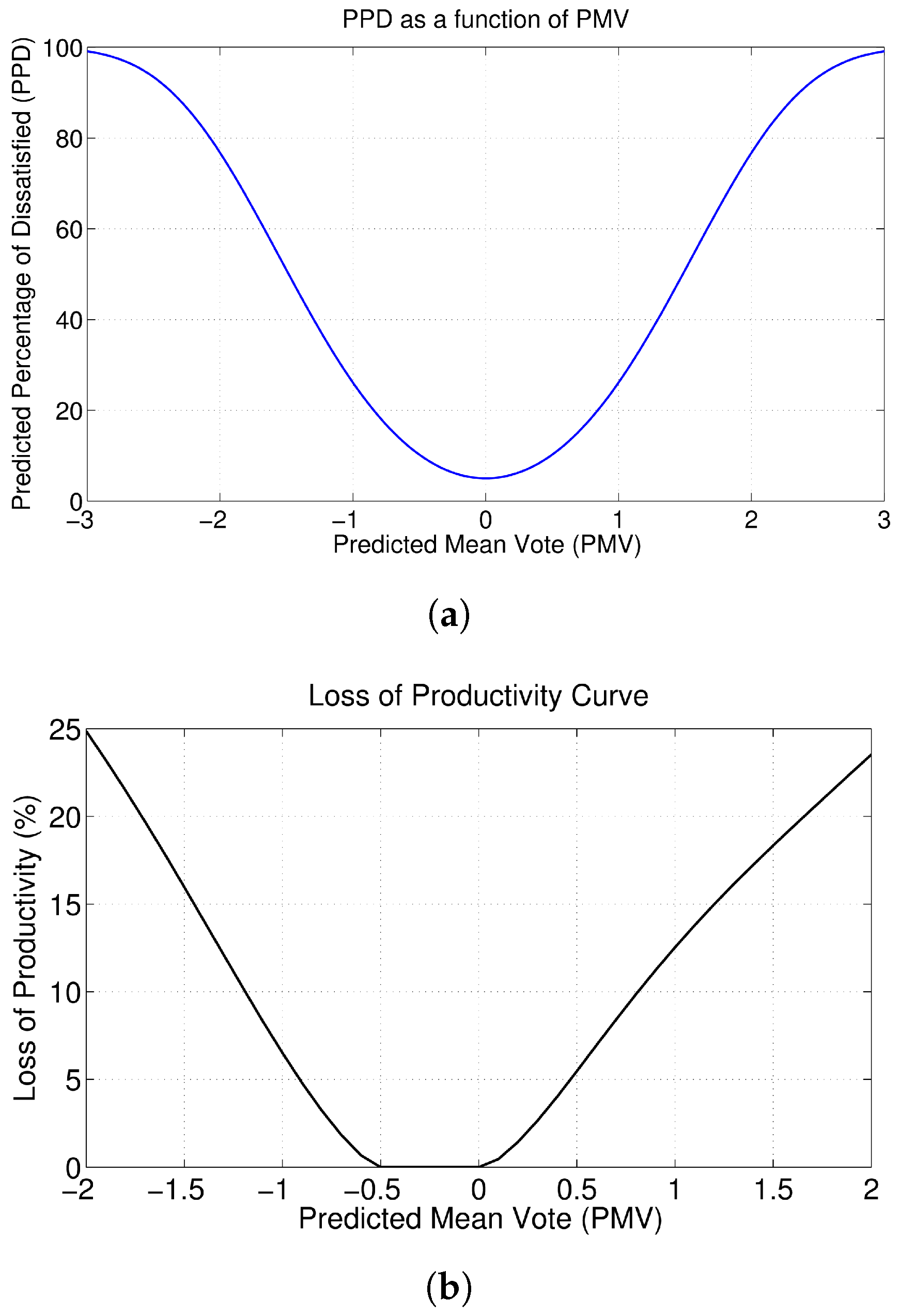
3.2.3. Zone Occupant Comfort Economic Objective Function Development
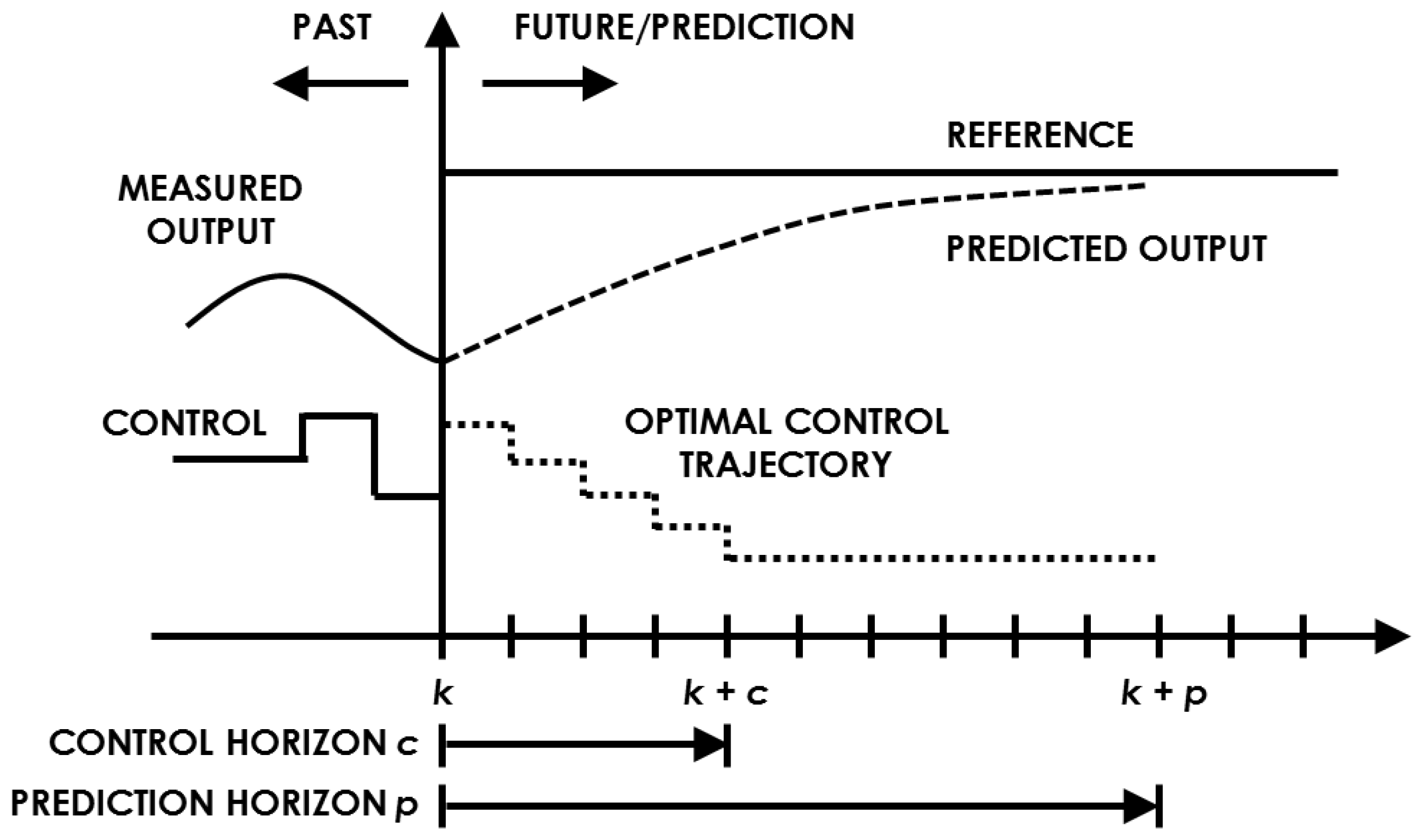
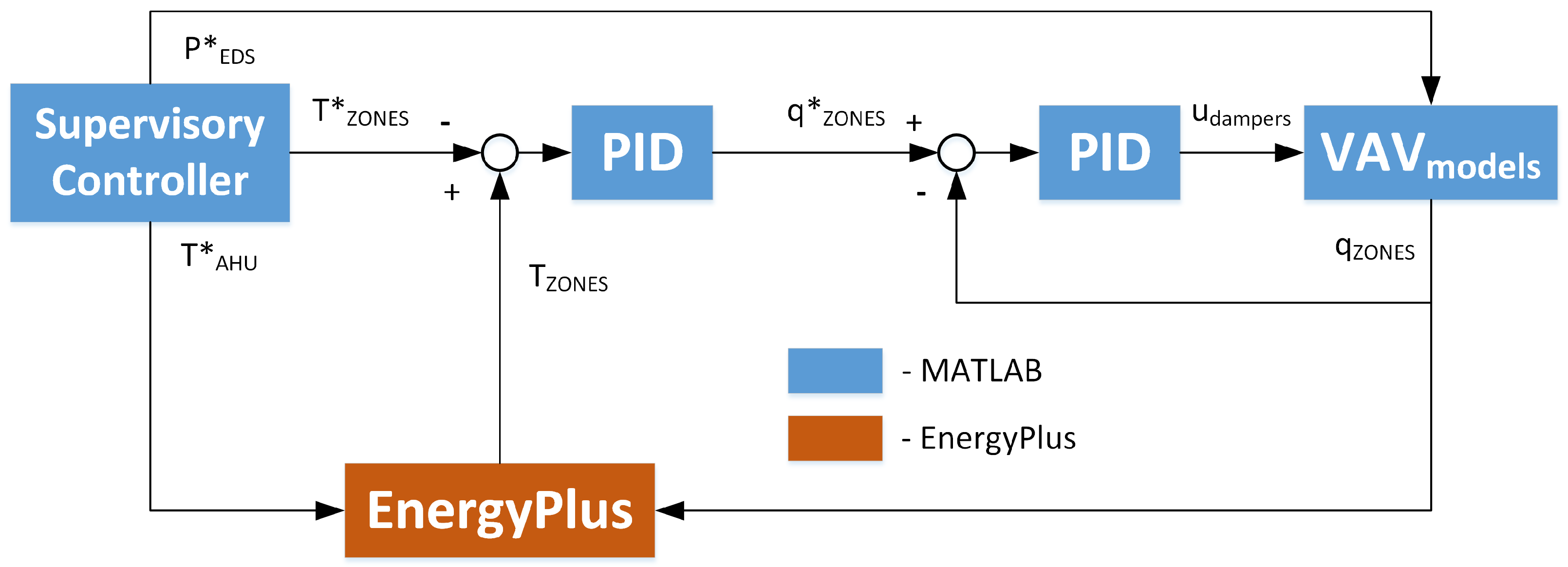
4. Simulation Design
5. Results
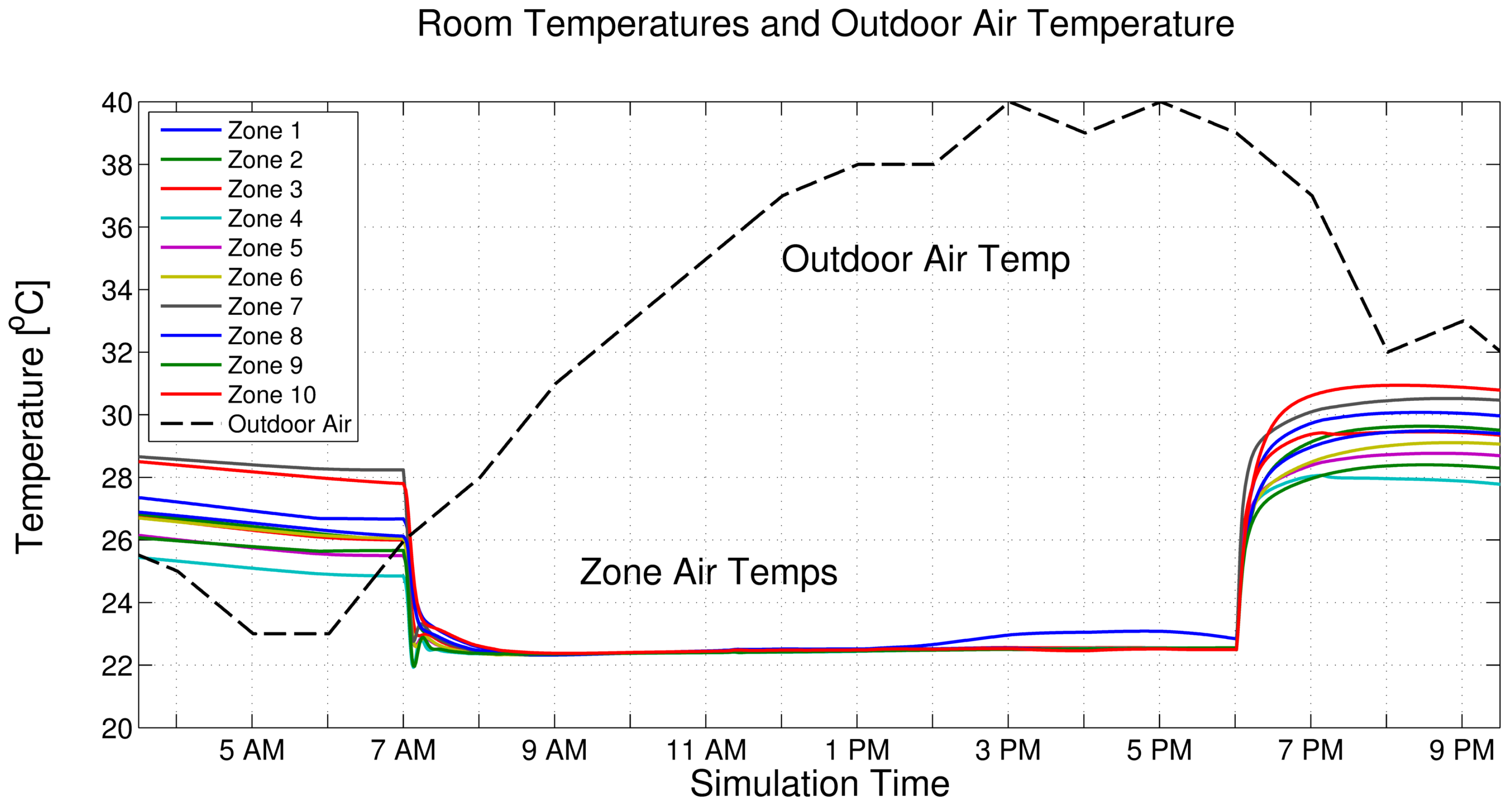
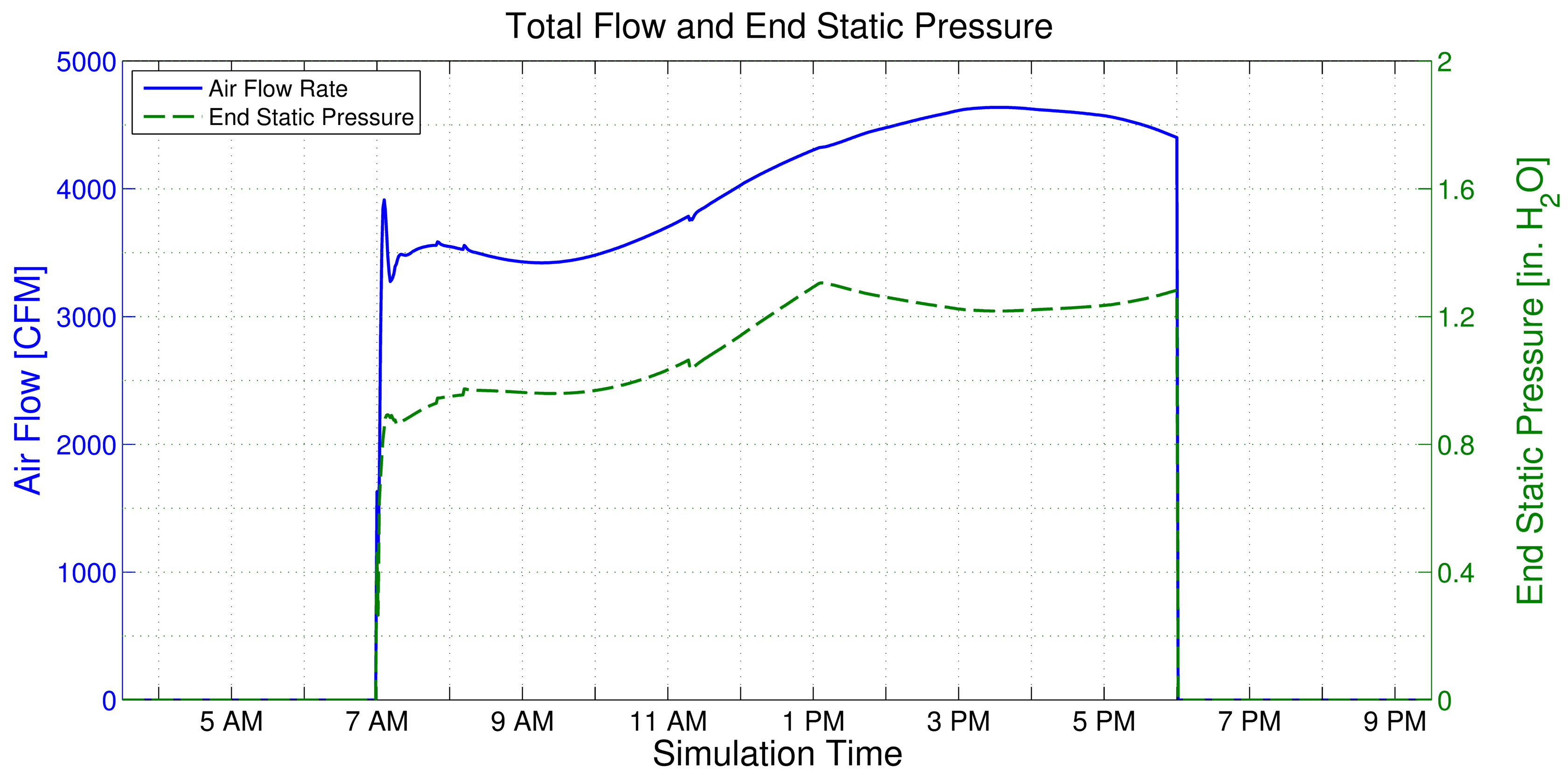
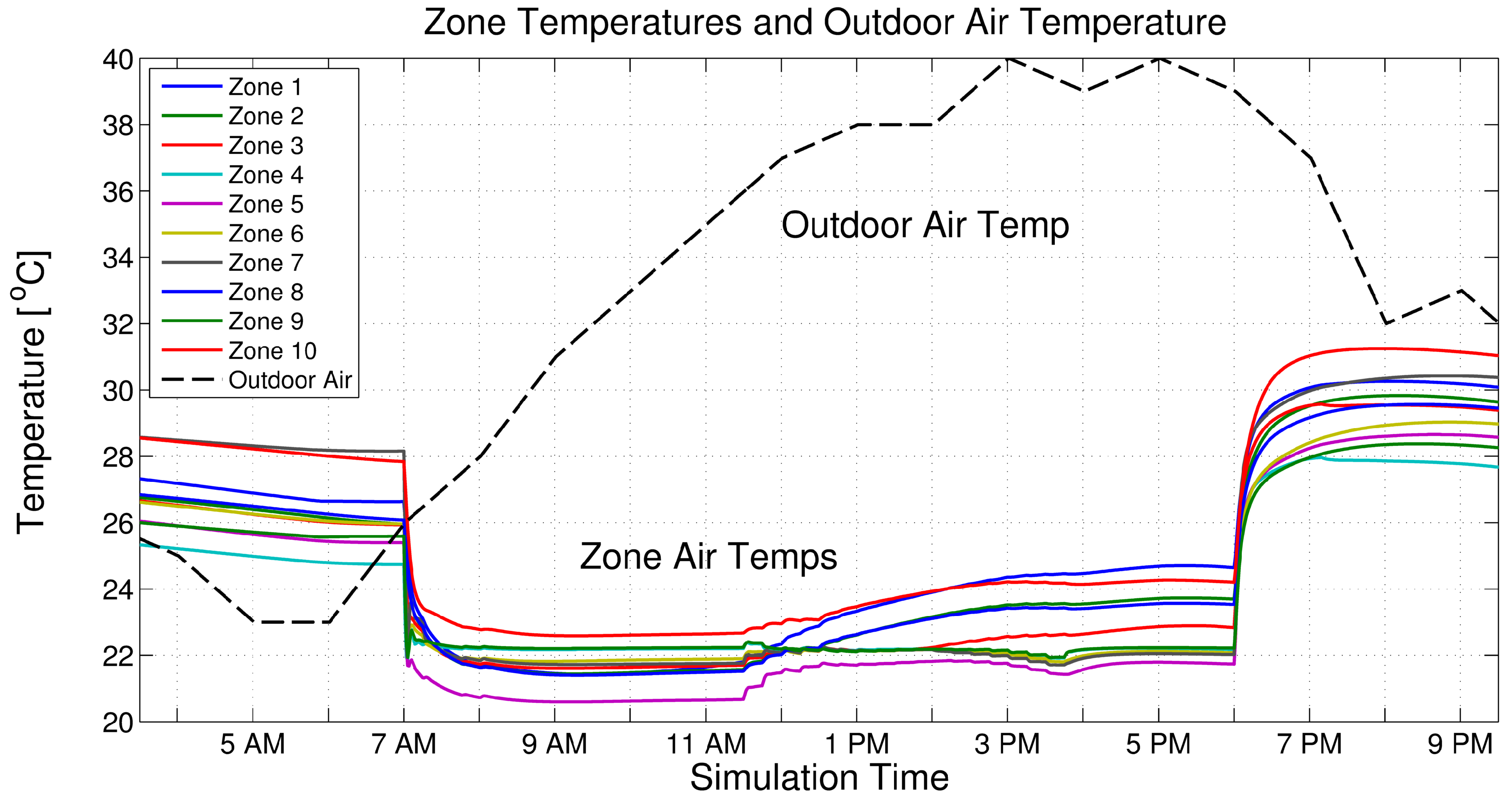
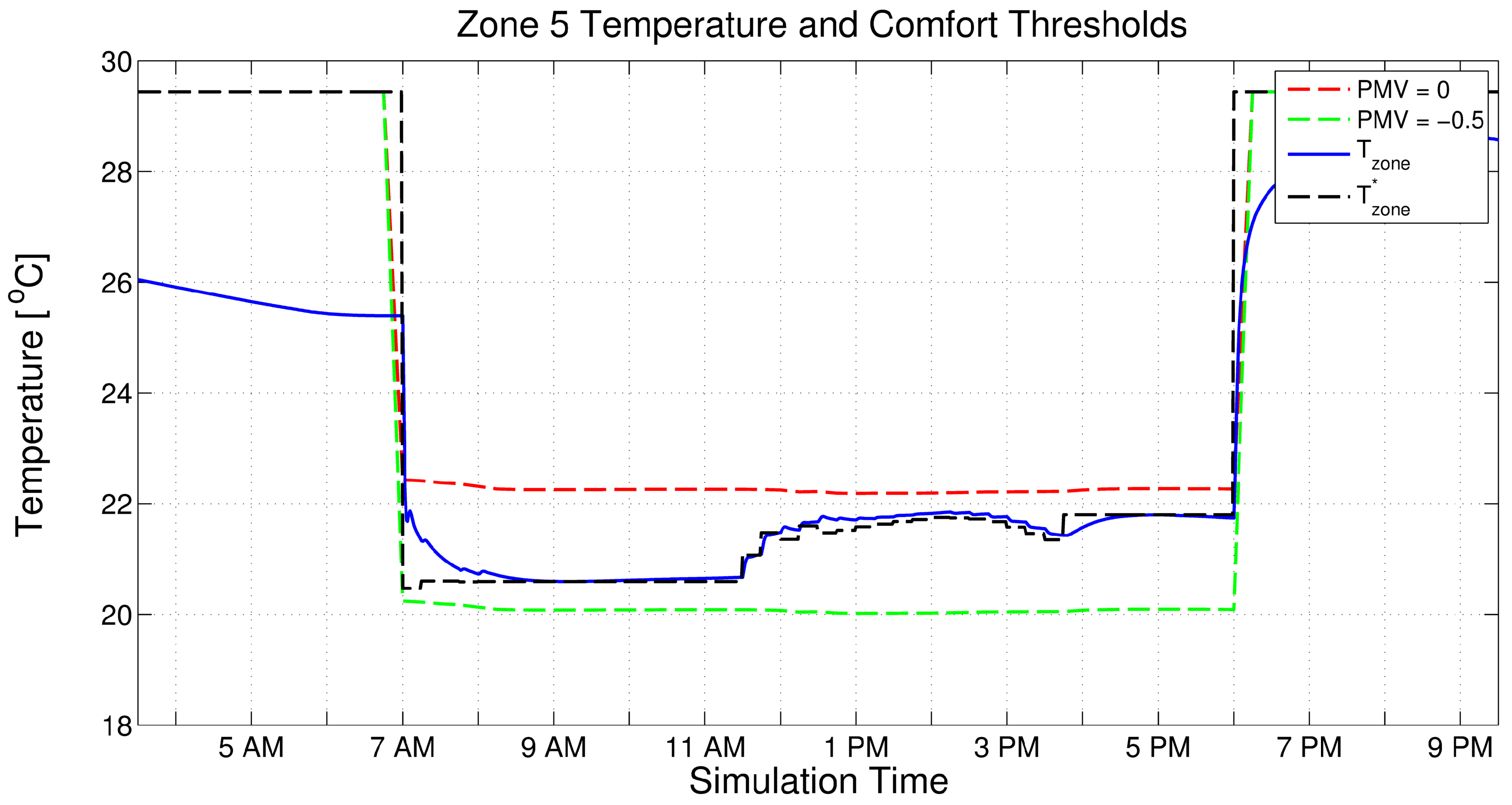
5.1. UBO Simulation with Current Building Controls
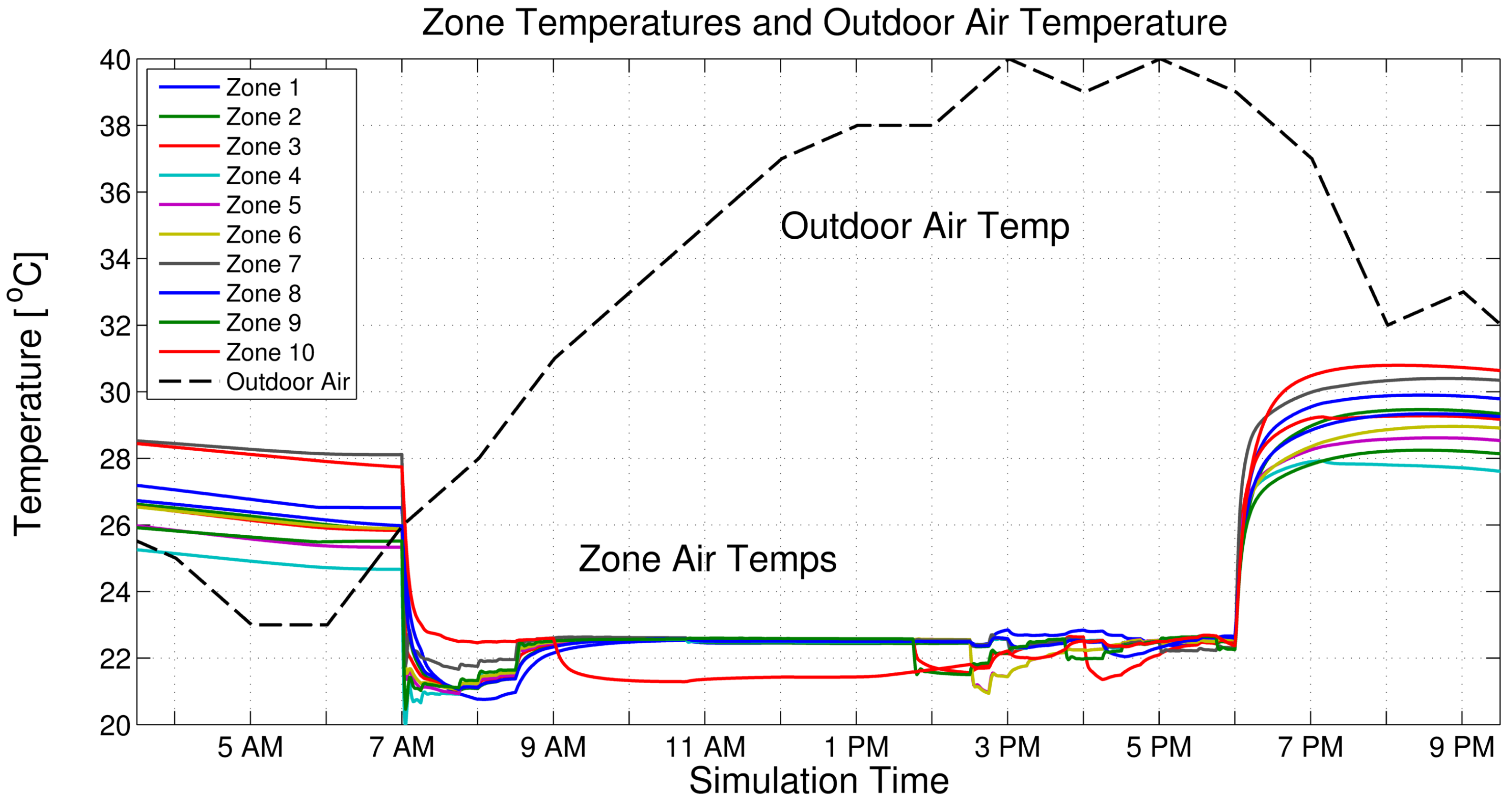
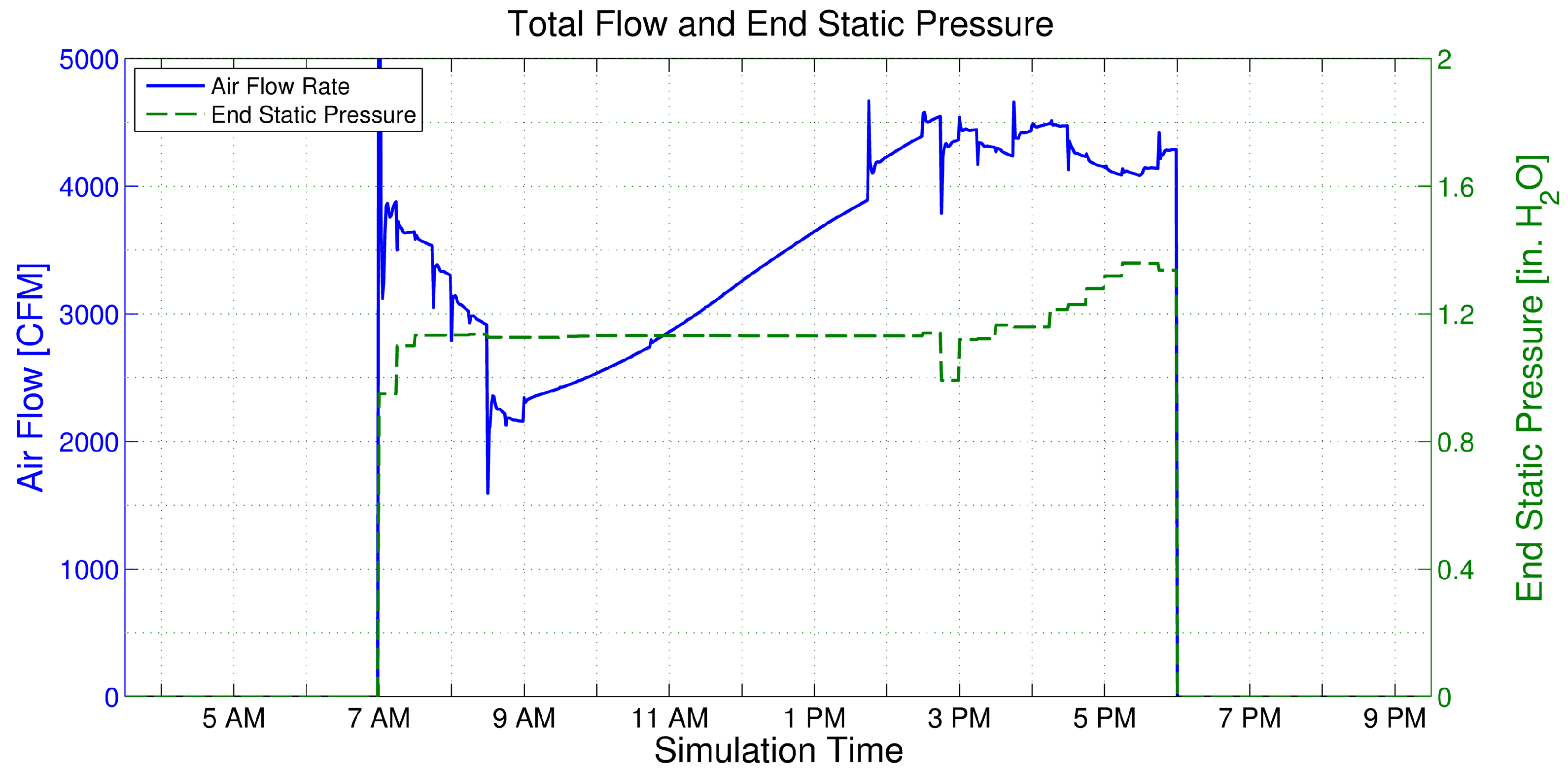
5.2. Steady-State Optimal Control Simulation
5.3. Very Important Person Simulation
6. Discussion
Future Directions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| AHU | Air Handling Unit |
| VAV | Variable Air Volume |
| E-MPC | Economic Model Predictive Control |
| HVAC | Heating, Ventilation, and Cooling |
| PMV | Predicted Mean Vote |
| PPD | Predicted Percentage of Dissatisfied |
| e | Error |
| Q | Weighting for quadratic error |
| R | Weighting for linear error |
| u | Control action |
| S | Weighting for quadratic control action |
| T | Weighting for linear control action |
| UEM | Utilities Energy Management |
| UBO | Utilities Business Office |
| PID | Proportional-Integral-Derivative |
| CHW | Chilled water |
| PI | Proportional-Integral |
| Proportional gain | |
| Integral gain | |
| Derivative gain | |
| End-static pressure demand setpoint | |
| End-static pressure demand | |
| End-static pressure setpoint | |
| End-static pressure | |
| Fan speed | |
| Cooling demand setpoint | |
| Cooling demand | |
| Discharge air temperature setpoint | |
| Discharge air temperature | |
| Chilled water valve position | |
| Zone temperature setpoint | |
| Zone temperature | |
| Damper position | |
| Fan power | |
| Air flow rate of the air handling unit | |
| Change in pressure across the fan | |
| Fan blade efficiency | |
| Fan belt efficiency | |
| Fan motor efficiency | |
| KiloWatt-hour | |
| Fan power cost | |
| Rate of electricity cost | |
| Sampling time | |
| Rate of change of heat | |
| Mass flow rate | |
| c | Specific heat |
| Difference in temperature | |
| Density | |
| q | Volume flow rate |
| Chilled water cost | |
| Maximum flow rate through the chilled water valve | |
| One million British thermal units | |
| ASHRAE | American Society of Heating, Refrigeration, and Air-Conditioning Engineers |
| LOP | Loss of productivity |
| Lost productivity in wages | |
| Annual salary | |
| Relative humidity of a zone | |
| Air temperature | |
| Total cost | |
| IDF | Energy Plus input file |
| DOE | Department of Energy |
| BCVTB | Building Controls Virtual Test Bed |
References and Note
- U.S. Energy Information Administration (EIA). Total Energy—Data; EIA: Washington, DC, USA, 2020.
- U.S. Energy Information Administration (EIA). Total Energy—Data; EIA: Washington, DC, USA, 2016.
- European Commission. Renewable Energy—Moving towards a Low Carbon Economy; European Commission: Brussels, Belgium, 2009. [Google Scholar]
- Department of Energy. 20% Wind Energy by 2030: Increasing Wind Energy’s Contribution to U.S. Electricity Supply; Department of Energy: Washington, DC, USA, 2008.
- U.S. Energy Information Administration. Annual Energy Review 2011; Technical Report; U.S. Department of Energy: Washington, DC, USA, 2012.
- U.S. Energy Information Administration. Emissions of Greenhouse Gases in the United States 2008; Technical Report; U.S. Department of Energy: Washington, DC, USA, 2009.
- U.S. Department of Energy. Building Share of U.S. Primary Energy Consumption (Percent). 2012. Available online: http://buildingsdatabook.eren.doe.gov (accessed on 1 January 2020).
- Putta, V.; Zhu, G.; Kim, D.; Hu, J.; Braun, J. Comparative Evaluation of Model Predictive Control Strategies for a Building HVAC System. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3455–3460. [Google Scholar]
- Gyalistras, D.; The OptiControl Team. Final Report: Use of Weather and Occupancy Forecasts for Optimal Building Climate Control (OptiControl); Technical Report; Terrestial Systems Ecology ETH: Zurich, Switzerland, 2010. [Google Scholar]
- Ghiaus, C.; Hazyuk, I. Calculation of optimal thermal load of intermittently heated buildings. Energy Build. 2010, 42, 1248–1258. [Google Scholar] [CrossRef]
- Ma, Y.; Borrelli, F.; Hencey, B.; Packard, A.; Bortoff, S. Model Predictive Control of Thermal Energy Storage in Building Cooling Systems. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 392–397. [Google Scholar] [CrossRef] [Green Version]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control Theory and Design; Nob Hill Pub: Madison, WI, USA, 2009. [Google Scholar]
- Hazyuk, I.; Ghiaus, C.; Penhouet, D. Optimal temperature control of intermittently heated buildings using Model Predictive Control: Part II—Control algorithm. Build. Environ. 2012, 51, 388–394. [Google Scholar] [CrossRef]
- Oldewurtel, F.; Parisio, A.; Jones, C.N.; Gyalistras, D.; Gwerder, M.; Stauch, V.; Lehmann, B.; Morari, M. Use of model predictive control and weather forecasts for energy efficient building climate control. Energy Build. 2012, 45, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Halvgaard, R.; Poulsen, N.K.; Madsen, H.; Jorgensen, J.B. Economic Model Predictive Control for Building Climate Control in a Smart Grid. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Morosan, P.D.; Bourdais, R.; Dumur, D.; Buisson, J. Building temperature regulation using a distributed model predictive control. Energy Build. 2010, 42, 1445–1452. [Google Scholar] [CrossRef]
- Touretzky, C.R.; Baldea, M. Integrating scheduling and control for economic MPC of buildings with energy storage. J. Process Control 2014, 24, 1292–1300. [Google Scholar] [CrossRef]
- Oldewurtel, F.; Parisio, A.; Jones, C.N.; Morari, M.; Gyalistras, D.; Gwerder, M.; Stauch, V.; Lehmann, B.; Wirth, K. Energy Efficient Building Climate Control Using Stochastic Model Predictive Control and Weather Predictions. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5100–5105. [Google Scholar] [CrossRef] [Green Version]
- Corbin, C.D.; Henze, G.P.; May-Ostendorp, P. A model predictive control optimization environment for real-time commercial building application. J. Build. Perform. Simul. 2013, 6, 159–174. [Google Scholar] [CrossRef]
- Oldewurtel, F.; Ulbig, A.; Parisio, A.; Andersson, G.; Morari, M. Reducing Peak Electricity Demand in Building Climate Control Using Real-Time Pricing and Model Predictive Control. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 1927–1932. [Google Scholar] [CrossRef]
- Molina, D.; Lu, C.; Sherman, V.; Harley, R.G. Model Predictive and Genetic Algorithm-Based Optimization of Residential Temperature Control in the Presence of Time-Varying Electricity Prices. IEEE Trans. Ind. Appl. 2013, 49, 1137–1145. [Google Scholar] [CrossRef]
- Alvarez, J.D.; Redondo, J.L.; Camponogara, E.; Normey-Rico, J.; Berenguel, M.; Ortigosa, P.M. Optimizing building comfort temperature regulation via model predictive control. Energy Build. 2013, 57, 361–372. [Google Scholar] [CrossRef]
- Ma, Y.; Borrelli, F.; Hencey, B.; Coffey, B.; Bengea, S.; Haves, P. Model Predictive Control for the Operation of Building Cooling Systems. IEEE Trans. Control Syst. Technol. 2012, 20, 796–803. [Google Scholar] [CrossRef] [Green Version]
- Bengea, S.C.; Kelman, A.D.; Borrelli, F.; Taylor, R.; Narayanan, S. Implementation of model predictive control for an HVAC system in a mid-size commercial building. HVAC&R Res. 2014, 20, 121–135. [Google Scholar] [CrossRef]
- West, S.R.; Ward, J.K.; Wall, J. Trial results from a model predictive control and optimisation system for commercial building HVAC. Energy Build. 2014, 72, 271–279. [Google Scholar] [CrossRef]
- Karlsson, H.; Hagentoft, C.E. Application of model based predictive control for water-based floor heating in low energy residential buildings. Build. Environ. 2011, 46, 556–569. [Google Scholar] [CrossRef]
- Duburcq, G.S. Advanced Control for Intermittent Heating. In Proceedings of the Clima 2000 Conference, Brussels, Belgium, 30 August to 2 September 1997. [Google Scholar]
- Yuan, S.; Perez, R. Multiple-zone ventilation and temperature control of a single-duct VAV system using model predictive strategy. Energy Build. 2006, 38, 1248–1261. [Google Scholar] [CrossRef]
- Fanger, P. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Elliott, M.; Rasmussen, B.P. Optimal Setpoints for HVAC Systems via Iterative Cooperative Neighbor Communication. J. Dyn. Syst. Meas. Control 2014, 137, 011006. [Google Scholar] [CrossRef]
- Bay, C.J. Advancing Embedded and Extrinsic Solutions for Optimal Control and Efficiency of Energy Systems in Buildings. Ph.D. Thesis, Texas A&M University, Uvalde, TX, USA, 2017. [Google Scholar]
- Roelofsen, P. The impact of office environments on employee performance: The design of the workplace as a strategy for productivity enhancement. J. Facil. Manag. 2002, 1, 247–264. [Google Scholar] [CrossRef]
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. A Standard Predictive Index of Human Response to the Thermal Environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Trimble. 3D modeling for everyone. 2017. [Google Scholar]
- Crawley, D.B.; Pedersen, C.O.; Lawrie, L.K.; Winkelmann, F.C. EnergyPlus: Energy Simulation Program. ASHRAE J. 2000, 42, 49–56. [Google Scholar]
- Bernal, W.; Behl, M.; Nghiem, T.X.; Mangharam, R. MLE+: A Tool for Integrated Design and Deployment of Energy Efficient Building Controls. In Proceedings of the 4th ACM Workshop On Embedded Sensing Systems For Energy-Efficiency In Buildings, (BuildSys’12), Toronto, ON, Canada, 6–9 November 2012. [Google Scholar]
- Wetter, M. Co-simulation of building energy and control systems with the Building Controls Virtual Test Bed. J. Build. Perform. Simul. 2011, 4, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Chintala, R.H. A Methodology for Automating the Implementation of Advanced Control Algorithms Such as Model Predictive Control on Large Scale Building HVAC Systems. Ph.D. Thesis, Texas A&M University, Uvalde, TX, USA, 2018. [Google Scholar]




| Controller | Reference | Feedback | Output | |||
|---|---|---|---|---|---|---|
| Supervisory Controller #1 | 12 | 0.1 | 0 | |||
| Fan Speed Controller | 0.5 | 0.15 | 0.1 | |||
| Supervisory Controller #2 | 12 | 0.01 | 2000 | |||
| Chilled Water Valve Controller | 20 | 1 | 10 | |||
| Supervisory Controller #3 | Deadband Controller | N/A | ||||
| Damper Controller | Set by Manufacturer | |||||
| Regression | Cold Side of | Warm Side of |
|---|---|---|
| Coefficients | PMV Comfort Zone | PMV Comfort Zone |
| 1.2802070 | −0.15397397 | |
| 15.995451 | 3.8820297 | |
| 31.507402 | 25.176447 | |
| 11.754937 | −26.641366 | |
| 1.4737526 | 13.110120 | |
| 0.0000000 | −3.1296854 | |
| 0.0000000 | 0.29260920 |
| Model Input | Model Output |
|---|---|
| Zone | |||||
|---|---|---|---|---|---|
| Comfort Cost | Total | ||||
| Control Method | (Productivity) | CHW Cost | Fan Cost | Utility Cost | Total Cost |
| Current Control with User Setpoints | $6869.38 | $4093.61 | $1255.67 | $7046.03 | $13,915.41 |
| Current Control with PMV Setpoints | $476.37 | $4562.48 | $1677.62 | $8131.19 | $8607.56 |
| Optimal Predicted Steady-State Setpoints with PMV Setpoints | $299.21 | $4383.28 | $1226.63 | $7426.72 | $7725.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bay, C.J.; Chintala, R.; Rasmussen, B.P. Steady-State Predictive Optimal Control of Integrated Building Energy Systems Using a Mixed Economic and Occupant Comfort Focused Objective Function. Energies 2020, 13, 2922. https://doi.org/10.3390/en13112922
Bay CJ, Chintala R, Rasmussen BP. Steady-State Predictive Optimal Control of Integrated Building Energy Systems Using a Mixed Economic and Occupant Comfort Focused Objective Function. Energies. 2020; 13(11):2922. https://doi.org/10.3390/en13112922
Chicago/Turabian StyleBay, Christopher J., Rohit Chintala, and Bryan P. Rasmussen. 2020. "Steady-State Predictive Optimal Control of Integrated Building Energy Systems Using a Mixed Economic and Occupant Comfort Focused Objective Function" Energies 13, no. 11: 2922. https://doi.org/10.3390/en13112922