Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review
Abstract
:1. Introduction
- Because of their higher efficiency, they consume less fuel and consequently produce lower CO2 and NOx emissions.
- The load demand following response is much faster than subcritical units.
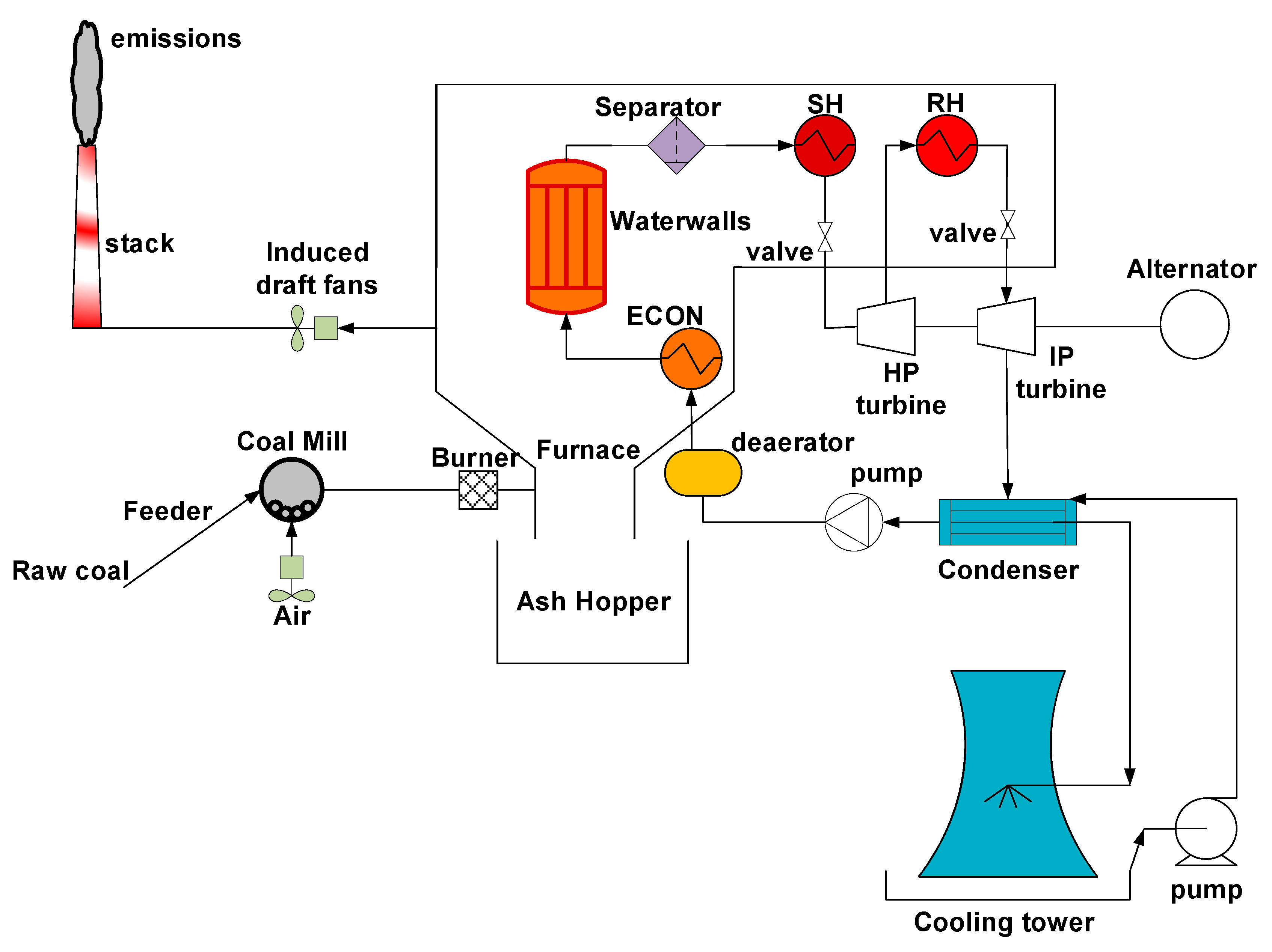
2. Coal-Fired Supercritical Power Generation Process
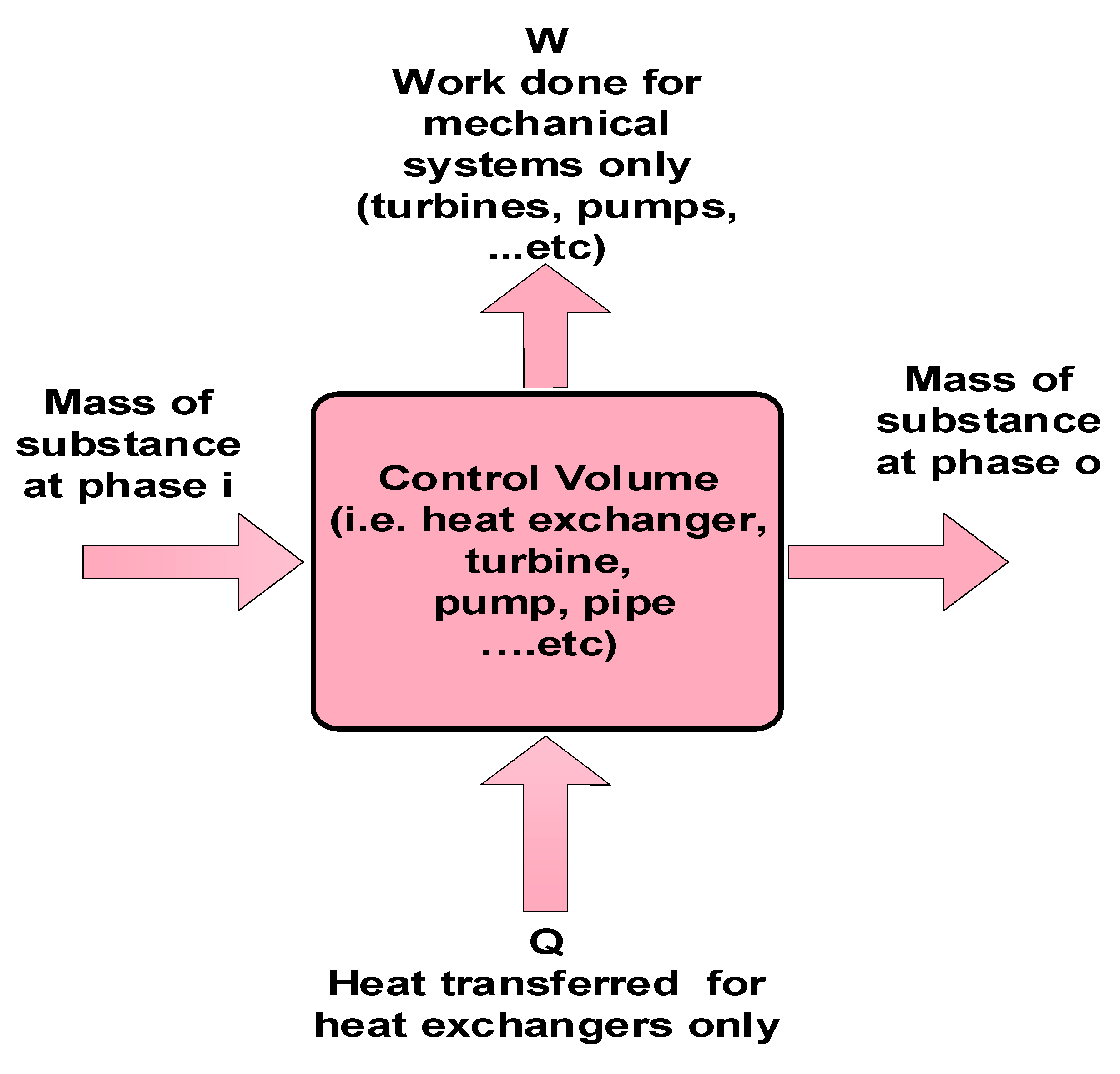
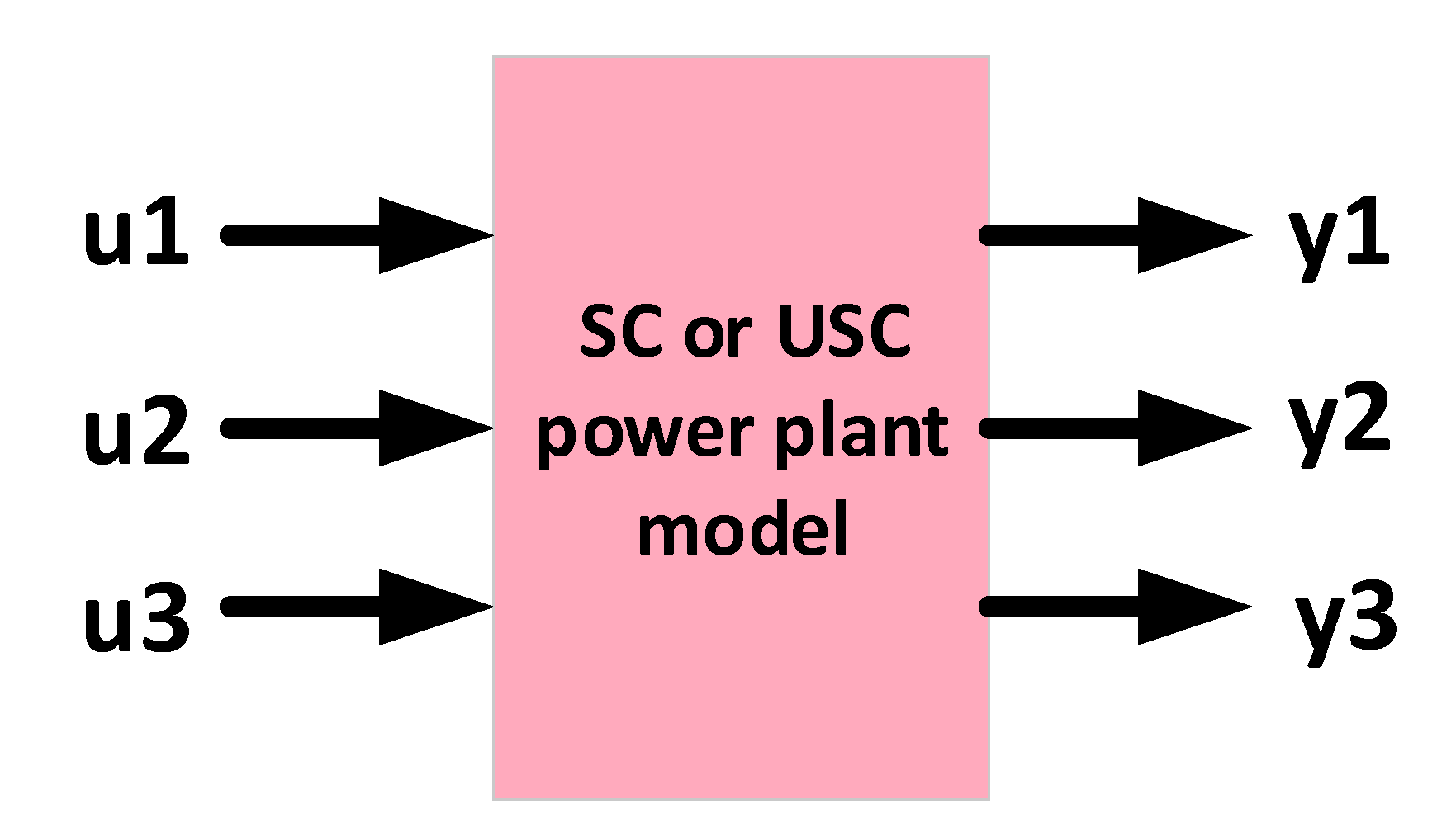
3. Supercritical Power Plant Modeling for Dynamic Performance Studies
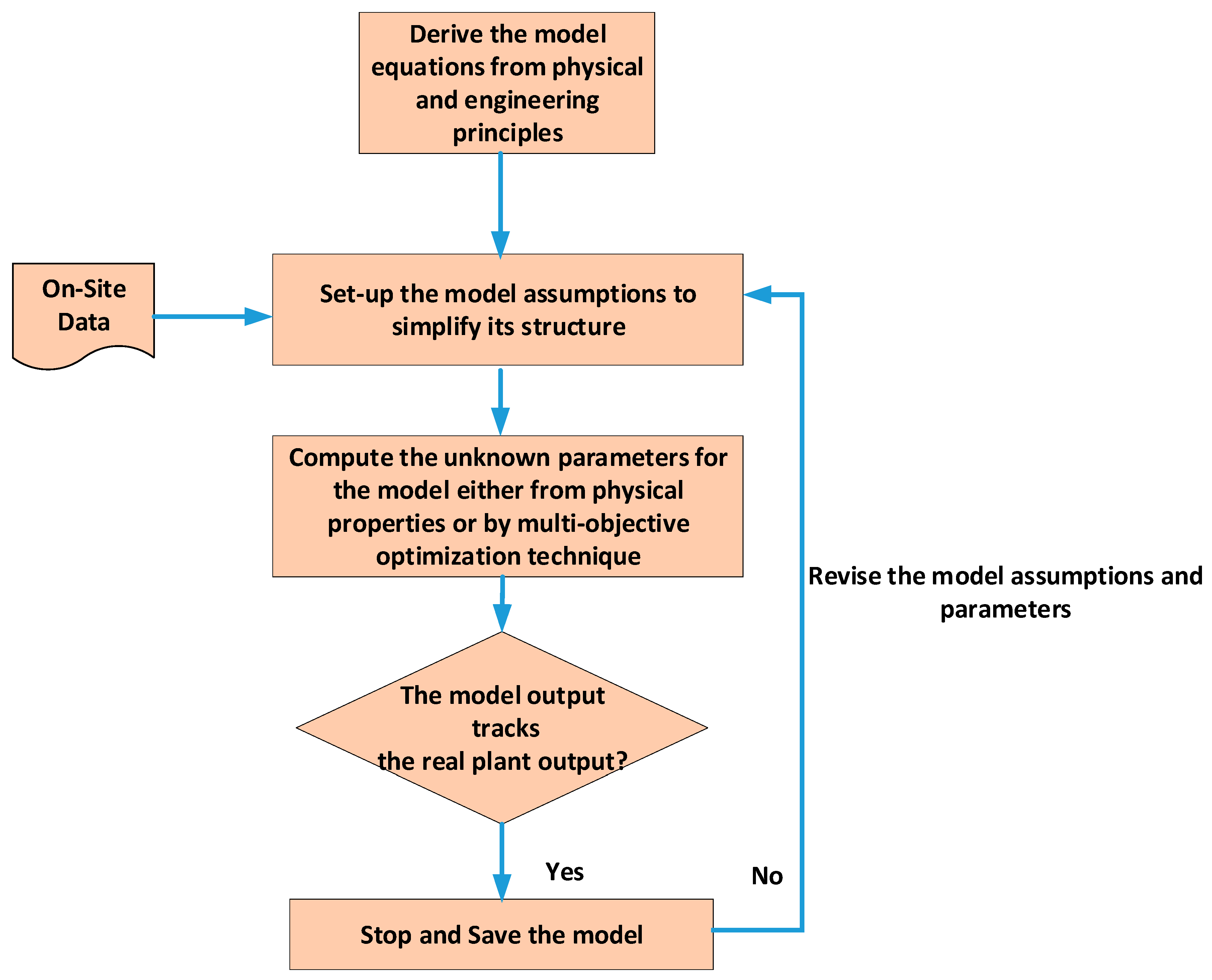
- Models rooted from thermodynamic and engineering principles or simply physical models and mathematical models.
- Empirical models or black-box modeling.
3.1. Physical and Mathematical Modeling of SC and USC Power Plants
3.2. Empirical Modeling of SC and USC Power Plants
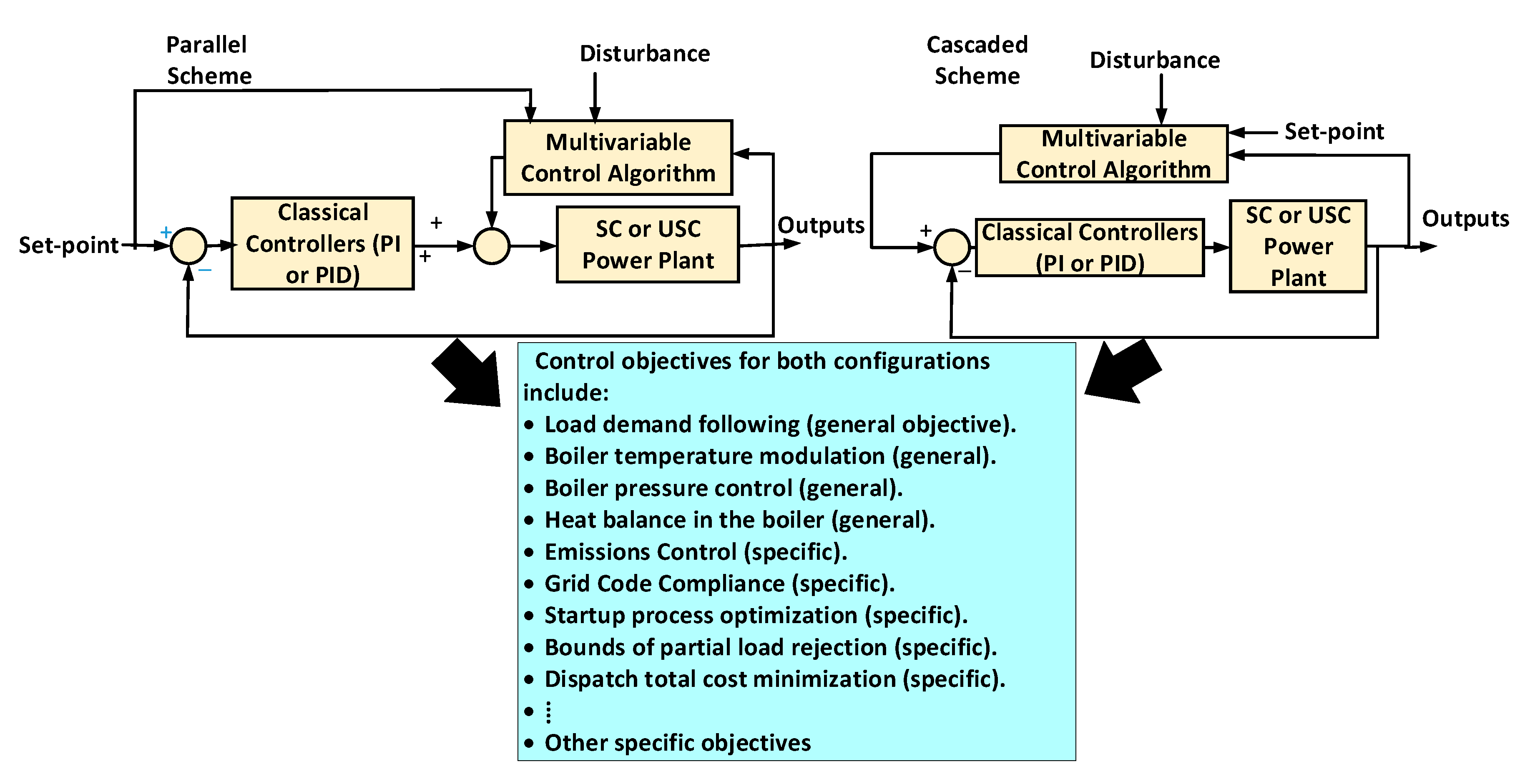
4. Control Strategies of SC and USC Power
5. Proposed New Trends
- Some system identification methods are found to be rewarding and have not been applied and verified on SC or USC power plants. Among the strong candidates of models, it has been found that Wiener, Hammerstein-Wiener, enhanced Wiener models, and Hammerstein structures, all worth investigation as they have brought notable improvements on modeling of other energy sources [98,99]. The approaches can be readily applied on supercritical and ultra-supercritical units and compared against other techniques.
- For physical and mathematical model part, there are some other parameter identification techniques that are found to be more robust than genetic algorithms and other evolutionary computation techniques. The proposed method in this section is to use gravitational search algorithm (GSA), which outperforms the evolutionary computation techniques in parameter identification of another energy conversion system [100]. Therefore, it is believed that the GSA approach will introduce enhanced results for SCPP and USC models’ identification.
- There is a lack of intelligent control applications on physics-based models as most reported articles for intelligent control of SCPP have been applied on neural network based models. Physics-based models are more compatible with system physics under normal and emergency conditions and offer the advantage of being easy to observe/estimate the intermediate variables, which are very difficult to observe or measure in practice. On the other hand, the NN controller is found to be more rigorous in following large load applications or rejections. Studying SCPP by this combination seems to be attractive and likely will bring improvements in the dynamic responses of SC and USC units.
- Startup process optimization is not extensively studied and seems to be forthcoming research proposal. Although these are published articles in this context [40,43], there are many alternative methods that can be applied. Multiple model predictive control (MMPC) is expected to a leading choice to optimize the startup process of SCPPs. Identified linear state-space models are preferable to cover the entire range of startup process in the MMPC algorithm and to facilitate the computation demands. Then, a comparative study can be conducted with and without MMPC to confirm how the proposed technique helps the operators in integrating the plant to the gird in a shorter time.
6. Conclusions
- The modeling review part has been classified into physical models and empirical models, in which the physical models includes the mathematical models that rooted originally and structurally from system physical and engineering principles, whereas the empirical models include data-based models that are built in the computer algorithm without any physical derivations. Although the later is found to be generally more accurate over wide range of operation, the former approach has the necessary physical verity that makes the intermediate variables that are difficult or expensive to measure available by reasonable inference. Furthermore, the simulations during emergency conditions, such as sudden loss of one of the mills, failure in the water-level control, and frequency excursions have given priority to physical models. Therefore, both methods have doubtless eligibility in modeling SC and USC units because of the salient merits of each method. The future recommendations for this part is to apply alternative system identification techniques as those proposed in Section 5 for more adequately accurate results. The proposed alternative model structures and identification algorithms have given prominent enhancement for other energy sources so they can be promising also in case of SC and USC processes.
- For control part, the review has focused on the control performance in load following capability, computation burdens, and the control scheme or configuration. Other modern objectives are included in recent control strategies, such as emissions control, energy efficiency improvements, and milling performance effects. The review reports the main articles, each has either parallel or cascade structure of two control levels: supervisory and regulatory. Despite all these promising achievements, there are still many issues to consider in the future as the ordinary way of control system philosophy is no longer sufficient to accomplish with all contemporary requirements. Intelligent techniques are one of the leading options, which need considerable background inartificial intelligence and power generation plants. The literature is also lack of extensive study for startup process optimization, which can be done by MPC, explicitly MPC or MMPC.
- The future recommendation is to study the suggested new points that are presented as proposed new trends in Section 5. Some state-of-the-art intelligent techniques for parameter identification and control applications are suggested that have not been applied to SCPP yet. It is believed that, these concise proposal open the way for more intensive research proposals in this area for future researchers subject to having favorable facilities, attaining the appropriate standard of the research, and hence more improved results.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| APD® | Aspen Plus Dynamics® |
| APROS® | Advanced Process Simulation Software® |
| ANN | Artificial Neural Networks |
| ARMAX | Autoregressive-Moving Average with Exogenous |
| CCGT | Combined Cycle Gas-Turbine |
| CCP | Carbon Capture Process |
| DMC | Dynamic Matrix Control |
| DNN | Deep Neural Network |
| DRNN | Diagonal Re-current Neural Network |
| ECON | Economizer |
| GA | Genetic algorithm |
| GB | Great Britain |
| HP | High pressure |
| HRSG | Heat Recovery Steam Generator |
| IP | Intermediate pressure |
| MPC | Model Predictive Control |
| MMPC | Multiple-Model Predictive Control |
| NMPC | Nonlinear Model Predictive Control |
| NN | Neural Network |
| RH | Reheater |
| SC | Supercritical |
| SCPP | Supercritical Power Plant |
| SH | Superheater |
| USC | Ultra-Supercritical |
Symbols
| E | Energy or Energies (KJ) |
| K | Unknown Fixed Parameter |
| m | mass (Kg) |
| Q | Heat Transfer (KJ) |
| t | Time (seconds) |
| u | Input |
| x | State variable (pressure or temperature for a heat exchanger) |
| y | Output |
Subscripts
| in | input |
| out | output |
| rh | Reheater |
| econ | Economizer |
| sh | Superheater |
| ww | Waterwall |
References
- Dipak, K.S. Steam generators. In Thermal Power Plant. Design and Operation; Elsevier: Amsterdam, The Netherlands, 2015; pp. 39–89. [Google Scholar]
- Franco, A. Analysis of small size combined cycle plants based on the use of supercritical HRSG. Appl. Eng. 2011, 31, 785–794. [Google Scholar] [CrossRef]
- Mohamed, O. Study of Energy-Efficient Supercritical Coal-Fired Power Plant Dynamic Responses and Control Strategies. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2012. [Google Scholar]
- Draganescu, M. Study of Supercritical Coal-Fired Power Plant Dynamic Responses and Control for Grid Code Compliance. Ph.D. Thesis, University of Warwick, Coventry, UK, 2015. [Google Scholar]
- Guo, S. Model Based Analysis of Power Plant Integrated with a Post Combustion Carbon Capture process. Ph.D. Thesis, University of Warwick, Coventry, UK, 2015. [Google Scholar]
- Agbonghae, E.O. Modelling and Optimization of Coal-Fired Power Plant Generation Systems with CO2 Capture. Ph.D. Thesis, University of Leeds, Leeds, UK, 2015. [Google Scholar]
- Kundur, P. A survey of utility experiences with power plant response during partial load rejection and system disturbances. IEEE Trans. Power Appar. Syst. 1981, 5, 2471–2475. [Google Scholar] [CrossRef]
- Garduno-Ramirez, R.; Lee, K.Y. Overall control of fossil-fuel power plants. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001. [Google Scholar]
- Alobaid, F.; Mertens, N.; Starkloff, R.; Lanz, T.; Heinze, C.; Epple, B. Progress in dynamic simulation of thermal power plants. Prog. Energy Combust. Sci. 2017, 59, 79–162. [Google Scholar] [CrossRef]
- Sonntag, R.; Borgnakke, C.; Van Wylen, G.J. Fundamentals of Thermodynamics, 5th ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Daren, Y.; Zhiqiang, X. Nonlinear coordinated control of drum boiler power unit based on feedback linearization. IEEE Trans. Energy Convers. 2005, 20, 204–210. [Google Scholar] [CrossRef]
- Adams, J.; Clark, D.R.; Luis, J.R.; Spanbaur, J.P. Mathematical modeling of once-through boiler dynamics. IEEE Trans. Power Appar. Syst. 1965, 84, 146–156. [Google Scholar] [CrossRef]
- Working Group on prime mover and energy supply models for system dynamic performance studies “Dynamic models for fossil fueled steam units in power system studies”. IEEE Trans. Power Syst. 1991, 6, 753–761. [CrossRef]
- De Mello, F.P. Boiler models for system dynamic performance studies. IEEE Trans. Power Syst. 1991, 6, 66–74. [Google Scholar] [CrossRef]
- Hogg, B.W.; Lu, S. “Power plant analyzer”_computer code for fossil power plant operation studies. IEEE Trans. Energy Convers. 1996, 11, 742–747. [Google Scholar]
- Usoro, P.B.; Wormley, D.N. Mathematical modeling of fossil-fueled steam power plants under normal and emergency conditions part I: Methodology. In Proceedings of the fifth power plant dynamics, control and testing symposium, Knoxville, TN, USA, 21 March 1983; pp. 601–622. [Google Scholar]
- Usoro, P.B.; Wormley, D.N. Mathematical modeling of fossil-fueled steam power plants under normal and emergency conditions part II: Simulation results. In Proceedings of the fifth power plant dynamics, control and testing symposium, Knoxville, TN, USA, 21 March 1983; pp. 623–638. [Google Scholar]
- Hogg, B.W.; Irwin, G.W.; Prasad, G.; Swidenbank, E. Plant-wide physical model based control for a thermal power plant. In Proceedings of the 38th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 1999; pp. 4631–4636. [Google Scholar]
- Astrom, K.J.; Bell, R.D. Drum boiler dynamics. Automatica 2000, 36, 363–378. [Google Scholar] [CrossRef]
- Hemmaplardh, K.; Esok, G.; Gate, R.A.; Hammond, S.A.S. Applications of dynamic models in dispatcher training simulator and in other system dynamic performance studies. IEEE Trans. Power Appar. Syst. 1985, 6, 1349–1355. [Google Scholar] [CrossRef]
- Lu, S.; Hogg, B.W. Dynamic nonlinear modeling of power plant by physical principles and neural networks. Int. J. Electr. Power Energy Syst. 2000, 22, 67–78. [Google Scholar] [CrossRef]
- Dimeo, R.; Lee, K.Y. Boiler-turbine control system design using a genetic algorithm. IEEE Trans. Energy Convers. 1995, 10, 752–759. [Google Scholar] [CrossRef]
- Ben-Abdennour, A.; Lee, K.Y. Multivariable robust control of a power plant deaerator. IEEE Trans. Energy Convers. 1993, 8, 123–129. [Google Scholar] [CrossRef]
- Cashar, E.E.; Hemmaplardh, K.; Lee, D.K.; Ramchandani, H.; Sackett, S.A. A Dispatcher Training Simulator Design with Multi-purpose Interfaces. IEEE Trans. Power Appar. Syst. 1985, 6, 1276–1280. [Google Scholar]
- Kola, V.; Bose, A.; Anderson, P.M. Power plant models for operator training simulators. IEEE Trans. Power Syst. 1989, 4, 559–565. [Google Scholar] [CrossRef]
- Chang-Liang, L.; Ji-Zhen, L.; Yu-Guang, N.; De-Liang, Z. Genetic algorithm-based multi-variables nonlinear model identification for 300 MW power unit. In Proceedings of the Second International Conference on Machine Learning and Cybernetics, Xi’an, China, 5 November 2003; Volume 1, pp. 314–317. [Google Scholar]
- Chaibakhsh, A.; Ghaffari, A. Steam turbine model. Simul. Model. Pract. Theory 2008, 16, 1145–1162. [Google Scholar] [CrossRef]
- Hoshmandi, K.; Montazeri, M. Long range predictive PID control for nonlinear boiler-turbine dynamics. In Proceedings of the IEEE International Conference on Industrial Technology, Gippsland, Australia, 10–13 February 2009; pp. 1–6. [Google Scholar]
- Maffezzoni, C. Boiler-turbine dynamics in power-plant control. Control. Eng. Pract. 1997, 5, 301–312. [Google Scholar] [CrossRef]
- Maffezzoni, C.; Cori, R. Practical-optimal control of a drum boiler power plant. Automatica 1984, 20, 163–173. [Google Scholar]
- Littman, B.; Chen, T.S. Simulation of bull run supercritical generation unit. IEEE Trans. Power Appar. Syst. 1966, 7, 711–722. [Google Scholar] [CrossRef]
- Laubli, F.; Fenton, F.H. The flexibility of the supercritical boiler as a partner in power system design and operation: Part I: Theoretical Relationship. IEEE Trans. Power Appar. Syst. 1971, 4, 1725–1733. [Google Scholar] [CrossRef]
- Laubli, F.; Fenton, F.H. The flexibility of the supercritical boiler as a partner in power system design and operation: Part II: Application and Field Test Results. IEEE Trans. Power Appar. Syst. 1971, 4, 1719–1724. [Google Scholar] [CrossRef]
- Suzuki, Y.; Sik, P.; Uchida, Y. Simulation of once-through supercritical boiler. Simulation 1979, 33, 181–193. [Google Scholar] [CrossRef]
- Shinohara, W.; Koditschek, D.E. A simplified model based supercritical power plant controller. In Proceedings of the 35th Conference on Decision and Control, Kobe, Japan, 13 December 1996; pp. 4486–4489. [Google Scholar]
- Inoue, T.; Taniguchi, H.; Ikeguchi, H. A model of fossil fueled plant with once-through boiler for power system frequency simulation studies. IEEE Trans. Power Syst. 2000, 15, 1322–1328. [Google Scholar] [CrossRef]
- Mohamed, O.; Wang, J.; Guo, S.; Al-Duri, B.; Wei, J. Modelling study of supercritical power plant and parameter identification using genetic algorithms. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010. [Google Scholar]
- Mohamed, O.; Wang, J.; Guo, S.; Al-Duri, B. Mathematical modeling of coal fired supercritical power plant and model parameter identification using genetic algorithms. In Electrical Engineering and Applied Computing. Lecture Notes in Electrical Engineering; Ao, S.I., Gelman, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 90. [Google Scholar]
- Liu, J.-Z.; Yan, S.; Zeng, D.-L.; Hu, Y.; Lv, Y. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit. Energy 2015, 93, 2069–2078. [Google Scholar] [CrossRef]
- Alobaid, F.; Strohle, J.; Epple, B.; Hyun-Gee, K. Dynamic simulation of a supercritical once-through heat recovery steam generator during load changes and start-up procedures. Appl. Energy 2009, 86, 1274–1282. [Google Scholar] [CrossRef]
- Deng, K.J.; Yang, C.; Chen, H.; Zhou, N.N.; Huang, S.L. Start-up and dynamic processes simulation of supercritical once-through boiler. Appl. Therm. Eng. 2017, 115, 937–946. [Google Scholar] [CrossRef]
- Sarda, P.; Hedrick, E.; Reynolds, K.; Bhattacharyya, D.; Zitney, E.S.; Omell, B. Development of a dynamic model and control system for load-following studies of supercritical pulverized coal power plants. Processes 2018, 6, 266. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Liu, M.; Li, B.; Liu, Y.; Yan, J. Thermodynamic analysis on the transient cycling of coal-fired power plants: Simulation study of a 660 MW supercritical unit. Energy 2017, 122, 505–527. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.F.; Su, Z.G.; Wang, B. A dynamic mathematical model of an ultra-supercritical coal fired once-through boiler-turbine unit. Appl. Energy 2017, 189, 654–666. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Cao, L.; Hu, P.; Li, B.; Li, Y. Model establishment and performance evaluation of a modified regenerative system for a 660 MW supercritical unit running at the IPT-setting mode. Energy 2019, 179, 908–915. [Google Scholar] [CrossRef]
- Zima, W.; Nowak-Ocłon, M.; Ocłon, P. Simulation of fluid heating in combustion chamber waterwalls of boilers for supercritical steam parameters. Energy 2015, 92, 117–127. [Google Scholar] [CrossRef]
- Zima, W.; Nowak-Ocłon, M.; Ocłon, P. Novel online simulation-ready models of conjugate heat transfer in combustion chamber waterwall tubes of supercritical power boilers. Energy 2018, 148, 809–823. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. Study of supercritical power plant integration with high temperature thermal energy storage for flexible operation. Energy Storage 2018, 20, 140–152. [Google Scholar] [CrossRef]
- Wu, H.; Yang, C.; He, H.; Huang, S.; Chen, H. A hybrid simulation of a 600 mw supercritical circulating fluidized bed boiler system. Appl. Therm. Eng. 2018, 143, 977–987. [Google Scholar] [CrossRef]
- Zhong-Xu, H.; Jian, F.; Hui, W.; Chuan, Z.; Zhi-qiang, K. Study on simulation mathematical model of supercritical boiler-turbine-generator unit. In Proceedings of the Power System Technology and IEEE Power India Conference, New Delhi, India, 2–15 October 2008; pp. 1–5. [Google Scholar]
- Kwang, Y.; Lee, J.S.; Jason, H.A.; Hoffman, S.-H.K.; Won-Hee, J. Neural network based modeling for large scale power plant. In Proceedings of the Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Liu, X.J.; Kong, X.B.; Hou, G.L.; Wang, J.H. Modeling of a 1000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods. Energy Convers. Manag. 2013, 53, 518–527. [Google Scholar] [CrossRef]
- Zhang, L.; Kong, X.; Lee, K.Y. Stacked auto-encoder modeling of an ultra-supercritical boiler-turbine system. Energies 2019, 12, 4035. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Chai, T.; Liu, X. Deep-neural-network-based economic model predictive control for ultra-supercritical power plant. IEEE Trans. Ind. Inform. 2020, 16, 5905–5913. [Google Scholar] [CrossRef]
- Mohamed, O.; Za’ter, M.E. comparative study between three modeling approaches for a gas turbine power generation system. Arab. J. Sci. Eng. 2020, 45, 1803–1820. [Google Scholar] [CrossRef]
- Nakamura, H.; Akaike, H. Use of statistical identification for optimal control of a supercritical thermal power plant. In Proceedings of the 5th IFAC Symposium on Identification and System Parameter Identification, Tokyo, Japan, 20 March 1979; pp. 221–232. [Google Scholar]
- Nakamura, H.; Akaike, H. Statistical identification for optimal control for supercritical thermal power plants. Automatica 1981, 17, 143–155. [Google Scholar] [CrossRef]
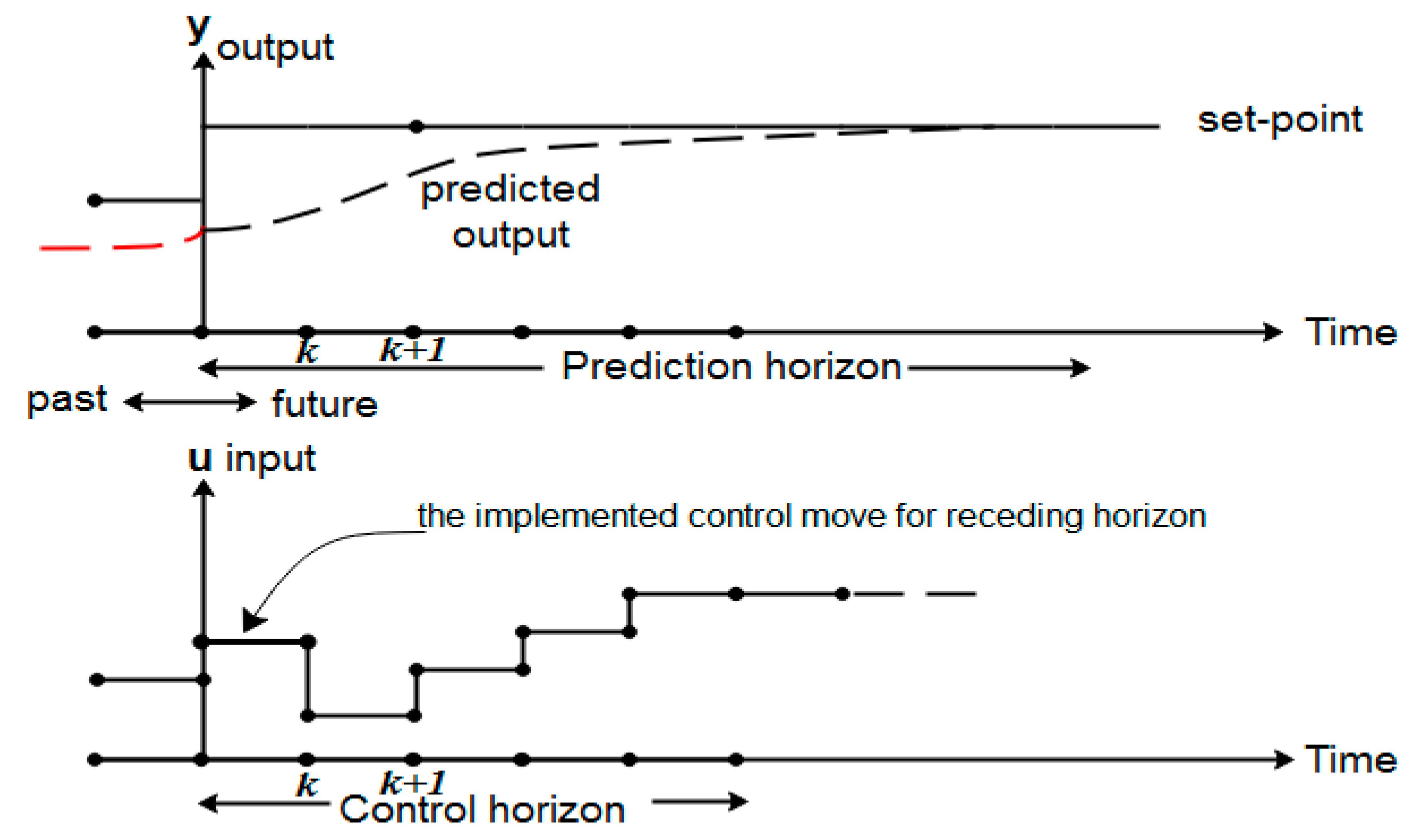
- Richalet, J. Industrial applications of model based predictive control. Automatica 1993, 29, 1251–1274. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraint; Addison-Wesley Educational Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Wang, L. Model. Predictive Control. System Design and Implementation Using MATLAB®; Springer: London, UK, 2010. [Google Scholar]
- Gibbs, B.P.; Weber, D.S.; Porter, D.W. Application of nonlinear model predictive control to fossil power plants. In Proceedings of the 30th Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 1850–1856. [Google Scholar]
- Rovnak, J.A.; Corlis, R. Dynamic matrix based control of fossil power plant. IEEE Trans. Energy Convers. 1991, 6, 320–326. [Google Scholar] [CrossRef]
- Mohamed, O.; Wang, J.; Al Duri, B.; Lu, J.; Gao, Q.; Xue, Y.; Liu, X. Predictive control of coal mills for improving supercritical power generation process dynamic responses. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 1709–1714. [Google Scholar]
- Mohamed, O.; Wang, J.; Al Duri, B. Predictive control strategy for a supercritical power plant and study of influences of coal mills control on its dynamic responses. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 918–923. [Google Scholar]
- Draganescu, M.; Guo, S.; Wojcik, J.; Wang, J.; Liu, X.; Hou, G.; Xue, Y.; Gao, Q. Generalized predictive control for superheated steam temperature regulation in a supercritical coal-fired power plant. CSEE J. Power Energy Syst. 2015, 1, 69–77. [Google Scholar] [CrossRef]
- Lee, T.; Han, E.; Moon, U.-C.; Lee, K.Y. supplementary control of air–fuel ratio using dynamic matrix control for thermal power plant emission. Energies 2020, 13, 226. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Jin, S.; Heo, J.; Hoffman, A.; Kim, S.-H.; Jung, W.-H. Modified predictive optimal control using neural network-based combined model for large-scale power plants. In Proceedings of the Power Engineering Society General Meeting, Calgary, AB, Canada 26–30 July 2007; pp. 1–8. [Google Scholar]
- Lu, S. Dynamic modelling and simulation of power plant systems. Proceedings of the institution of mechanical engineers, part A. J. Power Energy 1999, 213, 7–22. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, G.; Zhang, J. Adaptive neuro-control system for superheated steam temperature of power plant over wide range operation. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications IEEE, Jinan, China, 16–18 October 2006; pp. 138–141. [Google Scholar]
- Lo, K.L.; Rathamarit, Y. State estimation of a boiler model using the unscented Kalman filter. Iet Gener. Transm. Distrib. 2008, 2, 917–931. [Google Scholar] [CrossRef]
- Gu, J.-J.; Zhang, L.; Li, J.-Q. Study on mathematical model of coordinated control system for supercritical unit. In Proceedings of the Eighth International Conference on Machine Learning and Cybernetics, Hebei, China, 12–15 July 2009; pp. 2158–2168. [Google Scholar]
- Sreedhar, R.; Fernandez, B.; Masada, G.Y. Sliding control retrofit for a thermal power plant. In Proceedings of the 4th IEEE Conference on Control Application, Albany, NY, USA, 28–29 September 1995; pp. 409–414. [Google Scholar]
- Moon, U.-C.; Lee, K.Y. Step response model development for dynamic matrix control of a drum-type boiler-turbine system. IEEE Trans. Energy Convers. 2019, 24, 423–430. [Google Scholar] [CrossRef]
- Ogata, K.; Matsumura, S.; Fujii, S.; Shiyoa, H. Adaptive control for the steam temperature of thermal power plants. In Proceedings of the 1998 IEEE International Conference on Control Applications, Trieste, Italy, 4 September 1998; pp. 1105–1109. [Google Scholar]
- Leyzerovich, A.S. Steam Turbines for Modern Fossil-Fuel Power Plant; The Fairmont Press, Inc.: Lilburn, GA, USA, 2007. [Google Scholar]
- Sato, T.; Kazuhiro, T.; Akir, I. Design of a pressure control system in furnace of a thermal power plant boiler using self tuning I-P and feed-forward compensator. Int. J. Innov. Comput. Inf. Control 2007, 3, 371–384. [Google Scholar]
- Li, S.; Liu, H.; Cai, W.-J.; Soh, Y.-C.; Xie, L.-H. A new coordinated control strategy for boiler-turbine system of coal-fired power plant. IEEE Trans. Control. Syst. Technol. 2005, 13, 943–954. [Google Scholar]
- Tan, W.; Marquez, H.J.; Chen, T. Multivariable robust controller design for a boiler system. IEEE Trans. Control. Syst. Technol. 2002, 10, 735–742. [Google Scholar] [CrossRef]
- Prasad, G.; Swidenbank, E.; Hogg, B.W. A neural net model-based multivariable long-range predictive control strategy applied in thermal power plant control. IEEE Trans. Energy Convers. 1998, 13, 176–182. [Google Scholar] [CrossRef]
- Brown, M.D.; Irwin, G.W.; Hogg, B.W.; Swindenbank, E. Modelling and control of generation units using neural network techniques. In Proceedings of the Third IEEE Conference on Control Applications, Glasgow, UK, 24–26 August 1994; Volume 1, pp. 735–740. [Google Scholar]
- Liu, H.; Li, S.; Chai, T. Intelligent decoupling control of power plant main steam pressure and power output. Int. J. Electr. Power Energy Syst. 2003, 25, 809–819. [Google Scholar] [CrossRef]
- Li, D.; Zeng, H.; Xue, Y.; Jiang, X. Multivariable nonlinear control design for boiler-turbine units. In Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 7518–7522. [Google Scholar]
- Zhao, W.-J.; Niu, Y.-U.; Liu, J.-Z. Multi-model adaptive control for the superheated steam temperature. In Proceedings of the 1st International conference on Machine Learning and Cybernetics, Beijing, China, 4–5 November 2002; pp. 269–272. [Google Scholar]
- Demello, F.P.; de Mello, F.; Dunlop, R.; Fenton, F.; Intrabartola, J.; Kundur, P.; Littman, B.; Russell, T. Guidelines for enhancing power plant response to partial load rejections. IEEE Trans. Power Appar. Syst. 1983, 6, 1501–1504. [Google Scholar]
- Ben-Abdennour, A.; Lee, K.Y. Improving boiler performance during partial load rejections using a mixed fuzzy logicand LQG/LTR approach. In Proceedings of the International Conference on Intelligent Systems Applications to Power Systems, Orlando, FL, USA, 28 January–2 February 1996; pp. 304–308. [Google Scholar]
- Ben-Abdennour, A. An intelligent supervisory system for drum type boilers during severe disturbances. Int. J. Electr. Power Energy Syst. 2000, 22, 381–387. [Google Scholar] [CrossRef]
- Emto, G.; Tsuda, A.; Takeshita, T.; Monical, M.T.; Nakagawa, S.; Fujita, K. Integrated large-scale multivariable control and real time optimization of a power system. In Proceedings of the IEEE Conference on Control Applications, Trieste, Italy, 4 September 1998; pp. 1368–1372. [Google Scholar]
- Tan, W.; Horacio, J.; Tongwan, C.M.; Liu, J. Analysis and control of nonlinear boiler-turbine unit. J. Process Control 2005, 15, 883–891. [Google Scholar] [CrossRef]
- Lu, S.; Hogg, B.W. Predictive co-ordinated control for power plant steam pressure and power output. Control. Eng. Pract. 1997, 5, 79–84. [Google Scholar] [CrossRef]
- Ramirez, G.; Lee, K.Y. Multiobjective optimal power plant operation through coordinated control with pressure set-point scheduling. IEEE Trans. Energy Convers. 2001, 16, 115–122. [Google Scholar] [CrossRef]
- Sáez, D.; Cipriano, A.; Ordys, A.W. Optimization of industrial processes at the supervisory level. In Advances in Industrial Control; Springer: London, UK, 2002. [Google Scholar]
- Bulut, B.; Katebi, M.R.; Johnson, M.A. Industrial application of model based predictive control as a supervisory system. In Proceedings of the 2000 American Control Conference ACC, Chicago, IL, USA, 28–30 June 2000; Volume 6, pp. 3763–3767. [Google Scholar]
- Lee, K.; Van Sickel, J.H.; Hoffman, J.A.; Jung, W.-H.; Kim, S.-H. Controller design for large-scale ultrasupercritical once-through boiler power plant. IEEE Trans. Energy Convers. 2010, 25, 1063–1070. [Google Scholar] [CrossRef]
- Li, Z.-J.; Li, Z.-X.; Tan, W.; Liu, J.-Z. Constrained dynamic matrix control for a boiler-turbine unit. In Proceedings of the Fifth International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006. [Google Scholar]
- Oluwande, G.A. Exploitation of advanced control techniques in power generation. Comput. Control. Eng. J. 2001, 12, 63–67. [Google Scholar] [CrossRef]
- Trangbaek, K. Constrained control of a once-through boiler with recirculation. In Proceedings of the 17th World Congress the International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008. [Google Scholar]
- Vocke, C. Supercritical boiler control & operational experience. In Proceedings of the Power Generation Control 2007 IET Seminar, Birmingham, UK, 6 December 2007; pp. 29–35. [Google Scholar]
- Mohammadi, E.; Montazeri-Gh, M. A new approach to the gray-box identification of wiener models with the application of gas turbine engine modeling. Asme J. Eng. Gas. Turbines Power 2015, 137, 12. [Google Scholar] [CrossRef]
- Van der Veen, G.; van Wingerden, J.; Verhaegen, M. Global identification of wind turbines using a hammerstein identification method. IEEE Trans. Control. Syst. Technol. 2013, 21, 1471–1478. [Google Scholar] [CrossRef]
- Díaz-Cortés, M.A.; Cuevas, E.; Rojas, R. Gravitational search algorithm applied to parameter identification for induction motors. In Engineering Applications of Soft Computing, Intelligent Systems Reference Library; Springer: Cham, Switzerland, 2017; pp. 45–57. [Google Scholar]

| Physical Modeling | Empirical Modeling | Hybrid Models | |||
|---|---|---|---|---|---|
| Parameters Computation | Processes Covered | Simulator Tool | Artificial Neural Networks (ANNs) | Algebraic Polynomial | [42,49] |
| Thermodynamic or Thermo-Physical properties or formulas. [5,31,34,40,41,42,43,48] Thermodynamic properties (online computation) [46,47] Direct comparison with another detailed simulator or on-site measurements data [32,34,35,36] Multi-Objective Intelligent Optimization to fit with on-site measurements GA [3,4,5,37,38,39] IGA [44] Remark: Two references cited repeatedly in two approaches means that both methods are used so the model contains fixed and dynamic parameters. | Coal mill- Boiler turbine- generator [3,4,5,37,38] Coal mill-boiler-turbine [39,44] Boiler-turbine- Generator [45,48] Boiler-turbine [32,33,36,42,43] Boiler [34,35,40,41,46,47] Functional process integrated with CCP: [5,42] Operational processes: Startup and load following [40,43] Load following [3,4,5,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. | APROS® [40,41] APD® [42] FORTRAN 95, SimuEngine [4] GSE [43] MATLAB® [3,4,5,37,38,39] Thermolib [3]. Remark: No detailed information is given in other references about the description of the computer tool. | Diagonal Recurrent Network (DRN) [51] Feed-forward Back-propagation(BP) with RBF [52] Deep Neural Network (DNN) [53,54] | [42,50] | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, O.; Khalil, A.; Wang, J. Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review. Energies 2020, 13, 2935. https://doi.org/10.3390/en13112935
Mohamed O, Khalil A, Wang J. Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review. Energies. 2020; 13(11):2935. https://doi.org/10.3390/en13112935
Chicago/Turabian StyleMohamed, Omar, Ashraf Khalil, and Jihong Wang. 2020. "Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review" Energies 13, no. 11: 2935. https://doi.org/10.3390/en13112935
APA StyleMohamed, O., Khalil, A., & Wang, J. (2020). Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review. Energies, 13(11), 2935. https://doi.org/10.3390/en13112935








