Boiling Heat Transfer Performance of Parallel Porous Microchannels

Abstract

Flow boiling in microporous layers has attracted a great deal of attention in the enhanced heat transfer field due to its high heat dissipation potential. In this study, flow boiling experiments were performed on both porous microchannels and a copper-based microchannel, using water as the coolant. As the heat flux was less than 80 W/cm², the porous microchannels presented significantly higher boiling heat transfer coefficients than the copper-based microchannel. This was closely associated with the promotion of the nucleation site density of the porous coating. With the further increase in heat flux, the heat transfer coefficients of the porous microchannels were close to those of the copper-based sample. The boiling process in the porous microchannel was found to be dominated by the nucleate boiling mechanism from low to moderate heat flux (<80 W/cm²).This switched to the convection boiling mode at high heat flux. The porous samples were able to mitigate flow instability greatly. A visual observation revealed that porous microchannels could suppress the flow fluctuation due to the establishment of a stable nucleate boiling process. Porous microchannels showed no advantage over the copper-based sample in the critical heat flux. The optimal thickness-to-particle-size ratio (δ/d) for the porous microchannel was confirmed to be between 2–5. In this range, the maximum enhanced effect on boiling heat transfer could be achieved.

1. Introduction

In order to meet higher cooling requirements, boiling heat transfer in microchannels has attracted increased attention in recent decades [1,2,3]. However, some difficulties, such as flow instability, need to be overcome. With the increase in heat flux, the boiling process becomes more unsteady and a flow instability phenomenon occurs. Numerous studies [3,4,5,6] have shown that the bubble dynamics of boiling in microchannels are different from in the macro channel. The rapid coalescence of bubbles in microchannels easily generates elongated bubbles. The bubbles expand in the upstream direction and cause reversal flow problems due to the limitation of the narrow channel. Large flow boiling instabilities, in the forms of temperature and pressure fluctuations, have a negative impact on the heat transfer system. Pressure fluctuations limit the effective transporting of the coolant, and temperature fluctuations induce thermal stresses on the substrate. In order to suppress the flow instability, various improvement methods had been proposed [7,8,9]. Porous structures have also attracted increased attention due to their large quantity of nucleation sites as well as re-entrance cavities.

Several studies [10,11,12,13] have been performed on investigating the augmentation effect of micro porous layers on boiling performance. Yang and Liu [14] investigated the effect of layer thickness on the boiling heat transfer coefficient (HFC) and critical heat flux (CHF) inside a confined space. The micro porous coating layer could enhance the HTC up to a factor of 4.5 compared to a plain surface. The optimal thickness is determined by the combination of three effects: the bubble departure resistance, extra thermal resistance and increased nucleation site density. Jun et al. [11] also studied the effect of microporous copper coatings on pool boiling. The wall superheating degrees decreased with an increase in particle size. The measured wall superheating degrees at 20 W/cm² were 7.8 K, 3.1 K, 2.1 K and 1.4 K for plain, 10 μm, 25 μm, and 67 μm-sized copper particle-coated surfaces, respectively. Both the HTC and CHF increased with the increase in particle size. The highest CHF and HTC were found to be approximately 210 W/cm² and 40 kW/m²·K for the coated surface of d = 67 μm. Sun [15] investigated subcooled flow boiling in a small flat channel. Three differently-sized copper particles (35 μm, 120 μm, and 240 μm) were selected. Under the optimum condition (120 μm particle size and 237 μm coating thickness), the microporous coating could produce a 178–200% enhancement for the HTC when compared to the smooth surface at G = 50–150 kg/m²·s. In parallel, progress was also being made for the porous-coated microchannel. Srikar and Peles [16] introduced the self-assembled method of forming thin porous layers on the surface of silicon microchannels to enhance the boiling heat transfer. Using ethanol as a working fluid, Bai et al. [17] studied enhanced flow boiling in the porous-coated microchannels using the sintering method. The porous-coated copper microchannels could improve the heat transfer performance dramatically compared to the bare microchannels, particularly under a low vapor quality regime. The enhancement mechanism of porous coatings was attributed to the increase of the nucleation site density. However, porous-coated microchannels possess some disadvantages, such as being difficult to make and experiencing performance degradation over time.

Owing to the development of the sintering method and metalfoam field, a microchannel can be produced directly by a porous material, which is called a porous microchannel. This combines the merits of the microchannel and porous structure in heat transfer and has attracted increased attention in recent years. Chou Chi-Sheng and Chen Yau-Ming [18], from National Taiwan University, found that the porous microchannel can enhance heat transfer performance by 300%andreduce pressure fluctuation by 66%. Their experiments used water as a working fluid under the condition of G = 103–207 kg/m²·s and P_sat = 1.4 bar. The copper-particle diameters investigated included 18 μm, 53 μm and 68 μm. Deng and Tang [19] studied the performance of Ω-shaped porous microchannels, fabricated by the wire EDM process on a sintered copper block. Compared with copper-based microchannels, the test results showed that porous microchannels presented a significant decrease of the wall superheat for boiling incipience, and a 2–5 fold enhancement in the heat transfer coefficient from low to moderate heat fluxes. They also found that nucleate boiling was predominant at low heat flux and vapor quality, while the convective flow boiling dominated at moderate to high heat fluxes. The heat in the nucleate boiling process was mainly dissipated through the generated bubbles on the heating surface. The heat transfer coefficient depends only on the heat flux and is unaffected by the velocity and vapor quality. The major flow patterns were bubbly flow and slug flow. However, the convective boiling mechanism was mainly determined by the evaporation process from the gas–liquid interface [19]. The heat transfer coefficient of this mechanism depends on both the velocity and vapor quality and is unaffected by the heat flux; the predominant flow pattern is annular flow.

In these studies, some mechanisms for enhancing the effect of a porous coating on boiling heat transfer have been widely accepted [6,20]. The nucleation site density is significantly increased, and the capillary force of the porous layer is helpful to supply more liquid to avoid the early occurrence of a drought problem. For a porous layer, both the particle diameter and thickness play important roles in combination on the boiling heat transfer process. In the same manner as the porous coating, there is also an optimal thickness-to-particle-size ratio for porous microchannels. The thickness represents the magnitude of the bottom layer of the porous microchannel and the particle represents the sintered copper particles. This is determined by the trade-off between conflicting factors such as the capillary liquid supply, additional thermal resistance and bubble dynamic process. At present, relevant research on porous microchannels is still lacking. There are some fundamental problems which need to be answered: What is the potential the heat transfer capability of the porous microchannel? How do the particle size and particle shape affect the flow boiling process? What is the relationship between heat transfer performance (HTC and CHF) and flow fluctuation? In this work, we focus on investigating the overall characteristics of rectangle porous microchannels in detail to help resolve these issues.

The purpose of our research is to study the heat transfer performance of porous microchannels further and explore the flow boiling mechanism in them. In the experiment, non-spheroid copper particles were chosen, and the working fluid was deionized water subject to P_out = 1 atm. Under different inlet conditions, the effects of the particle size and the bottom thickness on the HTC of porous microchannels were investigated in comparison with a copper-based microchannel. The boiling instabilities of porous microchannels are also discussed.

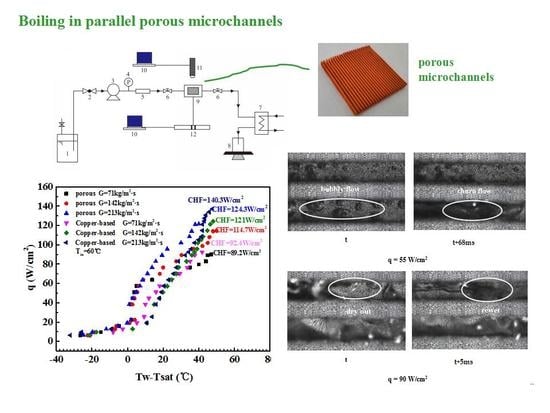
2. Experimental Setup and Procedure

2.1. Testing System

The open-loop testing system is schematically shown in Figure 1. Deionized water was used as the working fluid. At a constant mass flow rate, the water from a thermostatic water bath was pumped into the test section via a micro magnetic-driving gear pump that could ensure the flow stability. The flow boiling process took place in the porous microchannels of the test section and removed heat from the copper surface, which was heated by the electric heating rods. One throttle valve was installed near the entrance of the test section, and another valve was set to control the outlet pressure of the test section. Then, the vapor away from the test section was cooled by a plate heat exchanger. Finally, the condensated water was collected into the water storage. The flow rate was measured by a rotameter and ranged from 1–15 L/h. The pressure drop across the test section was measured by two pressure transducers of the diffused-silicon piezoresistive type (FSCK), with a response time of 2 ms and an uncertainty of ±0.25% in the range of 0–2 bar (absolute pressure). Two PT100 sensors of 3 mm in diameter were screwed at the inlet and outlet of the test section to monitor the fluid temperatures of the inlet and outlet, respectively. Three K-type shielded thermocouples were inserted into the copper block to measure the stream-wise surface temperature distributions. The axial positions of these thermocouples were 5, 15, and 25 mm, respectively. Temperature and pressure measurement data were displayed on the computer in real-time through the data acquisition module. In this experiment, the data acquisition system had to satisfy fast response requirements due to the pressure and temperature pulsation of the microchannel boiling process. The flow visualization system consisted of a high-speed camera and microscope. A camera adapter was used to connect the microscope (10 times magnification) to a high-speed camera. The high-speed camera, with a frame rate of 4000 fps at a full resolution of 912 × 888 pixels, was employed to visualize flow boiling patterns in the microchannels.

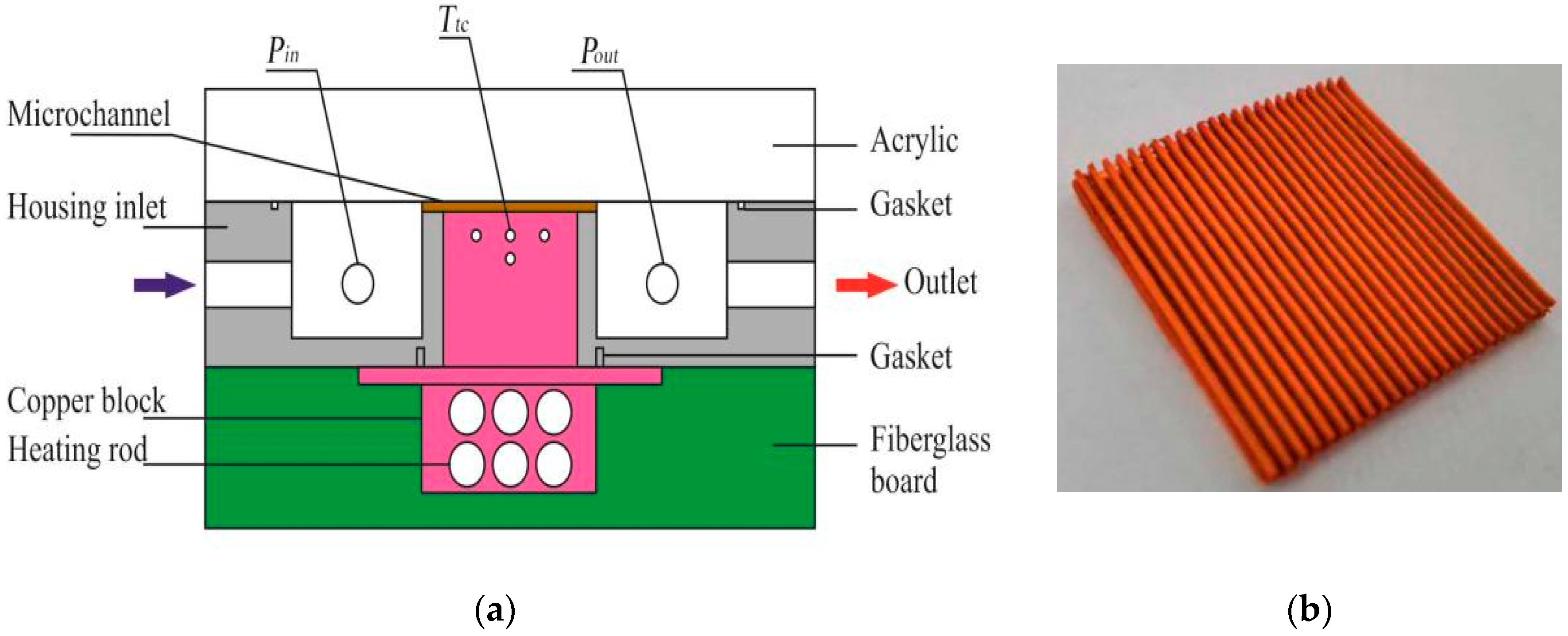
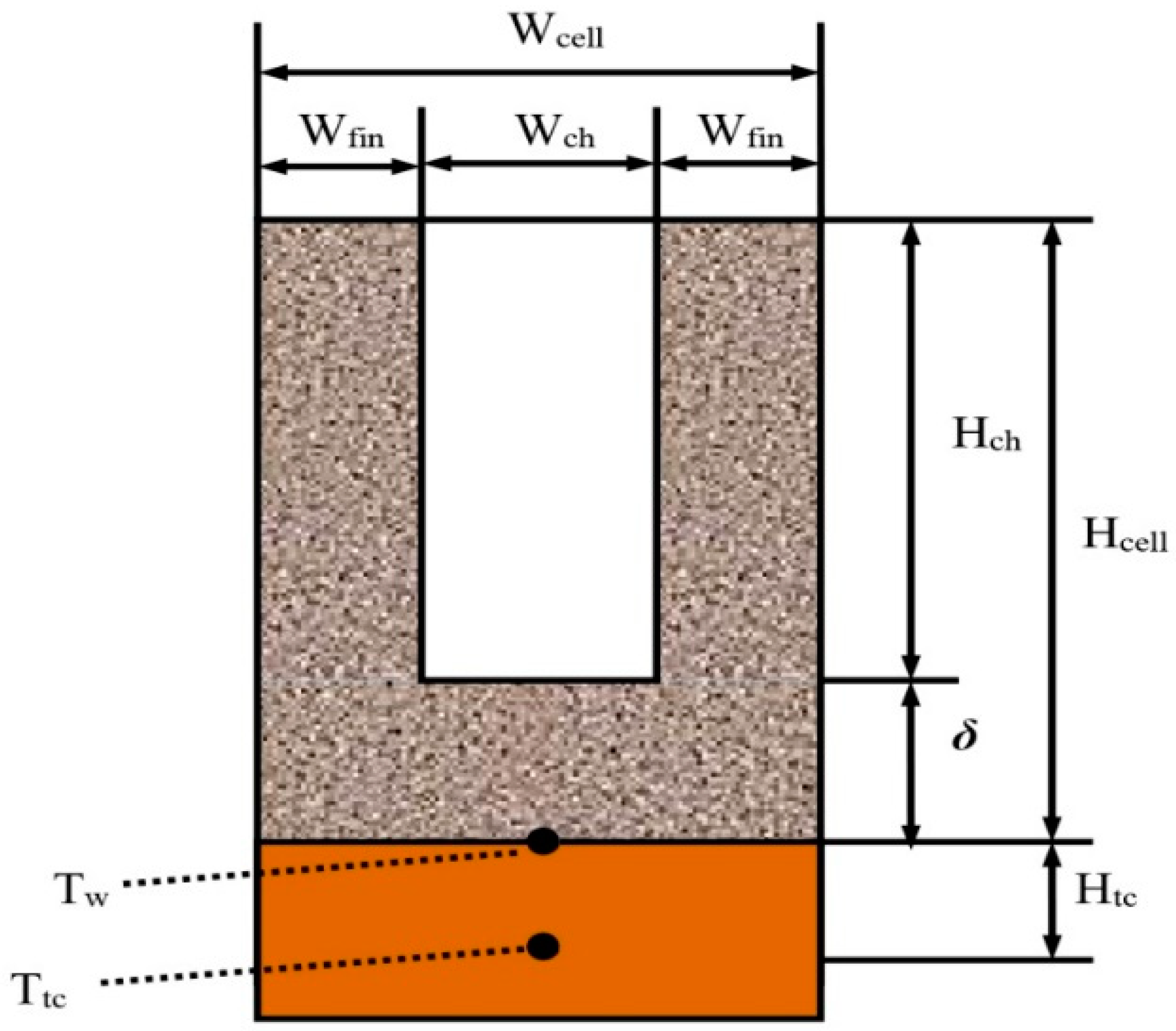
2.2. Test Section

In the design of the heat sink, a total number of 23 flow channels of 600 μm in width and 1200 μm in depth were selected. The structural parameters are shown in

Table 1. Uncertainties in variables.

Parameters	Materials
Thermocouple	±0.5 K
Pt100	±0.3 K
Flow rate	±4%
Pressure	±0.25%
Heat power Q	±0.5%
Thickness of solder (0.2 mm)	±3%
Thermal conductivity of solder (50 W/m·K)	±3%
Heat loss	±5%
Copper surface area	±2%
Local saturated temperature Ts	±0.5%
The distance of surface (0.75 cm)	±5%
Wcell (1.2 mm) and Wch (0.6 mm)	±3%
Hch (1.2 mm)	±4%
Wall temperature	±1–2%
Effective heat flux	±5%
Pressure drop	±0.35%
Heat transfer coefficient	±13.3–40.0%

. The test section consisted of a polycarbonate cover plate, a PEEK (Polyetheretherketone) housing, a copper block heating module and a Bakelite insulating block, as illustrated in Figure 2a. The porous microchannel is shown in Figure 2b. The microchannel sample was soldered on top of the copper block using low-temperature solder (Pb-Sn-Ag-Sb, λ_s = 50 W/m·K) under the protection of nitrogen gas. The cover plate and Bakelite insulating block were bolted on top of the housing to form a heat sink module. This sandwich-like design ensured the thermal insulation and reduced the heat loss greatly. The cover plate was manufactured by a polycarbonate plate (PC material), withstanding a high temperature of over 350 °C. The transparency of the PC material facilitated visual observation. The housing was made of the PEEK material with a melting point of 334 °C. The PEEK was suitable for high-accuracy requirements due to the high mechanical strength and was little affected by the temperature and humidity. A Bakelite insulating block at the bottom was wrapped around the copper block to minimize the heat loss.

2.3. Experimental Procedures

The mass flux in tests ranged from 71–213 kg/m²·s. Powered by the micro gear pump, subcooled deionized water at a certain temperature flowed across the test section. The inlet pressure was controlled by a throttle valve near the entrance. Six cartridge heaters on the bottom of the copper block were used as an analog heat source and adjusted by a voltage transformer. The heating power was specified as 50 W initially and increased by 50 W at each step after the flow rate and the inlet fluid temperature were stabilized. When heated to a certain value, the surface temperature of the copper block would surge abruptly and could not reach a steady state, indicating the emergence of the CHF condition. The previous steady-state heat flux plus half of the heat flux increment was considered to be the CHF value.

2.4. Data Reduction

The mass flux is calculated as follows:

$$G=\frac{\dot{m}}{N{A}_{ch}}$$

(1)

where $\dot{m}$ is the mass flow rate, N is the number of each of microchannels, and A_ch is the cross-section area of the single microchannel. The effective heat flux of the test section is as follows:

$$q_{eff}=\frac{Q_{eff}}{A_{base}}=\frac{Q_{eff}}{WL}$$

(2)

where A_base is the top surface area of the copper block, and W and L are the width and length of the microchannel sample, respectively; q_eff is the effective heat flux, and Q_eff is the effective heat input after the heat loss (Q_loss):

$$Q_{eff}=Q_{total}-Q_{loss}$$

(3)

where Q_total is the total input heating power, and Q_loss is the heat losses between the heat sink and environment. The heat loss quantity is mainly influenced by the flow rate, inlet temperature, input heat flux and temperature difference between the copper surface and environment. From single-phase heat transfer experiments, the linear functions between the heat losses and temperature differences are fitted by the least square method at different flow rates. The heat losses to the environment were evaluated not to exceed ±5% at G = 142 kg/m²s.

Applying the fin analysis method to the unit cell in Figure 3, the boiling heat transfer coefficient in the microchannel is then derived by the following energy balance:

$$q_{eff}\cdot W_{\mathrm{ce}ll}=h\cdot (T_w-T_{sat})\cdot (W_{ch}+2\eta \cdot H_{ch})$$

(4)

where T_w is the surface temperature at the midpoint, and T_sat is the corresponding saturation temperature at the midpoint. The wall superheat ΔT_sup is the difference between T_s and T_sat. The left-hand side of Equation (4) represents the heat input to the unit cell, and the right-hand side the heat dissipation rate by the flow boiling process from the channel walls. The thin fin approximation is applied to both sidewalls by introducing the fin efficiency:

$$\eta =\frac{\tanh (m{H}_{ch})}{m{H}_{ch}}$$

(5)

where $\dot{m}$ is the fin parameter.

$$m=\sqrt{\frac{h}{\lambda \cdot W_{ch}}}$$

(6)

On the condition of 2500 ≤ h ≤ 100,000 (W/m·K), Equation (5) can be simplified [18]:

$$\eta \approx 1.0$$

For parallel porous microchannels, the local heat transfer is given as follows:

$$h=\frac{q_{eff}\cdot W_{cell}}{(T_w-T_{sat})\cdot (W_{ch}+2H_{ch})}$$

(7)

In Equation (7), the surface temperature T_w at the midpoint is derived from the temperature of the uppermost thermocouple point, assuming one-dimensional heat conduction between thermocouples and the wall. In the experiment, three thermocouples are set below the copper surface:

$$T_w=T_{tc}-\frac{q_{eff}\cdot \mathsf{\Delta }y}{{\lambda }_{copper}}$$

(8)

where q_eff is the effective heat flux, Δy is the vertical distance of the uppermost thermocouple point from the top surface, T_w is the derived surface temperature of copper block, T_tc is the measured temperature of the uppermost thermocouple in the channel midpoint, and λ_copper is the thermal conductivity of copper.

The saturation temperature T_sat in the channel is obtained by using the saturated pressure at the specific moment. After both the inlet pressure P_in and outlet pressure P_out are measured, the saturated pressure of the working fluid in the midpoint can be obtained by the linear interpolation method.

The vapor quality x at the midpoint is calculated as follows:

$$x=\frac{1}{h_{fg}}[\frac{q_{eff}}{\dot{m}}\frac{L_i}{L}-c_p(T_{sat}-T_{in})]$$

(9)

where h_fg is the latent heat of vaporization, L_i is the distance from the inlet to the temperature measurement location, L is the microchannel length, and $\dot{m}$ is the mass flow rate.

The measuring errors of related physical variables are presented in Table 1. The uncertainties of the flow rate, pressure of the inlet and outlet, and input heat power are ±4%, ±0.25% and ±0.5%, respectively. The fluid temperatures of the inlet and outlet are measured by two thermal resistance sensors (PT100) with uncertainties of ±0.3 K. The three thermocouples, used in copper surface temperature measurement, had an uncertainty of ±0.5 K with a response time of 0.1 s after being calibrated. Following the procedure described by the standard error analysis method, the heat transfer coefficients were estimated to be in the range of 13.3–40.0%. The large uncertainty occurred near the onset of nucleation boiling (ONB) point due to the low superheat degrees in porous microchannels.

3. Fabrication Processes of Porous Microchannel

The porous microchannel was made by the powdersintering method. The structural parameters of the porous microchannel were found to be greatly influenced by the particle shape, particle size and sintering temperature. A higher sintering temperature would result in the low porosity of the sample, while a lower temperature would lead to poor mechanical strength. If the sintering temperature is lower than 850 °C, the poor mechanical strength may lead to the collapse of the porous sample. However, an overly high sintering temperature may lower the pore porosity of the porous microchannels. After repeated attempts, the sintering temperature of 900 °C was selected to ensureboth appropriate structure parameters and sufficient mechanical strength. The manufacturing process was as follows: firstly, the graphite mold was manufactured by the wire-electrode cutting method; secondly, the copper powders were evenly filled into the graphite mold; then, the graphite mold was placed in a sintering furnace for about 60 min at 900 °C under a hydrogen-reducing atmosphere to prevent oxidation; and finally, the sintered porous microchannel was demolded very carefully. The constructed porous microchannel is shown in Figure 2b. The structural parameters of both kinds of microchannels are listed in

Table 2. Structural parameter of porous microchannels.

Width, Wch (μm)	Depth, Hch (μm)	Wall Thickness, Wfin (μm)	Hydraulic Diameter, dh (μm)	Number of Trenches N
600	1200	600	800	23

. After removing the oxide layer in the citric acid aqueous solution, porous microchannels showed good hydrophilicity. The contact-angle measuring apparatus was used to capture the instantaneous state of water droplets contacting the porous surface. The water droplet was sucked into the porous layer within almost 1.5 s for one porous microchannel sample (d = 90 μm, δ = 200 μm).

4. Experimental Results

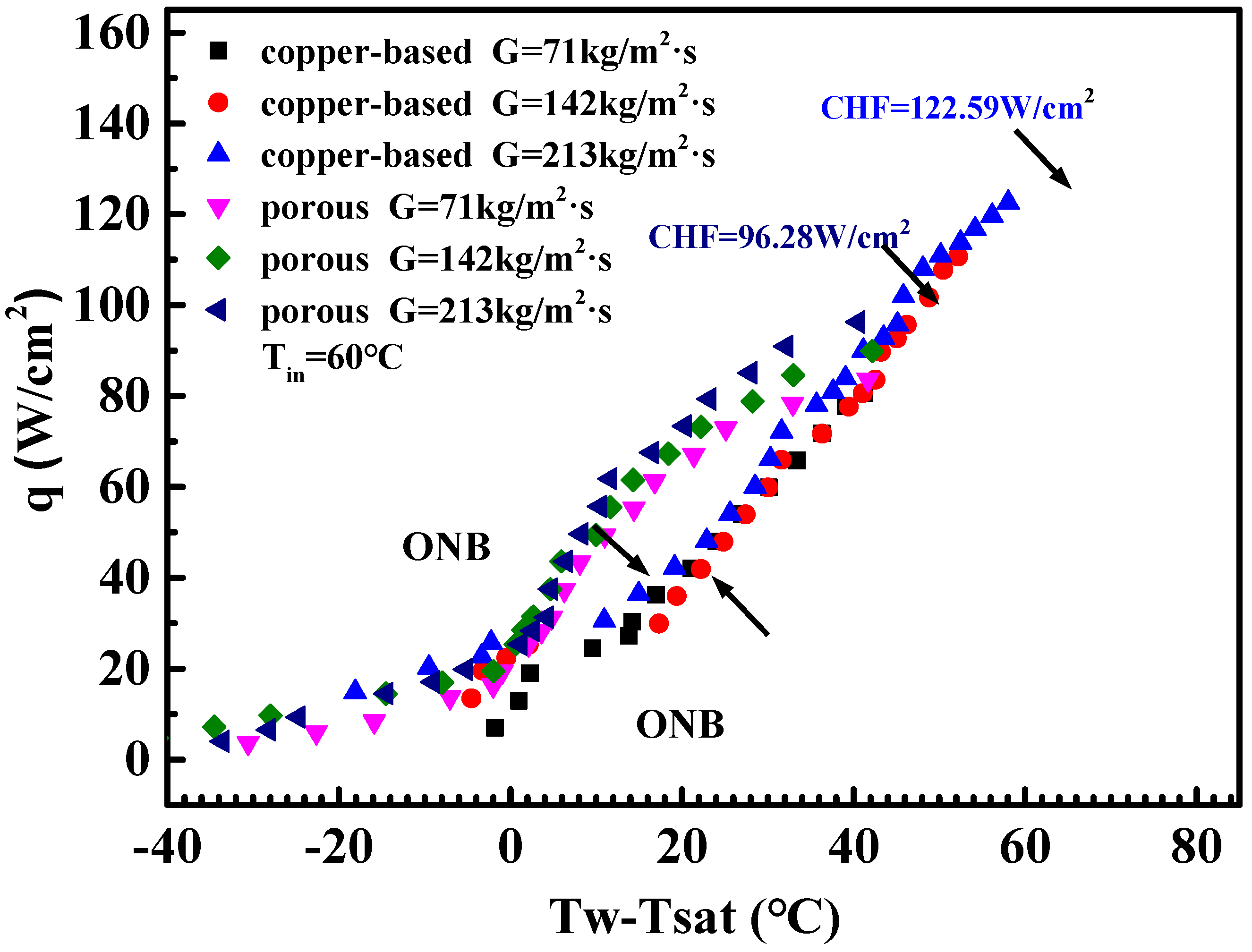
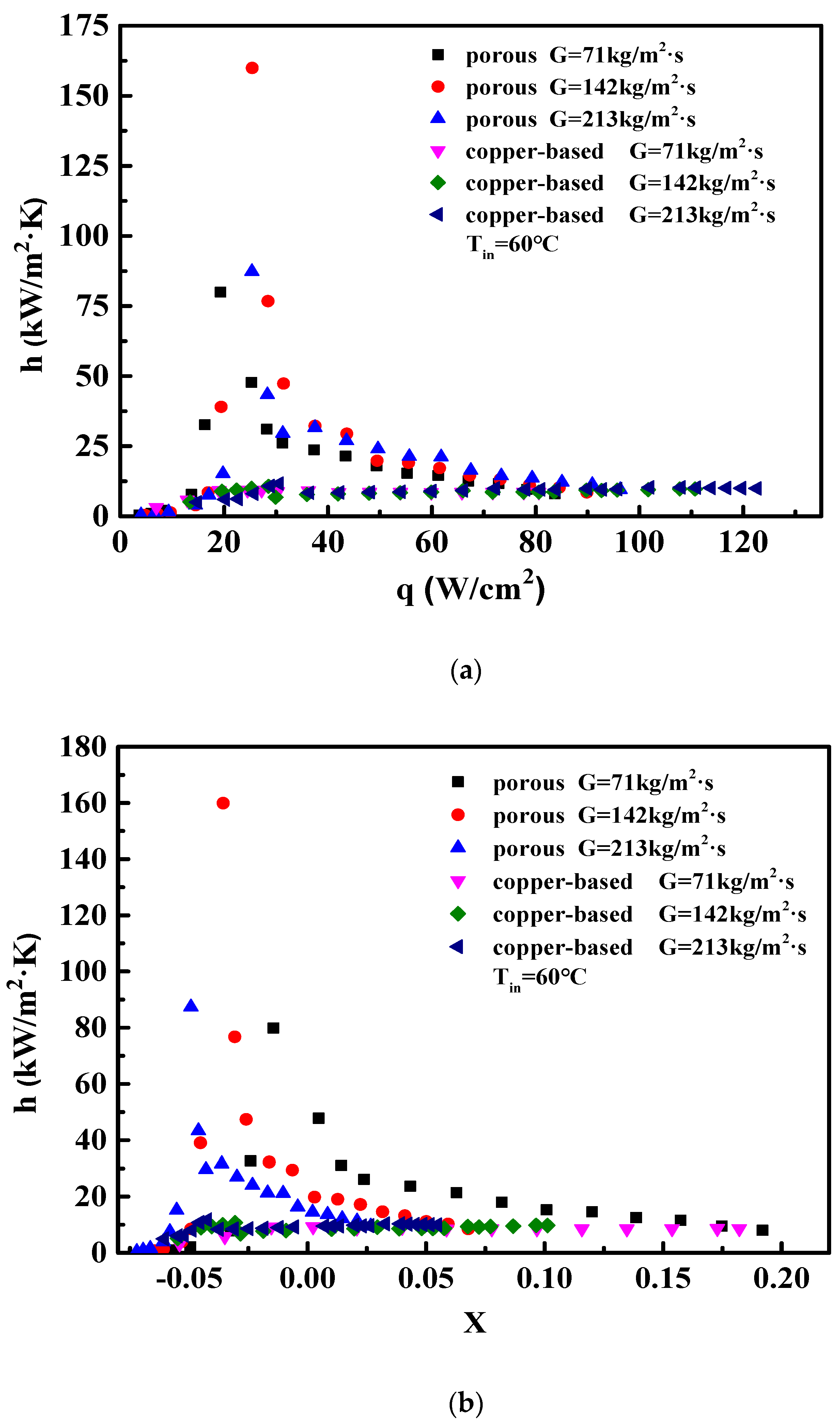
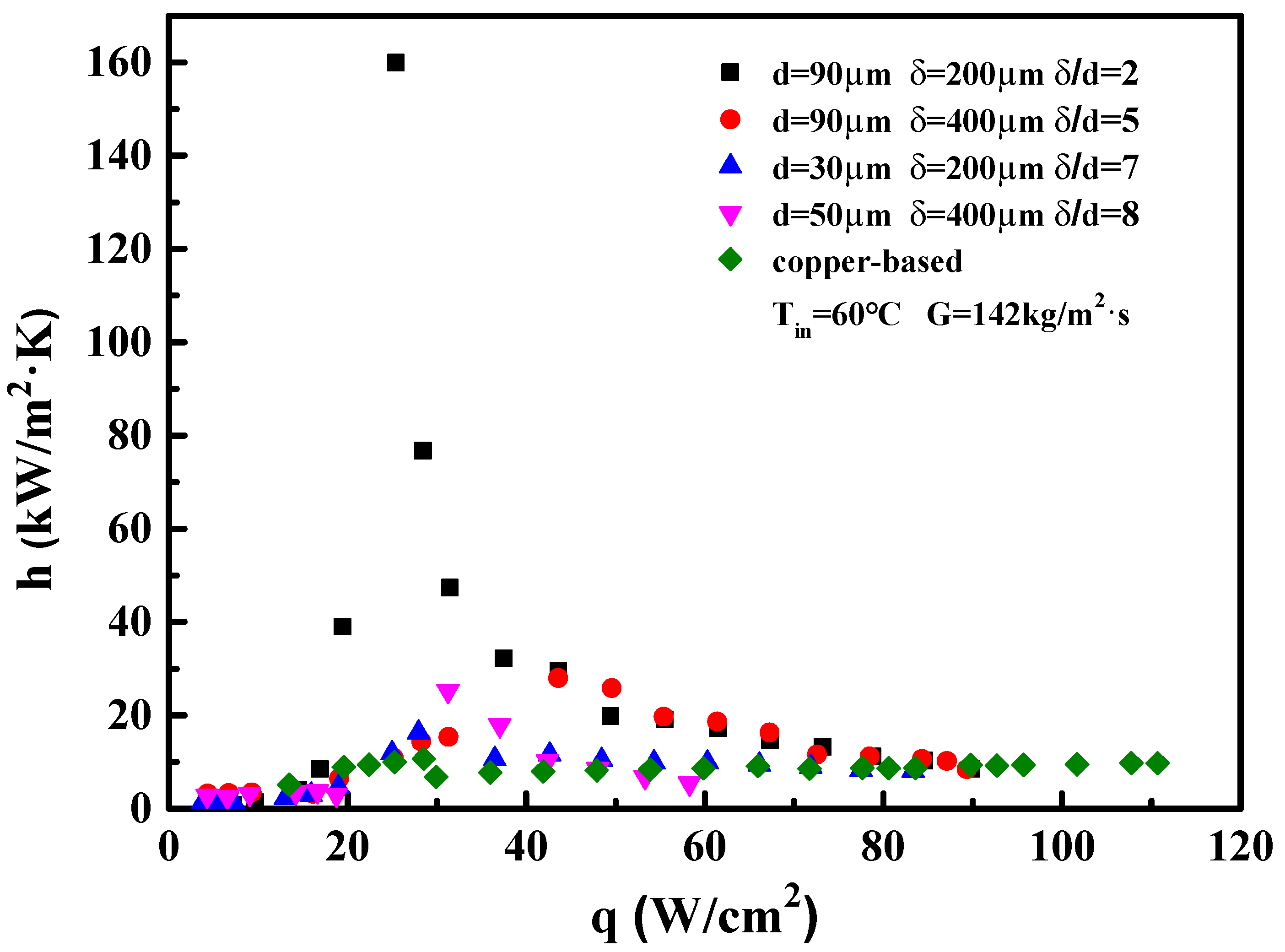
4.1. Flow Boiling Heat Transfer Coefficient of Microchannels

As the inlet temperature reaches 60 °C (ΔT_sub = 40 °C), the flow boiling curves of porous microchannels are as illustrated in Figure 4, where they are compared with the copper-based microchannel. This porous sample with a bottom thickness of 200 μm was sintered from the particle size of 90 μm. As shown in Figure 4, in the liquid phase region, the performance of the porous microchannel is almost identical to that of copper-based one. At low heat fluxes, the slope of all curves is fairly constant, which is indicative of single-phase heat transfer. When the heat flux increases to about 20.0 W/cm², the slope of the boiling curve begins to increase sharply, indicating that flow boiling had commenced at the midpoint. The onset of nucleation boiling (ONB) can be identified at the point where the boiling curve presents a radical change in slope. As shown in Figure 4, the wall superheat of the porous microchannel to initiate the boiling behavior is significantly lower than that of the copper-based microchannel. A very small temperature overshoot, 1.0–3.0 °C, is observed for the porous microchannel, while 10.0–14.0 °C is observed for the copper-based channel. For porous microchannels, the boiling curves in different mass fluxes collapse into one line between 40.0–80.0 W/cm², suggesting that the HTC in this range is only affected by heat flux. This is typical of the nucleate boiling heat transfer mechanism. Since the heat flux exceeds 80.0 W/cm², the boiling curves at different mass fluxes would begin to separate, and the slopes tend to be gentle. This indicates that the effect of heat flux on heat transfer becomes weakened and mass flux gradually comes into play. Under the same heat flux, the wall superheat of the porous microchannels decreases with the increasing mass flux.

In the experiment, temperatures at three points along the microchannel were measured. The heat transfer coefficients took the temperature at the midpoint as the basis of calculation. For the porous microchannels and copper-based channel, the HTC was plotted against the heat flux in Figure 5a in different mass fluxes. At low heat flux, the trend of the heat transfer coefficient will hit a peak and then decline gradually as the heat flux increases. After q > 80.0 W/cm², the HTC curves of porous microchannels tend to flatten out and become closer to those of the copper-based microchannel. The limiting value of the HTC was about 10 kW/m²·K for the copper-based microchannel, which is the same magnitude as the values shown in similar studies from Bai [17] and Deng [19].

Figure 5b displays the HTC as the function of the vapor quality at the midpoint corresponding to heat flux. Negative vapor qualities represent a single phase state. It is observed that the HTC was very high near x~0. This result implies rapid nucleation, bubble growth and departure in the porous surface. The latent heat of the liquid–vapor phase change process is released vigorously, and then the local boiling heat transfer coefficient drops very sharply and reaches a constant value after x~0.06. This tendency is analogous to that measured by Kuo and Peles [9], as well as the results of Deng [19,21] and Chen [20]. Note that the maximum HTCs near x~0 in our work are higher than those of Deng [19,21] under similar inlet conditions (T_in = 60 °C and G = 213 kg/m²·s). In Deng’s design [19,21] of a reentrant porous microchannel, the porous layer thickness below the Ω-shaped microchannel was about 900 μm, which would induce extra thermal conductivity and large bubble departure resistance. As for the problem of the rapid decline trend near x~0, a possible explanation is the transition of the two-phase flow pattern. Caused by bubble coalescence, the emergence of churn flow or slug flow may suppress the nucleate boiling and inhibit the heat transfer process in porous microchannel. Figure 6 provides a visual depiction using images taken from a high-speed camera (4000 fps). Under the condition of q = 55 W/cm², G = 71 kg/m²·s and T_in = 60 °C, the flow transition processes were clearly captured. There was one cycle of alternating flow patterns, from bubbly flow to coalesced bubbly flow, churn flow, and slug flow. This phenomenon presented the periodic characteristics. Even if the elongated bubbles were formed in the porous microchannel, the reverse flow was rarely observed in this condition. This indicates that the coalesced bubbles could not overcome the upstream inflow pressure.

At the initial stage of boiling, the HTC of the porous microchannel is only affected by heat flux and almost independent of mass flux and vapor quality. With the increase in heat flux, the heat transfer performance of the porous microchannel is increasingly influenced by the mass flux. This reveals that a different boiling heat transfer mechanism occurs in the porous microchannel. Under low and medium heat fluxes, the heat transfer mechanism of the porous microchannel is governed by the nucleate boiling mode; however, up to high heat flux, the heat transfer mechanism of the porous microchannel changes to a convection boiling mode. Figure 7a–c displays the typical visualization results for three input heat fluxes at G = 213 kg/m²·s. Figure 7a is the nucleation boiling condition for q = 33 W/cm². Some bubbles grow to large sizes on the wall and then are swept away before blocking the microchannel by upstream flow. For a higher heat flux of q = 55 W/cm², bubbly/annular alternating flow patterns are often observed in the porous microchannel, as shown in Figure 7b. As the input heat flux increases to q = 90 W/cm², local dry out occurs in the channel and is captured instantaneously, as shown in Figure 7c. However, this zone is soon rewetted by incoming coolant. In this condition, the status in the channel is close to the CHF. Until the drought crisis extends to most regions in the porous channels, the onset of CHF would be triggered and lead to a rapid surge in surface temperature.

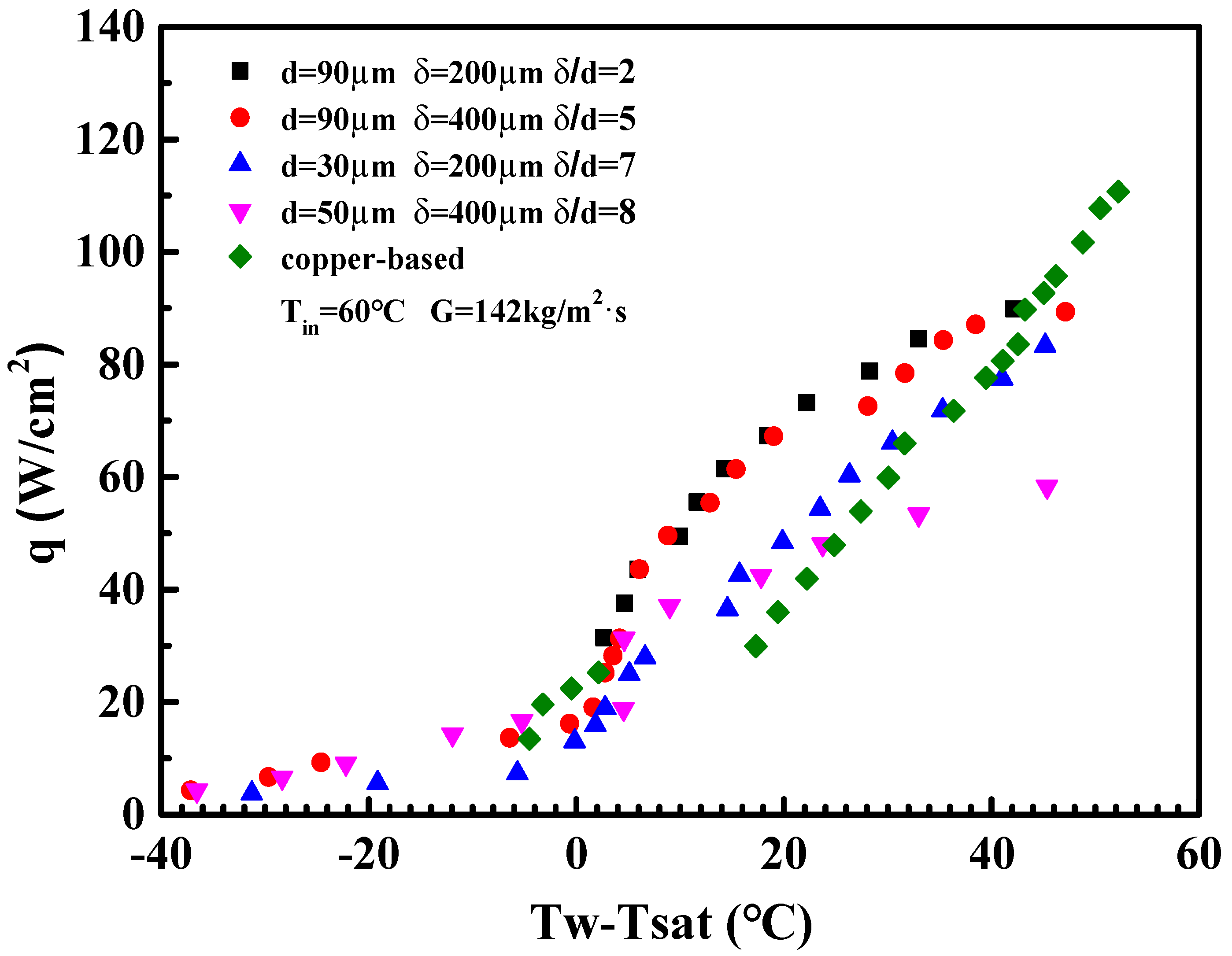
4.2. The Influence of Porous Structural Parameters

To test porous microchannels, the effects of the thickness-to-particle-size ratio (δ/d) were studied in detail. Four porous microchannel samples with different ratios of δ/d were investigated. The characteristic parameters of these porous samples are listed in

Table 3. Specification of parameters of porous microchannels.

Sample	ParticleSize, d (μm)	Sintering Thickness, δ (μm)	Sintering Temperature (℃)	δ/d
1	30	200	900	7
2	50	400	900	8
3	90	200	900	2
4	90	400	900	5

, showing the combination of three kinds of particle diameter (30 μm, 50 μm, 90 μm) and two kinds of sintering thickness (200 μm and 400 μm). The boiling curves of these porous samples and the copper-based microchannel are shown in Figure 8. The wall superheats of all porous microchannels are significantly lower than that of the copper-based microchannel. However, as for the critical heat flux (CHF), porous microchannels show no advantage over the copper-based microchannel.

At the same flow rate, Figure 9 shows the variation of the HTCs versus heat fluxes for different porous samples. With the increase in heat flux, the HTCs of the copper-based microchannel remain unchanged while those of the porous microchannels decrease gradually. After q ≥ 80 W/cm², the heat transfer performance of all porous samples approaches that of the copper-based sample, indicating no pronounced enhancing effect in this region.

Within the range of q = 40–80 W/cm², two porous samples made of d = 90 μm could reduce the wall temperature by almost 15 degrees compared to the copper-based microchannel from Figure 8. As the thickness-to-particle-size ratio is between 2–5, the HTCs of the porous microchannels are significantly higher than that of the copper-based microchannel. As the δ/d is increased further up to 7, the enhancing effect of the porous microchannel becomes degraded, especially after a heat flux larger than 80 W/cm². After repeated measurements for other samples with a larger δ/d, it is concluded that the optimal thickness-to-particle-size ratio ranges from 2–5. This is consistent with the experimental results of Taiwan University [18]. Thus, the heat transfer performance of porous microchannels is mainly determined by the ratio of δ/d, rather than only by one of the parameters. There is a trade-off of multifaceted factors such as the liquid supply, nucleation process and bubble dynamics. For a certain particle diameter, the layer thickness, large or small, will be not favorable to the improvement of the HTC in a microchannel.

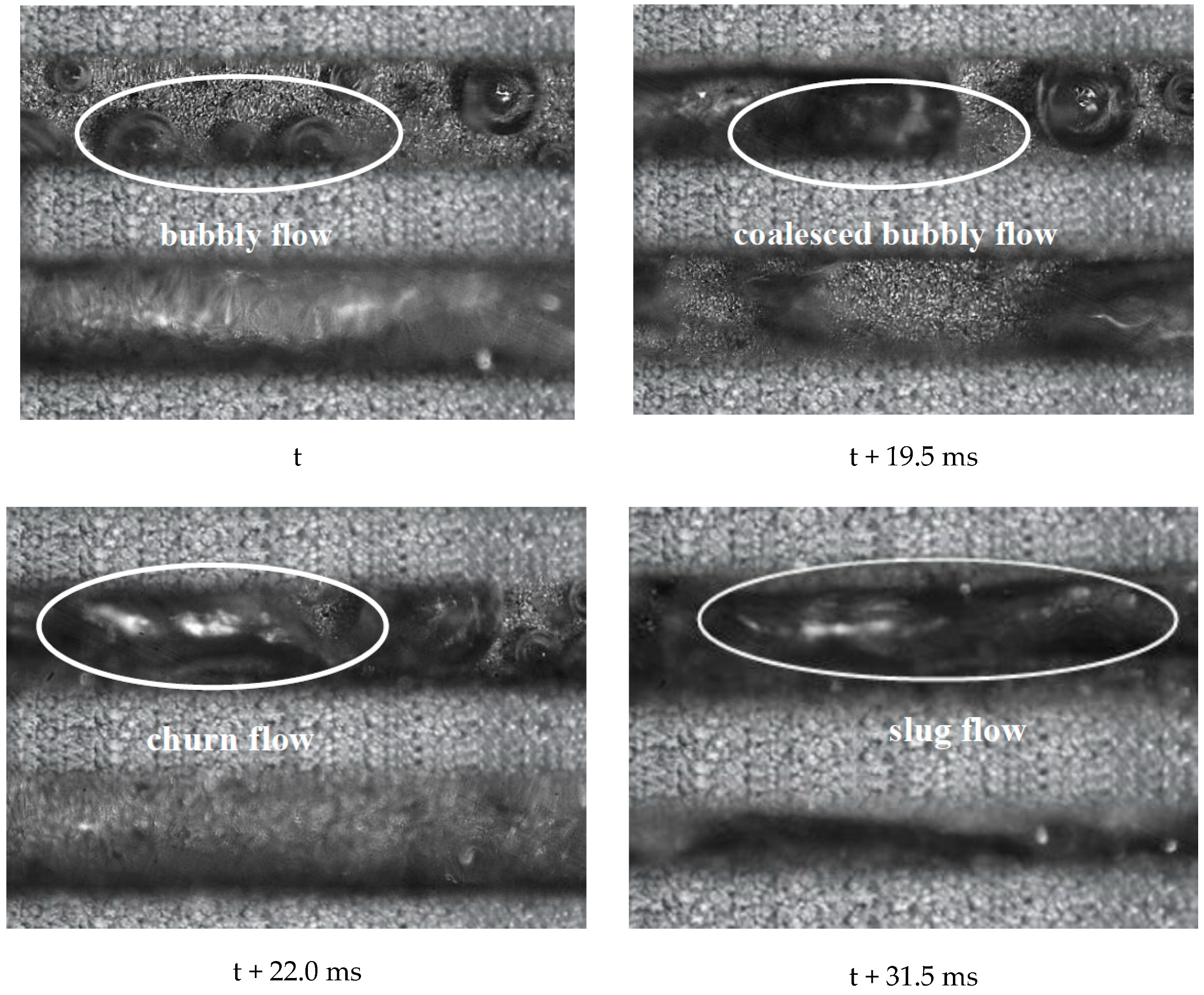
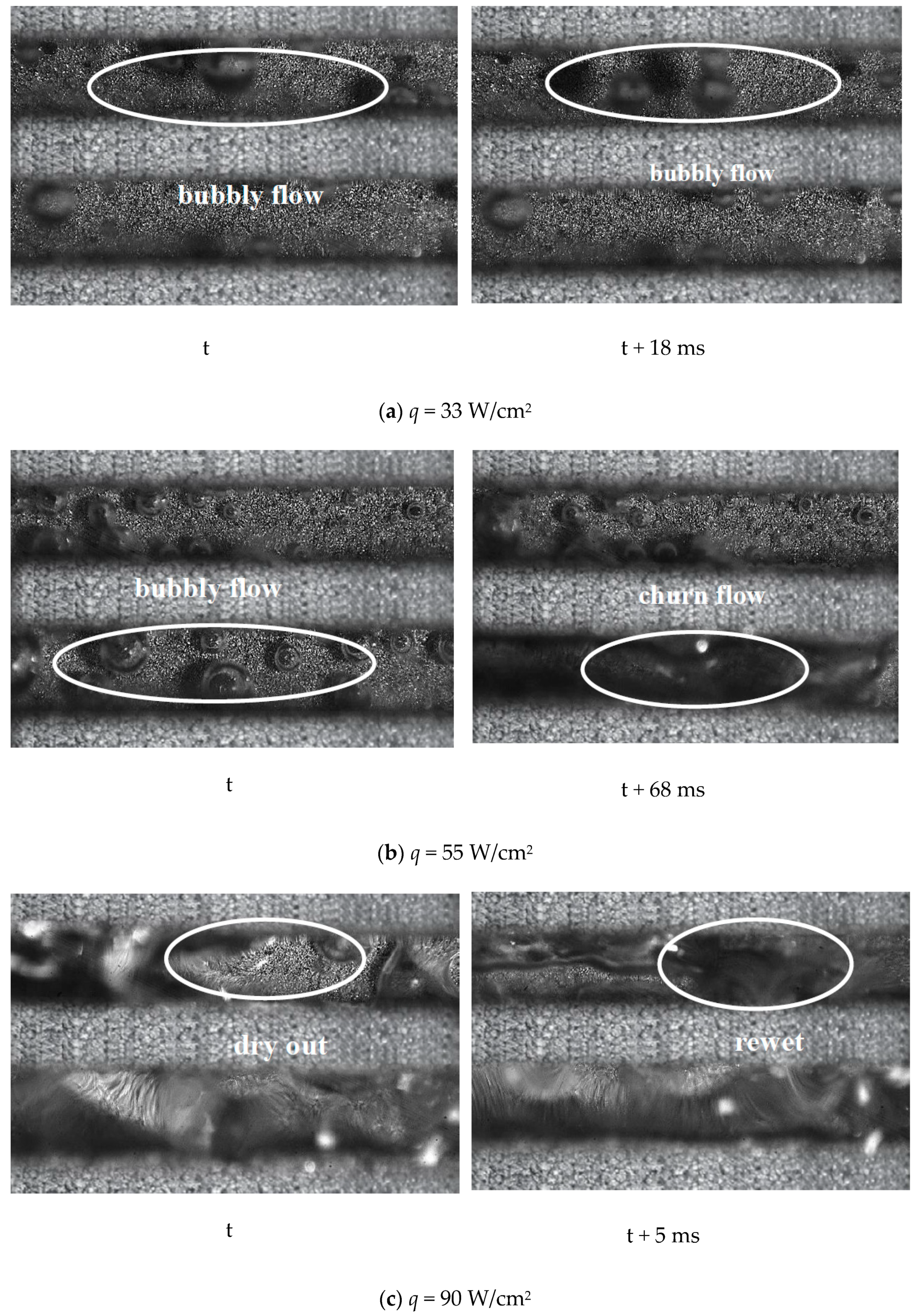
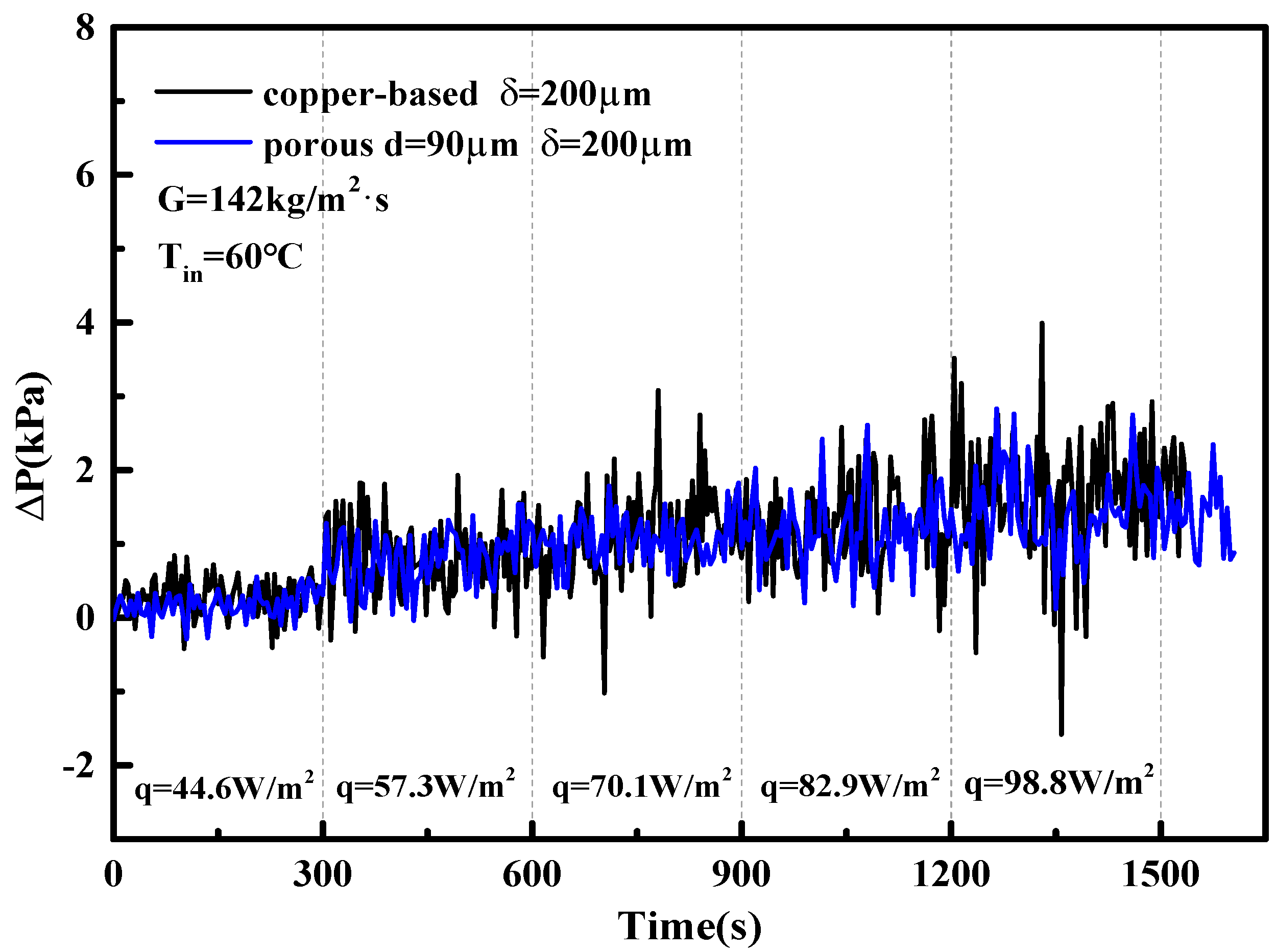
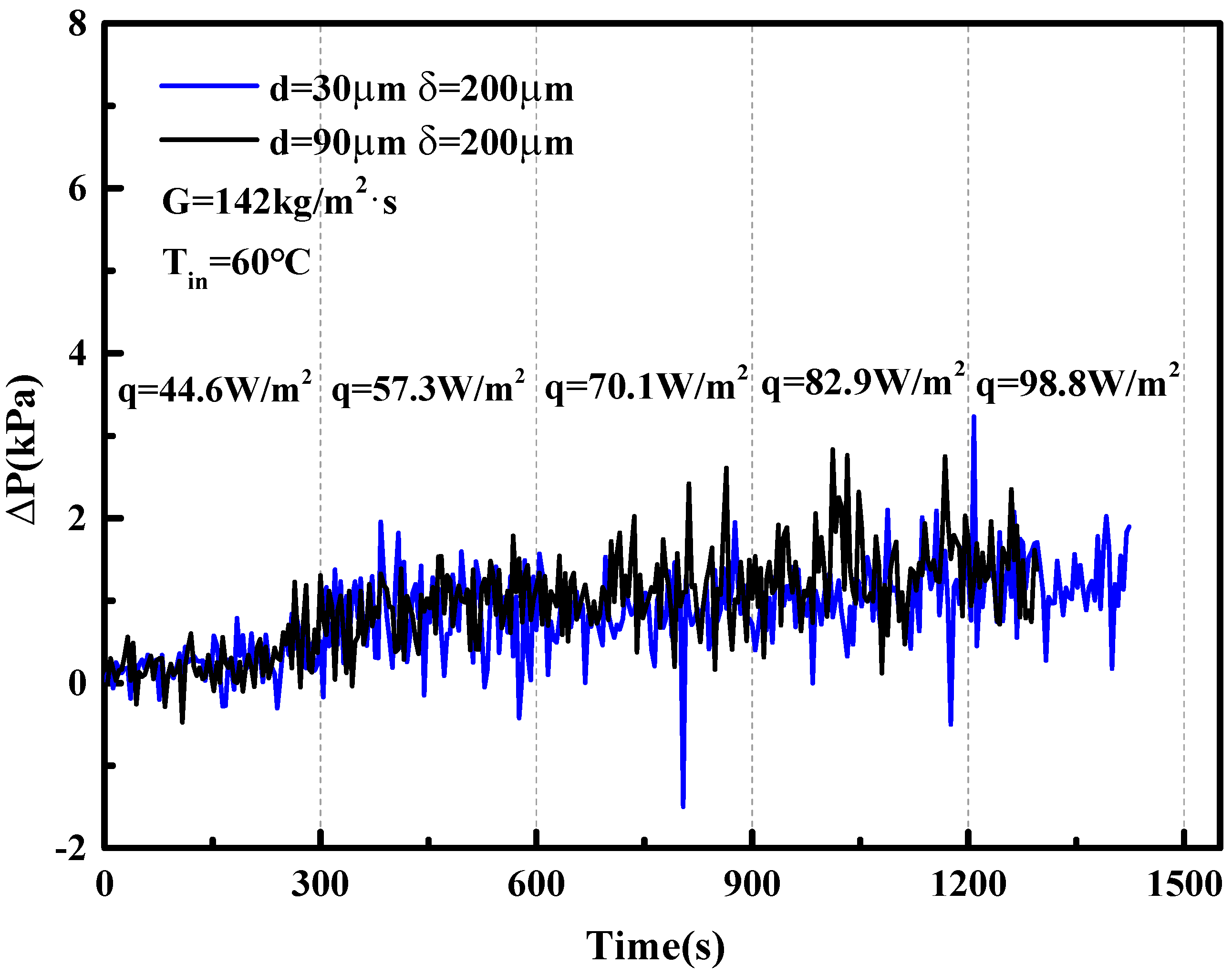
5. Two-Phase Flow Instability of Porous Microchannel

The boiling instability phenomenon is of concern in the microchannel phase-change system and could cause the severe fluctuation of the flow rate and wall temperature of the heat sink. The main sources of boiling instability include the upstream compressible instability and parallel channel interaction [1,2]. This limits the practical application of the microchannel phase-change cooling system. As discussed previously, the porous microchannel may facilitate the mitigation of the boiling instability. In our experiment, porous structural parameters on the flow boiling instability in the microchannel were investigated in detail.

The comparison of the pressure drop fluctuation between both kinds of microchannels is illustrated in Figure 10 at G = 142 kg/m²·s and T_in = 60 °C. The porous microchannel could suppress the flow pulsation of the boiling process significantly. With the increase in the heat flux, the fluctuation amplitude of the pressure drop increases gradually for the copper-based sample but remains almost invariable for the porous microchannel. The maximum fluctuation amplitude is about 6.0 kPa in the copper-based microchannel but only 3.0 kPa in the porous microchannel. Under the same inlet condition, the porous microchannel can reduce the pressure fluctuation by 50% more than the copper-based microchannel. As observed in [15], the bubble discharge diameter in a porous surface is only about 40–50% of that in a copper surface, and the bubble discharge frequency increases by about 2 times at most. It is helpful to establish a steadier boiling process by reducing the bubble coalescence effect. Moreover, the surface of the porous channel can be viewed as a permeable wall. Such a kind of surface could alleviate the pressure fluctuation effectively as the coalesced bubbles expand both in upstream and downstream directions.

Figure 11 shows the pressure drop fluctuation of two porous microchannels (d = 30 μm and 90 μm while δ = 200 μm); the corresponding thickness-to-particle-size ratios are 2 and 7, respectively. The pressure drop fluctuation begins to increase when the heat fluxes are larger than 80 W/cm². The maximum amplitude of the porous sample of d = 90 μm is about 2.0 kPa, while that of the sample of d = 30 μm is about 4.0 kPa. As shown in Figure 8, the sample with d = 90 μm and δ = 200 μm shows better heat transfer performance than the sample with d = 30 μm and δ = 200 μm within the range of q = 20–80 W/cm². This also reveals the relation between the boiling heat transfer performance and pressure fluctuation indirectly. The mechanism of how the δ/d affects the boiling heat transfer process is still not fully understood. The thickness-to-particle-size ratio could be considered as the ratio of the heat transfer area to the flow resistance of liquid and vapor. For a certain particle diameter, an excessive thickness of the porous layer causes serious difficulties for the liquid supply and bubble discharge, while overly thin layers result in an insufficient heat exchange area. A clarification of this mechanism is still required.

6. Conclusions

The subcooling flow boiling heat transfer of porous microchannels was investigated in detail, under three different mass fluxes at a 60 °C inlet fluid temperature. The key findings from present study are summarized as follows:

• The wall superheats for the boiling incipience in porous microchannels were much lower than in the copper-based one. The HTC of the porous microchannel was significantly higher than that of the copper-based microchannel at low and moderate heat fluxes. At high heat flux, the heat transfer performance of the porous samples approached that of the copper-based microchannel.
• The boiling heat transfer mechanism in the porous microchannel was mainly governed by the nucleate boiling mode, and the HTC was determined only by heat flux under low and moderate heat flux. Up to high flux condition, the heat transfer mechanism in the porous microchannel was converted into convection boiling mode; thus, the HTCs were dependent on both the flow velocity and heat flux.
• The optimal thickness-to-particle-size ratio ranged between 2–5 for porous microchannels. As the δ/d was further increased up to 7, the enhancing effect of the porous microchannel became degraded.
• The porous microchannel could suppress the flow fluctuation from low to moderate heat fluxes. The bubble coalescence effects in porous microchannels were less than in the copper-based microchannel. Porous microchannels were helpful to establish a stable nucleate boiling process; this was the typical mechanism for the porous microchannel to alleviate the flow fluctuation.

In subsequent study, an exploration of how to enhance convection boiling performance at high heat flux for a porous microchannel is required.