Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows
Abstract
:1. Introduction
2. Numerical Model
2.1. Homogenous Condensation
2.2. Heterogeneous Condensation
3. Internal Flow
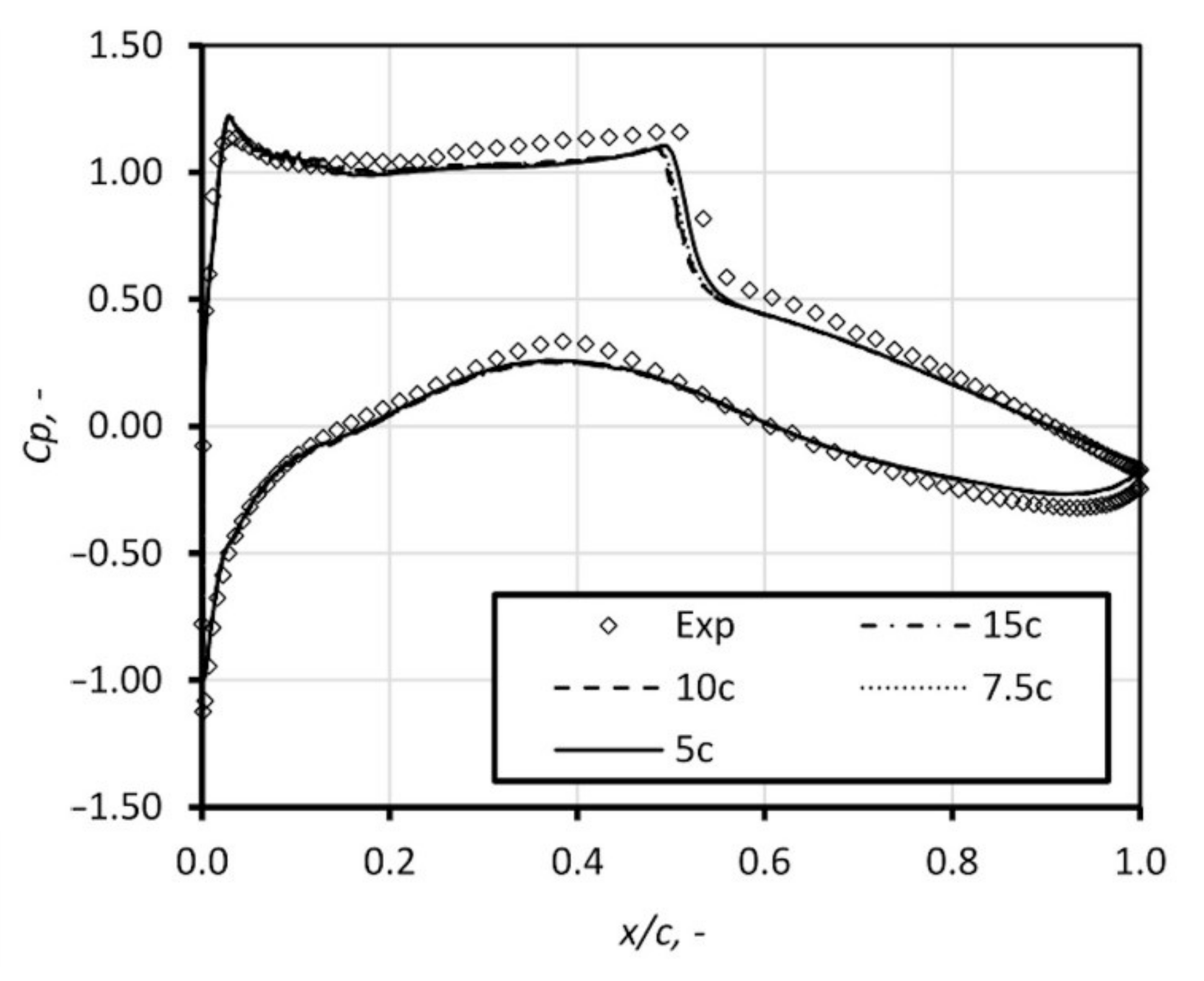
3.1. Circular Nozzle
3.2. Parallel Nozzle
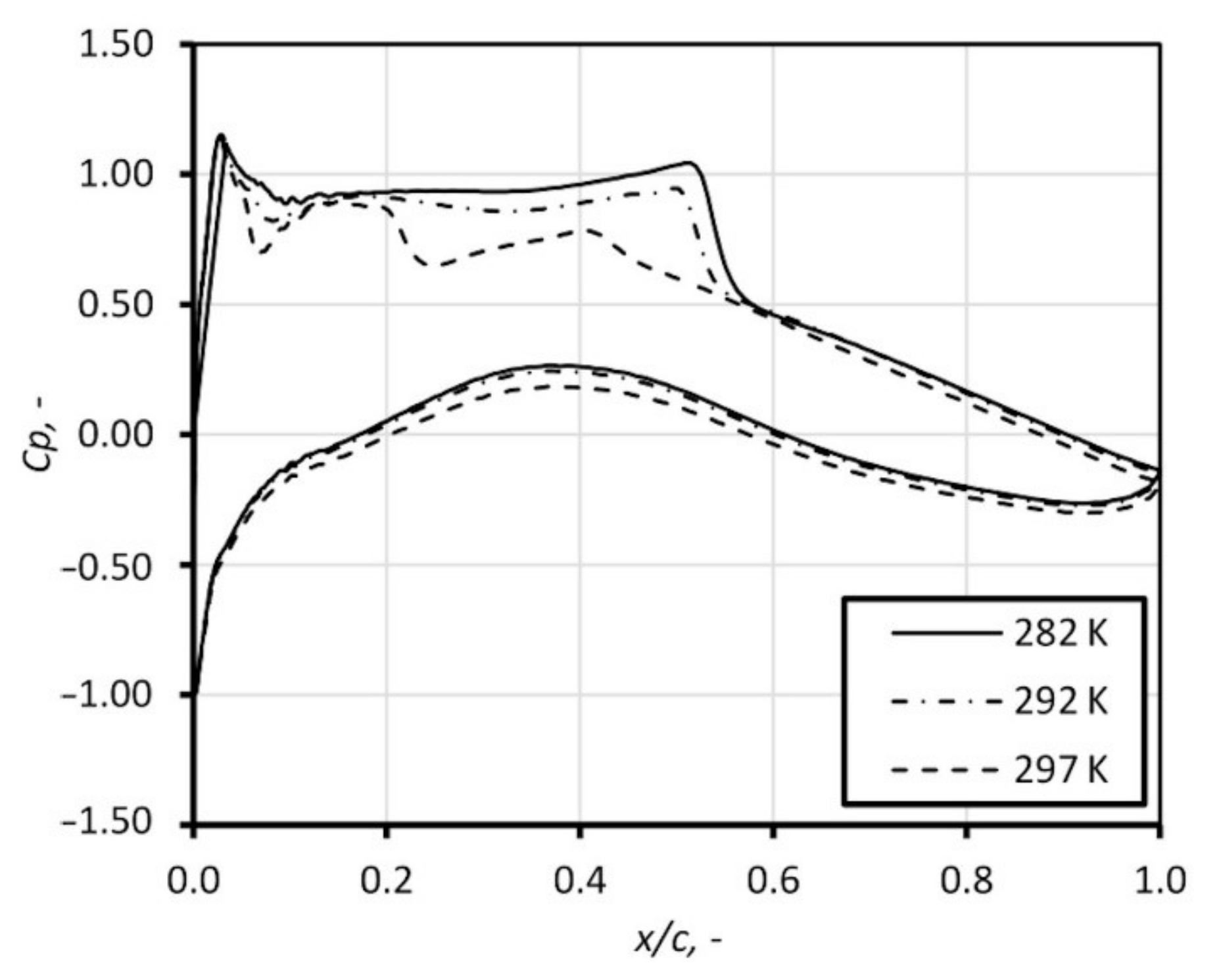
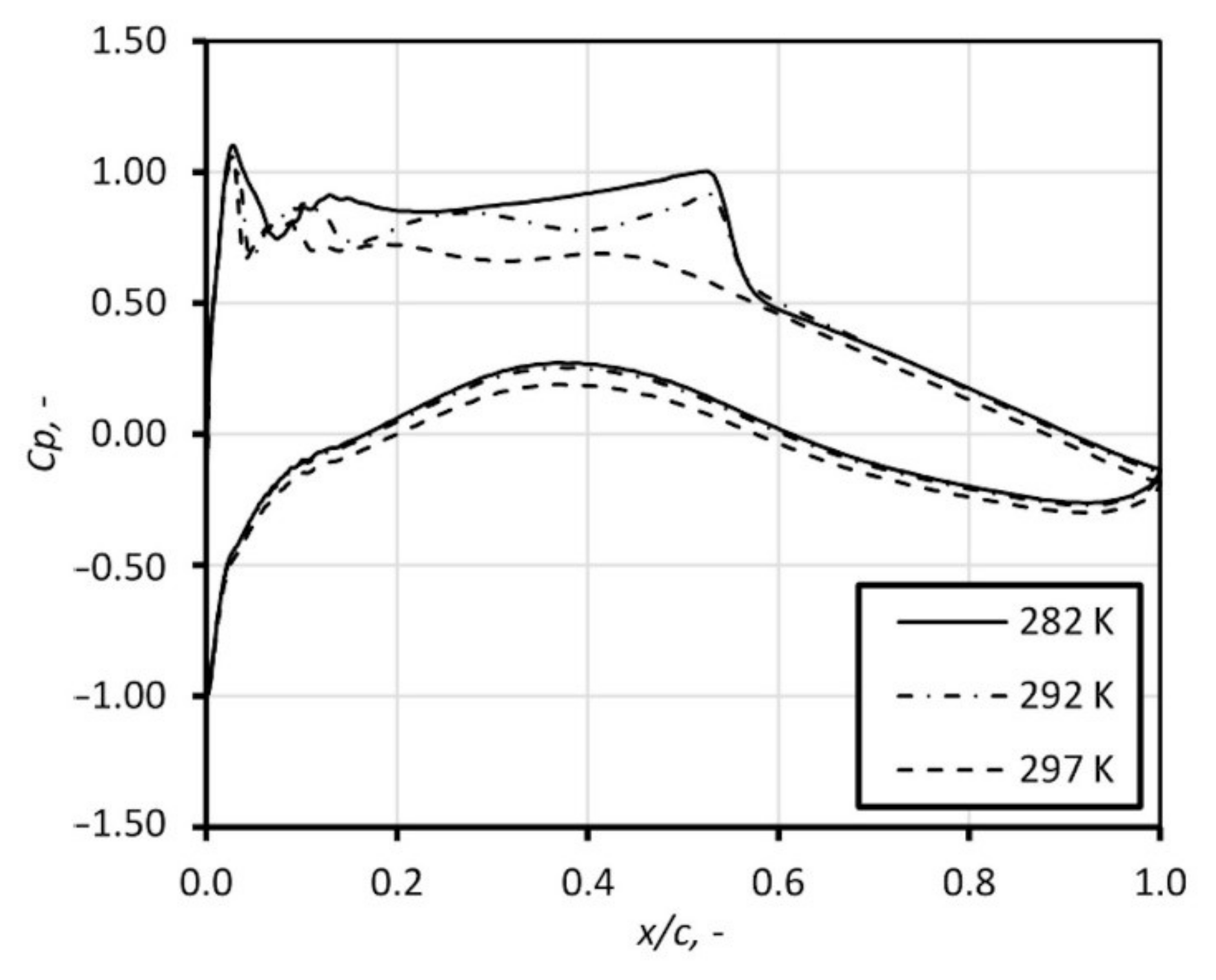
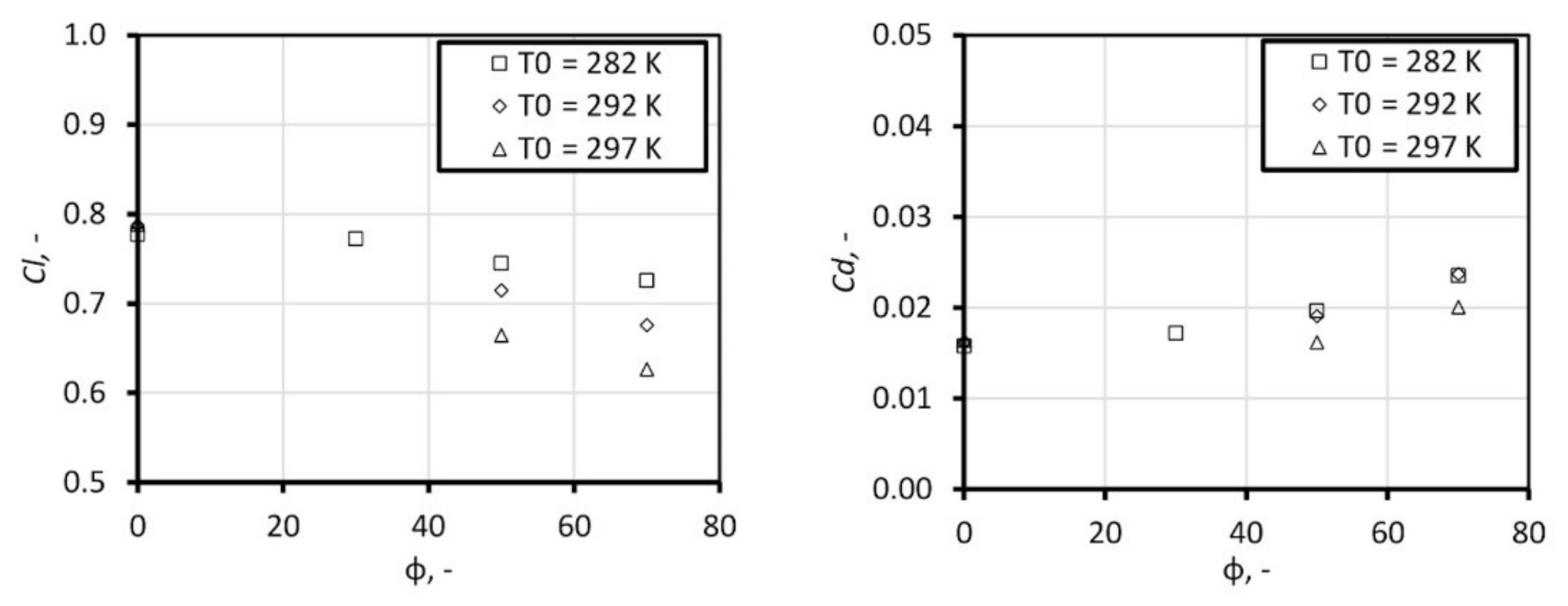
4. External Flow
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yammamoto, S.; Hagari, H.; Murayama, M. Numerical simulation of condensation around the 3-D Wing. Trans. Jpn. Soc. Aeronaut. Space Sci. 2000, 42, 182–189. [Google Scholar]
- Schnerr, G.H.; Mundinger, G. Similarity, drag, and lift in transonic flow with given internal heat addition. Eur. J. Mech. B Fluids 1993, 12, 597–611. [Google Scholar]
- Schnerr, G.H.; Dohrmann, U. Transonic flow around airfoils with relaxation and energy supply by homogeneous condensation. AIAA J. 1990, 28, 1187–1193. [Google Scholar] [CrossRef]
- Adam, S. Numerische und Experimentelle Untersuchung Instationarer Dusenstromungen mit Energiezufuhr Durch Homogene Kondensation; Universität Karlsruhe: Karlsruhe, Germany, 1996. [Google Scholar]
- Dykas, S.; Majkut, M.; Smołka, K. Influence of air humidity on transonic flows with weak shock waves. J. Therm. Sci. 2019. [Google Scholar] [CrossRef] [Green Version]
- Goodheart, K.A. 3-D Transonic Flow Dynamics with Nonequilibrium Condensation Munich; Universitätsbibliothek der TU München: München, Germany, 2004. [Google Scholar]
- Karabelas, S.J.; Markatos, N.C. Water vapor condensation in forced convection flow over an airfoil. Aerosp. Sci. Technol. 2008, 12, 150–158. [Google Scholar] [CrossRef]
- Dykas, S. Badania Przepływów Transonicznych z Kondensacją Pary Wodnej; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2006. [Google Scholar]
- Cook, P.H.; McDonald, M.A.; Firmin, M.C. Aerofoil Rae 2822: Pressure Distributions, and Boundary Layer and Wake Measurements, Experimental Data Base for Computer Program Assessment; AGARD Report ar 138; AGARD: Neuilly sur Seine, France, 1979. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Dykas, S.; Majkut, M.; Smołka, K.; Strozik, M. Analiza Zjawisk Cieplno-Przepływowych W Okołodźwiękowych Przepływach Powietrza Wilgotnego w Dyszach; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2017. [Google Scholar]
- Dykas, S.; Majkut, M.; Smołka, K.; Strozik, M. Numerical analysis of the impact of pollutants on water vapour condensation in atmospheric air transonic flows. Appl. Math. Comput. 2018, 338, 451–465. [Google Scholar] [CrossRef]
- Dykas, S.; Majkut, M.; Smołka, K.; Strozik, M. Comprehensive investigations into thermal and flow phenomena occurring in the atmospheric air two-phase flow through nozzles. Int. J. Heat Mass Transf. 2017, 114, 1072–1085. [Google Scholar] [CrossRef]
- Frenkel, J. Kinetic Theory of Liquids; Dover: New York, NY, USA, 1955. [Google Scholar]
- Kantrowitz, A. Nucleaton in very rapid vapor expansions. J. Chem. Phys. 1951, 19, 1097–1100. [Google Scholar] [CrossRef]
- Główny Inspektorat Ochrony Środowiska (Chief Inspectorate for Environmental Protection). 2020. Available online: https://powietrze.gios.gov.pl/pjp/content/annual_assessment_air_acceptable_level?lang=pl (accessed on 27 April 2020).
- World Health Organization. 2020. Available online: https://www.who.int/news-room/fact-sheets/detail/ambient-(outdoor)-air-quality-and-health (accessed on 27 April 2020).
- Chris, N.; Julianne, D. NPARC Alliance Validation Archive. 2008. Available online: https://www.grc.nasa.gov/WWW/wind/valid/raetaf/raetaf05/raetaf05.html (accessed on 23 April 2020).
- TU Berlin. Available online: https://www.cfd.tu-berlin.de/research/thermofluid/transport/node6.html (accessed on 27 April 2020).

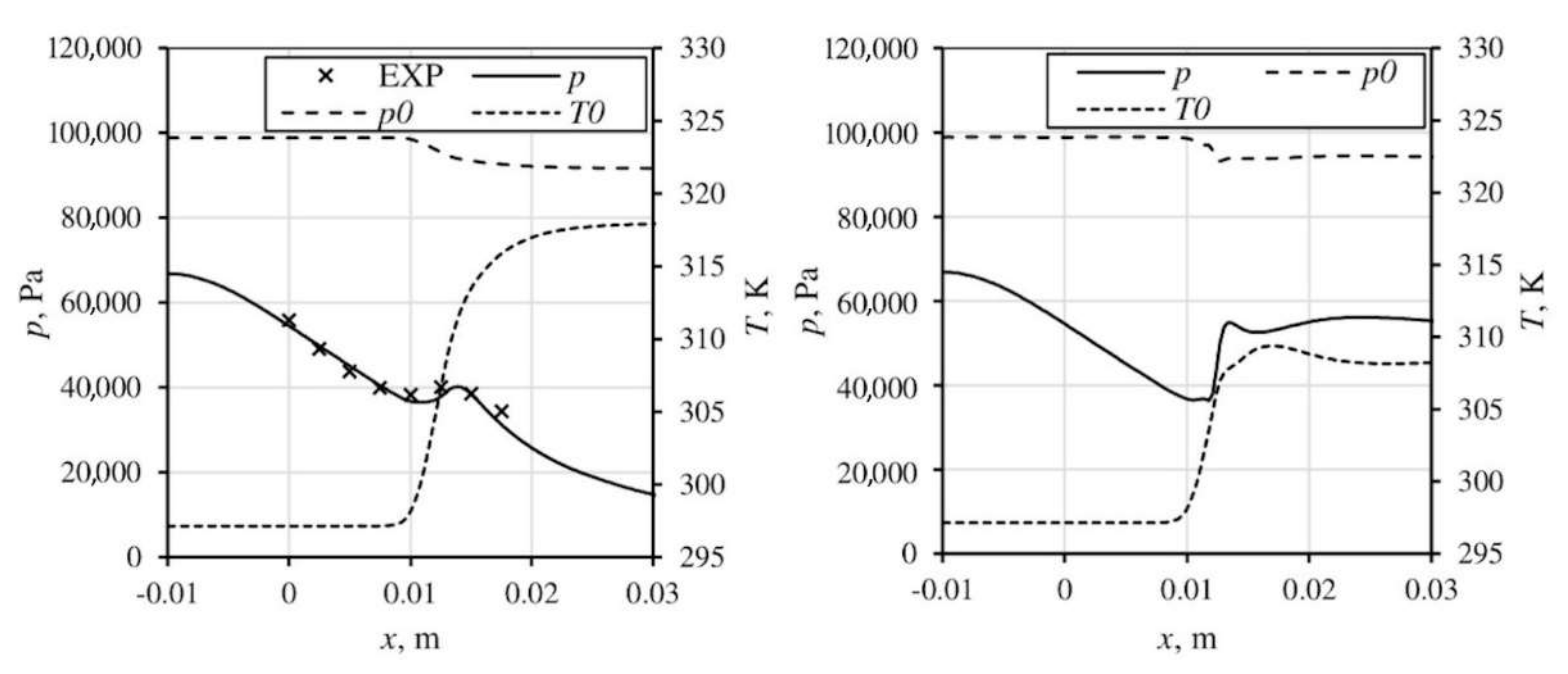
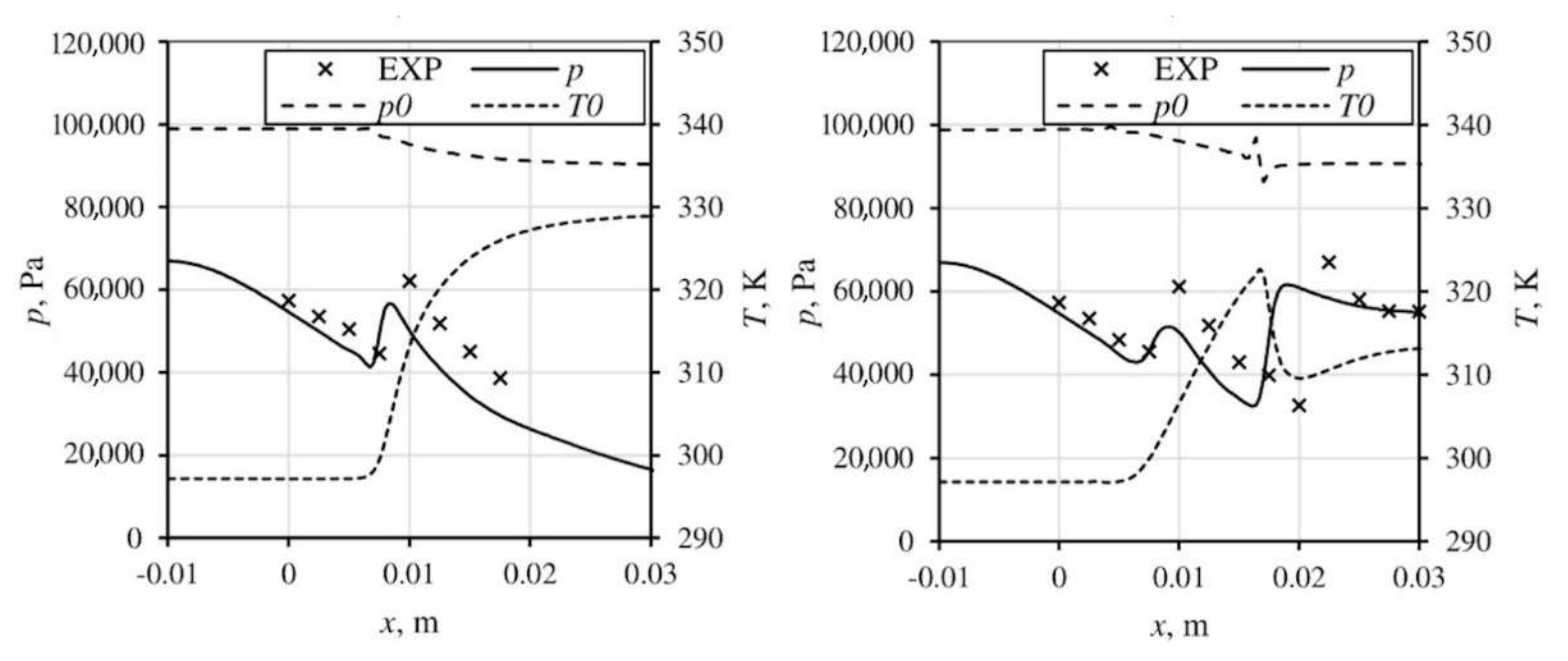
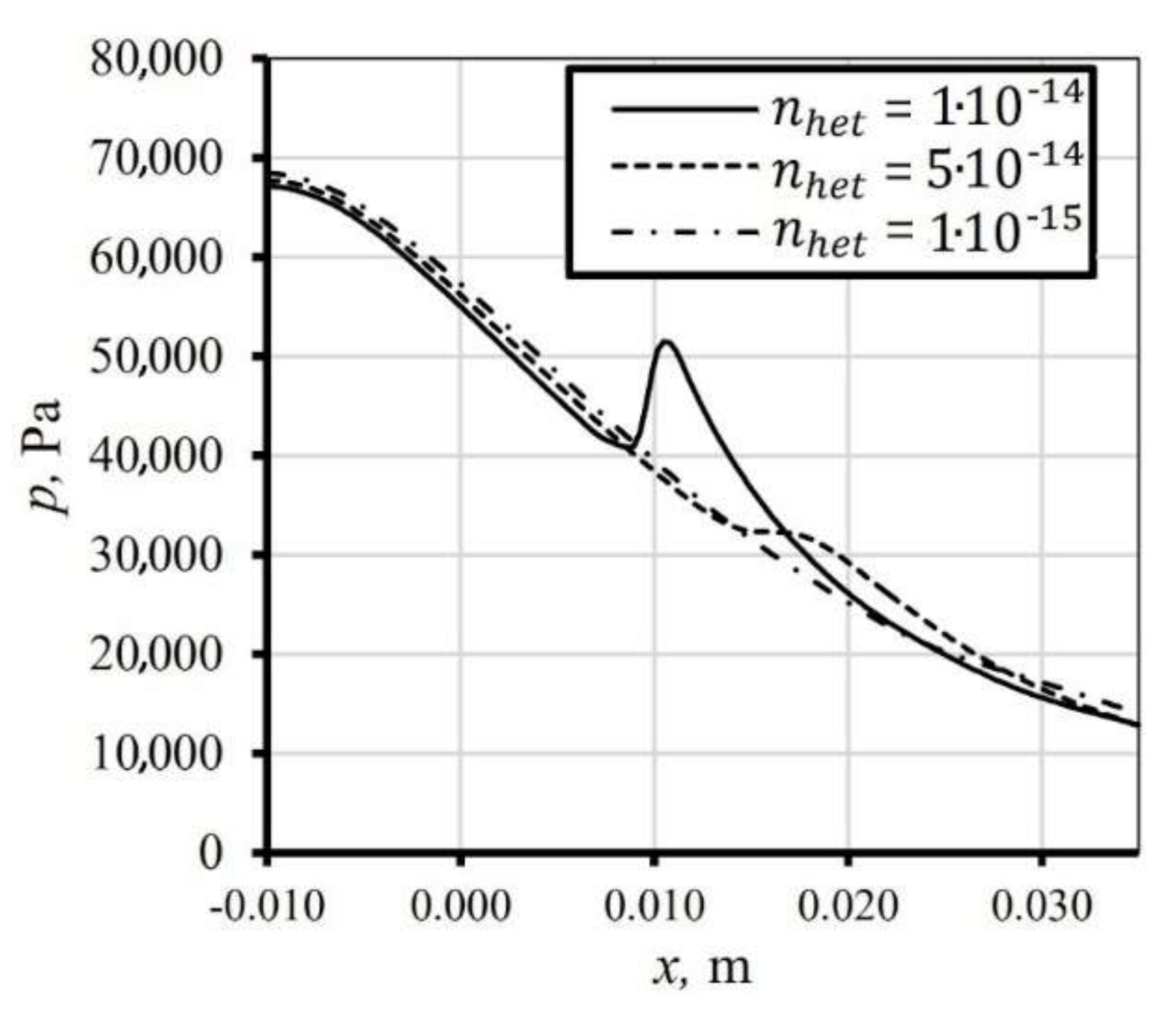
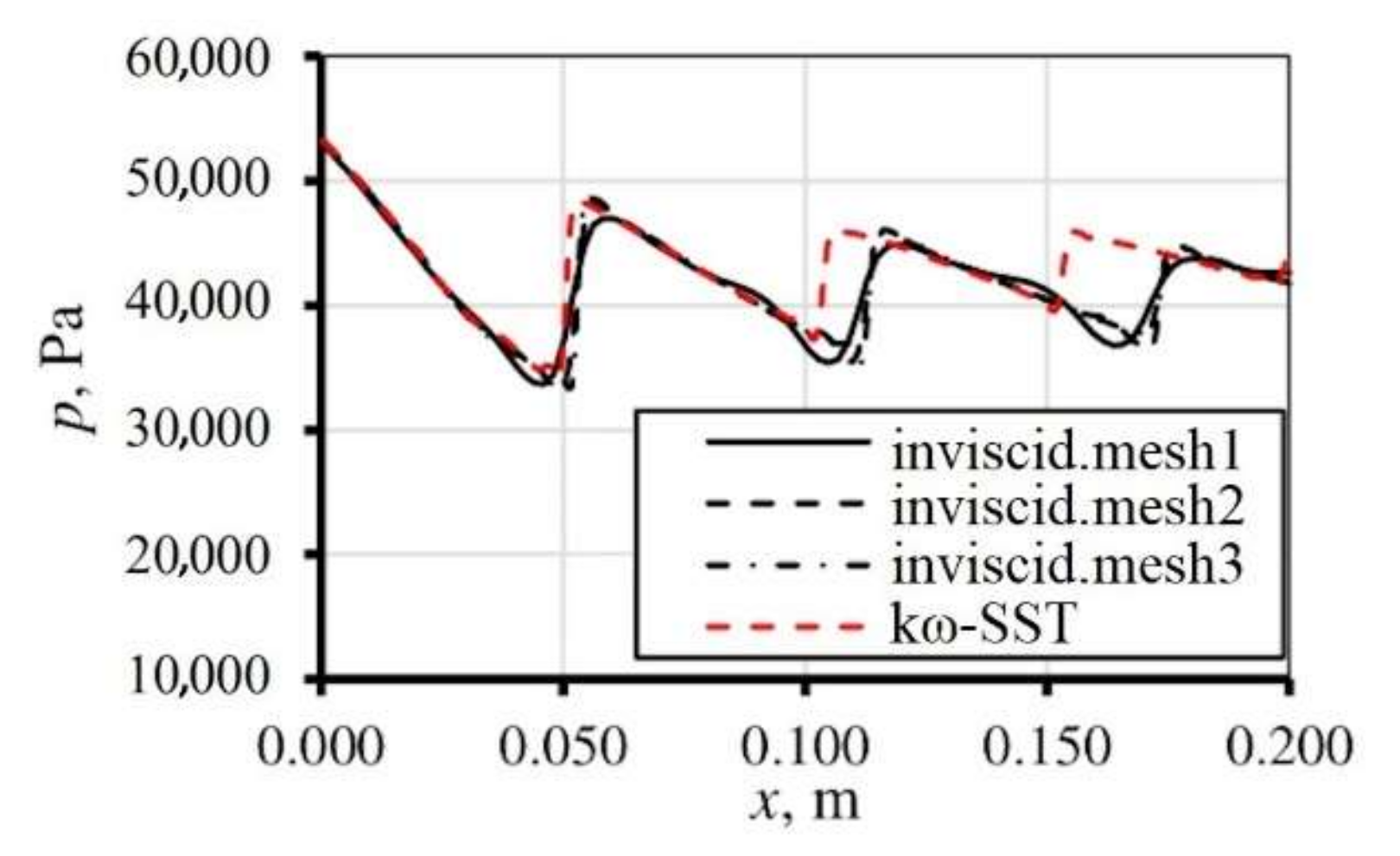


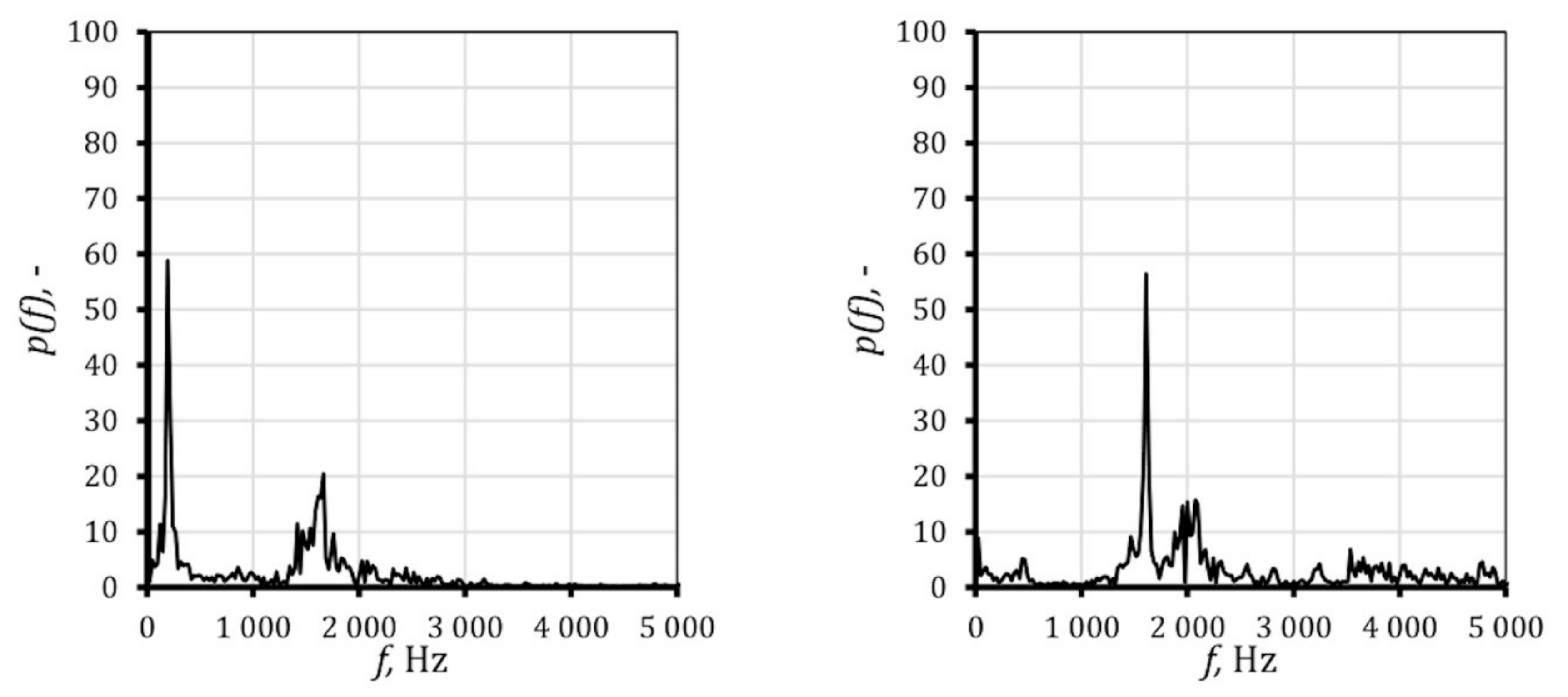


| T01, K | p01, Pa | φ, % | fexp, Hz | finvis, Hz | fkω-SST, Hz |
|---|---|---|---|---|---|
| 292.8 | 99,800 | 51.6 | 225 | 195 1661 | 1610 |
| 288.2 | 100,000 | 82.0 | 905 | 984 | 984 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiśniewski, P.; Dykas, S.; Yamamoto, S. Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows. Energies 2020, 13, 3153. https://doi.org/10.3390/en13123153
Wiśniewski P, Dykas S, Yamamoto S. Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows. Energies. 2020; 13(12):3153. https://doi.org/10.3390/en13123153
Chicago/Turabian StyleWiśniewski, P., S. Dykas, and S. Yamamoto. 2020. "Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows" Energies 13, no. 12: 3153. https://doi.org/10.3390/en13123153
APA StyleWiśniewski, P., Dykas, S., & Yamamoto, S. (2020). Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows. Energies, 13(12), 3153. https://doi.org/10.3390/en13123153






