Development of Future Compact and Eco-Friendly HVDC Gas-Insulated Systems: Shape Optimization of a DC Spacer Model and Novel Materials Investigation

Abstract

Testing and validating the electrical insulation performance of full-size compact high-voltage direct current (HVDC) gas-insulated systems, gas-insulated transmission lines (GIL) and gas-insulated switchgears (GIS) is very costly and take long time. Therefore, a reduced scale system was designed and constructed to study thoroughly the spacer’s performance when subjected to higher electric fields under HVDC with different shapes, made of new advanced materials, and housed in new SF₆-free gas environment. Since the stationary DC electric field distribution along the spacer is controlled by spacer material conductivity and strongly depends upon its shape, this, the first part of two articles, proposes in a first step based on electric field calculations with COMSOL Multiphysics software, an optimized shape of a spacer model using a standard high-voltage alternating current (HVAC) alumina-filled epoxy material. Then, two novel types of materials were introduced and investigated: (i) modified filled epoxy material with a lower temperature-dependent conductivity than that of the standard HVAC material, which is interpreted by a lower thermal activation energy; and (ii) nonlinear resistive field grading material with a low nonlinearity coefficient, with and without the presence of a temperature gradient which occurs under operating service load. The numerical results show that, despite that the DC optimized profile of the spacer made of standard HVAC, alumina-filled epoxy is very effective in relaxing the electric field magnitudes along the spacer under uniform temperature—its distribution is significantly affected by the presence of a high temperature gradient causing the maximum electric field shifts along the spacer surface towards the earthed flange. Under this condition, the modified filled epoxy material with a weaker temperature-dependent conductivity results in a significant reduction of the electric field enhancement, representing thus a relevant key solution for HVDC GIL/GIS applications. Nonlinear resistive field grading material is also effective but seems unnecessary. The optimized DC spacer models are being fabricated for tests verification with C4-Perfluoronitrile (C4-PFN, 3M^TM Novec^TM 4710)/CO₂ and Trifluoroiodomethane (CF₃I)/CO₂ gas mixtures in the reduced scale gas-insulated test prototype.

1. Introduction

While high voltage gas-insulated switchgears (GIS) and gas-insulated transmission lines (GIL) have been in use for high-voltage alternating current (HVAC) electricity transmission for more than 50 years, they cannot be used for high-voltage direct current (HVDC) applications and they are currently being developed for operation under 500 kV and higher voltage levels. The main reason is that the electric field distribution within the insulation of GIL/GIS, which consists of SF₆ gas and epoxy insulators (also called spacers) employed to separate gas compartments and to provide mechanical support for high-voltage (HV) conductors, is controlled by their permittivity (ε_SF6, ε_insulator) during HVAC operation, since the electric field distribution is derived from the relation: div (ε·E) = 0 (no free charges are initially present) and the permittivity does not change or varies weakly with temperature. Conversely, the electric field distribution in the case of HVDC operation is controlled by the electric conductivity, σ, of the SF₆ gas and the epoxy insulators through the formula div (σ·E) = 0, where σ depends strongly on temperature.

Furthermore, besides the electric conductivity effect, the shape of the solid epoxy spacer influences significantly the distribution of the electric field resulting in local electric field intensification in the gas at the gas–spacer interface and particularly at the contacts: the HV conductor/grounded enclosure-gas-epoxy spacer, called triple junctions [1,2]. Consequently, the spacer shape must be optimized in a suitable manner for HVDC operation and verified by testing.

On the other hand, even though the employed SF₆ gas is an excellent electrical insulating and arc extinguishing gas it is a potent greenhouse gas, and the reduction of its usage, which means developing compact GIL/GIS withstanding higher electric fields, and its replacement by other suitable alternative environmental gases are today of paramount importance. Recently, promising candidate substitutes to SF₆ have been found, such as Trifluoroiodomethane (CF₃I)-CO₂ gas mixture (its electric breakdown performance has been investigated by the authors’ group [3]); C5-perfluoroketone (C5-PFK, 3M^TM Novec^TM 5110); and C4-Perfluoronitrile (C4-PFN, 3M^TM Novec^TM 4710)-based gas mixtures with CO₂ or CO₂–O₂ [4]. A clearer understanding of the compatibility of these alternative gases with the spacer’s materials is essential to design reliable future eco-friendly HVDC compact gas-insulated systems.

Therefore, a reduced scale gas-insulated test setup was designed and constructed with the objective to investigate thoroughly HVDC spacer models with different appropriate shapes and made of novel epoxy-based materials by using CF₃I (30%)/CO₂ (70%) and C4-PFN (4%)/CO₂ (96%) gas mixtures, since the manufacturing of full-size spacers, their HV testing and validation in the full-size HVDC GIS/GIL arrangements are very expensive and take a long time. Such experimental investigation will bring useful information.

In [5], we presented our first results of the electric field analysis along an initial HVAC spacer model design under DC energization. The spacer was assumed of standard HVAC-filled epoxy and two nonlinear resistive field grading materials with high and small non-linearity.

The aim of this paper is to present, based on field calculations using COMSOL Multiphysics software, an optimized shape of a spacer model stressed by a DC voltage of 131.3 kV corresponding approximately to the voltage level of 500 kV of the full-size GIL/GIS; and to explore the effect of two novel types of epoxy-based materials which have not been yet investigated for such application: (i) modified filled epoxy with a lower temperature-dependent conductivity than that of the HVAC standard material expressed by a lower thermal activation energy; and (ii) nonlinear resistive field grading material with a moderate (less than 8) nonlinearity coefficient of its conductivity, with and without the presence of a temperature gradient that occurs when the GIL/GIS is under load operation. Furthermore, since under DC voltage charges tend to accumulate on the spacer’s surface and their amount can be deduced from the calculated electric fields, they are also presented and discussed in this work.

2. Initial Spacer Shape

The initial shape of the spacer model to be optimized for DC use is shown in Figure 1. It is based on a commercial conventional full-size cone spacer used in HVAC 420 kV gas-insulated system reduced to ¼ scale. Namely the dimensions of the full-size gas-insulated system with respect to the central conductor outer diameter (D_c), the enclosure inner diameter (D_E), and the spacer shape (thickness and height) are all downsized by a factor of ¼ (0.25).

It should be noted that the ¼-size gas-insulated system has been chosen to reproduce the design of the commercial full-size HVAC 420 kV GIL/GIS in such a way to obtain approximately the same applied electric fields at the central HV conductor and at the grounded enclosure that are respectively given by E_C = 2 V/[D_C·Ln (D_C/D_E)] and E_E = 2 V/[D_E·Ln (D_C/D_E)]. Furthermore, since our goal is to develop spacers for 500 kV DC GIL/GIS use, to be able to verify by HV testing the spacer models subjected to the voltage of 131.3 kV that corresponds approximately to 500 kV using our DC power supply, rated to 150 kV.

3. Electric Field and Surface Charges Calculations

The electric field magnitude, E, distribution around the spacer under stationary DC voltage is obtained from the following equations:

$$\mathrm{div}\overrightarrow{{\mathrm{J}}_{\mathrm{C}}}=\mathrm{div}\left(\mathsf{\sigma }\overrightarrow{\mathrm{E}}\right)=0,$$

(1)

$$\overrightarrow{\mathrm{E}}=-\mathrm{grad}\mathrm{V},$$

(2)

where $\overrightarrow{{\mathrm{J}}_{\mathrm{C}}}$ is the current density (A/m²), $\mathsf{\sigma }$ is the conductivity (S/m), V is the electric potential (V).

The steady-state accumulated charges on the spacer surface can be calculated directly from the obtained electric fields by using Gauss’s law as follows:

$${\mathsf{\rho }}_{\mathrm{S}}={\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{\mathrm{G}}{\mathrm{E}}_{\mathrm{GN}}-{\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{\mathrm{I}}{\mathrm{E}}_{\mathrm{IN}},$$

(3)

where ε_G is the relative permittivity of the gas, ε_I the relative permittivity of the spacer material and ε₀ the permittivity of vacuum. E_GN and E_IN are the normal components of the electric field in the gas side and the spacer side, respectively.

The values of the electric potential, V, are fixed on the central conductor (applied voltage) and on the enclosure (ground voltage) according to Dirichlet boundary conditions. Von-Neumann boundary conditions are used to specify the continuity of the normal derivative of the electric potential at the interface gas-epoxy spacer.

Since the electric conductivity of the spacer’s material varies with the temperature, the profile of this latter inside the reduced scale gas-insulated system must be first determined to get the electric field distribution. To simplify the calculations, heat transfer by thermal conduction through both the gas and the spacer under thermal steady state condition is considered according to Equation (4):

$$\mathrm{div}\left(\mathrm{k}\mathrm{gradT}\right)=0,$$

(4)

where k is the thermal conductivity (W/m·K)

The temperatures at the central HV conductor T_c and at the grounded enclosure T_e are given and lie within the permissible temperatures during HVDC GIS/GIL operation; namely, 105 °C at the HV conductor and 70 °C at the grounded enclosure.

4. Physical Properties of the HVDC GIS/GIL Insulation

4.1. Alternative Gas Mixture

Since we are intending to use CF₃I (30%)/CO₂ (70%) and C4-PFN (4%)/CO₂ (96%) gas mixtures, and so far there are no published information data available about the DC electrical conductivity, relative permittivity and thermal conductivity of these new gas mixtures, we have assumed in our calculations that their physical parameters are similar to those of SF₆, namely an electric conductivity of 10⁻¹⁸ S/m [6], a thermal conductivity of 0.0145 W/m·K and a relative permittivity of 1. It is noteworthy that in case the electric conductivity of the gas mixture might be higher, with a value up to 10⁻¹⁵ S/m for example, the final results of the electric field distribution would not be affected as we found in our published work [5].

4.2. Spacer’s Epoxy-Based Materials

Three types of epoxy-based materials were investigated: (i) conventional epoxy resin matrix filled with 60 to 66 wt.% of micro-sized alumina (Al₂O₃) commonly used in HVAC GIS/GIL systems, (ii) modified filled epoxy, and (iii) nonlinear resistive electric field grading material (FGM). Their thermal conductivity corresponds to 0.675 W/m·K [7], and the relative permittivity is equal to 5 for (i) and (ii) and to 10 for (iii). The electric conductivity of the materials is electric field and temperature dependent whose models are described below.

This investigation will allow us to determine which material type yields a better electric field distribution. Using numerical simulations, the most appropriate approach for the fabrication of DC spacer models can be selected and allow their tests verification in the reduced scale GIL/GIS.

4.2.1. Conventional Alumina-Filled Epoxy

According to published literature [8,9,10], the behavior of the DC electric conductivity with electric field and temperature, σ (E, T), of alumina-filled epoxy material has been found to be weakly dependent on the electric field up to 10 kV/mm and strongly dependent on temperature where the conductivity increases by 2 to 3 decades from 20 °C to the maximum operating temperature of 105 °C. In general, the conductivity is expressed by the following two empirical models:

$${\mathsf{\sigma }}_{\mathrm{Alumina}-\mathrm{filled}\mathrm{epoxy}}\left(\mathrm{E},\mathrm{T}\right)={\mathsf{\sigma }}_0{\mathrm{e}}^{\mathsf{\alpha }\mathrm{T}+\mathsf{\beta }\mathrm{E}},$$

(5)

$${\mathsf{\sigma }}_{\mathrm{Alumina}-\mathrm{filled}\mathrm{epoxy}}\left(\mathrm{E},\mathrm{T}\right)={\mathsf{\sigma }}_0{\mathrm{e}}^{-\frac{{\mathrm{W}}_{\mathrm{a}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}{\mathrm{e}}^{\mathsf{\beta }\mathrm{E}},$$

(6)

where β is the field dependency coefficient (mm/kV), α is the temperature dependency coefficient (K⁻¹), σ₀ is a specific conductivity constant (S/m), k_B is Boltzmann constant (eV/K), and W_a is the thermal activation energy (eV).

In this paper, the conductivity formula of Equation (6) is used, where the characteristics of the alumina-filled epoxy as function of E and T are shown in Figure 2 with σ₀ = 19.9 S/m, β = 0.08 mm/kV, W_a = 0.95 eV and K_B = 8.62 × 10⁻⁵ eV/K.

4.2.2. Modified Filled Epoxy

The modified filled epoxy material exhibits a lower increase of the electric conductivity with temperature compared to the conventional HVAC alumina-filled epoxy, which is represented by a decreased value of the thermal activation energy W_a. Indeed, for the development of HVDC cables, it has been found that improved cross-linked polyethylene (XLPE) based insulating materials with reduced temperature-dependent conductivity is one of the key solutions to obtain a desired electric field distribution compared to conventional HVAC XLPE materials [11]. Therefore, this approach is considered to verify whether the reduced temperature dependence of the conductivity could be also beneficial for the improvement of the filled epoxy materials for HVDC GIL/GIS applications.

Practically, such modified filled epoxy material can be obtained by careful selection and tuning the constituents of the epoxy material formulation: nature of the epoxy base resin, hardener type, catalyst, other additives as well as the type of filler (alumina, silica (SiO₂), etc.), its shape, size and concentration.

The behavior of the electric conductivity of the modified filled epoxy fits also the expression given in Equation (6) namely ${\mathsf{\sigma }}_{\mathrm{modified}\mathrm{filled}\mathrm{epoxy}}\left(\mathrm{E},\mathrm{T}\right)={\mathsf{\sigma }}_0{\mathrm{e}}^{-\frac{{\mathrm{W}}_{\mathrm{a}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}{\mathrm{e}}^{\mathsf{\beta }\mathrm{E}}$, where β = 0.08 mm/kV, W_a = 0.5 eV and σ₀ = 3.64 × 10⁻⁷ S/m. The latter was deduced from assuming that at 20 °C and under low applied electric field, its initial conductivity is equal to that of the conventional epoxy material. Figure 3 plots the electric conductivity of the modified filled epoxy as function of the electric field at 30 °C and 90 °C together with the conventional alumina-filled epoxy with W_a = 0.95 eV to show the difference of the electric conductivity increase with temperature between the two materials.

4.2.3. Nonlinear Resistive Field Grading Material (FGM)

Electric field grading materials are used to reduce the local enhancements of the electric field in high-voltage electrical apparatus. Nonlinear resistive electric field grading materials (FGM) are composite materials whose electric conductivity increases from a low value σ₀ at low electric fields to a high value at the switching field E₁ where the FGM becomes active. Among the mathematical models that describe such nonlinear behavior of σ_FGM (E), the following two expressions were reported [12,13]:

$${\mathsf{\sigma }}_{\mathrm{FGM}}\left(\mathrm{E}\right)={\mathsf{\sigma }}_{\mathrm{o}}\frac{1+{\left(\frac{\mathrm{E}}{{\mathrm{E}}_1}\right)}^{\mathsf{\gamma }-1}}{1+{\left(\frac{\mathrm{E}}{{\mathrm{E}}_2}\right)}^{\mathsf{\gamma }-1}},$$

(7)

$${\mathsf{\sigma }}_{\mathrm{FGM}}\left(\mathrm{E}\right)={\mathsf{\sigma }}_{\mathrm{o}}\frac{\sqrt[{\mathrm{N}}_1]{1+{10}^{\mathrm{mN}1\left(\mathrm{E}-{\mathrm{E}}_1\right)}}}{\sqrt[{\mathrm{N}}_2]{1+{10}^{\mathrm{mN}2\left(\mathrm{E}-{\mathrm{E}}_2\right)}}},$$

(8)

where σ₀ is the base conductivity (S/m), E₁ is the switching field strength (kV/mm), E₂ is the saturation field strength (kV/mm), γ and m are the slopes of nonlinearity, N₁ and N₂ are the smoothing parameters.

In this paper, the conductivity of Equation (7) is used. For the FGM to work, the base conductivity σ₀ should be higher than the conductivity of the adjacent gas insulation and its maximum value should not lead to excessive heat losses. The switching electric field strength, E₁, can be approximated to E = (applied voltage)/(spacer surface length). By considering the temperature effect, Equation (7) becomes:

$${\mathsf{\sigma }}_{\mathrm{FGM}}\left(\mathrm{E},\mathrm{T}\right)={\mathsf{\sigma }}_{\mathrm{o},\mathrm{T}}{\mathrm{e}}^{-\frac{{\mathrm{W}}_{\mathrm{a}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\frac{1+{\left(\frac{\mathrm{E}}{{\mathrm{E}}_1}\right)}^{\mathsf{\gamma }-1}}{1+{\left(\frac{\mathrm{E}}{{\mathrm{E}}_2}\right)}^{\mathsf{\gamma }-1}},$$

(9)

where σ_0,T is the specific conductivity constant (S/m).

Among the different composite electric field grading materials that have been investigated for use in HVDC GIL/GIS applications, and which are still under development, there are: (i) zinc oxide (ZnO) microvaristor-filled epoxy material [14], which has a strong field dependence, or high nonlinearity coefficient (γ > 20), of its conductivity. However, ZnO microvaristor filler is composed of other metal oxides (Bi₂O₃, Sb₂O₃, etc.), requires a well-controlled sintering process at temperatures above 900 °C, and its fabrication is mastered by only few ZnO varistors manufacturers. (ii) Epoxy filled with Iriotec 7000 particles (Merck Global) that consist of flake shaped mica particles covered with a nanoscale semiconducting antimony doped tin oxide (ATO) layer [15]. This material shows a modest nonlinearity where the measured electric conductivity is in the range 10⁻¹³–10⁻¹¹ S/m. (iii) silicon carbide (SiC)/Al₂O₃-filled epoxy [16].

In this work, we are particularly interested in verifying the effectiveness of another novel FGM type with a moderate nonlinearity coefficient (γ < 8) that can be obtained by filling the epoxy resin matrix with two types of fillers (n/p doped semiconducting SiC with conducting/semiconducting bridging particles) namely doped SiC/CB (carbon black) or doped SiC/ATO. It should be noted that doped SiC/CB mixed with a rubber matrix was employed for electric field control in commercial HVDC cable accessories [17,18]. Such novel type of epoxy-based FGM has a nonlinear resistive conductivity σ_FGM (E, T) behavior that can match approximately the theoretical trend illustrated in Figure 4 where σ_0,T = 3.83 × 10⁻³ S/m, E₁ = 1 kV/mm, E₂ = 5 kV/mm, W_a = 0.5 eV, γ = 6.

5. Simulation Results

5.1. Optimization of DC Spacer Shape

In order to obtain the desirable shape of the spacer model minimizing local electric field enhancements at the critical regions under DC voltage, the following optimization criteria were considered when applying a direct voltage of 131.3 kV corresponding approximately, as mentioned previously, to the voltage 500 kV of the full-size GIL/GIS:

• A minimum value of electric field magnitude at both the HV and the ground triple junctions (spacer–gas–HV conductor/grounded flange);
• A small normal electric field on the spacer surface in order to minimize surface charge accumulation as recommended in [19];
• Sufficient creepage distance to prevent surface flashover caused by a high tangential electric field;
• Minimized field enhancement along the spacer surface.

To fulfil these requirements, the geometrical modifications that have been carried out with respect to the initial shape and the flange (Figure 1) are shown in Figure 5, and they are as follow:

• Increasing the radius (R) of the flange corner;
• Introducing a small gas gap (g) at the spacer–flange interface to lower the electric field at the ground triple junction;
• Increasing the spacer thickness (T) at the HV conductor contact to reduce the electric field at the HV triple junction;
• Increasing the spacer inclination angle (θ) to lower the normal component of the electric field and, hence, minimize the surface charges accumulation;
• Varying the distance (s) between the end of the flange radius and the spacer;
• Varying the radius (r) of the spacer edge near the ground side.

It is important to recall that modifying the contact condition between the grounded flange and the epoxy spacer by the introduction of a gas gap (g) [20] and increasing the spacer inclination angle (θ) [21] has been found to be effective in avoiding local electric field intensification under DC voltage application.

COMSOL Multiphysics software was used to perform the numerical analysis of the electric field distribution and the geometrical optimization of the spacer model made of conventional HVAC alumina-filled epoxy with the electric conductivity behavior shown in Figure 3, under a uniform temperature set to T_c = T_e = 30 °C.

The optimization procedure has been performed without the use of any mathematical optimization algorithm but by using the parametric sweep method according to the following steps: (i) the selected geometrical controllable parameters (R, g, s, T, r, θ) are given with the ranges of their variation indicated in

Table 1. Controlled geometrical parameters and final optimized values.

Geometrical Parameter	Initial Value	Variation Range	Optimized Value
Flange radius (R)	0 mm	0–15 mm	15 mm
Gas gap (g)	0 mm	0–5 mm	5 mm
Distance (s)	0 mm	0–8 mm	4 mm
Thickness (T)	10 mm	10–25 mm	23 mm
Radius (r)	0 mm	0–5 mm	5 mm
Inclination angle (θ)	17°	17°, 45°, 60°	60°

; (ii) the electric field distribution along the spacer is calculated under DC voltage energization over the variation ranges of the geometrical parameters; (iii) the stored electric field distribution results are displayed and analyzed to find the optimum values whose electric field distribution matches the targeted requirements of Section 5. The obtained final optimized values are indicated in Table 1.

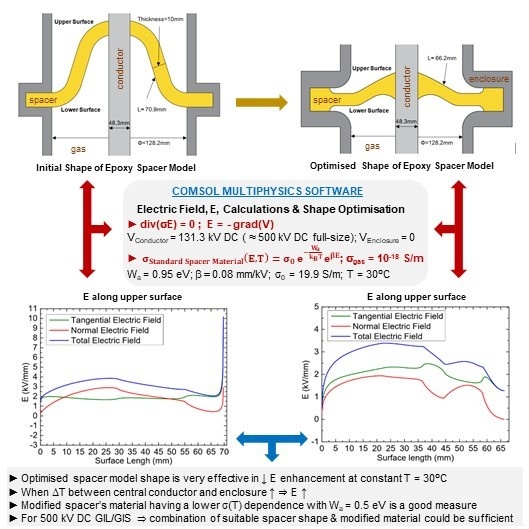
The resulting optimized configuration is illustrated in Figure 6, and the obtained results of its electric field distributions (tangential, normal and total) are illustrated in Figure 7a for the upper surface of the spacer and Figure 8a for the lower surface of the spacer in comparison with those of the initial spacer profile presented in Figure 7b and Figure 8b.

As can be seen in Figure 7b and Figure 8b of the spacer’s initial profile, the maximum electric field values at both upper and lower surfaces occur at the critical ground triple junction (gas–spacer–grounded flange) and are 10 kV/mm at the upper side and 8 kV/mm at the lower side, thus exceeding the maximum applied electric value of 5.6 kV/mm at the inner conductor, whereas the maximum electric field of the improved optimized spacer is not located at the critical ground triple junction and is much lower, with 3.4 kV/mm at the upper surface side and 3.2 kV/mm at the lower one (Figure 7a and Figure 8a). At the ground triple junction, the maximum electric field is 1.2 kV/mm and is lower than the ground applied electric field of 2.1 kV/mm. Furthermore, the maximum value of the normal component of the electric field which is responsible for surface charges accumulation is about 3 kV/mm for the initial shape, whilst it is 2 kV/mm for the optimized one.

5.2. Effects of the Spacer’s Material and Temperature Gradient on the Electric Field Distribution

To account for the load conditions of the DC GIS/GIL, the temperatures of the HV conductor T_c and the grounded flange T_e were set to 90 °C and 50 °C, respectively, with a temperature gradient ΔT = 40 °C. The calculated temperature distribution around the optimized spacer model is shown in Figure 9.

The results of the electric field distributions around the optimized spacer made of different types of epoxy-based materials at uniform temperature (30 °C) and in the presence of a temperature gradient of 40 °C are given in Figure 10.

As can be seen in Figure 10, the presence of a temperature gradient influences the electric field distribution around the spacer for all types of materials where the maximum electric field strength is shifted towards the grounded flange compared to the uniform temperature case ΔT = 0 °C. It is important to note that such a phenomenon of electric field displacement towards cooler regions where the electric conductivity is lower than the one of the warmer regions near the HV conductor is well known when HVDC GIL/GIS are under load operation, and this was reported in many works, such as [22].

However, a significant increase in the electric field is observed for the conventional HVAC alumina-filled epoxy. Furthermore, it is worth emphasizing that the electric field is also intensified at the flange’s rounded edges where it reaches 11.5 kV/mm instead of 3.5 kV/mm at the upper side and 10 kV/mm instead of 2.2 kV/mm at the lower side.

The total electric field E_total distributions along the upper surface of the optimized spacer model made of the AC standard alumina-filled epoxy material, the modified filled epoxy material and the FGM, are presented in Figure 11a,b for uniform temperature (ΔT = 0 °C) and temperature gradient (ΔT = 40 °C), respectively, under a DC voltage of 131.3 kV.

With a uniform temperature of 30 °C (Figure 11a), the obtained electric field distributions for the standard alumina-filled epoxy and the modified filled epoxy material are the same, since, as shown in Figure 3, both materials have the same weakly electric field-dependent conductivity (β = 0.08 mm/kV) and the conductivity difference at 30 °C for both materials is low. However, for the FGM, although the maximum value of the total electric field remained unchanged, the electric field at the ground triple junction is increased to 2.4 kV/mm compared to the other two materials, where it is 1.2 kV/mm.

In the presence of a high temperature gradient (ΔT = 40 °C), as can be seen in Figure 11b, the most relevant finding is that the use of modified filled epoxy material with the reduced temperature dependence of the conductivity represented by a lower thermal activation energy (W_a = 0.5 eV) compared with the conventional alumina-filled epoxy with W_a = 0.95 eV results in a significant reduction of the electric field enhancement. Compared with the standard alumina-filled epoxy, the maximum value of the total electric field is decreased from 6.5 kV/mm to 4.5 kV/mm without exceeding the maximum applied conductor electric field of 5.57 kV/mm. Furthermore, the electric field at the critical ground triple junction is lowered from 4.5 kV/mm to 2.8 kV/mm. The electrical field enhancement at the rounded edges of the flange is much improved, too (Figure 10). The FGM with a low nonlinearity coefficient does not add any further minimization of the electric field at the critical ground triple junction.

5.3. Surface Charges Accumulation

Figure 12a,b present the accumulated charges along the spacer’s upper surface under stationary DC applied voltage of 131.3 kV at a uniform temperature of 30 °C (ΔT = 0 °C) and a thermal gradient of ΔT = 40 °C between the central HV conductor (90 °C) and the earthed flange (50 °C), respectively, for the standard AC alumina-filled epoxy, modified filled epoxy and FGM. As can be seen, positive charges accumulate on the whole surface of the spacer. Numerical electric field computations and the use of Equation (3) to obtain the normal component of electric field at the gas side, E_GN, revealed that the highest values in regions where the electric conductivity is very low (10⁻¹⁸ S/m) and that, at the spacer side, E_IN is negligible. Furthermore, the direction of the normal electric field lines is outward, from the surface from the spacer towards the gas.

At uniform temperature, the maximum surface charge density is 34.2 µC/m² for both the standard AC alumina-filled epoxy and modified filled epoxy, since they have the same weak electric field-dependent conductivity, and 38.9 µC/m² for the FGM.

However, for ΔT = 40 °C, the surface charge density increases for the three materials (Figure 12b). Such impact of temperature gradient on surface charges accumulation on spacers has been also obtained in the thermo-electrical simulation investigation of the work on insulators in 500 kV DC-GIL [23].

The most significant increase concerns the standard AC alumina-filled epoxy material exhibiting a higher temperature-dependent electric conductivity (W_a = 0.95 eV) where the maximum surface charge density is more than two times larger (75.3 µC/m²) than without a thermal gradient (34.2 µC/m²). The surface charge density of modified filled epoxy with a weaker temperature-dependent electric conductivity (W_a = 0.5 eV) is reduced with a value of 51.4 µC/m² and of the FGM is 44.4 µC/m². This indicates that a weak dependence of the electric conductivity with temperature may be very effective in reducing surface charge formation under DC energization, and thus modified filled epoxy should be used in HVDC GIL/GIS spacers.

6. Conclusions

The relevant findings of this work can be summarized as follows:

• The geometrically optimized spacer model profile for DC operation is very effective in reducing the enhancement of the electric field at the critical locations where the resulting maximum electric field along the spacer is within the acceptable range.
• The presence of a high temperature gradient has a significant influence on the electric field distribution along the spacer and shifts the maximum electric field from the central HV conductor towards the grounded flange side. One of the key mitigations to reduce this electric field enhancement is by using new modified filled epoxy material with a weakly temperature-dependent conductivity, namely a lower thermal activation energy than that of the conventional AC alumina-filled epoxy.
• The increase in temperature gradient leads also to charge accumulation increase on the spacer surface with the highest surface charge density when using the AC standard material.
• A novel nonlinear resistive field grading material (FGM) with a moderate nonlinearity coefficient (γ < 8) is also effective but does not add further improvement.
• The most relevant finding is that once the spacer profile had been initially well optimized for DC energization the use of modified filled epoxy may be sufficient for 500 kV DC GIL/GIS applications, provided that the maximum temperature gradient (ΔT) during load operation is not very high.
• Current and future work involves the fabrication and testing of the optimized scaled DC spacer. The scaled GIL/spacer will be experimentally characterized with alternative gases mixtures using CF₃I/CO₂ and C4-PFN/CO₂.