Development of Test-Bed Controller for Powertrain of HEV
Abstract
:1. Introduction
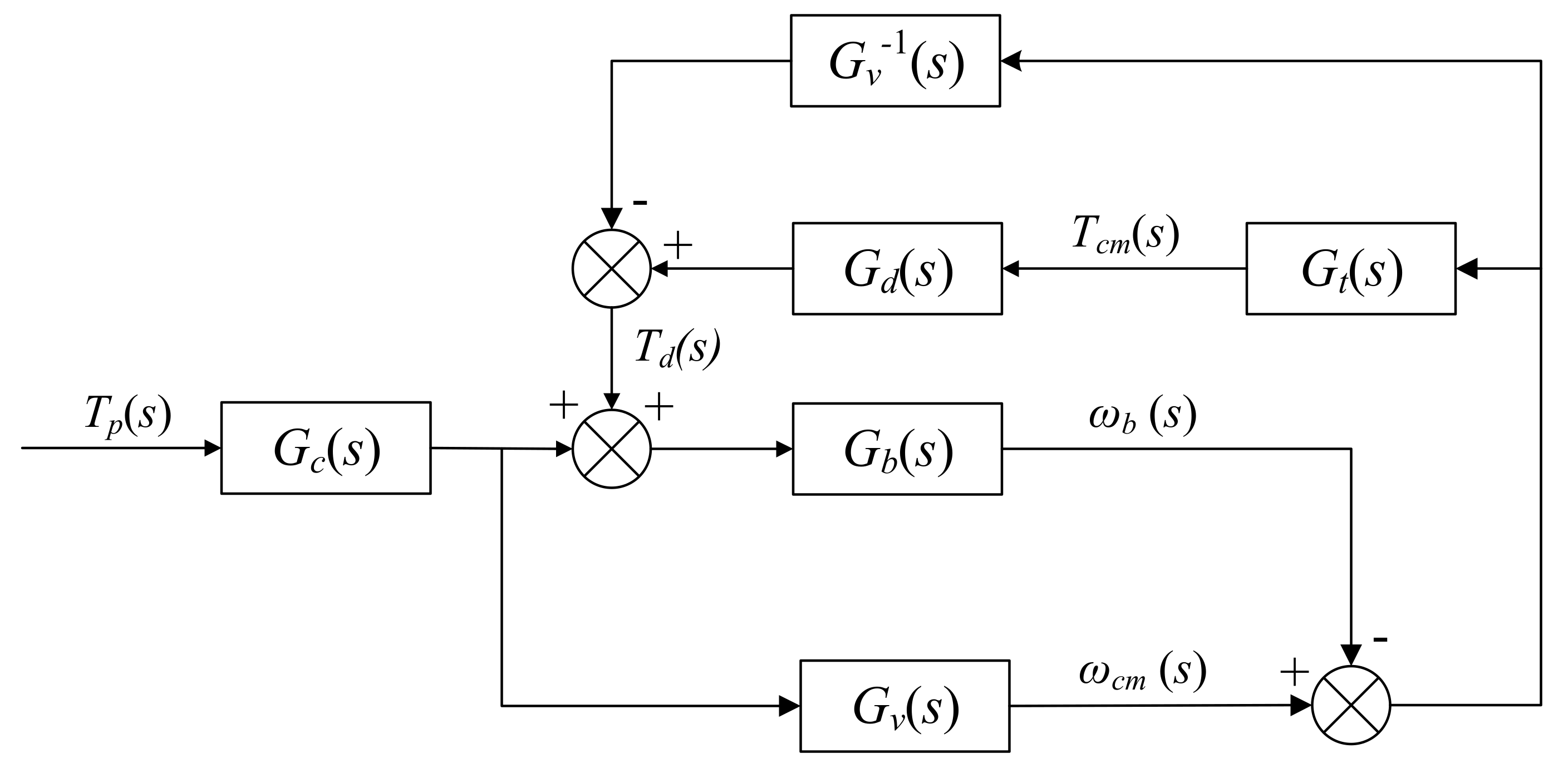
2. Structure of Test-Bed
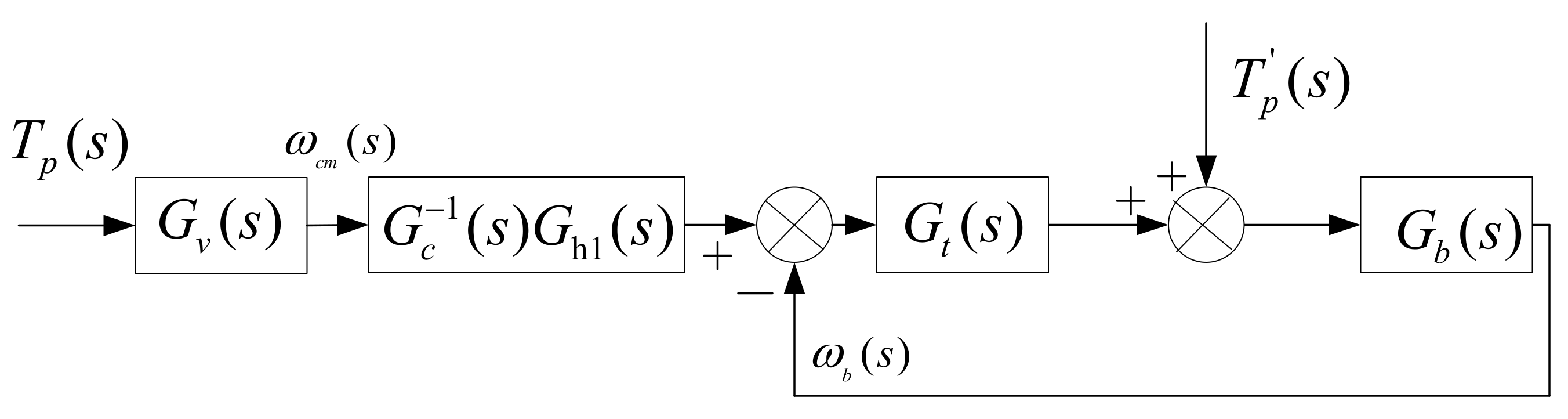
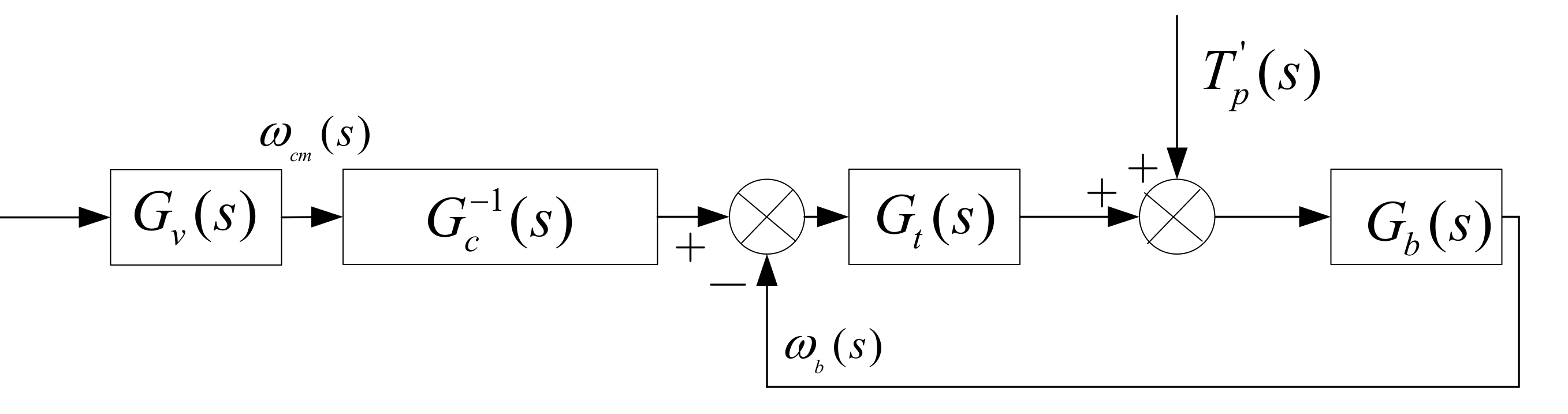
3. Test-Bed Control Strategy
3.1. RLS with a Penalty Function Based on a Forward Model
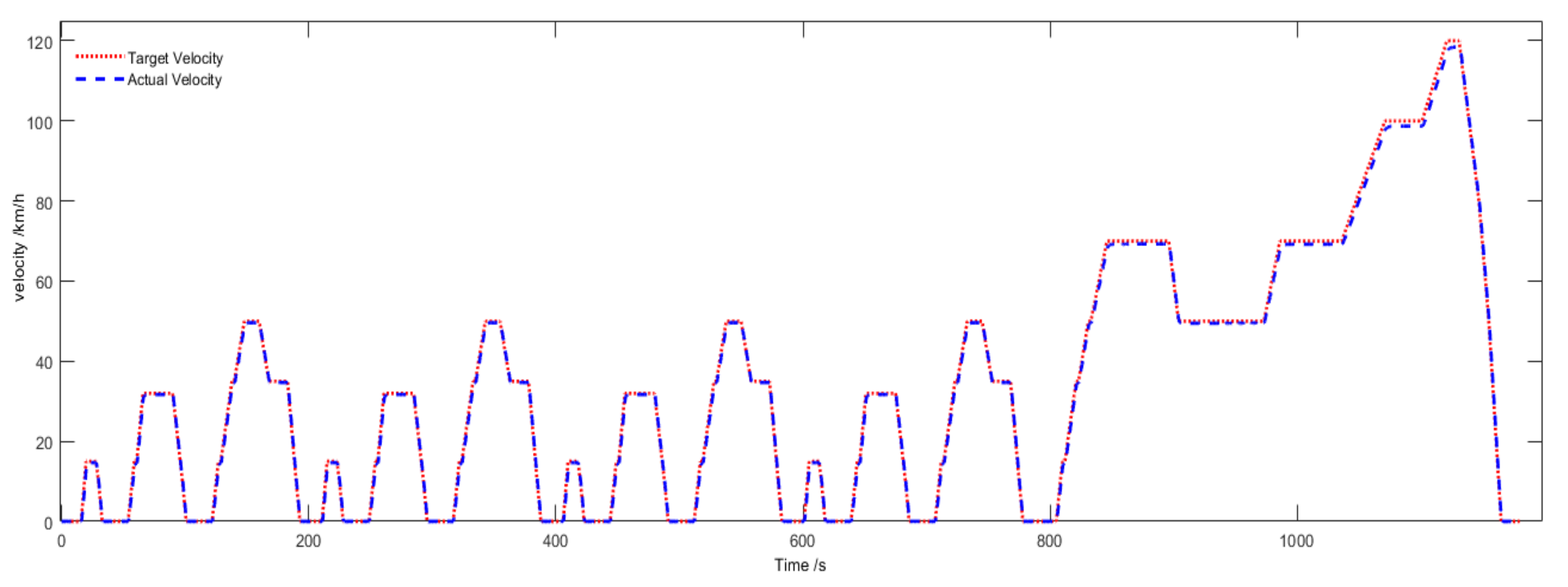
3.2. Driver Model
4. Simulation and Results Discussion
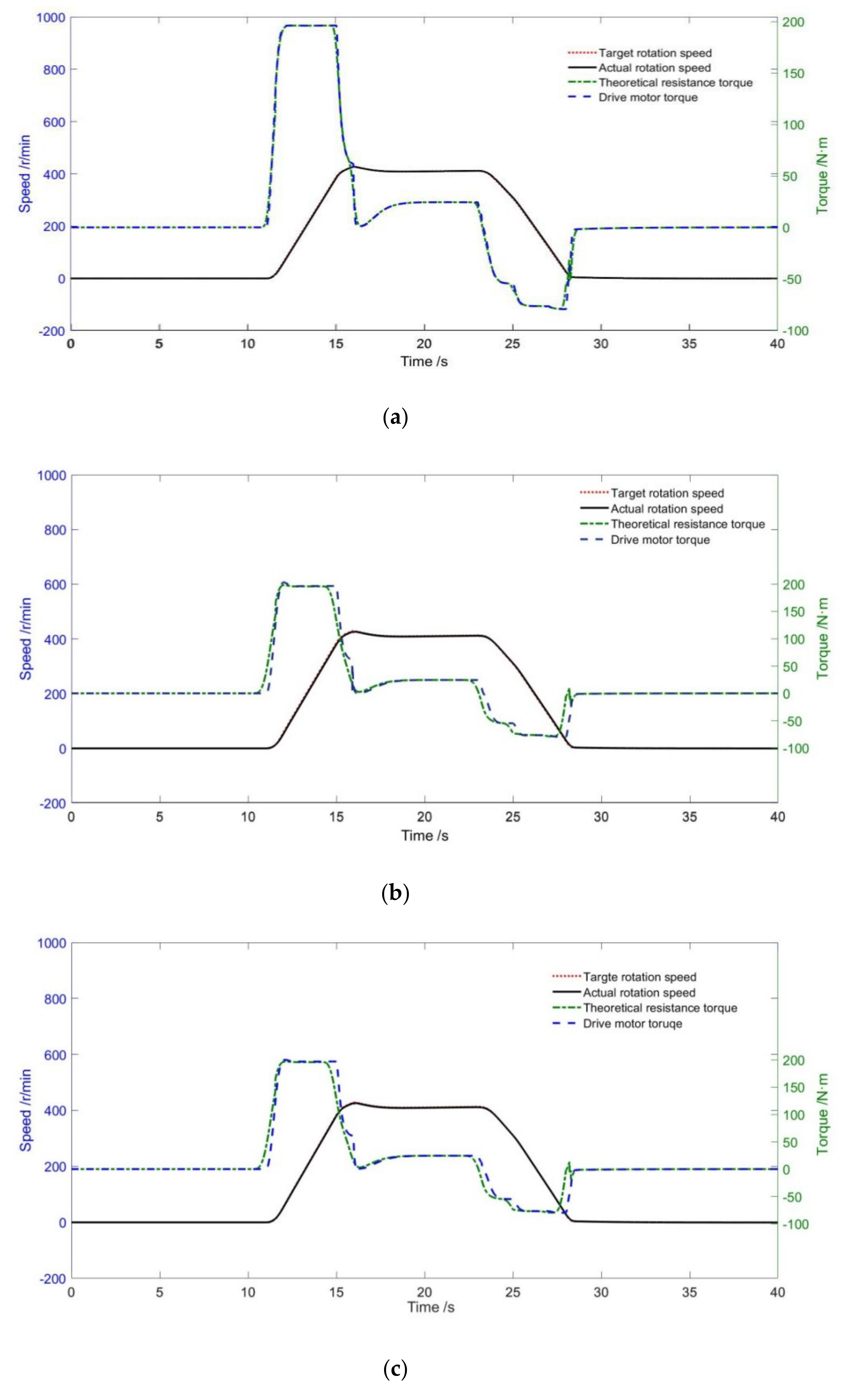
4.1. Impact of Inertia on RLS
4.2. Impact of the Sampling Frequency on RLS
4.3. Engine Simulation
5. Test Platform Construction and Experiment
5.1. Test Platform Construction
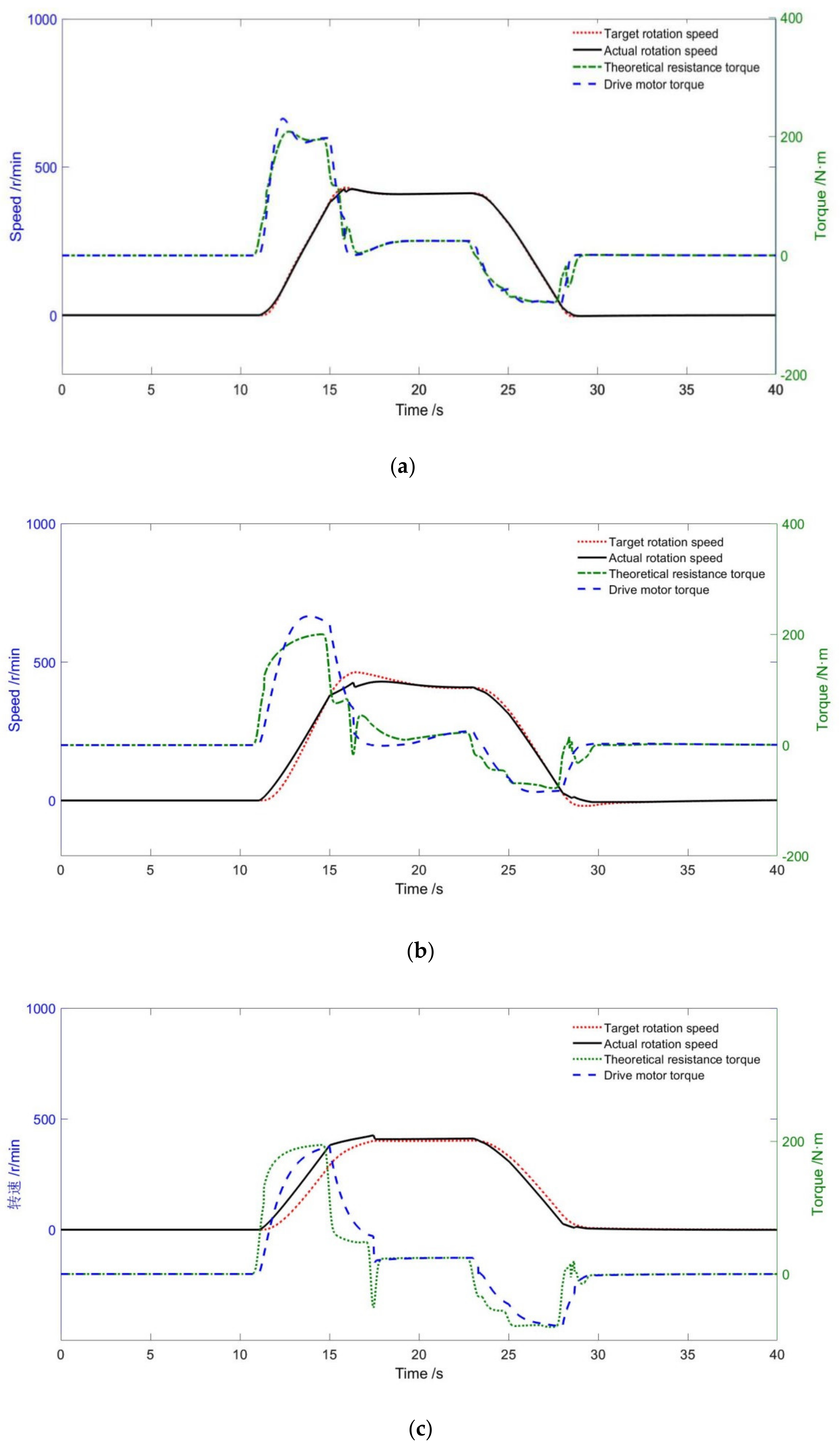
5.2. RLS Experiment
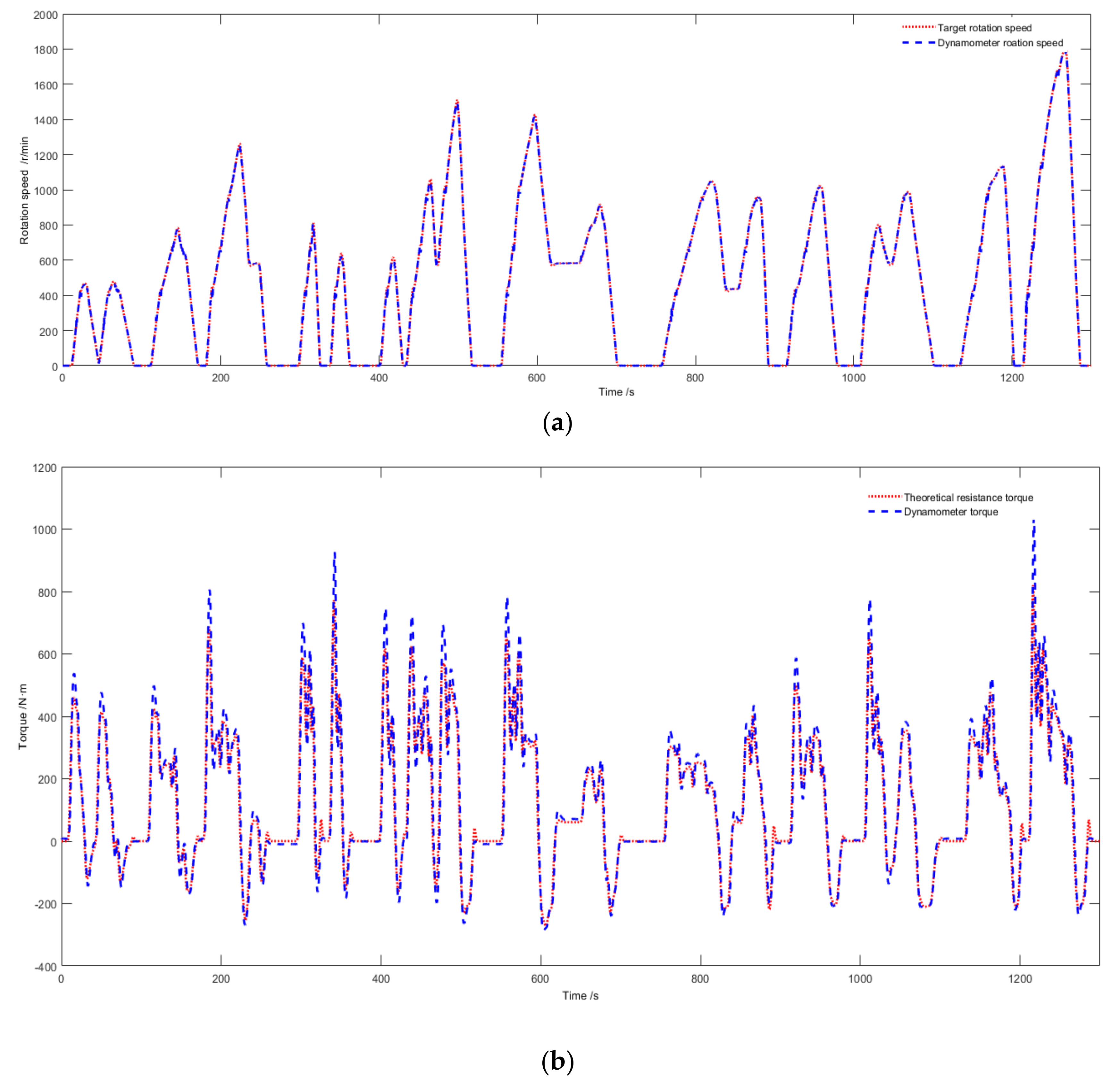
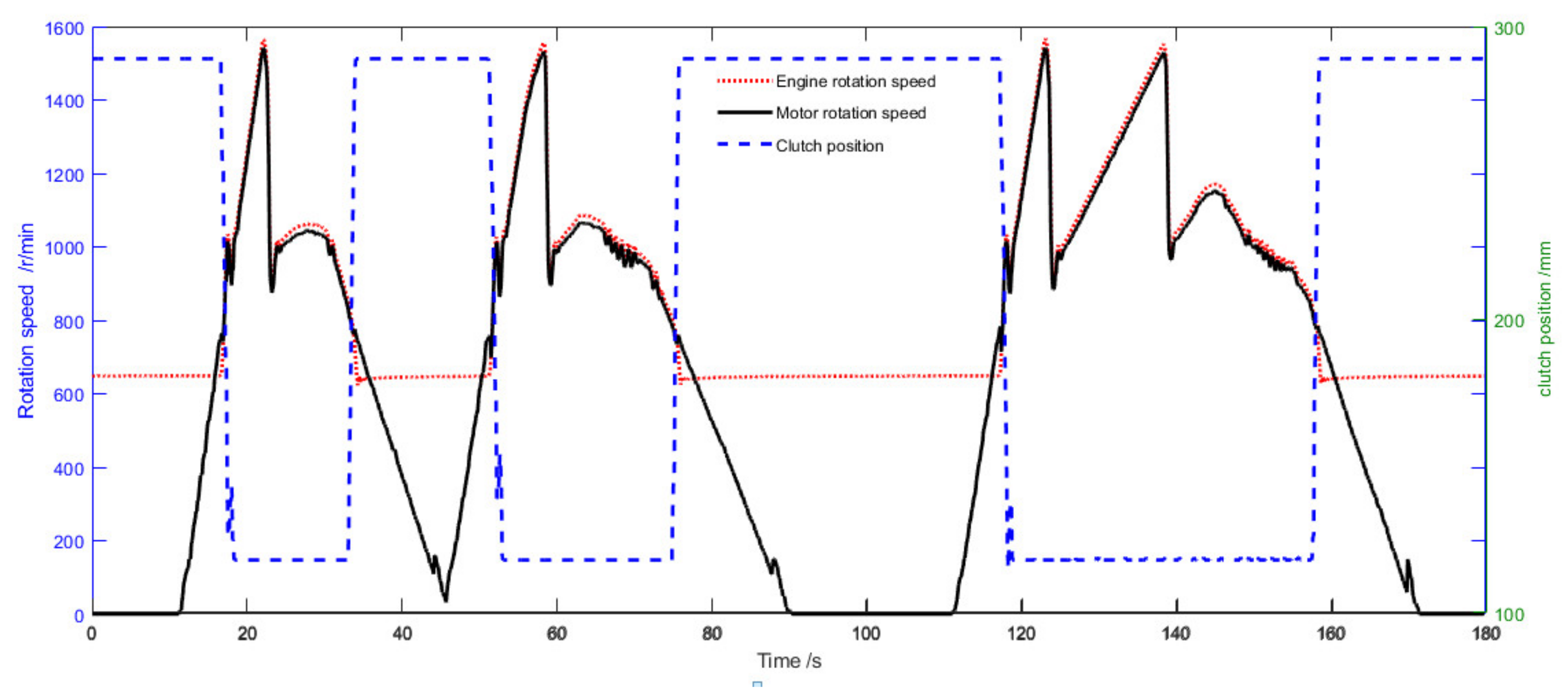
5.3. Engine Simulation Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ouyang, M. Development and Prospect of New Energy Vehicles in China. Sci. Technol. Rev. 2016, 34, 13–20. [Google Scholar]
- Niu, J.G.; Pei, F.L.; Zhou, S.; Zhang, T. Multi-objective Optimization Study of Energy Management Strategy for Extended-Range Electric Vehicle. Adv. Mater. Res. 2013, 694–697, 2704–2709. [Google Scholar] [CrossRef]
- Gong, C.; Hu, M.; Li, S.; Zhan, S.; Qin, D. Equivalent consumption minimization strategy of the hybrid electric vehicle considering the impact of driving style. Proc. Inst Mech. Eng. Part D J. Automob. Eng. 2018, 233, 2610–2623. [Google Scholar] [CrossRef]
- Omer, A.M. Energy and environment: Applications and sustainable development. Br. J. Environ. Clim. Chang. 2011, 1, 118–158. [Google Scholar] [CrossRef] [PubMed]
- Gehringer, M.A.; Defenderfer, E.J. Road Load Simulation Testing for Improved Assessment of Powertrain Noise and Vibration. SAE Int. J. Engines 2011, 4, 1210–1216. [Google Scholar] [CrossRef]
- Newton, R.W.; Betz, R.E.; Penfold, H.B. Emulating dynamic load characteristics using a dynamic dynamometer. In Proceedings of the IEEE International Conference on Power Electronics Drive Systems, Singapore, 21–24 February 1995. [Google Scholar]
- Ye, X.; Jin, Z.H.; Gao, D.W.; Lu, Q.C. Dynamometer Controller Algorithm for Road Load Emulations. J. Tsinghua Univ. (Sci. Technol.) 2013, 53, 1492–1497. [Google Scholar]
- Hewson, C.R.; Sumner, M.; Asher, G.M.; Wheeler, P.W. Dynamic mechanical load emulation test facility to evaluate the performance of AC inverters. Power Eng. J. 2000, 14, 21–28. [Google Scholar] [CrossRef]
- Arellano-Padilla, J.; Asher, G.; Sumner, M. Control of an AC Dynamometer for Dynamic Emulation of Mechanical Loads with Stiff and Flexible Shafts. IEEE Trans. Ind. Electron. 2006, 53, 1250–1260. [Google Scholar] [CrossRef]
- Akpolat, Z.H.; Asher, G.M.; Clare, J.C. Experimental dynamometer emulation of nonlinear mechanical loads. IEEE Trans. Ind. Appl. 2002, 35, 1367–1373. [Google Scholar] [CrossRef]
- Rodic, M.; Jezernik, K.; Trlep, M. Dynamic emulation of mechanical loads: An advanced approach. IEEE Proc.-Electr. Power Appl. 2006, 153, 159–166. [Google Scholar] [CrossRef]
- Wu, Z. Development of bench test systems for new energy vehicles. Master’s Thesis, Tsinghua University, Beijing, China, , 2016; pp. 28–34. [Google Scholar]
- Zhu, F.S.; Chen, X.M.; Ye, R.K.; Bao, J.Q. Urban Low-carbon Transport, Model of Pure Electric Vehicle Development Typical Research Based on Hangzhou Pure Electric Taxi Demonstration Operations. In Proceedings of 2013 International Conference on Future Energy & Materials Research, Madison, WI, USA, 24 September 2013. [Google Scholar]
- Zheng, X. Research on chassis dynamometer test technology based on rolling resistance dynamic loading and motion parameter prediction. Master’s Thesis, Zhejiang University, Zhejiang, China, 2018; pp. 32–36. [Google Scholar]
- Li, Q.; Zhao, X. Electrical simulation of resistance of chassis dynamometer based on rapid prototype. Agric. Equip. Veh. Eng. 2019, 57, 7–10. [Google Scholar]














| Name of Parameters | Values | |
|---|---|---|
| Vehicle | 1745 | |
| 4.35 | ||
| 0.012 | ||
| 2.34 | ||
| 0.38 | ||
| 0.4046 | ||
| Test-bed | Rotational inertia | 0.5 |
| Rotational damping | 0.05 | |
| Maximum mechanical | 1500 | |
| 0.01 | ||
| 0.02 |
| RLS | Inertia | Maximum Torque Difference () | Maximum Speed Difference () |
|---|---|---|---|
| With the penalty function | 0.5 | 15 | 2.2 |
| Without the penalty function | 0.1 | 20 | 3.5 |
| 0.5 | 30 | 4 | |
| 5 | 40 | 20 |
| Sample Frequencies | Maximum Torque Difference () | Maximum Speed Difference () |
| 100 | 2.2 | 15 |
| 10 | 4 | 30 |
| 1 | 5 | 50 |
| 100 without a penalty function | 7 | 60 |
| Name of Parameters | Values | |
|---|---|---|
| Vehicle mass | 12,000 | kg |
| Final reduction gear ratio | 5.7 | - |
| Rolling resistance coefficient | 0.014 | - |
| Frontal area | 8.25 | m2 |
| Aerodynamic drag coefficient | 0.6 | - |
| The radius of wheels | 0.5 | m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Jin, Z.; Hua, Y.; Zhang, L. Development of Test-Bed Controller for Powertrain of HEV. Energies 2020, 13, 3372. https://doi.org/10.3390/en13133372
Liu P, Jin Z, Hua Y, Zhang L. Development of Test-Bed Controller for Powertrain of HEV. Energies. 2020; 13(13):3372. https://doi.org/10.3390/en13133372
Chicago/Turabian StyleLiu, Peng, Zhenhua Jin, Yuwei Hua, and Lu Zhang. 2020. "Development of Test-Bed Controller for Powertrain of HEV" Energies 13, no. 13: 3372. https://doi.org/10.3390/en13133372
APA StyleLiu, P., Jin, Z., Hua, Y., & Zhang, L. (2020). Development of Test-Bed Controller for Powertrain of HEV. Energies, 13(13), 3372. https://doi.org/10.3390/en13133372




