Energy Efficiency Maximization of Two-Time-Slot and Three-Time-Slot Two-Way Relay-Assisted Device-to-Device Underlaying Cellular Networks

Abstract

The continuous development of fifth generation (5G) communication and Internet of Thing (IoT) inevitably necessitates more advanced systems that can satisfy the growing wireless data rate demand of future equipment. Device-to-Device (D2D) communication, whose performance is evaluated in terms of the overall throughput, energy efficiency (EE) and spectral efficiency (SE), is considered a promising solution for the aforementioned problem. Thereby, this paper aims at improving the performance of the D2D communication underlaying cellular networks operating on multiple bands by maximizing the EE in its uplink. Thanks to the stochastic geometry theory, it is possible to derive the closed-form expressions for the successful transmission probability (STP), the total average transmission rate (TATR), and the total average energy efficiency (TAEE) of cellular and D2D users in different time slot setting. Particularly investigated and compared in this study, there are one-hop, direct, D2D communication in two time slots (2TS), and multi-hop, indirect, D2D communication in three time slots (3TS) with an additional D2D user acting as a two-way relay to assist the communication. Moreover, an optimization problem is formulated to calculate the maximum TAEE of D2D users and the optimum transmission power of both the cellular and D2D users. Herein this optimization study, which is proven to be non-convex, the Quality of Service (QoS) is ensured as the STP on every link is considered. The herein approach is referred to as relay-assisted D2D communication which is capable of delivering a notably better QoS and lower transmission power for communication among distant D2D users.

1. Introduction

The more the world is progressing toward building more IoT systems and smart cities, the more important the development of the D2D communication becomes. Because it is the foundation for the 5G wireless networks upon which the aforementioned structures are built [1]. Focuses of D2D communication underlaying cellular networks infrastructure studies are paid on the cellular capacity increase, user throughput improvement, and battery lifespan extension of the user equipment units (UEs) by deploying the physical proximity between devices in the communication, along with reusing the spectrum resources [2,3,4].

Proximate devices can communicate with each other, and thanks to this, D2D communication can deliver higher data rate, SE and EE with noticeably lower latency and power consumption to the services [5,6,7,8]. Nonetheless, as the spectrum is shared between the cellular users in D2D communication, it inevitably produces problems that require knowledge about interference management. Besides, it should be mentioned that D2D communication can operate on a licensed band (in-band), or an unlicensed band (out-band). Specifically, in-band communication is classified into overlay and underlay, in which there are dedicated spectrum and shared spectrum, respectively.

Paper [9] studied the power controlling in D2D communications aiming at minimizing the total downlink transmission power, which is under the influence of the QoS from UEs. For better scalability of D2D communications, a certain number of different resource allocation methods were investigated in [10]. Moreover, interference management for better reliability was discussed in [11]. Accordingly, there are state-of-the-art mechanisms utilized for interference management in D2D networks which are investigated in [12,13]. Paper [14] described the D2D communications under influence of several users in Multiple-Input and Multiple-Output (MIMO) channels. Last but not least, the author group in [15] proposed a dynamic graph optimization framework specifically developed for multi-hop D2D communication underlaying cellular networks.

To solve the aforementioned interference problem, there is a need for an effective power allocation method. One of the solutions for this is to have a relay user placed in between the D2D pair [16]. This is referred to as relay-assisted D2D communication and was proven to be an efficient approach which provides better QoS and lower transmission power for communications among distant D2D users. In a relay-assisted D2D communication network, the relay works as a middle contact point which receives and then forwards the signal from a source to a destination. This technique is well-known since it is capable of delivering notably high SE and EE for cellular networks [17]. A relay-assisted network is categorized depending on how the signal is transmitted in the network. There are three types of network relay: one-way, two-way, and multi-way. A two-way relaying network (TWRN) provides higher SE in comparison with the one-way one as it permits the relay user to conduct concurrent communication with two D2D end users. Recent studies have proven that by utilizing two-way relays to assist a D2D communication, network designers can significantly improve the system performance (indicated by the improvement of outage probability (OP) and sum rate) [18,19].

The throughput performance of two-way relay-assisted D2D communication networks studies were presented in [20,21,22]. Specifically, in [20], the ergodic capacity, the finite signal-to-noise ratio (SNR), and the OP of simultaneous wireless information and power transfer (SWIPT) protocol for an amplify-and-forward (AF) TWRN were studied. The author group in [21] proposed three time switching based energy harvesting policies - namely, dual-source (DS) power transfer, single-fixed-source (SFS) power transfer, and single-best-source (SBS) power transfer. Last but not least, there are two relaying protocols designed in SWIPT, which were presented in [22]—namely, power time splitting-based two-slot (PTSTW), and power time splitting-based three-slot (PTSTH). Moreover, a so-called time switching-based network coding relaying (TSNCR) protocol was utilized for two-way energy harvesting and presented in [23]. Notwithstanding, the time slot processing problems have to be taken into account to balance the information transmission and energy harvesting process. Otherwise, the two-way transmission performance can not be improved. Besides, in [24] proposed a framework to compromise among D2D network parameters, specifically, the density of D2D users and the transmit power, to optimize the ergodic capacity while ensuring minimization of the overall power consumption. Recent study such as [25] even considered applying a potential game-based power adjustment in in-band multi-hop relay-assisted D2D communication to improve the EE and throughput in the downlink resulting in better coverage quality.

1.1. Related Work

There are several pieces of research conducted on the EE of the D2D communications underlaying cellular networks. Before discussing these studies further, it should be noted that the EE metric is important for such wireless networks because it indicates how efficiently the energy is utilized. Thereby, for instance, to improve the system performance, [26] studied the EE of D2D communications whereas the channel reuse was removed. The D2D communications deployed in heterogeneous networks results in better EE in comparison with the full small-cell deployment, hence, a greener solution for cellular network deployment. Likewise, the EE of D2D systems with cellular network deployment was analyzed and presented in [17,27]. Specifically in [27], the authors studied the compromise between the EE and the delay in D2D systems under stochastic traffic arrivals and time-varying channel conditions. Moreover, in [28], a D2D system whereas every user is self-seeking and individually attempts to maximize its EE was investigated. Therein, the EE and SE were studied provided that the system was constrained by the SE and the maximum transmission power limit. In [29], the extended radio resource management algorithms were integrated into one-way relay-assisted D2D communications aiming to balance off the SE and EE under constraints of mode selection and resource allocation. In the context of one-way D2D communications, the authors in [16,30] studied the system’s maximum achievable transmission capacity. The OP for both cellular and D2D link was guaranteed during this study. In [31], network users were modelled based on the stochastic geometry on multiple bands and the D2D users’ EE was maximized. Nevertheless, therein the study, the D2D communication was investigated in one way only, given that the influence of the transmission power of the cellular users was neglected. Differing itself from the above papers, this study focuses on the maximization and comparison study of the EE, which is henceforward addressed interchangeably as the TAEE, of the two-way D2D communication underlaying cellular networks in 2TS and 3TS scenario.

1.2. Main Contributions

As aforementioned, based on the stochastic geometry theory, an effective solution to maximize the EE of the cellular network in two-way D2D multi-hop communication is investigated. Accordingly, the optimum power of multiple bands is derived. In particular, the users are spatially and randomly distributed within the network following the homogeneous Poisson point process (PPP). It should be noted that the D2D and the cellular users in each band are distributed with different density levels. Additionally, the number of users participating in the transmission process is different. Because of the resource fluctuation and the developing network conditions of 5G, studies conducted in multi-hop scenario are considered more practical than one-hop ones. Besides, the dynamic behaviour of the system in those studies can as well be observed. Moreover, to manage the variation of the wireless channel parameters so as to enhance the network EE, multi-hop D2D communication as 2TS and 3TS mode with each possessing its adjustable power transmission is studied. Last but not least, as there are multiple bands for multiple hops, the D2D users, cellular users and other devices do not interfere with each other. This reduces considerably the complication of the interference management and improves the D2D communication performance.

Listed below are the main contributions of this paper:

• Firstly, the closed-form expressions for the STP, the TATR, and the TAEE for the cellular users and D2D users in 2TS and 3TS mode of the two-way D2D communication network are derived.
• Secondly, there is a proposed optimization problem aiming at maximizing the EE of D2D users while ensuring the QoS of the cellular and D2D users. This problem is solved thanks to a DB algorithm formulated from the fact that the multi-hop D2D users are subject to transmission power and OP constraints. This problem is proven to be non-convex and separated into two sub-problems. Solving the first sub-problem provides the maximized EE of the D2D users along with the optimum transmission power of the direct (one-hop) D2D user in 2TS mode. In the second sub-problem, an objective function is formulated to calculate the maximized EE and the optimum transmission power of the D2D users in 3TS mode with a two-way relay assisting the communication (multi-hop). It is noteworthy that the objective function is a sum of a number of sub-functions. When all of the sub-functions are maximized, by summing them up, it is possible to obtain the optimal result for the second sub-problem.
• Finally, a comparison between this study and the study in [31,32] given similar system model and assumptions is done. It can be observed from the simulation results that the DB algorithm provides a near-optimal solution in 2TS and an outstanding performance in 3TS comparing to the conventional Branch and Bound (BB) algorithm [33].

Ones can find in Section 2 the scenario and system model descriptions. Section 3 describes the analytical studies and the problem formulation on multiple bands, especially the EE optimization problem. Section 4 describes in details the proposed DB algorithm utilized to solve the aforementioned optimization problem. Accordingly, Section 5 presents the simulation results. Section 6 concludes this paper.

Notations: $\mathrm{E}\left\{.\right\}$ denotes expectation operation, $\mathrm{Pr}\left\{.\right\}$ is OP function. $\mathcal{L}\left(x\right)$ is Laplace transform of x. $\mathrm{\Gamma }\left(.\right)$ is the gamma function with $\mathrm{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$.

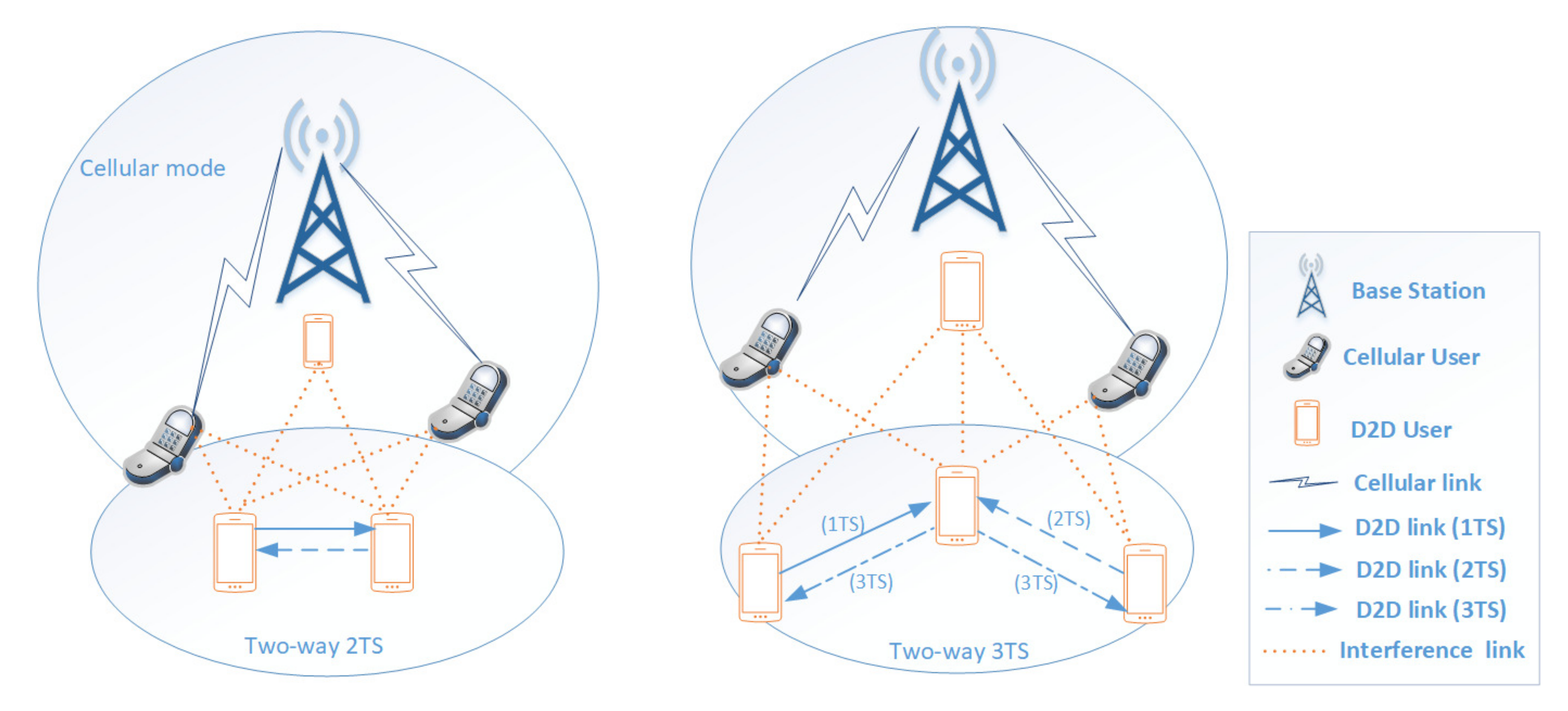
2. System Model

A. Scenario Description: In this study, a D2D communication underlaying a general cellular network is considered. It should be noted that the cellular network’s uplink frequency resources are shared with the D2D communication. The resource allocation of the whole network is handled by a base station (BS). Moreover, there are network and channel model depicted. Dissimilar to [34] where the authors conducted a power allocation problem study on a single band, the power allocation on multiple bands is considered in this paper. As its name suggests, the cellular network operates in a spectrum that is split into K number of bands, whereas each K has a subscript i indicating the $i_{th}$ band, given that $i=1,2,‥,K$. Figure 1 depicts the two transmission modes focused in this study. The two are based on a cellular network with cellular links between cellular users and the BS receiver. As D2D users exchange information with one another in multiple bands scenario, they operate in two modes:

• Two-time-slot (2TS) mode: direct, one-hop communication.
• Three-time-slot (3TS) mode: indirect, via an in-between D2D user working as a two-way relay to assist the signal transmission, multi-hop communication.

B. Network Models: There are four assumptions that are made based on the stochastic geometry theory in this study:

Assumption A1. 

There is a two-dimensional plane ℜ symbolized by ${\mathrm{\Phi }}_{c,i}$. Herein, by utilizing the homogeneous PPP, the random spatial distribution of the cellular users in the $i_{th}$ band can be carried out given that the density is ${\delta }_{c,i}$. To denote the cellular users’ transmission power in the $i_{th}$ band, $P_{c,i}$ is used. The total transmission power of all the cellular users, according to [35], is calculated as $P_c=\sum _{i=1}^K{P}_{c,i}$.

Assumption A2. 

On ℜ, in the same manner with modelling cellular users, D2D users are distributed with homogeneous PPP ${\mathrm{\Phi }}_{d,i}$, and density ${\delta }_{d,i}$. Every transmitter D2D user is coupled with a receiver D2D user which is a distance $R_{d,i}$ away from each other, and assigned with a Rayleigh fading coefficient $f_{d,i}$. Similarly, there is a denotation for transmission power of D2D users in the $i_{th}$ band, $P_{d,i}$, and $P_d=\sum _{i=1}^K{P}_{d,i}$ to sum them up.

Assumption A3. 

The statistics of the PPP are not influenced by the presence of any typical receiver at the origin, as stated in Palm theory, [36]. Thus, at the ℜ’s origin, a typical receiver is placed. It plays the role of a BS typically utilized for cellular uplink transmitting task and a typical D2D receiver assisting the D2D communication. This BS is studied in combination with the D2D users. Moreover, there are presumed reciprocal, invariant uplink and downlink channels founded on consecutive equal time slots model.

Assumption A4. 

If a pair of D2D users, D2D${}_a$ and D2D${}_b$, are considerably distanced from each other, there is a need for another D2D user placed in the middle of the two to assist their signal transmission. This device works as a two-way relay which is denoted as D2D${}_r$, given that the transmission power of the relay nodes (RNs) equals to the D2D power in the $i_{th}$ band, $P_{r,i}=P_{d,i}$. Communication between D2D${}_a$ and D2D${}_b$ is realized utilizing decode-and-forward (DF) protocol with the assistance of D2D${}_r$. The three D2D users are distributed on ℜ following the stationary PPP ${\mathrm{\Phi }}_{r,i}$, with density ${\delta }_{r,i}$. Furthermore, the distances from D2D${}_r$ to D2D${}_a$ and D2D${}_b$, denoted respectively as $R_{d,i}^{ar}$ and $R_{d,i}^{rb}$, are constrained so that they can not be equal to or greater than $R_{d,i}$, being the distance between D2D${}_a$ and D2D${}_b$. To formulate the relation between the distances, α fraction is deployed so that $R_{d,i}^{ar}=R_{d,i}\left(\frac{1}{1+\alpha }\right)$, and $R_{d,i}^{rb}=R_{d,i}\left(\frac{\alpha }{1+\alpha }\right)$. Moreover, for fading channels, the $f_{d,i,lk}$ is used to indicate the the Rayleigh fading coefficient of l-k link ($l,k=a,b,r$) which satisfies $f_{d,i,lk}=f_{d,i,kl}$.

C. Channel Models: The whole network is a combination of a cellular system and D2D communication. In this context, from [36], the path loss and Rayleigh fading are placed in a propagation channel model and their effects on the network are studied. Accordingly, a parameter namely received power for either cellular users or D2D users, ${\mathrm{P}}_{rx}$, is proposed and its expression is given as follows

$${\mathrm{P}}_{rx}=P_{tx}f{R}^{-m},$$

(1)

whereas $P_{tx}$ is the transmit power. f is the Rayleigh fading coefficient. It should be noted that f follows an independent exponential distribution, and is conditioned so that the unit mean is assigned for every communication link in the system. R denotes the distance between the transmitter and the receiver. m stands for the path-loss exponent given that it is an even number and $m\ge 2$.

Remark 1. 

Upon reusing the cellular resources, the D2D communication will cause interference to the typical receiver. This interference is generated by the cellular users, the D2D users, and last but not least, the RNs.

3. Problem Formulation

This section presents the work of maximizing the network’s EE in two modes. Firstly, the signal-to-interference-plus-noise ratio (SINR) and the STP of typical receivers are considered. Then, following the STP formula, the closed-form expressions for the TATR and TAEE of D2D communication of multiple bands are calculated. Eventually, the EE maximization, treated as an optimization problem, is formulated.

3.1. The Signal to Noise Plus Interference Ratio

The performance analysis of the cellular transmission and D2D communication in two-way relay-assisted setup is conducted and presented in this subsection. In particular, as the D2D pair and two-way relay user share common cellular spectrum resources, the D2D communication in two modes, 2TS and 3TS, are investigated.

A. Two Time Slot Communications Mode

A.1. D2D Pair between the Direct Links and Cellular Links

In this mode, the D2D pair formed between the direct and cellular links, UED${}_a$ and UED${}_b$, is investigated. They are in charge of exchanging information via direct one-hop D2D link in maximum two time slots without the two-way relay assisting the D2D transmission in the overlapping region.

According to [37], the received signal at the D2D receiver can be calculated in the $i_{th}$ band utilizing the following formula

$$y_{d,i}^{2TS}={\mathcal{I}}_{d,00,i}+{\mathcal{I}}_{id,c0,i}+{\mathcal{I}}_{id,d0,i}+N_0,$$

(2)

whereas the signal from D2D user is ${\mathcal{I}}_{d,00,i}=\sqrt{P_{d,i}{R}_{d,00,i}^{-m}{f}_{d,00}}$. Herein, there are $f_{d,00}$ being the Rayleigh fading channel coefficient, and $R_{d,00,i}$ being the distance from the D2D transmitter to its corresponding D2D receiver in the $i_{th}$ band. Similarly, the interference caused by the cellular users is formulated as ${\mathcal{I}}_{id,c0,i}=\sum _{j\in {\mathrm{\Phi }}_{c,i}}\sqrt{P_{c,i}{R}_{c,j0,i}^{-m}{f}_{c,j0}}$, in which $f_{c,j0}$ is the Rayleigh fading channel coefficient, and $R_{c,j0,i}$ is the distance from the $j_{th}$ cellular user to the typical D2D in the $i_{th}$ band. Moreover, there is the interference caused by the D2D users ${\mathcal{I}}_{id,d0,i}=\sum _{l\in {\mathrm{\Phi }}_{d,i}}\sqrt{P_{d,i}{R}_{d,l0,i}^{-m}{f}_{d,l0}}$. It is constructed of $f_{d,l0}$ being the Rayleigh fading channel coefficient and $R_{d,l0,i}$ being the distance from the $l_{th}$ D2D user as the transmitter to its corresponding receiver in the $i_{th}$ band. Last but not least, there is the thermal noise term $N_0$.

Due to the nature of the wireless broadcasting process, a typical receiver has to suffer the interference caused by the cellular and D2D communication in the same network. As aforementioned, the D2D communication operates utilizing the same uplink frequency resources of the cellular system. This, indeed, makes the interference an important parameter in this study. The whole network now is interference limited with neglect-able thermal noise. It should be noted that, in this scenario, the D2D pair communicates in 2TS mode. Accordingly, SINR is rewritten as the signal-to-interference ratio (SIR) of the typical D2D receiver in the $i_{th}$ band and expressed as

$${\gamma }_{d,i}^{2TS}=\frac{f_{d,00}{R}_{d,00,i}^{-m}}{\sum _{l\in {\mathrm{\Phi }}_{d,i}}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{j\in {\mathrm{\Phi }}_{c,i}}\frac{P_{c,i}}{P_{d,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}}.$$

(3)

A.2. Cellular Transmissions of the Typical BS

As aforementioned, the cellular and D2D transmission process cause interference to the typical receiver. Thus, to calculate the signal receiver that a typical BS, and, accordingly, its cellular user in the $i_{th}$ band, ones can utilize the following formula

$$y_{c,i}^{2TS}={\mathcal{I}}_{c,00,i}+{\mathcal{I}}_{ic,c0,i}+{\mathcal{I}}_{ic,d0,i}+N_0,$$

(4)

whereas ${\mathcal{I}}_{c,00,i}=\sqrt{P_{c,i}{R}_{c,00,i}^{-m}{f}_{c,00}}$ is the cellular signal of the typical BS. As in (2), ${\mathcal{I}}_{ic,c0,i}=\sum _{j\in {\mathrm{\Phi }}_{c,i}}\sqrt{P_{c,i}{R}_{c,j0,i}^{-m}{f}_{c,j0}}$, and ${\mathcal{I}}_{ic,d0,i}=\sum _{l\in {\mathrm{\Phi }}_{d,i}}\sqrt{P_{d,i}{R}_{d,l0,i}^{-m}{f}_{d,l0}}$ are the interference from the cellular users to the typical BS, and the interference from D2D users to the typical BS, respectively, in the $i_{th}$ band.

The SIR of the typical cellular receiver in the $i_{th}$ band can be obtained in the same manner as in (3). Thus, it is written as

$${\gamma }_{c,i}=\frac{f_{c,00}{R}_{c,00,i}^{-m}}{\sum _{l\in {\mathrm{\Phi }}_{d,i}}\frac{P_{d,i}}{P_{c,i}}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{j\in {\mathrm{\Phi }}_{c,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}}.$$

(5)

B. Three Time Slot Communications Mode

This session presents the study conducted on 3TS communication whereas a D2D communication in stochastic geometry, specifically in this case, a relay-assisted D2D link, aids a pair of other D2D users in information exchange with physical-layer network coding scheme [38]. The main focus is paid on the EE of the 3TS transmission given that the UER is embedded with DF protocol.

In two-way 3TS communication mode, a two-way relay D2D user is placed in between the two D2D users to assist the data transmission. In the first and second time slots, information is respectively transmitted from the two D2D users, D2D${}_a$ and D2D${}_b$, to the two-way relay, D2D${}_r$, with power $P_{d,i}$. Then, within the third time slot, D2D${}_r$ decodes the information sent from the two aforementioned sources. These two information flows are mixed utilizing some network coding technique, for example, the XOR coding operation. As a result, the information is network-coded and broadcasted back to the D2D${}_a$ and D2D${}_b$. The assisting task of the D2D${}_r$ is accomplished so far as the information transmission is finished. The two D2D users then can extract the information they need from the returned mixed flow of information.

The signals received by the D2D${}_r$ user in the first and second time slot are expressed as follows

$$y_{ar,i}={\mathcal{I}}_{ar,00,i}+{\mathcal{I}}_{ir,c0,i}+{\mathcal{I}}_{ir,d0,i}+{\mathcal{I}}_{ir,r0,i}+N_0,$$

(6)

and

$$y_{br,i}={\mathcal{I}}_{br,00,i}+{\mathcal{I}}_{ir,c0,i}+{\mathcal{I}}_{ir,d0,i}+{\mathcal{I}}_{ir,r0,i}+N_0,$$

(7)

whereas there are formulas for calculating the signal from the two typical D2D users $I_{ar,00,i}=\sqrt{P_{d,i}{\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^{-m}{f}_{ar,00}}$, and ${\mathcal{I}}_{br,00,i}=\sqrt{P_{d,i}{\left(\frac{\alpha R_{d,00,i}}{1+\alpha }\right)}^{-m}{f}_{br,00}}$. The $f_{ar,00}$ and $f_{br,00}$ are the Rayleigh fading channel coefficient between the two D2D users and the two-way relay which assists the D2D user communication in the $i_{th}$ band. Moreover, there are the received interference power from the cellular user, ${\mathcal{I}}_{ir,c0,i}=\sum _{j\in {\mathrm{\Phi }}_{c,i}}{P}_{c,i}{f}_{c,j0}{R}_{c,j0,i}^{-m}$, from the D2D user ${\mathcal{I}}_{ir,d0,i}=\sum _{l\in {\mathrm{\Phi }}_{d,i}}{P}_{d,i}{f}_{d,l0}{R}_{d,l0,i}^{-m}$, and from the two-way relay assisting the D2D users to the typical receiver ${\mathcal{I}}_{ir,r0,i}=\sum _{k\in {\mathrm{\Phi }}_{r,i}}{P}_{d,i}{f}_{r,k0}{R}_{r,k0,i}^{-m}$.

Within the third time slot, a portion $\beta$, ($0<\beta <1$), of the transmission power at the two-way relay D2D user, $P_{d,i}$, is utilized by the D2D${}_r$ to broadcast the mixed flow of the signal to the two D2D users. Particularly, $\beta P_{d,i}$ is allocated for transmission from D2D${}_r$ to D2D${}_a$, and $\left(1-\beta \right)P_{d,i}$ for D2D${}_r$ to D2D${}_b$. Hence, at D2D${}_a$ and D2D${}_b$, the resulting received signals are calculated respectively as follows

$$y_{ra,i}={\mathcal{I}}_{ra,00,i}+{\mathcal{I}}_{ir,c0,i}+{\mathcal{I}}_{ir,d0,i}+{\mathcal{I}}_{ir,r0,i}+N_0,$$

(8)

and

$$y_{rb,i}={\mathcal{I}}_{rb,00,i}+{\mathcal{I}}_{ir,c0,i}+{\mathcal{I}}_{ir,d0,i}+{\mathcal{I}}_{ir,r0,i}+N_0,$$

(9)

whereas $I_{ra,00,i}=\sqrt{\beta P_{d,i}{\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^{-m}{f}_{ra,00}}$, and $I_{rb,00,i}=\sqrt{\left(1-\beta \right)P_{d,i}{\left(\frac{\alpha R_{d,00,i}}{1+\alpha }\right)}^{-m}{f}_{rb,00}}$.

Similar to what is previously done, the SIR in the $i_{th}$ band of the typical D2D receivers, D2D${}_a$ and D2D${}_b$ user, via D2D${}_r$ user transmission with DF protocol is obtained from

$${\gamma }_{a,i}^{3TS}=min\left({\gamma }_{ar,i},{\gamma }_{br,i},{\gamma }_{ra,i}\right),$$

(10)

and

$${\gamma }_{b,i}^{3TS}=min\left({\gamma }_{ar,i},{\gamma }_{br,i},{\gamma }_{rb,i}\right),$$

(11)

whereas with regard to the Assumption 3, the instantaneous SIR in the first, second and third time slot can be calculated as

$$\begin{array}{ccc}{\gamma }_{ar,i}\hfill & =& P_{d,i}{f}_{ar,00}{\mathcal{J}}_a,\end{array}$$

(12)

$$\begin{array}{ccc}{\gamma }_{br,i}\hfill & =& P_{d,i}{f}_{br,00}{\mathcal{J}}_b,\end{array}$$

(13)

$$\begin{array}{ccc}{\gamma }_{ra,i}\hfill & =& \beta P_{d,i}{f}_{ra,00}{\mathcal{J}}_a,\end{array}$$

(14)

$$\begin{array}{ccc}{\gamma }_{rb,i}\hfill & =& (1-\beta )P_{d,i}{f}_{rb,00}{\mathcal{J}}_b,\end{array}$$

(15)

$$\begin{array}{ccc}{\mathcal{J}}_a\hfill & =& \frac{{\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^{-m}}{\sum _{j\in {\mathrm{\Phi }}_{c,i}}{P}_{c,i}{f}_{c,j0}{R}_{c,j0,i}^{-m}+\sum _{l\in {\mathrm{\Phi }}_{d,i}}{P}_{d,i}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{k\in {\mathrm{\Phi }}_{r,i}}{P}_{d,i}{f}_{r,k0}{R}_{d,k0,i}^{-m}},\end{array}$$

(16)

$$\begin{array}{ccc}{\mathcal{J}}_b\hfill & =& \frac{{\left(\frac{\alpha R_{d,00,i}}{1+\alpha }\right)}^{-m}}{\sum _{j\in {\mathrm{\Phi }}_{c,i}}{P}_{c,i}{f}_{c,j0}{R}_{c,j0,i}^{-m}+\sum _{l\in {\mathrm{\Phi }}_{d,i}}{P}_{d,i}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{k\in {\mathrm{\Phi }}_{r,i}}{P}_{d,i}{f}_{r,k0}{R}_{d,k0,i}^{-m}}.\end{array}$$

(17)

Ones can find the derivation of the STP of the typical D2D receiver in the next subsection.

3.2. The Successful Transmission Probability of Typical Receivers

Herein this subsection, the STP of typical receivers is derived. Signal transmission is considered successful as long as the transmitter can send the signal packet to its receivers within the third time slot given that the SIR recorded at the receivers is not lower than the whole D2D communication’s threshold value. On the other hand, negative feedback is sent to the D2D communication and the failed-to-be-sent packet is put back on top of the queue waiting for another transmission round.

A. Two Time Slot Communications Mode

A.1. D2D Pair Communication

The Proposition 1 below defines the STP of a typical D2D user receiver when it accomplishes one round of communication in the duration of two time slots.

Proposition 1. 

The SIR threshold of the D2D communication in the $i_{th}$ band is denoted as ${\zeta }_{d,i}$. From (2), the STP of the typical D2D pair receivers in the $i_{th}$ band has to satisfy

$$Pr\left({\gamma }_{d,i}^{2TS}\ge {\zeta }_{d,i}\right)=e^{-{\Theta }_{d,i}^{2TS}\left[{\delta }_{c,i}{\left(\frac{P_{c.i}}{P_{d,i}}\right)}^{\frac{2}{m}}+{\delta }_{d,i}\right]},$$

(18)

whereas ${\Theta }_{d,i}^{2TS}=\pi {\zeta }_{d,i}^{\frac{2}{m}}{R}_{d,00,i}^2\mathrm{\Gamma }(1+\frac{2}{m})\mathrm{\Gamma }(1-\frac{2}{m})$.

Proof. 

As aforementioned in the network model section, $f_{d,00}$ is independently and exponentially distributed with unit mean. In combination with the (2), the STP of the typical D2D receiver in the $i_{th}$ band is written as follows

$$\begin{array}{c}Pr\left\{{\gamma }_{d,i}^{2TS}\ge {\zeta }_{d,i}\right\}=Pr\left\{\frac{f_{d,00}{R}_{d,00,i}^{-m}}{\sum _{l\in {\mathrm{\Phi }}_{d,i}}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{j\in {\mathrm{\Phi }}_{c,i}}\frac{P_{c,i}}{P_{d,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}}\ge {\zeta }_{d,i}\right\}.\hfill \end{array}$$

(19)

As the study is conducted on 2D planes and ${\gamma }_{d,i}^{2TS}$ follows the independent exponential distribution of D2D users and cellular channel gains, with regard to the (19), the STP can be rewritten as

$$\begin{array}{c}Pr\left\{{\gamma }_{d,i}^{2TS}\ge {\zeta }_{d,i}\right\}=Pr\left\{f_{d,00}\ge {\zeta }_{d,i}{R}_{d,00,i}^m\left(\sum _{l\in {\mathrm{\Phi }}_{d,i}}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{j\in {\mathrm{\Phi }}_{c,i}}\frac{P_{c,i}}{P_{d,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}\right)\right\}\hfill \\ =1-{\int }_0^{x=\infty }x{\zeta }_{d,i}{R}_{d,00,i}^{m}d\left[Pr\left(\sum _{l\in {\mathrm{\Phi }}_{d,i}}{f}_{d,l0}{R}_{d,l0,i}^{-m}+\sum _{j\in {\mathrm{\Phi }}_{c,i}}\frac{P_{c,i}}{P_{d,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}\le x\right)\right]\hfill \\ =\mathrm{E}\left[\prod _{l\in {\mathrm{\Phi }}_{d,i}}{\mathrm{e}}^{\left(-{\zeta }_{d,i}{R}_{d,00,i}^m{f}_{d,l0}{R}_{d,l0,i}^{-m}\right)}\right]\times \mathrm{E}\left[\prod _{j\in {\mathrm{\Phi }}_{c,i}}{\mathrm{e}}^{\left(-{\zeta }_{d,i}{R}_{d,00,i}^m\frac{P_{c,i}}{P_{d,i}}{f}_{c,j0}{R}_{c,j0,i}^{-m}\right)}\right]\hfill \\ ={\mathcal{L}}_{f_{d,l0}}\left({\zeta }_{d,i}{R}_{d,00,i}^m\right)\times {\mathcal{L}}_{f_{c,j0}}\left({\zeta }_{d,i}{R}_{d,00,i}^m\right)\hfill \end{array}.$$

(20)

From Laplace transform definition and stochastic geometry theory in [35], below equations are obtained

$$\begin{array}{c}{\mathcal{L}}_{f_{d,l0}}\left({\zeta }_{d,i}{R}_{d,00,i}^m\right)={\mathrm{e}}^{\left(-{\delta }_{d,i}{\int }_0^{x=\infty }\mathrm{E}\left(f_{d,l0}\right)\left(1-e^{-{\zeta }_{d,i}{R}_{d,00,i}^m{x}^{-m}}\right)dx\right)}\hfill \\ ={\mathrm{e}}^{\left(-{\delta }_{d,i}\pi R_{d,00,i}^2{\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right)\right)}\hfill \end{array},$$

(21)

whereas $\mathrm{\Gamma }\left(x\right)={\int }_0^{\infty }{e}^{-t}{t}^{x-1}dt$.

Similarly, the function Laplace transformation of ${\mathcal{I}}_{id,c0,i}$ as

$$\begin{array}{c}{\mathcal{L}}_{f_{c,j0}}\left({\zeta }_{d,i}{R}_{d,00,i}^m\right)={\mathrm{e}}^{\left(-{\delta }_{c,i}{\int }_0^{x=\infty }\left(f_{c,j0}\right)\left(1-{\mathrm{e}}^{-{\zeta }_{d,i}{R}_{d,00,i}^m\frac{P_{c,i}}{P_{d,i}}{x}^{-m}}\right)dx\right)}\hfill \\ ={\mathrm{e}}^{\left(-{\delta }_{c,i}\pi {\zeta }_{d,i}^{\frac{2}{m}}{R}_{d,00,i}^2{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right)\right)}\hfill \end{array}.$$

(22)

By substituting (21) and (22) into (20), the result in (18) can be obtained. The proof for Proposition 1 ends here. □

Remark 2. 

Proposition 1 discloses the relation between a certain number of the network’s key parameters and the typical D2D receiver’s STP. In particular, as the threshold value in the $i_{th}$ band, ${\zeta }_{d,i}$, increases, the ${\gamma }_{d,i}\ge {\zeta }_{d,i}$ condition becomes more difficult to be satisfied leading to the decrease of STP. Moreover, as $R_{d,00,i}$ increases, the STP decreases. This is because the increase in the distance makes the channel fading more serious. On the other hand, the lower the density of the D2D users ${\delta }_{d,i}$ or cellular users ${\delta }_{c,i}$, the higher the STP. This can be utilized for alleviating the network interference resulted from different users. Moreover, $P_{d,i}$ decrease is associated with the STP decrease. Last but not least, ${\zeta }_{d,i}$, $R_{d,00,i}$, ${\delta }_{c,i}$, ${\delta }_{d,i}$, and $P_{c,i}$ increase will lead to the STP decrease. The parameters mentioned in the two previous sentences characterize the cellular transmission power, all of which, after being modified as stated, will introduce interference to the D2D communication, thus, causing the decline of the STP.

A.2. Typical Base Station

The STP of the typical D2D pair transmission and the typical BS in the $i_{th}$ band are derived similarly. This formula for the typical BS is presented in the Proposition 2 below.

Proposition 2. 

The STP of the typical BS in the $i_{th}$ band has to satisfy

$$Pr\left({\gamma }_{c,i}\ge {\zeta }_{c,i}\right)=e^{-{\Theta }_{c,i}\left[{\delta }_{c,i}+{\delta }_{d,i}{\left(\frac{P_{d,i}}{P_{c,i}}\right)}^{\frac{2}{m}}\right]},$$

(23)

whereas ${\zeta }_{c,i}$ denotes the SIR threshold of cellular transmission, and ${\Theta }_{c,i}=\pi {\zeta }_{c,i}^{\frac{2}{m}}{R}_{c,00,i}^2\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right)$.

Proof. 

This proof is similar to the proof of Proposition 1. □

Remark 3. 

From Proposition 2, it should be noticed that the typical BS varies dependently on the network key parameters. As stated previously, there is interference caused by the transmission power of the D2D communication to the network. Thus, the increase in $P_{d,i}$, and decrease in ${\zeta }_{c,i}$, $R_{d,00,i}$, ${\delta }_{c,i}$, ${\delta }_{d,i}$, and $P_{c,i}$ will result in the STP decrease. Furthermore, the more the power usage for the cellular transmission, the higher the ${\gamma }_{c,i}$, followed by the higher STP.

B. Three Time Slot Communication Mode

Proposition 3. 

The STP of the typical receiver D2D user through D2D${}_r$ with DF protocol at D2D${}_a$, D2D${}_b$, is given respectively by

$$Pr\left({\gamma }_{a,i}^{3TS}\ge {\zeta }_{d,i}\right)=e^{-{\Theta }_{a,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(24)

and

$$Pr\left({\gamma }_{b,i}^{3TS}\ge {\zeta }_{d,i}\right)=e^{-{\Theta }_{b,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(25)

whereas ${\Theta }_{a,i}^{3TS}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2\left(1+{\alpha }^2+{\beta }^{-\frac{2}{m}}\right)$, ${\Theta }_{b,i}^{3TS}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2\left(1+{\alpha }^2+{\alpha }^2{\left(1-\beta \right)}^{-\frac{2}{m}}\right)$.

Proof. 

Utilizing Proposition 1, with regard to (12), (16), the STP in the first time slot is formulated as

$$Pr\left\{{\gamma }_{ar,i}\ge {\zeta }_{d,i}\right\}=e^{-{\Theta }_{ar,i}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(26)

whereas ${\Theta }_{ar,i}=\pi {\zeta }_{d,i}^{\frac{2}{m}}{\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right)$.

Likewise, from (13) and (17), the STP in the second time slot is formulated as

$$Pr\left\{{\gamma }_{br,i}\ge {\zeta }_{d,i}\right\}=e^{-{\Theta }_{br,i}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(27)

whereas ${\Theta }_{br,i}=\pi {\zeta }_{d,i}^{\frac{2}{m}}{\left(\frac{\alpha R_{d,00,i}}{1+\alpha }\right)}^2\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right)$.

In the third time slot, based on (14)–(17), the STP at D2D${}_a$ and D2D${}_b$ are respectively formulated as

$$Pr\left\{{\gamma }_{ra,i}\ge {\zeta }_{d,i}\right\}=e^{-{\Theta }_{ra,i}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(28)

and

$$Pr\left\{{\gamma }_{rb,i}\ge {\zeta }_{d,i}\right\}=e^{-{\Theta }_{rb,i}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]},$$

(29)

whereas ${\Theta }_{ra,i}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2{\left(\frac{1}{\beta }\right)}^{\frac{2}{m}}$, and ${\Theta }_{rb,i}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{\alpha R_{d,00,i}}{1+\alpha }\right)}^2{\left(\frac{1}{1-\beta }\right)}^{\frac{2}{m}}$.

As aforementioned, in 3TS mode, one cycle of signal transmission consists of three links indicating the flows of information: D2D${}_a$→ D2D${}_r$, D2D${}_b$→ D2D${}_r$, then D2D${}_r$→ D2D${}_a$ and D2D${}_b$. At the start of every cycle, the D2D user attempts to send some packets from its queue. To evaluate the success of the packet sending to the D2D${}_r$, the SIR value at the D2D${}_r$ is compared with the SIR threshold value of the overall D2D transmission. If the D2D${}_r$’s SIR is greater than the network’s SIR, an acknowledgement (ACK) message is forwarded to the D2D user indicating that the transmission is successful. Those packets are then removed from the queue. On the other hand, the packets remain on top of the queue waiting for another transmission round.

Hence, the STP end-to-end SIR with DF protocol at UED${}_a$ in the 3TS mode can be given by

$$\begin{array}{c}Pr\left({\gamma }_{a,i}^{3TS}\ge {\zeta }_{d,i}\right)=Pr\left({\gamma }_{ar,i}\ge {\zeta }_{d,i}\right)Pr\left({\gamma }_{br,}\ge {\zeta }_{d,i}\right)Pr\left({\gamma }_{ra,i}\ge {\zeta }_{d,i}\right)\\ =e^{-{\Theta }_{a,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]}\end{array},$$

(30)

whereas ${\Theta }_{a,i}^{3TS}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2\left(1+{\alpha }^2+{\beta }^{-\frac{2}{m}}\right)$.

Similarly, the STP end-to-end SIR with DF protocol at UED${}_b$ in the 3TS mode can be given by

$$\begin{array}{c}Pr\left({\gamma }_{b,i}^{3TS}\ge {\zeta }_{d,i}\right)=Pr\left({\gamma }_{i,ar}\ge {\zeta }_{d,i}\right)Pr\left({\gamma }_{i,br}\ge {\zeta }_{d,i}\right)Pr\left({\gamma }_{i,rb}\ge {\zeta }_{d,i}\right)\\ =e^{-{\Theta }_{b,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]}\end{array},$$

(31)

whereas ${\Theta }_{b,i}^{3TS}=\pi {\zeta }_{d,i}^{\frac{2}{m}}\mathrm{\Gamma }\left(1+\frac{2}{m}\right)\mathrm{\Gamma }\left(1-\frac{2}{m}\right){\left(\frac{R_{d,00,i}}{1+\alpha }\right)}^2\left(1+{\alpha }^2+{\alpha }^2{\left(1-\beta \right)}^{-\frac{2}{m}}\right)$. This is the end of the proof for Proposition 3. □

4. Performance Energy Efficiency

Herein this section, the D2D communication performance in the K bands is studied in 2TS and 3TS mode. One of the factors to consider is the influence of the cellular system given that the D2D users and two-way relay assisting the communication to share the same cellular spectrum resources. So far, the STP of typical D2D receivers is derived. This is an important indicator for assessing the D2D network performance. In the following subsection, there are two others investigated indicators so-called total average transmissions rate (TATR), and total average energy efficiency (TAEE) of D2D communication.

Total Average Transmissions Rate and Total Average Energy Efficiency

In this subsection, the exact expression of the TATR is derived. The TAEE of D2D communication on multiple bands is then calculated. Subsequently, the TAEE optimizing formulation is done.

A. Two Time Slot Communication

According to Proposition 1, let $TAT{R}_{d,i}^{2TS}$ denoted the TATR of a D2D pair operating in 2TS mode on the $i_{th}$ band, in one round of communication, is given by [39]

$$\begin{array}{cc}TAT{R}_{d,i}^{2TS}& =2\times {\delta }_{d,i}\left[W_i{log}_2\left(1+{\zeta }_{d,i}\right)Pr({\gamma }_{d,i}^{2TS}\ge {\zeta }_{d,i})\right]\\ & =2W_i{\delta }_{d,i}{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{d,i}^{2TS}\left[{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}+{\delta }_{d,i}\right]}\end{array},$$

(32)

whereas the $W_i$ is the bandwidth of the $i_{th}$ band.

The TAEE is defined as the TATR divided by the total power consumption as a product of ${\delta }_{d,i}{P}_{d,i}$ in [40]. Accordingly, the TAEE of D2D communication in K bands can be formulated as

$$\begin{array}{c}TAE{E}_d^{2TS}=\sum _{i=1}^K\frac{TAT{R}_{d,i}^{2TS}}{{\delta }_{d,i}{P}_{d,i}}\hfill \\ =\sum _{i=1}^K\frac{{\mathcal{A}}_i^{2TS}}{P_{d,i}}{\mathrm{e}}^{-{\mathcal{B}}_i^{2Ts}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}\hfill \end{array},$$

(33)

whereas ${\mathcal{A}}_i^{2TS}=2W_i{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{d,i}^{2TS}{\delta }_{d,i}}$, and ${\mathcal{B}}_i^{2TS}={\Theta }_{d,i}^{2TS}{\delta }_{c,i}{\left(P_{c,i}\right)}^{\frac{2}{m}}$.

B. Three Time Slot Communication

Given the STP of typical receiver D2D user through two-way relay-assisted D2D user in (24), the average (data) transmission rate (ATR) at D2D${}_a$ in the $i_{th}$ band is formulated as

$$\begin{array}{c}AT{R}_{a,i}^{3TS}=W_i{log}_2\left(1+{\zeta }_{d,i}\right)Pr\left({\gamma }_{a,i}^{3TS}\ge {\zeta }_{d,i}\right)\hfill \\ =W_i{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{a,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]}\hfill \end{array}.$$

(34)

Similarly, from (25), the ATR at D2D${}_b$ in the $i_{th}$ band is formulated as

$$\begin{array}{c}AT{R}_{b,i}^{3TS}=W_i{log}_2\left(1+{\zeta }_{d,i}\right)Pr\left\{{\gamma }_{b,i}^{3TS}\ge {\zeta }_{d,i}\right\}\hfill \\ =W_i{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{b,i}^{3TS}\left[{\delta }_{d,i}+{\delta }_{r,i}+{\delta }_{c,i}{\left(\frac{P_{c,i}}{P_{d,i}}\right)}^{\frac{2}{m}}\right]}\hfill \end{array}.$$

(35)

Utilizing (34) and (35), the TATR of typical receiver D2D user through the assisting relay with DF protocol in 3TS can be obtained as follows

$$TAT{R}_{d,i}^{3TS}={\delta }_{d,i}\left(AT{R}_{a,i}^{3TS}+AT{R}_{b,i}^{3TS}\right).$$

(36)

Correspondingly, the TAEE of the typical receiver D2D user in 3TS mode in the K bands is formulated as follows

$$\begin{array}{c}TAE{E}_{d,i}^{3TS}=\sum _{i=1}^K\frac{TAT{R}_{d,i}^{3TS}}{{\delta }_{d,i}{P}_{d,i}}\hfill \\ =\sum _{i=1}^K\frac{{\mathcal{A}}_{a,i}^{3TS}}{P_{d,i}}{e}^{-{\mathcal{B}}_{a,i}^{3TS}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}+\sum _{i=1}^K\frac{{\mathcal{A}}_{b,i}^{3TS}}{P_{d,i}}{e}^{-{\mathcal{B}}_{b,i}^{3TS}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}\hfill \end{array},$$

(37)

whereas ${\mathcal{A}}_{a,i}^{3TS}=W_i{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{a,i}^{3TS}\left({\delta }_{d,i}+{\delta }_{r,i}\right)}$, ${\mathcal{B}}_{a,i}^{3TS}={\Theta }_{a,i}^{3TS}{\delta }_{c,i}{\left(P_{c,i}\right)}^{\frac{2}{m}}$, ${\mathcal{A}}_{b,i}^{3TS}=W_i{log}_2\left(1+{\zeta }_{d,i}\right)e^{-{\Theta }_{b,i}^{3TS}\left({\delta }_{d,i}+{\delta }_{r,i}\right)}$, and ${\mathcal{B}}_{b,i}^{3TS}={\Theta }_{b,i}^{3TS}{\delta }_{c,i}{\left(P_{c,i}\right)}^{\frac{2}{m}}$.

Specifically, the TAEE of D2D communication in 2TS and 3TS mode are the objective functions of the optimization problems in this paper. Their formulations are presented in the following section.

5. Optimization Problem

The main focus of this section is on the optimization problem of the TAEE formulation given the network constraints. It should be noted that individual users’ EE is affected by the interference introduced by the cellular and D2D transmission.

5.1. Optimization Total Average Energy Efficiency in 2TS

An optimization problem is formulated aiming at maximizing the TAEE of the D2D users in this subsection. This formulation, according to (33), applied in the K bands, is rewritten as

$$\begin{array}{cc}\underset{P_{d,i}}{max}\hfill & TAE{E}_d^{2TS}=\sum _{i=1}^K\frac{{\mathcal{A}}_i^{2TS}}{P_{d,i}}{\mathrm{e}}^{-{\mathcal{B}}_i^{2Ts}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}\\ \mathrm{subject}\mathrm{to}\hfill & \left(i\right),\left(ii\right),\left(iii\right),\left(iv\right)\end{array},$$

(38)

whereas given that (i) $\sum _{i=1}^K{P}_{d,i}\le P_d$; (ii) $0\le P_{d,i}\le P_{d,i,max}$; (iii) $\left[1-Pr({\gamma }_{d,i}^{2TS}\ge {\zeta }_{d,i})\right]\le {\epsilon }_{d,i}$; and (iv) $\left[1-Pr({\gamma }_{c,i}\ge {\zeta }_{c,i})\right]\le {\epsilon }_{c,i}$.

The optimal resource allocation scheme aims at maximizing the $TAE{E}_d^{2TS}$ in (38) considering the $P_{d,i}$ under certain constraints being (i) the total transmission power of the D2D users over all the bands must not exceed the threshold value of $P_d$; (ii) the power of D2D users in each band is greater than or equal to zero and does not exceed the allowable threshold value of $P_{d,i,max}$; respectively in (iii) and (iv), the threshold values ${\epsilon }_{c,i}$ and ${\epsilon }_{d,i}$ are established as the upper limits for the OP of the cellular and D2D users in order to maintain the QoS for the network users.

With regard to the Proposition 1 and Proposition 2, in combination with (ii), (iii), and (iv) in (38), the optimization problem is simplified utilizing the feasible regions of $P_{d,i}$ as follows

$$P_{d,i,down}^{2TS}\le P_{d,i}\le P_{d,i,up}^{2TS},$$

(39)

whereas $P_{d,i,down}^{2TS}=P_{c,i}{\left[\left(-\frac{ln\left(1-{\epsilon }_{d,i}\right)}{{\Theta }_{d,i}^{2TS}}-{\delta }_{d,i}\right)\frac{1}{{\delta }_{c,i}}\right]}^{-\frac{m}{2}}$, and $P_{d,i,up}^{2TS}=\min \left\{P_{c,i}{\left[\left(-\frac{ln\left(1-{\epsilon }_{c,i}\right)}{{\Theta }_{c,i}^{2TS}}-{\delta }_{c,i}\right)\frac{1}{{\delta }_{d,i}}\right]}^{-\frac{m}{2}},P_{d,i,max}\right\}$.

Hence, (38) can be transformed to

$$\begin{array}{cc}\underset{P_{d,i}}{max}\hfill & TAE{E}_d^{2TS}=\sum _{i=1}^K\underset{f_i\left(P_{d,i}\right)}{\underbrace{\frac{{\mathcal{A}}_i^{2TS}}{P_{d,i}}{\mathrm{e}}^{-{\mathcal{B}}_i^{2Ts}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}}}\\ \mathrm{subject}\mathrm{to}\hfill & \left(a\right)\end{array},$$

(40)

whereas $\left(a\right)$ following $P_{d,i,down}^{2TS}\le P_{d,i}\le P_{d,i,up}^{2TS}$, and $\sum _{i=1}^K{P}_{d,i}=P_d$ for $f_i\left(P_{d,i}\right)$ constraint.

5.2. Optimization Total Average Energy Efficiency in 3TS

Similar to the previous subsection, the optimal transmission power of the two-way relay-assisted D2D communication with DF protocol in 3TS mode in K bands is calculated as follows

$$\begin{array}{cc}\underset{P_{d,i}}{max}\hfill & TAE{E}_d^{3TS}=\sum _{i=1}^K\underset{f_{a,i}\left(P_{d,i}\right)}{\underbrace{\frac{{\mathcal{A}}_{a,i}^{3TS}}{P_{d,i}}{e}^{-{\mathcal{B}}_{a,i}^{3TS}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}}}+\sum _{i=1}^K\underset{f_{b,i}\left(P_{d,i}\right)}{\underbrace{\frac{{\mathcal{A}}_{b,i}^{3TS}}{P_{d,i}}{e}^{-{\mathcal{B}}_{b,i}^{3TS}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}}}\\ \mathrm{subject}\mathrm{to}\hfill & \left(b\right)\end{array}$$

(41)

whereas in $\left(b\right)$, there are $P_{d,i,down}^{3TS}\le P_{d,i}\le P_{d,i,up}^{3TS}$, $\sum _{i=1}^K{P}_{d,i}=P_d$ for constraining $f_{a,i}\left(P_{d,i}\right)$ and $f_{b,i}\left(P_{d,i}\right)$ in the $i_{th}$ band.

Using Proposition 3, and from (39), ones can obtain $P_{d,i,down}^{3TS}=max\left\{P_{c,i}{\left[\left(-\frac{ln\left(1-{\epsilon }_{d,i}\right)}{{\Theta }_{a,i}^{3TS}}-{\delta }_{d,i}-{\delta }_{r,i}\right)\frac{1}{{\delta }_{c,i}}\right]}^{-\frac{m}{2}},P_{c,i}{\left[\left(-\frac{ln\left(1-{\epsilon }_{d,i}\right)}{{\Theta }_{b,i}^{3TS}}-{\delta }_{d,i}-{\delta }_{r,i}\right)\frac{1}{{\delta }_{c,i}}\right]}^{-\frac{m}{2}}\right\}$, and $P_{d,i,up}^{3TS}=\min \left\{P_{c,i}{\left[\left(-\frac{ln\left(1-{\epsilon }_{c,i}\right)}{{\Theta }_{c,i}^{2TS}}-{\delta }_{c,i}\right)\frac{1}{{\delta }_{d,i}}\right]}^{-\frac{m}{2}},P_{d,i,max}\right\}$.

However, having been proven to be non-convex, the objective function TAEE in (40) and (41) can not be solved by convex optimization theory. Besides, being different from the previous optimization problem where only a single band is considered [28,32,34,41,42], a Derivative-Based (DB) algorithm is proposed to solve the problem in case of multiple bands and presented in the next subsection.

5.3. Derivative-Based Algorithm

This subsection presents the DB algorithm proposed to solve the aforementioned non-convex TAEE optimization problem. In the existing literature, there is the BB algorithm [33] adopted to solve a number of challenging optimization problems in wireless communication networks [42,43]. However, having considered the limit of the BB algorithm, the authors instead establish a DB algorithm to solve the (40) and (41). This method exploits the objective function property of being the sum of several sub-functions and attempts to maximize those sub-functions. Firstly, the study is conducted on a D2D pair in 2TS mode.

A. Two Time Slot Communication

As in (33), it can be observed that $TAE{E}_d^{2TS}$ is a sum of K sub-functions. Eliminating the constraint of $\sum _{i=1}^K{P}_{d,i}=P_d$ in (40) makes every $P_{d,i}$ become independent on each other. Consequently, the maximum $TAE{E}_d^{2TS}$ can be acquired as $E{E}_{d,i}$ is maximum on the feasible region. It is obvious that maximizing one at a time every EE in $i_{th}$ band is more practical than having the (40) solved.

Thereby, the global maximum $P_{d,i,max}$ of the $E{E}_{d,i}$ of D2D communication in the $i_{th}$ band can be calculated given that it is in the range of $\left[P_{d,i,down}^{2TS},P_{d,i,up}^{2TS}\right]$. The $f_i\left(P_{d,i}\right)$ is maximized when $P_{d,i}=P_{d,i,max}$.

Accordingly, re-defining $P_{d,i}=P_{d,i,max}$ for $i=1,2,\dots ,K$ band is done. The $P_{d,i}$ is then adjusted so that it satisfies $\sum _{i=1}^K{P}_{d,i}=P_d$ and produces the lowest EE reduction. Based on this principal, the DB algorithm is proposed, and is implemented in details henceforward. Firstly, the $P_{d,i,max}$ is calculated in the following Theorem 1.

Theorem 1. 

The global maximum point of $f_i\left(P_{d,i}\right)$ on the feasible region $\left[P_{d,i,down}^{2TS},P_{d,i,up}^{2TS}\right]$ in (40) is given by

$$P_{d,i,max}=\left\{\begin{array}{c}{P}_{d,i,up}^{2TS},P_{d,i,up}^{2TS}\le {\left(\frac{2{\mathcal{B}}_i^{2TS}}{m}\right)}^{\frac{m}{2}}\hfill \\ {\left(\frac{2{\mathcal{B}}_i^{2TS}}{m}\right)}^{\frac{m}{2}},P_{d,i,down}^{2TS}<{\left(\frac{2{\mathcal{B}}_i^{2TS}}{m}\right)}^{\frac{m}{2}}<P_{d,i,up}^{2TS}\hfill \\ P_{d,i,down}^{2TS},P_{d,i,down}^{2TS}\ge {\left(\frac{2{\mathcal{B}}_i^{2TS}}{m}\right)}^{\frac{m}{2}}\hfill \end{array}\right..$$

(42)

Proof. 

From (40), $f_i\left(P_{d,i}\right)$ is derived

$$\frac{\partial f_i\left(P_{d,i}\right)}{\partial P_{d,i}}=\frac{{\mathcal{A}}_i^{2TS}}{P_{d,i}^2}\times e^{-{\mathcal{B}}_i^{2TS}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}}\times \left(\frac{2{\mathcal{B}}_i^{2TS}}{m}{\left(\frac{1}{P_{d,i}}\right)}^{\frac{2}{m}}-1\right)$$

(43)

It appears that in (43), the first and second term are greater than zero. Thus, focus is paid only on the last term $\frac{\partial f_i\left(P_{d,i}\right)}{\partial P_{d,i}}$ given that it results in positive value in $\left(0,{\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}\right)$ and negative in $\left({\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}},+\infty \right)$. Its global maximum is at $P_{d,i}={\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$.

It can be easily observed that $f_i\left(P_{d,i}\right)$ increases up to the demarcation point being the maximum ${\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$, then decreases as $P_{d,i}$ continues to increase. Before discussing further, it should be noted that the calculated derivatives are in accordance with the $f_i\left(P_{d,i}\right)$, the above analysis is, thus, proven to be correct.

Subsequently, there are three cases to be considered given the relationship between the feasible region of $f_i\left(P_{d,i}\right)$ and the ${\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$ as follows

• Provided that $P_{d,i,up}\le {\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$, then there is a monotonic increase of $f_i\left(P_{d,i}\right)$ on the feasible region. Hence, $f_i\left(P_{d,i}\right)$ reaches its maximum at $P_{d,i}=P_{d,i,up}$ leading to $P_{d,i,max}=P_{d,i,up}$.
• Provided that $P_{d,i,down}<{\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}<P_{d,i,up}$, then the global maximum of $f_i\left(P_{d,i}\right)$ is located within the feasible region leading to $P_{d,i,max}={\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$.
• Provided that $P_{d,i,down}\ge {\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$, then there is a monotonic decrease of $f_i\left(P_{d,i}\right)$ on the feasible region. Hence, $f_i\left(P_{d,i}\right)$ reaches its maximum at $P_{d,i,max}=P_{d,i,down}$.

Theorem 1 holds true having considered the aforementioned cases in (42). □

As stated in Theorem 1, $P_{d,i,max}$ can be defined utilizing the relationship between ${\left(2B_i^{2TS}/\phantom{2B_i^{2TS}m}m\right)}^{\frac{m}{2}}$ and the feasible region $\left[P_{d,i,low}^{2TS},P_{d,i,up}^{2TS}\right]$ of $f_i\left(P_{d,i}\right)$.

Hence forward, the current $P_{d,i}$ value will be denoted as $P_{d,i,index}$. The method adopted to adjust the value of $P_{d,i}$ after assigning $P_{d,i,max}$ to $P_{d,i}$ is presented as follows

Assuming that $d=\sum _{i=1}^K{P}_{d,i,max}-P_d$, and $f=\frac{d}{n}$, whereas the adjustment step of $P_{d,i}$ is denoted as f and is controlled by parameter n. Because the global maximum point of $f_i\left(P_{d,i}\right)$ on the feasible region in (40) is adjusted, the $P_{d,i}$ is caused to deviate from $P_{d,i,max}$ following the below condition

$$f_i\left(P_{d,i,index}\right)>f_i\left(P_{d,i,index}-f\right).$$

(44)

Referring to Taylor’s theorem in [43], the $f_i\left(P_{d,i}\right)$ at $P_{d,i}=P_{d,i,index}$ by the first order Taylor polynomial is approximated as

$$f_i\left(P_{d,i,index}-f\right)\approx f_i\left(P_{d,i,index}\right)+f_i^{{}^{\prime }}\left(P_{d,i,index}\right)f.$$

(45)

Provided that $P_{d,i}$ is adjusted from $P_{d,i,index}$ to $P_{d,i,index}-f$, then, $E{E}_d$ is reduced by an amount of $\left|f_i\left(P_{d,i,index}\right)-f_i\left(P_{d,i,index}-f\right)\right|$. The reduced value is determined predominantly by $\left|f_i^{{}^{\prime }}\left(P_{d,i,index}\right)\right|$ as stated in (45). Thus, the $\left|f_i^{{}^{\prime }}\left(P_{d,i,index}\right)\right|$ is calculated for $i=1,2,\dots ,K$ and $P_{d,j}$ is adjusted from $P_{d,j,index}$ to $P_{d,j,index}-f$, whereas j satisfies the condition of $\left|f_j^{{}^{\prime }}\left(P_{d,j,index}\right)\right|\le \left|f_i^{{}^{\prime }}\left(P_{d,i,index}\right)\right|,\forall i=1,2,\dots ,K$. This process is replicated for a minimum of n times until which the condition $\sum _{i=1}^K{P}_{d,i}=P_d$ is satisfied, then, the near-optimal solution to (40) is obtained.

Based on the aforementioned analysis, the DB algorithm is formulated in the following Algorithm 1. Key steps are presented in details as follows

Algorithm 1: The DB algorithm for 2TS

B. Three Time Slot Communication

Being approached as the same manner as in Algorithm 1, the DB algorithm for solving the non-convex TAEE optimization problem of the two-way relay-assisted D2D communication with DF protocol in 3TS mode in K bands, as mentioned in (41), is shown in the following Algorithm 2.

Algorithm 2: The DB algorithm for 3TS

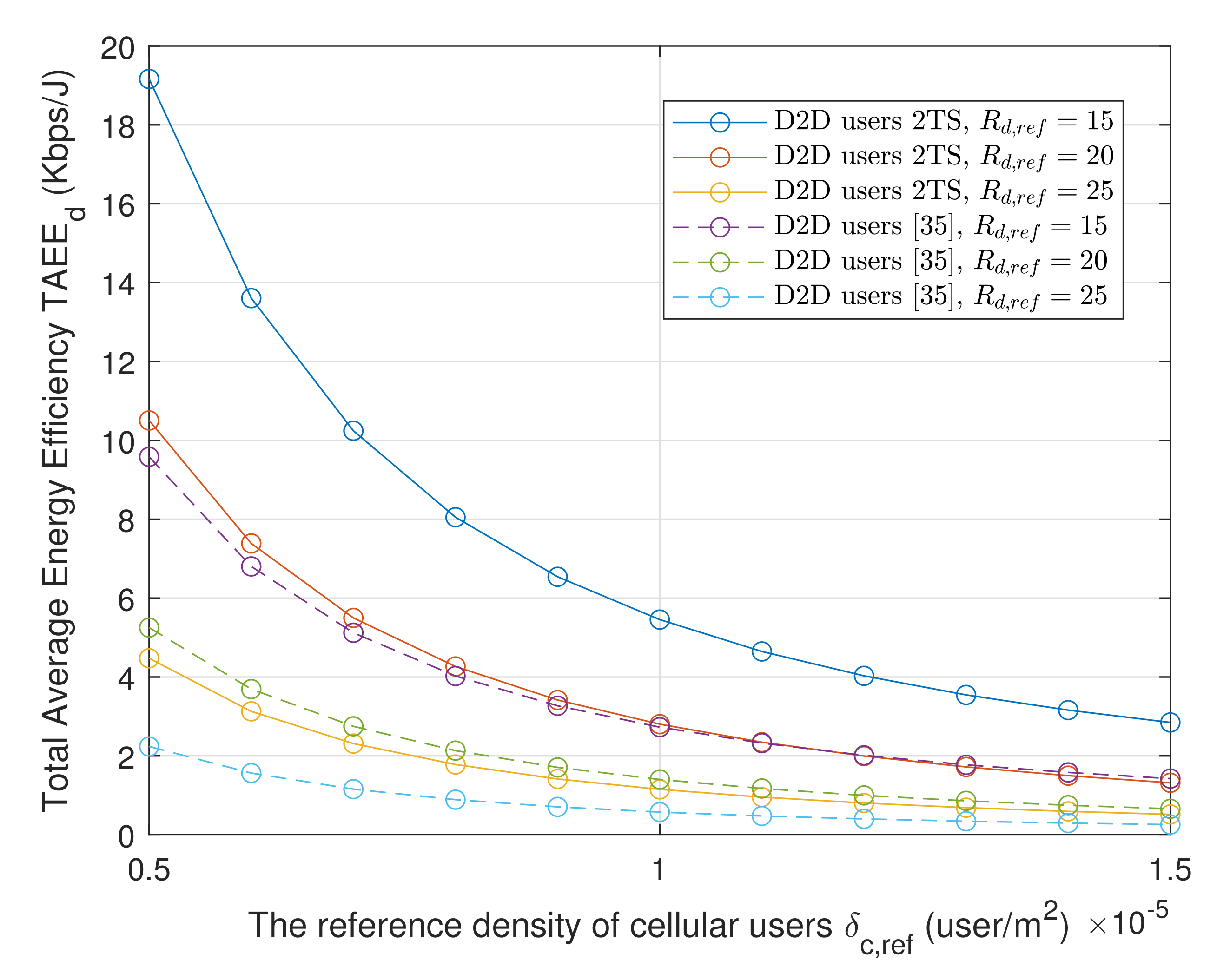
6. Numerical Results

Herein this section, the TAEE performance of the D2D communication in the 2TS and 3TS case is studied with the help of the DB algorithm in the K bands. The

Table 1. Simulation parameters.

Primary Parameters	Description	Values
K	Number of bands	5
$W_i$	Bandwidth ith	20 MHz
$P_{c,i}$	Cellular transmission power	125 mW
$P_{d,i}$	D2D user transmission power	60 mW
$P_{d,i,up}$	D2D user transmission power threshold	20 mW
m	Path loss coefficient	4
$\alpha$	Distances fraction between relay and D2D user	0.5
$\beta$	Power allocation at relay D2D user	0.5
${\epsilon }_{c,i}$	Cellular OP threshold	0.05
${\epsilon }_{d,i}$	D2D user OP threshold	0.05
${\zeta }_{c,i}$	Cellular SIR threshold	0 dB
${\zeta }_{d,i}$	D2D user SIR threshold	0 dB
$\left[R_{c,00,1},R_{c,00,2},\cdots ,R_{c,00,K}\right]$	Cellular link distance	$\left[50,60,70,80,90\right]$
$\left[R_{d,00,1},R_{d,00,2},\cdots ,R_{d,00,K}\right]$	D2D link distance	$\left[10,20,30,20,10\right]$
$\left[{\delta }_{c,1},{\delta }_{c,2},\cdots ,{\delta }_{c,K}\right]$	Cellular user density	$\left[10,1,10,10,10\right]\times {10}^{-5}$
$\left[{\delta }_{d,1},{\delta }_{d,2},\cdots ,{\delta }_{d,K}\right]$	D2D user density	$\left[10,1,10,10,10\right]\times {10}^{-4}$
$\left[{\delta }_{r,1},{\delta }_{r,2},\cdots ,{\delta }_{d,K}\right]$	Potential two-way relay D2D user density	$\left[10,1,10,10,10\right]\times {10}^{-4}$

below lists out the primary simulation parameters [32].

Figure 2 and Figure 3 plot the TAEE in all bands versus the density of D2D users, along with the transmission power of the cellular users calculated from the DB algorithm, in respectively 2TS and 3TS mode. There is the density setting of $\left[{\delta }_{d,1},{\delta }_{d,2},\cdots ,{\delta }_{d,5}\right]={\delta }_{d,\mathrm{ref}}\times [10,1,10,10,10]$. It can be observed that the TAEE obtained from the DB algorithm is nearly coincident with the optimal solution. On the other hand, there exists a considerable gap between the performance plot of the DB algorithm and the conventional BB algorithm [33]. It can be concluded that the DB algorithm yields near-optimal results and significantly outperforms the ones from conventional BB algorithm.

The two figures under consideration share the same common pattern being that after rising to a certain peak, the TAEE gradually declines as the ${\delta }_{d,ref}$ continues to increase further. This is because as the density of the users is small, the interference they cause through spectrum sharing is insignificant. This remains true up to a certain checkpoint. Hence, from the beginning, as ${\delta }_{d,ref}$ rises together with the ATR, the rise of the interference stays neglect-able resulting in higher and higher TAEE. Nevertheless, as ${\delta }_{d,ref}$ reaches its peak and continues to grow, the interference turns to be significant as there is a higher demand for energy consumption to coordinate the interference which causes the decline of the TAEE. To the direction of the black arrow indicating the $P_{c,i}$, the lowest curve corresponds to the highest $P_{c,i}$ and the highest curve corresponds to the lowest $P_{c,i}$. Accordingly, it can be observed that the TAEE curve tends to shift downward as the transmission power of the cellular users $P_{c,i}$ increases. In fact, the rise in $P_{c,i}$ results in more severe interference caused by the cellular transmission to the D2D communication. This rises as well the power demand for coordinating the interference thus causing the TAEE in overall to decrease.

It can be observed that TAEE performance in 3TS mode is remarkably better than in 2TS mode. This is because, in 2TS mode, the D2D direct link is utilized for signal transmission without two-way relay D2D users assisting the transmission with distance extension, Algorithms 1 and 2, resulting in lower performance. On the other hand, in two-way relay-assisted case, with small ${\delta }_{d,ref}$, the TAEE performance of the D2D network is highly boosted with the two-way relay’s assistance. In particular, the TAEE rises sharply as ${\delta }_{d,ref}$ increases from 1 to 3. The TAEE continues to increase with a lower rate in association with the increase of the D2D user density. The TAEE in 2TS and 3TS reaches its maximum value at ${\delta }_{d,ref}$ equals respectively to 5 or 6. Then, as the D2D user density increases further causing excessive interference to the D2D network, the TAEE performance gradually shrinks.

Figure 4 and Figure 5 plot the TAEE versus the cellular user density ${\delta }_{c,ref}$ in 2TS and 3TS mode. The higher the cellular user density, the lower the TAEE. This is because more cellular users introduce higher interference on D2D users. The D2D users, thus, have to consume more power to maintain the QoS leading to the exponential decline of the TAEE. It can be observed that the DB algorithm performs better than the conventional BB one. Nevertheless, as a very high-density level, there is not much difference between them since the TAEE at this level can not be enhanced further. Moreover, the TAEE is plotted for different $R_{d,ref}$ being the distance between two D2D users. As the $R_{d,ref}$ becomes higher, the TAEE tends to shift further downward since maintaining the QoS over longer distance requires higher power usage. Moving to the next figure, it can be seen that the TAEE performance in 3TS mode is similar to the 2TS mode but with an overall higher level. This further emphasizes the role of the communication mode in optimizing the transmission power of the cellular users. Besides, the two-way TAEE in 2TS and 3TS mode is compared with the one-way direct link TAEE in [31]. The TAEE is calculated by first solving the transmission power of the D2D users as in (40) and (41). Accordingly, after putting the transmission power of the cellular users, which is assumed to be constant, $P_{c,i}=325$ mW, and the power of devices into the DB algorithm, the TAEE is obtained. Similar to the TAEE in 2TS, the ${\delta }_{c,ref}$ increase is associated with the increase of the cellular users’ interference causing the TAEE to decline exponentially. The fact that higher overall TAEE is achieved in 3TS mode helps as well to enhance the D2D network in all bands. The TAEE, in the beginning, is considerably higher calculated from Algorithm 2 because they operate at the optimum transmission power.

7. Conclusions

This paper presents the maximization study of the TAEE of the D2D communication underlaying cellular networks in multi-hop 2TS and 3TS communication mode. First of all, by utilizing the stochastic geometry theory, the closed-form expressions for the STP and the TATR of both cellular and D2D users on multiple bands are derived. Accordingly, the optimization problem of maximizing the TAEE is formulated having considered the STP as the QoS of the cellular and D2D users in multi-hop two-way relay-assisted D2D network. Having proven that the TAEE optimization problem is non-convex, by taking advantage of the property of the objective function to be a sum of several sub-functions, a DB algorithm is proposed to collectively optimize the sub-functions to achieve the near-optimal solution for the objective one. The simulation results reveal that the performance of the authors’ proposed scheme is better than the currently known schemes in the literature. Besides, there is a remarkable EE enhancement accomplished by joint optimization of the transmission power of the cellular and D2D users. Developers can consider applying this method to the D2D communication of the 5G wireless networks in the future. Furthermore, it can be observed from the simulation results that the D2D direct link distance in 2TS mode; the one-way communication of cellular and D2D pair; and the D2D two-way relay user density in 3TS mode are the three factors that cause interference to the overall D2D network with different intensity. For the future study, band selection and power allocation can be considered for cross-tier interference minimization between the cellular and D2D users.