Can Effects of Temperature on Two-Phase Gas/Oil-Relative Permeabilities in Porous Media Be Ignored? A Critical Analysis
Abstract
1. Introduction
2. Fundamentals
2.1. Irreducible Water, Residual Oil, Critical Gas, and Liquid Saturation
2.2. Endpoint-Relative Permeability to Oil and Gas
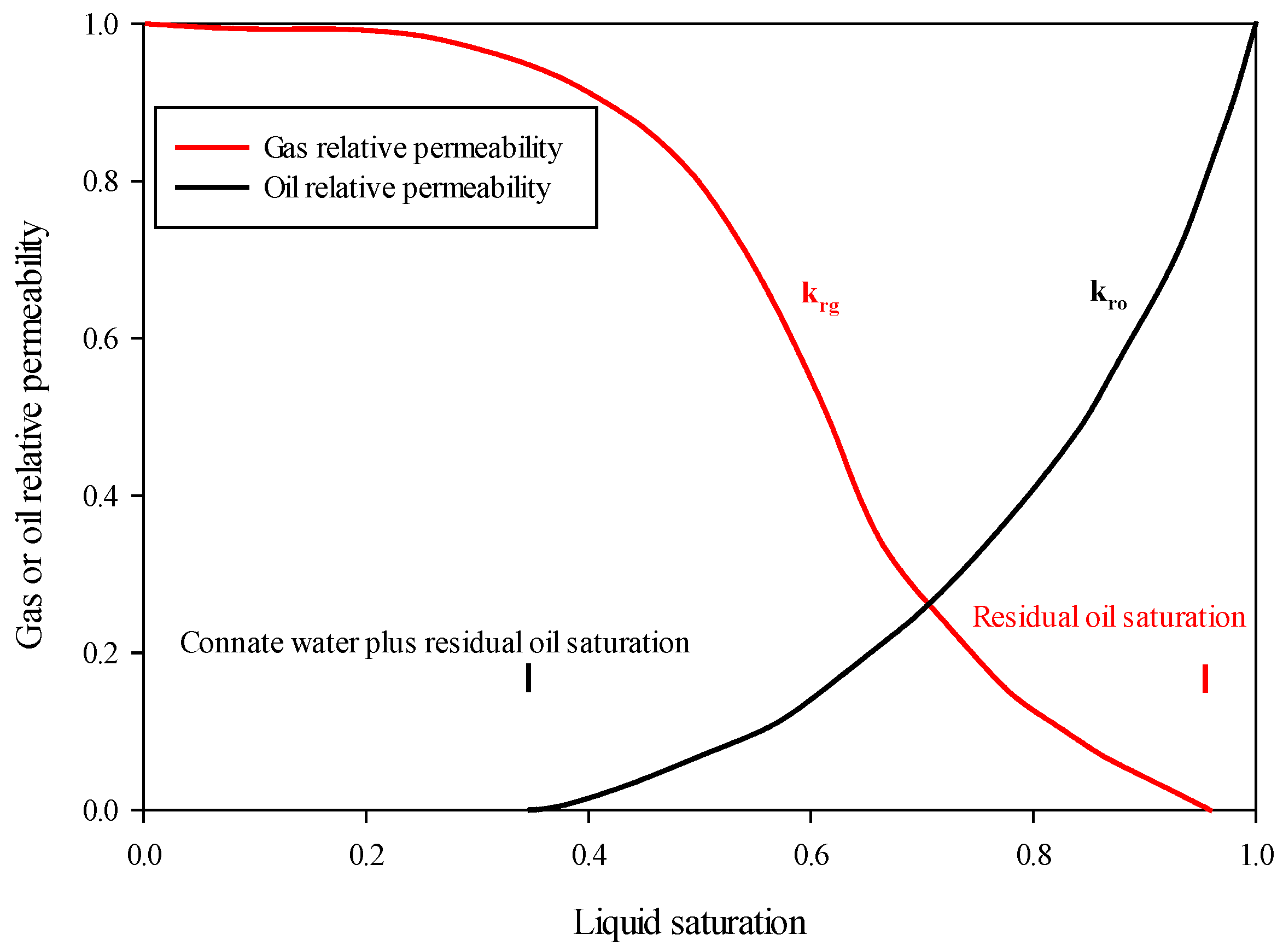
2.3. Shapes of Oil and Gas Relative Permeability Curves
3. Techniques for Measuring Gas/Oil-Relative Permeability
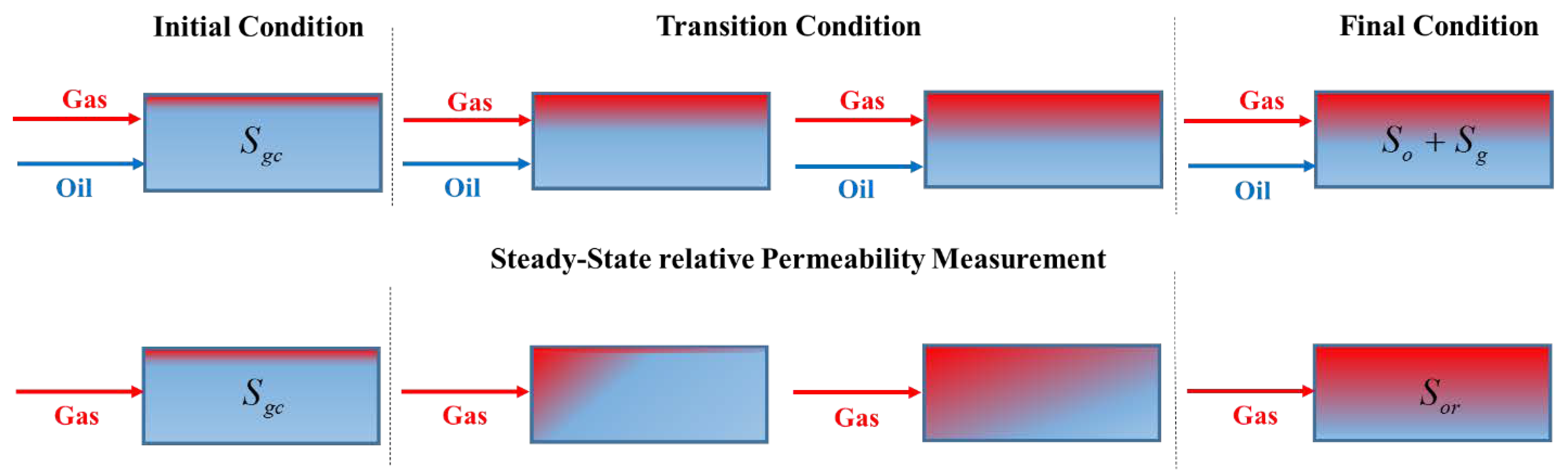
3.1. Steady-State Approach
3.2. Unsteady-State Approach
4. Challenges in Measuring Gas/Liquid-Relative Permeability
4.1. Gas Slippage Effect
4.2. Measurement Challenges
5. Effect of Temperature on Rock/Fluid Interactions and Properties
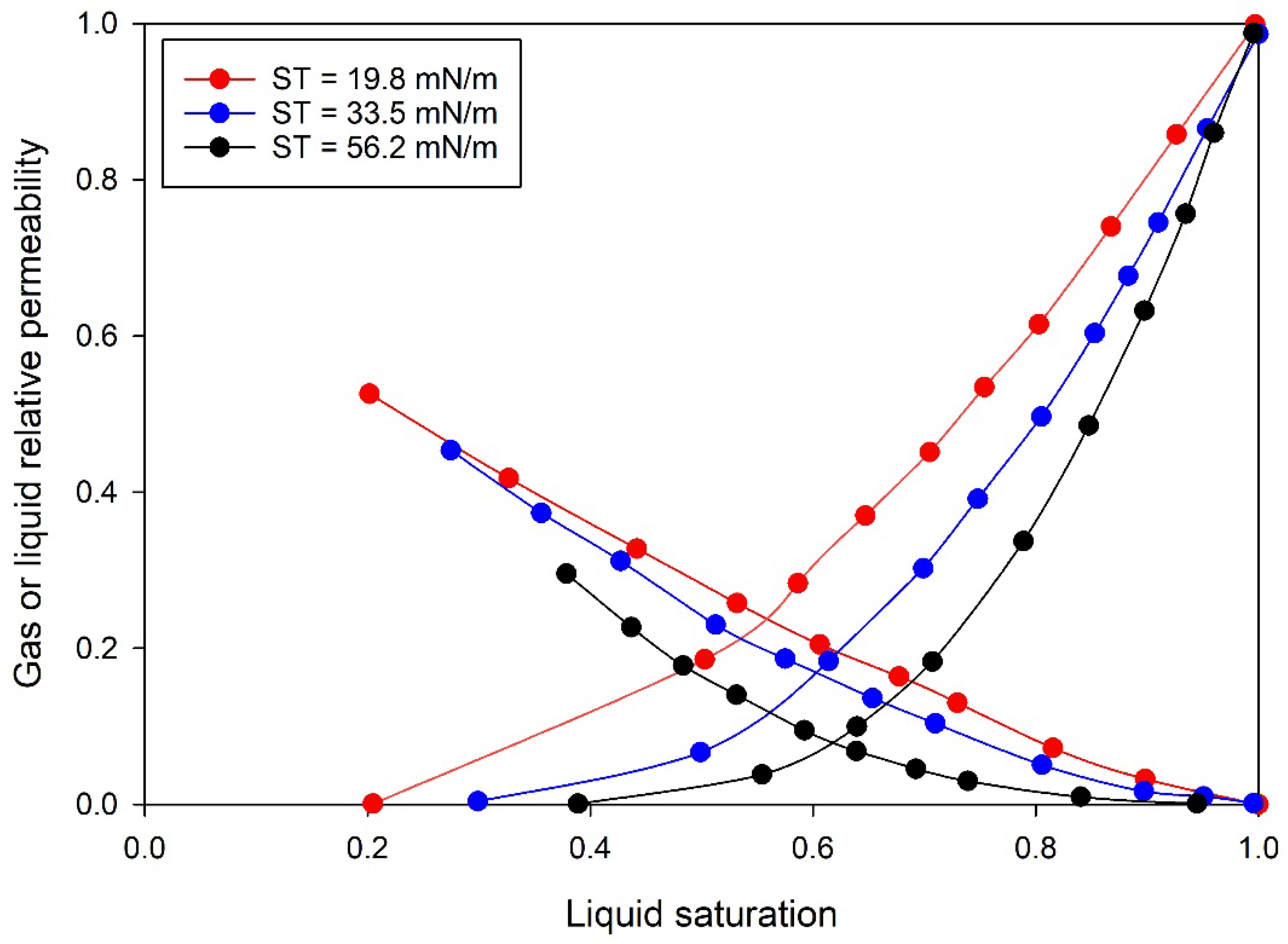
5.1. Surface Tension
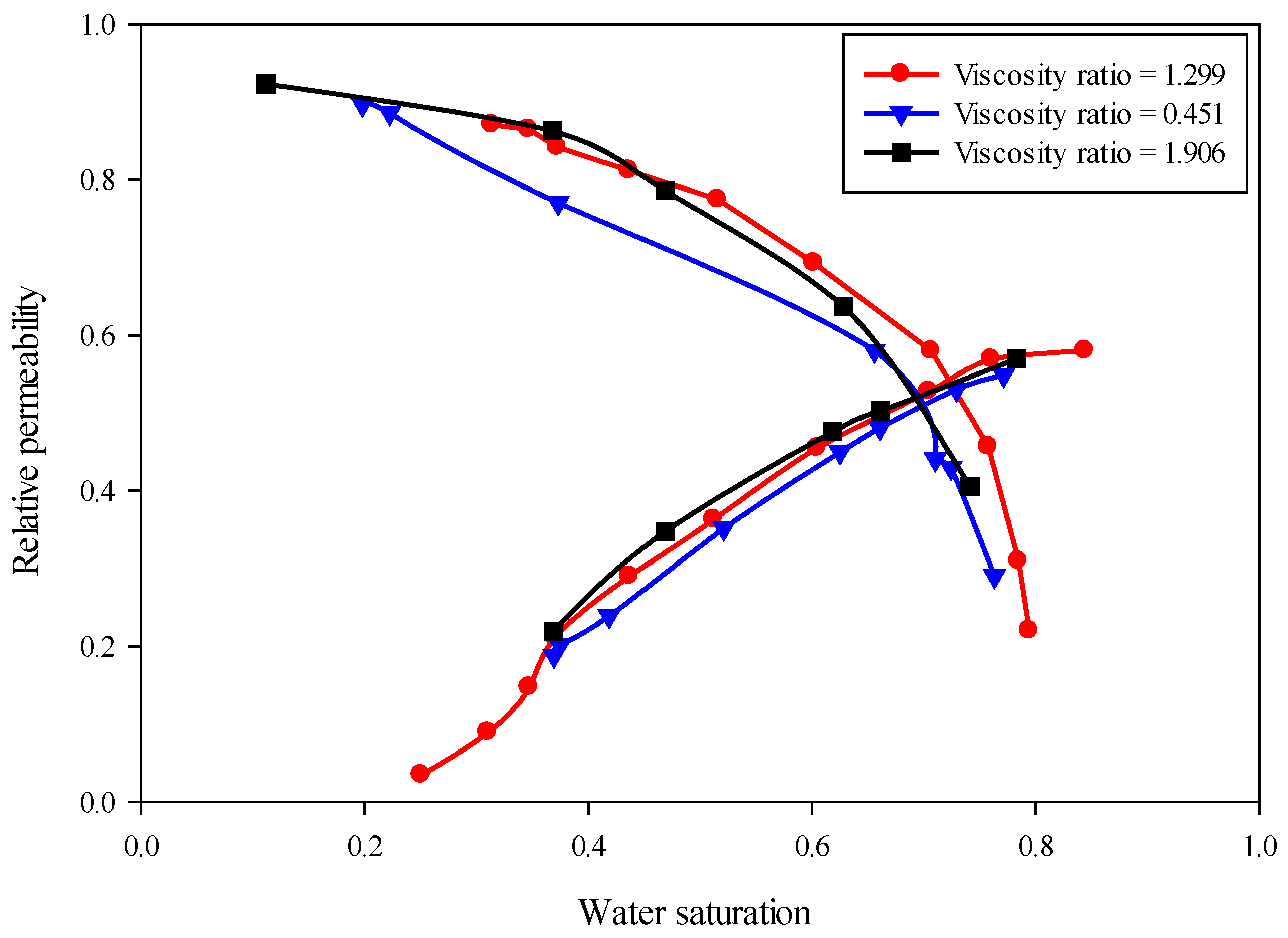
5.2. Viscosity Ratio
5.3. Wettability
6. Effect of Temperature on Gas/Oil-Relative Permeability Curves
6.1. Irreducible Water Saturation
6.2. Residual Oil Saturation
6.3. Critical Gas Saturation
7. Summary of Discussions
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| Notations | Meanings |
| Slip factor | |
| Absolute permeability to liquid | |
| Relative Permeability | |
| Relative Permeability to Gas | |
| Relative Permeability to Liquid | |
| Endpoint Relative Permeability to Liquid | |
| Mean pressure | |
| Saturation | |
| Oil Saturation | |
| Residual Oil Saturation | |
| Mean free path of the gas | |
| N/R | Not Reported |
| wt% | Weight percent |
| Proportionality factor | |
| Relative Permeability to Oil | |
| Absolute permeability to gas | |
| Relative Permeability to Water | |
| intrinsic permeability to gas at an infinite pressure | |
| Capillary number | |
| Average size of the capillaries | |
| Water Saturation | |
| Critical Gas Saturation | |
| Residual Liquid Saturation | |
| ST | Surface Tension |
| HP/HT | High pressure/high temperature |
References
- Ghoodjani, E.; Kharrat, R.; Vossoughi, M.; Bolouri, S.H. A review on thermal enhanced heavy oil recovery from fractured carbonate reservoirs. J. Pet. Environ. Biotehnol. 2011, 2. [Google Scholar] [CrossRef]
- Jiang, Q.; Thornton, B.; Russel-Houston, J.; Spence, S. Review of thermal recovery technologies for the clearwater and lower grand rapids formations in the cold lake area in Alberta. J. Can. Pet. Technol. 2010, 49, 2–13. [Google Scholar] [CrossRef]
- Irani, M.; Cokar, M. Understanding the Impact of Temperature-Dependent Thermal Conductivity on the Steam-Assisted Gravity-Drainage (SAGD) process. Part 1: Temperature front prediction. In Proceedings of the Heavy Oil Conference-Canada, Calgary, AB, Canada, 10–12 June 2014. [Google Scholar]
- Ashrafi, M.; Souraki, Y.; Torsaeter, O. Investigating the temperature dependency of oil and water relative permeabilities for heavy oil systems. Trans. Porous Med. 2014, 105, 517–537. [Google Scholar] [CrossRef]
- Hamouda, A.; Karoussi, O. Effect of temperature, wettability and relative permeability on oil recovery from oil-wet chalk. Energies 2008, 1, 19–34. [Google Scholar] [CrossRef]
- Punase, A.; Zou, A.; Elputranto, R. How do thermal recovery methods affect wettability alteration? J. Pet. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Kantzas, A.; Bryan, J.; Taheri, S. Fundamentals of fluid flow in porous media. Chapter 2: Pore size distribution. In Engineering Fluid Mechanics; Springer: Singapore, 2012; pp. 155–169. [Google Scholar]
- Klinkenberg, L. The Permeability of Porous Media to Liquids and Gases; American Petroleum Institute: New York, NY, USA, 1941. [Google Scholar]
- Letham, E.; Bustin, R. Klinkenberg gas slippage measurements as a means for shale pore structure characterization. Geofluids 2016, 16, 264–278. [Google Scholar] [CrossRef]
- Wu, K.; Li, X.; Guo, C.; Wang, C.; Chen, Z. A unified model for gas transfer in nanopores of shale-gas reservoirs: Coupling pore diffusion and surface diffusion. SPE J. 2016, 21, 1583–1611. [Google Scholar] [CrossRef]
- Anderson, W.G. Wettability literature survey-part 6: The effects of wettability on waterflooding. J. Pet. Technol. 1987, 39, 1605–1622. [Google Scholar] [CrossRef]
- Buckley, S.E.; Leverett, M. Mechanism of fluid displacement in sands. Trans. AIME 1942, 146, 107–116. [Google Scholar] [CrossRef]
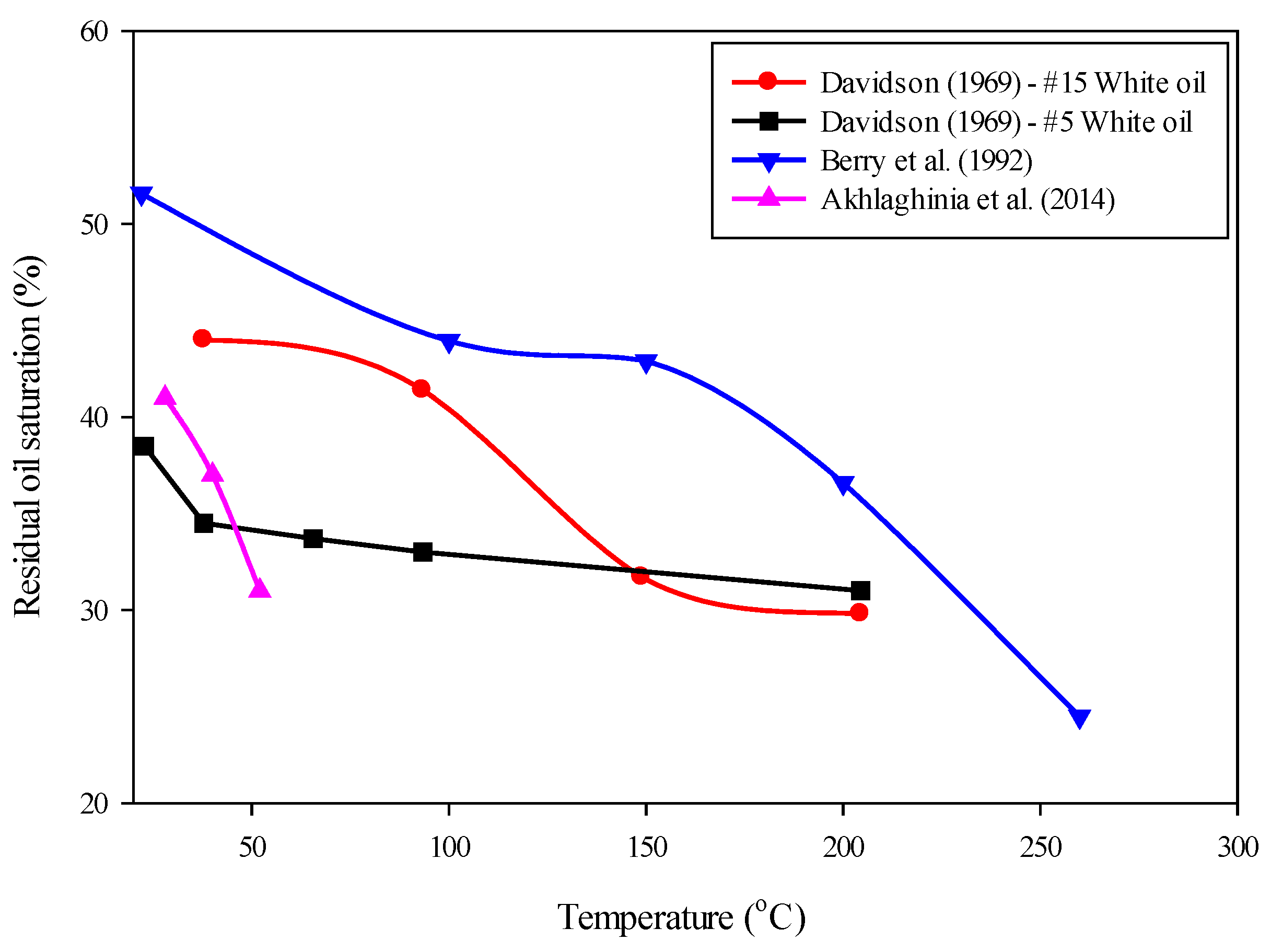
- Akhlaghinia, M.; Torabi, F.; Chan, C.W. Experimental investigation of temperature effect on three-phase relative permeability isoperms in heavy oil systems. Fuel 2014, 118, 281–290. [Google Scholar] [CrossRef]
- Berry, J.; Little, A.; Skinner, R. Differences in gas/oil and gas/water relative permeability. In Proceedings of the SPE/DOE Enhanced Oil Recovery Symposium, Tulsa, OK, USA, 22–24 April 1992. [Google Scholar]
- Longeron, D. Influence of very low interfacial tensions on relative permeability. Soc. Pet. Eng. J. 1980, 20, 391–401. [Google Scholar] [CrossRef]
- Modaresghazani, J. Experimental and Simulation Study of Relative Permeabilities in Heavy Oil/Water/Gas Systems. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, March 2015. [Google Scholar]
- Muqeem, M.A. Effect of Temperature on Three-Phase Relative Permeability. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1996. [Google Scholar]
- McCaffery, F.G. The Effect of Wettability on Relative Permeability and Imbibition in Porous Media. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 1973. [Google Scholar]
- Esmaeili, S.; Sarma, H.; Harding, T.; Maini, B. Review of the effect of temperature on oil-water relative permeability in porous rocks of oil reservoirs. Fuel 2019, 237, 91–116. [Google Scholar] [CrossRef]
- Egermann, P.; Vizika, O. Critical gas saturation and relative permeability during depressurization in the far field and the near-wellbore region. In Proceedings of the Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Maini, B.; Kokal, S.; Jha, K. Measurements and correlations of three-phase relative permeability at elevated temperatures and pressures. In Proceedings of the Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–11 October 1989. [Google Scholar]
- Ahmed, T. Chapter 11: Oil recovery mechanisms and the material balance equation. In Reservoir Engineering Handbook, 3rd ed.; Gulf Professional Publishing: Huston, TX, USA, 2006. [Google Scholar]
- Honarpour, M.M. Relative Permeability of Petroleum Reservoirs; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Li, K.; Horne, R.N. Comparison of methods to calculate relative permeability from capillary pressure in consolidated water-wet porous media. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Sarma, H.; Maini, B.; Jha, K. An unsteady-state technique for three-phase relative permeability measurements. J. Can. Pet. Technol. 1994, 33. [Google Scholar] [CrossRef]
- Counsil, J.R. Steam-Water Relative Permeability. Ph.D. Thesis, Stanford University, Stanford, CA, USA, May 1979. [Google Scholar]
- Estes, R.K.; Fulton, P.F. Gas slippage and permeability measurements. J. Pet. Technol. 1956, 8, 69–73. [Google Scholar] [CrossRef]
- Fulton, P.F. The effect of gas slippage on relative permeability measurements. Prod. Mon. 1951, 15, 14–19. [Google Scholar]
- Li, K.; Horne, R.N. Gas slippage in two-phase flow and the effect of temperature. In Proceedings of the Western Regional Meeting, Bakersfield, CA, USA, 26–30 March 2001. [Google Scholar]
- Mahiya, G.F. Experimental Measurement of Steam-Water Relative Permeability; Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Sampath, K.; Keighin, C.W. Factors affecting gas slippage in tight sandstones of cretaceous age in the Uinta basin. J. Pet. Technol. 1982, 34, 2715–2720. [Google Scholar] [CrossRef]
- Wei, K.; Morrow, N.; Brower, K. Effect of fluid, confining pressure, and temperature on absolute permeabilities of low-permeability sandstones. SPE Form. Eval. 1986, 1, 413–423. [Google Scholar] [CrossRef]
- Rose, W.D. Permeability and gas-slippage phenomena. API Drill. Prod. Pract. 1948, 234, 127–135. [Google Scholar]
- Maini, B. Is it futile to measure relative permeability for heavy oil reservoirs? J. Can. Pet. Technol. 1998, 37, 56–62. [Google Scholar] [CrossRef]
- Kadeethum, T.; Sarma, H.; Maini, B. Overcome viscous fingering effect in heavy oil reservoirs by an optimized smart water injection scheme. In Proceedings of the Canada Heavy Oil Technical Conference, Calgary, AB, Canada, 15–16 February 2017. [Google Scholar]
- Sarma, H. Viscous fingering: One of the main factors behind poor flood efficiencies in petroleum reservoirs. Powder Technol. 1986, 48, 39–49. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO 2-brine systems. Environ. Geol. 2008, 54, 1707–1722. [Google Scholar] [CrossRef]
- Cai, B.-Y.; Yang, J.-T.; Guo, T.-M. Interfacial tension of hydrocarbon + water/brine systems under high pressure. J. Chem. Eng. Data 1996, 41, 493–496. [Google Scholar] [CrossRef]
- Esmaeili, S.; Sarma, H.; Harding, T.; Maini, B. The effect of temperature on two-phase oil/water relative permeability in different rock/fluid systems. In Proceedings of the Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar]
- Maini, B.; Batycky, J. Effect of temperature on heavy-oil/water relative permeabilities in horizontally and vertically drilled core plugs. J. Pet. Technol. 1985, 37, 1500–1510. [Google Scholar] [CrossRef]
- Polikar, M.; Ferracuti, F.; Decastro, V.; Puttagunta, R.; Ali, S. Effect of temperature on bitumen-water end point relative permeabilities and saturations. J. Can. Pet. Technol. 1986, 25, 5. [Google Scholar] [CrossRef]
- Poston, S.; Ysrael, S.; Hossain, A.; Montgomery, E., III. The effect of temperature on irreducible water saturation and relative permeability of unconsolidated sands. Soc. Pet. Eng. J. 1970, 10, 171–180. [Google Scholar] [CrossRef]
- Rosman, A. Experimental studies of low IFT displacement by CO2 injection. In Proceedings of the Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 9–12 October 1977. [Google Scholar]
- Zuo, Y.-X.; Stenby, E.H. Prediction of interfacial tensions of reservoir crude oil and gas condensate systems. SPE J. 1998, 3, 134–145. [Google Scholar] [CrossRef]
- Navascues, G. Liquid surfaces: Theory of surface tension. Rep. Prog. Phys. 1979, 42, 1131. [Google Scholar] [CrossRef]
- Fulcher, R., Jr.; Ertekin, T.; Stahl, C. Effect of capillary number and its constituents on two-phase relative permeability curves. J. Pet. Technol. 1985, 37, 249–260. [Google Scholar] [CrossRef]
- Harbert, L. Low interfacial tension relative permeability. In Proceedings of the Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. [Google Scholar]
- Asar, H.; Handy, L.L. Influence of interfacial tension on gas/oil relative permeability in a gas-condensate system. SPE Reserv. Eng. 1988, 3, 257–264. [Google Scholar] [CrossRef]
- Honarvar, B.; Azdarpour, A.; Karimi, M.; Rahimi, A.; Afkhami Karaei, M.; Hamidi, H.; Ing, J.; Mohammadian, E. Experimental investigation of interfacial tension measurement and oil recovery by carbonated water injection: A case study using core samples from an iranian carbonate oil reservoir. Energ. Fuels 2017, 31, 2740–2748. [Google Scholar] [CrossRef]
- Yang, D.; Tontiwachwuthikul, P.; Gu, Y. Interfacial tensions of the crude oil + reservoir brine + CO2 systems at pressures up to 31 MPa and temperatures of 27 °C and 58 °C. J. Chem. Eng. Data 2005, 50, 1242–1249. [Google Scholar] [CrossRef]
- Chalbaud, C.; Robin, M.; Egermann, P. Interfacial tension of brine CO2 systems under reservoirs conditions. In Proceedings of the Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Wan, T.; Yang, S.; Wang, L.; Sun, L. Experimental investigation of two-phase relative permeability of gas and water for tight gas carbonate under different test conditions. Oil Gas Sci. Technol. 2019, 74, 23. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Ayatollahi, S.; Ghazanfari, M.-H.; Masihi, M. Experimental determination of interfacial tension and miscibility of the CO2–crude oil system; temperature, pressure, and composition effects. J. Chem. Eng. Data 2013, 59, 61–69. [Google Scholar] [CrossRef]
- Saraf, D.N.; McCaffery, F.G. Two-and Three-Phase Relative Permeabilities: A Review; Petroleum Recovery Institute: Calgary, AB, Canada, 1981. [Google Scholar]
- Pruteanu, C.G.; Ackland, G.J.; Poon, W.C.; Loveday, J.S. When immiscible becomes miscible—Methane in water at high pressures. Sci. Adv. 2017, 3, e1700240. [Google Scholar] [CrossRef] [PubMed]
- Leverett, M.C. Flow of oil-water mixtures through unconsolidated sands. Trans. AIME 1939, 132, 149–171. [Google Scholar] [CrossRef]
- Leverett, M.; Lewis, W. Steady flow of gas-oil-water mixtures through unconsolidated sands. Trans. AIME 1941, 142, 107–116. [Google Scholar] [CrossRef]
- Yuster, S. Theoretical considerations of multiphase flow in idealized capillary systems. In Proceedings of the Third World Petroleum Congress, Hague, The Netherlands, 28 May–6 June 1951; pp. 437–445. [Google Scholar]
- Wyckoff, R.; Botset, H. The flow of gas-liquid mixtures through unconsolidated sands. Physics 1936, 7, 325–345. [Google Scholar] [CrossRef]
- Craig, F.; Forrest, F. The Reservoir Engineering Aspects of Waterflooding; Society of Petroleum Engineers: New York, NY, USA, 1975; Volume 3. [Google Scholar]
- Doherty, H.L. Memorial Fund of AIME; Society of Petroleum Engineers: New York, NY, USA, 1971; Volume 3. [Google Scholar]
- Sandberg, C.; Gournay, L.; Sippel, R. The Effect of Fluid-Flow Rate and Viscosity on Laboratory Determinations of Oil-Water Relative Permeabilities; Society of Petroleum Engineers: New York, NY, USA, 1958. [Google Scholar]
- Odeh, A.S. Effect of Viscosity Ratio on Relative Permeability (Includes Associated Paper 1496-G); Society of Petroleum Engineers: New York, NY, USA, 1959. [Google Scholar]
- Baker, P. Discussion of effect of viscosity ratio on relative permeability. J. Pet. Technol 1960, 219, 65. [Google Scholar]
- Downie, J.; Crane, F. Effect of viscosity on relative permeability. Soc. Pet. Eng. J. 1961, 1, 59–60. [Google Scholar] [CrossRef]
- Niz Velásquez, E.; Niz Velasquez, E. A Numerical and Physical Study of Relative Permeability in High-Pressure Air Injection Process; University of Calgary: Calgary, AB, Canada, 2009. [Google Scholar]
- Donaldson, E.C.; Thomas, R.D.; Lorenz, P.B. Wettability determination and its effect on recovery efficiency. Soc. Pet. Eng. J. 1969, 9, 13–20. [Google Scholar] [CrossRef]
- Gao, S.; Meegoda, J.N.; Hu, L. Simulation of dynamic two-phase flow during multistep air sparging. Trans. Porous Med. 2013, 96, 173–192. [Google Scholar] [CrossRef]
- Xia, H.; Wang, D.; Wu, W.; Jiang, H. Effect of the visco-elasticity of displacing fluids on the relationship of capillary number and displacement efficiency in weak oil-wet cores. In Proceedings of the Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 30 October–1 November 2007. [Google Scholar]
- Nazari, J.; Nasiry, F.; Seddiqi, N.; Honma, S. Influence of relative permeability and viscosity ratio on oil displacement by water in petroleum reservoir. Proc. Schl. Eng. Tokai Univ. 2015, 40, 15–20. [Google Scholar]
- Peters, E.J.; Flock, D.L. The onset of instability during two-phase immiscible displacement in porous media. Soc. Pet. Eng. J. 1981, 21, 249–258. [Google Scholar] [CrossRef]
- Johnson, E.; Bossler, D.; Bossler, V. Calculation of Relative Permeability from Displacement Experiments; Society of Petroleum Engineers: New York, NY, USA, 1959. [Google Scholar]
- Jiang, G. Gas Wettability of Reservoir Rock Surfaces with Porous Media; Gulf Professional Publishing: Huston, TX, USA, 2018. [Google Scholar]
- Moore, T.; Slobod, R. The effect of viscosity and capillarity on the displacement of oil by water. Prod. Mon. 1956, 20, 20–30. [Google Scholar]
- Wagner, O.; Leach, R. Improving oil displacement efficiency by wettability adjustment. Trans. AIME 1959, 216, 65–72. [Google Scholar] [CrossRef]
- Froning, H.; Leach, R. Determination of chemical requirements and applicability of wettability alteration flooding. J. Pet. Technol. 1967, 19, 839–843. [Google Scholar] [CrossRef]
- Penny, G.; Conway, M.; Briscoe, J. Enhanced load water-recovery technique improves stimulation results. In Proceedings of the Proceedin of the Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. [Google Scholar]
- Conway, M.W.; Smith, K.; Thomas, T.; Schraufnagel, R.A. The effect of surface active agents on the relative permeability of brine and gas in porous media. In Proceedings of the International Symposium on Oilfield Chemistry, San Antonio, TX, USA, 14–17 February 1995. [Google Scholar]
- Al-Siyabi, Z.; Danesh, A.; Tohidi, B.; Todd, A. Measurement of gas-oil contact angle at reservoir conditions. In Proceedings of the 9th European Symposium on Improved Oil Recovery (IOR 1997), Hague, The Netherlands, 20–22 October 1997. [Google Scholar]
- Morrow, N.; McCaffery, F. Displacement Studies in Uniformly Wetted Porous Media; Academic Press: New York, NY, USA, 1978; Volume 289. [Google Scholar]
- Zisman, W.A. Relation of the equilibrium contact angle to liquid and solid constitution. Adv. Chem. 1964. [Google Scholar] [CrossRef]
- Dake, L. The Practice of Reservoir Engineering. In Developments in Petroleum Science; Elsevier Science and Technology: Amsterdam, The Netherlands, 1994; pp. 370–371. [Google Scholar]
- Li, K.; Firoozabadi, A. Phenomenological modeling of critical condensate saturation and relative permeabilities in gas/condensate systems. SPE J. 2000, 5, 138–147. [Google Scholar] [CrossRef]
- Habowski, E. The Effects of Large Temperature Change on Relative Permeability Ratios; Pennsylvania State University: Pennsylvania, PA, USA, 1966. [Google Scholar]
- Wang, W.; Gupta, A. Investigation of the effect of temperature and pressure on wettability using modified pendant drop method. In Proceedings of the Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar]
- Karyampudi, R. Evaluation of cyclic steam performance and mechanisms in a mobile heavy oil reservoir at Elk point thermal pilot. J. Can. Pet. Technol. 1995, 34, 1. [Google Scholar] [CrossRef]
- Blevins, T.; Duerksen, J.; Ault, J. Light-oil steamflooding an emerging technology. J. Pet. Technol. 1984, 36, 1115–1122. [Google Scholar] [CrossRef]
- Escrochi, M.; Nabipour, M.; Ayatollahi, S.S.; Mehranbod, N. Wettability alteration at elevated temperatures: The consequences of asphaltene precipitation. In Proceedings of the International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 13–15 February 2008. [Google Scholar]
- Larsen, J.K.; Fabricius, I.L. Interpretation of water saturation above the transitional zone in chalk reservoirs. SPE Reserv. Eval. Eng. 2004, 7, 155–163. [Google Scholar] [CrossRef]
- Tang, G.-Q.; Firoozabadi, A. Effect of pressure gradient and initial water saturation on water injection in water-wet and mixed-wet fractured porous media. SPE Reserv. Eval. Eng. 2001, 4, 516–524. [Google Scholar] [CrossRef]
- Wheaton, R. Fundamentals of Applied Reservoir Engineering: Appraisal, Economics and Optimization; Gulf Professional Publishing: Huston, TX, USA, 2016. [Google Scholar]
- Narahara, G.; Pozzi, A., Jr.; Blackshear, T., Jr. Effect of connate water on gas/oil relative permeabilities for water-wet and mixed-wet berea rock. Adv. Technol. Series 1993, 1, 114–122. [Google Scholar] [CrossRef]
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Moss, J.; White, P.; McNiel, J., Jr. In Situ Combustion Process-Results of a Five-Well Field Experiment in Southern Oklahoma; Society of Petroleum Engineers: New York, NY, USA, 1959. [Google Scholar]
- Naar, J.; Henderson, J. An imbibition model—Its application to flow behavior and the prediction of oil recovery. Soc. Pet. Eng. J. 1961, 1, 61–70. [Google Scholar] [CrossRef]
- Davidson, L. The effect of temperature on the permeability ratio of different fluid pairs in two-phase systems. J. Pet. Technol. 1969, 21, 1037–1046. [Google Scholar] [CrossRef]
- Lo, H.Y.; Mungan, N. Effect of temperature on water-oil relative permeabilities in oil-wet and water-wet systems. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Las Vegas, NV, USA, 30 September–3 October 1973. [Google Scholar]
- Kumar, S.; Jain, R.; Chaudhary, P.; Mahto, V. Development of inhibitive water based drilling fluid system with synthesized graft copolymer for reactive Indian shale formation. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 4–6 April 2017. [Google Scholar]


| Authors | Year | Measurement Techniques | Porous Media | Type of System | Temperature Range (°C) | Effect of Temperature on Relative Permeability |
|---|---|---|---|---|---|---|
| Longeron [15] | 1980 | Unsteady-state | Core | Oil/Gas | 20–71 | kr of both phases increased |
| Berry et al. [14] | 1992 | Unsteady-state | Core | Oil/Gas | Ambient to 93 | kro increased and krg was independent |
| Muqeem (Ph.D. Thesis) [17] | 1994 | Unsteady-state | Core | Oil/Gas | 75–125 | kro has been increased but krg was not affected |
| Akhlaghinia et al. [13] | 2014 | Unsteady-state | Sand pack | Oil/CH4 gas | 28–52 | krg increased but kro decreased from 28 to 40 °C and then increased dramatically above 40 °C |
| Akhlaghinia et al. [13] | 2014 | Unsteady-state | Sand pack | Oil/CO2 gas | 28–52 | krg increased but kro decreased from 28 to 40 °C and then increased dramatically above 40 °C |
| Punase et al. [6] | 2014 | N/R | N/R | Oil/Gas | Not Reported | Both phases affected with temperature when wettability changed |
| Modaresghazani (Ph.D. Thesis) [16] | 2015 | Steady- and unsteady-state | Sand pack | Oil/Gas | Not Reported | Both kro and krg were affected |
| Authors | Year | Porous Media–Fluid System | Temperature and Pressure | Effect of Pressure and Temperature on ST | Effect of ST on Relative Permeability |
|---|---|---|---|---|---|
| Longeron [15] | 1980 | Fontainebleau sandstone core–methane and heptane | 71.1 °C (constant) 2.76–24.13 MPa | ST reduced with an increase in pressure at a constant temperature. | Both liquid and gas-relative permeability increased linearly with a decrease in ST. |
| Asar and Handy [48] | 1988 | Consolidated Berea sandstone core–methane and propane | 21 °C (constant) 7.58–9.55 MPa | Reduction in ST from 0.03 to 0.82 mN/m with an increase in pressure at a constant temperature. | Oil-relative permeability decreased more rapidly comparing to gas-relative permeability with an increase in ST |
| Yang et al. [50] | 2005 | N/R-CO2/Brine and Crude Oil | 27–58 °C 0.12–13 MPa | Below 8.50 MPa, the ST decreased with an increase in temperature and vice versa were observed when pressure was above the 8.50 MPa. | N/R |
| Chalbaud et al. [51] | 2006 | N/R-CO2/brine | 27–100 °C 0.12–13 MPa | At specified temperature, with an increase in pressure, the ST decreased. At lower pressure, the ST decreased with an increase in temperature. | N/R |
| Bachu and Bennion [37] | 2008 | Sandstone core–CO2/brine | 41–125 °C 1–27 MPa | ST decreased with an increase in pressure at a constant temperature but at lower pressure, the ST reduced with increase in temperature and vice versa at high pressure. | Relative permeability to gas and brine both increased with decrease in ST. |
| Honarvar et al. [49] | 2017 | Iranian carbonate core–CO2/brine | 40–100 °C 13.79 MPa | ST reduced with increase in temperature, but no effect of pressure has been reported. | N/R |
| Wan et al. [52] | 2019 | Carobonate (dolomite) core–nitrogen/brine | Ambient–80 °C | Increase in temperature decreased the ST from 71.25 to 50.12. | Changes the relative permeability curves for both the liquid and gas. |
| Authors | Year | Viscosity Ratio Range (cP) | Intrinsic Permeability Range (Darcy) |
|---|---|---|---|
| Leverett [56] | 1939 | 0.057–90.0 | 3.2–6.8 |
| Leverett and Lewis [57] | 1941 | 1.86–20.2 | 5.4–16.2 |
| Yuster [58] | 1951 | 1–10 | N/R |
| Wyckoff and Botset [59] | 1936 | 9–29 | 0.45–0.49 |
| Craig [60] | 1971 | 1.4–125 | 0.80–0.82 |
| Sandberg et al. [61] | 1958 | 0.48–2.02 | 0.413–0.757 |
| Odeh [62] | 1959 | 0.44–82.7 | 0.0021–0.405 |
| Baker [63] | 1960 | N/R | N/R |
| Downie and Crane [64] | 1961 | 9.29–51.54 | 0.13–0.16 |
| Velásquez [65] | 2009 | 0.4–75.4 | 0.041–0.521 |
| Donaldson, et al. [66] | 1969 | 35–78 | 0.76–1.20 |
| Gao et al. [67] | 2013 | N/R | N/R |
| Berry et al. [14] | 1992 | 41.53–170.5 | 0.79–0.11 |
| Muqeem [17] | 1996 | 215.35–22500 | 3.29–3.44 |
| Modaresghazani [16] | 2015 | 16.90–50.88 | 10.03–10.95 |
| Authors | Year | Porous Media–Fluid System | Contact Angle | Pressure and Temperature | Effect of Wettability on Relative Permeability |
|---|---|---|---|---|---|
| Moore and Slobod [73] | 1956 | Core–oil/gas | N/R | N/R | Both the relative permeability curves of gas and oil has been affected |
| Wagner and Leach [74] | 1959 | Quartz–Soltrol C/gas | 30 to 130° | 3.45 MPa and 35 to 57.2 °C | N/R |
| Zisman [80] | 1964 | Silica surface–hexadecane/gas | N/R | N/R | N/R |
| Habowski [83] | 1966 | Sandstone–oil/gas | N/R | N/R | Change in relative permeability curves for both the phases have been observed. |
| Froning and Leach [75] | 1967 | Sandstone–crude oil/gas | N/R | N/R | N/R |
| Morrow and McCaffery [79] | 1978 | Artificial PTFE (teflon)–n-Alkanes and air | 22 to 108° | N/R | Gas-relative permeability increased with increase as system becomes neutrally-wet or gas-wet. |
| Penny et al. [76] | 1983 | Ottawa sand–oil/gas | N/R | 62 MPa and 82.2 °C | Relative permeability to oil enhanced |
| Blevins et al. [86] | 1984 | Carbonate (dolomite) core–nitrogen/brine | N/R | Ambient–80 °C | Changes the relative permeability curves for both the liquid and gas. |
| Conway et al. [77] | 1995 | Blue Creek coal–brine/methane gas | N/R | N/R | Brine-relative permeability enhanced but not effect on gas-relative permeability has been observed. |
| Wang and Gupta [84] | 1995 | Quartz crystal–crude oil/gas | 22 to 135° | 20.68 MPa and 65 to 135 °C | N/R |
| Karyampudi [85] | 1995 | Sandstone–crude oil/gas | 32 to 172° | 4.4 MPa and 24 to 196 °C | Oil-relative permeability declined sharply |
| Al-Siyabi et al. [78] | 1997 | Teflon | N/R | N.R | N/R |
| Li and Firoozabadi [82] | 2000 | Consolidated sandstone core and capillary tube–water/gas and oil/gas | 0 to 118° for water/gas and 0 to 60° for oil/gas | N/R | Both the oil- and gas-relative permeability enhanced with the increase in contact angle and wettability alteration. |
| Escrochi et al. [87] | 2008 | Viscous crude oil/gas | 20 to 126° | NR and 23 to 93 °C | N/R |
| Jiang [72] | 2018 | Water/gas | 11 to 89° | N/R | N/R |
| Authors | Year | Irreducible Water Saturation (Swir) Range (%) | Effect of Swir on Relative Permeability |
|---|---|---|---|
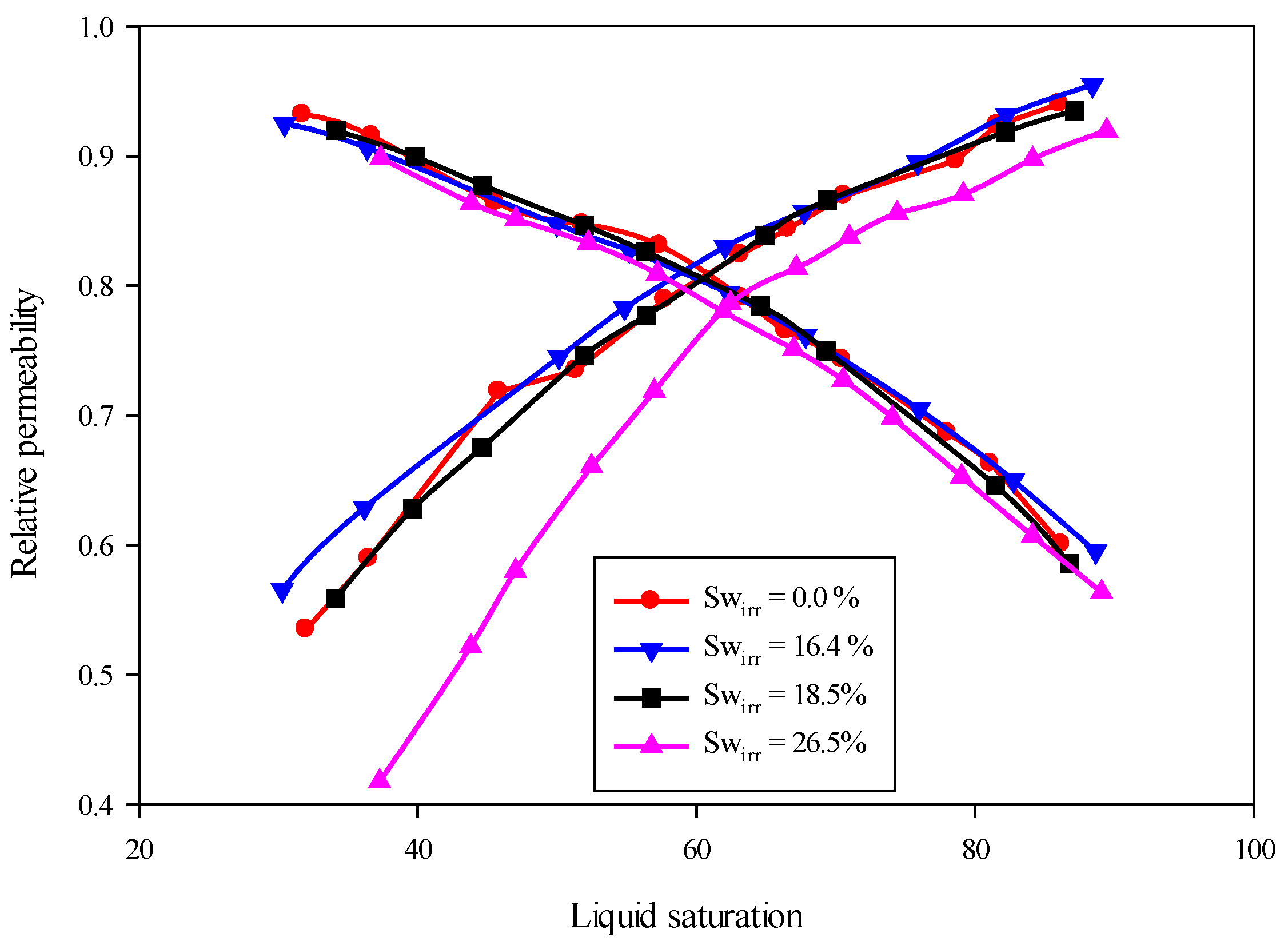
| Narahara et al. [91] | 1993 | 0–26.5 | Oil-relative permeability changed and no effect on gas-relative permeability has been observed |
| Corey [92] | 1954 | N/R | Liquid-relative permeability has been affected |
| Moss and McNiel [93] | 1959 | 0–13 | Relative permeability curves to both the phases gas and oil has been changed |
| Naar and Henderson’s [94] | 1961 | 6–18 | N/R |
| Davidson [95] | 1969 | 4–4.12 | N/R |
| Lo et al. [96] | 1973 | 5–523 | N/R |
| Berry et al. [14] | 1983 | 0.20–0.25 | Relative permeability curve for both the phase gas and oil has been changed. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Esmaeili, S.; Sarma, H.; Maini, B. Can Effects of Temperature on Two-Phase Gas/Oil-Relative Permeabilities in Porous Media Be Ignored? A Critical Analysis. Energies 2020, 13, 3444. https://doi.org/10.3390/en13133444
Kumar S, Esmaeili S, Sarma H, Maini B. Can Effects of Temperature on Two-Phase Gas/Oil-Relative Permeabilities in Porous Media Be Ignored? A Critical Analysis. Energies. 2020; 13(13):3444. https://doi.org/10.3390/en13133444
Chicago/Turabian StyleKumar, Saket, Sajjad Esmaeili, Hemanta Sarma, and Brij Maini. 2020. "Can Effects of Temperature on Two-Phase Gas/Oil-Relative Permeabilities in Porous Media Be Ignored? A Critical Analysis" Energies 13, no. 13: 3444. https://doi.org/10.3390/en13133444
APA StyleKumar, S., Esmaeili, S., Sarma, H., & Maini, B. (2020). Can Effects of Temperature on Two-Phase Gas/Oil-Relative Permeabilities in Porous Media Be Ignored? A Critical Analysis. Energies, 13(13), 3444. https://doi.org/10.3390/en13133444






