Model of R134a Liquid–Vapor Two-Phase Heat Transfer Coefficient for Pulsating Flow Boiling in an Evaporator Using Response Surface Methodology
Abstract
:1. Introduction
2. Experimental Approach, Test Conditions, and Data Source
2.1. Pulsating Flow Boiling Facility
2.2. Test Conditions and Data Reduction
3. Results and Discussions
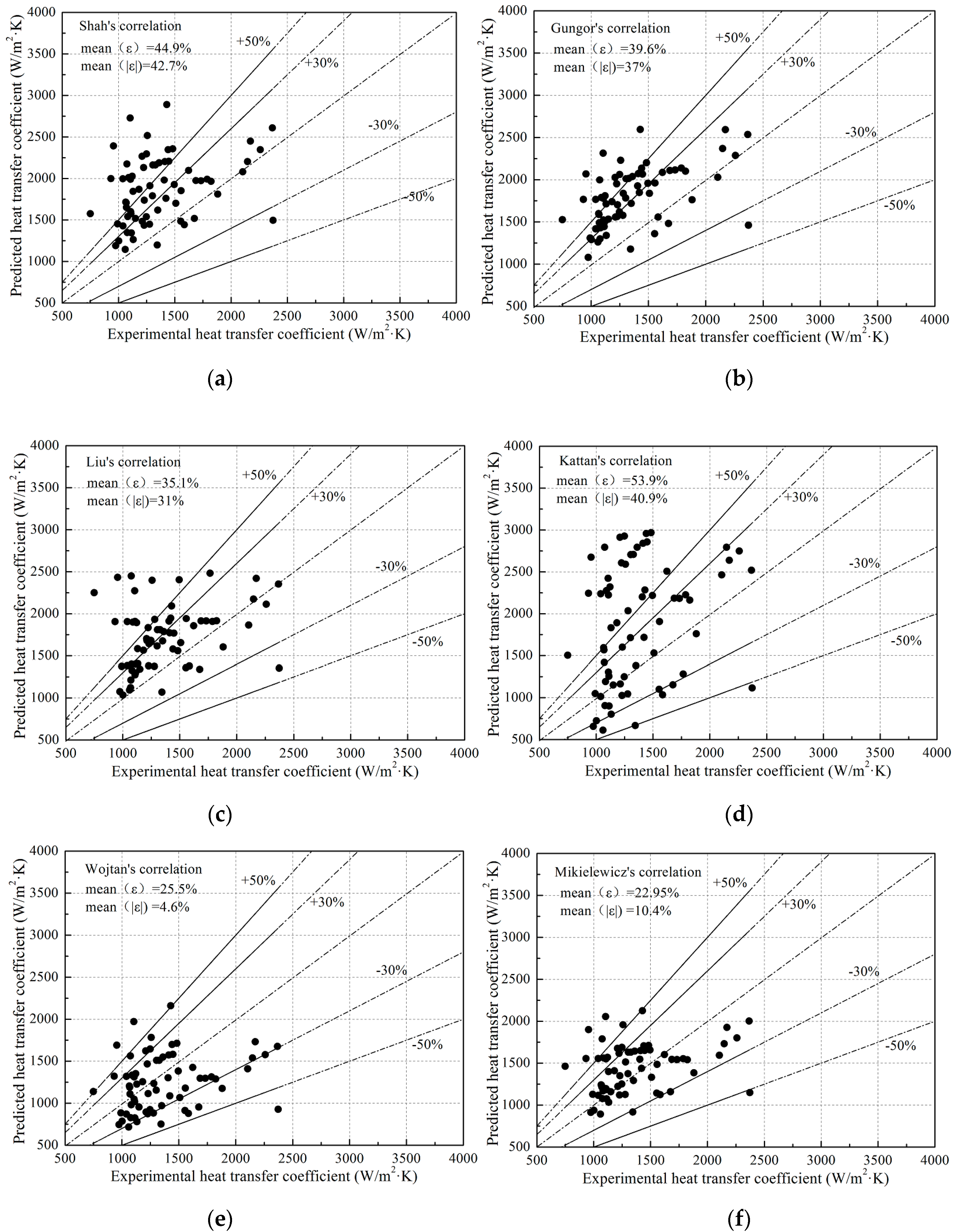
3.1. HTC Correlations in the Two-Phase Continuous Flow
3.2. Model of the HTC Ratio for Two-Phase Pulsating Flow Using RSM
3.2.1. Description about RSM
3.2.2. Rearrangement of Experimental Data
3.2.3. Analysis of Variance (ANOVA)
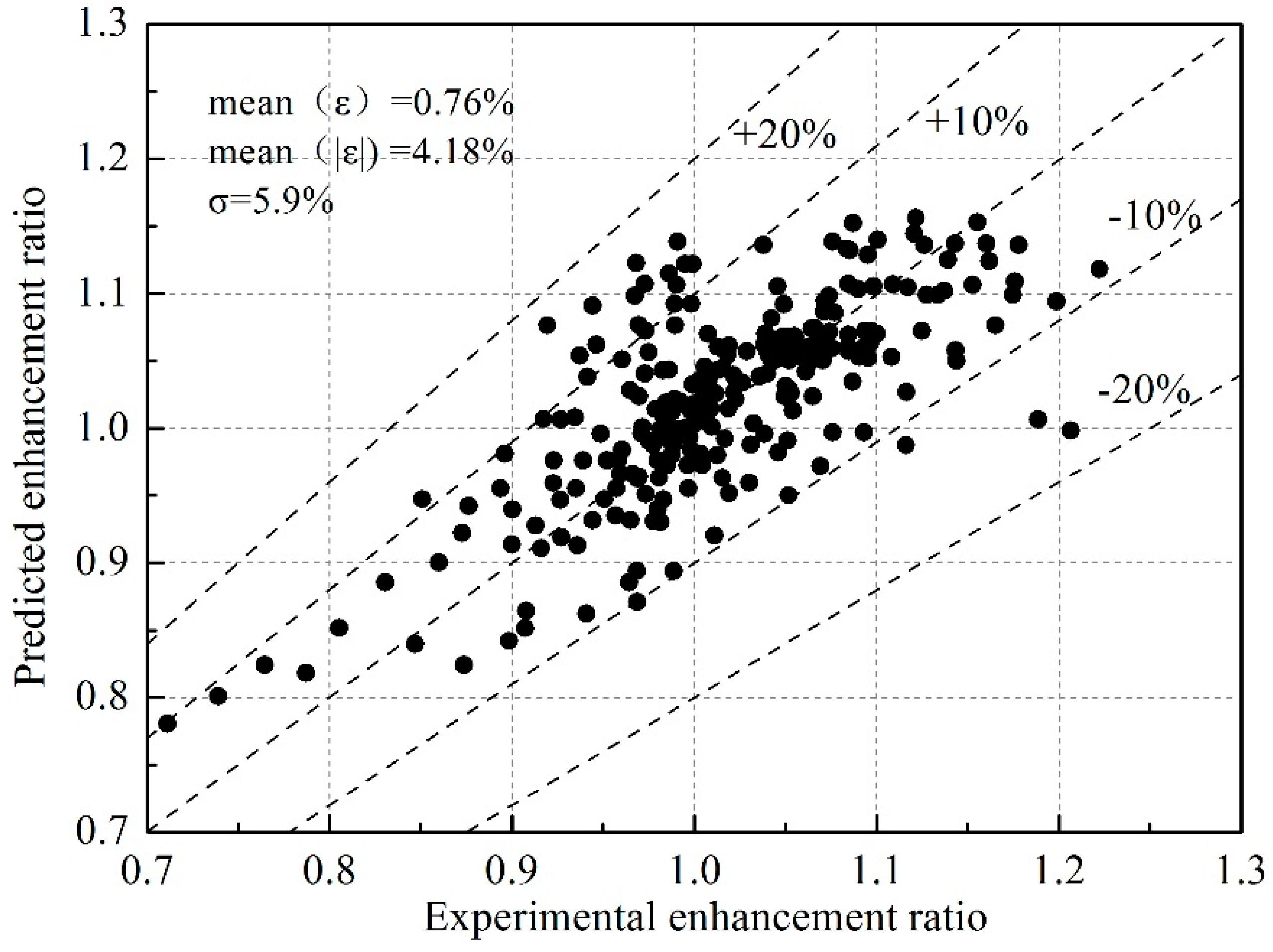
3.2.4. RSM Regression Model for the HTC Ratio
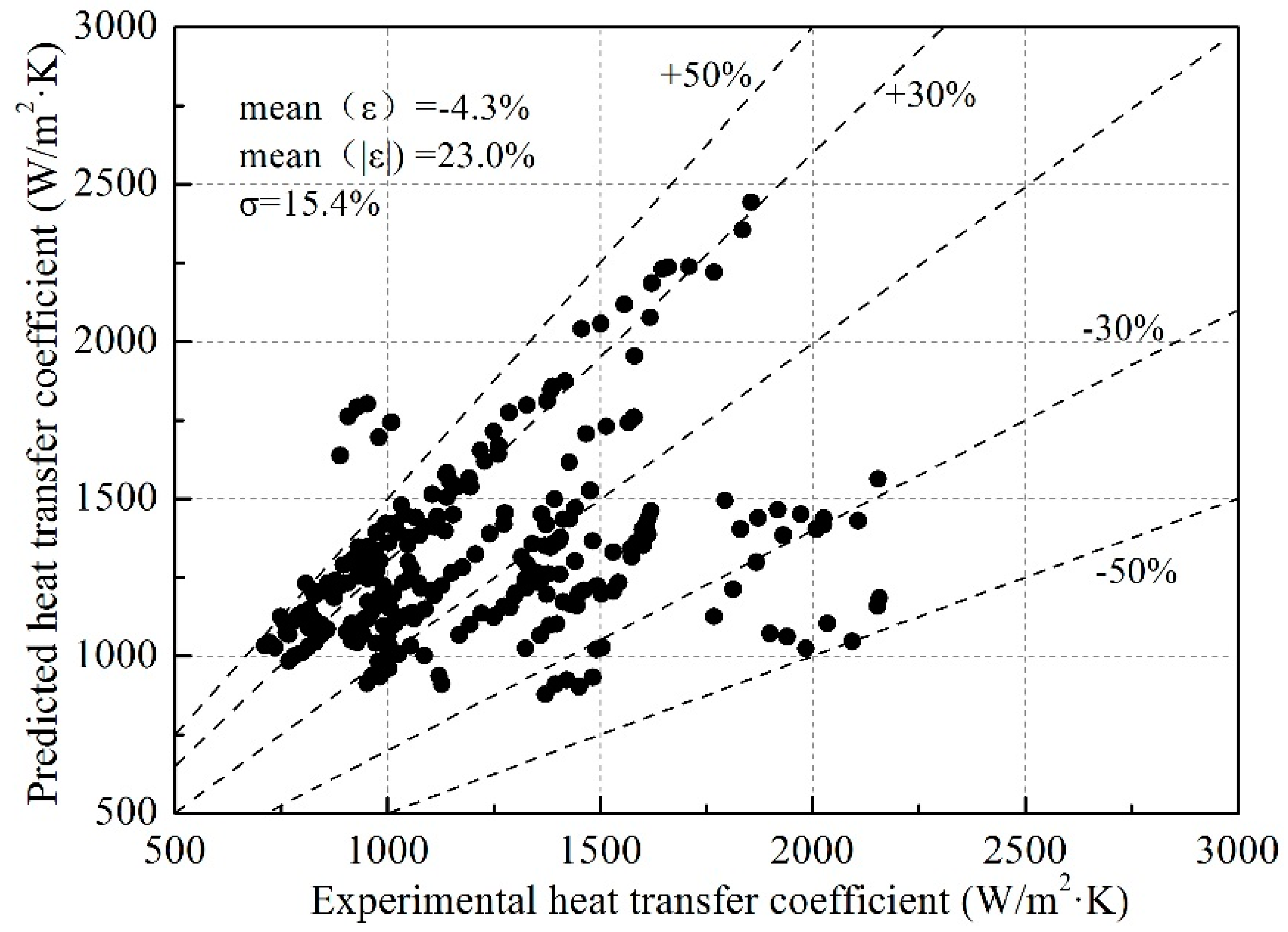
3.3. HTC model for R134a Two-Phase Pulsating Flow Boiling
4. Conclusions
- (1)
- Six existing models for heat transfer in the two-phase continuous flow were compared with our experimental data. Results show that the Wojtan’s model had the smallest mean error and the most data lying in the ±50% error window. Therefore, the Wojtan’s model was selected as a basis for predicting HTC in the R134a two-phase continuous flow.
- (2)
- RSM was carried out to rearrange the experimental data to obtain the regression model for the HTC ratio. ANOVA was performed to test the statistical significance of the model. The small error between RSM predicted data and experimental results shows that the model was satisfactory.
- (3)
- A new model for HTC in the R134a two-phase pulsating flow was finally obtained by multiplying the Wojtan’s model in continuous flow with the RSM regression model for the ratio. The new correlation produced a small error of −4.3% and a standard deviation of 15.4% compared with experimental results, indicating that the new model can predict the HTC in the R134a two-phase pulsating flow boiling well.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Bo | boiling number |
| Co | convective number |
| Cp | specific heat (J/(kg·K)) |
| D | internal diameter (m) |
| f | pulsation frequency (1/s) |
| F | intensifier factor |
| Fr | Froude number |
| G | refrigerant mass velocity (kg/(m2·s)) |
| h | heat transfer coefficient (W/(m2·K)) or Enthalpy (J/kg) |
| h* | heat transfer coefficient ratio for pulsating flow |
| k | thermal conductivity (W/(m·K)) |
| Pr | Prandtl number |
| Re | Reynolds number |
| S | suppression factor |
| St | Strouhal number |
| u | velocity (m/s) |
| We | Weber number |
| x | vapor quality |
| Xtt | Martinelli parameter |
| Greek symbols | |
| ε | error |
| σ | standard deviation |
| μ | viscosity coefficient (Pa·s) |
| ρ | density (kg/m3) |
| θdry | dry angle of tube diameter (rad) |
| θstrat | stratified flow angle of tube diameter (rad) |
| Subscripts | |
| g/G/v | vapor |
| l/L | liquid |
| pool/nb | pool boiling/nucleate boiling |
| tp | two-phase |
| sp | single-phase |
| in | inlet of heat exchanger |
| out | outlet of heat exchanger |
Appendix A
| Runs | Factors | Response | ||
|---|---|---|---|---|
| ln(St) | ln(xin) | ln(xout) | ln(h*) | |
| 1 | −3.551 | −2.303 | −0.223 | 0.0450 |
| 2 | −4.244 | −2.303 | −0.223 | 0.0073 |
| 3 | −4.937 | −2.303 | −0.223 | 0.0126 |
| 4 | −5.342 | −2.303 | −0.223 | 0.0592 |
| 5 | −5.630 | −2.303 | −0.223 | −0.0308 |
| 6 | −5.853 | −2.303 | −0.223 | −0.0168 |
| 7 | −6.035 | −2.303 | −0.223 | −0.0254 |
| 8 | −3.838 | −2.303 | −0.223 | 0.0919 |
| 9 | −4.531 | −2.303 | −0.223 | 0.0811 |
| 10 | −5.225 | −2.303 | −0.223 | 0.0608 |
| 11 | −5.630 | −2.303 | −0.223 | 0.0484 |
| 12 | −5.918 | −2.303 | −0.223 | 0.0093 |
| 13 | −6.141 | −2.303 | −0.223 | 0.0033 |
| 14 | −6.323 | −2.303 | −0.223 | −0.0197 |
| 15 | −3.754 | −2.303 | −0.357 | 0.0813 |
| 16 | −4.447 | −2.303 | −0.357 | 0.0894 |
| 17 | −5.140 | −2.303 | −0.357 | 0.0610 |
| 18 | −5.546 | −2.303 | −0.357 | −0.0277 |
| 19 | −5.834 | −2.303 | −0.357 | −0.0110 |
| 20 | −6.057 | −2.303 | −0.357 | 0.0003 |
| 21 | −6.239 | −2.303 | −0.357 | −0.0230 |
| 22 | −3.676 | −2.303 | −0.511 | 0.0833 |
| 23 | −4.370 | −2.303 | −0.511 | 0.0518 |
| 24 | −5.063 | −2.303 | −0.511 | 0.0631 |
| 25 | −5.468 | −2.303 | −0.511 | 0.0125 |
| 26 | −5.756 | −2.303 | −0.511 | 0.0051 |
| 27 | −5.979 | −2.303 | −0.511 | −0.0020 |
| 28 | −6.161 | −2.303 | −0.511 | −0.0191 |
| 29 | −3.930 | −2.303 | −0.105 | 0.0398 |
| 30 | −4.623 | −2.303 | −0.105 | 0.0398 |
| 31 | −5.316 | −2.303 | −0.105 | 0.0114 |
| 32 | −5.722 | −2.303 | −0.105 | 0.0732 |
| 33 | −6.010 | −2.303 | −0.105 | 0.0668 |
| 34 | −6.233 | −2.303 | −0.105 | 0.0503 |
| 35 | −6.415 | −2.303 | −0.105 | −0.0225 |
| 36 | −4.061 | −2.303 | −0.223 | 0.0481 |
| 37 | −4.755 | −2.303 | −0.223 | 0.0430 |
| 38 | −5.448 | −2.303 | −0.223 | 0.0030 |
| 39 | −5.853 | −2.303 | −0.223 | −0.0863 |
| 40 | −6.141 | −2.303 | −0.223 | −0.1096 |
| 41 | −6.364 | −2.303 | −0.223 | −0.0803 |
| 42 | −6.546 | −2.303 | −0.223 | −0.1052 |
| 43 | −3.977 | −2.303 | −0.357 | 0.0919 |
| 44 | −4.670 | −2.303 | −0.357 | 0.0713 |
| 45 | −5.364 | −2.303 | −0.357 | 0.0507 |
| 46 | −5.769 | −2.303 | −0.357 | 0.0516 |
| 47 | −6.057 | −2.303 | −0.357 | 0.0319 |
| 48 | −6.280 | −2.303 | −0.357 | −0.0017 |
| 49 | −6.462 | −2.303 | −0.357 | −0.0413 |
| 50 | −3.900 | −2.303 | −0.511 | 0.0055 |
| 51 | −4.593 | −2.303 | −0.511 | 0.0431 |
| 52 | −5.286 | −2.303 | −0.511 | 0.0681 |
| 53 | −5.691 | −2.303 | −0.511 | 0.0489 |
| 54 | −5.979 | −2.303 | −0.511 | 0.0526 |
| 55 | −6.202 | −2.303 | −0.511 | 0.0377 |
| 56 | −6.385 | −2.303 | −0.511 | −0.0128 |
| 57 | −4.244 | −2.303 | −0.223 | 0.0954 |
| 58 | −4.937 | −2.303 | −0.223 | 0.0700 |
| 59 | −5.630 | −2.303 | −0.223 | 0.0628 |
| 60 | −6.035 | −2.303 | −0.223 | 0.0500 |
| 61 | −6.323 | −2.303 | −0.223 | 0.0154 |
| 62 | −6.546 | −2.303 | −0.223 | −0.0203 |
| 63 | −6.729 | −2.303 | −0.223 | −0.0756 |
| 64 | −4.160 | −2.303 | −0.357 | 0.0697 |
| 65 | −4.853 | −2.303 | −0.357 | 0.0535 |
| 66 | −5.546 | −2.303 | −0.357 | 0.0393 |
| 67 | −5.951 | −2.303 | −0.357 | −0.0122 |
| 68 | −6.239 | −2.303 | −0.357 | −0.0115 |
| 69 | −6.462 | −2.303 | −0.357 | −0.0346 |
| 70 | −6.644 | −2.303 | −0.357 | −0.0761 |
| 71 | −4.082 | −2.303 | −0.511 | 0.0910 |
| 72 | −4.775 | −2.303 | −0.511 | 0.0189 |
| 73 | −5.468 | −2.303 | −0.511 | −0.0174 |
| 74 | −5.874 | −2.303 | −0.511 | −0.0082 |
| 75 | −6.161 | −2.303 | −0.511 | −0.0094 |
| 76 | −6.385 | −2.303 | −0.511 | 0.0124 |
| 77 | −6.567 | −2.303 | −0.511 | −0.0316 |
| 78 | −4.398 | −2.303 | −0.223 | 0.0384 |
| 79 | −5.091 | −2.303 | −0.223 | 0.0180 |
| 80 | −5.784 | −2.303 | −0.223 | −0.0132 |
| 81 | −6.190 | −2.303 | −0.223 | −0.0425 |
| 82 | −6.477 | −2.303 | −0.223 | −0.0504 |
| 83 | −6.700 | −2.303 | −0.223 | −0.1360 |
| 84 | −6.883 | −2.303 | −0.223 | −0.1507 |
| 85 | −4.447 | −2.303 | −0.357 | 0.1178 |
| 86 | −5.140 | −2.303 | −0.357 | 0.0812 |
| 87 | −5.834 | −2.303 | −0.357 | 0.0223 |
| 88 | −6.239 | −2.303 | −0.357 | 0.0304 |
| 89 | −6.527 | −2.303 | −0.357 | 0.0297 |
| 90 | −6.750 | −2.303 | −0.357 | −0.0441 |
| 91 | −6.932 | −2.303 | −0.357 | −0.1055 |
| 92 | −4.531 | −1.204 | −0.511 | 0.1339 |
| 93 | −5.225 | −1.204 | −0.511 | 0.1188 |
| 94 | −5.918 | −1.204 | −0.511 | 0.1422 |
| 95 | −6.323 | −1.204 | −0.511 | 0.1529 |
| 96 | −6.611 | −1.204 | −0.511 | 0.1345 |
| 97 | −6.834 | −1.204 | −0.511 | 0.1100 |
| 98 | −3.930 | −1.609 | −0.223 | 0.1201 |
| 99 | −4.623 | −1.609 | −0.223 | 0.1032 |
| 100 | −5.316 | −1.609 | −0.223 | 0.0688 |
| 101 | −5.722 | −1.609 | −0.223 | 0.0377 |
| 102 | −6.010 | −1.609 | −0.223 | 0.0212 |
| 103 | −6.233 | −1.609 | −0.223 | 0.0057 |
| 104 | −6.415 | −1.609 | −0.223 | −0.0289 |
| 105 | −4.153 | −1.609 | −0.223 | 0.1107 |
| 106 | −4.846 | −1.609 | −0.223 | 0.0861 |
| 107 | −5.540 | −1.609 | −0.223 | 0.0640 |
| 108 | −5.945 | −1.609 | −0.223 | 0.0155 |
| 109 | −6.233 | −1.609 | −0.223 | −0.0157 |
| 110 | −6.456 | −1.609 | −0.223 | −0.0295 |
| 111 | −6.638 | −1.609 | −0.223 | −0.0627 |
| 112 | −4.336 | −1.609 | −0.223 | 0.0810 |
| 113 | −5.029 | −1.609 | −0.223 | 0.0712 |
| 114 | −5.722 | −1.609 | −0.223 | 0.0645 |
| 115 | −6.127 | −1.609 | −0.223 | 0.0507 |
| 116 | −6.415 | −1.609 | −0.223 | −0.0041 |
| 117 | −6.638 | −1.609 | −0.223 | −0.0800 |
| 118 | −6.821 | −1.609 | −0.223 | −0.1123 |
| 119 | −4.623 | −0.916 | −0.511 | 0.0690 |
| 120 | −5.316 | −0.916 | −0.511 | 0.0480 |
| 121 | −6.010 | −0.916 | −0.511 | −0.0550 |
| 122 | −6.415 | −0.916 | −0.511 | −0.0010 |
| 123 | −6.703 | −0.916 | −0.511 | −0.0759 |
| 124 | −6.926 | −0.916 | −0.511 | −0.0406 |
| 125 | −7.108 | −0.916 | −0.511 | −0.0309 |
| 126 | −4.031 | −1.204 | −0.223 | 0.0866 |
| 127 | −4.724 | −1.204 | −0.223 | 0.0727 |
| 128 | −5.418 | −1.204 | −0.223 | 0.0353 |
| 129 | −5.823 | −1.204 | −0.223 | 0.0090 |
| 130 | −6.111 | −1.204 | −0.223 | 0.0166 |
| 131 | −6.334 | −1.204 | −0.223 | −0.0038 |
| 132 | −6.516 | −1.204 | −0.223 | −0.0437 |
| 133 | −4.437 | −1.204 | −0.223 | 0.0711 |
| 134 | −5.130 | −1.204 | −0.223 | 0.0416 |
| 135 | −5.823 | −1.204 | −0.223 | 0.0186 |
| 136 | −6.229 | −1.204 | −0.223 | 0.0450 |
| 137 | −6.516 | −1.204 | −0.223 | −0.0033 |
| 138 | −6.739 | −1.204 | −0.223 | −0.0356 |
| 139 | −6.922 | −1.204 | −0.223 | −0.0877 |
| 140 | −4.837 | −0.916 | −0.223 | 0.0890 |
| 141 | −5.530 | −0.916 | −0.223 | 0.0002 |
| 142 | −6.223 | −0.916 | −0.223 | −0.0188 |
| 143 | −6.629 | −0.916 | −0.223 | −0.0321 |
| 144 | −6.917 | −0.916 | −0.223 | −0.0967 |
| 145 | −7.140 | −0.916 | −0.223 | −0.1659 |
| 146 | −7.322 | −0.916 | −0.223 | −0.2395 |
| 147 | −4.271 | −0.916 | −0.105 | −0.1614 |
| 148 | −4.964 | −0.916 | −0.105 | −0.1319 |
| 149 | −5.657 | −0.916 | −0.105 | −0.0662 |
| 150 | −6.063 | −0.916 | −0.105 | −0.0363 |
| 151 | −6.350 | −0.916 | −0.105 | −0.0608 |
| 152 | −6.573 | −0.916 | −0.105 | −0.1071 |
| 153 | −6.756 | −0.916 | −0.105 | −0.1350 |
| 154 | −4.676 | −0.916 | −0.105 | −0.0172 |
| 155 | −5.369 | −0.916 | −0.105 | −0.0910 |
| 156 | −6.063 | −0.916 | −0.105 | −0.1855 |
| 157 | −6.468 | −0.916 | −0.105 | −0.2166 |
| 158 | −6.756 | −0.916 | −0.105 | −0.2684 |
| 159 | −6.979 | −0.916 | −0.105 | −0.3023 |
| 160 | −7.161 | −0.916 | −0.105 | −0.3411 |
References
- Fernández-Seara, J.; Pardiñas, Á.Á.; Diz, R. Heat transfer enhancement of ammonia pool boiling with an integral-fin tube. Int. J. Refrig. 2016, 69, 175–185. [Google Scholar] [CrossRef]
- Kærn, M.R.; Elmegaard, B.; Meyer, K.E.; Palm, B.; Holst, J. Continuous versus pulsating flow boiling. Experimental comparison, visualization, and statistical analysis. Sci. Technol. Built Environ. 2017, 23, 983–996. [Google Scholar]
- Li, G.; Zheng, Y.; Hu, G.; Zhang, Z.; Xu, Y. Experimental study of the heat transfer enhancement from a circular cylinder in laminar pulsating cross-flows. Heat Transf. Eng. 2016, 37, 535–544. [Google Scholar] [CrossRef]
- Bohdal, T.; Kuczyński, W. Investigation of boiling of refrigeration medium under periodic disturbance conditions. Exp. Heat Transf. 2005, 18, 135–151. [Google Scholar] [CrossRef]
- Chen, C.A.; Chang, W.R.; Lin, T.F. Time periodic flow boiling heat transfer of R-134a and associated bubble characteristics in a narrow annular duct due to flow rate oscillation. Int. J. Heat Mass Transf. 2010, 53, 3593–3606. [Google Scholar] [CrossRef]
- Roh, C.W.; Kim, M.S. Enhancement of heat pump performance by pulsation of refrigerant flow using a solenoid-driven control valve. Int. J. Refrig. 2012, 35, 1547–1557. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 2012, 12, 3–22. [Google Scholar] [CrossRef]
- Shah, M.M. Chart correlation for saturated boiling heat transfer: Equations and further study. ASHRAE Trans. 1982, 88, 185–196. [Google Scholar]
- Jabardo, J.S.; Bandarra Filho, E.P.; Lima, C.U. New correlation for convective boiling of pure halocarbon refrigerants flowing in horizontal tubes. J. Braz. Soc. Mech. Sci. 1999, 21, 245–258. [Google Scholar]
- Chaddock, J. Film coefficients for in-tube evaporation of ammonia and R-502 with and without small percentages of mineral oil. Ashrae Trans. 1986, 92, 22–40. [Google Scholar]
- Wattelet, J.P.; Chato, J.C.; Jabardo, J.M.; Panek, J.S.; Renie, J.P. An experimental comparison of evaporation characteristics of HFC-134a and CFC-12. In Proceedings of the XVIIIth International Congress of Refrigeration, Montreal, QC, Canada, 10–17 August 1991. [Google Scholar]
- Panek, J.S. Evaporation Heat Transfer and Pressure Drop in Ozone-Safe Refrigerants and Refrigerant-Oil Mixtures; Air Conditioning and Refrigeration Center, College of Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1992. [Google Scholar]
- Tran, T.N.; Wambsganss, M.W.; France, D.M. Small circular-and rectangular-channel boiling with two refrigerants. Int. J. Multiph. Flow 1996, 22, 485–498. [Google Scholar] [CrossRef]
- Kew, P.A.; Cornwell, K. Correlations for the prediction of boiling heat transfer in small-diameter channels. Appl. Therm. Eng. 1997, 17, 705–715. [Google Scholar] [CrossRef]
- Lazarek, G.M.; Black, S.H. Evaporative heat transfer, pressure drop and critical heat flux in a small vertical tube with R-113. Int. J. Heat Mass Transf. 1982, 25, 945–960. [Google Scholar] [CrossRef]
- da Silva Lima, R.J.; Quibén, J.M.; Thome, J.R. Flow boiling in horizontal smooth tubes: New heat transfer results for R-134a at three saturation temperatures. Appl. Therm. Eng. 2009, 29, 1289–1298. [Google Scholar] [CrossRef]
- Mikielewicz, D. A new method for determination of flow boiling heat transfer coefficient in conventional-diameter channels and minichannels. Heat Transf. Eng. 2010, 31, 276–287. [Google Scholar] [CrossRef]
- Sardeshpande, M.V.; Ranade, V.V. Two-phase flow boiling in small channels: A brief review. Sadhana 2013, 38, 1083–1126. [Google Scholar] [CrossRef]
- Cooper, M.G. Saturated Nucleate Pool Boiling-A Simple Correlation. IChemE Symp. Ser. 1984, 86, 786. [Google Scholar]
- Gungor, K.E.; Winterton, R.H. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
- Gungor, K.E.; Winterton, R.H.S. Simplified general correlation for saturated flow boiling and comparisons of correlations with data. Chem. Eng. Res. Des. 1987, 65, 148–156. [Google Scholar]
- Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat Mass Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
- Kattan, N.; Thome, J.R.; Favrat, D. Flow boiling in horizontal tubes: Part 3—Development of a new heat transfer model based on flow pattern. J. Heat Transf. 1998, 120, 156–165. [Google Scholar] [CrossRef]
- Wojtan, L.; Ursenbacher, T.; Thome, J.R. Investigation of flow boiling in horizontal tubes: Part II—Development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes. Int. J. Heat Mass Transf. 2005, 48, 2970–2985. [Google Scholar] [CrossRef]
- Wang, X.; Tang, K.; Hrnjak, P.S. Evaporator performance enhancement by pulsation width modulation (PWM). Appl. Therm. Eng. 2016, 99, 825–833. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, Y.; Wang, X.; Liu, Y.W. Heat transfer measurement and flow regime visualization of two-phase pulsating flow in an evaporator. Int. J. Heat Mass Transf. 2018, 127, 1014–1024. [Google Scholar] [CrossRef]
- ASME. Measurement of Fluid Flow in Pipes Using Orifice, Nozzle, and Venture; Standard MFC-3M-2004; American Society of Mechanical Engineers: New York, NY, USA, 2004. [Google Scholar]
- ASME. Flow Measurement; ANSI/ASME Standard PTC 19.5–2004 (RA13); American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Kim, N.H.; Youn, B.; Webb, R.L. Air-side heat transfer and friction correlations for plain fin-and-tube heat exchangers with staggered tube arrangements. J. Heat Transf. 1999, 121, 662–667. [Google Scholar] [CrossRef]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B (Methodol.) 1951, 13, 1–38. [Google Scholar] [CrossRef]
- Yang, P.; Liu, Y.W.; Zhong, G.Y. Prediction and parametric analysis of acoustic streaming in a thermoacoustic Stirling heat engine with a jet pump using response surface methodology. Appl. Therm. Eng. 2016, 103, 1004–1013. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Liang, L.; Liu, X.; Li, J. Thermodynamic optimization of the recuperative heat exchanger for Joule–Thomson cryocoolers using response surface methodology. Int. J. Refrig. 2015, 60, 155–165. [Google Scholar] [CrossRef]
- Hariharan, N.M.; Sivashanmugam, P.; Kasthurirengan, S. Optimization of thermoacoustic primemover using response surface methodology. HVAC R Res. 2012, 18, 890–903. [Google Scholar]

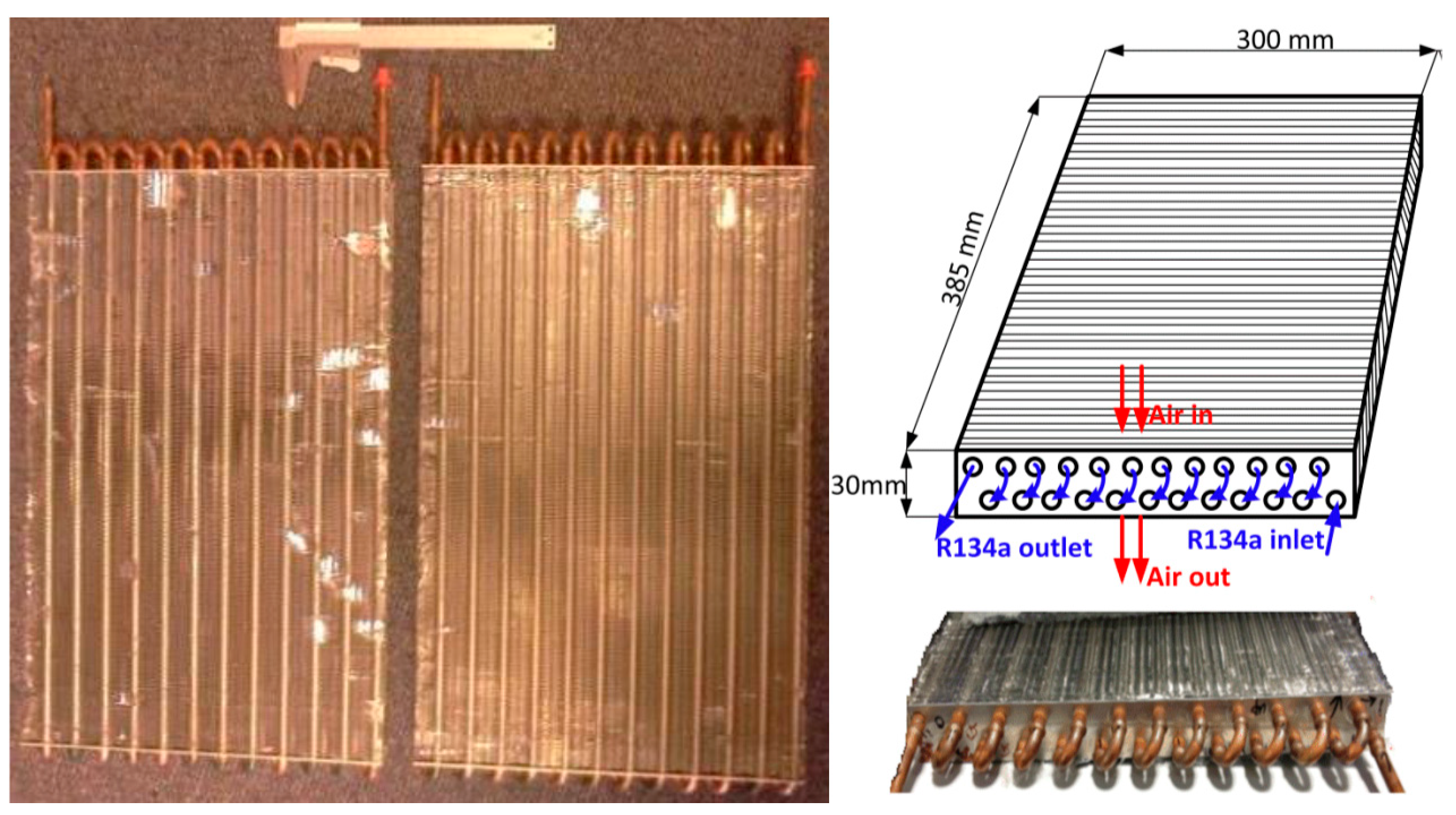


| Variables | Refrigerant Side | Air Side |
|---|---|---|
| Flow rate | Continuous flow: 75–250 kg/(m2·s) | 0.8–8.0 m/s |
| Pulsating flow: double | ||
| Temperature | Evaporation Temperature: 15 °C | Inlet Temperature: 25 °C |
| Superheat Temperature: 35–40 °C | (room temperature) | |
| Vapor quality | Inlet of heat exchanger: 0.1–0.4 | - |
| Outlet of heat exchanger: 0.6–0.9 | ||
| Operating mode | Continuous flow | Continuous flow |
| Pulsating flow: period 2–24 s |
| Heat Transfer Side | Measured Parameters/Unit | Sensors | Range | Accuracy |
|---|---|---|---|---|
| Air side | Temperature/°C | Copper-constantan T type | −10–80 | ±0.1/°C |
| Pressure drop/kPa | Setra Model 264 | 0–0.623 | ±1% FS | |
| Refrigerant side | Mass flow rate/(g/s) | Micromotion DS006S | 0–18 | ±0.1% RS |
| Pressure (inlet of HX)/kPa | Sensotec Model Z | 0–1034 | ±0.25% RS | |
| Pressure (outlet of HX)/kPa | Sensotec Model TJE | 0–689 | ±0.25% RS | |
| Temperature/°C | Copper-constantan T type | −10–80 | ±0.1/°C | |
| Pressure drop/kPa | Rosemount 1151DP4E2A | 0–37.36 | ±0.25% RS | |
| Heat power/W | AC Watt Transducer PC5 | 0–1000 | ±0.02 W | |
| Overall HTC/W·m−2·K−1 | ±10.4% | |||
| Refrigerant side HTC/W·m−2·K−1 | ±12%~±16.5% |
| Author | Correlation |
|---|---|
| Shah [8] | |
| Gungor [20] | |
| Liu [22] | |
| Kattan [23] | |
| Wojtan [24] | |
| Slug/Annular/Intermittent zone θdry = 0 | |
| Stratified-wavy zone | |
| Slug-stratified wavy zone | |
| Mikielewicz [17] | |
| For Laminar flow, n = 2 | |
| For turbulent flow, n = 0.9 | |
| For conventional channels, m = 0 | |
| For small-diameter channels and mini channels, m = −1 |
| Correlation | Mean Error (%) | Abs. Mean Error (%) | Standard Deviation (%) | Points Inside an Error Window of | |
|---|---|---|---|---|---|
| ±30 (%) | ±50 (%) | ||||
| Shah | 42.7 | 44.9 | 37.9 | 47 | 62 |
| Gungor | 37.0 | 39.6 | 29.1 | 45.5 | 73.5 |
| Liu | 31.0 | 35.2 | 40.1 | 55.8 | 82.4 |
| Kattan | 40.9 | 53.9 | 57.2 | 51.5 | 61.8 |
| Wojtan | −4.6 | 25.5 | 29.6 | 86.7 | 94.1 |
| Mikielewicz | 10.5 | 22.9 | 29.9 | 79.4 | 91.2 |
| Variables | Equation (10) | Equation (11) |
|---|---|---|
| Constant term | lnC | β0 |
| Coefficients of xi (i = 1, …, n−1) | ||
| Coefficient of xn | an | βn + βnnxn |
| Variables | Ranges | |
|---|---|---|
| St | 0.0007 | 0.0287 |
| xin | 0.1 | 0.4 |
| xout | 0.6 | 0.9 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F | Significance |
|---|---|---|---|---|---|---|
| Model | 0.8193 | 9 | 0.0910 | 47.71 | <0.0001 | * |
| ln(St) | 0.2087 | 1 | 0.2087 | 109.38 | <0.0001 | * |
| ln(xin) | 0.0100 | 1 | 0.0100 | 5.25 | 0.0233 | * |
| ln(xout) | 0.1072 | 1 | 0.1072 | 56.21 | <0.0001 | * |
| ln(St) ln(xin) | 0.0029 | 1 | 0.0029 | 1.51 | 0.2215 | |
| ln(St) ln(xout) | 0.0067 | 1 | 0.0067 | 3.52 | 0.0625 | |
| ln(xin) ln(xout) | 0.0586 | 1 | 0.0586 | 30.70 | <0.0001 | * |
| (ln(St))2 | 0.0583 | 1 | 0.0583 | 30.56 | <0.0001 | * |
| (ln(xin))2 | 0.0753 | 1 | 0.0753 | 39.49 | <0.0001 | * |
| (ln(xout)) 2 | 0.0028 | 1 | 0.0028 | 1.48 | 0.2250 | |
| Residual | 0.2862 | 150 | 0.0019 | |||
| Lack of Fit | 0.2300 | 121 | 0.0019 | 0.98 | 0.5503 | |
| Pure Error | 0.0562 | 29 | 0.0019 | |||
| Cor Total | 1.1054 | 159 | ||||
| Adeq Precision | 34.433 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Zhang, T.; Zhang, Y.; Wang, S.; Liu, Y. Model of R134a Liquid–Vapor Two-Phase Heat Transfer Coefficient for Pulsating Flow Boiling in an Evaporator Using Response Surface Methodology. Energies 2020, 13, 3540. https://doi.org/10.3390/en13143540
Yang P, Zhang T, Zhang Y, Wang S, Liu Y. Model of R134a Liquid–Vapor Two-Phase Heat Transfer Coefficient for Pulsating Flow Boiling in an Evaporator Using Response Surface Methodology. Energies. 2020; 13(14):3540. https://doi.org/10.3390/en13143540
Chicago/Turabian StyleYang, Peng, Ting Zhang, Yuheng Zhang, Sophie Wang, and Yingwen Liu. 2020. "Model of R134a Liquid–Vapor Two-Phase Heat Transfer Coefficient for Pulsating Flow Boiling in an Evaporator Using Response Surface Methodology" Energies 13, no. 14: 3540. https://doi.org/10.3390/en13143540
APA StyleYang, P., Zhang, T., Zhang, Y., Wang, S., & Liu, Y. (2020). Model of R134a Liquid–Vapor Two-Phase Heat Transfer Coefficient for Pulsating Flow Boiling in an Evaporator Using Response Surface Methodology. Energies, 13(14), 3540. https://doi.org/10.3390/en13143540





