Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods
Abstract
:1. Introduction
- It is a combination of ST and DT methods for accurately detecting and classifying nine stationary and non-stationary PQ disturbances
- It responds to the automatic PQ disturbance classification in real-time analysis
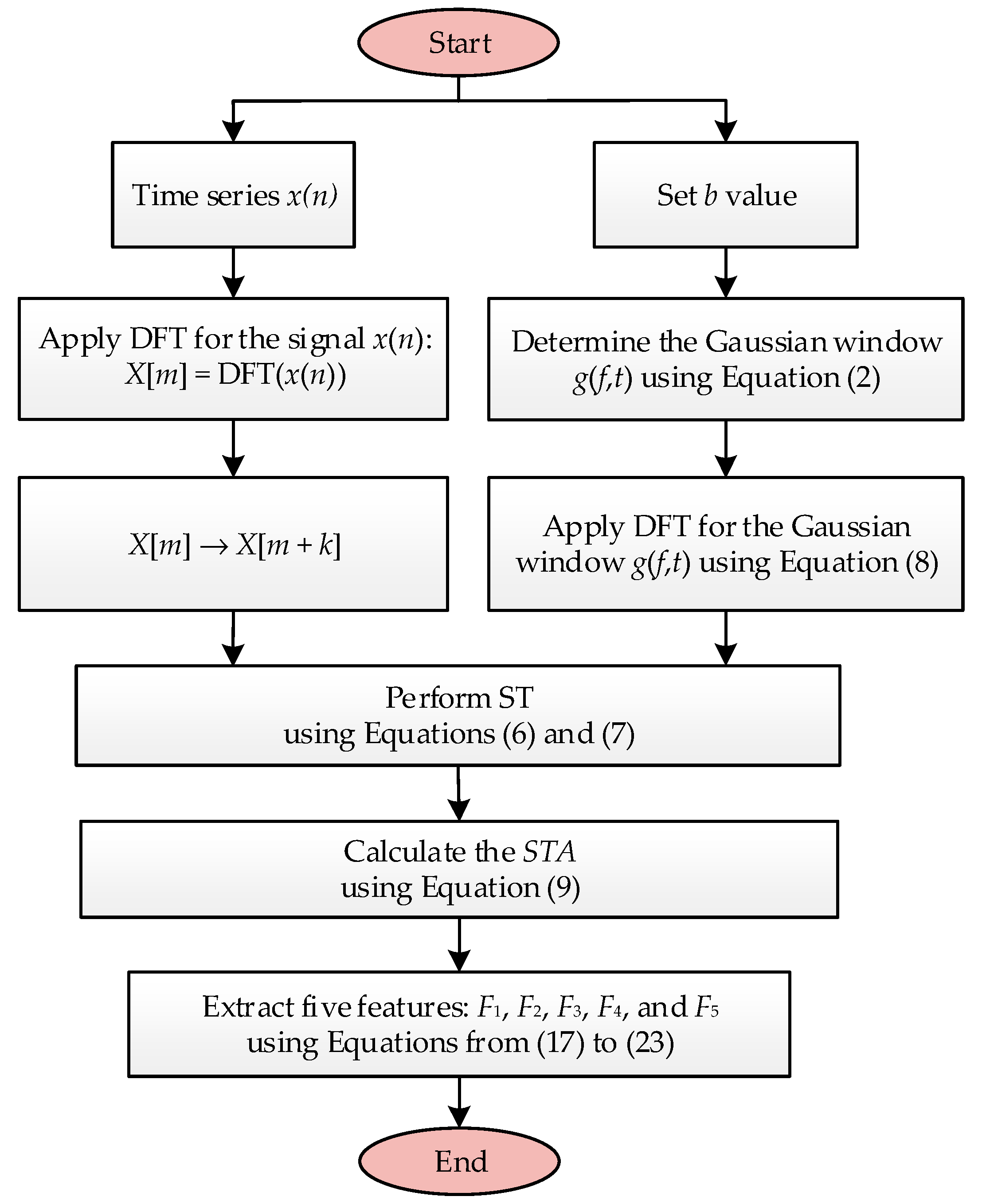
2. Stockwell Transform Method
3. Decision Tree Method
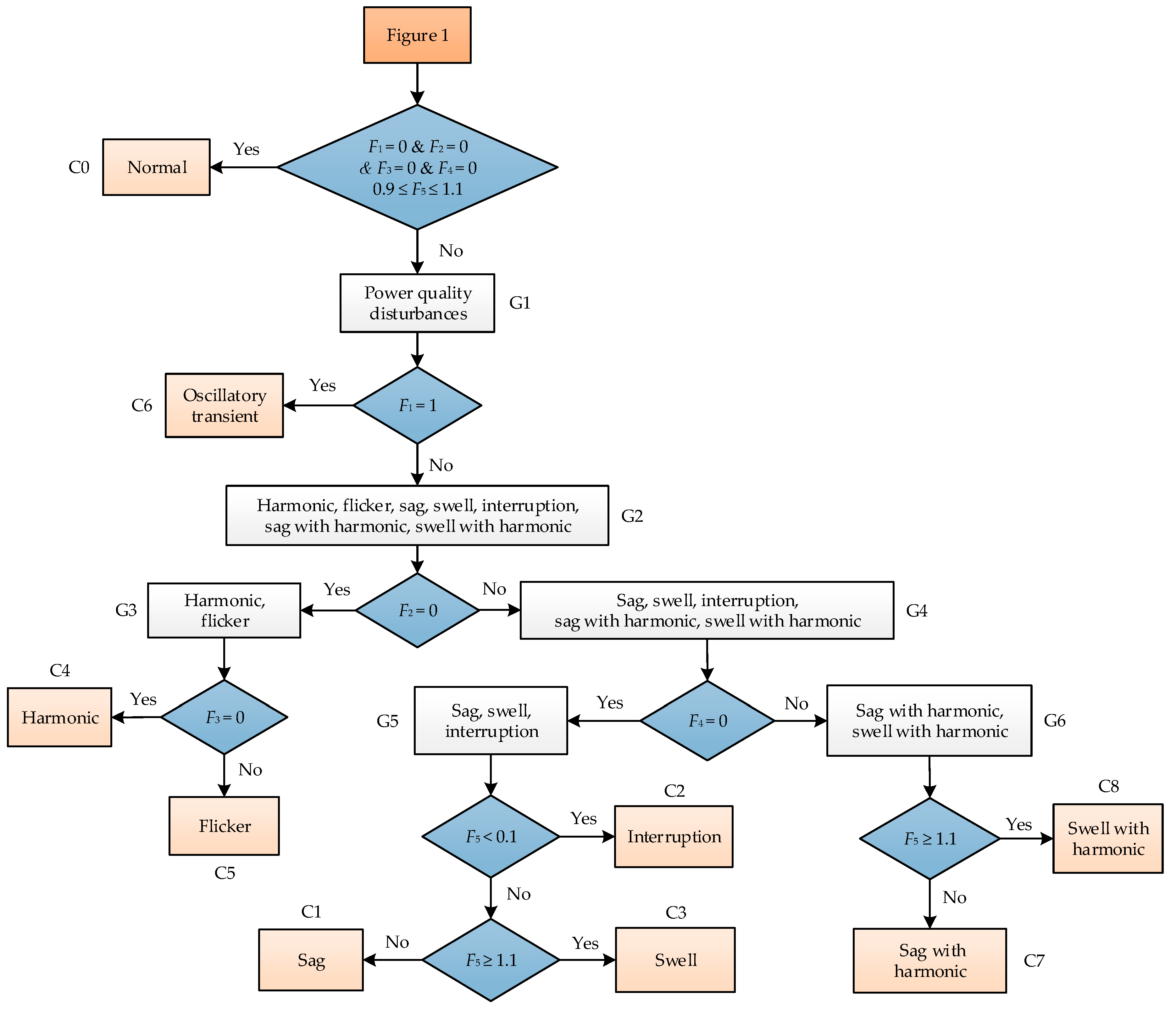
4. Detection and Classification Features of the PQ Disturbances
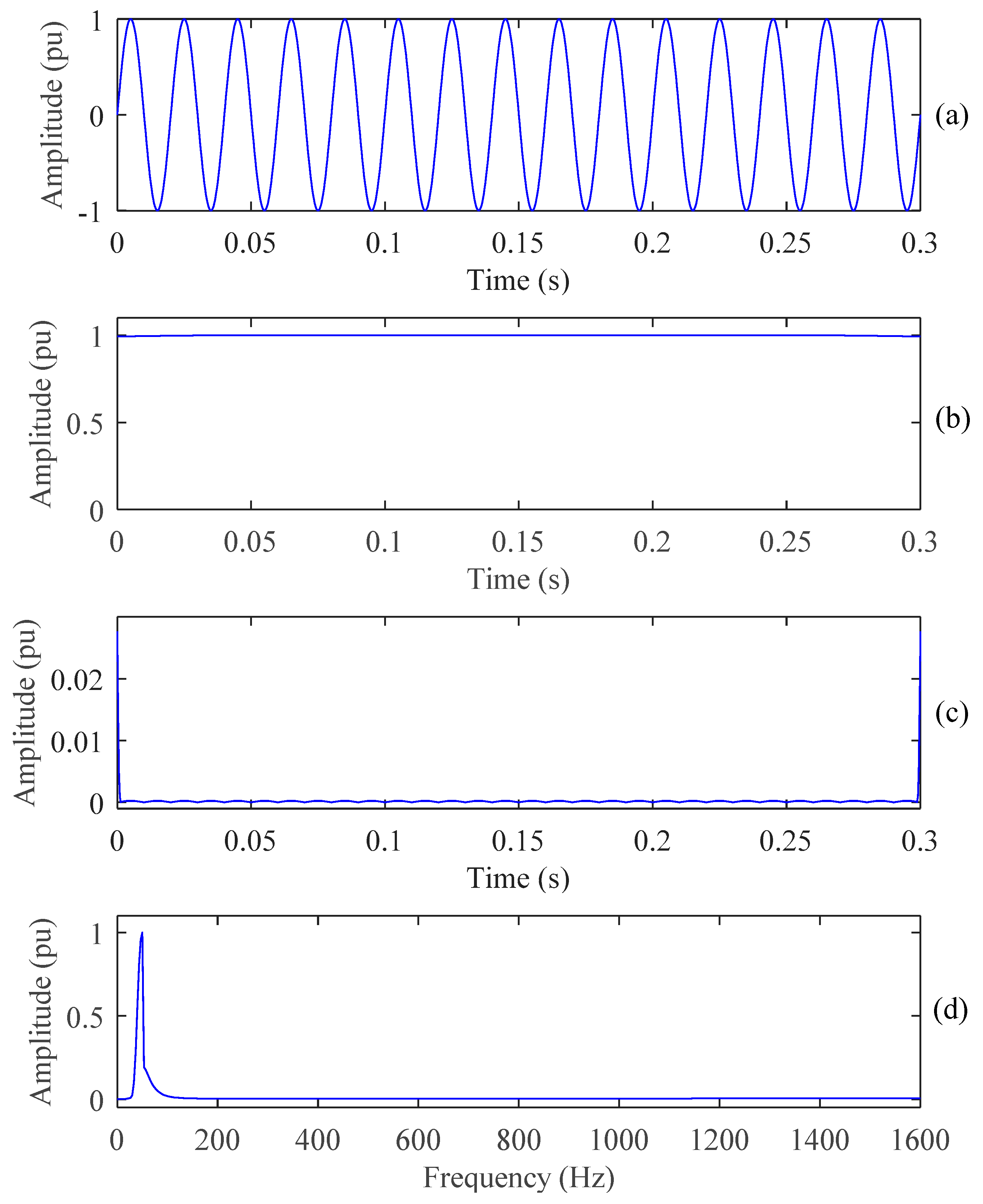
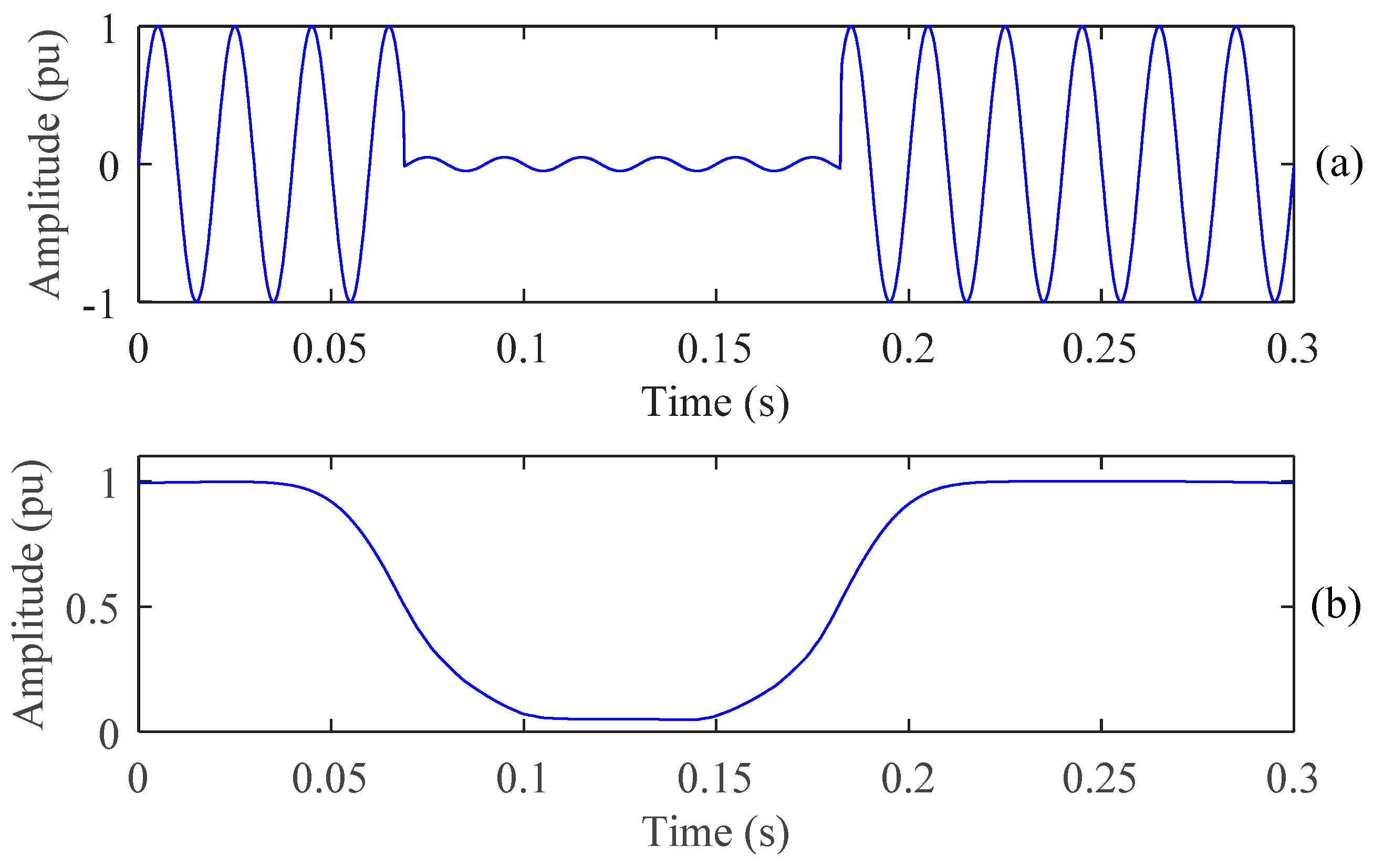
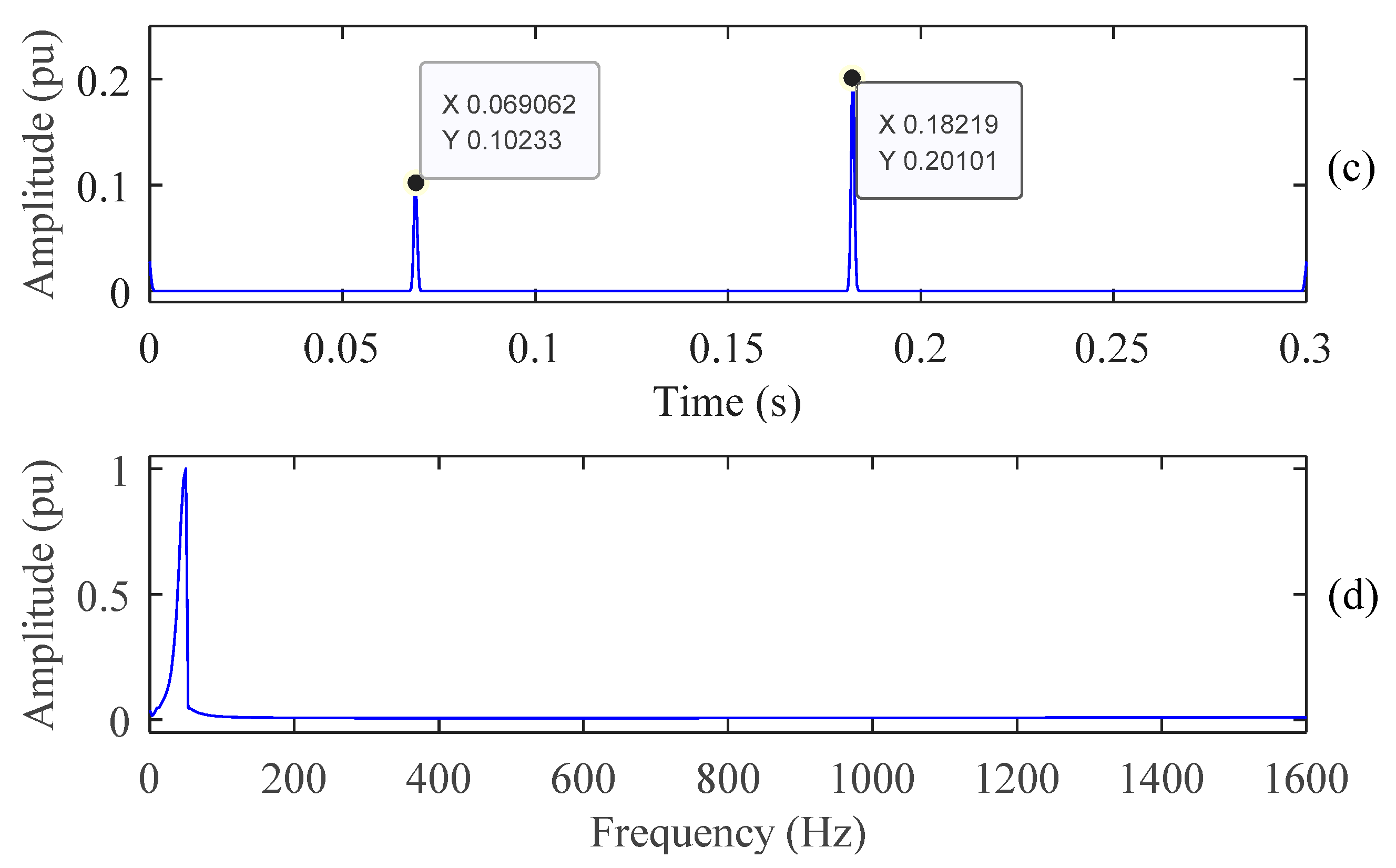
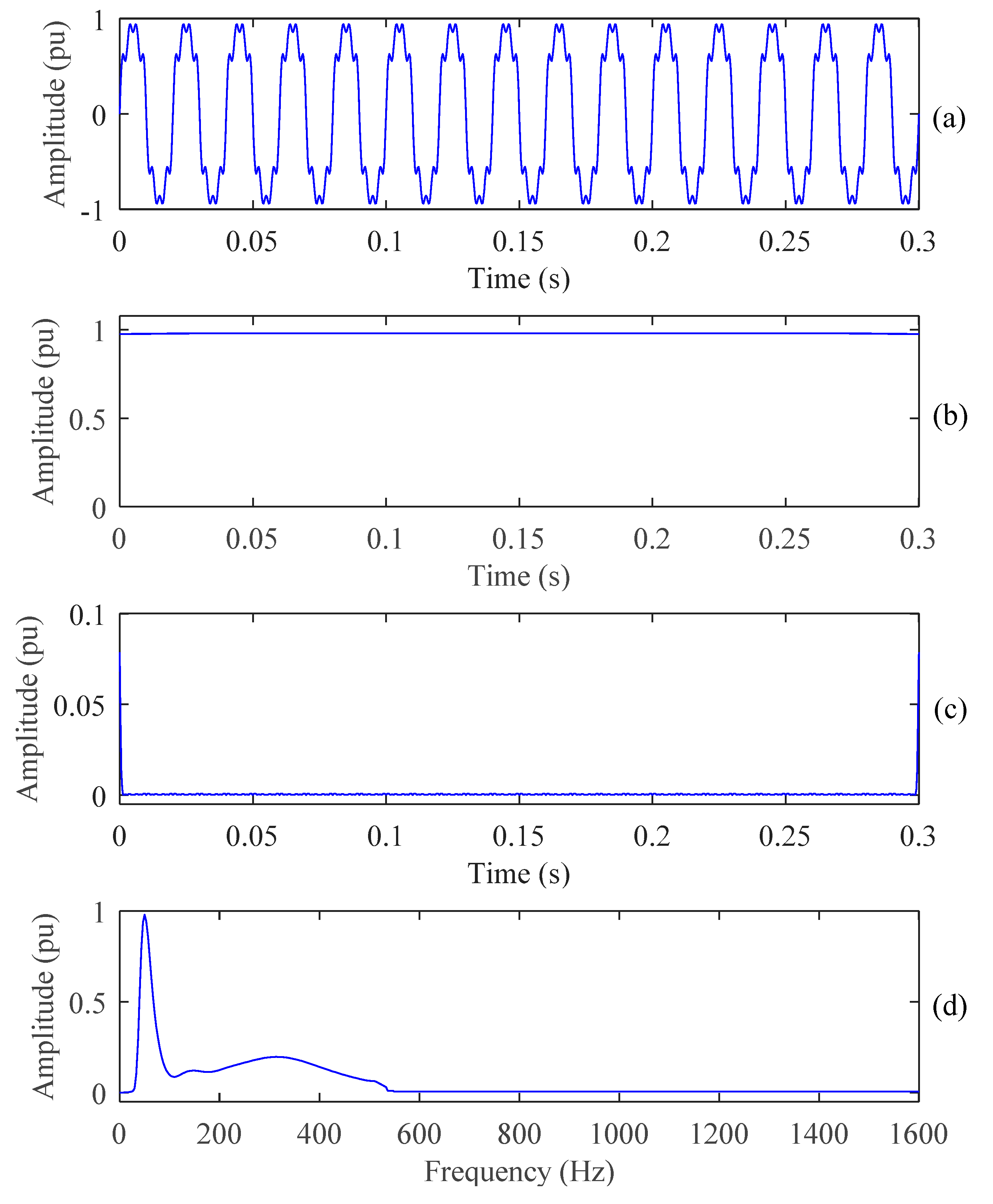
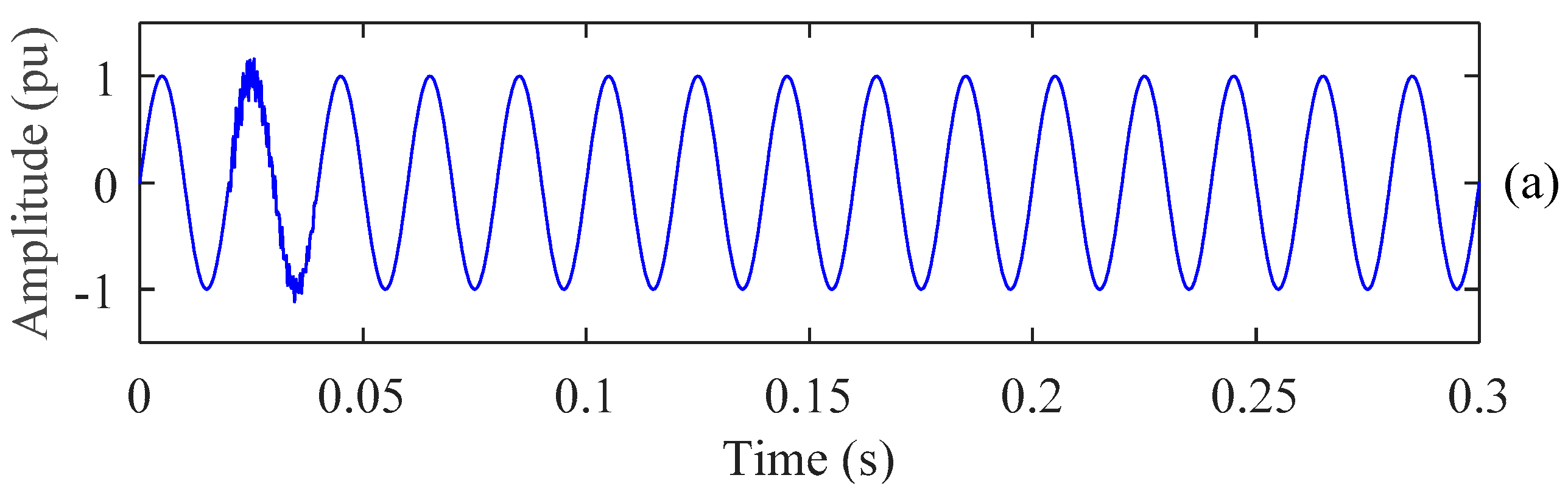
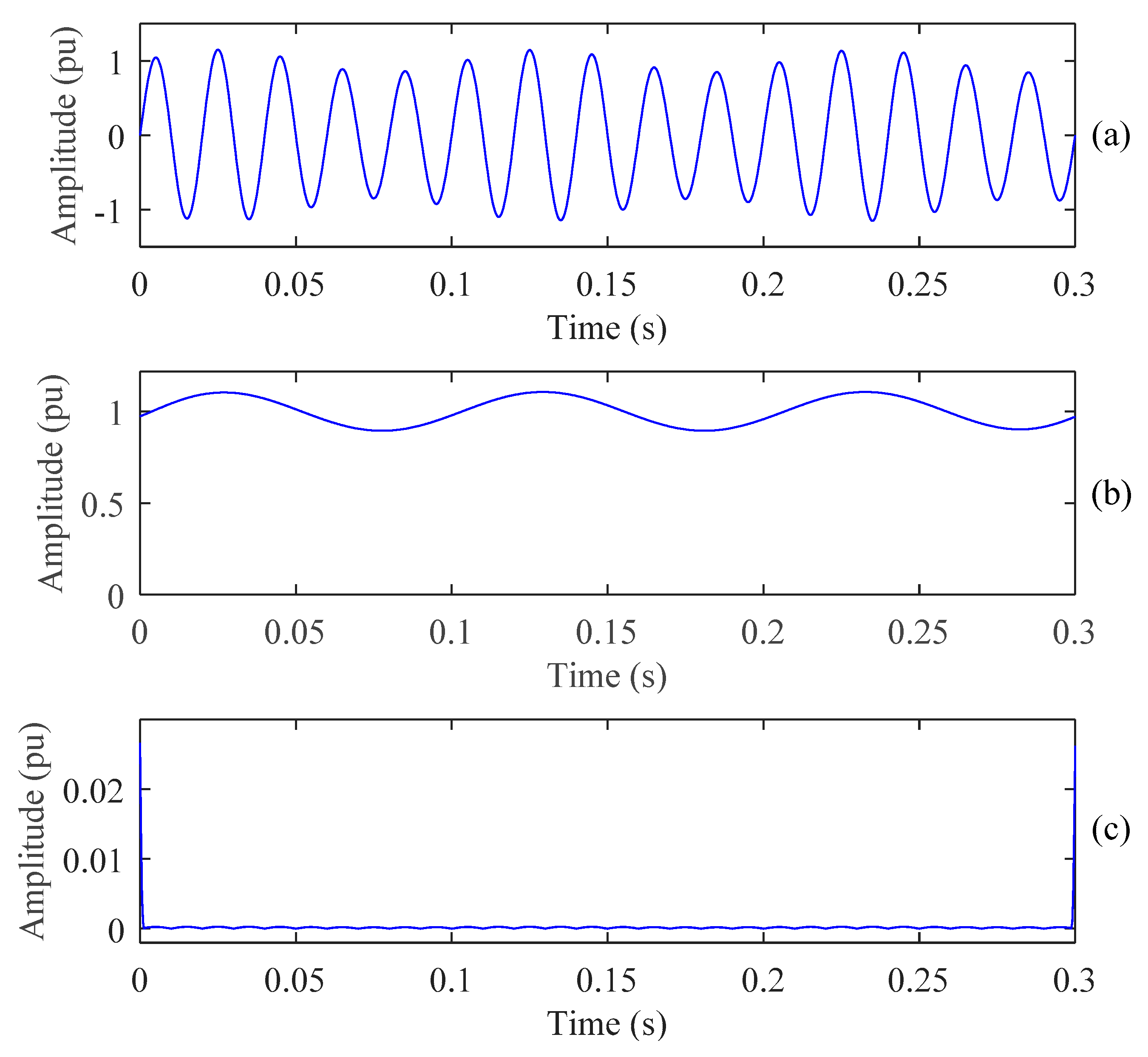
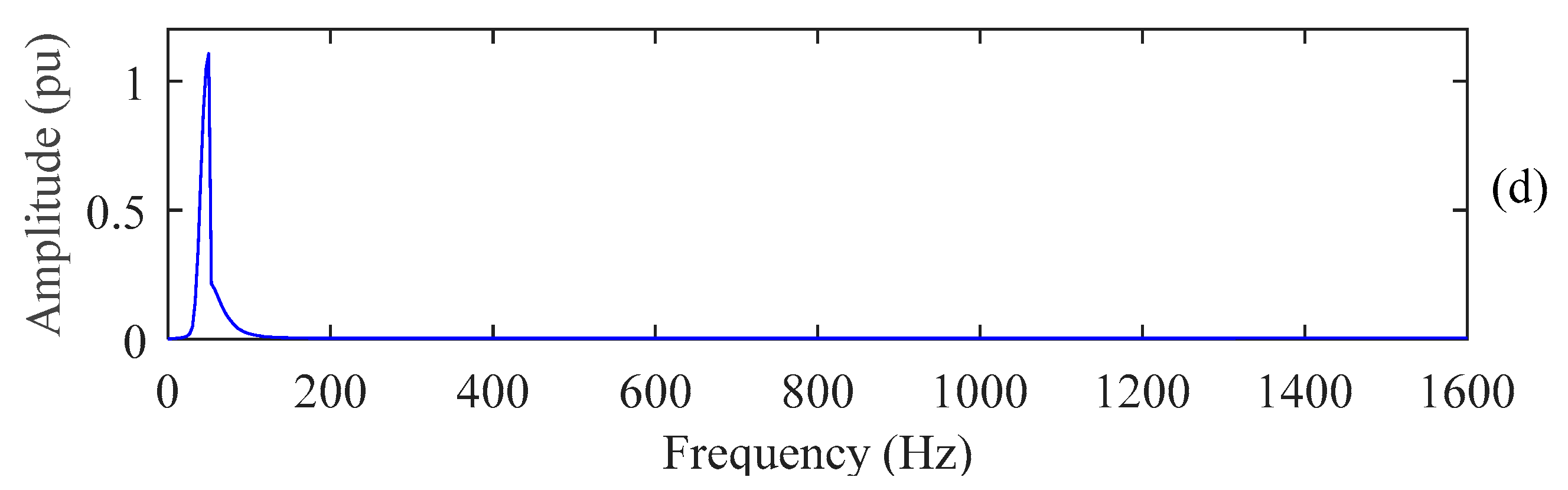
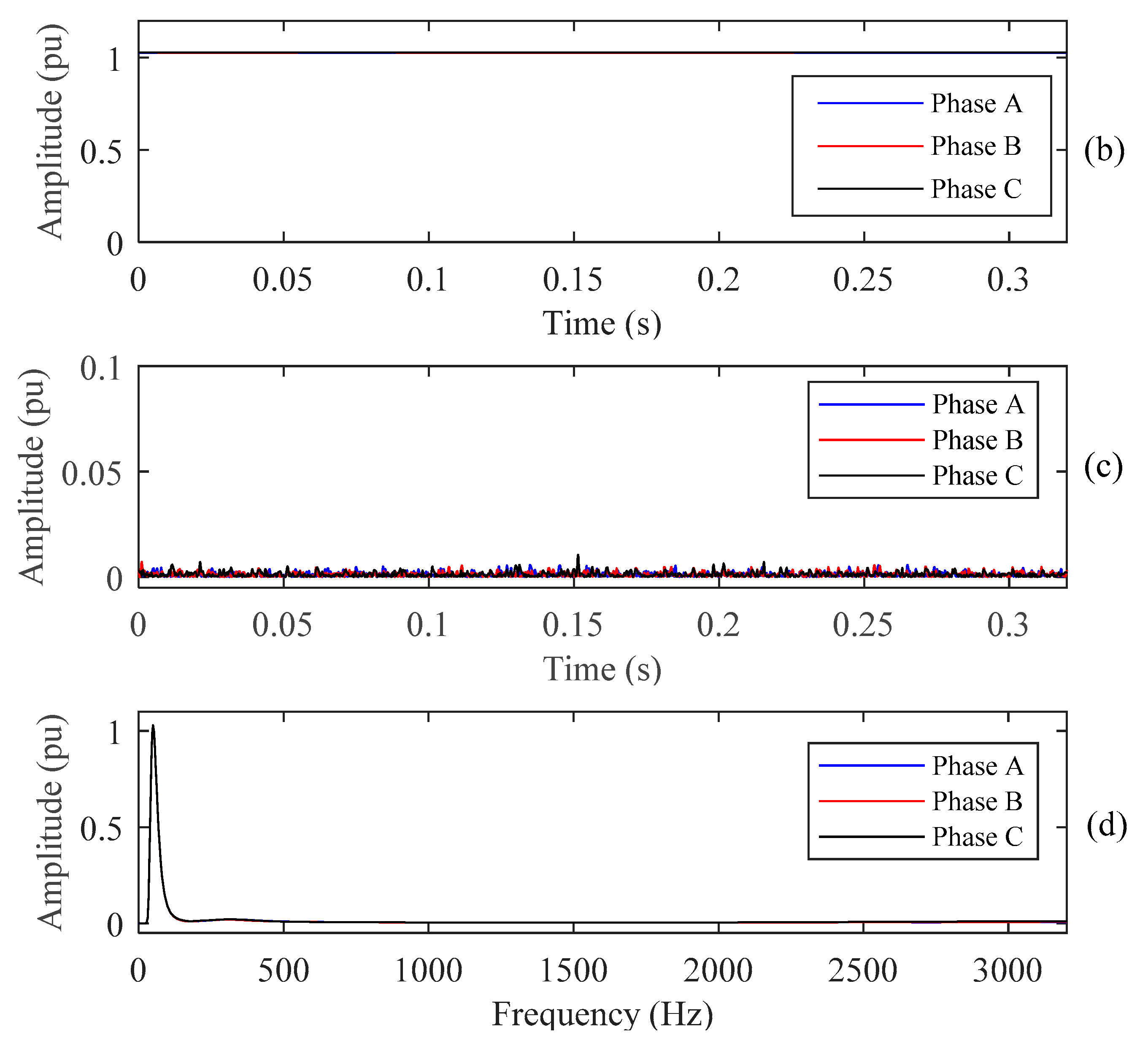
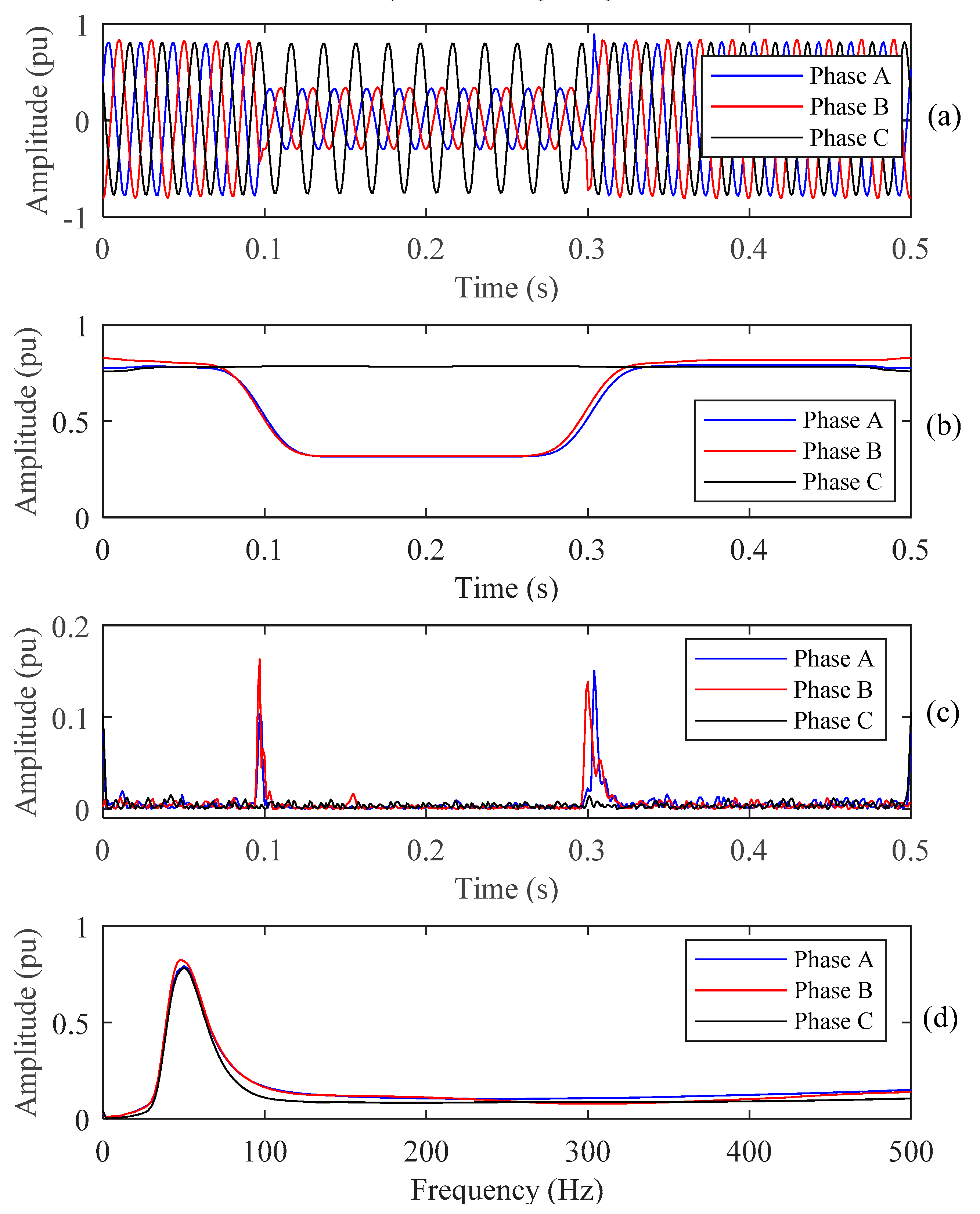
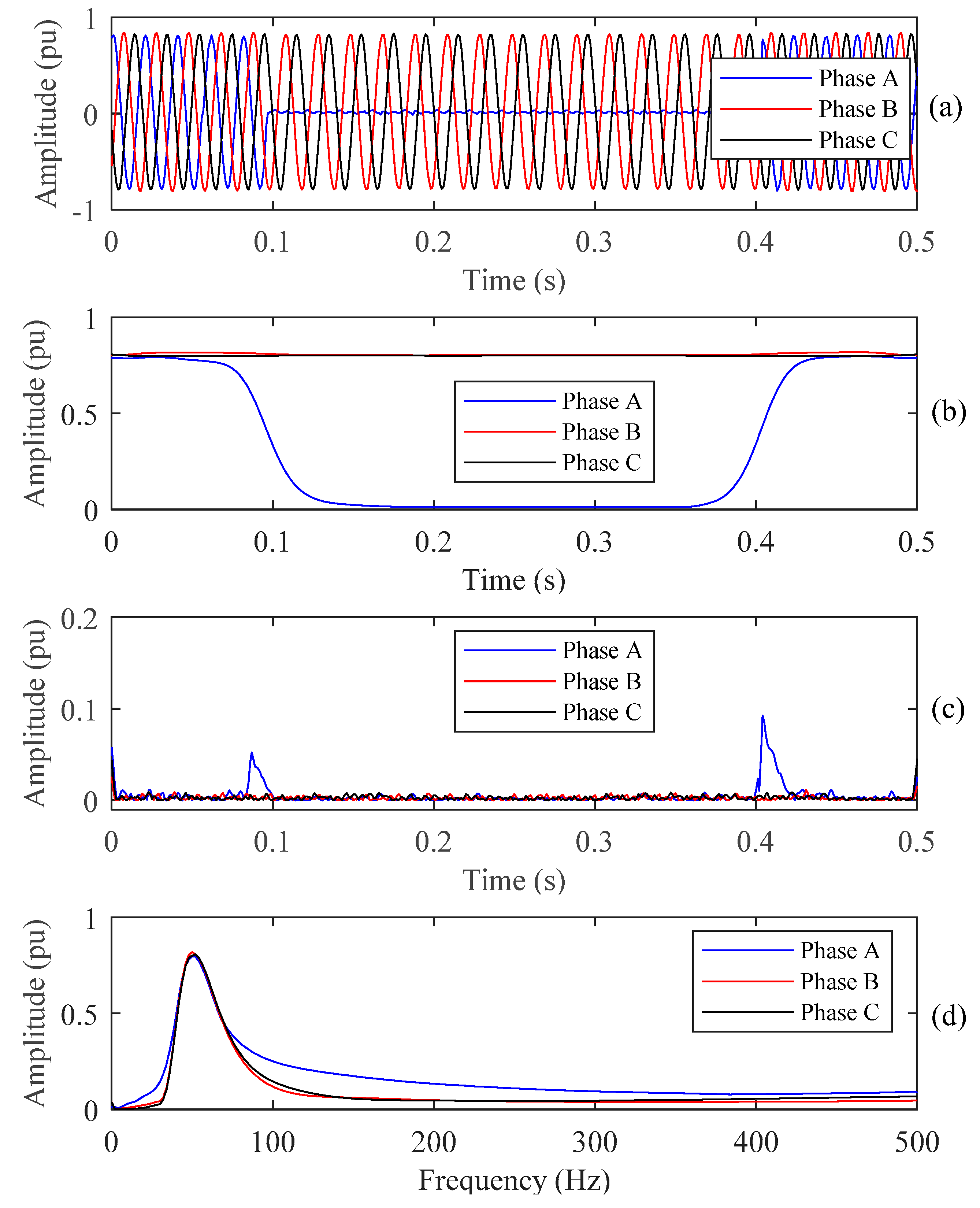
4.1. PQ Disturbances Analysis Using ST
4.2. Features Extraction
4.3. PQ Disturbances Analysis
4.4. Proposed Method
5. Tests and Discussion
5.1. Performance Evaluation
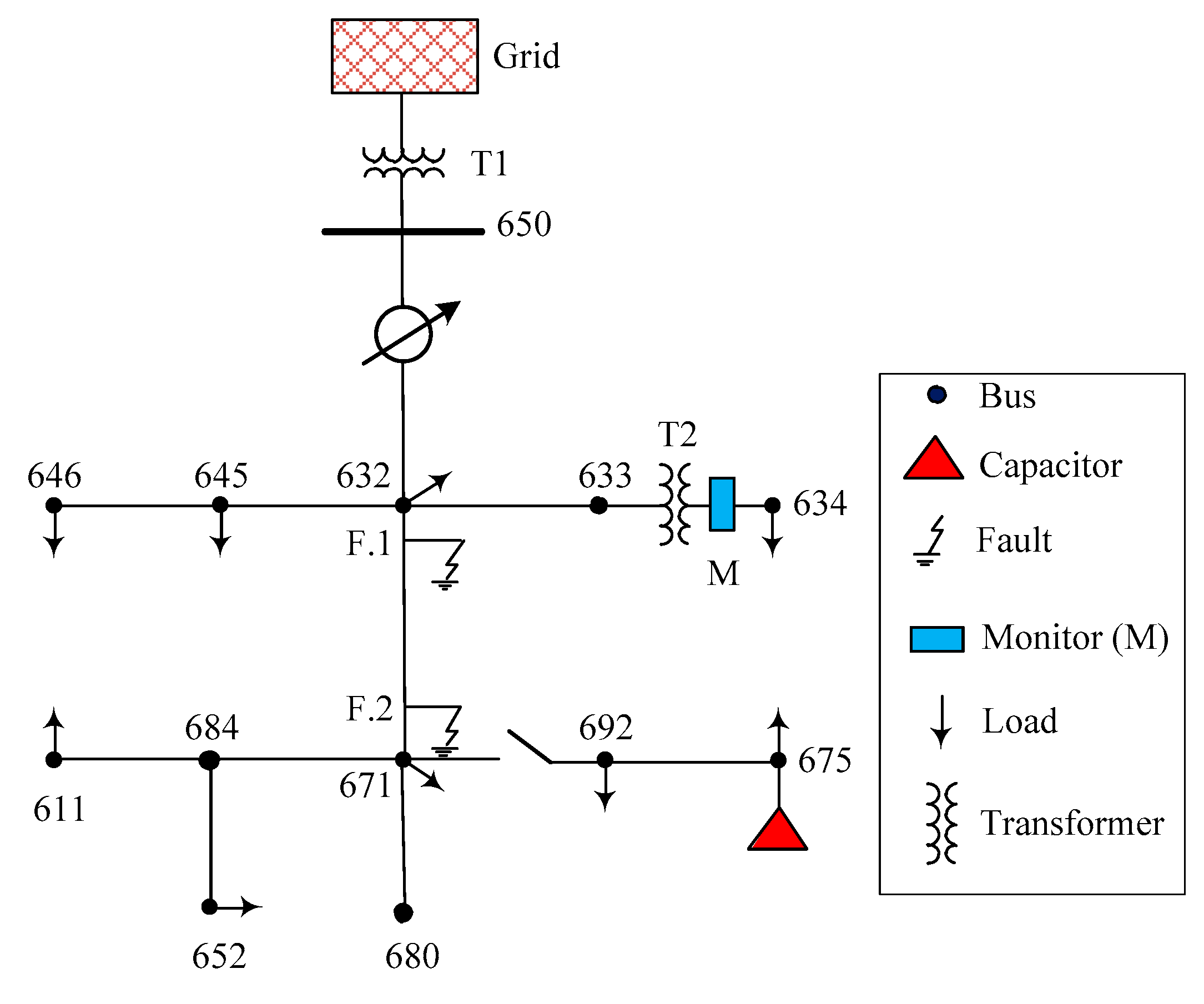
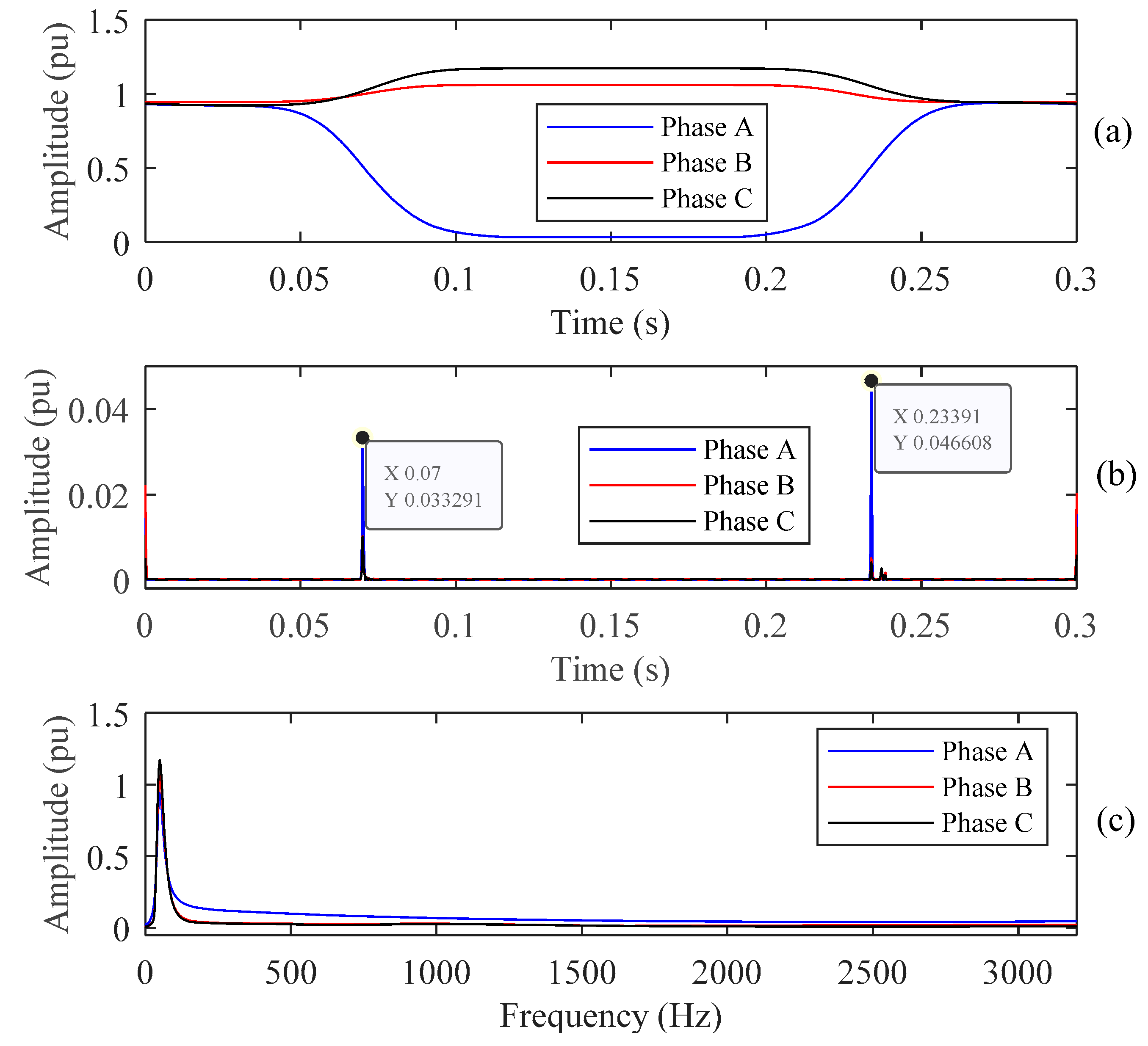
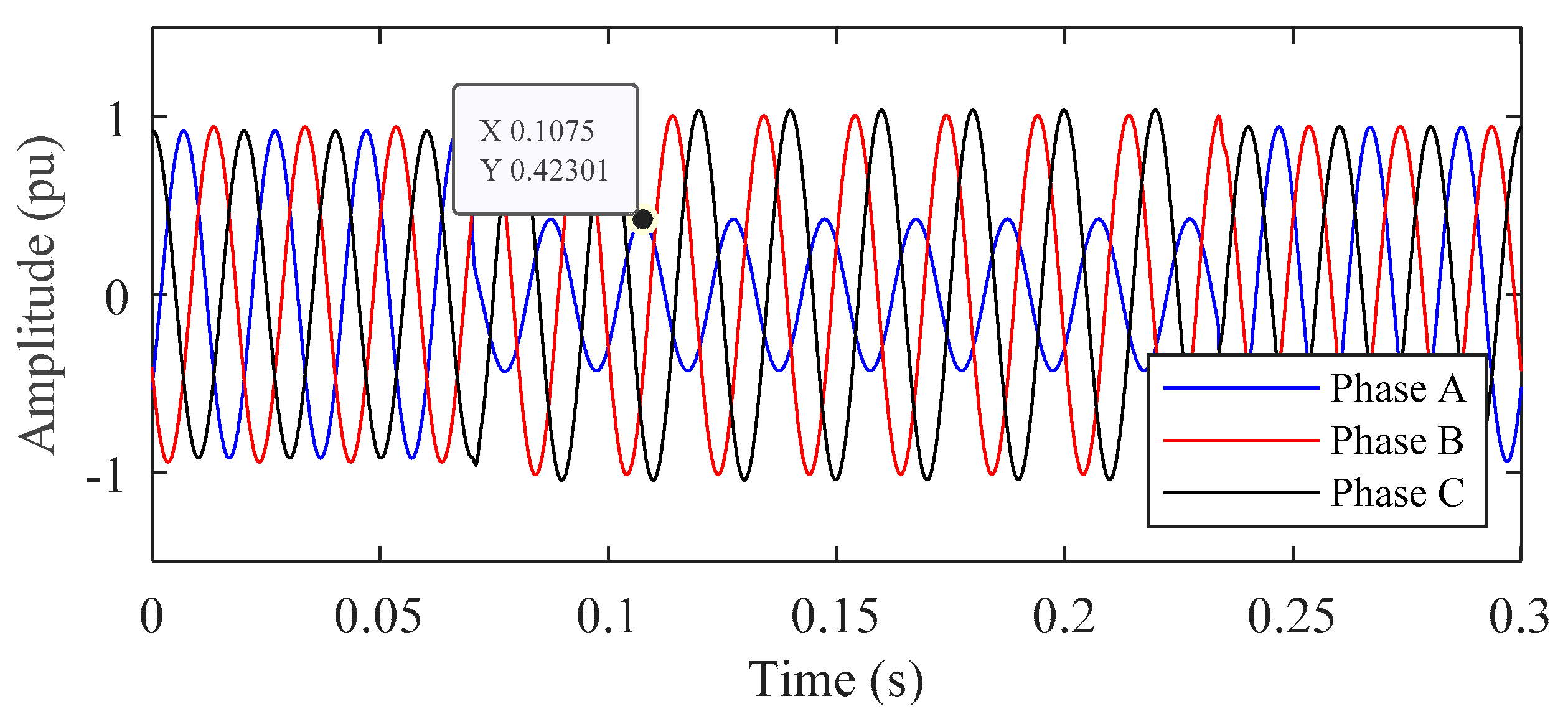
5.2. Test the PQ Disturbance on Standard IEEE Network
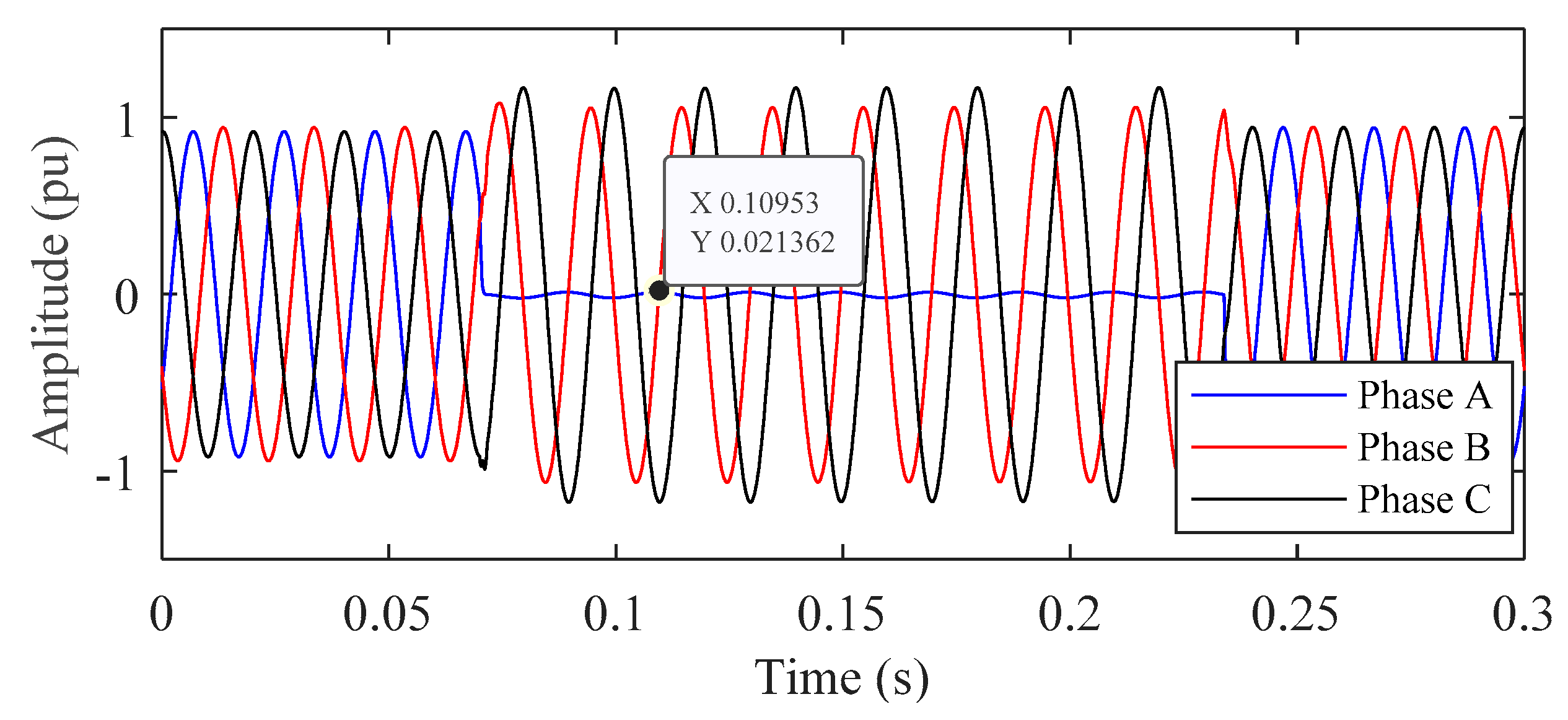
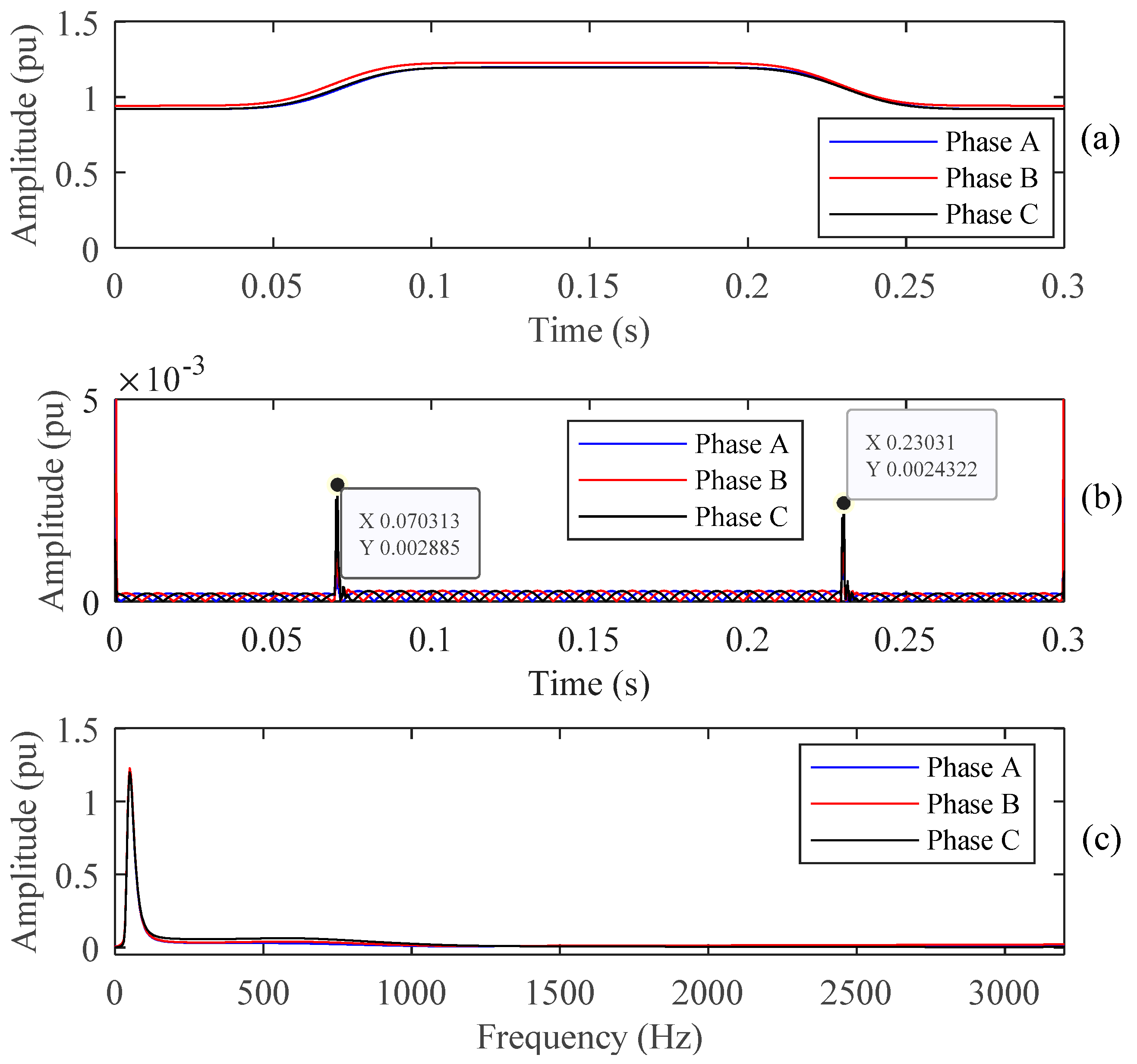
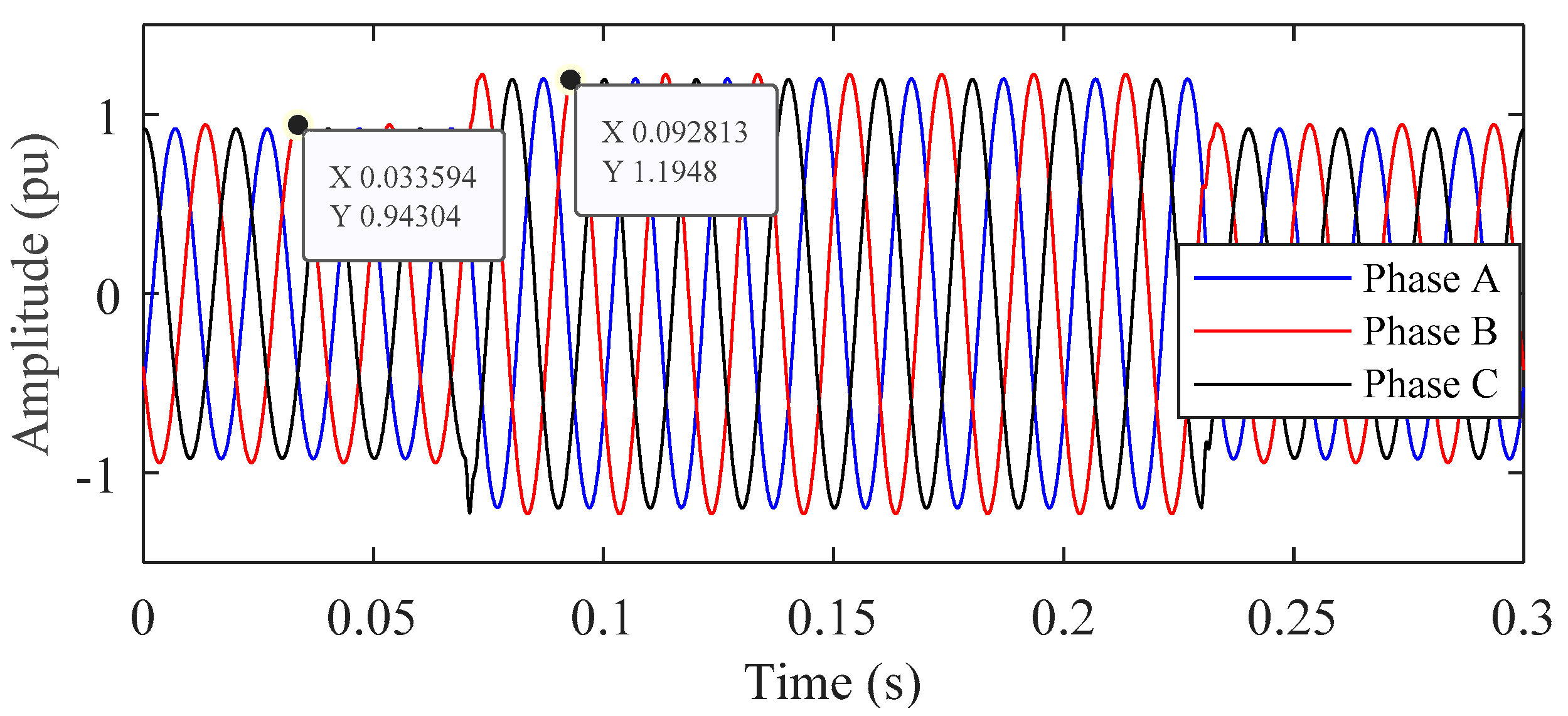
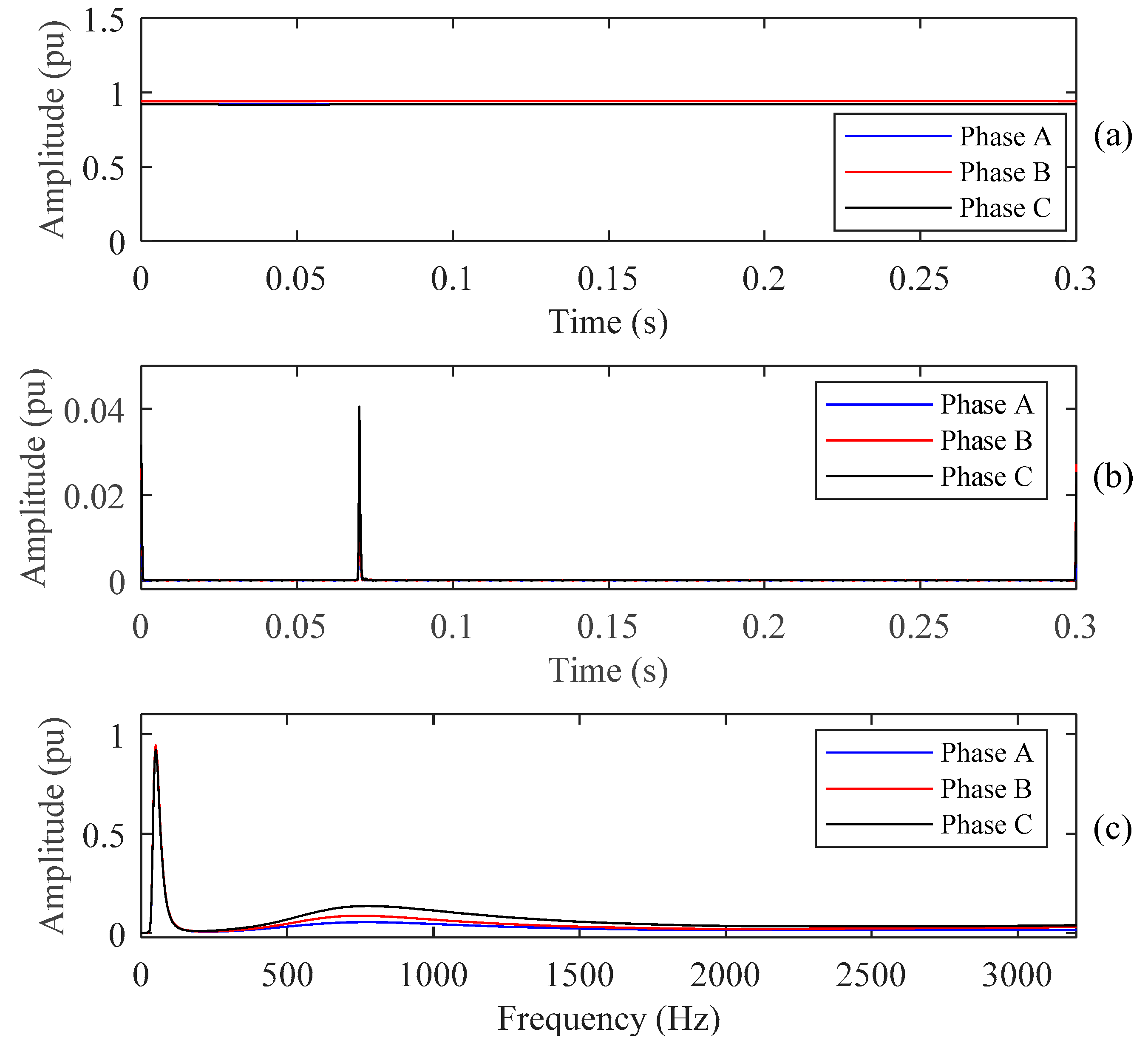
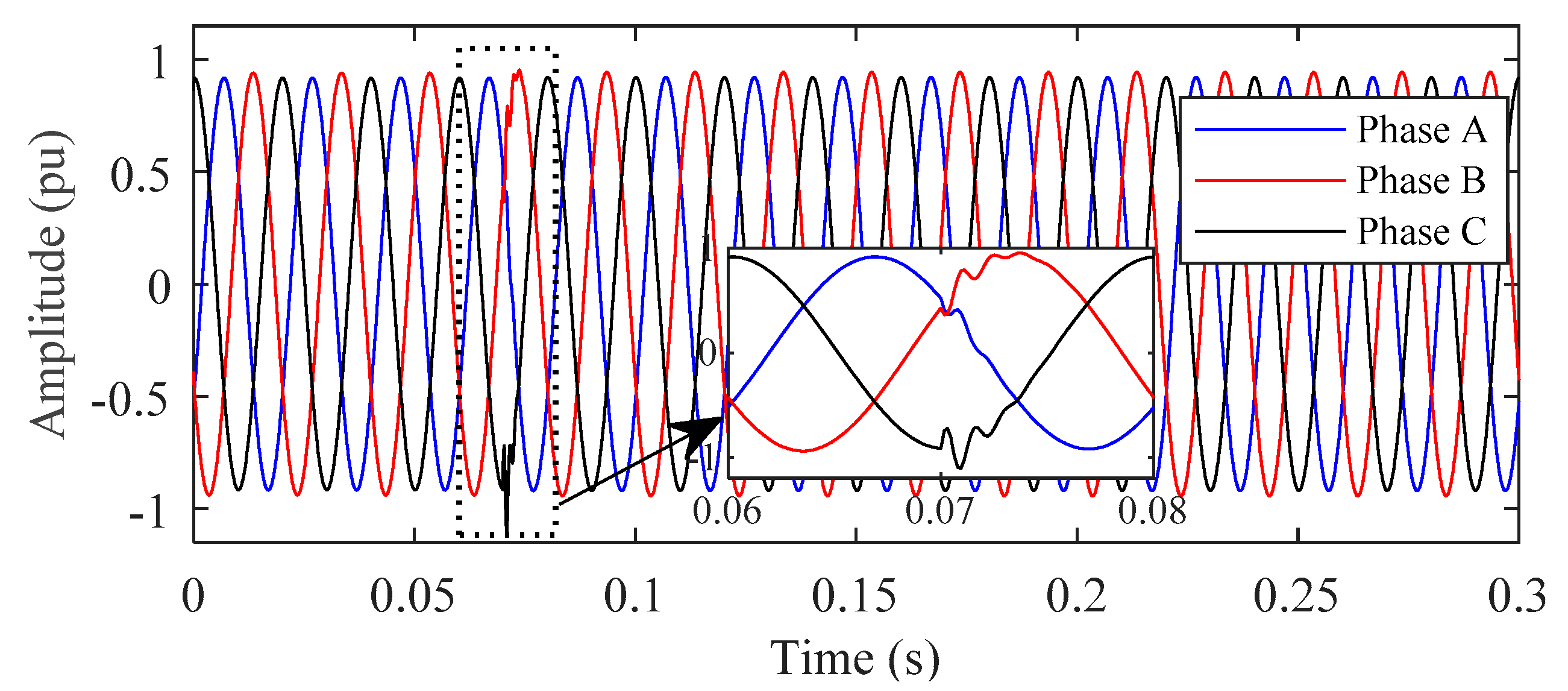
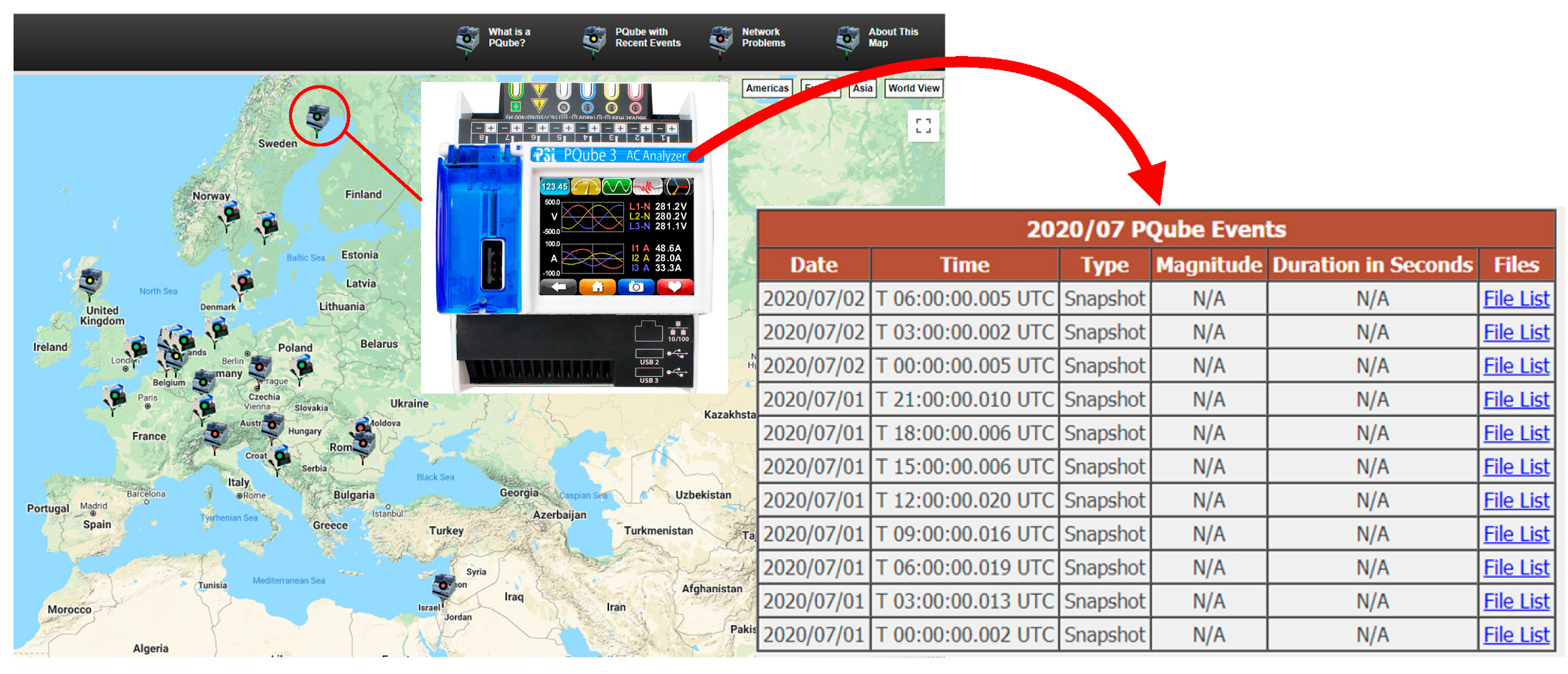
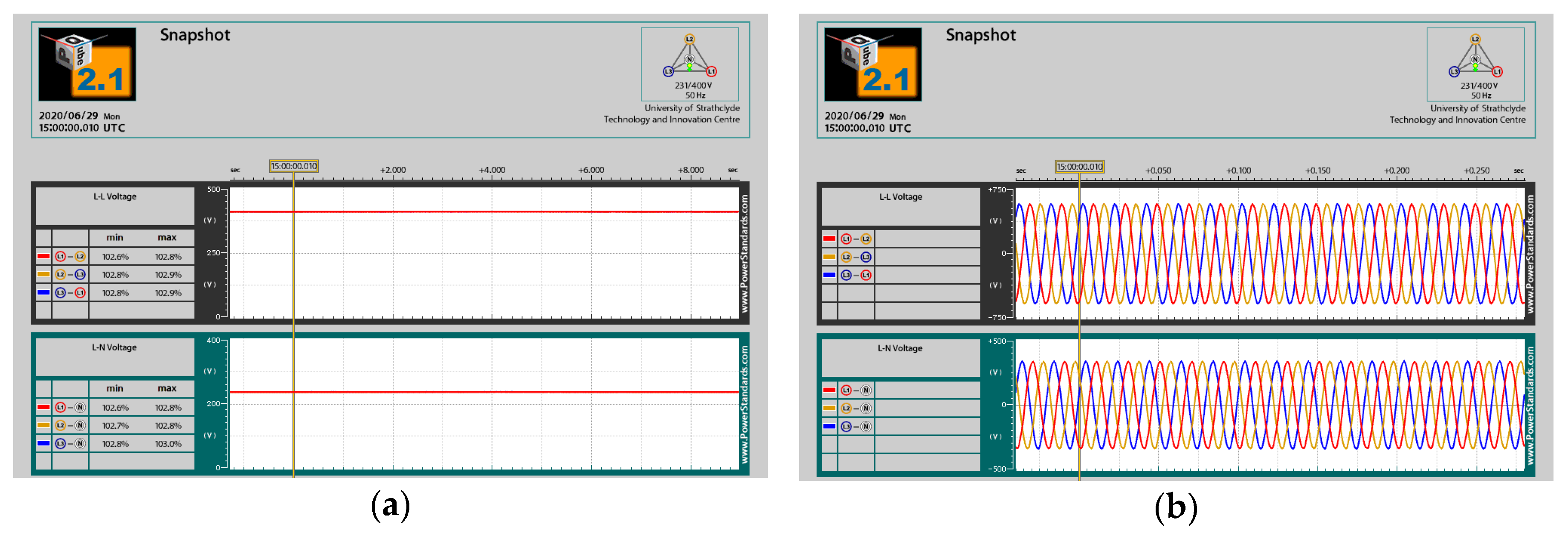
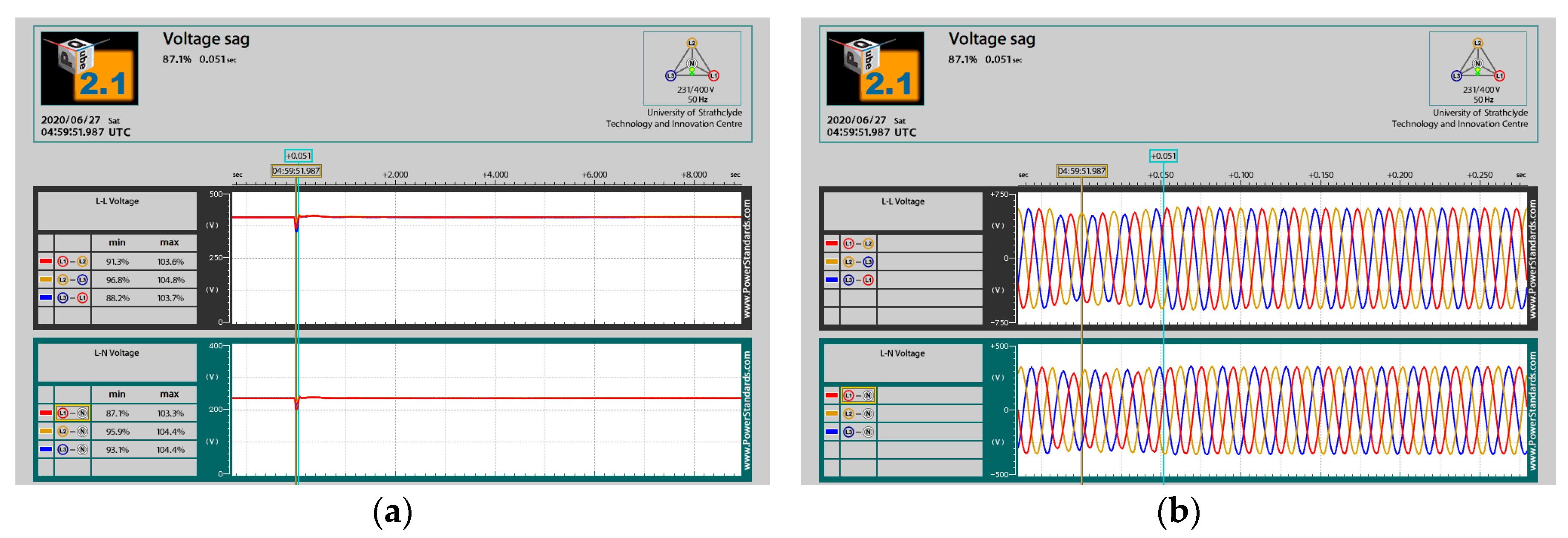
5.3. Test the PQ Disturbance on Recorded Real Data of PQube
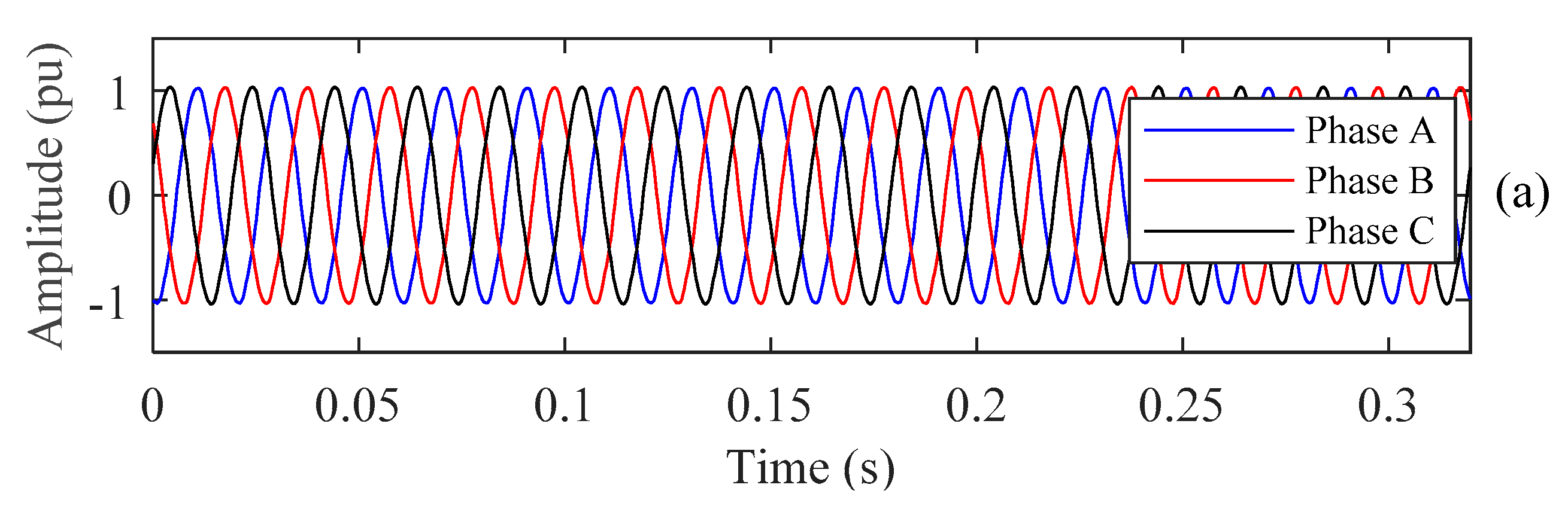
5.4. Test PQ Disturbance in Laboratory Environment
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liao, H.; Milanović, J.V. On capability of different FACTS devices to mitigate a range of power quality phenomena. IET Gen. Trans. Distr. 2017, 11, 1202–1211. [Google Scholar] [CrossRef] [Green Version]
- Saini, K.M.; Beniwal, R.K. Detection and classification of power quality disturbances in wind-grid integrated system using fast time-time transform and small residual-extreme learning machine. Int. Trans. Electr. Energy Syst. 2018, 28, 2519. [Google Scholar] [CrossRef]
- Jones, G.A.; Layer, D.H.; Osenkowsky, T.G. National Association of Broadcasters Engineering Handbook: NAB Engineering Handbook; Taylor & Francis: New York, NY, USA, 2013. [Google Scholar]
- Wang, M.; Rowe, G.I.; Mamishev, A.V. Classification of power quality events using optimal time-frequency representations—Part 2: Application. IEEE Trans. Power Del. 2004, 19, 1496–1503. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Cobben, S. Consequences of poor power quality—An overview. In Power Quality; Intech Open: Rijeka, Croatia, 2011. [Google Scholar]
- IEEE. IEEE Standard Definitions for the Measurement of Electric Power Quantities under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions; IEEE Std.1459-2010; IEEE Standards: Piscataway, NJ, USA, 2010; pp. 1–50. [Google Scholar]
- Hooshmand, R.A.; Enshaee, A. Detection and classification of single and combined power quality disturbances using fuzzy systems oriented by particle swarm optimization algorithm. Electr. Power Syst. Res. 2010, 80, 1552–1561. [Google Scholar] [CrossRef]
- Gu, Y.H.; Bellon, M.H.J. Time-frequency and time-scale domain analysis of voltage disturbances. IEEE Trans. Power Del. 2000, 15, 1279–1284. [Google Scholar] [CrossRef]
- Jaramillo, S.H.; Heydt, G.T.; O’Neill-Carrillo, E. Power quality indices for aperiodic voltages and currents. IEEE Trans. Power Del. 2000, 15, 784–790. [Google Scholar] [CrossRef]
- Heydt, G.; Fjeld, P.S.; Liu, C.C.; Pierce, D.; Tu, L.; Hensley, G. Applications of the windowed FFT to electric power quality assessment. IEEE Trans. Power Del. 1999, 14, 1411–1416. [Google Scholar] [CrossRef]
- Barros, J.; Diego, R.I. Application of the wavelet-packet transform to the estimation of harmonic groups in current and voltage waveforms. IEEE Trans. Power Del. 2006, 21, 533–535. [Google Scholar] [CrossRef]
- Zhang, M.; Li, K.; Hu, Y. A real-time classification method of power quality disturbances. Electr. Power Syst. Res. 2011, 81, 660–666. [Google Scholar] [CrossRef]
- Chilukuri, M.V.; Dash, P.K. Multiresolution S-Transform-Based Fuzzy Recognition System for Power Quality Events. IEEE Trans. Power Del. 2004, 19, 323–330. [Google Scholar] [CrossRef]
- Axelberg, P.G.V.; Gu, I.Y.; Bollen, M.H.J. Support Vector Machine for classification of voltage disturbances. IEEE Trans. Power Del. 2007, 22, 1297–1303. [Google Scholar] [CrossRef]
- Dash, P.K.; Panigrahi, B.K.; Sahoo, P.K.; Panda, G. Power quality disturbance data compression, detection and classification using integrated spline wavelet and S-transform. IEEE Trans. Power Del. 2003, 18, 595–600. [Google Scholar] [CrossRef]
- Uyara, M.; Yildirima, S.; Gencoglub, M.T. An effective wavelet-based feature extraction method for classification of power quality disturbance signals. Electr. Power Syst. Res. 2008, 78, 1747–1755. [Google Scholar] [CrossRef]
- Lin, W.M.; Wu, C.H.; Lin, C.H.; Chen, F.S. Detection and classification of multiple power-quality disturbances with wavelet multiclass SVM. IEEE Trans. Power Del. 2008, 23, 2575–2582. [Google Scholar] [CrossRef]
- Poisson, O.; Rioual, P.; Meunier, M. Detection and measurement of power quality disturbances using wavelet transform. IEEE Trans. Power Del. 2000, 15, 1039–1044. [Google Scholar] [CrossRef]
- Masoum, M.; Jamali, S.; Ghaffarzadeh, N. Detection and classification of power quality disturbances using discrete wavelet transform and wavelet networks. IET Sci. Meas. Technol. 2010, 4, 193–205. [Google Scholar] [CrossRef]
- Khokhar, S.; Mohd Zin, A.A.; Mokhtar, A.S.; Zareen, N. Automatic pattern recognition of single and multiple power quality disturbances. Aust. J. Electr. Electron. Eng. 2016, 13, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Decanini, J.G.M.S.; Tonelli-Neto, M.S.; Malange, F.C.V.; Minussi, C.R. Detection and classification of voltage disturbances using a Fuzzy-ARTMAP-wavelet network. Electr. Power Syst. Res. 2011, 81, 2057–2065. [Google Scholar] [CrossRef]
- Gaouda, A.M.; Salama, M.M.A.; Sultan, M.R.; Chikhani, A.Y. Power quality detection and classification using wavelet-multiresolution signal decomposition. IEEE Trans. Power Del. 1999, 14, 1469–1476. [Google Scholar] [CrossRef]
- Reddy, M.J.B.; Mohanta, D.K.; Sagar, K. A Multifunctional Real-Time Power Quality Monitoring System Using Stockwell Transform. IET Sci. Meas. Technol. 2014, 8, 155–169. [Google Scholar] [CrossRef]
- Granados-Lieberman, D.; Romero-Troncoso, R.J.; Osornio-Rios, R.A.; Garcia-Perez, A.; Cabal-Yepez, E. Techniques and methodologies for power quality analysis and disturbances classification in power systems: A review. IET Gener. Transm. Distrib. 2011, 5, 519–529. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal. Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hu, H.W.; Tang, K. Constructing a decision tree from data with hierarchical class labels. Expert Syst. Appl. 2009, 36, 4838–4847. [Google Scholar] [CrossRef]
- Ray, P.; Kishor, N.; Mohanty, S. Islanding and power quality disturbance detection in grid-connected hybrid power system using wavelet and S-transform. IEEE Trans. Smart Grid 2012, 3, 1082–1094. [Google Scholar] [CrossRef]
- Dash, P.K.; Panigrahi, B.K.; Panda, G. Power quality analysis using S-Transform. IEEE Trans. Power Del. 2003, 18, 406–411. [Google Scholar] [CrossRef]
- Parvez, I.; Aghili, M.; Sarwat, A.I.; Rahman, S.; Fahmida, A. Online power quality disturbance detection by support vector machine in smart meter. J. Mod. Power Syst. Clean Energy 2019, 7, 1328–1339. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Qunzhan, L.I.; Fulin, Z. Transient power quality disturbance denoising and detection based on improved iterative adaptive kernel regression. J. Mod. Power Syst. Clean Energy 2019, 7, 644–657. [Google Scholar]
- Zhong, T.; Zhang, S.; Cai, G.; Li, Y.; Yang, B.; Chen, Y. Power Quality Disturbance Recognition Based on Multiresolution S-Transform and Decision Tree. IEEE Access 2019, 7, 88380–88392. [Google Scholar] [CrossRef]
- Lin, L.; Wang, D.; Zhao, S.; Chen, L.; Huang, N. Power quality disturbance feature selection and pattern recognition based on image enhancement techniques. IEEE Access 2019, 7, 67889–67904. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Detection and characterization of multiple power quality disturbances with a fast S-transform and decision tree based classifier. Digit. Signal. Proc. 2013, 23, 1071–1083. [Google Scholar] [CrossRef]
- Gargoom, A.M.; Ertugrul, N.; Soong, W.L. Automatic classification and characterization of power quality events. IEEE Trans. Power Del. 2008, 23, 2417–2425. [Google Scholar] [CrossRef] [Green Version]
- Tan, R.H.; Ramachandaramurthy, V.K. Numerical model framework of power quality events. Eur. J. Sci. Res. 2010, 43, 30–47. [Google Scholar]
- Uyar, M.; Yildirim, S.; Gencoglu, M.T. An expert system based on S-transform and neural network for automatic classification of power quality disturbances. Expert Syst. Appl. 2009, 36, 5962–5975. [Google Scholar] [CrossRef]
- Mishra, S.; Bhende, C.N.; Panigrahi, B.K. Detection and classification of power quality disturbances using S-transform and probabilistic neural network. IEEE Trans. Power Del. 2007, 23, 280–287. [Google Scholar] [CrossRef]
- Manimala, K.; Selvi, K.; Ahila, R. Optimization techniques for improving power quality data mining using wavelet packet based support vector machine. Neurocomputing 2012, 77, 36–47. [Google Scholar] [CrossRef]
- Ahila, R.; Sadasivam, V.; Manimala, K. An integrated PSO for parameter determination and feature selection of ELM and its application in classification of power system disturbances. Appl. Soft Comput. 2015, 32, 23–37. [Google Scholar] [CrossRef]
- Dehghani, H.; Vahidi, B.; Naghizadeh, R.A.; Hosseinian, S.H. Power quality disturbance classification using a statistical and wavelet-based Hidden Markov Model with Dempster–Shafer algorithm. Int. J. Electr. Power Energy Syst. 2013, 47, 368–377. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001. [Google Scholar]
- Christe, A.; Negrashov, S.; Johnson, P. Open Power Quality: An open source framework for power quality collection, analysis, visualization, and privacy. In Proceedings of the 2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016. [Google Scholar]
- Rönnberg, S.; Gil de Castro, A.; Espin Delgado, A. Variations in Supraharmonic Levels in Low Voltage Networks. In Proceedings of the 25th International Conference on Electricity Distribution, Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Available online: http://map.pqube.com (accessed on 30 June 2020).
- Available online: http://map.pqube.com/glasgow/2020/Month%2006/Day%2029/T%2015-00-00-010%20Snapshot/FilesList.htm (accessed on 30 June 2020).
- Available online: http://map.pqube.com/glasgow/2020/Month%2006/Day%2027/T%2004-59-51-987%20Voltage%20Sag/FilesList.htm (accessed on 30 June 2020).








| Type of Voltage Signals | Syb. | The Values of Features | ||||
|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | ||
| Normal | C0 | 0 | 0 | 0 | 0 | (≥0.9) and (≤1.1) |
| Sag | C1 | 0 | 1 | - | 0 | (≥0.1) and (≤0.9) |
| Interruption | C2 | 0 | 1 | - | 0 | ≤ 0.1 |
| Swell | C3 | 0 | 1 | - | 0 | (≥1.1) and (≤1.8) |
| Harmonic | C4 | 0 | 0 | 0 | 1 | - |
| Flicker | C5 | 0 | 0 | 1 | - | - |
| Oscillatory transient | C6 | 1 | 1 | - | - | - |
| Harmonic voltage sag | C7 | 0 | 1 | - | 1 | (≥0.1) and (≤0.9) |
| Harmonic voltage swell | C8 | 0 | 1 | - | 1 | (≥1.1) and (≤1.8) |
| Type of Voltage Signal | Classification result | |||
|---|---|---|---|---|
| Total Samples | Correct Samples | Incorrect Samples | Classification Accuracy | |
| Normal | 100 | 100 | 0 | 100% |
| Sag | 100 | 100 | 0 | 100% |
| Interruption | 100 | 98 | 2 | 98% |
| Swell | 100 | 100 | 0 | 100% |
| Harmonic | 100 | 100 | 0 | 100% |
| Flicker | 100 | 100 | 0 | 100% |
| Oscillatory transient | 100 | 100 | 0 | 100% |
| Harmonic voltage sag | 100 | 100 | 0 | 100% |
| Harmonic voltage swell | 100 | 100 | 0 | 100% |
| Total | 900 | 898 | 2 | 99.78% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minh Khoa, N.; Van Dai, L. Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods. Energies 2020, 13, 3623. https://doi.org/10.3390/en13143623
Minh Khoa N, Van Dai L. Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods. Energies. 2020; 13(14):3623. https://doi.org/10.3390/en13143623
Chicago/Turabian StyleMinh Khoa, Ngo, and Le Van Dai. 2020. "Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods" Energies 13, no. 14: 3623. https://doi.org/10.3390/en13143623
APA StyleMinh Khoa, N., & Van Dai, L. (2020). Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods. Energies, 13(14), 3623. https://doi.org/10.3390/en13143623






