Assessment of Material Durability of Steam Pipelines Based on Statistical Analysis of Strength Properties—Selected Models
Abstract
:1. Introduction
- Collection of results of diagnostic tests (mechanical properties of steam pipelines) from various power units.
- Creation of a database containing the following results: tensile strength (Rm), conventional yield point (Rp), elongation (A), and Vickers hardness (V) correlated with the operating time and medium type (FS and SSS) for elbows of steam pipelines.
- Selection of nonlinear-linearized models, which may be reduced to a linear form after transformation and treated (approximately) as linear models.
- Selection of statistical linear models defining the course of changes between the selected strength properties and the operating time of steam pipeline elbows.
- Forecast determination of the number of hours, after which further exploitation of the pipeline should cease or the pipeline should be subjected to a thorough inspection of diagnostic supervision services.
2. Materials and Methods
- Type of steam flowing through the pipeline:
- Fresh steam (steel grades: 14MoV6-3, 13CrMo4-5)—designation FS;
- Secondarily super-heated steam (steel grade 10CrMo9-10)—designation SSS;
- Sampling location for tests of mechanical properties in the elbow area (Figure 1a):
- Elbow “bend” on the side of maximum bending zone (compression or stretching);
- Elbow straight section;
- Location of sample cutting for static tensile test (Figure 1b):
- Longitudinal—along the steam pipeline axis;
- Crosswise—across the pipeline axis.
- -
- Exponential:
- -
- Hyperbolic:
- -
- Quadratic:
- -
- Modified exponential:which—because the course of changes in mechanical properties is “inversely proportional” to the exponential model—better reflects the occurring changes in properties during the operation of pipe elbows,
- y—selected mechanical property (Vickers hardness, Rm, Rp, A);
- x—operating time of the tested steam pipeline elbow;
- a, b—coefficients of the given function;
- c—correction coefficient, obtained by maximization (to a value equal to 1) of the coefficient of determination R2 of the exponential, hyperbolic, or quadratic function.
- Rm: 640 (USL)–440 (LSL) MPa for FS and 590(USL)–440 (LSL) MPa for SSS,
- Rp: 440 (USL)–295 (LSL) MPa for FS and 410 (USL)–275 (LSL) MPa for SSS,
- A: 0 (LSL)–21 (USL) % for FS and 0 (LSL)–20 (USL) % for SSS,
- V: above 140 V for FS and for SSS steel group.
3. Results
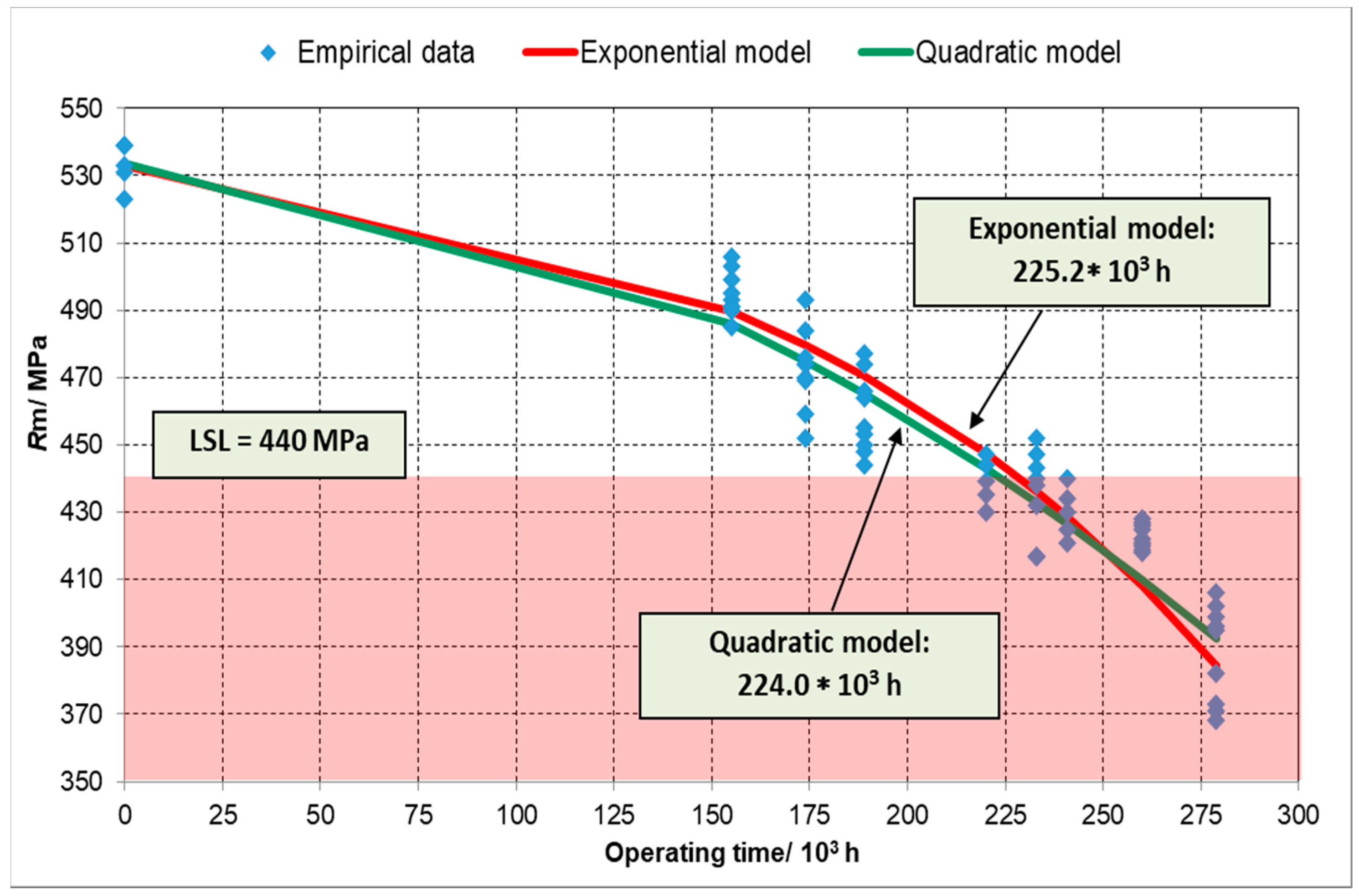
3.1. Determining the Forecast of Operating Time on the Statistical Results of Tensile Strength (Rm) Change
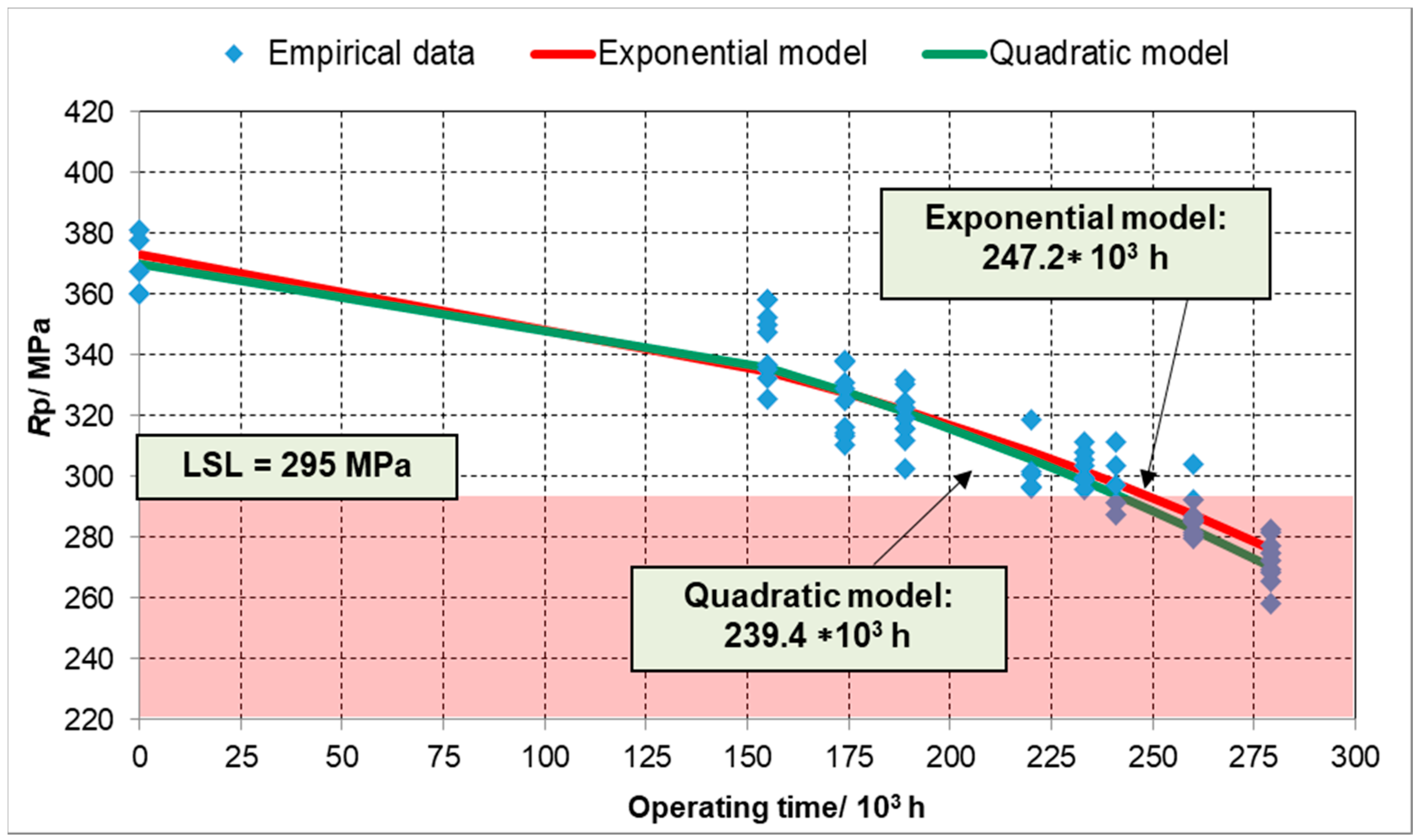
3.2. Determining the Forecast of Operating Time on the Statistical Results of Conventional Yield Point (Rp) Change
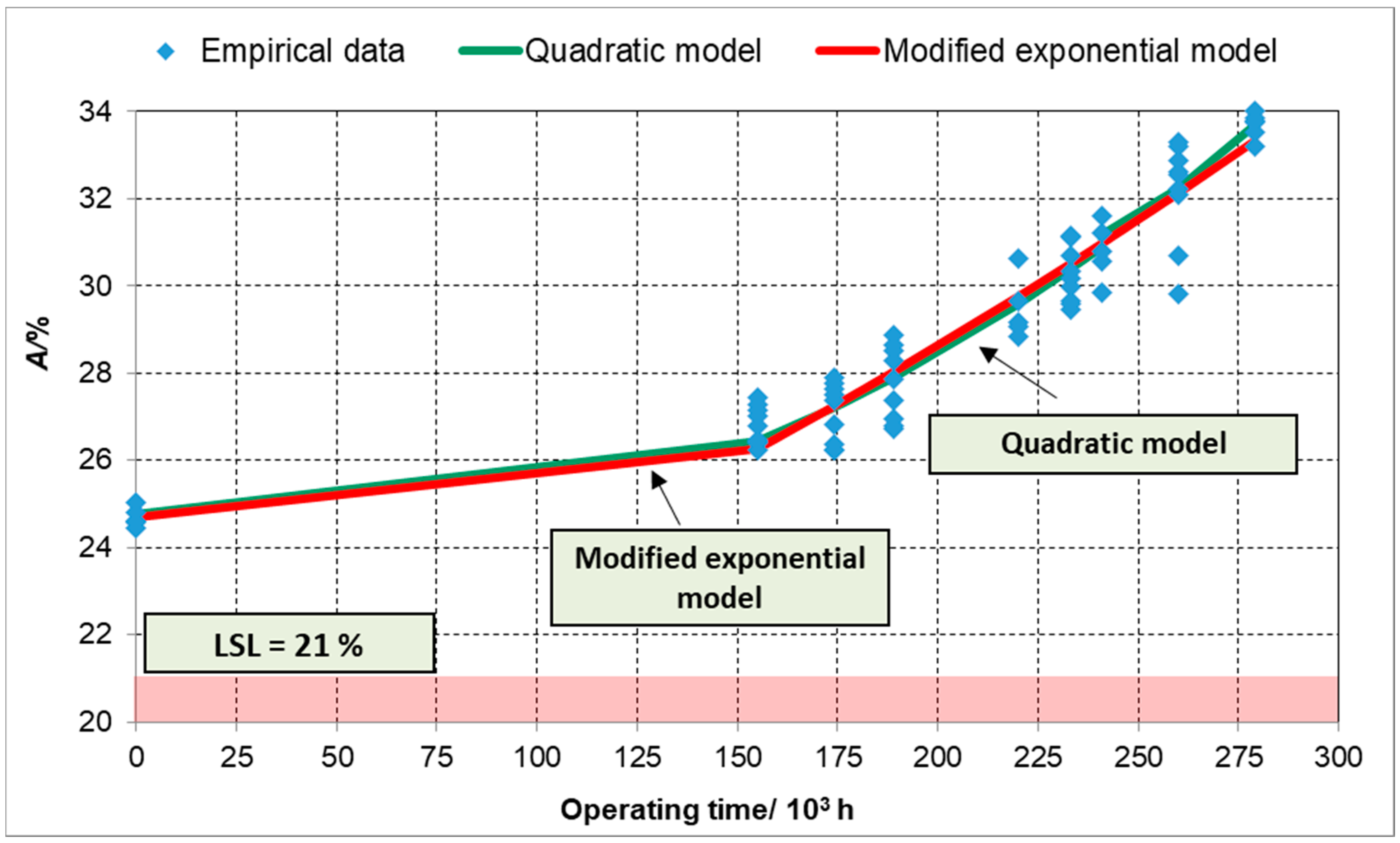
3.3. Determining the Forecast of Operating Time on the Statistical Results of Elongation (A) Change
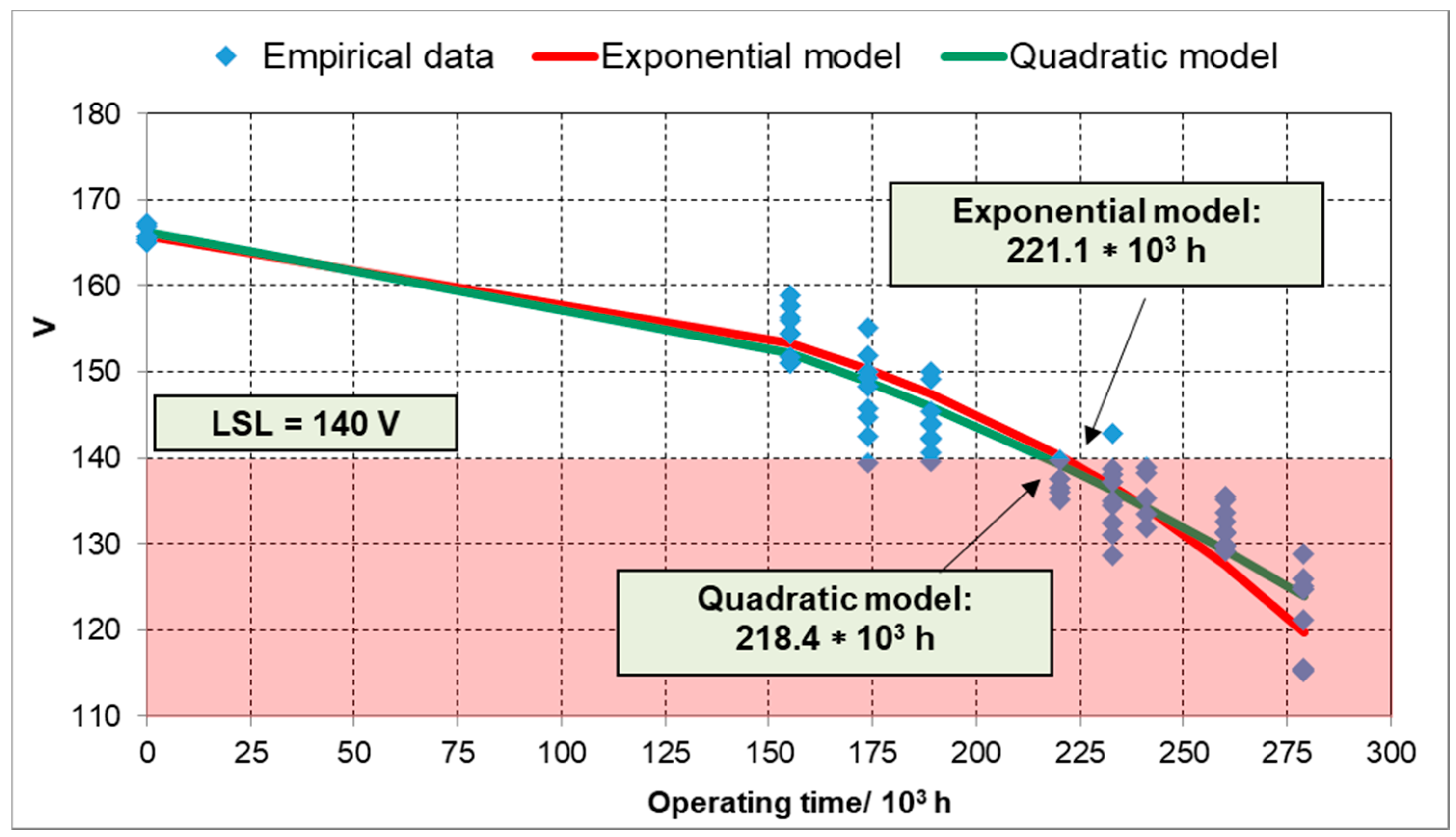
3.4. Determining the Forecast of Operating Time on the Statistical Results of Vickers Hardness Change
4. Discussion
5. Conclusions
- The presented methodology fort statistical tests may be used for estimation of operational reliability forecast, as a derivative of evaluation of material durability of elements of pressurized facilities, including the elbows of steam pipelines.
- Statistical forecasting of failure-free operation time (in the range reported) should be considered a method supporting the decision process, supplementing conventional tests of structure degradation of steel used for steam pipelines.
- Statistical calculations on the base of the Rm results indicate that the working time forecast is from about 200,000 to 228,000 h (for fresh steam) and from about 193,000 to 258,000 h for secondarily super-heated steam. Based on a comparison of the obtained Rm results, one may ascertain that the shortest operating time of the tested elbow element of a steam pipeline is determined on the basis of circumferential location for secondarily super-heated steam, while the longest operating time may be forecast using the results pertaining to fresh steam.
- Statistical calculations on the base of Rp results for fresh steam indicate that the working time forecast is from about 226,000 to 247,000 h. For secondarily super-heated steam: from 245,000 to 293,000 h.
- Statistical calculations on the base of Vickers hardness results for fresh steam indicate that the working time forecast is from about 192,000 to 221,000 h. For secondarily super-heated steam: from 193,000 to 247,000 h.
- The results of elongation indicate that on the basis of the course of the studied functions, a forecast of failure-free operation time of steam pipeline elbows is not possible.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Będkowski, L.; Dąbrowski, T. Basics of Operation. P. II Basics of Operational Reliability; Military University of Technology Publishing House: Warsaw, Poland, 2006. [Google Scholar]
- Szopa, T. Reliability and Safety; Warsaw University of Technology Publishing House: Warsaw, Poland, 2009. [Google Scholar]
- Sołowiej, A.D. Analytical Methods in Reliability Theory; WNT: Warsaw, Poland, 1983. [Google Scholar]
- Warszyński, M. Reliability in Structural Calculations; PWN: Warsaw, Poland, 1988. [Google Scholar]
- Available online: http://www.statsoft.pl/textbook/stprocan.html (accessed on 28 January 2018).
- Kleinbaum, D.G.; Kupper, L.L.; Muller, K.E.; Nizam, A. Applied Regression Analysis and Other Multivariable Methods; Duxbury Press: Pacific Grove, CA, USA, 1998. [Google Scholar]
- Konecki, W. Statistics for Engineers; PWN: Warsaw, Poland, 1999. [Google Scholar]
- Maliński, M. Computer-Aided Mathematical Statistics; Silesian University of Technology Publishing House: Gliwice, Poland, 2000. [Google Scholar]
- Sobol, I.M. Monte Carlo Method; Science Publishing House: Moscow, Russia, 2017. (In Russian) [Google Scholar]
- Winkelmann, K. Calculation of Reliability of Engineering Structures by Simulation Methods and the Response Surface Method; Gdańsk University of Technology: Gdańsk, Poland, 2013; Available online: www.pbc.gda.pl/Kontent/34300/phd (accessed on 22 February 2018).
- Kolanek, K. Analysis and Reliability Optimization of Structures by Adaptive Simulation Methods. Ph.D. Thesis, PAS Institute of Fundamental Technological Research, Warsaw, Poland, 2006. [Google Scholar]
- Pacut, A. Probability, Theory, Probabilistic Modeling in Technology; WNT: Warsaw, Poland, 1985. [Google Scholar]
- Akram, M.; Hayat, A. Comparison of Estimators of the Weibull Distribution; Financial Econometrics Series; School Working Paper; Deakin University Australia: Geelong, Australia, 2013. [Google Scholar]
- Almeida, J.B. Application of Weibull statistics to the failure of coatings. J. Mater. Process. Technol. 1999, 93, 257–263. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kateri, M. On the maximum likelihood estimation of parameters of Weibull distribution based on complete and censored data. Stat. Probab. Lett. 2008, 78, 2971–2975. [Google Scholar] [CrossRef]
- Basu, B.; Tiwari, D.; Kundu, D.; Prasad, R. Is Weibull distribution the most appropriate statistical strength distribution for brittle materials? Ceram. Int. 2009, 35, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Dobosiewicz, J. (Ed.) Guidelines for Life Extension of Thermo-Mechanical Equipment of 200 MW Power Units; Sprawozdanie PN/20.2900; Pro Novum sp. z o.o.: Katowice, Poland, 2013. [Google Scholar]
- Polish Standard PN-EN 12952:2015. Water-Tube Boilers and Auxiliary Installations—Part 1: General. Part 2: Materials for Pressure Parts of Boilers and Accessories. Part 3: Design and Calculation for Pressure Parts; Polish Committee for Standardization: Warsaw, Poland, 2015.
- Polish Standard PN-EN 13480-3:2017-10. Metallic Industrial Piping—Part 3: Design and Calculation; Polish Committee for Standardization: Warsaw, Poland, 2017.
- Polish Standard PN-EN 10216-2:2014. Seamless Steel Tubes for Pressure Purposes—Technical Delivery Conditions—Part 2: Non-Alloy and Alloy Steel Tubes with Specified Elevated Temperature Properties; Polish Committee for Standardization: Warsaw, Poland, 2014.
- Polish Standard PN-83 N-04041/10:2011. Reliability in Technical Engineering—Reliability Structures of Technical Systems; Data Collection and Handling System, and N-04041/05 General Testing Principles; Polish Committee for Standardization: Warsaw, Poland, 2011.
- UDT Guidelines, No. 1/2015. Principles of Diagnostics and Operational Durability Assessment of Boiler and Pipeline Elements Working in Creep Conditions; Publisher UDT: Warsaw, Poland, 2015; Available online: www.dt-b.pl/wytyczne-udt-nr-1-2015 (accessed on 20 May 2020).
- Dobrzański, J. Materials science interpretation of the life of steels for power plants. Open Access Libr. J. 2011, 3, 1–228. [Google Scholar]
- Dobrzański, J. Material diagnostics of components in the pressure part of steam boilers and pipelines operating under creep conditions much beyond the design service life. Energetyka 2002, 12, 937–946. [Google Scholar]
- Hernas, A.; Dobrzański, J. Durability and Deterioration of Elements of Steam Boilers and Turbines; Monograph; Silesian University of Technology Publishing House: Gliwice, Poland, 2003. [Google Scholar]
- Dobrzański, L.A.; Sroka, M.; Dobrzański, J. Application of neural networks to classification of internal damages in steel working in creep service. J. Achiev. Mater. Manuf. Eng. 2007, 20, 303–306. [Google Scholar]
- Dobrzański, L.A.; Dobrzański, J.; Sroka, M.; Sitek, W.; Krupiński, M. Computer aided for classification of damage of steel working in creep conditions. Hut. Wiadomości Hut. 2005, 3, 176–181. [Google Scholar]
- Hernas, A. Heat Durability of Steels and Alloys; Silesian University of Technology Publishing House: Gliwice, Poland, 2000. [Google Scholar]
- Dobrzański, J.; Purzyńska, H. The life-time fractures rule in the assessment of exhaustion degree. Energetyka 2015, 10, 653–656. Available online: http://www.elektroenergetyka.pl (accessed on 26 February 2018).
- Dobrzański, J. Diagnostics of Damages to Pressure Components of Powder Devices in Assessment of Reasons for Failures Based on Materials Testing; Institute for Ferrous Metallurgy: Gliwice, Poland, 2009; Volume 61, pp. 36–45. [Google Scholar]
- Hernas, A. Material and technological issues in development of power industry. In Proceedings of the III Scientific and Technical Conference Energo-Tech-Mat, Ustroń, Poland, 20–24 May 1998; pp. 8–15. [Google Scholar]
- Dobrzański, J.; Zieliński, A. Assessment of Operational Durability of Power Engineering Steels Working above the Boundary Temperature Based on Shortened Creep Tests; Institute for Ferrous Metallurgy: Gliwice, Poland, 2009. [Google Scholar]
- Klepacki, F. Methodology of Calculations of Durability Elements Working in Creep Conditions Based on Harmonized European Standards; Dozór Techniczny: Warsaw, Poland, 2015. [Google Scholar]
- Brunne, W.; Rajca, S. Usefulness of Non-destructive Tests for Life Time Forecasting of HP Steam Pipelines. Energetyka 2002, 20, 929–933. [Google Scholar]
- Gause, D.C.; Weinberg, G.M. Exploring Requirements; Dorset House: New York, NY, USA, 1989. [Google Scholar]
- Trzeszczyński, J. Material diagnosis on-line of power station thermo-mechanical installations. Energetyka 2008, 4, 279–283. [Google Scholar]
- Słowiński, B. Fundamentals of Testing and Assessment of the Reliability of Technical Objects; Koszalin University of Technology: Koszalin, Poland, 2002. [Google Scholar]
- Bucior, J. Fundamentals of Reliability Theory and Engineering; Publishing House Rzeszow University of Technology: Rzeszów, Poland, 2004. [Google Scholar]
- Szymszal, J. Reliability Assessment of AlSi(Me) Alloys Casts on the Basis of Statistical Material Reliability Indices Based on Weibull Analysis; Monograph; Silesian University of Technology Publishing House: Gliwice, Poland, 2009. [Google Scholar]
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Mesjasz, A.; Piątkowski, J. The reasons of steam pipeline rupture. Arch. Foundry Eng. 2016, 16, 67–70. [Google Scholar] [CrossRef]
- Anaya-Lara, O.; Acha, E. Modeling and analysis of custom power systems by PSCAD/EMTDC Power Delivery. IEEE Trans. Power Deliv. 2002, 17, 266–272. [Google Scholar] [CrossRef]
- McCarthy, R.W.; Ogden, J.M.; Sperling, D. Assessing reliability in energy supply systems. Energy Policy 2007, 35, 2151–2162. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-Y.; Park, J.-K. The modeling and analysis of shunt type custom power device. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 1, pp. 186–191. [Google Scholar]
- Pohjenheimo, P.; Lakervi, E. Steady State Modeling of Custom Power Components in Power Distribution Networks. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 January 2000. [Google Scholar]
- Celin, R.; Kmetric, D. A wet-steam pipeline fracture. Mater. Technol. 2007, 41, 151–154. [Google Scholar]
- Balyts’kyi, O.I.; Ripei, I.V.; Protsakh, K.A. Reliability of steam pipelines of thermal power plants in the course of long-term operation. Mater. Sci. 2006, 42, 421–425. [Google Scholar] [CrossRef]
- Rudzinskas, V.; Valiulis, A.V.; Chernashejus, O. Operation reliability of bent elbows of steam pipelines. In Mechatronic Systems and Materials, Solid State Phenomena Book Series, Proceedings of the 1st International Conference on Mechatronic Systems and Materials, Vilnius, 20–23 October 2006; Trans Tech Publications Ltd.: Baech, Switzerland, 2006; Volume 113, pp. 577–582. [Google Scholar]
- Burzić, Z.; Gačo, D.; Burzić, M.; Prokić-Cvetković, R. The effect of operating conditions on service behaviour of high alloyed steel X20. In Proceedings of the 12th International Research/Expert Conference: Trends in the Development of Machinery and Associated Technology, Istanbul, Turkey, 26–30 August 2008; pp. 1365–1368. [Google Scholar]
- Electricity—Today’s Technologies—Tomorrow’s Alternatives; Electric Power Research Institute: Palo Alto, CA, USA, 1987.
- Agenda 2030, Sustainability Development Program for UE. Available online: https://www.gov.pl/web/rozwoj/agenda-2030 (accessed on 20 May 2020).
- Polish Information and Foreign Investment Agency. Energy Sector in Poland. Available online: www.paiz.gov.pl (accessed on 20 April 2020).
- Viswanathan, R. Damage Mechanisms and Life Assessment of High Temperature Components, 3rd ed.; ASM International: Metals Park, OH, USA, 1989; Available online: https://books.google.pl/books?hl=pl&lr=&id=psNWNNXB02EC&oi=fnd&pg=PA1&dq=Demage+of+steam+pipies&ots=0UFs_rUUUf&sig=AtPjfJGJVX9HEe88J7JhIVHG2xM&redir_esc=y#v=onepage&q=Demage%20of%20steam%20pipies&f=false (accessed on 20 March 2020).
- Clouston, J.; Sundaram, A.; Woodley, N.H. Eletricity Today, Custom Power: The Utility Solution to Distribution Power Quality. In Proceedings of the CIRED 13 International Conference on Electricity Distribution, Brussels, Belgium, 20 May 1995. [Google Scholar]
- Shankran, C. Power Quality; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Ghosh, A.; Ledwich, G. Power Quality Enhancement Using Custom Power Devices; Kluwer Acadamic Publishers: New York, NY, USA, 2002; pp. 114–116. [Google Scholar]
- Hingorani, N.G. Overview of Custom Power Applications. In Proceedings of the Summer Meeting Panel Session on Application of Custom Power Devices for Enhanced Power Quality; IEEE/PES: Piscataway, NJ, USA, 1998. [Google Scholar]
- He, C.; Li, F. Static Transfer Switch (STS) Model in EMTP Works RV. In Proceedings of the Canadian Conference on Electrical and Computer Engineering 2004 (CCECE 2004), Niagara Falls, ON, Canada, 2–5 May 2004; pp. 111–116. [Google Scholar]
- Rusin, A.; Bieniek, M. Maintenance planning of power plant elements based on avoided risk value. Energy 2017, 134, 672–680. [Google Scholar] [CrossRef]
- Zhong, W.; Feng, H.; Wang, X.; Wu, D.; Xue, M. Online hydraulic calculation and operation optimization steam heating networks considering heat dissipation in pipes. Energy 2015, 87, 566–577. [Google Scholar] [CrossRef]
- Dong, Z.Y.; Saha, T. Power Quality & Equipment Protection. ELEC4301 2004, 1–34. [Google Scholar] [CrossRef]
- Dittmann, P. Forecasting in an Enterprise; Oficyna Ekon.: Cracow, Poland, 2004. [Google Scholar]
- Zeliaś, A. Statistical Methods; PWE Publisher: Warsaw, Poland, 2000. [Google Scholar]
- Goryl, A.; Jędrzejczyk, A.; Kukuła, K.; Osiewalski, J.; Walkosz, A. Introduction to Econometrics in Examples and Problems; PWN Publisher: Warsaw, Poland, 2007. [Google Scholar]
- De Smith, M.J. Statistical Analysis Handbook; The Winchelsea Press, Drumlin Security Ltd.: Edinburgh, UK, 2018. [Google Scholar]
- Altman, D.G. Practical Statistics for Medical Research; Chapman and Hall: London, UK, 1991. [Google Scholar]
- Stanisz, A. An Easy Course of Statistics Using STATISTICA PL on Examples from Medicine; StatSoft Publisher: Cracow, Poland, 2006. [Google Scholar]
- Wieczorkowska, G. Statistics; Scholar Publisher: Warsaw, Poland, 2003. [Google Scholar]
- Snarska, A. Statistics, Econometrics, Forecasting—Exercises with Excel; Placet Publisher: Warsaw, Poland, 2005. [Google Scholar]
- Aczel, A.D. Statistics in Management; Polish Scientific Publishers PWN: Warsaw, Poland, 2000. [Google Scholar]
- Hong, Y. Probability and Statistics for Economists; World Scientific: Singapore, 2017. [Google Scholar]
- Keller, G. Statistics for Management and Economics; Cenage Learning: Boston, MA, USA, 2017. [Google Scholar]
- Peck, R.; Short, T. Statistics—Learning from Data; Cengage: Boston, MA, USA, 2018. [Google Scholar]
- Hayhurst, D.R. The Role of Creep Damage in Structural Mechanics. Engineering Approaches to High Temperature; Wilshire, B., Owen, D.R.J., Eds.; Pineridge Press: Swansea, UK, 1983; pp. 85–176. [Google Scholar]
- Hyde, T.H.; Sun, W.; Becker, A. Effects of End Loading on the Creep Failure Behaviour of CrMoV Welds in Main Steam Pipelines—Damage & Fracture Mechanics VI.; Brebbia, C.A., Selvadurai, A.P.S., Eds.; WIT Press: Southampton, UK, 2000; pp. 415–424. [Google Scholar]
- Pearson, J.M.; Anderson, R.W. Reliability and durability from large heat recovery steam generators. Proc. Inst. Mech. Eng. Part A 1999, 213, 151–168. [Google Scholar] [CrossRef] [Green Version]
- Chicherin, S.V. New approach to determination of corrosion damage degree of pipeline system elements. Bull. Tomsk Polytech. Univ.—GEO Assets Eng. 2016, 327, 110–115. [Google Scholar]
- Gofman, Y.M. Estimation of the reliability of testing welded joints of steam pipelines of thermal power plants. Russ. J. Nondestruct. Test. 2003, 39, 230–231. [Google Scholar] [CrossRef]
- Rogalev, A.; Kocherova, A.; Komarov, I.; Garanin, I.; Kurdiukova, G. Development of new flow stabilizers for increasing the reliability and efficiency of power equipment. WIT Trans. Ecol. Environ. 2015, 195, 475–484. [Google Scholar]
- Zaryankin, A.; Rogalev, N.; Rogalev, A.; Kocherova, A.; Strielkowski, W. Line summary of approaches for improving vibrational reliability of thermomechanical equipment and its interconnecting pipelines at thermal power plant. Contemp. Eng. Sci. 2014, 7, 1793–1806. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.Y.; Jia, J.H.; Wang, N.; Xia, X.M.; Wang, Z.D.; Tu, S.T. Design and test of an extensometer for strain monitoring of high temperature pipelines. J. Press. Vessel Technol. Trans. ASME 2012, 134, 044501. [Google Scholar] [CrossRef]

| Steel Group | Elbow Element | Sampling Location | Designated Model Type (y = Rm) | R2 | Working Time Forecast * /103 h | |
|---|---|---|---|---|---|---|
| FS | Bend | circumferential | quadratic | (1) y = −0.0018x2 + 0.0899x + 509.66 | 0.9224 | 223.3 |
| exponential | y = 519 − e0.0098 + 2.131 | 0.9161 | 228.4 | |||
| longitudinal | quadratic | y = −0.0016x2 − 0.0597x + 533.63 | 0.9151 | 224.0 | ||
| exponential | y = 550 − e0.00815x + 2.865 | 0.9247 | 225.2 | |||
| Straight section | longitudinal | quadratic | y = −0.0023x2 + 0.1215x + 520.51 | 0.9186 | 215.0 | |
| exponential | y = 542 − e0.00793x + 2.867 | 0.8278 | 221.7 | |||
| circumferential | hyperbolic | y = (555.8x − 121255.2)/(x − 290.68) | 0.8456 | 204.3 | ||
| quadratic | y = −0.0029x2 + 0.1617x + 546.01 | 0.9303 | 200.1 | |||
| exponential | y = 587 − e0.00105x + 2.403 | 0.9532 | 203.2 | |||
| SSS | Bend | circumferential | quadratic | (2) y = −0.0024x2 + 0.0921x + 546.62 | 0.9590 | 231.2 |
| hyperbolic | y = (607.2x − 204319.1)/(x − 375.06) | 0.9967 | 235.0 | |||
| exponential | y = 567 − e0.00815x + 2.393 | 0.9391 | 234.2 | |||
| longitudinal | quadratic | y = −0.0016x2 + 0.0013x + 546.01 | 0.8910 | 256.2 | ||
| exponential | y = 579 − e0.00633x + 3.313 | 0.7923 | 258.3 | |||
| Straight section | longitudinal | quadratic | y = −0.0022x2 + 0.1883x + 518.23 | 0.8167 | 236.3 | |
| exponential | y = 528 − e0.0115x + 1.757 | 0.8231 | 236.6 | |||
| circumferential | hyperbolic | y = (554.7x − 158158.3)/(x − 307.76) | 0.9862 | 198.2 | ||
| quadratic | y = −0.0027x2 + 0.1334x + 515.13 | 0.9619 | 193.4 | |||
| exponential | y = 525 − e0.0119x + 2.111 | 0.9213 | 195.9 | |||
| Statistics: Parameters, Tests, Errors | ||||
|---|---|---|---|---|
| a | b | c | ||
| −0.00178 | 0.08992 | 509.7 | ||
| Standard error | 0.00021 | 0.057242 | 3.7961 | |
| R = 0.9604 | R2 = 0.9224 | Se = 8.498 | ||
| F Stat. | 291.037 | df (I) | ||
| 49 | ||||
| SS Regression | 42036.4 | 3538.7 | SS Residual Standard | |
| −8.44284 | 1.57093 | 134.26130 | t Stat | |
| Significance level: p = | 0.0000 | 0.01226 | 0.0000 | |
| Statistics: Parameters; Tests; Errors | ||||
|---|---|---|---|---|
| a | b | c | ||
| −0.00240 | 0.09209 | 546.6 | ||
| Standard error | 0.00016 | 0.044039 | 3.1465 | |
| R = 0.9788 | R2 = 0.9580 | Se = 9.454 | ||
| F Stat. | 752.145 | df (I) | ||
| 66 | ||||
| SS Regression | 134456.1 | 5899.2 | SS Residual Standard | |
| −14.84802 | 2.09108 | 173.72309 | t Stat | |
| Significance level: p = | 0.0000 | 0.0404 | 0.0000 | |
| Steel Group | Elbow Element | Sampling Location | Designated Model Type (y = Rp) | R2 | Working Time Forecast * /103 h | |
|---|---|---|---|---|---|---|
| FS | Bend | longitudinal | quadratic | y = −0.0011x2 − 0.050x + 370.01 | 0.8904 | 239.4 |
| exponential | y = 410 − e0.0046x + 3.6078 | 0.9103 | 247.2 | |||
| circumferential | quadratic | y = − 0.0013x2 + 0.0342x + 361.63 | 0.9055 | 242.0 | ||
| exponential | y = 370 − e0.0106x + 1.878 | 0.8074 | 242.6 | |||
| Straight section | longitudinal | quadratic | y = −0.0012x2 + 0.0006x + 363.45 | 0.8513 | 239.1 | |
| exponential | y = 388 − e0.00609x + 3.0482 | 0.7605 | 243.7 | |||
| circumferential | quadratic | y = −0.0011x2 − 0.0401x + 361.81 | 0.8735 | 228.5 | ||
| exponential | y = 380 − e0.00715x + 2.828 | 0.8818 | 225.8 | |||
| SSS | Bend | longitudinal | quadratic | y = −0.0011x2 − 0.1272x + 368.53 | 0.8878 | 254.4 |
| exponential | y = 429 − e0.00393x + 4.079 | 0.8988 | 259.8 | |||
| circumferential | quadratic | y = −0.0016x2 − 0.0988x + 366.24 | 0.8608 | 284.3 | ||
| exponential | y = 388 − e0.00750x + 2.540 | 0.8208 | 293.2 | |||
| Straight section | longitudinal | quadratic | y = −0.0016x2 − 0.0150x + 364.24 | 0.8867 | 260.9 | |
| exponential | y = 378 − e0.00932x + 2.441 | 0.8545 | 245.3 | |||
| circumferential | quadratic | y = −0.0015x2 − 0.0041x + 361.02 | 0.9272 | 251.6 | ||
| exponential | y = 383 − e0.0069x + 2.996 | 0.8731 | 257.2 | |||
| Steel Group | Elbow Element | Sampling Location | Designated Model Type (y = A) | R2 | |
|---|---|---|---|---|---|
| FS | Bend | longitudinal | quadratic | y = −0.00171x2 − 0.01574x + 24.769 | 0.9394 |
| mod. exponential | y = 19.503e0.00815x | 0.9075 | |||
| circumferential | quadratic | y = 0.000208x2 − 0.01958x + 23.750 | 0.9376 | ||
| mod. exponential | y = 17.511e0.00242x | 0.9171 | |||
| Straight section | longitudinal | quadratic | y = 0.000179x2 − 0.014528x + 24.288 | 0.9028 | |
| mod. exponential | y = 19.660e0.00187x | 0.8286 | |||
| circumferential | quadratic | y = 0.000199x2 − 0.01890x + 24.741 | 0.9140 | ||
| mod. exponential | y = 19.125e0.00204x | 0.8045 | |||
| SSS | Bend | longitudinal | quadratic | y = 0.000187x2 − 0.01978x + 24.787 | 0.9020 |
| mod. exponential | y = 18.238e0.00221x | 0.8685 | |||
| circumferential | quadratic | y = 0.000159x2 − 0.011108x + 24.343 | 0.9444 | ||
| mod. exponential | y = 19.077e0.00202x | 0.9175 | |||
| Straight section | longitudinal | quadratic | y = 0.000167x2 − 0.01244x + 24.290 | 0.8746 | |
| mod. exponential | y = 19.855e0.00181x | 0.7925 | |||
| circumferential | quadratic | y = 0.000175x2 − 0.0153x + 24.553 | 0.9163 | ||
| mod. exponential | y = 19.835e0.00183x | 0.8645 | |||
| Steel Group | Elbow Element | Sampling Location | Designated Model Type (y = V) | R2 | Working Time Forecast * /103 h | |
|---|---|---|---|---|---|---|
| FS | Bend | longitudinal | quadratic | y = −0.00049x2 − 0.01488x + 166.3 | 0.8987 | 218.4 |
| exponential | y = 170 −e0.008915x + 1.4303 | 0.9295 | 221.0 | |||
| circumferential | quadratic | y = −0.00055x2 + 0.02828x + 159.4 | 0.9075 | 215.3 | ||
| exponential | y = 170 − e0.005294x + 2.2614 | 0.8845 | 215.3 | |||
| Straight section | longitudinal | quadratic | y = −0.00065x2 + 0.02031x + 163.9 | 0.8806 | 208.0 | |
| exponential | y = 171 − e0.008179x + 1.680 | 0.8621 | 214.5 | |||
| circumferential | hyperbolic | y = (173.6x − 46757.5)/(x − 285.80) | 0.9970 | 199.7 | ||
| quadratic | y = −0.00094x2 + 0.05406x + 164.3 | 0.9299 | 192.1 | |||
| exponential | y = 173 − e0.008072x + 1.936 | 0.7911 | 197.0 | |||
| SSS | Bend | longitudinal | quadratic | y = −0.00051x2 − 0.00285x + 171.1 | 0.8796 | 244.2 |
| exponential | y = 184 − e0.00509x + 2.528 | 0.8019 | 246.8 | |||
| circumferential | hyperbolic | y = (185.2x − 60062.75)/(x − 185.196) | 0.9960 | 226.0 | ||
| quadratic | y = −0.00078x2 + 0.04215x + 170.0 | 0.9485 | 225.0 | |||
| exponential | y = 177 − e0.008483x + 1.682 | 0.7636 | 225.7 | |||
| Straight section | longitudinal | quadratic | y = −0.00068x2 + 0.03072x + 163.4 | 0.8386 | 209.5 | |
| exponential | y = 168 − e0.009345x + 1.336 | 0.8235 | 213.6 | |||
| circumferential | hyperbolic | y = (170.86x − 46239.78)/(x − 287.5) | 0.9971 | 198.2 | ||
| quadratic | y = −0.00082x2 + 0.03838x + 161.5 | 0.9724 | 193.4 | |||
| exponential | y = 170 − e0.007336x + 2.027 | 0.9098 | 195.9 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piątkowski, J.; Gajdzik, B.; Mesjasz, A. Assessment of Material Durability of Steam Pipelines Based on Statistical Analysis of Strength Properties—Selected Models. Energies 2020, 13, 3633. https://doi.org/10.3390/en13143633
Piątkowski J, Gajdzik B, Mesjasz A. Assessment of Material Durability of Steam Pipelines Based on Statistical Analysis of Strength Properties—Selected Models. Energies. 2020; 13(14):3633. https://doi.org/10.3390/en13143633
Chicago/Turabian StylePiątkowski, Jarosław, Bożena Gajdzik, and Aleksander Mesjasz. 2020. "Assessment of Material Durability of Steam Pipelines Based on Statistical Analysis of Strength Properties—Selected Models" Energies 13, no. 14: 3633. https://doi.org/10.3390/en13143633
APA StylePiątkowski, J., Gajdzik, B., & Mesjasz, A. (2020). Assessment of Material Durability of Steam Pipelines Based on Statistical Analysis of Strength Properties—Selected Models. Energies, 13(14), 3633. https://doi.org/10.3390/en13143633






