1. Introduction
The flux-switching motor is a type of double-salient structured motor with two windings in the stator, including an armature winding and a field winding, which could be replaced by a permanent magnet. The flux-switching motor has several advantages, including a robust structure, a sinusoidal back-electromotive force (back-EMF) waveform, and a reasonable torque density [
1,
2]. Several researchers have investigated the design of different types of flux-switching motors [
3,
4,
5]. Recently, field-excited flux-switching motors have become more and more popular due to there being no need for a permanent magnet and the good flux-weakening operational characteristics [
6]. Many papers have investigated field-excited flux-switching motors. For example, Ullah et al. proposed a field-excited linear flux-switching motor [
7]. Gaussens proposed an analytical method of air-gap modeling for a field-excited flux-switching motor, by which the flux linkage and torque were derived [
8].
Several papers have studied the control of flux-switching motor drive systems. For instance, Zhao et al. employed a model predictive controller for a flux-switching drive system to decrease its torque and flux ripples and to enhance the quality of the drive system [
9]. Moreover, Zhao et al. investigated the low copper-loss control of a field-excited flux-switching drive system to improve its adjustable speed range and efficiency [
10]. Zhao et al. implemented vector control of a field-excited flux-switching drive to maximize its output torque by using particle swarm optimization [
11]. Yang et al. studied flux-weakening control of a hybrid flux-switching motor to increase its output torque and high-speed operating range [
12]. Wu et al. investigated field-oriented control and direct torque control for a five-phase flux-switching motor drive system with a fault-tolerant capability to improve its dynamics during faulty conditions [
13]. Nguyen et al. proposed rotor position sensorless control of a field-excited flux-switching motor drive system using a high-frequency square-wave voltage injecting method to replace an encoder [
14]. Zhang proposed model reference adaptive control to improve the dynamics of a sensorless flux-switching motor drive system [
15].
Several researchers have proposed sensorless methods for motor drives. For example, Fan et al. proposed sensorless control of a five-phase interior permanent magnet synchronous motor (IPMSM) based on a high-frequency sinusoidal voltage injection [
16]. Wang et al. investigated a position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame [
17]. Compared to previously published papers [
9,
10,
11,
12,
13,
14,
15,
16,
17], this paper is the first to propose predictive controllers for a sensorless field-excited flux-switching motor drive system. To the authors’ best knowledge, this idea is an original idea. This is the first time that a multi-step predictive speed controller is developed and compared to a single-step predictive speed controller for a flux-switching motor drive system. This is another main contribution of the paper. The implemented drive system could be applied for grass cutters and vacuum cleaners due to its robustness, lack of need for a permanent magnet, and high torque. In addition, the high torque ripple, large volume, and serious acoustic noise may not be the main issues for the applications of vacuum cleaners and grass cutters.
2. Flux-Switching Motor
This paper investigates a 3-phase, 6-slot armature winding stator, 7-salient-tooth rotor, field-excited, flux-switching motor, which is shown in
Figure 1. The armature winding is located inside the motor, and the salient-tooth rotor is located outside of the motor. In
Figure 1, the A1, A2, B1, B2, C1, and C2 are armature windings, and F1, F2, F3, F4, F5, and F6 are field windings. All of them are located on the teeth of the stator. Between the stator and rotor, there is a non-uniform air gap.
To explain the basic principle of the flux-switching motor,
Figure 2a–d illustrate the different rotor positions between the rotor and the stator, in which
,
, and
are the slot numbers of the stator.
Figure 3 shows the induced flux linkage and its related back-EMF.
Figure 2a illustrates that the flux linkage of the F1 field winding rises, but the flux linkage of the F2 field winding decreases. As a result, the total flux linkage in the A2 armature winding is zero. This situation is also indicated at the a-point in
Figure 3. Here the flux linkage of the A2 armature winding is zero, but the back-EMF of the A2 armature winding reaches its maximum value.
Figure 2b illustrates that both the F1 and F2 field windings provide rising flux at the A2 armature winding. As a result, the total flux of the A2 armature winding reaches its maximum value, and the back-EMF of the A2 armature winding is zero, which is shown at the b-point in
Figure 3.
Figure 2c illustrates that the flux linkage of the field winding F1 also rises, but the flux linkage of the field winding F2 also decreases. As a result, the total flux linkage of the A2 armature winding is zero, and the back-EMF of the A2 armature winding reaches its negative minimum value, which is shown at the c-point of
Figure 3.
Figure 2d illustrates that both the flux linkage of the F1 and F2 field windings decrease. As a result, the total flux linkage of the A2 armature winding reaches its negative minimum value, and the back-EMF of the A2 armature winding is zero. This is illustrated as the d-point in
Figure 3. In
Figure 3,
is the electric rotor speed of the rotor and
is the flux linkage of the stator when rotor rotates. According to the above analysis, it is feasible to generate a flux linkage waveform and a back-EMF waveform, which are sinusoidal and cosine waveforms, respectively, and are illustrated in
Figure 3. By using the back-EMF from the armature winding, torque is generated and the motor rotates smoothly.
3. Mathematical Model of a Flux-Switching Motor
The synchronous frame d-q axis stator voltage of a flux-switching motor is expressed as follows:
where
and
are the d- and q-axis voltages,
is the rotor resistance,
and
are the d- and q-axis self-inductances,
is the mutual inductance between the d-axis of the armature winding and the field winding,
is the mutual inductance between the q-axis of the armature and the field winding,
is the electrical rotor speed,
is the differential operator,
and
are the d- and q-axis currents, and
is the field current.
The flux linkage of the field winding,
, can be expressed as follows:
where
is the total flux linkage of the field winding,
is the self-inductance of the field winding, and
is the mutual inductance between the field winding and the d-axis winding. The voltage of the field winding is expressed as follows:
where
is the voltage of the field winding, and
is the resistance of the field winding. The total torque is shown as follows:
The mechanical speed of the motor is
where
is the mechanical speed of the rotor,
is the inertia of the motor and load,
is the total output torque,
is external load, and
is the total viscous friction coefficient. The differential of the mechanical position of the motor is
4. Rotor Position Estimator Design
In this paper, assuming
, the d-q-f axis high-frequency voltages and high- frequency currents can be described as follows:
where
,
, and
are the high-frequency d-axis, q-axis, and field winding voltages,
is the self-inductance of the d- and q-axis,
is the mutual inductance between the d-axis or q-axis and the field winding inductance, and
is the high-frequency self-inductance of the field winding. From
Figure 4, the coordinate transformation between d-q-f and
can be expressed as
where
and
are the d- and q-axis voltages or currents,
and
are the
- and
-axis voltages or currents, and
is the coordinate transformation matrix. Substituting Equation (8) into (7), one can obtain
where
,
, and
are the
,
, and field winding voltages, and
,
, and
are the
,
, and field winding currents.
From Equation (9), after doing some mathematical processes, one can obtain
From Equation (10), one can derive the following equation:
In this paper, a high-frequency voltage
, which is injected into the field winding, is expressed as follows:
Substituting Equation (12) into (11) and doing some mathematical processes, one can obtain the high-frequency
-axis and β-axis currents as follows:
After using a low-pass filter to remove the high-frequency components, one can obtain the following equation:
where
,
, and
are the high-frequency currents after a band-pass filtering. From Equation (14), the estimated rotor position,
, can be derived as follows:
The estimated speed can be described as follows:
where
is the estimated speed and
is the sampling interval. In this paper, a speed state estimator is constructed [
18]. A high-order speed estimator is employed to avoid the high-frequency noise caused by the difference operator.
Figure 4 shows the relationship between the estimated rotor position
and the real position
.
Figure 5 demonstrates the control block diagram of the sensorless drive system, which includes the current control of the armature winding, the current control of the field winding, the rotor position estimation, and the rotor speed control.
6. Implementation
To evaluate the correctness and feasibility of the proposed method, a field-excited flux-switching sensorless flux-switching motor drive system is implemented. The implemented block diagram of the drive system is displayed in
Figure 9a, which includes a voltage-source inverter, a field-excited flux-switching motor, an H-bridge circuit that controls the excited field winding, a digital signal processor, Hall-effect sensors, and A/D converters. The switching frequency of the inverter is 10 kHz, and the switching frequency of the H-bridge circuit is 20 kHz. In addition, the sampling time of the current control is 100
and the sampling time of the speed control is 1
ms. The DC voltages of the inverter and H-bridge are both 250 V. The digital signal processor (DSP) is manufactured by Texas Instruments, type TMS-320-F2808 [
23]. To obtain a closed-loop high performance drive system, the DSP reads the a-phase current, b-phase current, and field winding current via A/D converters. After that, the DSP executes the rotor position estimation and all of the predictive control algorithms, and it also determines the inverter and H-bridge triggering signals.
A photograph of the implemented hardware circuit is displayed in
Figure 9b, including a DSP, two drivers, two Hall-effect current sensors, an inverter, and an H-bridge circuit. The insulated gate bipolar transistor (IGBT) modules are made by the Mitsubishi Company, type CM200dy-12NF. The photo-couple gate drivers are manufactured by Avago Company, type HCPL-3120. The Hall-effect sensors are manufactured by the Swiss LEM company, type LA25-NP with a 100 kHz bandwidth. The A/D converters with fast conversion time are made by Analog Devices, type AD7655.
Figure 9c displays the photograph of the flux-switching motor, which is connected to the dynamometer, in which a DC generator is used as an external load. The field-excited flux-switching motor is a seven stator salient teeth motor, with rated specifications of a power of 540 W, a speed of 600 r/min, and a current of 6 A. Its parameters include a stator resistance of 1.3
, a d-axis inductance of 18.9 mH, a q-axis inductance of 23 mH, an inertia of 0.0143 kg-m
, and a friction coefficient of 0.0047 N.m.s/rad. The motor was assembled in our laboratory because it is not available on the market.
The details of the control algorithms are shown in
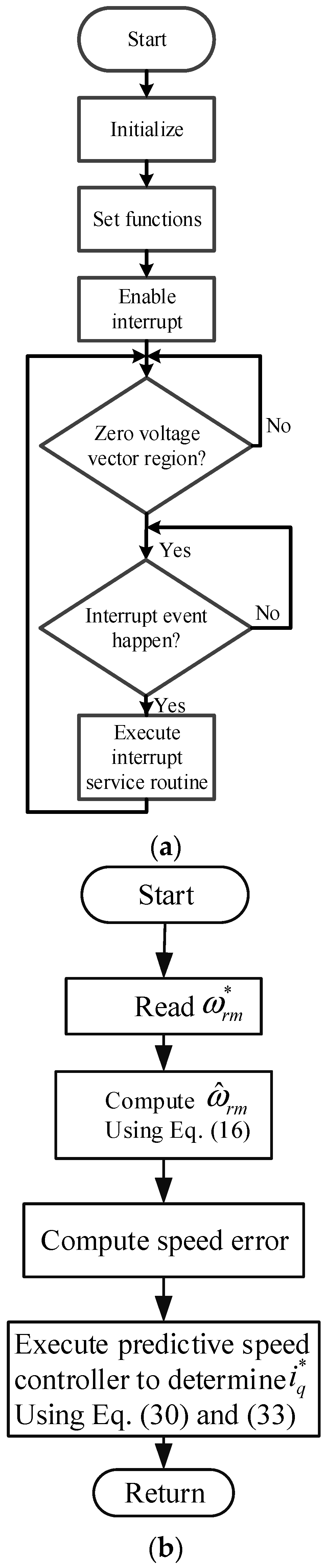
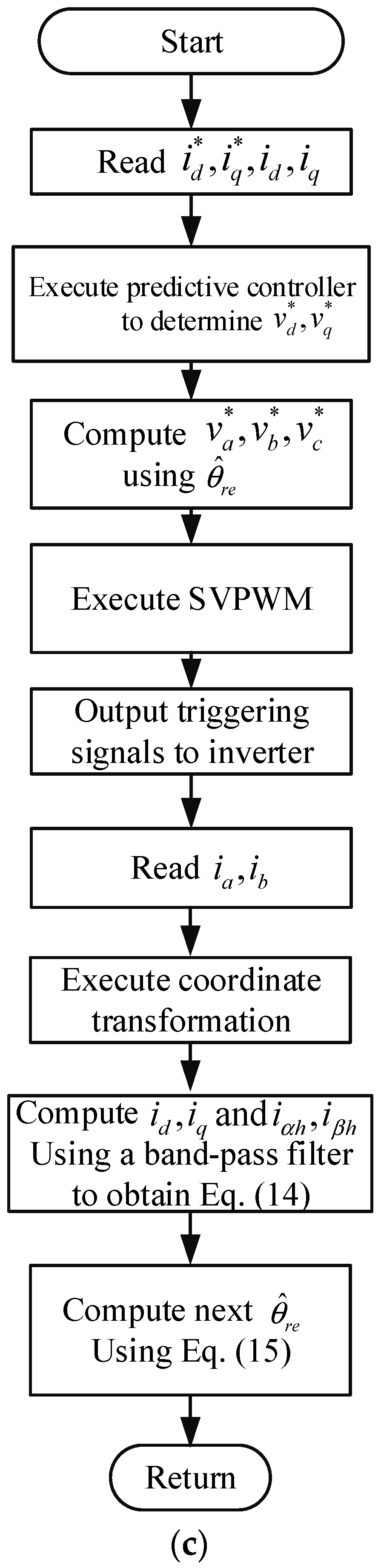
Figure 10a–d, which are the flowcharts of the DSP.
Figure 10a is the flowchart of the main program, which waits for the zero-voltage vector to detect currents.
Figure 10b is the speed-loop interrupt service routine, which uses Equation (16) to compute
and Equations (30) and (33) to determine
.
Figure 10c is the current loop interrupt service routine, which uses Equation (8) to execute the coordinate transformation, the band-pass filtering to obtain
, and finally computes
.
Figure 10d is the flowchart of the H-bridge field current control. The principle is measuring the current and comparing it with the field current command. Then, proportional-integral (PI) controller is used as the current controller to obtain the field voltage. Finally, the high-frequency voltage is injected and pulse-width modulation (PWM) is executed.
7. Experimental Results
To verify the proposed methods, our experimental results are illustrated in this section. The input DC voltage of the inverter and the H-bridge are both 250 V. The switching frequency of the inverter is 10 kHz, and the switching frequency of the H-bridge is 20 kHz. The sampling time of the a-b-c axis current control is 100 , and the sampling time of the speed control is 1 ms. The selection of the sampling intervals is based on the required computation time of the current loop and the speed loop. In addition, a synchronous relationship, in which the current loop executes 10 times and then the speed loop executes one time, is employed in this paper. The injection high-frequency voltage of the field winding is , which is near 10% of the DC bus voltage of the H-bridge.
Figure 11a demonstrates the measured a-phase current at 300 r/min and a 2 N.m load. The current is influenced by the different switching frequencies of the inverter and field winding. The measured a-phase current is a near sinusoidal waveform with high-frequency harmonics. The b-phase and c-phase are similar to the a-phase with a 120 degree phase shift.
Figure 11b demonstrates the measured current of the field winding, which is clearly influenced by an injection of high-frequency voltage, which is 1 kHz.
Figure 11c demonstrates the measured 1 kHz and 25 V high-frequency voltage, which is used to inject into the field winding.
Figure 12a demonstrates the measured speed responses of step input at 300 r/min. The rise time is 0.23 s, and the speed reaches its steady-state condition at 0.41 s. In addition, the estimated speed
is very close to the speed
.
Figure 12b demonstrates the estimated and real rotor positions and both of them are very close.
Figure 12c demonstrates the errors of the estimated position and they are near
2 electrical degrees.
Figure 13a shows the different PI parameters of transient responses;
Figure 13b shows the different PI parameters of 2 N.m load disturbance responses. From
Figure 13a,b, the best PI parameters, considering both transient responses and load disturbance responses, can be obtained as
and
, which is designed by pole assignment with the following two distinct poles,
and
.
Figure 14a demonstrates the measured speed responses using different controllers, including a multi-step predictive speed controller (
, a single-step predictive speed controller (
, and a PI speed controller. As one can observe, the multi-step predictive speed controller has a very smooth response, but the single-step controller has a quicker response with larger overshoot. The PI controller performs the worst, with the slowest response and largest overshoot.
Figure 14b demonstrates the measured load disturbance responses. The multi-step controller has a very similar response to the single-step controller. The PI controller, however, has the largest speed drop and the slowest recovery time.
Figure 15a demonstrates the measured speed responses of a triangular command by using an encoder for comparison. The multi-step controller has a similar response to the single-step controller.
Figure 15b demonstrates the measured speed responses of a triangular command by using the proposed sensorless method. The speed ripples are increased when compared with using an encoder.
Figure 16a demonstrates the measured speed responses of a trapezoidal command using an encoder. The multi-step controller has similar responses to the single-step controller.
Figure 16b demonstrates the measured speed responses of a trapezoidal command using the proposed sensorless method.
Figure 16c shows the measured responses of a step-input command using the proposed sensorless method. The multi-step controller with a small weighting factor has a slower but smoother response than the multi-step controller, which has a weighting factor of 1.
Figure 17a–c demonstrate the comparison of different speed operations.
Figure 17a demonstrates the highest speed by using a field-weakening control, which is 1550 r/min with an 1 N.m external load. The control method effectively reduces the d-axis flux to extend the operational speed range. In addition,
Figure 17a also demonstrates the highest operational speed without using a field-weakening control, which is 1080 r/min.
Figure 17b demonstrates the mid-speed operational range from 100 to 600 r/min with a 2 N.m external load. All of the different speeds have linear responses.
Figure 17c demonstrates the lowest operational speed, which is near 4 r/min with a 0.5 N.m external load. The lowest speed has obvious speed ripples.
Figure 18a demonstrates the measured line-to-line voltage,
, which has high-frequency PWM modulation pulses.
Figure 18b demonstrates the excited winding voltage,
, which is controlled by an H-bridge circuit.
Figure 18c demonstrates the excited winding current,
, during the transient time interval of the field current regulated control, which is controlled by an H-bridge circuit. The additional high-frequency flux on the core created core loss, which increases core loss and reduces the efficiency of the motor. Roughly speaking, this increased high frequency core loss is near 2% of the total losses of the motor. Comparing the torque and efficiency for analogously dimension PM and induction motors, for a 0.5 KW motor, the efficiency of a PM is near 90%, the efficiency of an induction motor is near 87%, and the efficiency of a field-excited flux-switching motor is 87%. For a 0.5 kW motor, the torque of a PM is 100% as a reference, the torque of an induction motor is 90%, and the torque of a field-excited flux-switching motor is 93%.
8. Conclusions
A rotor position estimator and three predictive controllers, which include a multi-step speed predictive controller, a single-step speed predictive controller, and a predictive current controller for a field-excited flux-switching motor drive system have been designed and implemented for this paper. A 1 kHz, high-frequency voltage is injected into the field winding to obtain the estimated rotor position. In addition, the high-frequency injection voltage does not occupy any available output voltages in the inverter. The methods in this paper provide more available voltage for the PWM modulation. The two different predictive controllers implemented in this research enhance the transient responses, decrease the speed drops of load disturbances, and improve tracking responses more effectively than previously published control methods for flux-switching drive systems. In addition, the multiple-step predictive controller provides smoother speed responses than the single-step predictive controller. These are the main contributions of this paper versus other similar research.
Experimental results show that the controllable speed range of the motor drive system discussed in this paper is from 4 r/min to 1500 r/min. Furthermore, the measured results demonstrate that the errors of the rotor position estimations are below 2 electrical degrees. Moreover, the proposed predictive controllers provide better performance than PI controllers at different speeds. However, all the considerations in the paper are based on a circuit model with fixed parameters. In the future, methods using field methods or online measuring methods will be thoroughly investigated.
Most functions of the rotor position estimators and predictive controllers are implemented by the DSP, and only simple hardware circuits are employed. This proposed flux-switching drive system can be easily applied to meet the high dynamic requirements for applications in household appliances, such as vacuum cleaners and lawn mowers.