Dynamics of Connectedness in Clean Energy Stocks
Abstract
:1. Introduction
2. Literature Review
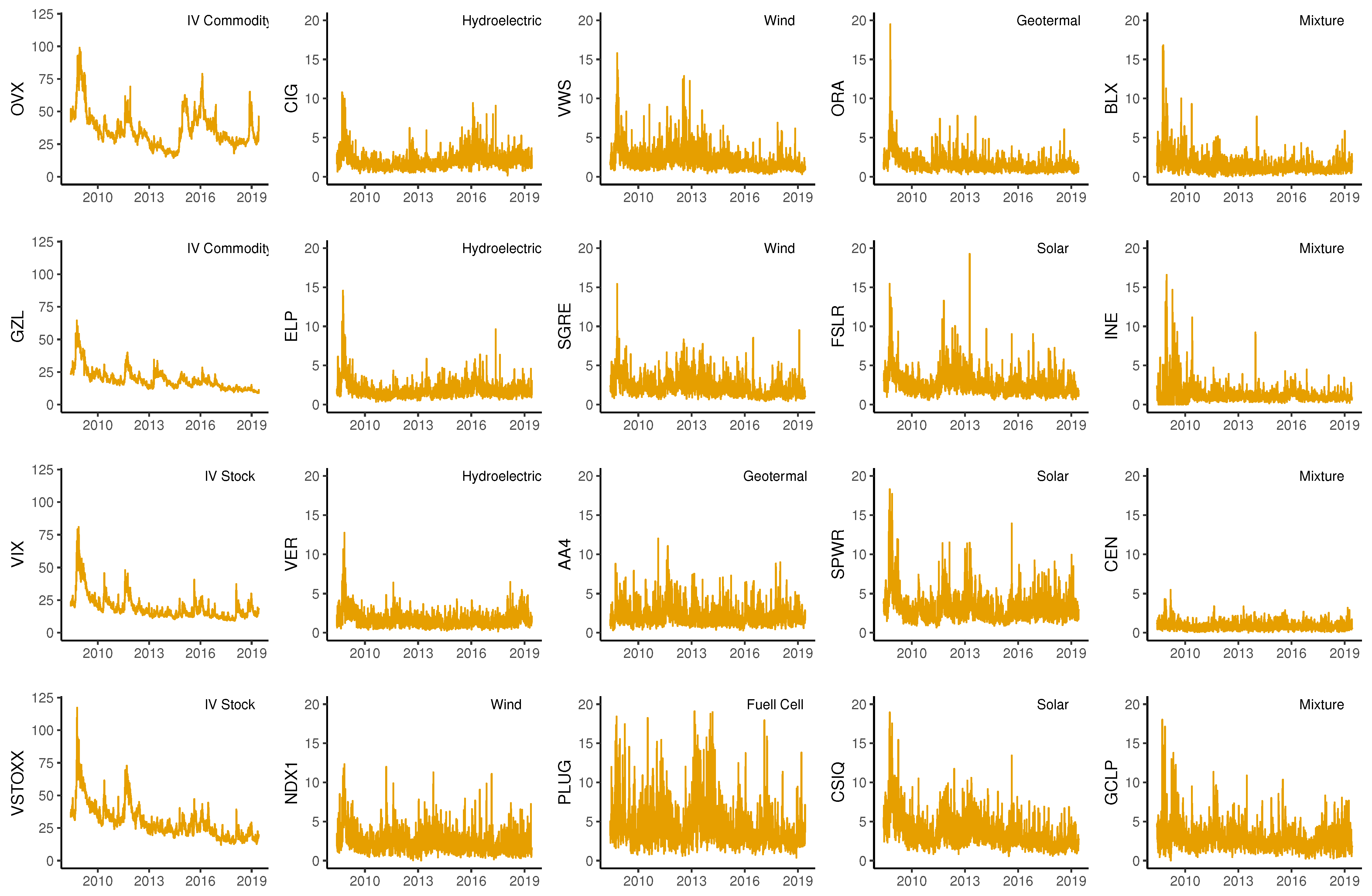
3. Data Description
4. Methodology
5. Empirical Results and Discussion
5.1. Full-Sample Analysis
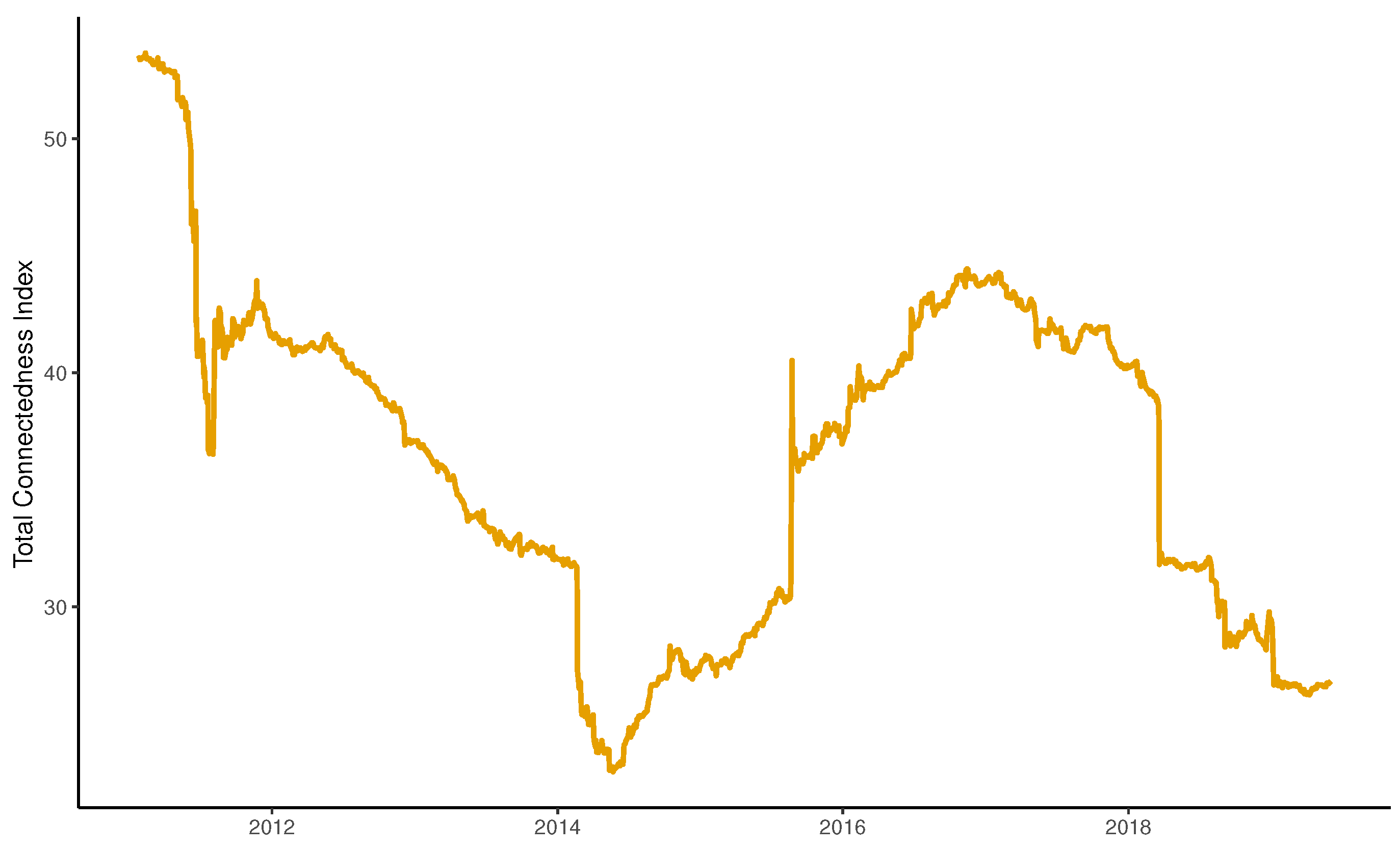
5.2. Rolling-Sample Analysis: Spillover Plots
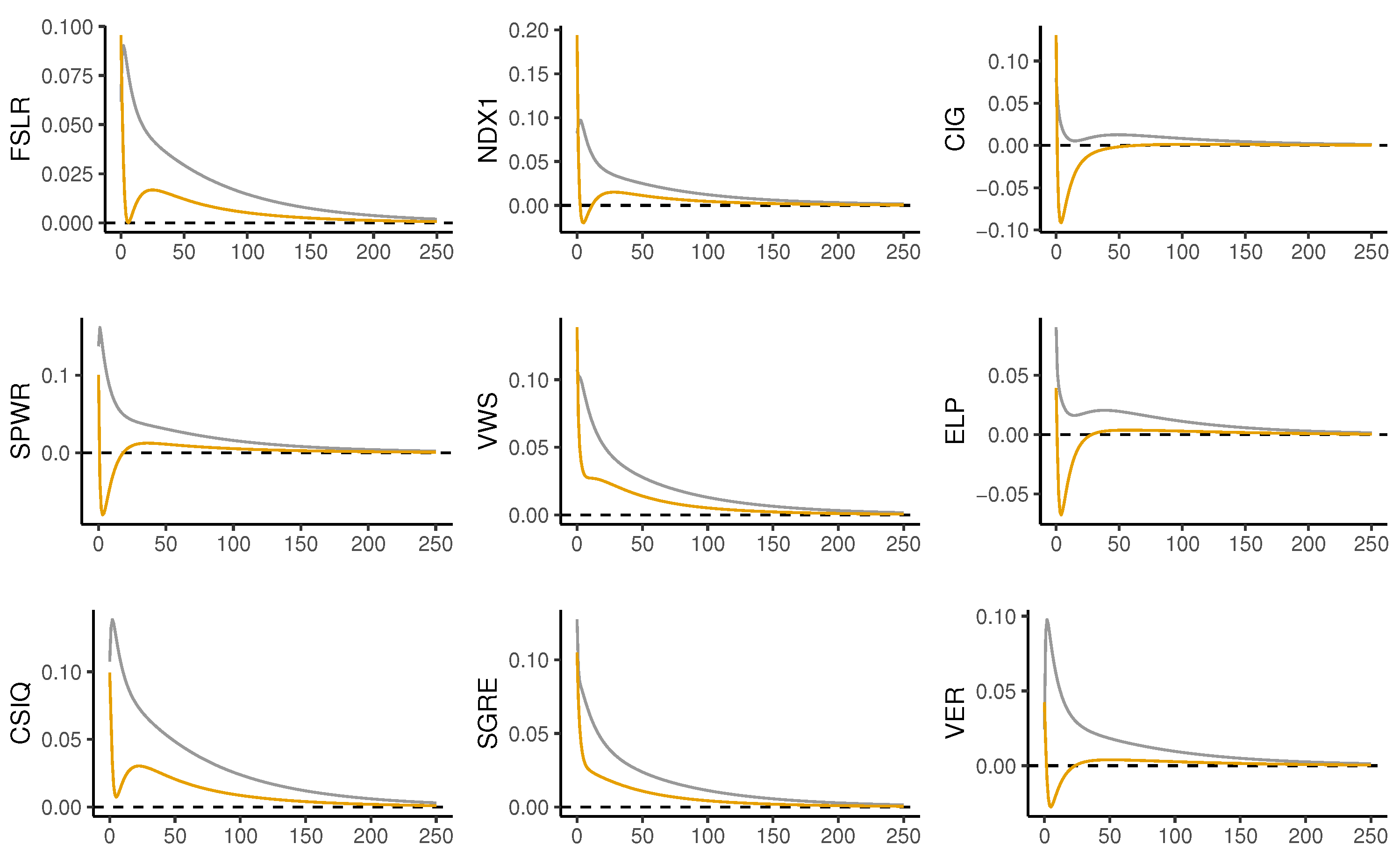
5.3. Impulse–Response Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mejdoub, H.; Ghorbel, A. Conditional dependence between oil price and stock prices of renewable energy: A vine copula approach. Econ. Political Stud. 2018, 6, 176–193. [Google Scholar] [CrossRef]
- Amran, Y.A.; Amran, Y.M.; Alyousef, R.; Alabduljabbar, H. Renewable and sustainable energy production in Saudi Arabia according to Saudi Vision 2030; Current status and future prospects. J. Clean. Prod. 2019, 247, 119602. [Google Scholar] [CrossRef]
- Valadkhani, A.; Smyth, R.; Nguyen, J. Effects of primary energy consumption on CO2 emissions under optimal thresholds: Evidence from sixty countries over the last half century. Energy Econ. 2019, 80, 680–690. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Paramati, S.R.; Ozturk, I.; Bhattacharya, S. The effect of renewable energy consumption on economic growth: Evidence from top 38 countries. Appl. Energy 2016, 162, 733–741. [Google Scholar] [CrossRef]
- Zeppini, P.; Van Den Bergh, J.C. Global competition dynamics of fossil fuels and renewable energy under climate policies and peak oil: A behavioural model. Energy Policy 2020, 136, 110907. [Google Scholar] [CrossRef]
- Malik, K.; Rahman, S.M.; Khondaker, A.N.; Abubakar, I.R.; Aina, Y.A.; Hasan, M.A. Renewable energy utilization to promote sustainability in GCC countries: Policies, drivers, and barriers. Environ. Sci. Pollut. Res. 2019, 26, 20798–20814. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Bouri, E.; Das, D.; Roubaud, D. Assessment and optimization of clean energy equity risks and commodity price volatility indexes: Implications for sustainability. J. Clean. Prod. 2020, 243, 118669. [Google Scholar] [CrossRef]
- Kocaarslan, B.; Soytas, U. Asymmetric pass-through between oil prices and the stock prices of clean energy firms: New evidence from a nonlinear analysis. Energy Rep. 2019, 5, 117–125. [Google Scholar] [CrossRef]
- Webb, J. New lamps for old: Financialised governance of cities and clean energy. J. Cult. Econ. 2019, 12, 286–298. [Google Scholar] [CrossRef]
- Pham, L. Do all clean energy stocks respond homogeneously to oil price? Energy Econ. 2019, 81, 355–379. [Google Scholar] [CrossRef]
- Dutta, A.; Bouri, E.; Noor, M.H. Return and volatility linkages between CO2 emission and clean energy stock prices. Energy 2018, 164, 803–810. [Google Scholar] [CrossRef]
- Kyritsis, E.; Serletis, A. Oil Prices and the Renewable Energy Sector. Energy J. 2019, 40, 337–364. [Google Scholar] [CrossRef]
- Maghyereh, A.I.; Awartani, B.; Abdoh, H. The co-movement between oil and clean energy stocks: A wavelet-based analysis of horizon associations. Energy 2019, 169, 895–913. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A. The impact of energy prices on clean energy stock prices. A multivariate quantile dependence approach. Energy Econ. 2018, 76, 136–152. [Google Scholar] [CrossRef]
- Bouri, E.; Jalkh, N.; Dutta, A.; Salah, G. Gold and crude oil as safe-haven assets for clean energy stock indices: Blended copulas approach. Energy 2019, 178, 544–553. [Google Scholar]
- Ahmad, W.; Sadorsky, P.; Sharma, A. Optimal hedge ratios for clean energy equities. Econ. Model. 2018, 72, 278–295. [Google Scholar] [CrossRef]
- Dutta, A. Oil price uncertainty and clean energy stock returns: New evidence from crude oil volatility index. J. Clean. Prod. 2017, 164, 1157–1166. [Google Scholar] [CrossRef]
- Park, J.; Ratti, R.A. Oil price shocks and stock markets in the US and 13 European countries. Energy Econ. 2008, 30, 2587–2608. [Google Scholar] [CrossRef]
- Kilian, L.; Park, C. The impact of oil price shocks on the US stock market. Int. Econ. Rev. 2009, 50, 1267–1287. [Google Scholar] [CrossRef]
- Ahmad, W. An analysis of directional spillover between crude oil prices and stock prices of clean energy and technology companies. Res. Int. Bus. Financ. 2017, 42, 376–389. [Google Scholar] [CrossRef]
- Henriques, I.; Sadorsky, P. Oil prices and the stock prices of alternative energy companies. Energy Econ. 2008, 30, 998–1010. [Google Scholar] [CrossRef]
- Reboredo, J.C. Is there dependence and systemic risk between oil and renewable energy stock prices? Energy Econ. 2015, 48, 32–45. [Google Scholar] [CrossRef]
- Kumar, S.; Managi, S.; Matsuda, A. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Econ. 2012, 34, 215–226. [Google Scholar] [CrossRef]
- Tully, E.; Lucey, B.M. A power GARCH examination of the gold market. Res. Int. Bus. Financ. 2007, 21, 316–325. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Raza, N.; Shahbaz, M.; Ali, A. Dependence of stock markets with gold and bonds under bullish and bearish market states. Resour. Policy 2017, 52, 308–319. [Google Scholar] [CrossRef] [Green Version]
- Diebold, F.X.; Yılmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Managi, S.; Okimoto, T. Does the price of oil interact with clean energy prices in the stock. Jpn. World Econ. 2013, 27, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Sadorsky, P. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Econ. 2012, 34, 248–255. [Google Scholar] [CrossRef]
- Demirer, M.; Diebold, F.X.; Liu, L.; Yilmaz, K. Estimating global bank network connectedness. J. Appl. Econom. 2018, 33, 1–15. [Google Scholar] [CrossRef]
- Ahmad, W. On the dynamic dependence and investment performance of crude oil and clean energy stocks. Res. Int. Bus. Financ. 2017, 42, 376–389. [Google Scholar] [CrossRef]
- Ahmad, W.; Rais, S. Time-varying spillover and the portfolio diversification implications of clean energy equity with commodities and financial assets. Emerg. Mark. Financ. Trade 2018, 54, 1837–1855. [Google Scholar] [CrossRef]
- Sadorsky, P. Modeling renewable energy company risk. Energy Policy 2012, 40, 39–48. [Google Scholar] [CrossRef]
- Bondia, R.; Ghosh, S.; Kanjilal, K. International crude oil prices and the stock prices of clean energy and technology companies: Evidence from non-linear cointegration tests with unknown structural breaks. Energy 2016, 101, 558–565. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A.; Ugolini, A. Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Econ. 2017, 61, 241–252. [Google Scholar] [CrossRef]
- Yahşi, M.; Çanakoğlu, E.; Ağralı, S. Carbon price forecasting models based on big data analytics. Carbon Manag. 2019, 10, 175–187. [Google Scholar] [CrossRef]
- Maghyereh, A.I.; Awartani, B.; Bouri, E. The directional volatility connectedness between crude oil and equity markets: New evidence from implied volatility indexes. Energy Econ. 2016, 57, 78–93. [Google Scholar] [CrossRef] [Green Version]
- Awartani, B.; Aktham, M.; Cherif, G. The connectedness between crude oil and financial markets: Evidence from implied volatility indices. J. Commod. Mark. 2016, 4, 56–69. [Google Scholar] [CrossRef] [Green Version]
- Garman, M.B.; Klass, M.J. On the estimation of security price volatilities from historical data. J. Bus. 1980, 53, 67–78. [Google Scholar] [CrossRef]
- Pesaran, H.H.; Shin, Y. Generalized impulse response analysis in linear multivariate models. Econ. Lett. 1998, 58, 17–29. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef] [Green Version]
- Diebold, F.X.; Liu, L.; Yilmaz, K. Commodity Connectedness; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2017.
- Polat, O. Systemic risk contagion in FX market: A frequency connectedness and network analysis. Bull. Econ. Res. 2019, 71, 585–598. [Google Scholar] [CrossRef]
- Gupta, D.; Kamilla, U. Dynamic linkages between implied volatility indices of developed and emerging financial markets: An econometric approach. Glob. Bus. Rev. 2015, 16, 46S–57S. [Google Scholar] [CrossRef]
- Ding, L.; Huang, Y.; Pu, X. Volatility linkage across global equity markets. Glob. Financ. J. 2014, 25, 71–89. [Google Scholar] [CrossRef]
- Shu, H.C.; Chang, J.H. Spillovers of volatility index: Evidence from US, European, and Asian stock markets. Appl. Econ. 2019, 51, 2070–2083. [Google Scholar] [CrossRef]
- Sarwar, G. Interrelations in market fears of US and European equity markets. N. Am. J. Econ. Financ. 2020, 41, 101136. [Google Scholar] [CrossRef]
- Antonakakis, N.; Kizys, R. Dynamic spillovers between commodity and currency markets. Int. Rev. Financ. Anal. 2015, 41, 303–319. [Google Scholar] [CrossRef] [Green Version]


| Econometric Methodology | Reference | Specification | Indices |
|---|---|---|---|
| VAR | Kumar et al. [23] | VAR | ECO, SPGCE, NEX, PSE, Oil, Carbon, Interest Rate, S&P 500 |
| Managi and Okimoto [27] | Markov Switching VAR | ECO, PSE, Oil, Interest Rate | |
| Volatility | Sadorsky [28] | BEKK, Diagonal, DCC, CCC | ECO, PSE, Oil |
| Ahmad et al. [16] | DCC, ADCC, GO-GARCH | ECO, Oil, Gold, VIX, OVX, Carbon, Bond | |
| Dutta et al. [11] | VAR-GARCH, DCC-GARCH | ECO, ERIX, Carbon | |
| Maghyereh et al. [13] | waveled MGARCH-DCC | ECO, Oil, FTSE ET50 | |
| Kyritsis and Serletis [12] | VAR-GARCH in mean | ECO, SPGCE, NEX, PSE, Oil | |
| Dutta et al. [7] | DCC-GARCH | ECO, SPGCE, MAC, OVX, GVZ, VXSLV | |
| Copulas | Reboredo [22] | TGARCH- Copula | ECO, SPGCE, ERIX, WIND, SOLAR, TECH, Oil |
| Mejdoub and Ghorbel [1] | TGARCH-Vine Copula | ECO, SPGCE, NEX, Oil | |
| Reboredo and Ugolini [14] | Multivariate Vine Copula | ECO, ERIX, Oil, Natural Gas, Coal, Electricity, S&P 500, Euro Stoxx 50 | |
| Bouri et al. [15] | EVT-Copulas | ECO, SPGCE, Oil, Gold | |
| Mixed | Sadorsky [32] | Beta model (CAPME extension) | PBW, Oil |
| Bondia et al. [33] | Threshold Cointegration Test, Granger Causality. | NEX, PSE, Oil, Interest Rate | |
| Reboredo et al. [34] | Wavelet based-test, Granger Causality | ECO, SPGCE, ERIX, Oil, WIND, SOLAR, TECH | |
| Dutta [17] | Range-based volatility measures. | ECO, Oil, OVX, Carbon | |
| Yahşi et al. [35] | Random Forest, Regression | SPGCE, DAX, Oil, Natural Gas, Coal, Carbon, Electricity | |
| Diebold-Yilmaz Connectedness | Ahmad [30] | Diebold-Yilmaz connectedness, BEKK, DCC, CCC | ECO, PSE, Oil |
| Ahmad and Rais [31] | Diebold-Yilmaz connectedness, ADCC | NEX, PSE, Oil, Heating, Gasoline, DJIMI, Market Indexes: WORLD-DS, US-DS, EUROPE-DS. | |
| Pham [10] | Diebold-Yilmaz connectedness, DCC, ADCC, GO-GARCH | Oil, NASDAQ OMX Clean Energy Indices. |
| Name | Ticker | Founded | Subsector |
|---|---|---|---|
| Cia Energetica de Minas Gerais Prf ADR | CIG | Brazil, 1952 | Hydro (Electric power) |
| Companhia Paranaense de Energia | ELP | Brazil, 1954 | Hydro (Electric power) |
| VERBUND AG | VER | Austria, 1947 | Hydro (Electric power) |
| Nordex SE | NDX1 | Germany, 1985 | Wind |
| Vestas Wind Systems AS | VWS | Denmark, 1945 | Wind |
| Siemens Gamesa Renewable Energy | SGRE | Spain, 1976 | Wind |
| Falckrenewables | AA4 | Italy, 2002 | Mixture |
| Plugpower | PLUG | USA, 1997 | Fuell Cell |
| Ormat Technologies | ORA | USA, 1965 | Geotermal |
| First Solar Inc | FSLR | USA, 1999 | Solar |
| Sunpower | SPWR | USA, 1985 | Solar |
| Canadian Solar Inc | CSIQ | Canada, 2001 | Solar |
| Boralex Inc. ’A’ | BLX | Canada, 1982 | Mixture |
| Innergex Renewable Energy Inc | INE | Canada, 1990 | Mixture |
| Contact Energy Ltd | CEN | New Zealand, 1996 | Mixture |
| GCL Poly Energy Holdings Ltd | GCLP | China, 2006 | Mixture |
| Ticker | Mean | Standard Deviation | Min | Max | Skewness | Kurtosis | Jarque– Bera | Box– Pierce | Phillips– Perron |
|---|---|---|---|---|---|---|---|---|---|
| OVX | 36.221 | 13.762 | 14.500 | 98.930 | 1.340 | 2.375 | 0.00 | 0.00 | 0.02 |
| GVZ | 19.145 | 7.801 | 8.880 | 64.530 | 2.062 | 5.917 | 0.00 | 0.00 | 0.01 |
| VIX | 19.378 | 9.624 | 9.150 | 80.860 | 2.543 | 8.362 | 0.00 | 0.00 | 0.01 |
| VSTOXX | 29.951 | 13.245 | 11.990 | 117.310 | 1.793 | 4.706 | 0.00 | 0.00 | 0.01 |
| CIG | 2.094 | 1.287 | 0.160 | 8.947 | 5.913 | 93.894 | 0.00 | 0.00 | 0.01 |
| ELP | 1.881 | 1.128 | 0.362 | 14.575 | 3.661 | 24.027 | 0.00 | 0.00 | 0.01 |
| VER | 1.630 | 0.978 | 0.156 | 12.743 | 2.877 | 17.235 | 0.00 | 0.00 | 0.01 |
| NDX1 | 2.362 | 1.563 | 0.000 | 12.322 | 2.083 | 6.580 | 0.00 | 0.00 | 0.01 |
| VWS | 2.127 | 1.477 | 0.303 | 15.802 | 2.854 | 13.427 | 0.00 | 0.00 | 0.01 |
| SGRE | 2.285 | 1.303 | 0.427 | 15.425 | 2.126 | 9.381 | 0.00 | 0.00 | 0.01 |
| AA4 | 2.189 | 1.283 | 0.294 | 11.997 | 1.943 | 5.977 | 0.00 | 0.00 | 0.01 |
| PLUG | 4.301 | 2.921 | 0.375 | 26.365 | 2.385 | 8.742 | 0.00 | 0.00 | 0.01 |
| ORA | 1.585 | 1.110 | 0.304 | 19.499 | 4.536 | 42.995 | 0.00 | 0.00 | 0.01 |
| FSLR | 2.599 | 1.537 | 0.566 | 19.270 | 3.018 | 16.715 | 0.00 | 0.00 | 0.01 |
| SPWR | 3.199 | 1.782 | 0.657 | 18.315 | 2.733 | 12.521 | 0.00 | 0.00 | 0.01 |
| CSIQ | 3.581 | 2.139 | 0.567 | 23.410 | 2.764 | 14.836 | 0.00 | 0.00 | 0.01 |
| BLX | 1.399 | 1.186 | 0.000 | 16.806 | 4.847 | 42.237 | 0.00 | 0.00 | 0.01 |
| INE | 1.217 | 1.182 | 0.000 | 16.579 | 5.533 | 46.376 | 0.00 | 0.00 | 0.01 |
| CEN | 0.863 | 0.505 | 0.000 | 5.473 | 1.823 | 7.434 | 0.00 | 0.00 | 0.01 |
| GCLP | 2.815 | 1.633 | 0.000 | 18.025 | 2.514 | 12.395 | 0.00 | 0.00 | 0.01 |
| OVX | GVZ | VIX | VSTOXX | CIG | ELP | VER | NDX1 | VWS | SGRE | AA4 | PLUG | ORA | FSLR | SPWR | CSIQ | BLX | INE | CEN | GCLP | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OVX | 61.09 | 7.08 | 15.75 | 7.81 | 2.38 | 1.29 | 0.70 | 0.40 | 0.41 | 0.34 | 0.20 | 0.16 | 0.83 | 0.10 | 0.39 | 0.28 | 0.44 | 0.33 | 0.01 | 0.00 | 39.00 | 1.4 |
| GVZ | 4.84 | 52.39 | 13.54 | 14.41 | 1.84 | 1.75 | 0.11 | 1.73 | 1.66 | 1.36 | 0.41 | 0.50 | 0.92 | 1.37 | 1.24 | 1.64 | 0.25 | 0.02 | 0.01 | 0.01 | 47.60 | 50.0 |
| VIX | 8.75 | 12.13 | 45.58 | 20.49 | 0.79 | 0.94 | 0.94 | 1.93 | 1.58 | 1.86 | 0.34 | 0.22 | 1.79 | 0.59 | 0.91 | 0.43 | 0.51 | 0.05 | 0.12 | 0.05 | 54.40 | 85.0 |
| VSTOXX | 6.19 | 13.21 | 28.09 | 40.66 | 0.79 | 0.47 | 0.37 | 1.95 | 1.99 | 2.35 | 0.89 | 0.20 | 0.74 | 0.71 | 0.47 | 0.41 | 0.29 | 0.12 | 0.10 | 0.01 | 59.40 | 38.0 |
| CIG | 3.46 | 4.26 | 3.41 | 2.77 | 52.32 | 19.97 | 1.27 | 1.53 | 1.01 | 0.27 | 0.27 | 0.19 | 1.79 | 1.70 | 2.31 | 1.77 | 1.50 | 0.07 | 0.03 | 0.09 | 47.60 | -2.8 |
| ELP | 2.83 | 7.19 | 4.83 | 1.72 | 18.66 | 47.57 | 1.44 | 2.30 | 0.97 | 0.64 | 0.04 | 0.48 | 3.43 | 1.65 | 2.48 | 2.59 | 0.85 | 0.15 | 0.03 | 0.17 | 52.40 | -7.2 |
| VER | 2.58 | 3.05 | 9.98 | 3.29 | 3.21 | 2.99 | 59.08 | 2.55 | 1.02 | 1.54 | 0.56 | 0.45 | 2.68 | 1.01 | 2.01 | 0.71 | 2.39 | 0.13 | 0.36 | 0.42 | 41.00 | -25.6 |
| NDX1 | 0.78 | 5.29 | 5.30 | 4.67 | 1.49 | 1.85 | 1.64 | 60.13 | 3.32 | 3.94 | 0.94 | 1.03 | 2.93 | 1.52 | 1.95 | 2.24 | 0.20 | 0.09 | 0.16 | 0.52 | 39.80 | -6.8 |
| VWS | 0.34 | 4.46 | 5.89 | 6.03 | 1.12 | 0.57 | 0.78 | 3.41 | 58.25 | 11.07 | 0.17 | 0.42 | 2.62 | 1.97 | 0.87 | 1.13 | 0.09 | 0.33 | 0.16 | 0.31 | 41.80 | -3.8 |
| SGRE | 0.80 | 3.98 | 6.16 | 6.44 | 0.39 | 0.52 | 1.00 | 4.18 | 11.36 | 59.17 | 0.29 | 0.21 | 1.65 | 1.52 | 1.06 | 0.94 | 0.05 | 0.07 | 0.05 | 0.18 | 40.80 | -7.6 |
| AA4 | 1.08 | 0.67 | 2.41 | 4.81 | 0.50 | 0.16 | 0.37 | 1.58 | 0.59 | 0.54 | 84.45 | 0.12 | 0.23 | 0.80 | 0.96 | 0.06 | 0.05 | 0.22 | 0.15 | 0.26 | 15.60 | -10.0 |
| PLUG | 0.44 | 3.83 | 1.75 | 1.27 | 0.25 | 0.47 | 0.03 | 1.42 | 0.93 | 0.33 | 0.08 | 83.70 | 1.07 | 0.34 | 1.44 | 2.22 | 0.13 | 0.10 | 0.08 | 0.12 | 16.20 | -5.2 |
| ORA | 1.86 | 7.53 | 10.67 | 6.00 | 3.17 | 4.04 | 1.30 | 2.87 | 3.39 | 2.03 | 0.16 | 0.78 | 47.55 | 2.29 | 2.05 | 2.44 | 1.34 | 0.37 | 0.13 | 0.04 | 52.40 | -20.8 |
| FSLR | 0.58 | 4.68 | 4.66 | 3.58 | 1.63 | 1.44 | 0.63 | 1.14 | 3.84 | 2.39 | 0.28 | 0.53 | 2.26 | 50.93 | 12.71 | 6.92 | 0.35 | 0.73 | 0.11 | 0.61 | 49.00 | -10.6 |
| SPWR | 0.85 | 5.19 | 6.95 | 2.18 | 1.70 | 2.19 | 0.60 | 1.33 | 1.62 | 1.77 | 0.42 | 1.04 | 1.72 | 12.56 | 51.16 | 7.43 | 0.33 | 0.64 | 0.09 | 0.21 | 48.80 | -7.6 |
| CSIQ | 1.04 | 7.20 | 6.67 | 4.85 | 1.66 | 2.65 | 0.55 | 2.31 | 2.31 | 1.62 | 0.09 | 2.01 | 3.07 | 7.71 | 8.12 | 47.00 | 0.29 | 0.33 | 0.11 | 0.41 | 53.00 | -18.6 |
| BLX | 1.93 | 5.70 | 5.47 | 3.16 | 4.39 | 2.48 | 2.64 | 0.95 | 0.30 | 0.31 | 0.04 | 1.53 | 2.47 | 0.35 | 1.31 | 1.17 | 65.12 | 0.53 | 0.10 | 0.08 | 34.80 | -25.4 |
| INE | 1.30 | 0.23 | 2.42 | 1.11 | 0.35 | 0.08 | 0.07 | 0.09 | 0.53 | 0.07 | 0.14 | 0.78 | 0.40 | 0.04 | 0.10 | 0.49 | 0.13 | 91.43 | 0.19 | 0.06 | 8.60 | -4.2 |
| CEN | 0.37 | 0.60 | 1.27 | 0.47 | 0.19 | 0.22 | 0.63 | 0.81 | 0.57 | 0.26 | 0.05 | 0.10 | 0.52 | 0.39 | 0.22 | 0.55 | 0.23 | 0.05 | 92.34 | 0.16 | 7.60 | -5.6 |
| GCLP | 0.47 | 1.29 | 4.12 | 2.26 | 0.28 | 1.12 | 0.27 | 0.44 | 0.52 | 0.54 | 0.32 | 0.25 | 0.44 | 1.81 | 0.65 | 1.01 | 0.07 | 0.13 | 0.09 | 83.92 | 16.00 | -12.2 |
| 40.40 | 97.60 | 139.4 | 97.40 | 44.80 | 45.20 | 15.40 | 33.00 | 38.00 | 33.20 | 5.60 | 11.00 | 31.60 | 38.40 | 41.20 | 34.40 | 9.40 | 4.40 | 2.00 | 3.80 | = 38.31% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes, F.; Herrera, R. Dynamics of Connectedness in Clean Energy Stocks. Energies 2020, 13, 3705. https://doi.org/10.3390/en13143705
Fuentes F, Herrera R. Dynamics of Connectedness in Clean Energy Stocks. Energies. 2020; 13(14):3705. https://doi.org/10.3390/en13143705
Chicago/Turabian StyleFuentes, Fernanda, and Rodrigo Herrera. 2020. "Dynamics of Connectedness in Clean Energy Stocks" Energies 13, no. 14: 3705. https://doi.org/10.3390/en13143705
APA StyleFuentes, F., & Herrera, R. (2020). Dynamics of Connectedness in Clean Energy Stocks. Energies, 13(14), 3705. https://doi.org/10.3390/en13143705






