Method of Averaging the Effective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers
Abstract
:1. Introduction
2. Thermal Response Test
- ρ—density of the medium, kg/m3,
- cp—specific heat of the ground, J/(kgK),
- λ—thermal conductivity of the ground, W/(mK),
- T—temperature, K,
- t—time, s,
- r—radius, m.
- q—unit heat transfer coefficient of the BHE, W/m,
- T0—initial temperature in the BHE, K.
- P—mean heating power during the TRT, W,
- H—depth of the borehole heat exchanger, m,
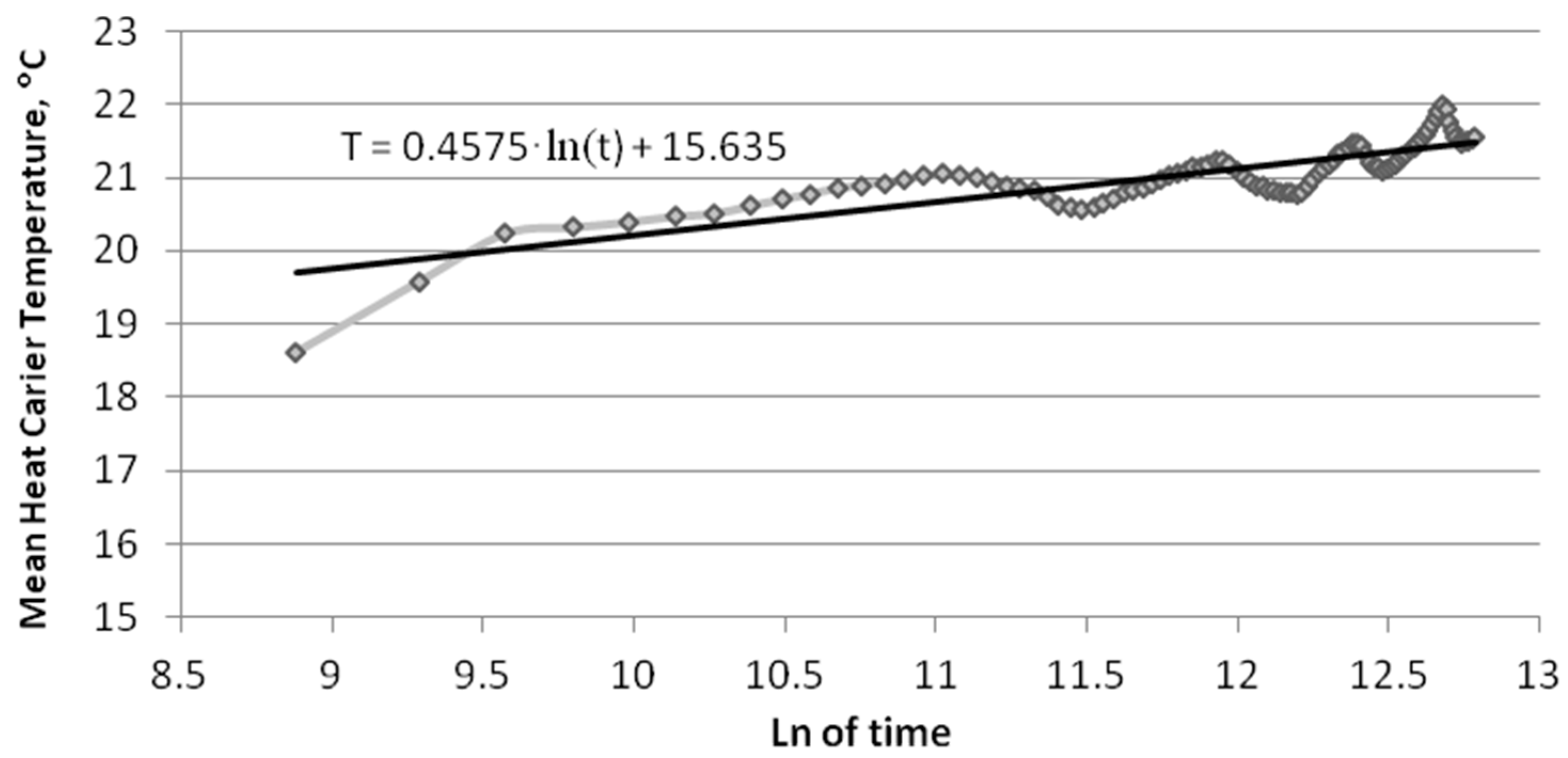
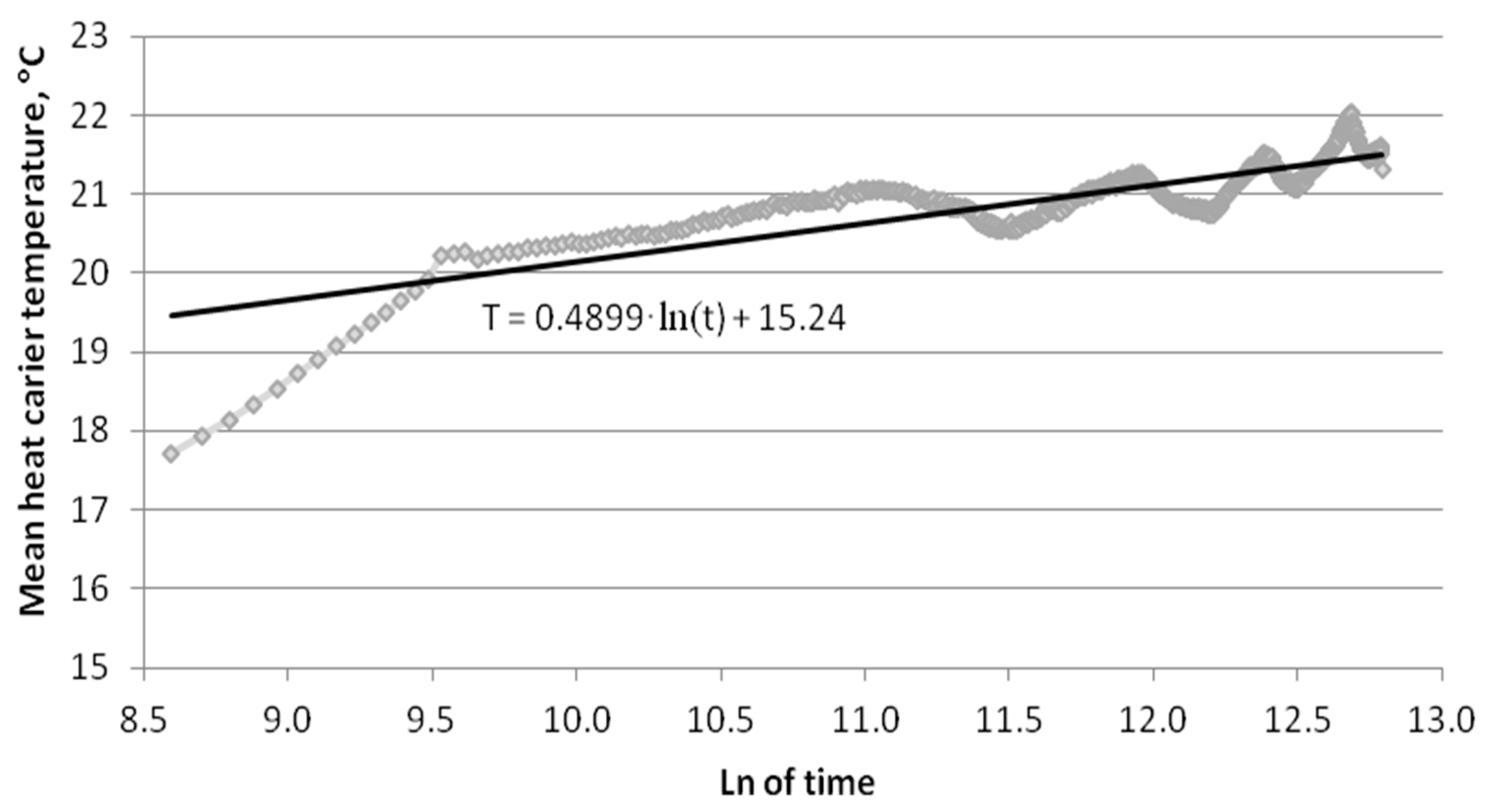
- k—the slope of the trend line—a straight line determined as the ratio of the mean temperature to the logarithm of the natural test time.
- the design of the borehole heat exchanger,
- TRT parameters, and
- how the measurement results are averaged, as shown in this article. Its aim is to show the diversity of the final measurement results, which can be regarded as a manifestation of their uncertainty.
3. The Scope of the Conducted Research
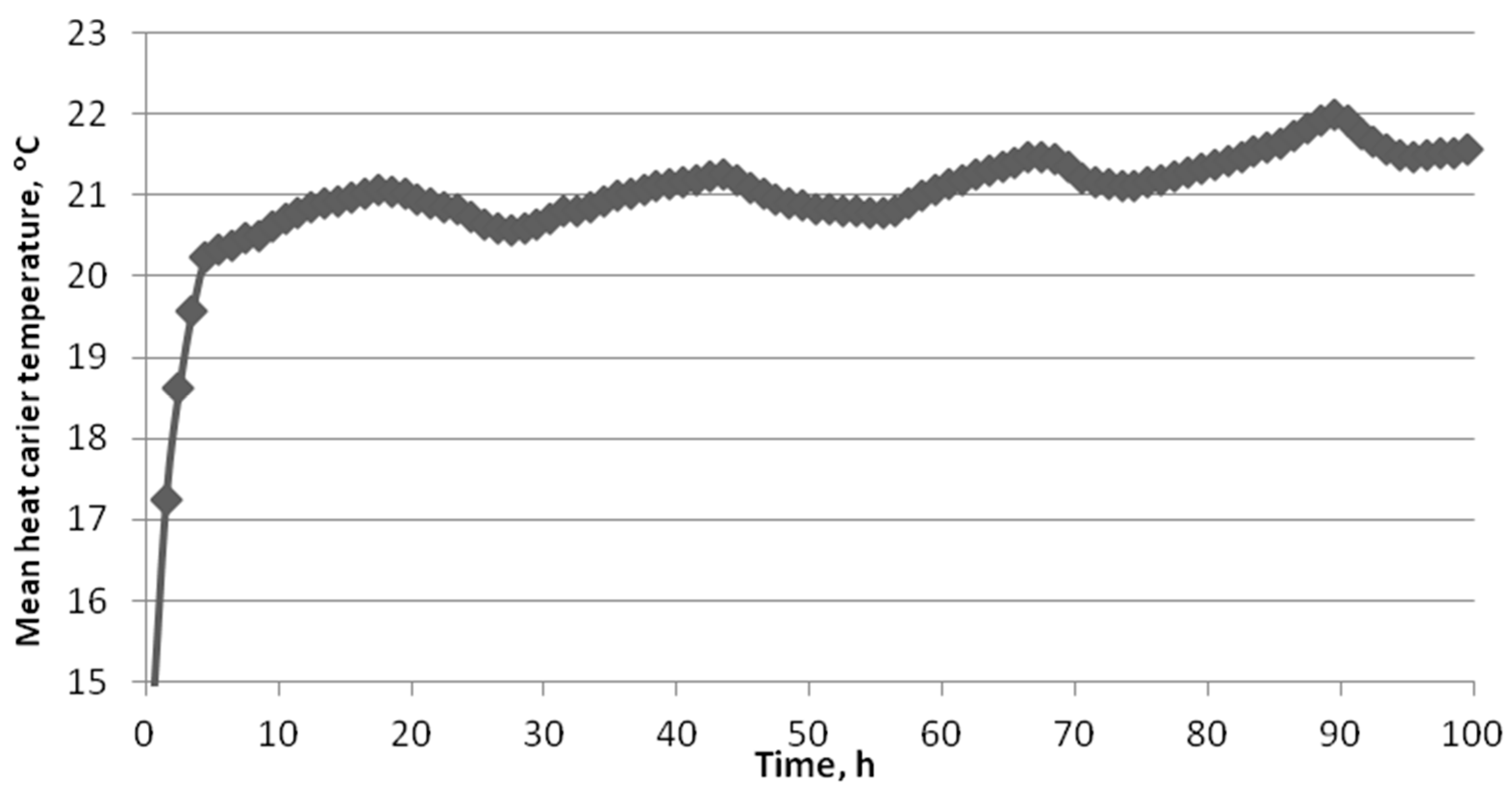
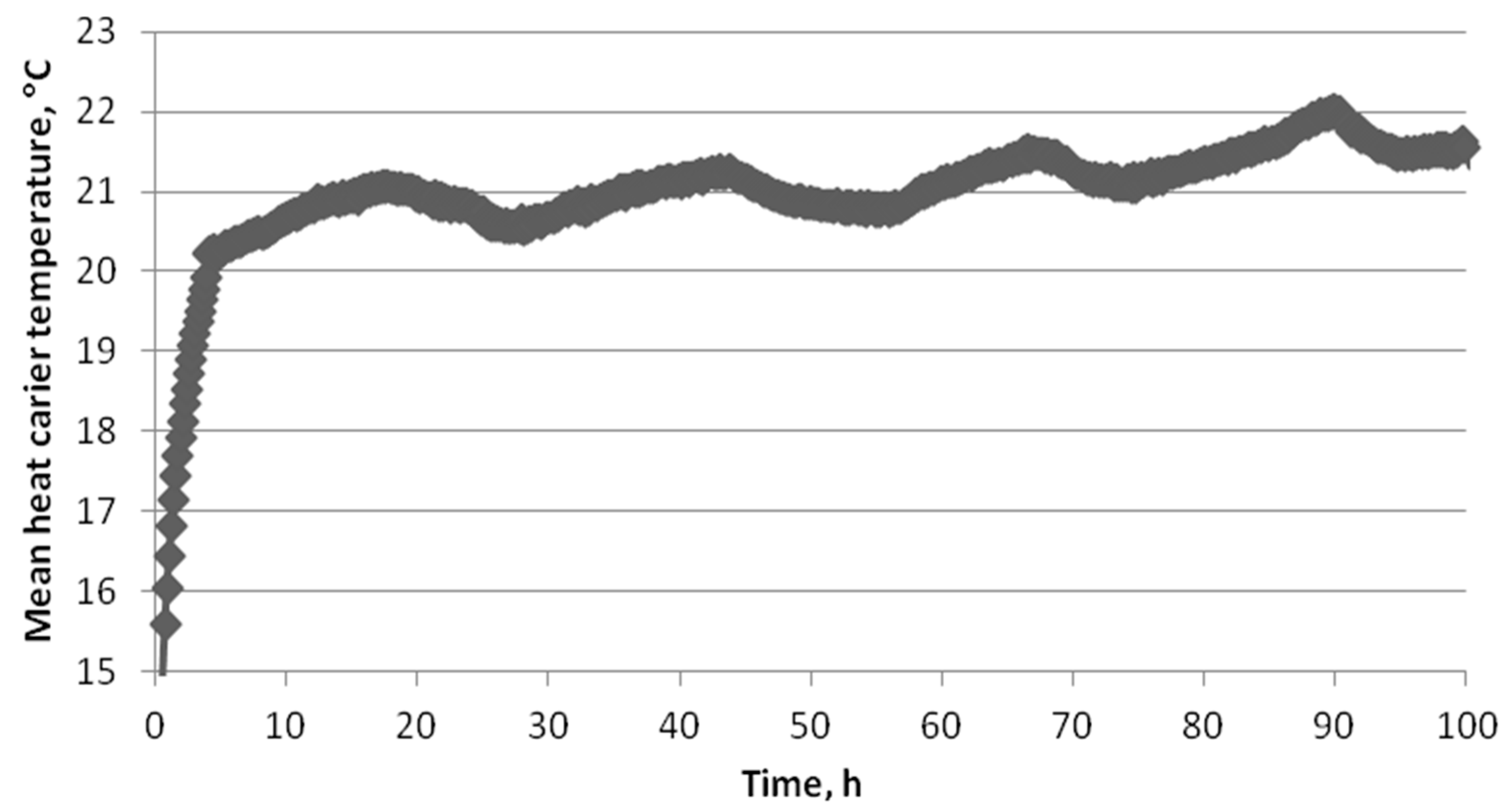
4. Measurement Results
5. Interpretation of TRT Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yoon, A.-Y.; Kang, H.-K.; Moon, S.-I. Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction. Energies 2020, 13, 862. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Pei, P.; Hao, D.; Wang, C. A Numerical Study on the Performance of Ground Heat Exchanger Buried in Fractured Rock Bodies. Energies 2020, 13, 1647. [Google Scholar] [CrossRef] [Green Version]
- Sliwa, T.; Gonet, A. Otworowe wymienniki ciepła jako źródło ciepła lub chłodu na przykładzie Laboratorium Geoenergetyki WWNiG AGH (Borehole heat exchangers as heat or cool source on the basis of Laboratory of Geothermics of Drilling, Oil and Gas Faculty in AGH University of Science and Technology). Wiert. Naft. Gaz 2011, 28, 419–430. Available online: http://journals.bg.agh.edu.pl/WIERTNICTWO/2011-1-2/W_2011_1-2_36.pdf (accessed on 10 April 2020). (In Polish).
- Sliwa, T.; Knez, D.; Gonet, A.; Sapińska-Śliwa, A.; Szłapa, B. Research and Teaching Capacities of the Geoenergetics Laboratory at Drilling, Oil and Gas Faculty AGH University of Science and Technology in Kraków (Poland). In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015; Paper No. 09012. pp. 1–14. Available online: https://www.geothermal-energy.org/pdf/IGAstandard/WGC/2015/09012.pdf (accessed on 10 April 2020).
- Sliwa, T.; Gołaś, A.; Wołoszyn, J.; Gonet, A. Numerical model of borehole heat exchanger in ANSYS CFX software. Arch. Min. Sci. 2012, 57, 375–390. [Google Scholar]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Gultekin, A.; Aydin, M.; Sisman, A. Thermal performance analysis of multiple borehole heat exchangers. Energy Convers. Manag. 2016, 122, 544–551. [Google Scholar] [CrossRef]
- Li, M.; Lai, A.C. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs): A perspective of time and space scales. Appl. Energy 2015, 151, 178–191. [Google Scholar] [CrossRef]
- Sliwa, T.; Sojczyńska, A.; Rosen, M.A.; Kowalski, T. Evaluation of temperature profiling quality in determining energy efficiencies of borehole heat exchangers. Geothermics 2019, 78, 129–137. [Google Scholar] [CrossRef]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 199–406. [Google Scholar] [CrossRef]
- Raymond, J.; Therrien, R.; Gosselin, L. Borehole temperature evolution during thermal response tests. Geothermics 2011, 40, 69–78. [Google Scholar] [CrossRef]
- Wagner, V.; Blum, P.; Kubert, M.; Bayer, P. Analytical approach to groundwater-influenced thermal response tests of grouted borehole heat exchangers. Geothermics 2013, 46, 22–31. [Google Scholar] [CrossRef]
- Liuzzo-Scorpo, A.; Nordell, B.; Gehlin, S. Influence of regional groundwater flow on ground temperature around heat extraction boreholes. Geothermics 2015, 56, 119–127. [Google Scholar] [CrossRef]
- Rouleau, J.; Gosselin, L.; Raymond, J. New concept of combined hydro-thermal response tests (H/TRTS) for ground heat exchangers. Geothermics 2016, 62, 103–114. [Google Scholar] [CrossRef]
- Bandos, T.V.; Montero, A.; Fernandez de Cordoba, P.; Urchueguía, J.F. Improving parameter estimates obtained from thermal response tests: Effect of ambient air temperature variations. Geothermics 2011, 40, 136–143. [Google Scholar] [CrossRef] [Green Version]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Gehlin, S. Thermal Response Test: Method Development and Evaluation. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2002. Available online: http://ltu.diva-portal.org/smash/get/diva2:991442/FULLTEXT01.pdf (accessed on 30 April 2020).
- Mogensen, P. Fluid to Duct Wall Heat Transfer in Duct System Heat Storage. In Proceedings of the Int. Conf. On Subsurface Heat Storage in Theory and Practice, Stockholm, Sweden, 1983; pp. 652–657. [Google Scholar]
- Nejad, P.E.; Badache, M.; Corcoran, A.; Bernier, M. Calibration of thermal response test (TRT) units with a virtual borehole. Geothermics 2019, 79, 105–113. [Google Scholar]
- Sun Chang, K.; Jun Kim, M. Thermal performance evaluation of vertical U-loop ground heat exchanger using in-situ thermal response test. Renew. Energy 2019, 87, 585–591. [Google Scholar] [CrossRef]
- Choi, W.; Kikumoto, H.; Choudhary, R.; Ooka, R. Bayesian inference for thermal response test parameter estimation and uncertainty assessment. Appl. Energy 2018, 209, 306–321. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D.; Spitler, J.D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis. Geothermics 2011, 40, 79–85. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Z.; Liu, Y. A review on thermal response test of ground-coupled heat pump systems. Renew. Sustain. Energy Rev. 2014, 40, 851–867. [Google Scholar] [CrossRef]
- Raymond, J.; Lamarche, L.; Malo, M. Field demonstration of a first thermal response test with low power source. Appl. Energy 2015, 147, 30–39. [Google Scholar] [CrossRef]
- Franco, A.; Moffat, R.; Toledo, M.; Herrera, P. Numerical sensitivity analysis of thermal response tests (TRT) in energy piles. Renew. Energy 2016, 86, 985–992. [Google Scholar] [CrossRef]
- Zarrella, A.; Emmi, G.; Graci, S.; De Carli, M.; Cultrera, M.; Santa, G.D.; Galgaro, A.; Bertermann, D.; Müller, J.; Pockelé, L.; et al. Thermal Response Testing Results of Different Types of Borehole Heat Exchangers: An Analysis and Comparison of Interpretation Methods. Energies 2017, 10, 801. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, A.-M.; Westerlund, L. Multi-injection rate thermal response test in groundwater filled borehole heat exchanger. Renew. Energy 2010, 35, 1061–1070. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P.; Liu, Y. An improved evaluation method for thermal performance of borehole heat exchanger. Renew. Energy 2015, 77, 142–151. [Google Scholar] [CrossRef]
- Loveridge, F.; Powire, W.; Nicholson, D. Comparison of two different models for pile thermal response test interpretation. Geothermics 2014, 9, 367–384. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Zhang, Y.; Deng, N.; Ma, H.; Dong, S. Thermal response test for ground source heat pump based on constant temperature and heat-flux methods. Appl. Therm. Eng. 2016, 93, 678–682. [Google Scholar] [CrossRef]
- Sliwa, T.; Gonet, A. Theoretical model of borehole heat exchanger. J. Energy Resour. Technol. 2005, 127, 142–148. [Google Scholar] [CrossRef]
- Signorelli, S.; Basetti, S.; Pahud, D.; Kohl, T. Numerical evaluation of thermal response tests. Geothermics 2007, 36, 141–166. Available online: 10.1016/j.geothermics.2006.10.006 (accessed on 10 April 2020). [CrossRef]
- Sliwa, T.; Kotyza, J. Application of existing wells as ground heat source for heat pumps in Poland. Appl. Energy 2003, 74, 3–8. [Google Scholar] [CrossRef]
- Sliwa, T.; Rosen, M.A.; Jezuit, Z. Use of Oil Boreholes in the Carpathians in Geoenergetic Systems: Historical and Conceptual Review. Res. J. Environ. Sci. 2014, 8, 231–242. [Google Scholar] [CrossRef] [Green Version]
- Sliwa, T.; Kruszewski, M.; Zare, A.; Assadi, M.; Sapińska-Śliwa, A. Potential application of vacuum insulated tubing for deep borehole heat exchangers. Geothermics 2018, 75, 58–67. [Google Scholar] [CrossRef]
- Sapińska-Śliwa, A.; Rosen, M.A.; Gonet, A.; Kowalczyk, J.; Sliwa, T. A new method based on thermal response tests for determining effective thermal conductivity and borehole resistivity for borehole heat exchangers. Energies 2019, 12, 1072. Available online: https://www.mdpi.com/1996-1073/12/6/1072/pdf (accessed on 10 April 2020).
- Sliwa, T.; Rosen, M.A. Natural and artificial methods for regeneration of heat resources for borehole heat exchangers to enhance the sustainability of underground thermal storages: A review. Sustainability 2015, 7, 13104–13125. [Google Scholar] [CrossRef] [Green Version]
- Perina, T. Derivation of the Theis (1935) Equation by Substitution. Ground Water 2010, 48, 6–7. [Google Scholar] [CrossRef] [PubMed]
- Eklöf, C.; Gehlin, S. TED—A Mobile Equipment for Thermal Response Test. Master’s Thesis, Lund University, Lund, Sweden, 1996. [Google Scholar]
- Gonet, A.; Sliwa, T.; Stryczek, S.; Sapińska-Śliwa, A.; Jaszczur, M.; Pająk, L.; Złotkowski, A. Metodyka Identyfikacji Potencjału Cieplnego Górotworu Wraz z Technologią Wykonywania i Eksploatacji Otworowych Wymienników Ciepła (Methodology for the Identification of Potential Heat of the Rock Mass Along with Technology Implementation and Operation of the Borehole Heat Exchangers), 1st ed.; Gonet, A., Ed.; Wydawnictwa AGH: Krakow, Poland, 2011; p. 439. (In Polish) [Google Scholar]
- Somerton, W.H. Thermal Properties and Temperature-Related Behavior of Rock/Fluid Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1992; p. 256. [Google Scholar]
- Plewa, S. Rozkład Parametrów Geotermalnych na Obszarze Polski, 1st ed.; Wydawnictwo CPPGSMiE PAN: Krakow, Poland, 1994; p. 138. (In Polish) [Google Scholar]
- Sapińska-Śliwa, A. Efektywność Pozyskiwania Ciepła z Górotworu w Aspekcie Sposobu Udostępniania Otworami Wiertniczymi (Effectiveness of Heat Recovery from Rock Mass in the Context of the Production Method by Means of Boreholes), 1st ed.; Wydawnictwa AGH: Krakow, Poland, 2019; p. 319. (In Polish) [Google Scholar]
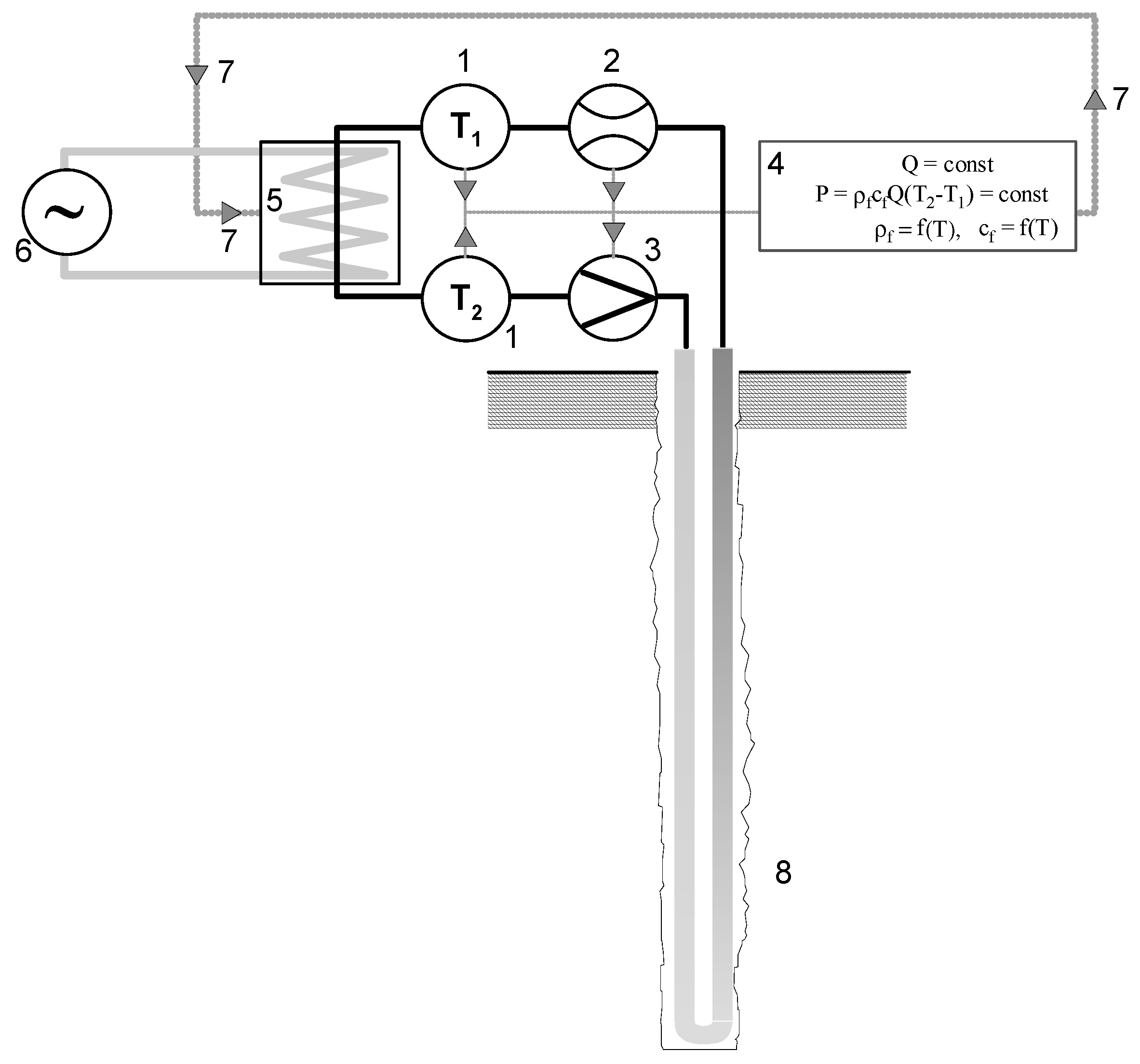


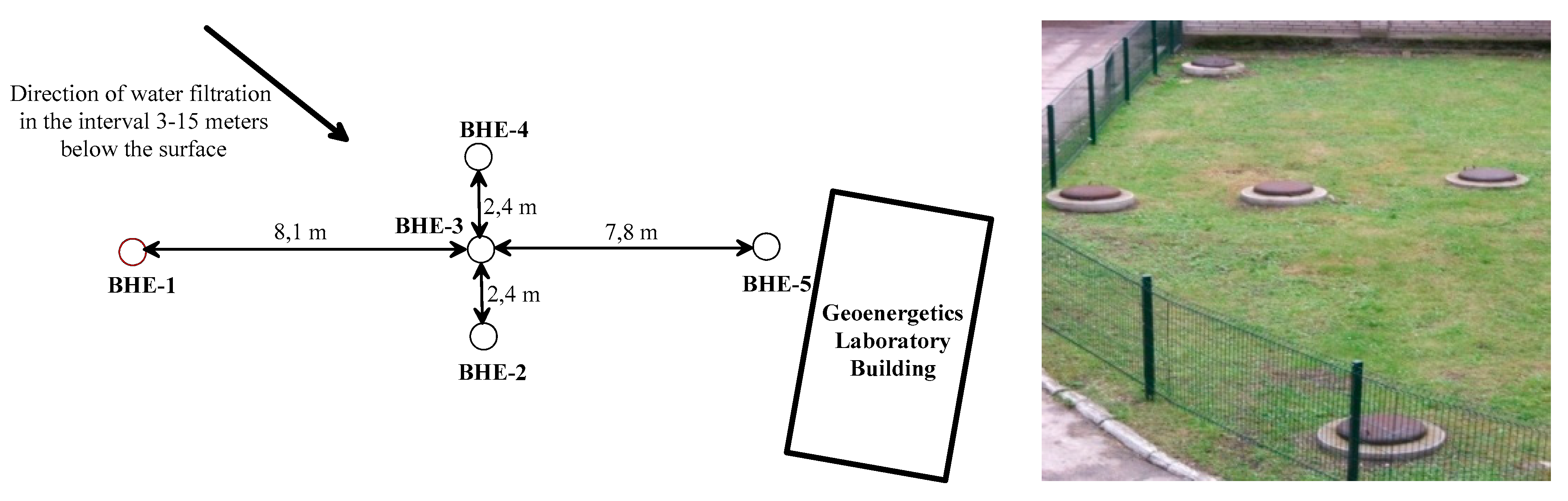




| BHE No. | Characteristics of the BHE Construction | Symbol |
|---|---|---|
| BHE-1 | Depth 76.4 m, coaxial design (pipe in pipe). Outer diameter of the outer pipe equals 90 mm, wall thickness 5.4 mm. Outer diameter of the inner pipe is 40 mm, with wall thickness 2.4 mm | 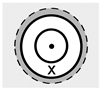 |
| BHE-3 | Depth 76.4 m, design consisting of a single U-tube. Distance between pipe axes equals 80 mm. Outer diameter of the exchanger pipes is 40 mm. Wall thickness 2.4 mm. Heat-improved sealing material (thermocem) with heat conduction λ = 2.0 W/(mK) | 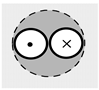 |
| BHE-5 | Depth 76.4 m, system with double U-tube. Distance between the pipe axes is 70 mm. Outer diameter of the pipes equals 32 mm, wall thickness 2.4 mm | 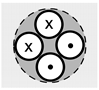 |
| No. of Layer | Top of the Layer, m | Bottom of the Layer, m | Thicness of the Layer, m | Lithology | Stratigraphy | Thermal Conductivity, λ, W⋅m−1K−1 | Volumetric Heat Capacity, cv, MJ⋅m−3K−1 |
|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 2.2 | 2.2 | Anthropogenic soil (dark gray bank with debris) | Quaternary (Pleistocene, Holocene) | 1.600 | 2.000 |
| 2 | 2.2 | 2.6 | 0.4 | Silt (gray soil) | 1.600 | 2.200 | |
| 3 | 2.6 | 4.0 | 1.4 | Fine and dusty sand, slightly argillaceous | 1.000 | 2.000 | |
| 4 | 4.0 | 6.0 | 2.0 | Fine sand | 1.200 | 2.500 | |
| 5 | 6.0 | 15.0 | 9.0 | All-in aggregate and gravel | 1.800 | 2.400 | |
| 6 | 15.0 | 30.0 | 15.0 | Gray loam | Tertiary (Miocene) | 2.200 | 2.300 |
| 7 | 30.0 | 78.0 | 48.0 | Gray shale | 2.100 | 2.300 | |
| Weighted average | 2.039 | 2.309 | |||||
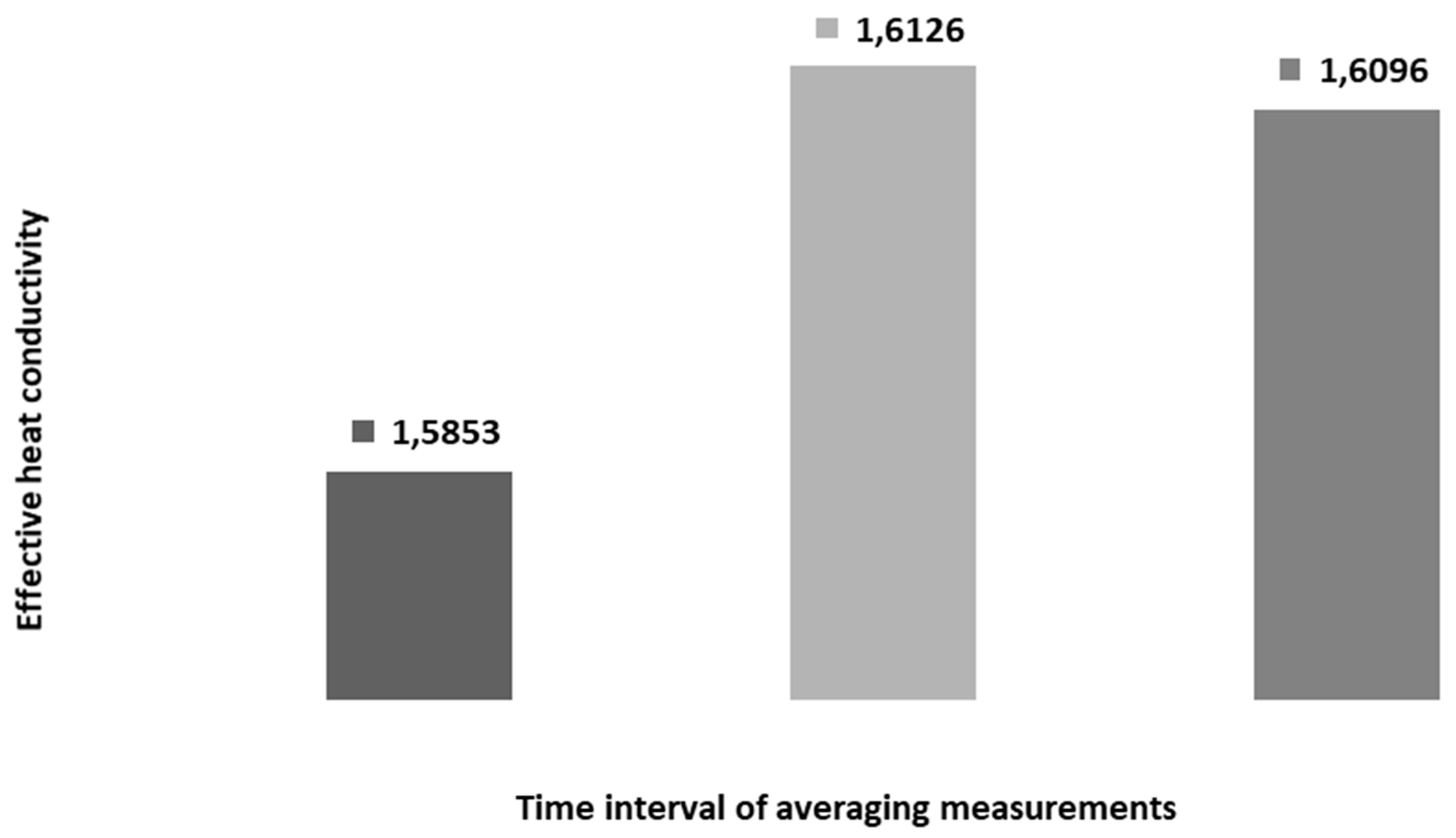
| BHE No. | Value of λeff with Interval of 1 min, Wm−1K−1 | Value of λeff with Interval of 10 min, Wm−1K−1 | Value of λeff with Interval of 1 h, Wm−1K−1 | Volatility * of the λeff Value, Wm−1K−1 |
|---|---|---|---|---|
| BHE-1 | 1.585 | 1.613 | 1.610 | 0.028 |
| BHE-3 | 1.540 | 1.539 | 1.529 | 0.011 |
| BHE-5 | 1.516 | 1.515 | 1.579 | 0.064 |
| BHE No. | Average λeff, Wm−1K−1 | Standard Deviation λeff,Wm−1K−1 | Coefficient of Variation,% |
| BHE-1 | 1.603 | 0.015 | 0.94 |
| BHE-3 | 1.536 | 0.006 | 0.39 |
| BHE-5 | 1.537 | 0.037 | 2.40 |
| Location of the Exchanger | Average Heating Power during TRT, W | Standard Deviation of Heating Power, W | Coefficient of Variation, % | Borehole Depth, m | Average Unit Heating Power, W/m | Slope of the Regression Line in a Semi-Logarithmic Plot |
|---|---|---|---|---|---|---|
| Łódź | 6645 | 127.36 | 1.92 | 120 | 55.38 | 1.8632 |
| Szczecin | 10,008 | 60.24 | 0.60 | 191 | 52.40 | 1.5816 |
| Polkowice | 7800 | 24.52 | 0.31 | 153 | 50.98 | 1.8542 |
| Rawa Mazowiecka | 2509 | 26.03 | 1.04 | 48 | 52.27 | 1.7100 |
| 7009 | 56.61 | 0.81 | 140 | 50.06 | 1.4352 | |
| Kraków I | 7823 | 383.32 | 4.90 | 150 | 52.15 | 1.9694 |
| Wolsztyn | 9523 | 86.99 | 0.91 | 200 | 47.62 | 2.1722 |
| Gola Dzierżoniowska | 7014 | 226.90 | 3.23 | 150 | 46.76 | 1.2513 |
| Żarów | 6000 | 79.97 | 1.33 | 120 | 50.00 | 1.5873 |
| 5997 | 124.74 | 2.08 | 120 | 49.98 | 1.4193 | |
| Białystok | 4390 | 245.75 | 5.60 | 100 | 43.90 | 1.4745 |
| Wrocław | 4072 | 141.12 | 3.47 | 133 | 30.62 | 1.4139 |
| Kraków II | 4813 | 154.05 | 3.20 | 150 | 32.09 | 1.2354 |
| Niepołomice | 4007 | 100.27 | 2.50 | 140 | 28.62 | 0.8564 |
| Kraków III | 8892 | 288.36 | 3.24 | 200 | 44.46 | 1.8384 |
| Location of the Exchanger | Average Heating Power during TRT, W | Standard Deviation of Heating Power, W | Coefficient of Variation, % | Borehole Depth, m | Average Unit Heating Power, W/m | Slope of the Regression Line in a Semi-Logarithmic Plot |
|---|---|---|---|---|---|---|
| Łódź | 6648 | 28.28 | 0.43 | 120 | 55.40 | 1.8463 |
| Szczecin | 10,008 | 14.87 | 0.15 | 191 | 52.40 | 1.4713 |
| Polkowice | 7799 | 38.83 | 0.5 | 153 | 50.97 | 1.8620 |
| Rawa Mazowiecka | 2509 | 12.13 | 0.48 | 48 | 52.27 | 1.4534 |
| 7008 | 24.28 | 0.35 | 140 | 50.06 | 1.8801 | |
| Kraków I | 7824 | 68.32 | 0.87 | 150 | 52.16 | 2.0785 |
| Wolsztyn | 9523 | 54.65 | 0.57 | 200 | 47.62 | 2.134 |
| Gola Dzierżoniowska | 7014 | 39.13 | 0.56 | 150 | 46.76 | 1.2995 |
| Żarów | 6000 | 39.06 | 0.65 | 120 | 50.00 | 1.4714 |
| 5998 | 73.58 | 1.23 | 120 | 49.98 | 1.4543 | |
| Białystok | 4387 | 137.96 | 3.15 | 100 | 43.87 | 1.3974 |
| Wrocław | 4071 | 176.86 | 4.34 | 133 | 30.61 | 1.4834 |
| Kraków II | 4813 | 121.38 | 2.52 | 150 | 32.09 | 1.2582 |
| Niepołomice | 4007 | 158.25 | 3.95 | 140 | 28.62 | 0.8629 |
| Kraków III | 8890 | 273.58 | 3.08 | 200 | 44.45 | 1.9976 |
| Location of the Exchanger | Average Heating Power during TRT, W | Standard Deviation of Heating Power, W | Coefficient of Variation, % | Borehole Depth, m | Average Unit Heating Power, W/m | Slope of the Regression Line in a Semi-Logarithmic Plot |
|---|---|---|---|---|---|---|
| Łódź | 6636 | 106.70 | 1.61 | 120 | 55.30 | 1.8421 |
| Szczecin | 10,009 | 4.01 | 0.04 | 191 | 52.40 | 1.8276 |
| Polkowice | 7800 | 2.18 | 0.03 | 153 | 50.98 | 1.8430 |
| Rawa Mazowiecka | 2508 | 10.42 | 0.42 | 48 | 52.25 | 1.4979 |
| 7009 | 5.38 | 0.08 | 140 | 50.06 | 2.0205 | |
| Kraków I | 7794 | 14.71 | 0.19 | 150 | 51.96 | 2.2584 |
| Wolsztyn | 9523 | 28.45 | 0.30 | 200 | 47.62 | 2.1623 |
| Gola Dzierżoniowska | 7014 | 14.19 | 0.20 | 150 | 46.76 | 1.4956 |
| Żarów | 6000 | 17.29 | 0.29 | 120 | 50.00 | 1.593 |
| 5996 | 33.78 | 0.56 | 120 | 49.97 | 1.4702 | |
| Białystok | 4390 | 99.77 | 2.27 | 100 | 43.90 | 1.3912 |
| Wrocław | 4077 | 227.82 | 5.59 | 133 | 30.65 | 1.484 |
| Kraków II | 4810 | 102.54 | 2.13 | 150 | 32.07 | 1.3227 |
| Niepołomice | 4008 | 130.54 | 3.26 | 140 | 28.63 | 0.9115 |
| Kraków III | 8889 | 242.48 | 2.73 | 200 | 44.45 | 2.0555 |
| BHE Location | Heating Power for an Interval of 1 min, W | Heating Power for an Interval of 10 min, W | Heating Power for an Interval of 60 min, W | Average Heating Power, W | Standard Deviation of Heating Power, W | Coefficient of Variation, % |
|---|---|---|---|---|---|---|
| Łódź | 6645 | 6648 | 6636 | 6643 | 5.10 | 0.077 |
| Szczecin | 10,008 | 10,008 | 10,009 | 1008.33 | 0.47 | 0.005 |
| Polkowice | 7800 | 7799 | 7800 | 7799.67 | 0.47 | 0.006 |
| Rawa Mazowiecka | 2509 | 2509 | 2508 | 2508.67 | 0.47 | 0.019 |
| 7009 | 7008 | 7009 | 7008.67 | 0.47 | 0.007 | |
| Kraków I | 7823 | 7824 | 7794 | 7813.67 | 13.91 | 0.178 |
| Wolsztyn | 9523 | 9523 | 9523 | 9523 | 0.00 | 0.000 |
| Gola Dzierżoniowska | 7014 | 7014 | 7014 | 7014 | 0.00 | 0.000 |
| Żarów | 6000 | 6000 | 6000 | 6000 | 0.00 | 0.000 |
| 5997 | 5998 | 5996 | 5997 | 0.82 | 0.014 | |
| Białystok | 4390 | 4387 | 4390 | 4389 | 1.41 | 0.032 |
| Wrocław | 4072 | 4071 | 4077 | 4073.33 | 2.62 | 0.064 |
| Kraków II | 4813 | 4813 | 4810 | 4812 | 1.41 | 0.029 |
| Niepołomice | 3998 | 4007 | 4008 | 4007.33 | 0.47 | 0.012 |
| Kraków III | 8892 | 8890 | 8889 | 8890.33 | 1.25 | 0.014 |
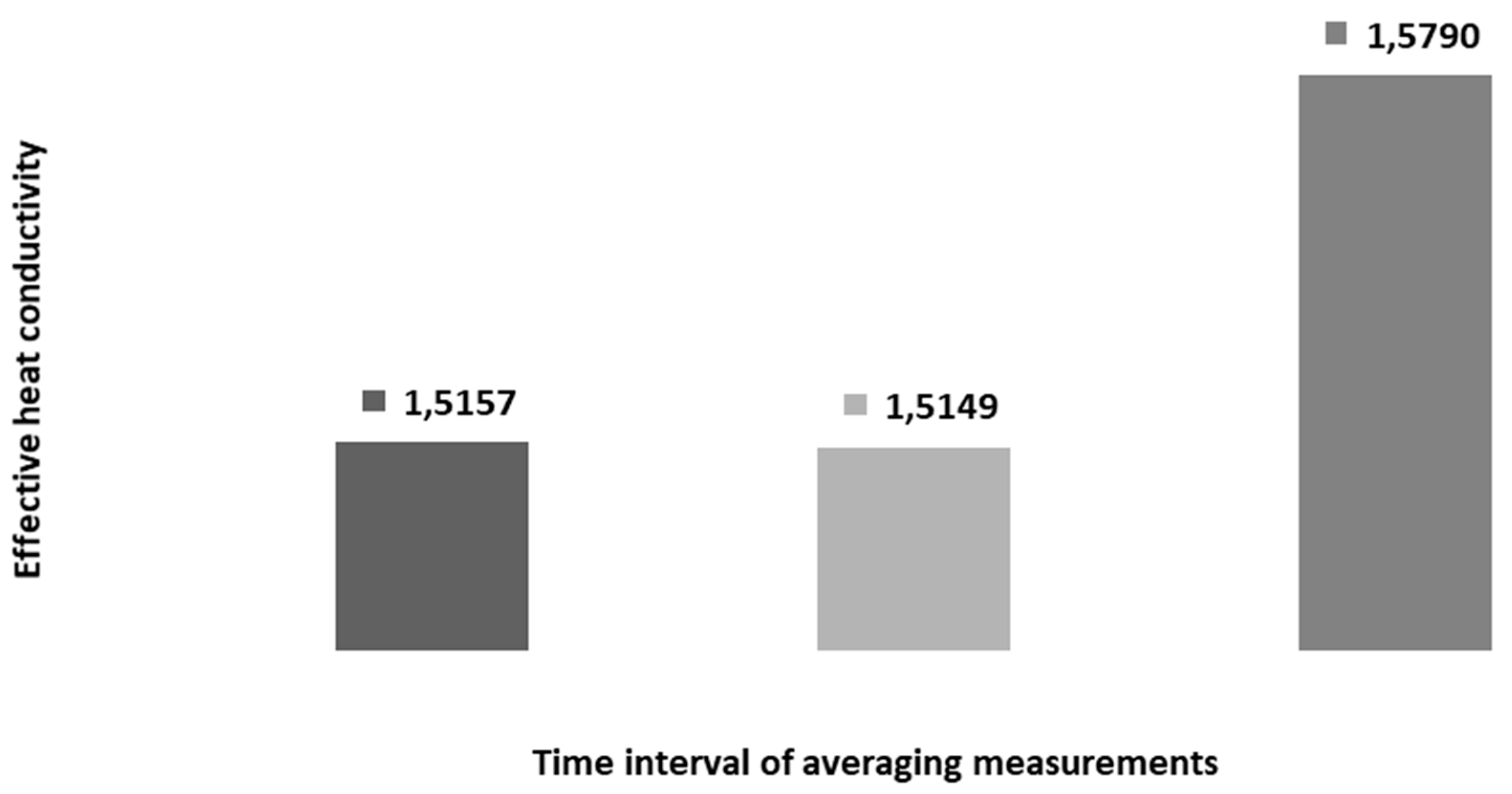
| BHE Location | BHE Design | λeff for an Interval of 1 min, Wm−1K−1 | λeff for an Interval of 10 min, Wm−1K−1 | λeff for an Interval of 60 min, Wm−1K−1 | Average λeff, Wm−1K−1 | Standard Deviation of λeff, Wm−1K−1 | Coefficient of Varition, % |
|---|---|---|---|---|---|---|---|
| Łódź | 2-U-tube | 2.37 | 2.39 | 2.39 | 2.38 | 0.010 | 0.42 |
| Szczecin | 1-U-tube | 2.63 | 2.83 | 2.28 | 2.58 | 0.230 | 8.91 |
| Polkowice | 1-U-tube | 2.19 | 2.18 | 2.20 | 2.19 | 0.010 | 0.46 |
| Rawa Mazowiecka | 1-U-tube | 2.33 | 2.12 | 1.97 | 2.14 | 0.150 | 7.01 |
| 1-U-tube | 2.90 | 2.86 | 2.77 | 2.84 | 0.050 | 1.76 | |
| Kraków I | 1-U-tube | 2.11 | 2.00 | 1.83 | 1.98 | 0.120 | 6.06 |
| Wolsztyn | 1-U-tube | 1.74 | 1.78 | 1.75 | 1.76 | 0.020 | 1.14 |
| Gola Dzierżoniowska | 1-U-tube | 2.97 | 2.86 | 2.50 | 2.78 | 0.200 | 7.19 |
| Żarów | 1-U-tube | 2.50 | 2.70 | 2.50 | 2.57 | 0.090 | 3.50 |
| 1-U-tube | 2.80 | 2.74 | 2.70 | 2.75 | 0.040 | 1.45 | |
| Białystok | 1-U-tube | 2.53 | 2.50 | 2.39 | 2.47 | 0.060 | 2.43 |
| Wrocław | 1-U-tube | 1.72 | 1.64 | 1.64 | 1.67 | 0.040 | 2.40 |
| Kraków II | 2-U-tube | 2.07 | 2.03 | 1.93 | 2.01 | 0.060 | 2.99 |
| Niepołomice | 1-U-tube | 2.66 | 2.64 | 2.50 | 2.60 | 0.070 | 2.69 |
| Kraków III | 2-U-tube | 1.92 | 1.77 | 1.72 | 1.80 | 0.080 | 4.44 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapińska-Śliwa, A.; Sliwa, T.; Twardowski, K.; Szymski, K.; Gonet, A.; Żuk, P. Method of Averaging the Effective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers. Energies 2020, 13, 3737. https://doi.org/10.3390/en13143737
Sapińska-Śliwa A, Sliwa T, Twardowski K, Szymski K, Gonet A, Żuk P. Method of Averaging the Effective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers. Energies. 2020; 13(14):3737. https://doi.org/10.3390/en13143737
Chicago/Turabian StyleSapińska-Śliwa, Aneta, Tomasz Sliwa, Kazimierz Twardowski, Krzysztof Szymski, Andrzej Gonet, and Paweł Żuk. 2020. "Method of Averaging the Effective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers" Energies 13, no. 14: 3737. https://doi.org/10.3390/en13143737
APA StyleSapińska-Śliwa, A., Sliwa, T., Twardowski, K., Szymski, K., Gonet, A., & Żuk, P. (2020). Method of Averaging the Effective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers. Energies, 13(14), 3737. https://doi.org/10.3390/en13143737






