Effects of Inflow Shear on Wake Characteristics of Wind-Turbines over Flat Terrain

Abstract

The scope of the present study was to understand the wake characteristics of wind-turbines under various inflow shears. First, in order to verify the prediction accuracy of the in-house large-eddy simulation (LES) solver, called RIAM-COMPACT, based on a Cartesian staggered grid, we conducted a wind-tunnel experiment using a wind-turbine scale model and compared the numerical and experimental results. The total number of grid points in the computational domain was about 235 million. Parallel computation based on a hybrid LES/actuator line (AL) model approach was performed with a new SX-Aurora TSUBASA vector supercomputer. The comparison between wind-tunnel experiment and high-resolution LES results showed that the AL model implemented in the in-house LES solver in this study could accurately reproduce both performances of the wind-turbine scale model and flow characteristics in the wake region. Next, with the LES solver developed in-house, flow past the entire wind-turbine, including the nacelle and the tower, was simulated for a tip-speed ratio (TSR) of 4, the optimal TSR. Three types of inflow shear, N = 4, N = 10, and uniform flow, were set at the inflow boundary. In these calculations, the calculation domain in the streamwise direction was very long, 30.0 D (D being the wind-turbine rotor diameter) from the center of the wind-turbine hub. Long-term integration of t = 0 to 400 R/U_in was performed. Various turbulence statistics were calculated at t = 200 to 400 R/U_in. Here, R is the wind-turbine rotor radius, and U_in is the wind speed at the hub-center height. On the basis of the obtained results, we numerically investigated the effects of inflow shear on the wake characteristics of wind-turbines over a flat terrain. Focusing on the center of the wind-turbine hub, all results showed almost the same behavior regardless of the difference in the three types of inflow shear.

1. Introduction

Offshore-located wind-turbines are always clustered in wind farms to limit overall installation and maintenance expenses. Today, the potential offshore market is also the main driver for the development of large wind-turbines. As shown in Figure 1, with the rotation of the blade of the wind-turbine, a region of wind-velocity deficit with temporal and spatial variations is formed downstream of the wind-turbine. This flow phenomenon is called wind-turbine wake. Wind-turbines in offshore wind farms operating in downwind wake flow are subjected to two main problems. One is decreased energy production due to the wind-velocity deficit, and the other is increased fatigue loading due to the added turbulence intensity generated by the upwind turbine. The mutual interference of wind-turbine wake, which is a strongly nonlinear flow phenomenon, occurs especially in large offshore wind farms consisting of multiple wind-turbine groups. The mutual interference of wind-turbine wakes is an essential and inherent problem in offshore wind farms. Therefore, in order to improve the power efficiency and lifetime of a wind-turbine, an accurate understanding of wake effects due to the mutual interaction between the wakes of the wind-turbines is extremely important [1,2,3,4,5,6,7,8,9,10,11,12,13,14].

For accurate evaluation of wind-turbine wake flows, field measurements and wind-tunnel experiments using a scale model are currently problematic. Therefore, engineering wake models (empirical/analytical wake models represented by Jensen [15]/Katic [16]), computational fluid dynamics (CFD) with the wake model using an actuator disk (AD) model [17], the actuator disk model with rotation (ADM-R) [18], actuator line (AL) model [19], actuator surface (AS) model [20], and numerical investigations based on fully resolved geometries combined with CFD simulations [21] are generally used.

In this study, we focused on the incoming flow conditions of a wind-turbine (two sheared and one uniform inflow) and examined the effects of inflow shear on the wake characteristics of wind-turbines over flat terrain. The effect of mean shear in conjunction with other effects (atmospheric stratification or turbulence intensity) on wind-turbine-wake recovery has been investigated. The effect of shear alone on wind-turbine wake recovery has not been investigated. For this purpose, the approach of CFD by large-eddy simulation (LES) was adopted. In this study, we constructed an in-house LES solver called RIAM-COMPACT [22,23,24,25,26,27] based on the Cartesian staggered grid. In this study, we adopted the AL model for the rotation of wind-turbine blades as a method in which numerical simulations for multiple wind-turbines are relatively easy.

The scope of the present study is to understand the wake characteristics of wind-turbines, under various inflow shears. First, in order to verify the prediction accuracy of the in-house LES solver based on a Cartesian staggered grid, RIAM-COMPACT, we conducted a wind-tunnel experiment using a wind-turbine scale model, and compared the numerical and experiment results. Next, with the developed in-house LES solver, flow past the entire wind-turbine (isolated wind-turbine), including the nacelle and the tower, was simulated for a tip speed ratio of 4, the optimal tip-speed ratio (TSR). On the basis of the obtained results, we numerically investigated the effects of inflow shear on the wake characteristics of wind-turbines over a flat terrain.

2. Wind-Tunnel Experiment Using Wind-Turbine Scale Model and Verification of Prediction Accuracy of In-House LES Solver

2.1. Overview of the Wind-Tunnel Experiment Using Wind-Turbine Scale Model

First, a wind-tunnel experiment using a wind-turbine scale model was conducted to verify the prediction accuracy of RIAM-COMPACT, the in-house LES solver based on a Cartesian staggered grid. The wind-tunnel facility used in this study is a boundary layer wind tunnel (15 m long × 3.6 m wide × 2.0 m high) owned by the Research Institute for Applied Mechanics (RIAM) of Kyushu University, as shown in Figure 2.

The small-scale wind-turbine model manufactured in this study is shown in Figure 3. The blades of the small-scale wind-turbine model were Mechanical Engineering Laboratory airfoils [28] with increased thickness. As shown in Figure 3, in the wind-tunnel experiment, only the blade portion of the wind-turbine was targeted for the scale model. To avoid the blockage effect, the side walls and ceiling of the wind tunnel were removed. As shown in Figure 4, inflow wind velocity U_in was set to 8 m/s in the wind-tunnel experiment. The optimal tip speed ratio (TSR = 4.0, about 610 rpm), at which power coefficient Cp of the wind-turbine scale model had the maximal value, was estimated by rotating the wind-turbine blades at multiple rotation speeds. Figure 5 shows the relationship between the TSR and Cp obtained by the TSR. Reynolds number Re = U_in D/ν defined with rotor diameter D = 1 m as the representative length was in the order of 10⁵. After that, the blades of the wind-turbine scale model were rotated at optimal TSR = 4.0 (about 610 rpm), and the I-type hot-wire anemometer was horizontally traversed at the position of x = 0.5 D in the near-wake region, and the time-series data of wind velocity in the streamwise direction (U-velocity) were acquired (see also Figure 6). The sampling frequency for flow measurement was 500 Hz, and the sampling time was 30 s. Therefore, the total number of units of data was 15,000. Time-averaged U-velocity was evaluated on the basis of these datasets.

2.2. Overview of LES-Based CFD Approach

The calculation by the in-house LES solver for a wind-turbine scale model (rotor diameter D = 1 m) was performed with optimal TSR = 4.0, as estimated in the wind-tunnel experiment. The in-house LES solver consisted of three-dimensional, unsteady, incompressible, filtered continuity, and Navier–Stokes equations in Cartesian co-ordinates. These governing equations were discretized by a finite-difference method (FDM). A mixed-time-scale (MTS) model [29] was used for the subgrid scale (SGS) model of LES. In this study, we adopted the AL model for the rotation of wind-turbine blades as a method in which numerical simulations for multiple wind-turbines are relatively easy. In the AL model approach, tangential and thrust forces generated by the rotating blade are added to Navier–Stokes equations as external terms that represent reaction forces exerted on the fluid in the direction of the streamwise flow and rotation. In the present study, because a Cartesian grid system was adopted, the component of the force in the direction of rotation is decomposed into the spanwise and vertical directions. In addition to the investigation of the decelerating effect of the wind-turbine simply as a drag-inducing body, the adopted AL model allowed the investigation of the effect of blade rotation on flow, which is considered a major benefit of the adopted modeling approach. Furthermore, the model was designed so that it allowed the user to simulate wind-turbine wake flows of various wind-turbines, by inputting only the dataset of the blade chord length, lift coefficient, drag coefficient, and angle of attack as a function of the distance from the center of the rotor.

2.3. Results and Discussion

Figure 5 shows that power coefficient Cp at the TSR = 2.0, 3.0, 4.0, and 5.0 obtained by numerical calculation was almost the same as that in the wind-tunnel experiment. From the comparison between the wind-tunnel experiment and LES results, it was shown that the AL model implemented in the in-house LES solver in this study could accurately reproduce the performance of the wind-turbine scale model.

Figure 6 shows the computational grid in the numerical simulation for the wind-tunnel experiment using a wind-turbine scale model. The total number of grid points in the computational domain was about 235 million (2021 (x) × 341 (y) × 341 (z), x+ = y+ = z+ < 5.0 behind the wind-turbine model). To recreate the conditions of the wind-tunnel experiments in the numerical simulations, configurations of the hub and support connected to the hub were reconstructed with a rectangular-grid approximation (Figure 6). In order to model the rotation of the wind-turbine blades, an actuator line (AL) model based on blade-element theory was applied. Wind velocity was set to zero at all grid points on the surface and in the interior of the hub and the support connected to the hub (see part indicated by A in Figure 6). Here, the motor part was not simulated. The time step was Δt = 5 × 10⁻⁴ (R/U_in). In this calculation, time integration from t = 0 to 65 (R/U_in) was performed. Various turbulence statistics were calculated at t = 32.5–65 (R/U_in).

Figure 7 shows spatial distribution of the instantaneous U-velocity and corresponding vorticity. Focusing on the top view shown in Figure 7a, the formation of a tip vortex could clearly be observed near the tip of the wind-turbine blade until x = 4.0 D in the near-wake region. The tip vortex gradually collapsed in the far-wake region after x = 4.0 D. As a result, a meandering motion was confirmed in the turbine wake flows. Next, the rear view in Figure 7b–g shows concentric wake flows that were formed with the formation of the tip vortex up to x = 4.0 D in the near-wake region. The region locally shown in red, that is, the region where the speed was locally increased, corresponded to the position of the blade tip of the wind-turbine. On the other hand, in the far-wake region beyond x = 4.0 D, concentric wake flows were greatly deformed due to the collapse of the tip vortex.

Figure 8 shows a comparison of the time variation of instantaneous U-velocity at measurement points (x = 0.5 D and y = 0.5 D) indicated by symbols in Figure 6. Both the horizontal and the vertical axis were normalized by radius R of the wind-turbine blade and the inflow wind velocity U_in. The results of the wind-tunnel experiment, in red, show that, since the position where the time-series data were acquired was x = 0.5 D in the near-wake region, clear periodic fluctuation was confirmed with the formation and passage of the tip vortex. It was confirmed that the LES results, in blue, showed good reproduction of the wind-tunnel experiment results shown in red. Specifically, the periodical shedding period of the tip vortex and the amplitude of the waveform showing its strength were qualitatively and quantitatively well-matched. This result showed that the AL model implemented in the in-house LES solver in this study could accurately reproduce the performance of the wind-turbine scale model.

Figure 9 shows the spatial distribution of time-averaged U-velocity corresponding to Figure 7. Looking at the top view shown in Figure 9a, we can see that the tip vortex disappeared from the near- to the far-wake region. Similarly, in the rear views shown in Figure 7b–g, none of the velocity distributions show a region of local acceleration associated with the formation of the tip vortex. In particular, at x = 6.0 D shown in Figure 9f and x = 8.0 D shown in Figure 9g, the wake flow was greatly deformed in the instantaneous flow field shown in Figure 7. However, it was observed that concentric wake regions were formed in the time-averaged flow field. From these visualization results shown in Figure 9a–g, it was confirmed that the wake–expansion rate was relatively small. Wake width is almost constant in the near- and far-wake regions. In other words, there was almost no spreading of the wake. In this study, we also examined the effect of the region size on the wake width (see Appendix B).

Figure 10 shows velocity vectors for the time-averaged flow fields at x = 0.5 D. The displayed position is on the measurement line at x = 0.5 D, described in Figure 6. The area of particular interest is the part surrounded by the dotted line in Figure 10. A large velocity shear occurred in this region due to the formation of the tip vortex and periodical shedding. Figure 11a shows a graph comparing the time-averaged U-velocity values of the velocity vector on the measurement line shown in Figure 10 with the results of the wind-tunnel experiment. The LES results in blue show good reproduction of the wind-tunnel experiment results shown in red. In particular, paying attention to the area shown by the dotted line in Figure 11a of the wind-tunnel experiment shown in red, the inflow wind speed was reduced by about 30%. This was due to the formation of the tip vortex and its periodical shedding. The LES results succeeded in reproducing the same amount of velocity deficit as that in the wind-tunnel experiment in the near-wake region. Figure 11b shows the distribution of nondimensional streamwise standard deviation corresponding to Figure 11a for the LES results in the near-wake region. In the area of the dotted line, the distribution of nondimensional streamwise standard deviation was remarkably large. Even in the far-wake region at x = 8.0 D shown in Figure 11c, it was shown that the numerical simulation results reproduce well the results of the wind-tunnel experiment. Even in the distribution of nondimensional streamwise standard deviation shown in Figure 11d corresponding to Figure 11c, a large value is clearly present near the tip of the wind-turbine blade due to the generation and collapse of the tip vortex (see the area of the dotted line).

As mentioned above, the AL model implemented in the in-house LES solver in this study showed that the results of wind-tunnel experiments using a wind-turbine scale model could be reproduced both qualitatively and quantitatively in the near- and far-wake region. As a result, we were able to verify the prediction accuracy of the in-house LES solver. The core technology of the in-house LES solver has already verified the prediction accuracy by comparing it with high-order turbulence statistics in atmospheric stable and unstable boundary layers with wind tunnel experiments [30,31]. In addition, the Reynolds-averaged Navier–Stokes (RANS) modeling results and the present LES results were compared in the latest findings [24,32], and the prediction accuracy of the present LES approach by comparison with wind tunnel experiments was discussed [23].

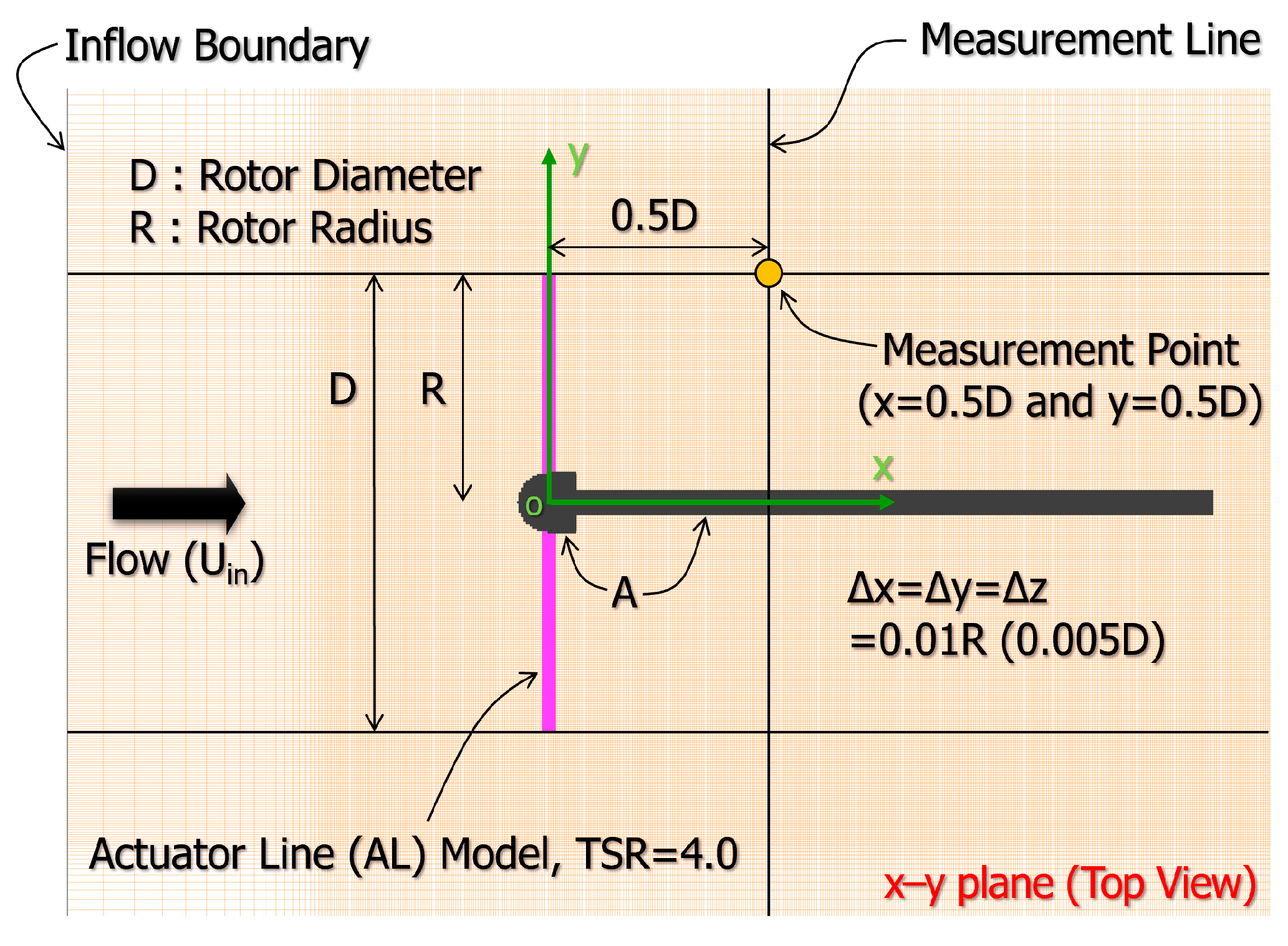
3. Effects of Inflow Shear on Wake Characteristics of Wind-Turbines over Flat Terrain

Here, as shown in Figure 12 and Figure 13, various inflow shears were assumed at the inflow boundary surface, and we conducted wind-turbine wake simulations installed on a flat terrain. On the basis of the obtained results, the effect of inflow shear on the flow characteristics in the wind-turbine wake region was considered. Similar to the calculation shown in Section 2, the wind-turbine blades were rotated at the optimal TSR = 4.0, at which the power coefficient Cp showed the maximum value. In order to reproduce the shape of the nacelle and tower, the spatial grid resolution in the vicinity of the wind-turbine was set to Δx = Δy = Δz = 0.005 D (x+ = y+ = z+ < 10.0). Here, D is the diameter of the wind-turbine blade. In order to eliminate the influence of the spatial-grid resolution on the reproduction accuracy of the wind-turbine wake as much as possible, the spatial-grid resolutions in the x direction were all the same downstream of the wind-turbine, and Δx = 0.01 D. The total number of grid points in the entire computational domain was about 85 million (3075 (x) × 171 (y) × 161 (z)). In particular, we focused on reproducing the generation and collapse of tip vortex, and set the spatial resolution in the streamwise direction (see Appendix C). The boundary conditions of velocity at the other boundaries except for the inflow boundary surface were as shown below. Slip conditions were imposed on the upper- and lateral-boundary surfaces. No-slip conditions were applied on the ground, and convection-type outflow conditions were applied on the outflow boundary surface. Boundary conditions for pressure were Neumann conditions on all boundary surfaces. Other conditions were the same as those in the calculation in Section 2. The time step was Δt = 1 × 10⁻³ R/U_in. In this calculation, the calculation domain in the x direction was very long, 30.0 D; thus, a long-term integration of t = 0 to 400 R/U_in was performed. Various turbulence statistics were calculated at t = 200 to 400 R/U_in. In this study, the some calculations were performed by changing the domain size, and its effect was also examined (see Appendix B). The calculations in this study were performed using a new SX-Aurora TSUBASA vector supercomputer. The CPU time required for each calculation is about several days.

Figure 14 shows spatial distribution of instantaneous U-velocity in the mid-span plane (side view) at t = 400 R/U_in. In all cases of N = 4 shown in Figure 14a, N = 10 shown in Figure 14b, and uniform flow shown in Figure 14c, periodic shedding of the tip vortex was clearly observed in the near-wake region of x = 5.0 D. In all cases, a vertical meandering motion of the wind-turbine wake occurred from around x = 6.0 D. After that, in the far-wake region where x = 10.0 D, the amount of change in vertical meandering motion was even larger. We can see the entrainment of ambient fluid into the wake-flow region. In other words, the rapid mixing and exchange of fluid volumes across the wake edge occurred.

Figure 15 shows the time variation of the three velocity components at the N = 4 measurement points (x = 0.5 D and z = 0.5 D, x = 30.0 D and z = 0.5 D) shown in Figure 14a (the mid-span plane and at the top-tip height). The current paper imposes inflow condition with no turbulent fluctuations. Therefore, at x = 0.5 D in the near-wake region shown in Figure 15a, a waveform that reflected the behavior of the tip vortex that was periodically formed and shed was clearly observed, as described above. On the other hand, at x = 30.0 D in the far-wake region shown in Figure 15b, it could be seen that the three velocity components greatly fluctuated, reflecting the vertical meandering motion. We considered that the mechanism by which the periodic shedding of the tip vortex formed from the tip of the wind-turbine blade collapsed, due to the instability of the strong velocity shear in the distance of the wind turbine, and the vertical meandering motion in the far-wake region subsequently formed. Due to the inflow condition with no turbulent fluctuations, the periodic generation and shedding of tip vortex and the subsequent collapse of tip vortex caused by shear instability directly affect the meandering motion in the far-wake region [12,13].

Figure 16 shows the spatial distribution of U-velocity in the mid-span plane (side view) for the time-averaged field calculated at t = 200–400 R/U_in. First, as expected, the periodic shedding of the tip vortex observed in Figure 14 disappeared with temporal averaging. On the other hand, it was clear that the decay of the wake velocity deficit in the far-wake region behind a wind-turbine clearly existed, even 30 times downstream of the diameter of the wind-turbine. The wind velocity deficit near the hub center was almost the same in all cases regardless of difference in inflow shear.

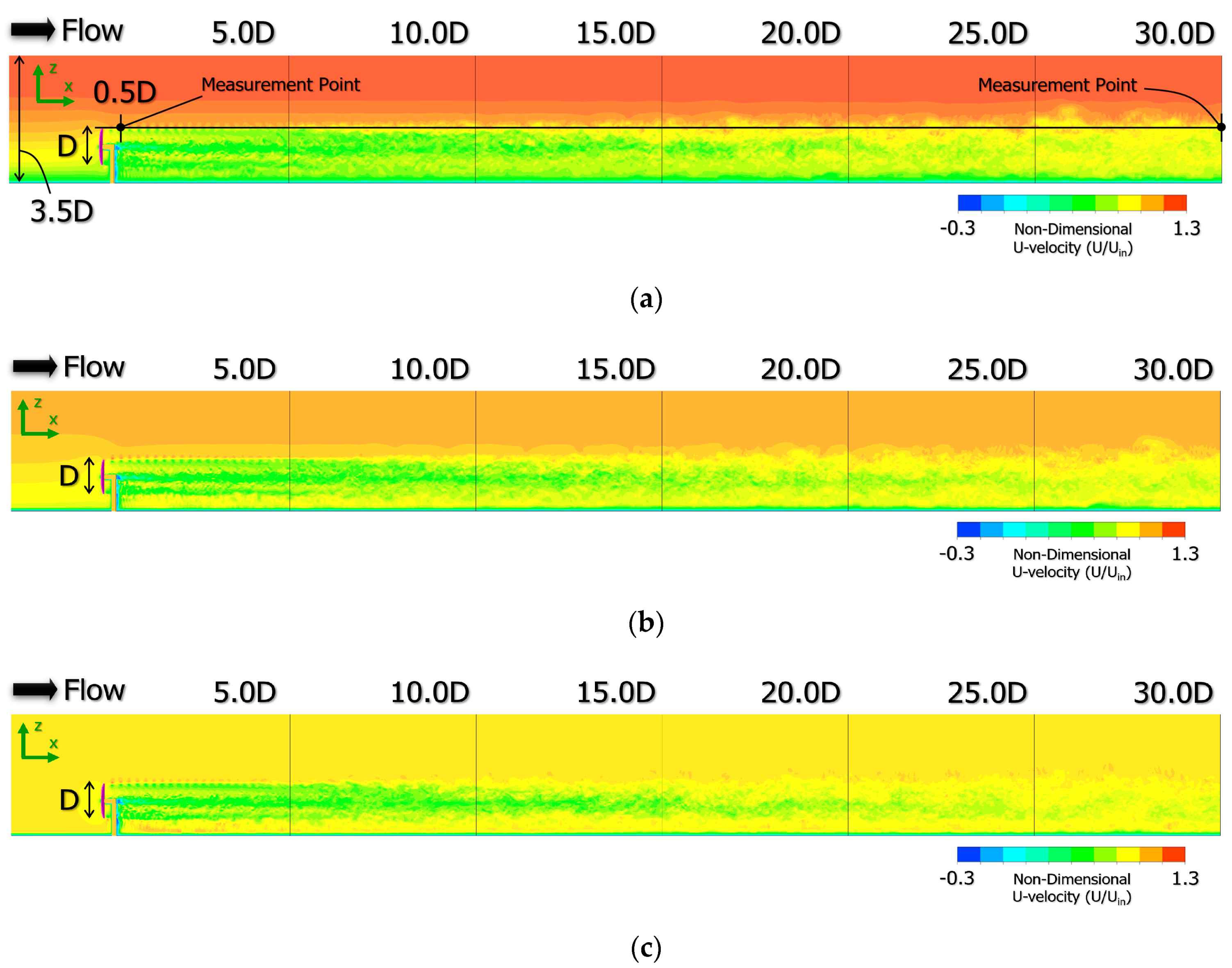
Figure 17 shows the spatial distribution of U-velocity in the y–z plane (front view) at x = 5.0 D to 30.0 D for the instantaneous flow field of t = 400 R/U_in. In all cases of N = 4 shown in Figure 17a, N = 10 shown in Figure 17b, and uniform flow shown in Figure 17c, an almost concentric wake region was formed behind the wind-turbine in the near-wake region with x = 5.0 D. In the far-wake region of x ≥ 10.0 D, the concentric wake region was greatly deformed with the occurrence of the vertical meandering motion. In the visualization result (Figure 18) for the time-averaged flow field corresponding to Figure 17, the distortion of wake flows in the far-wake region with x ≥ 10.0 D also clearly existed. As described above, Figure 18 also shows that the wind velocity deficit near the hub center of the wind-turbine was almost the same in all cases, regardless of the difference in inflow shear.

Figure 19 shows the spatial distribution of nondimensional streamwise standard deviation in the y–z plane (front view) at x = 5.0 D to 30.0 D. Regardless of the difference in velocity shear, spatial distribution was almost the same at each x coordinate position. We also examined the spatial distribution of turbulence kinetic energy (TKE) corresponding to Figure 19. The results are shown in Appendix E. In Figure 19 and Figure 20, the discernible difference in the flow fields depending on the sheared and uniform inflow conditions could not be observed clearly.

Figure 20 shows a comparison of vertical distribution of time-averaged U-velocity at x = 5.0 D and 30.0 D. It is very interesting that, regardless of difference in inflow shear, the vertical distribution of time-averaged U-velocity showed almost the same tendency in the entire swept area of the wind-turbine at both x = 5.0 D and 30.0 D. At x = 5.0 D in the near-wake region shown in Figure 20a, a large velocity shear occurred at z/R = 1 in all cases, as described above. The time-averaged U-velocity exhibited sharp corners below the swept area (especially in the case of the uniform flow). This means that the flow here is locally accelerated. We performed additional calculations using very fine grid, and investigated the reason for this flow phenomenon. The results are shown in Appendix D. On the other hand, at x = 30.0 D in the far-wake region shown in Figure 20b, an approximately conical wake profile was formed in all cases of N = 4, N = 10, and uniform flow. We arranged the vertical distribution of time-averaged U-velocity for every three cases of N = 4, N = 10, and uniform flow. The results are shown in Appendix A.

Figure 21 shows the comparison of vertical distribution of nondimensional streamwise standard deviation at x = 5.0 and 30.0 D, corresponding to Figure 20. At x = 5.0 D in the near-wake region shown in Figure 21a, almost the same numerical values were shown in the entire swept area of the wind-turbine, regardless of the difference in speed shear. At the top position of the wind-turbine blade, z/R = 1, and at the bottom position of the wind-turbine blade, z/R = −1, maximal values are clearly shown. The maxima at these two locations are due to the passage of the periodically formed tip vortex. On the other hand, the differences within the swept area for different values of shear are significant at x = 30.0 D (see dotted line in Figure 21b).

Figure 22 shows a comparison of time-averaged U-velocity distribution at the hub center of the wind-turbine. As described above, time-averaged U-velocity distribution at the hub center of the wind-turbine behaved in almost the same way in all three cases, regardless of differences in inflow shear. In all three cases, the wake velocity deficit in the far-wake region behind a wind-turbine gradually and linearly recovered with x, and its recovery rate was very small. As shown by the orange dotted line in the figure, the recovery rate changed in the far-wake region of x ≥ 12.0 D. This was thought to be due to the occurrence of vertical meandering motion in the far-wake region and the increase in vertical fluctuation. In all cases, 10% velocity deficit was clearly present even in the far-wake region of x = 30.0 D, as shown in the figure.

Figure 23 shows a comparison of nondimensional standard deviation distribution at the hub center of the wind-turbine, corresponding to Figure 22. Similar to Figure 22, the nondimensional standard deviation distribution at the hub center of the wind-turbine showed almost the same values in all cases of Figure 23a–c, regardless of difference in inflow shear. Furthermore, as in Figure 23, the slope at which the nondimensional standard deviation decayed changed in the far-wake region of x ≥ 12.0 D. As shown in the figure, the numerical value at x = 30.0 D in the far-wake region gradually decreased in the order of the (a) streamwise, (b) spanwise, and (c) vertical directions. There are some points to note here. As shown in Figure 21b, in the far-wake region, there is a significant difference in standard deviation, especially in the upper part of the swept area, due to the influence of inflow shear.

4. Conclusions

The scope of the present study was to understand the wake characteristics of wind-turbines under various inflow shears. First, in order to verify the prediction accuracy of RIAM-COMPACT, the in-house LES solver based on a Cartesian staggered grid, we conducted a wind-tunnel experiment using a wind-turbine scale model and compared the numerical and experimental results. The total number of grid points in the computational domain was about 235 million. Parallel computation based on a hybrid LES/AL model approach was performed with a new SX-Aurora TSUBASA vector supercomputer. From the comparison between the wind-tunnel experiment and the high-resolution LES results, the AL model that was implemented in the in-house LES solver in this study could accurately reproduce both the performance of the wind-turbine scale model and the flow characteristics in the wake region.

Next, using the LES solver developed in-house, the flow past the entire wind-turbine, including the nacelle and the tower, was simulated for a tip speed ratio of 4, the optimal TSR with a new SX-Aurora TSUBASA vector supercomputer. Three types of inflow shear, namely, N = 4, N = 10, and uniform flow, were set at the inflow boundary. In these calculations, the calculation domain in the streamwise direction was very long, 30.0 D (D being the wind-turbine rotor diameter) from the center of the wind-turbine hub. Therefore, long-term integration of t = 0 to 400 R/U_in was performed. Various turbulence statistics were calculated at t = 200 to 400 R/U_in. Here, R is the wind-turbine rotor radius, and U_in is the wind speed at the hub center height. On the basis of the obtained results, we numerically investigated the effects of inflow shear on the wake characteristics of wind-turbines over a flat terrain.

Focusing on the center of the wind-turbine hub, all results showed almost the same behavior regardless of difference in the three types of inflow shear. In all cases, 10% velocity deficit was clearly present even in the far-wake region of x = 30.0 D. The nondimensional standard deviation distribution at the hub center of the wind-turbine showed almost the same values in all cases, regardless of difference in inflow shear. Furthermore, the slope at which the nondimensional standard deviation decayed changed in the far-wake region of x ≥ 12.0 D. The numerical value at x = 30.0 D in the far-wake region gradually decreased in the order of the (a) streamwise, (b) spanwise, and (c) vertical directions.

Through the comparison of vertical distribution of time-averaged U-velocity at x = 5.0 D and 30.0 D, we obtained the following findings. It is very interesting that, regardless of difference in inflow shear, the vertical distribution of time-averaged U-velocity showed almost the same tendency in the entire swept area of the wind-turbine at both x = 5.0 D and 30.0 D. At x = 5.0 D in the near-wake region, a large velocity shear occurred at z/R = 1 in all cases. On the other hand, at x = 30.0 D in the far-wake region, an approximately conical wake profile was formed in all cases of N = 4, N = 10, and uniform flow.

Regarding the comparison of vertical distribution of nondimensional streamwise standard deviation at x = 5.0 and 30.0 D, the following findings were obtained. At x = 5.0 D in the near-wake region, almost the same numerical values were shown in the entire swept area of the wind-turbine, regardless of the difference in speed shear. At the top position of the wind-turbine blade and at the bottom position of the wind-turbine blade, maximal values are clearly shown. The maxima at these two locations are due to the passage of the periodically formed tip vortex. On the other hand, the differences within the swept area for different values of shear are significant at x = 30.0 D.