Automated Data Filtering Approach for ANN Modeling of Distributed Energy Systems: Exploring the Application of Machine Learning
Abstract
:1. Introduction
- How can machine-learning techniques help the automated processing of a large amount of operational data in a real-time fashion?
- Can the dataset obtained from an automated data-filtering method be error-free and used to develop reliable predictive models with high prediction accuracy?
- How can an interdisciplinary approach with a combination of domain knowledge from energy systems and computer science pave the way for the successful implementation of this smart solution in energy systems?
- In contrast to previous studies, where the manual and demanding data-filtering method was used, this research has proposed an automated data processing that has the capability to filter large amounts of data from outliers in a real-time fashion, providing error-free datasets for data-driven predictive models.
- A machine-learning-based data clustering method, DBSCAN, has been employed to identify the outliers in the raw dataset obtained from the MGT test rig. The filtered datasets were used to train and further test the ANN models. It should be noted that, for a comparative performance assessment between the manual and automated filtering methods, the optimum ANN setup, as it was used in [16], was identically considered in the present study.
- The present investigation has brought together researchers from energy systems, AI and data science to realize the potential of interdisciplinary research, contributing in a smart and reliable automated data-filtering tool that can work in real-time applications. This approach bridges the current knowledge gaps mainly caused by narrow focusing on a certain field of competence rather than an interdisciplinary approach that combines the strengths of different disciplines to solve real-world problems.
- The benefits of the proposed methodology have been demonstrated using available real-life data that allowed the validation of the developed tool to a level that could be suitable for real-life implementations not only in MGT applications but, also, in other types of DG systems.
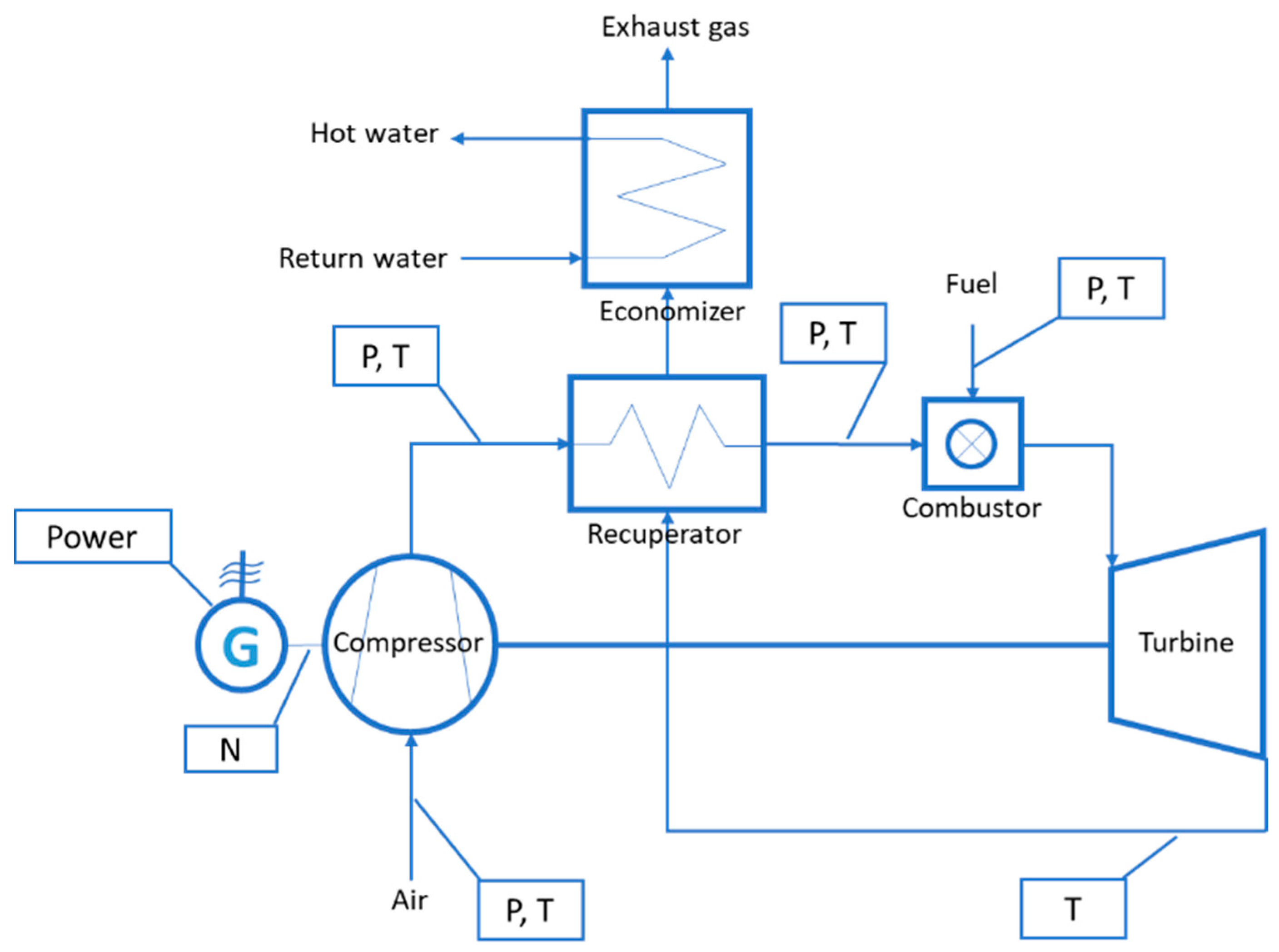
2. Micro Gas Turbine System
3. Methodology
3.1. Preprocessing on the Dataset to Detect Outliers
3.2. Data Normalization
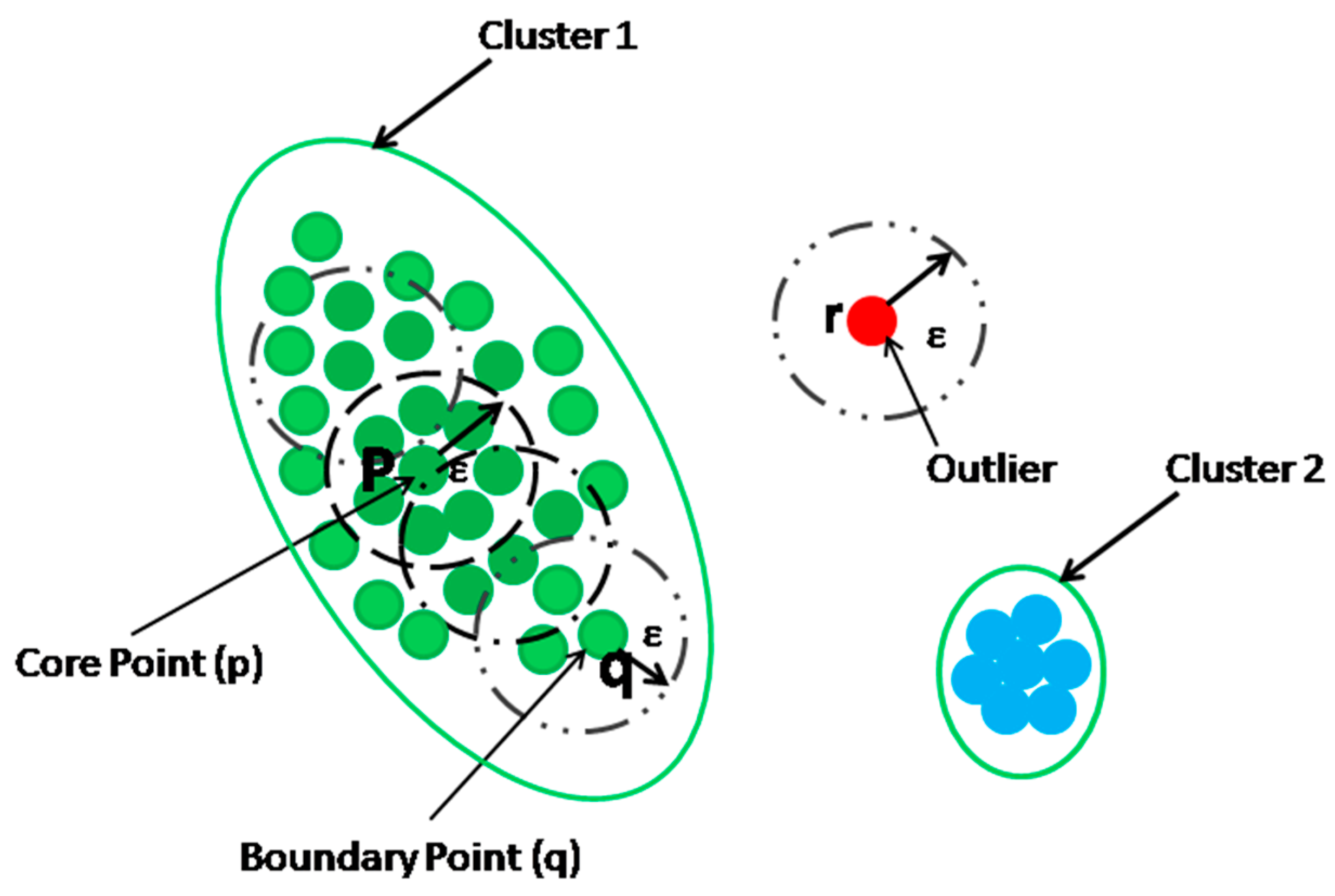
3.3. Data Clustering Approach for Outlier Detection
3.4. DBSCAN Algorithm
| Algorithm 1. DBSCAN (a density-based clustering algorithm) |
| Inputs: Dataset having X number of objects with F number of features ε: reachability distance or radius minpts: minimum number of points to form a cluster Outputs: A set of density-based clusters and an outlier set Method of feature-wise outlier detection using DBSCAN: Begin // Start of method let outliers_set = { } // initially null For each feature f in F //Start of 1st For loop let unvisited_set = { } unvisited_set = Dataset //add all objects of Dataset to unvisited_set For each point p in unvisited_set //Start of 2nd For loop unvisited_set = unvisited_set – {p} //remove p from unvisited_set let N = NEIGHBOUR(p, ε, f); //calculate neighbourhood of p If |N| < minpts outliers_set = outliers_set U { p} // include p to outlier_set Else create a new cluster C and add p to cluster C For each point point q in N //Start of 3rd For loop N = N – {q} //remove q from N If q is in unvisited_set remove q from unvisited set let Q = NEIGHBOUR(q, ε, f); If |Q| >= minpts N = N U Q //add all elements of Q to N EndIf EndIf If q is not a member of any Cluster add q to cluster C EndIf If q is in outliers_set outliers_set = outliers_set – {q} //remove q from outliers_set EndIf EndFor //End of of 3rd For loop EndIf EndFor //End of of 2nd For loop EndFor //End of of 1st For loop Return outliers_set End // End of method Method of calculating neighbourhood of a point p: Begin// Start of method let neighbour_set = { } //initially null For each point d in Dataset: If |d[f] – p[f]| is less than or equal to ε neighbour_set = neighbour_set U {d} //include d in neighbour_set EndIf EndFor return neighbor_set End// End of method |
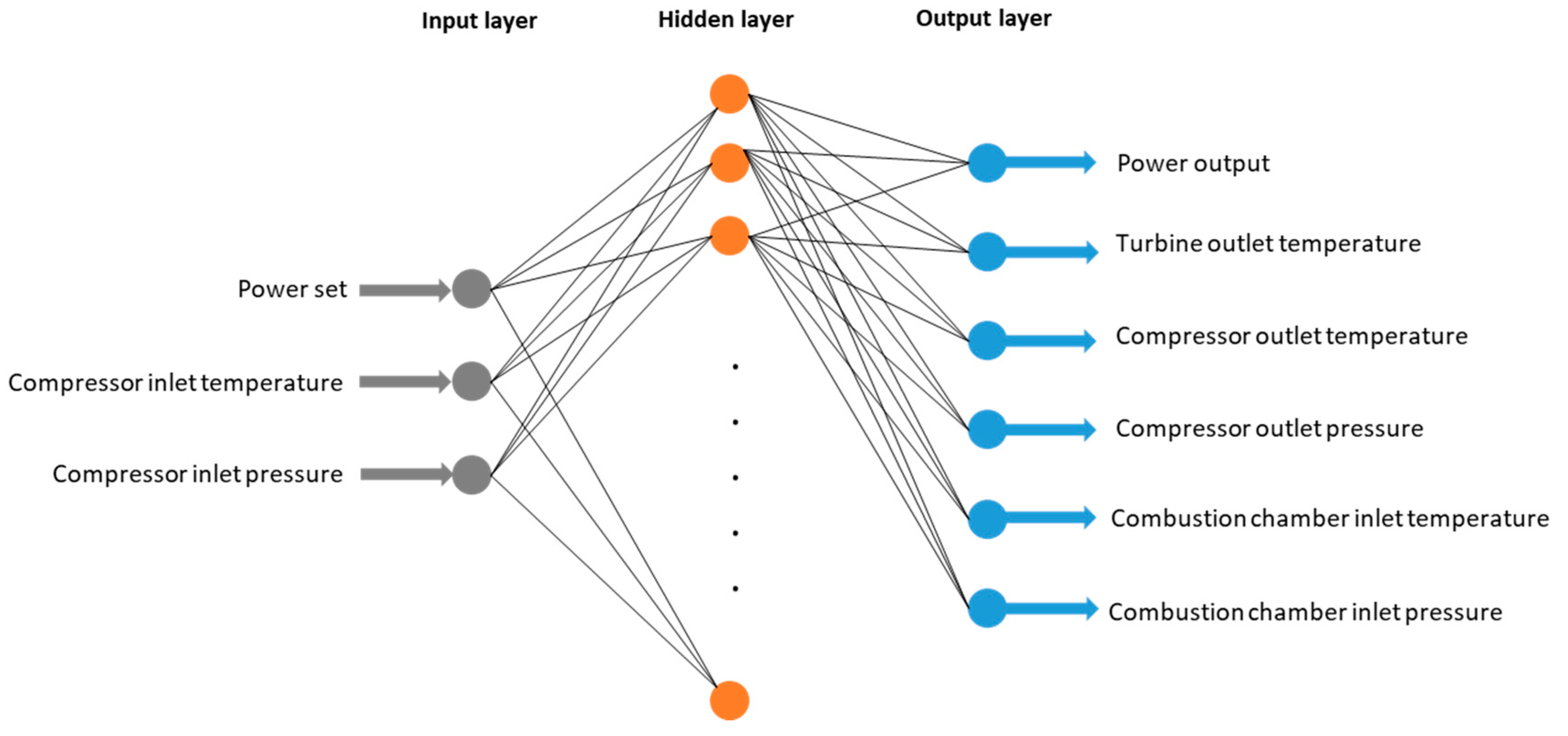
3.5. ANN Model Development
4. Results and Analysis
4.1. DBSCAN for Outlier Detection
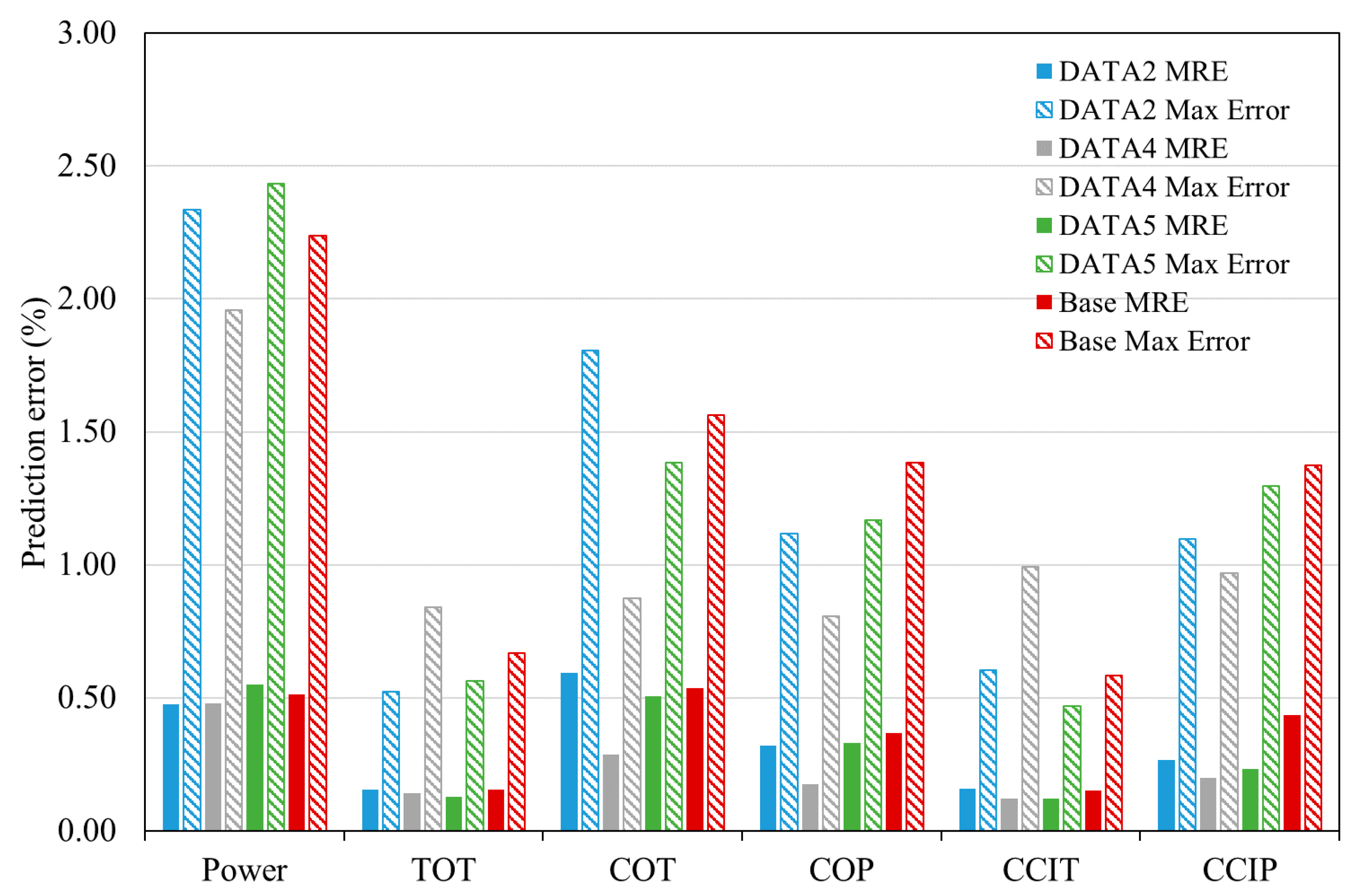
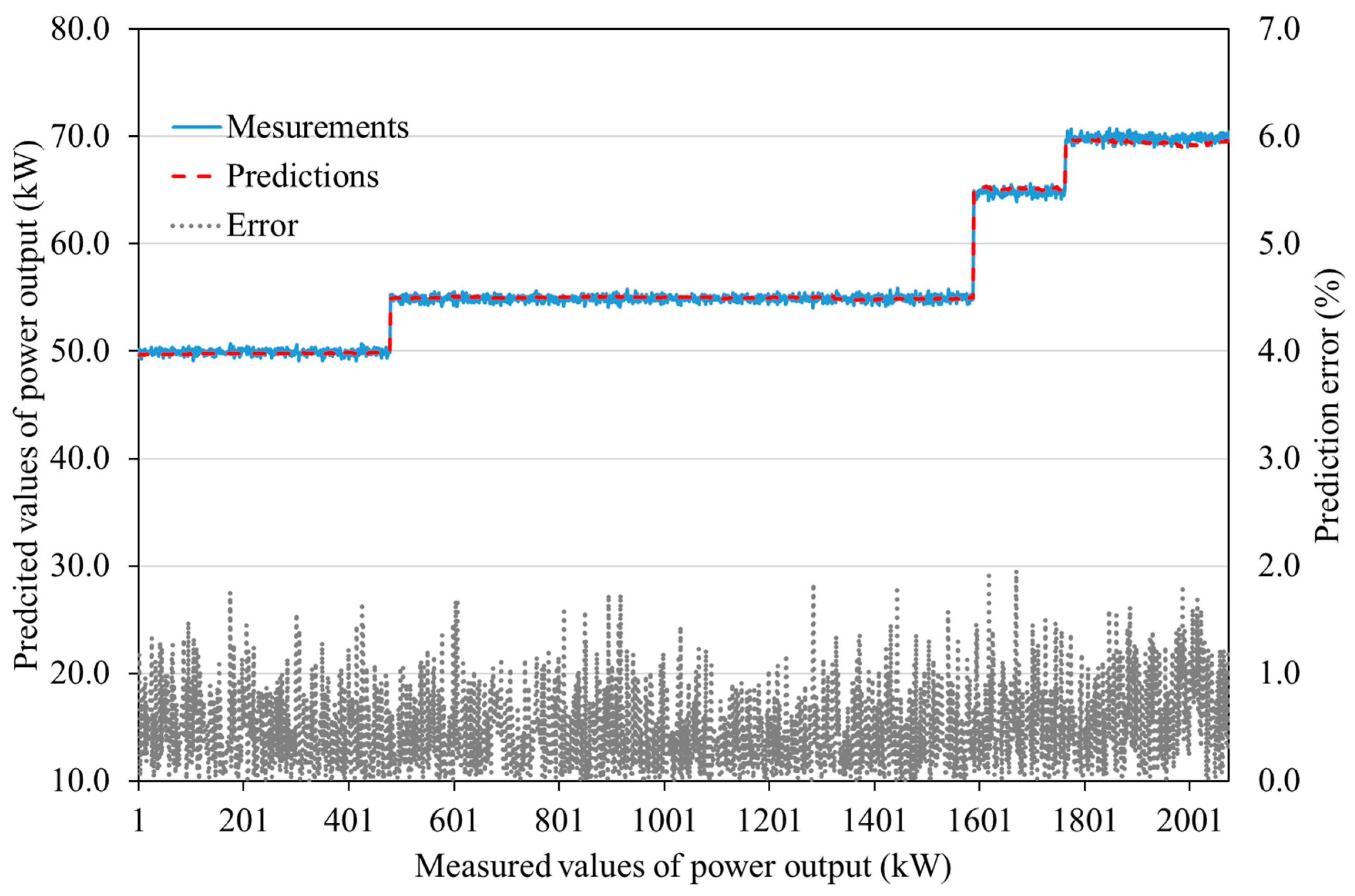
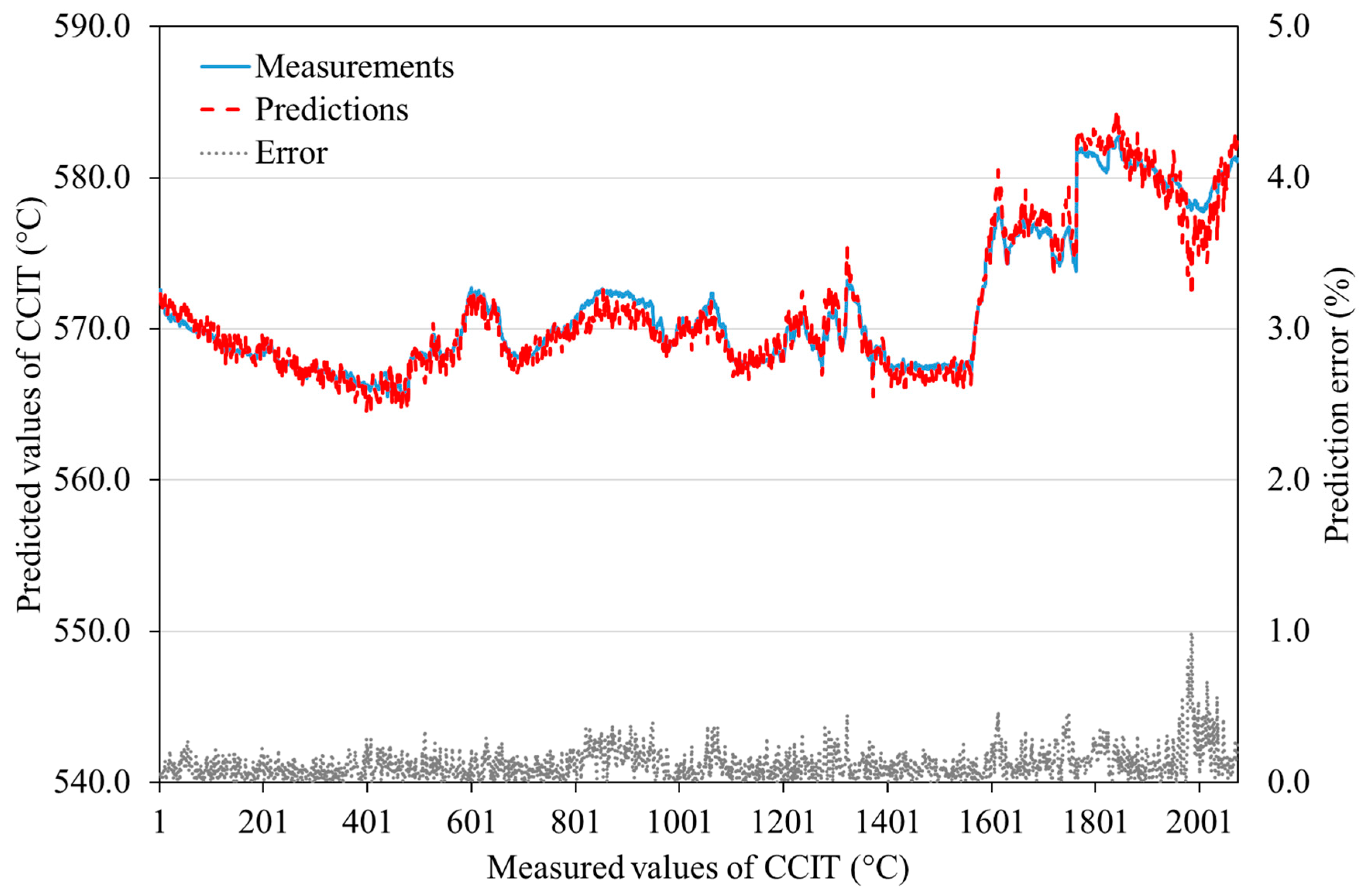
4.2. ANN Modeling Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Perera, A.T.D.; Nik, V.M.; Mauree, D.; Scartezzini, J.L. Electrical hubs: An effective way to integrate non-dispatchable renewable energy sources with minimum impact to the grid. Appl. Energy 2017, 190, 232–248. [Google Scholar] [CrossRef]
- Rahman, M.; Zaccaria, V.; Zhao, X.; Kyprianidis, K. Diagnostics-Oriented Modelling of Micro Gas Turbines for Fleet Monitoring and Maintenance Optimization. Processes 2018, 6, 216. [Google Scholar] [CrossRef] [Green Version]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef] [Green Version]
- Powering the Digital Transformation of Electricity. GE Power. 2016. Available online: https://www.ge.com/digital/sites/default/files/download_assets/Power%20Digital%20Solutions%20Product%20Catalog.pdf (accessed on 1 June 2020).
- Ingimundarson, A.; Stefanopoulou, A.G.; McKay, D.A. Model-based detection of hydrogen leaks in a fuel cell stack. IEEE Trans. Control Syst. Technol. 2008, 16, 1004–1012. [Google Scholar] [CrossRef]
- Mahmood, M.; Martini, A.; Traverso, A.; Bianchi, E. Model Based Diagnostics of AE-T100 Micro Gas Turbine. in ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. Am. Soc. Mech. Eng. 2016, 49828, V006T05A021. [Google Scholar]
- Diez-Olivan, A.; Pagan, J.A.; Khoa, N.L.D.; Sanz, R.; Sierra, B. Kernel-based support vector machines for automated health status assessment in monitoring sensor data. Int. J. Adv. Manuf. Tech. 2018, 95, 327–340. [Google Scholar] [CrossRef]
- Hanachi, H.; Liu, J.; Mechefske, C. Multi-mode diagnosis of a gas turbine engine using an adaptive neuro-fuzzy system. Chin. J. Aeronaut. 2018, 31, 1–9. [Google Scholar] [CrossRef]
- Yoon, J.E.; Lee, J.J.; Kim, T.S.; Sohn, J.L. Analysis of performance deterioration of a micro gas turbine and the use of neural network for predicting deteriorated component characteristics. J. Mech. Sci. Tech. 2008, 22, 2516. [Google Scholar] [CrossRef]
- Talaat, M.; Gobran, M.H.; Wasfi, M. A hybrid model of an artificial neural network with thermodynamic model for system diagnosis of electrical power plant gas turbine. Eng. Appl. Artif. Intell. 2018, 68, 222–235. [Google Scholar] [CrossRef]
- Zabihi-Hesari, A.; Ansari-Rad, S.; Shirazi, F.A.; Ayati, M. Fault detection and diagnosis of a 12-cylinder trainset diesel engine based on vibration signature analysis and neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 1910–1923. [Google Scholar] [CrossRef]
- Fast, M.; Assadi, M.; De, S. Development and multi-utility of an ANN model for an industrial gas turbine. Appl. Energy 2009, 86, 9–17. [Google Scholar] [CrossRef]
- Palme, T.; Breuhaus, P.; Assadi, M.; Klein, A.; Kim, M. New Alstom monitoring tools leveraging artificial neural network technologies. in ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. Am. Soc. Mech. Eng. 2011, 54631, 281–292. [Google Scholar]
- Palmé, T.; Breuhaus, P.; Assadi, M.; Klein, A.; Kim, M. Early warning of gas turbine failure by nonlinear feature extraction using an auto-associative neural network approach. in ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. Am. Soc. Mech. Eng. 2011, 54631, 293–304. [Google Scholar]
- Smrekar, J.; Pandit, D.; Fast, M.; Assadi, M.; De, S. Prediction of power output of a coal-fired power plant by artificial neural network. Neural Comput. Appl. 2010, 19, 725–740. [Google Scholar] [CrossRef]
- Nikpey, H.; Assadi, M.; Breuhaus, P. Development of an optimized artificial neural network model for combined heat and power micro gas turbines. Appl. Energy 2013, 108, 137–148. [Google Scholar] [CrossRef]
- Nikpey, H.; Assadi, M.; Breuhaus, P.; Mørkved, P.T. Experimental evaluation and ANN modeling of a recuperative micro gas turbine burning mixtures of natural gas and biogas. Appl. Energy 2014, 117, 30–41. [Google Scholar] [CrossRef]
- Milos Milojevic, F.N. Digital Industrial Revolution with Predictive Maintenance; CXP Group: Nanterre, Île-de-France, 2018. [Google Scholar]
- Khamis, A.; Ismail, Z.; Haron, K.; Tarmizi Mohammed, A. The effects of outliers data on neural network performance. J. Appl. Sci. 2005, 5, 1394–1398. [Google Scholar]
- Das, N.G. Statistical Methods; McGraw Hill Companies: New Delhi, India, 2017. [Google Scholar]
- Han, J.; Pei, J.; Kamber, M. Data mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Almeida, J.A.S.; Barbosa, L.M.S.; Pais, A.A.C.C.; Formosinho, S.J. Improving hierarchical cluster analysis: A new method with outlier detection and automatic clustering. Chemom. Intell. Lab. Syst. 2007, 87, 208–217. [Google Scholar] [CrossRef] [Green Version]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD, Portland, Oregon, 2–4 August 1996. [Google Scholar]
- Çelik, M.; Dadaşer-Çelik, F.; Dokuz, A.Ş. Anomaly detection in temperature data using DBSCAN algorithm. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, 15–18 June 2011. [Google Scholar]
- Thang, T.M.; Kim, J. The anomaly detection by using DBSCAN clustering with multiple parameters. In Proceedings of the 2011 International Conference on Information Science and Applications, Jeju Island, Korea, 26–29 April 2011. [Google Scholar]
- Bruno, J.; Coronas, A. Distributed generation of energy using micro gas turbines: Polygeneration systems and fuel flexibility. In Proceedings of the International Conference on Renewable Energy and Power Quality, ICREPQ’04, Barcelona, Spain, 31 March–2 April 2004. [Google Scholar]
- Onovwiona, H.I.; Ugursal, V.I. Residential cogeneration systems: Review of the current technology. Renew. Sustain. Energy Rev. 2006, 10, 389–431. [Google Scholar] [CrossRef]
- Pilavachi, P.A. Mini- and micro-gas turbines for combined heat and power. Appl. Therm. Eng. 2002, 22, 2003–2014. [Google Scholar] [CrossRef]
- Razbani, O.; Assadi, M. Artificial neural network model of a short stack solid oxide fuel cell based on experimental data. J. Power Sources 2014, 246, 581–586. [Google Scholar] [CrossRef]
- D10293. Technical Description–T100 Microturbine CHP System, Ver 4.0; Turbec AB: Malmo, Sweden, 2000. (In English) [Google Scholar]
- Nikpey, H.; Assadi, M.; Breuhaus, P. Development of an artificial neural network model for combined heat and power micro gas turbines. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012. [Google Scholar]



| ε | minpts | Number of Outliers | |
|---|---|---|---|
| DATA1 | 0.014 | 5 | 39 |
| DATA2 | 0.012 | 5 | 53 |
| DATA3 | 0.016 | 35 | 99 |
| DATA4 | 0.012 | 35 | 468 |
| DATA5 | 0.020 | 100 | 599 |
| Power | TOT | COT | COP | CCIT | CCIP | ||
|---|---|---|---|---|---|---|---|
| DATA1 | MRE (%) | 0.71 | 0.11 | 0.42 | 0.39 | 0.09 | 0.25 |
| Maximum error (%) | 3.00 | 0.52 | 1.36 | 1.63 | 0.39 | 1.37 | |
| DATA2 | MRE (%) | 0.48 | 0.16 | 0.59 | 0.32 | 0.16 | 0.27 |
| Maximum error (%) | 2.34 | 0.52 | 1.81 | 1.12 | 0.60 | 1.10 | |
| DATA3 | MRE (%) | 0.63 | 0.13 | 0.39 | 0.36 | 0.08 | 0.31 |
| Maximum error (%) | 3.50 | 0.50 | 1.39 | 2.03 | 0.37 | 2.11 | |
| DATA4 | MRE (%) | 0.48 | 0.14 | 0.29 | 0.18 | 0.12 | 0.20 |
| Maximum error (%) | 1.96 | 0.84 | 0.88 | 0.81 | 0.99 | 0.97 | |
| DATA5 | MRE (%) | 0.55 | 0.13 | 0.51 | 0.33 | 0.12 | 0.23 |
| Maximum error (%) | 2.43 | 0.57 | 1.38 | 1.17 | 0.47 | 1.30 | |
| Baseline | MRE (%) | 0.51 | 0.16 | 0.54 | 0.37 | 0.15 | 0.44 |
| Maximum error (%) | 2.24 | 0.67 | 1.56 | 1.38 | 0.58 | 1.38 |
| < 0.5% | 0.5–1.0% | 1.0–1.5% | 1.5–2% | 2–2.5% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best ANN | Baseline | Best ANN | Baseline | Best ANN | Baseline | Best ANN | Baseline | Best ANN | Baseline | |
| Power | 59.9% | 57.4% | 30.1% | 29.7% | 9% | 11.0% | 1.1% | 1.6% | - | 0.3% |
| TOT | 98.2% | 99.7% | 1.8% | 0.3% | - | - | - | - | - | - |
| COT | 76.3% | 50% | 23.7% | 39.4% | - | 10.6% | - | - | - | - |
| CCIT | 99.2% | 99.7% | 0.8% | 0.3% | - | - | - | - | - | - |
| COP | 97.6% | 69.0% | 2.4% | 29.8% | - | 1.2% | - | - | - | - |
| CCIP | 93.6% | 61.5% | 6.4% | 36.6% | - | 1.9% | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikpey Somehsaraei, H.; Ghosh, S.; Maity, S.; Pramanik, P.; De, S.; Assadi, M. Automated Data Filtering Approach for ANN Modeling of Distributed Energy Systems: Exploring the Application of Machine Learning. Energies 2020, 13, 3750. https://doi.org/10.3390/en13143750
Nikpey Somehsaraei H, Ghosh S, Maity S, Pramanik P, De S, Assadi M. Automated Data Filtering Approach for ANN Modeling of Distributed Energy Systems: Exploring the Application of Machine Learning. Energies. 2020; 13(14):3750. https://doi.org/10.3390/en13143750
Chicago/Turabian StyleNikpey Somehsaraei, Homam, Susmita Ghosh, Sayantan Maity, Payel Pramanik, Sudipta De, and Mohsen Assadi. 2020. "Automated Data Filtering Approach for ANN Modeling of Distributed Energy Systems: Exploring the Application of Machine Learning" Energies 13, no. 14: 3750. https://doi.org/10.3390/en13143750
APA StyleNikpey Somehsaraei, H., Ghosh, S., Maity, S., Pramanik, P., De, S., & Assadi, M. (2020). Automated Data Filtering Approach for ANN Modeling of Distributed Energy Systems: Exploring the Application of Machine Learning. Energies, 13(14), 3750. https://doi.org/10.3390/en13143750








