Optimal Chiller Loading for Energy Conservation Using an Improved Fruit Fly Optimization Algorithm
Abstract
:1. Introduction
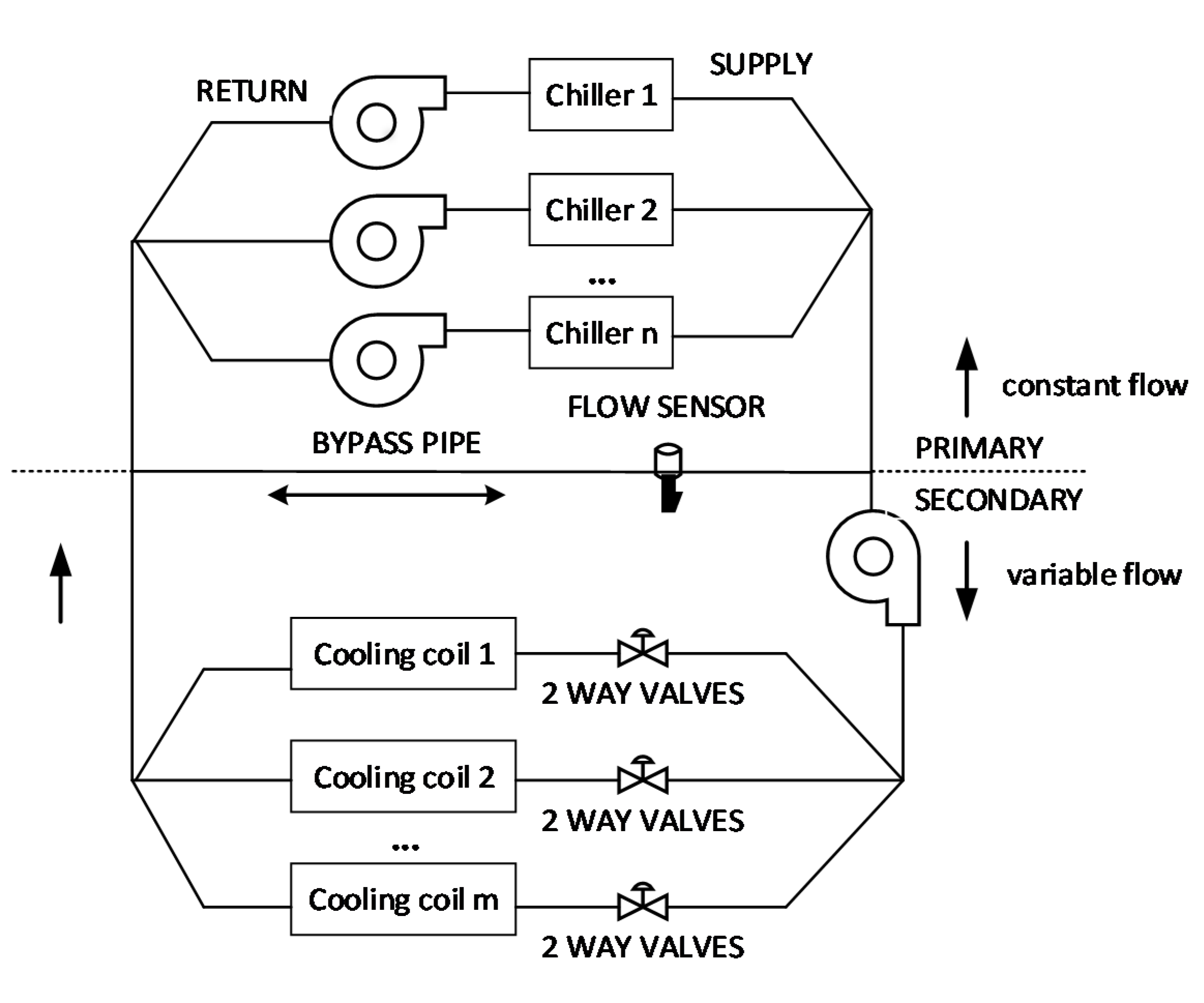
2. Problem Description
3. Canonical FOA and Analysis
3.1. Canonical FOA Overview
3.2. Disadvantages of Canonical FOA
- (1)
- Nonuniform generation of candidate solutions
- (2)
- Poor search ability
4. Improved FOA Algorithm Based on Dynamic Search Radius
| Algorithm 1. Improved fruit fly optimization algorithm (IFOA) algorithm |
| Parameters: PS, Itermax, rmax, rmin |
| Output: Solution X* |
| //Initialization |
| Set PS, Itermax, rmax, rmin |
| Fori = 1, 2, …, PS |
| //Generate the locations of PS individuals |
| Endfor |
| //Set swarm location |
| Iter = 0, X* = X_axis |
| Repeat |
| //Osphresis foraging phase |
| For i = 1, 2, …, PS |
| Endfor |
| //Vision foraging phase |
| if Smellbest > bestSmell then |
| Smellbest = bestSmell |
| Iter = Iter + 1 |
| UntilIter == Itermax |
5. Implementation of IFOA on OCL Problem
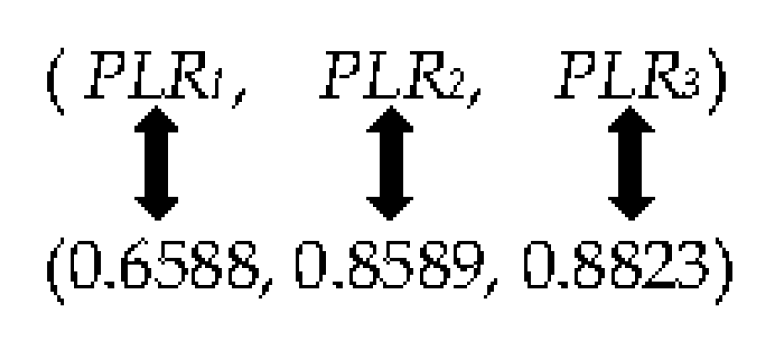
- P1 = 100.95 + 818.61 × 0.6588 − 973.43 × (0.6588)2 + 788.55 × (0.6588)3 = 443.235317 KW,
- P2 = 481.473064 KW, P3 = 478.487741 KW,
- J = P1 + P2 + P3 = 1403.196121 KW,
- 0.6588 × 800 + 0.8589 × 800 + 0.8823 × 800 = 1920RT, 1920RT = CL.
6. Simulation Results
6.1. Cases Used in Experiments
6.1.1. Case with Six Chillers
6.1.2. Case with Four Chillers
6.1.3. Cases with Three Chillers
6.2. Results and Analysis
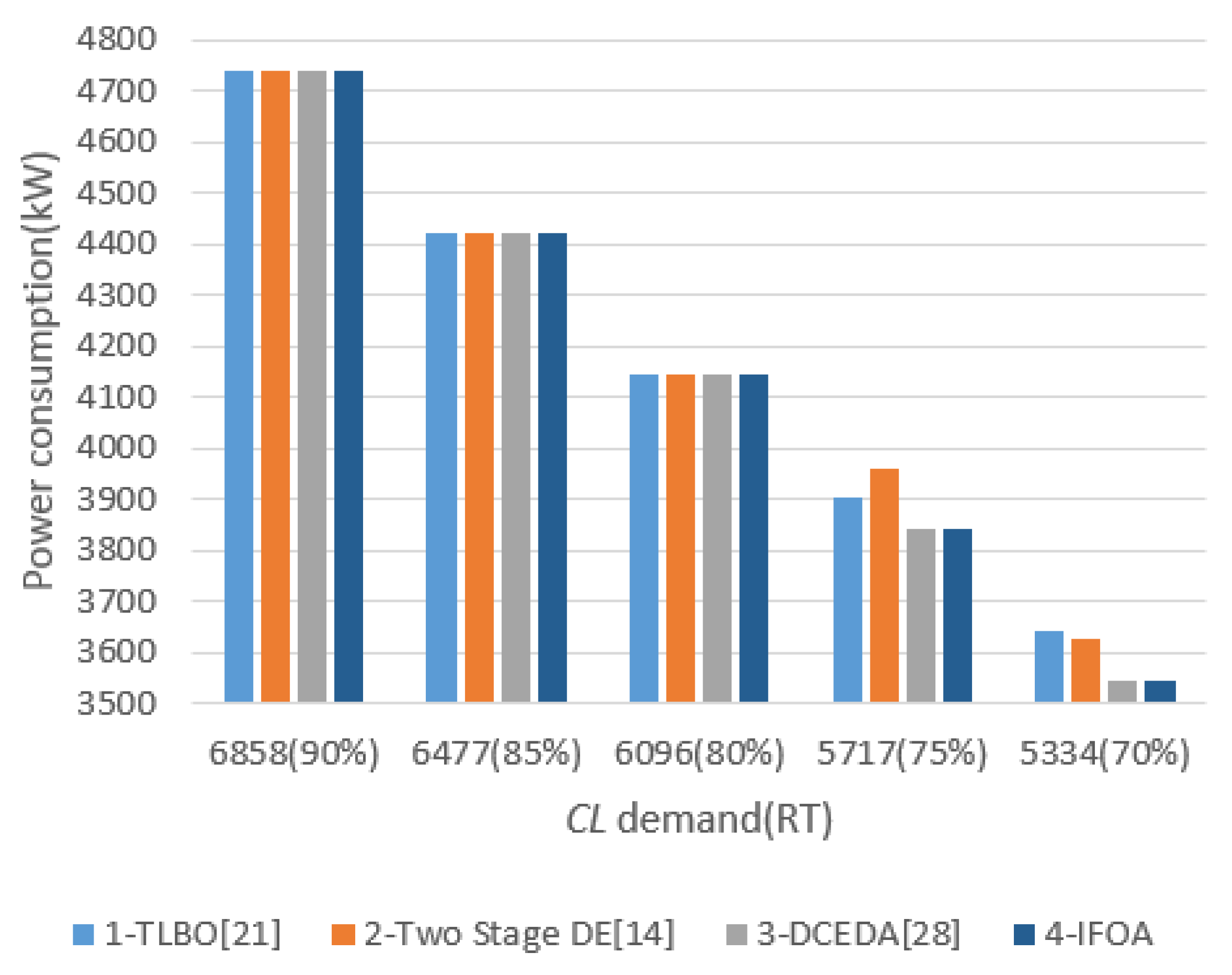
6.2.1. Comparisons of the First Case Experiment
- P1 = 399.345 − 122.12 × 0.843243 + 770.46 × (0.843243)2 = 844.210495 KW,
- P2 = 287.116 + 80.04 × 0.783222 + 700.48 × (0.783222)2 = 779.505229 KW,
- P3 = −120.505 + 1525.99 × 0.000000 – 502.14 × (0.000000)2 = −120.505 KW,
- P4 = 781.488298 KW, P5 = 755.200502 KW, P6 = 798.313427 KW,
- J = = 3838.212951 KW.
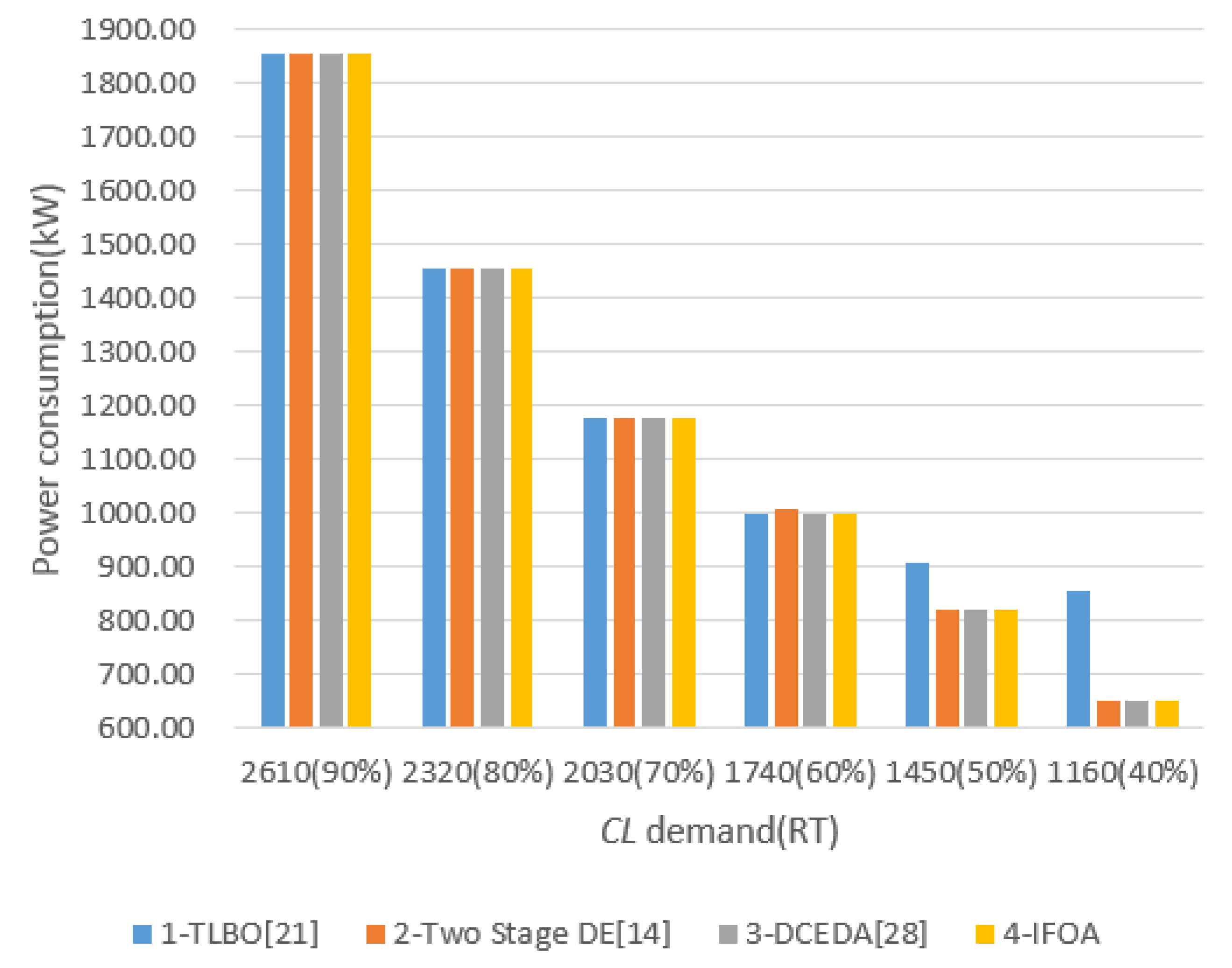
6.2.2. Comparisons of the Second Case Experiment
6.2.3. Comparisons of the Third Case Experiment
6.2.4. Results of Comparison of Three Case Experiments
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PLR | partial load ratio | Smellbest | the best smell concentration in vision foraging phase |
| CL | cooling load | r | the search radius |
| RT | design capacity | IFOA | improved fruit fly optimization algorithm |
| ON | the state of the chiller | GA | genetic algorithm |
| P | power consumption | SA | simulated annealing |
| a | coefficients of the chiller KW-PLR curve | PSO | particle swarm optimization |
| b | GRG | generalized reduced gradient | |
| c | DS | differential search | |
| d | DCSA | differential cuckoo search algorithm | |
| J | the total energy consumption of multi-chiller system | LGM | Lagrangian method |
| B&B | branch and bound | ||
| n | the total number of chillers | ES | evolution strategy |
| PS | population size | GM | gradient method |
| Iter | the number of iterations | DE | differential evolution |
| LR | the fruit fly swarm location range | IFA | improved firefly algorithm |
| FR | the flight range | NNPSO | neural networks model with particle swarm optimization |
| X | horizontal coordinate | GAMS | general algebraic modeling system |
| Y | vertical coordinate | TLBO | teaching-learning-based optimization |
| DIST | the distance between the individual and the origin | EIWO | improved invasive weed optimization |
| EMA | exchange market algorithm | ||
| S | the smell concentration judgment value | CGOA | improved grasshopper optimization algorithm |
| Smell | the smell concentration | VAFSA | improved artificial fish swarm algorithm |
| bestSmell | the best smell concentration in osphresis foraging phase | IGDT | information gap decision theory |
| bestIndex | location with the best smell concentration | DCEDA | distributed chaotic estimation of distribution algorithm |
References
- Ardakani, A.J.; Ardakani, F.F.; Hosseinian, S.H. A novel approach for optimal chiller loading using particle swarm optimization. Energy Build. 2008, 40, 2177–2187. [Google Scholar] [CrossRef]
- Linton, R.; Frutiger, T.; Blanc, S.; Hydeman, M.; Brambley, M.; Branson, D.; O’Neill, P.; Cagwin, D.; Kammers, B.; Carpenter, P. Ashrae Handbook; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2008. [Google Scholar]
- Chang, Y.C. A novel energy conservation method―optimal chiller loading. Electr. Power Syst. Res. 2004, 69, 221–226. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lin, F.A.; Lin, C.H. Optimal chiller sequencing by branch and boun method for saving energy. Energy Convers. Manag. 2005, 46, 2158–2172. [Google Scholar] [CrossRef]
- Chang, Y.C. Genetic algorithm based optimal chiller loading for energy conservation. Appl. Therm. Eng. 2005, 25, 2800–2815. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lin, J.K.; Chuang, M.H. Optimal chiller loading by genetic algorithm for reducing energy consumption. Energy Build. 2005, 37, 147–155. [Google Scholar] [CrossRef]
- Chang, Y.C. An innovative approach for demand side management—Optimal chiller loading by simulated annealing. Energy 2006, 31, 1547–1560. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Chen, W.-H.; Lee, C.-Y.; Huang, C.-N. Simulated annealing based optimal chiller loading for saving energy. Energy Convers. Manag. 2006, 47, 2044–2058. [Google Scholar] [CrossRef]
- Lee, W.S.; Lin, L.C. Optimal chiller loading by particle swarm algorithm for reducing energy consumption. Appl. Therm. Eng. 2009, 29, 1730–1734. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lee, C.Y.; Chen, C.R.; Chou, C.J.; Chen, W.H.; Chen, W.H. Evolution Strategy Based Optimal Chiller Loading For Saving Energy. Energy Convers. Manag. 2009, 50, 132–139. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chan, R.-S.; Lee, R.-S. Economic dispatch of chiller plant by gradient method for saving energy. Appl. Energy 2010, 87, 1096–1101. [Google Scholar] [CrossRef]
- Zong, W.G. Solution quality improvement in chiller loading optimization. Appl. Therm. Eng. 2011, 31, 1848–1851. [Google Scholar]
- Lee, W.S.; Chen, Y.T.; Kao, Y. Optimal chiller loading by differential evolution algorithm for reducing energy consumption. Energy Build. 2011, 43, 599–604. [Google Scholar] [CrossRef]
- Lin, C.-M.; Wu, C.-Y.; Tseng, K.-Y.; Ku, C.-C.; Lin, S.-F. Applying Two-Stage Differential Evolution for Energy Saving in Optimal Chiller Loading. Energies 2019, 12, 622. [Google Scholar] [CrossRef] [Green Version]
- Coelho, L.D.S.; Mariani, V.C. Improved firefly algorithm approach applied to chiller loading for energy conservation. Energy Build. 2013, 59, 273–278. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Ibrahim, H.; Daniyal, H.; Mohamed, M.R. A New Swarm Intelligence Approach for Optimal Chiller Loading for Energy Conservation. Procedia Soc. Behav. Sci. 2014, 129, 483–488. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.L.; Chang, Y.C.; Chan, T.S. Applying smart models for energy saving in optimal chiller loading. Energy Build. 2014, 68, 364–371. [Google Scholar] [CrossRef]
- Coelho, L.D.S.; Klein, C.E.; Sabat, S.L.; Mariani, V.C. Optimal chiller loading for energy conservation using a new differential cuckoo search approach. Energy 2014, 75, 237–243. [Google Scholar] [CrossRef]
- Salari, E.; Askarzadeh, A. A new solution for loading optimization of multi-Chiller systems by general algebraic modeling system. Appl. Therm. Eng. Des. Process. Equip. Econ. 2015, 84, 429–436. [Google Scholar] [CrossRef]
- Saeedi, M.; Moradi, M.; Hosseini, M.; Emamifar, A.; Ghadimi, N. Robust optimization based optimal chiller loading under cooling demand uncertainty. Appl. Therm. Eng. 2019, 148, 1081–1091. [Google Scholar] [CrossRef]
- Duan, P.Y.; Li, J.Q.; Wang, Y.; Sang, H.Y.; Jia, B.X. Solving chiller loading optimization problems using an improved teaching-Learning-Based optimization algorithm. Optim. Control Appl. Methods 2017, 39, 65–77. [Google Scholar] [CrossRef]
- Sohrabi, F.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S. Optimal chiller loading for saving energy by exchange market algorithm. Energy Build. 2018, 169, 245–253. [Google Scholar] [CrossRef]
- Wenhan, X.; Yuanxing, W.; Di, Q.; Rouyendegh, B.D. Improved grasshopper optimization algorithm to solve energy consuming reduction of chiller loading. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 1–14. [Google Scholar] [CrossRef]
- Zheng, Z.X.; Li, J. Optimal chiller loading by improved invasive weed optimization algorithm for reducing energy consumption. Energy Build. 2018, 161, 80–88. [Google Scholar] [CrossRef]
- Zheng, Z.-X.; Li, J.-Q.; Duan, P.-Y. Optimal chiller loading by improved artificial fish swarm algorithm for energy saving. Math. Comput. Simul. 2019, 155, 227–243. [Google Scholar] [CrossRef]
- Shi, E.; Jabari, F.; Anvari-Moghaddam, A.; Mohammadpourfard, M.; Mohammadi-ivatloo, B. Risk-Constrained Optimal Chiller Loading Strategy Using Information Gap Decision Theory. Appl. Sci. 2019, 9, 1925. [Google Scholar] [CrossRef] [Green Version]
- Qiu, S.; Li, Z.; Li, Z.; Zhang, X. Model-Free optimal chiller loading method based on Q-Learning. Sci. Technol. Built Environ. 2020, 1–17. [Google Scholar] [CrossRef]
- Yu, J.; Liu, Q.; Zhao, A.; Qian, X.; Zhang, R. Optimal chiller loading in HVAC System Using a Novel Algorithm Based on the distributed framework. J. Build. Eng. 2020, 28, 101044. [Google Scholar] [CrossRef]
- Pan, W.T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Shi, X. Advanced Fruit Fly Optimization Algorithm and Its Application to Irregular Subarray Phased Array Antenna Synthesis. IEEE Access 2019, 7, 165583–165596. [Google Scholar] [CrossRef]
- Peng, L.; Zhu, Q.; Lv, S.-X.; Wang, L. Effective long short-term memory with fruit fly optimization algorithm for time series forecasting. Soft Comput. 2020, 1–21. [Google Scholar] [CrossRef]
- Ding, G.; Dong, F.; Zou, H. Fruit fly optimization algorithm based on a hybrid adaptive-Cooperative learning and its application in multilevel image thresholding. Appl. Soft Comput. 2019, 84, 84. [Google Scholar] [CrossRef]
- Hu, J.; Chen, P.; Yang, Y.; Liu, Y.; Chen, X. The Fruit Fly Optimization Algorithms for Patient-Centered Care Based on Interval Trapezoidal Type-2 Fuzzy Numbers. Int. J. Fuzzy Syst. 2019, 21, 1270–1287. [Google Scholar] [CrossRef]
- Jiang, W.; Wu, X.; Gong, Y.; Yu, W.; Zhong, X. Holt–Winters smoothing enhanced by fruit fly optimization algorithm to forecast monthly electricity consumption. Energy 2020, 193. [Google Scholar] [CrossRef]
- Shao, Z.; Pi, D.; Shao, W. Hybrid enhanced discrete fruit fly optimization algorithm for scheduling blocking flow-shop in distributed environment. Expert Syst. Appl. 2020, 145, 113147. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Y.; Li, S.; Zeng, Y.-R. New fruit fly optimization algorithm with joint search strategies for function optimization problems. Knowl. Based Syst. 2019, 176, 77–96. [Google Scholar] [CrossRef]
- Tian, X.; Li, J. A novel improved fruit fly optimization algorithm for aerodynamic shape design optimization. Knowl. Based Syst. 2019, 179, 77–91. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, X.; Jia, S.; Li, X. A novel phase angle-encoded fruit fly optimization algorithm with mutation adaptation mechanism applied to UAV path planning. Appl. Soft Comput. 2018, 70, 371–388. [Google Scholar] [CrossRef]
- Guo, Q.; Quan, Y.; Jiang, C. Object Pose Estimation in Accommodation Space using an Improved Fruit Fly Optimization Algorithm. J. Intell. Robot. Syst. 2018, 95, 405–417. [Google Scholar] [CrossRef]
- Wang, T.; Shen, X.; Zhou, J.; Yin, Y.; Ji, X.; Zhou, Q. Optimal Gating System Design of Steel Casting by Fruit Fly Optimization Algorithm Based on Casting Simulation Technology. Int. J. Met. 2018, 13, 561–570. [Google Scholar] [CrossRef]
- Wang, H.; Song, W.; Zio, E.; Kudreyko, A.; Zhang, Y. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Measurement 2020, 161. [Google Scholar] [CrossRef]
- Dan, S.; Cao, G.H.; Dong, H. LGMS-FOA: An Improved Fruit Fly Optimization Algorithm for Solving Optimization Problems. Math. Probl. Eng. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Li, J.Q.; Han, Y.Q.; Duan, P.Y.; Han, Y.Y.; Niu, B.; Li, C.D.; Zheng, Z.X.; Liu, Y.P. Meta-heuristic algorithm for solving vehicle routing problems with time windows and synchronized visit constraints in prefabricated systems. J. Clean. Prod. 2020, 250, 119464. [Google Scholar] [CrossRef]
- Han, Y.; Gong, D.; Jin, Y.; Pan, Q. Evolutionary Multi-Objective Blocking Lot-Streaming Flow Shop Scheduling with Machine Breakdowns. IEEE Trans. Cybern. 2017, 49, 1–14. [Google Scholar]
- Li, J.Q.; Deng, J.W.; Li, C.Y.; Han, Y.Y.; Tian, J.; Zhang, B.; Wang, C.G. An improved Jaya algorithm for solving the flexible job shop scheduling problem with transportation and setup times. Knowl. Based Syst. 2020, 200, 106032. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.; Gong, D.; Sang, H. Multi-Objective migrating birds optimization algorithm for stochastic lot-streaming flow shop scheduling with blocking. IEEE Access 2018, 7, 5946–5962. [Google Scholar] [CrossRef]
- Gong, D.; Han, Y.; Sun, J. A novel hybrid multi-Objective artificial bee colony algorithm for blocking lot-streaming flow shop scheduling problems. Knowl. Based Syst. 2018, 148, 115–130. [Google Scholar] [CrossRef]
- Li, J.; Pan, Q.; Duan, P.; Sang, H.; Gao, K. Solving multi-Area environmental U+002F economic dispatch by Pareto-based chemical-Reaction optimization algorithm. IEEE/CAA J. Autom. Sin. 2017, 99, 1–11. [Google Scholar] [CrossRef]
- Li, J.Q.; Han, Y.Q. A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system. Clust. Comput 2019, 1–17. [Google Scholar] [CrossRef]
- Li, J.Q.; Tao, X.R.; Jia, B.X.; Han, Y.Y.; Liu, C.; Duan, P.; Zheng, Z.X.; Sang, H.Y. Efficient multi-Objective algorithm for the lot-Streaming hybrid flowshop with variable sub-Lots. Swarm Evol. Comput. 2020, 52, 100600. [Google Scholar] [CrossRef]

| Chiller | c1i | c2i | c3i | Capacity (RT) |
|---|---|---|---|---|
| 1 | 399.345 | −122.12 | 770.46 | 1280 |
| 2 | 287.116 | 80.04 | 700.48 | 1280 |
| 3 | −120.505 | 1525.99 | −502.14 | 1280 |
| 4 | −19.121 | 898.76 | −98.15 | 1280 |
| 5 | −95.029 | 1202.39 | −352.16 | 1250 |
| 6 | 191.750 | 224.86 | 524.04 | 1250 |
| Chiller | c1i | c2i | c3i | c4i | Capacity (RT) |
|---|---|---|---|---|---|
| 1 | 104.09 | 166.57 | −430.13 | 512.53 | 450 |
| 2 | −67.15 | 1177.79 | −2174.53 | 1456.53 | 450 |
| 3 | 384.71 | −779.13 | 1151.42 | −63.20 | 1000 |
| 4 | 541.63 | 413.48 | −3626.50 | 4021.41 | 1000 |
| Chiller | c1i | c2i | c3i | c4i | Capacity (RT) |
|---|---|---|---|---|---|
| 1 | 100.95 | 818.61 | −973.43 | 788.55 | 800 |
| 2 | 66.598 | 606.34 | −380.58 | 275.95 | 800 |
| 3 | 130.09 | 304.50 | 14.377 | 99.80 | 800 |
| Symbol | Meaning | Value |
|---|---|---|
| PS | population size of Case 1 | 200 |
| population size of Case 2 and Case 3 | 50 | |
| Itermax | maximum number of iterations | 5000 |
| rmin | minimum value of search radius | 0.00001 |
| rmax | maximum value of search radius | 1.0 |
| CL(RT) | Chiller | TLBO [21] | Two Stage DE [14] | DCEDA [28] | IFOA | Energy Saving/KW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | PLRi | Power (KW) (A) | PLRi | Power (KW) (B) | PLRi | Power (KW) (C) | PLRi | Power (KW) (D) | D-A | D-B | D-C | |
| 6858(90%) | 1 | 0.8186 | 4738.54 | 0.81273 | 4738.575 | 0.8126 | 4738.58 | 0.8127 | 4738.575 | 0.035 | 0 | 0 |
| 2 | 0.7523 | 0.749554 | 0.7489 | 0.7496 | ||||||||
| 3 | 1.0000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 4 | 1.0000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 5 | 1.0000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 6 | 0.8297 | 0.838621 | 0.8395 | 0.8386 | ||||||||
| 6477(85%) | 1 | 0.727731 | 4421.65 | 0.720409 | 4421.6486 | 0.7280 | 4421.65 | 0.7279 | 4421.649 | 0 | 0 | 0 |
| 2 | 0.656132 | 0.634290 | 0.6564 | 0.6561 | ||||||||
| 3 | 1.000000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 4 | 1.000000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 5 | 1.000000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 6 | 0.716524 | 0.746387 | 0.7160 | 0.7164 | ||||||||
| 6096(80%) | 1 | 0.6431 | 4143.64 | 0.642368 | 4143.7064 | 0.6431 | 4143.71 | 0.6427 | 4143.706 | 0.066 | 0 | 0 |
| 2 | 0.5621 | 0.562711 | 0.5622 | 0.5628 | ||||||||
| 3 | 1.0000 | 0.999999 | 1.0000 | 1.0000 | ||||||||
| 4 | 1.0000 | 0.999999 | 1.0000 | 1.0000 | ||||||||
| 5 | 1.0000 | 0.999999 | 1.0000 | 1.0000 | ||||||||
| 6 | 0.5946 | 0.594798 | 0.5946 | 0.5944 | ||||||||
| 5717(75%) | 1 | 0.55765 | 3904.70 | 0.843243 | 3838.2079 | 0.0000 | 3843.07 | 0.0000 | 3842.553 | −62.147 | −116.16 | −0.517 |
| 2 | 0.46918 | 0.783222 | 0.7144 | 0.7150 | ||||||||
| 3 | 0.99995 | 0.000000 | 1.0000 | 1.0000 | ||||||||
| 4 | 1.00000 | 0.999999 | 1.0000 | 1.0000 | ||||||||
| 5 | 1.00000 | 0.999999 | 1.0000 | 1.0000 | ||||||||
| 6 | 0.47250 | 0.882499 | 0.7941 | 0.7934 | ||||||||
| 5334(70%) | 1 | 0.64179 | 3642.51 | 0.758176 | 3507.269 | 0.0000 | 3546.48 | 0.0000 | 3546.437 | −96.073 | −81.337 | −0.043 |
| 2 | 0.66219 | 0.689668 | 0.5831 | 0.5835 | ||||||||
| 3 | 0.33009 | 0.000000 | 1.0000 | 1.0000 | ||||||||
| 4 | 0.99059 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 5 | 0.99900 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 6 | 0.58047 | 0.760606 | 0.6221 | 0.6217 | ||||||||
| Optimization Method | Load CL (RT) | Power (KW) | Standard Deviation | CPU Time (s) | ||
|---|---|---|---|---|---|---|
| Max | Min | Mean | ||||
| IFOA | 6858(90%) | 4738.577 | 4738.575 | 4738.576 | 7.746 × 10−4 | 0.74 |
| DCEDA | 6858(90%) | 4739.08 | 4738.58 | 4738.66 | 0.113 | 0.73 |
| IFOA | 6477(85%) | 4421.651 | 4421.649 | 4421.649 | 5.477 × 10−4 | 0.73 |
| DCEDA | 6477(85%) | 4422.83 | 4421.65 | 4421.78 | 0.232 | 0.71 |
| IFOA | 6096(80%) | 4143.708 | 4143.706 | 4143.707 | 6.325 × 10−4 | 0.72 |
| DCEDA | 6096(80%) | 4144.31 | 4143.71 | 4143.78 | 0.116 | 0.70 |
| IFOA | 5717(75%) | 3844.036 | 3842.553 | 3842.652 | 3.947 × 10−1 | 0.68 |
| DCEDA | 5717(75%) | 3845.16 | 3842.55 | 3842.85 | 0.557 | 0.68 |
| IFOA | 5334(70%) | 3546.438 | 3546.437 | 3546.437 | 5.477 × 10−4 | 0.68 |
| DCEDA | 5334(70%) | 3562.39 | 3546.44 | 3547.09 | 2.338 | 0.66 |
| CL(RT) | Chiller | TLBO [21] | Two Stage DE [14] | DCEDA [28] | IFOA | Energy Saving/KW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | PLRi | Power (KW) (A) | PLRi | Power (KW) (B) | PLRi | Power (KW) (C) | PLRi | Power (KW) (D) | D-A | D-B | D-C | |
| 2610(90%) | 1 | 0.992 | 1857.3 | 0.990491 | 1857.297 | 0.9909 | 1857.30 | 0.9908 | 1857.30 | 0 | 0 | 0 |
| 2 | 0.908 | 0.905503 | 0.9059 | 0.9059 | ||||||||
| 3 | 1.000 | 1.000000 | 1.0000 | 1.0000 | ||||||||
| 4 | 0.755 | 0.756791 | 0.7564 | 0.7565 | ||||||||
| 2320(80%) | 1 | 0.82570 | 1455.70 | 0.822981 | 1455.733 | 0.8291 | 1455.66 | 0.8289 | 1455.66 | −0.04 | −0.073 | 0 |
| 2 | 0.80305 | 0.801856 | 0.8055 | 0.8055 | ||||||||
| 3 | 0.89931 | 0.885369 | 0.8965 | 0.8966 | ||||||||
| 4 | 0.68776 | 0.685549 | 0.6879 | 0.6879 | ||||||||
| 2030(70%) | 1 | 0.72446 | 1178.79 | 0.725289 | 1178.138 | 0.7262 | 1178.14 | 0.7262 | 1178.14 | −0.65 | 0 | 0 |
| 2 | 0.76312 | 0.739752 | 0.7402 | 0.7402 | ||||||||
| 3 | 0.71095 | 0.722185 | 0.7215 | 0.7216 | ||||||||
| 4 | 0.64959 | 0.648549 | 0.6486 | 0.6485 | ||||||||
| 1740(60%) | 1 | 0.60049 | 997.18 | 0.745135 | 0.6034 | 998.53 | 0.6036 | 998.53 | 1.35 | −10.679 | 0 | |
| 2 | 0.65995 | 0.000000 | 0.6577 | 0.6576 | ||||||||
| 3 | 0.55975 | 0.748647 | 0.5648 | 0.5648 | ||||||||
| 4 | 0.60999 | 0.656017 | 0.6077 | 0.6077 | ||||||||
| 1450(50%) | 1 | 0.5995 | 907.39 | 0.599201 | 0.6069 | 820.07 | 0.6068 | 820.07 | −87.32 | −0.043 | 0 | |
| 2 | 0.3555 | 0.000000 | 0.0000 | 0.0000 | ||||||||
| 3 | 0.4395 | 0.571431 | 0.5683 | 0.5683 | ||||||||
| 4 | 0.57992 | 0.656017 | 0.6086 | 0.6087 | ||||||||
| 1160(40%) | 1 | 0.32975 | 856.84 | 0.000000 | 0.0000 | 651.09 | 0.0000 | 651.07 | −205.77 | −0.004 | −0.02 | |
| 2 | 0.32025 | 0.000012 | 0.0000 | 0.0000 | ||||||||
| 3 | 0.32982 | 0.556082 | 0.5569 | 0.5551 | ||||||||
| 4 | 0.53625 | 0.603912 | 0.6031 | 0.6049 | ||||||||
| Optimization Method | Load CL (RT) | Power (KW) | Standard Deviation | CPU Time (s) | ||
|---|---|---|---|---|---|---|
| Max | Min | Mean | ||||
| IFOA | 2610(90%) | 1857.299 | 1857.299 | 1857.299 | 0 | 0.68 |
| DCEDA | 2610(90%) | 1858.62 | 1857.30 | 1857.43 | 0.314 | 0.67 |
| IFOA | 2320(80%) | 1455.665 | 1455.665 | 1455.665 | 0 | 0.66 |
| DCEDA | 2320(80%) | 1457.41 | 1455.66 | 1455.77 | 0.283 | 0.67 |
| IFOA | 2030(70%) | 1178.137 | 1178.137 | 1178.137 | 0 | 0.65 |
| DCEDA | 2030(70%) | 1178.72 | 1178.14 | 1178.20 | 0.096 | 0.64 |
| IFOA | 1740(60%) | 998.533 | 998.533 | 998.533 | 0 | 0.63 |
| DCEDA | 1740(60%) | 1000.56 | 998.53 | 998.61 | 0.627 | 0.62 |
| IFOA | 1450(50%) | 820.073 | 820.073 | 820.073 | 0 | 0.55 |
| DCEDA | 1450(50%) | 822.36 | 820.07 | 820.24 | 0.463 | 0.54 |
| IFOA | 1160(40%) | 651.072 | 651.072 | 651.072 | 0 | 0.47 |
| DCEDA | 1160(40%) | 656.72 | 651.09 | 651.35 | 1.708 | 0.48 |
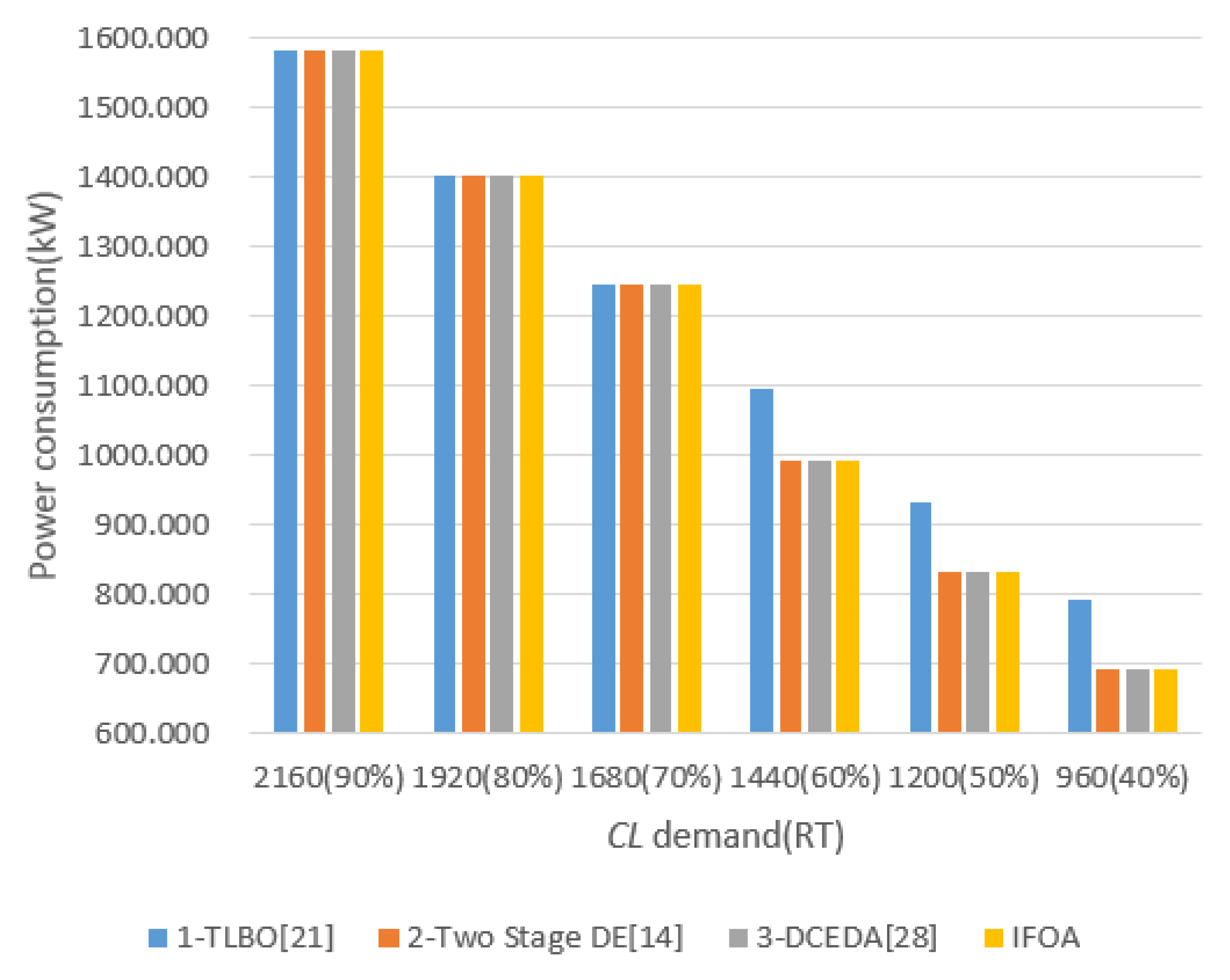
| CL(RT) | Chiller | TLBO [21] | Two Stage DE [14] | DCEDA [28] | IFOA | Energy Saving/KW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | PLRi | Power (KW) (A) | PLRi | Power (KW) (B) | PLRi | Power (KW) (C) | PLRi | Power (KW) (D) | D-A | D-B | D-C | |
| 2160(90%) | 1 | 0.725 | 1583.82 | 0.7253 | 1583.81 | 0.7265 | 1583.81 | 0.7254 | 1583.81 | −0.01 | 0 | 0 |
| 2 | 0.975 | 0.9747 | 0.9735 | 0.9746 | ||||||||
| 3 | 1.000 | 1.0000 | 1.0000 | 1.0000 | ||||||||
| 1920(80%) | 1 | 0.66 | 1403.20 | 0.6591 | 1403.20 | 0.6609 | 1403.20 | 0.6588 | 1403.20 | 0 | 0 | 0 |
| 2 | 0.86 | 0.8585 | 0.8557 | 0.8589 | ||||||||
| 3 | 0.88 | 0.8824 | 0.8834 | 0.8823 | ||||||||
| 1680(70%) | 1 | 0.59415 | 1244.34 | 0.5961 | 1244.32 | 0.5942 | 1244.32 | 0.5959 | 1244.32 | −0.02 | 0 | 0 |
| 2 | 0.74365 | 0.7447 | 0.7455 | 0.7453 | ||||||||
| 3 | 0.76220 | 0.7591 | 0.7603 | 0.7588 | ||||||||
| 1440(60%) | 1 | 0.000 | 1094.55 | 0.0000 | 993.60 | 0.0000 | 993.60 | 0.0000 | 993.60 | −100.95 | 0 | 0 |
| 2 | 0.885 | 0.8855 | 0.8858 | 0.8854 | ||||||||
| 3 | 0.915 | 0.9145 | 0.9142 | 0.9146 | ||||||||
| 1200(50%) | 1 | 0.000 | 933.275 | 0.0000 | 832.33 | 0.0000 | 832.33 | 0.0000 | 832.33 | −100.945 | 0 | 0 |
| 2 | 0.743 | 0.7435 | 0.7425 | 0.7431 | ||||||||
| 3 | 0.757 | 0.7565 | 0.7575 | 0.7569 | ||||||||
| 960(40%) | 1 | 0.00 | 793.201 | 0.0000 | 692.25 | 0.0000 | 692.25 | 0.0000 | 692.25 | −100.951 | 0 | 0 |
| 2 | 0.57 | 0.5699 | 0.5683 | 0.5700 | ||||||||
| 3 | 0.63 | 0.6301 | 0.6317 | 0.6300 | ||||||||
| Optimization Method | Load CL (RT) | Power(KW) | Standard Deviation | CPU Time (s) | ||
|---|---|---|---|---|---|---|
| Max | Min | Mean | ||||
| IFOA | 2160(90%) | 1583.807 | 1583.807 | 1583.807 | 0 | 0.13 |
| DCEDA | 2160(90%) | 1585.24 | 1583.81 | 1583.98 | 0.295 | 0.12 |
| IFOA | 1920(80%) | 1403.196 | 1403.196 | 1403.196 | 0 | 0.12 |
| DCEDA | 1920(80%) | 1405.01 | 1403.20 | 1403.32 | 0.272 | 0.11 |
| IFOA | 1680(70%) | 1244.325 | 1244.325 | 1244.325 | 0 | 0.12 |
| DCEDA | 1680(70%) | 1244.83 | 1244.32 | 1244.37 | 0.087 | 0.11 |
| IFOA | 1440(60%) | 993.602 | 993.602 | 993.602 | 0 | 0.10 |
| DCEDA | 1440(60%) | 995.07 | 993.60 | 993.66 | 0.209 | 0.10 |
| IFOA | 1200(50%) | 832.325 | 832.325 | 832.325 | 0 | 0.10 |
| DCEDA | 1200(50%) | 834.30 | 832.33 | 832.42 | 0.316 | 0.10 |
| IFOA | 960(40%) | 692.251 | 692.251 | 692.251 | 0 | 0.10 |
| DCEDA | 960(40%) | 695.22 | 692.25 | 692.39 | 0.485 | 0.10 |
| Number of Optimal Results | Ratio of Optimal Result | |
|---|---|---|
| Case 1 | 3 | 60% (3/5) |
| Case 2 | 5 | 83.3% (5/6) |
| Case 3 | 6 | 100% (6/6) |
| Total | 14 | 82.4% (14/17) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, M.-Y.; Li, J.-Q.; Han, Y.-Y.; Dong, J.-X. Optimal Chiller Loading for Energy Conservation Using an Improved Fruit Fly Optimization Algorithm. Energies 2020, 13, 3760. https://doi.org/10.3390/en13153760
Qi M-Y, Li J-Q, Han Y-Y, Dong J-X. Optimal Chiller Loading for Energy Conservation Using an Improved Fruit Fly Optimization Algorithm. Energies. 2020; 13(15):3760. https://doi.org/10.3390/en13153760
Chicago/Turabian StyleQi, Min-Yong, Jun-Qing Li, Yu-Yan Han, and Jin-Xin Dong. 2020. "Optimal Chiller Loading for Energy Conservation Using an Improved Fruit Fly Optimization Algorithm" Energies 13, no. 15: 3760. https://doi.org/10.3390/en13153760
APA StyleQi, M.-Y., Li, J.-Q., Han, Y.-Y., & Dong, J.-X. (2020). Optimal Chiller Loading for Energy Conservation Using an Improved Fruit Fly Optimization Algorithm. Energies, 13(15), 3760. https://doi.org/10.3390/en13153760





