Multiphase PMSM with Asymmetric Windings for Electric Drive
Abstract
:1. Introduction
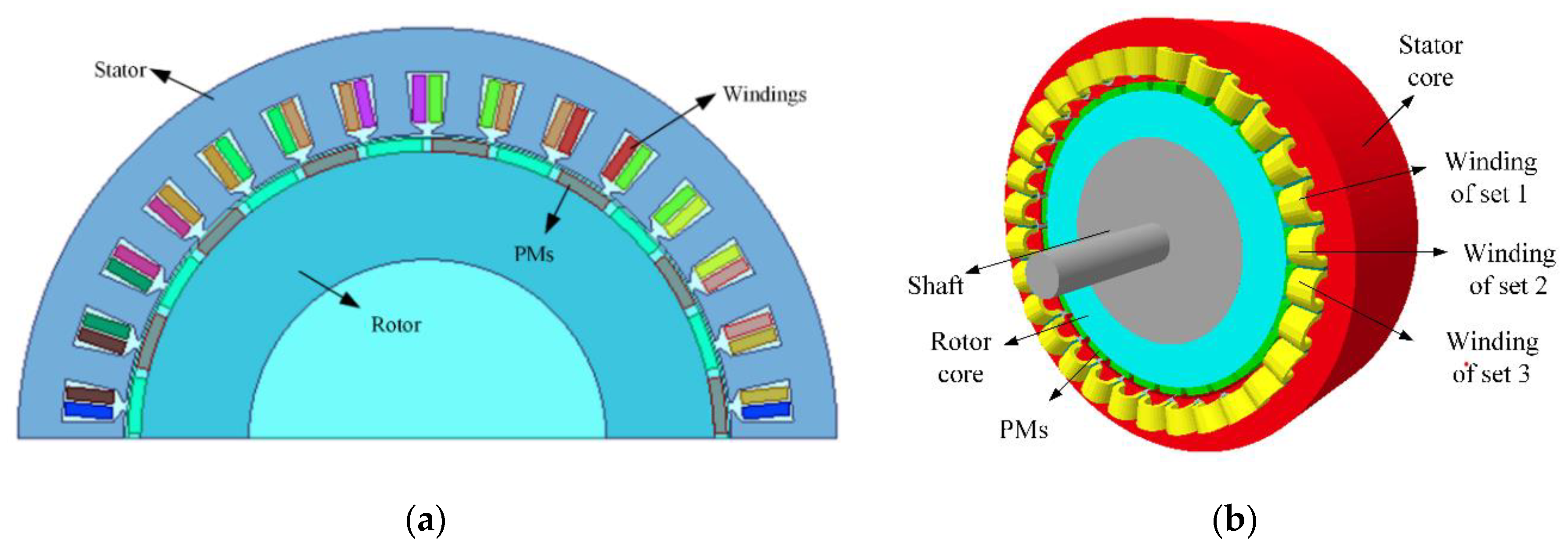
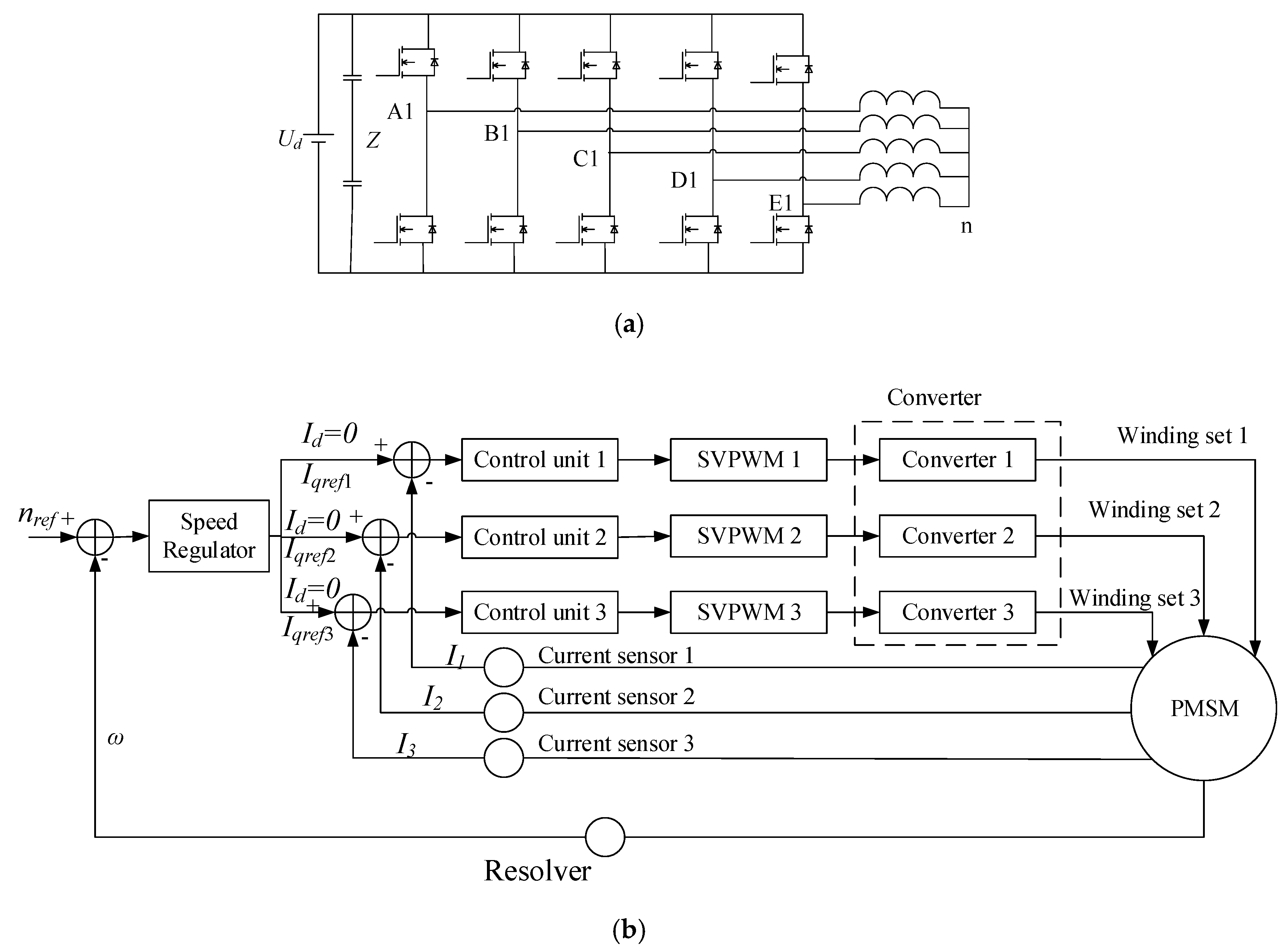
2. Asymmetric Winding Multiphase Motor and Its Model
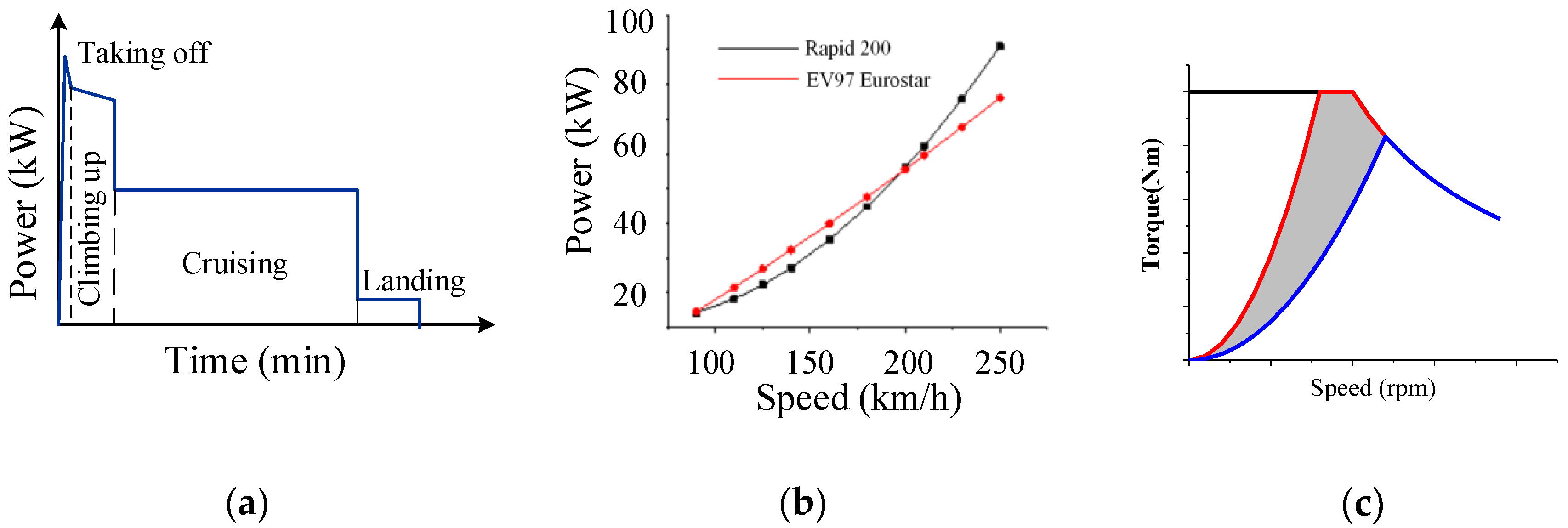
2.1. Work Area of Propulsion Motor
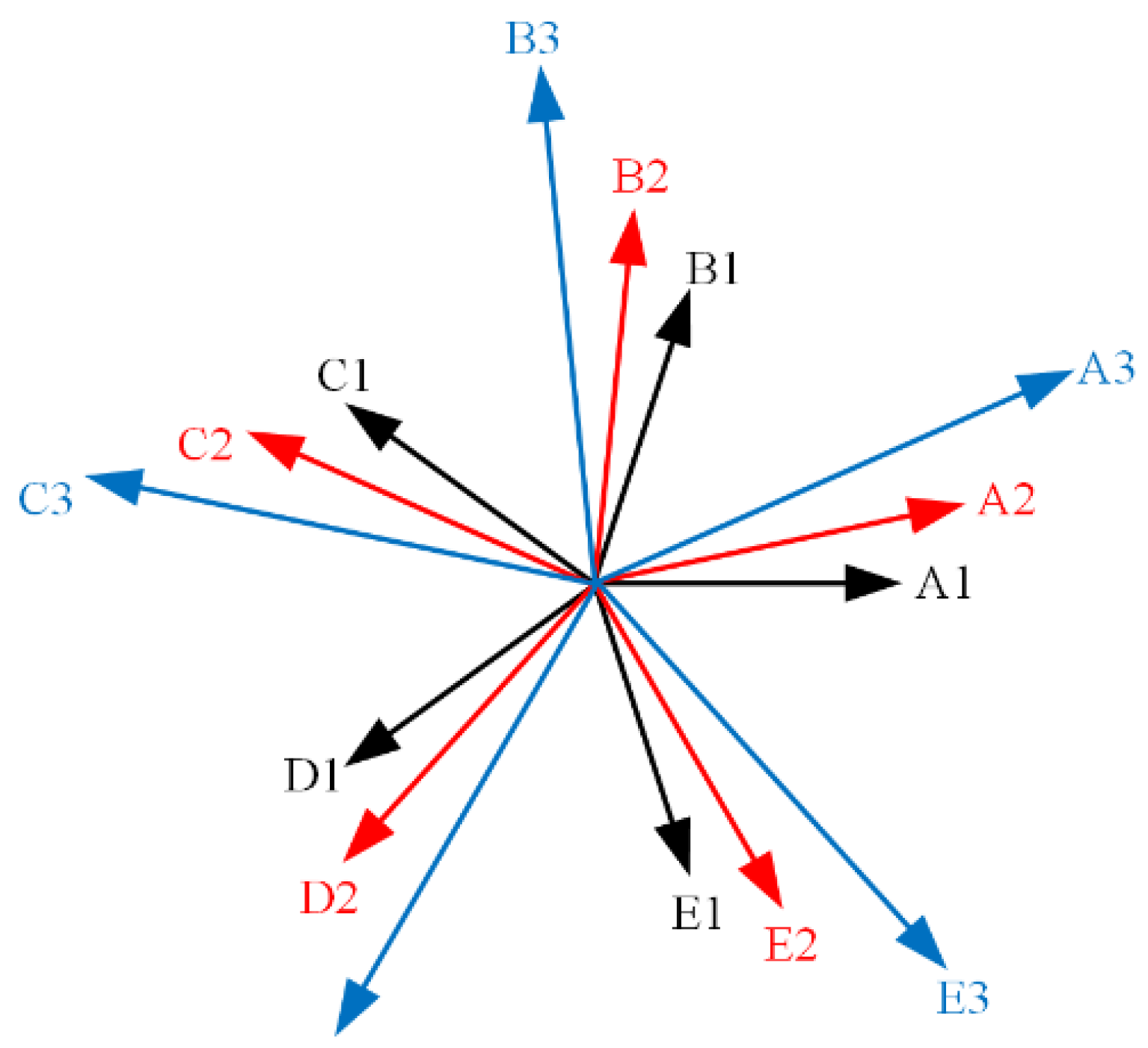
2.2. Matching Mode of Windings
- Equal torque mode: the three sets of windings have same rated torque but different rated speed;
- Equal speed mode: the three sets of windings have same rated speed but different rated torque;
- Equal power mode: the three sets of windings have same rated power but different rated speed and torque.
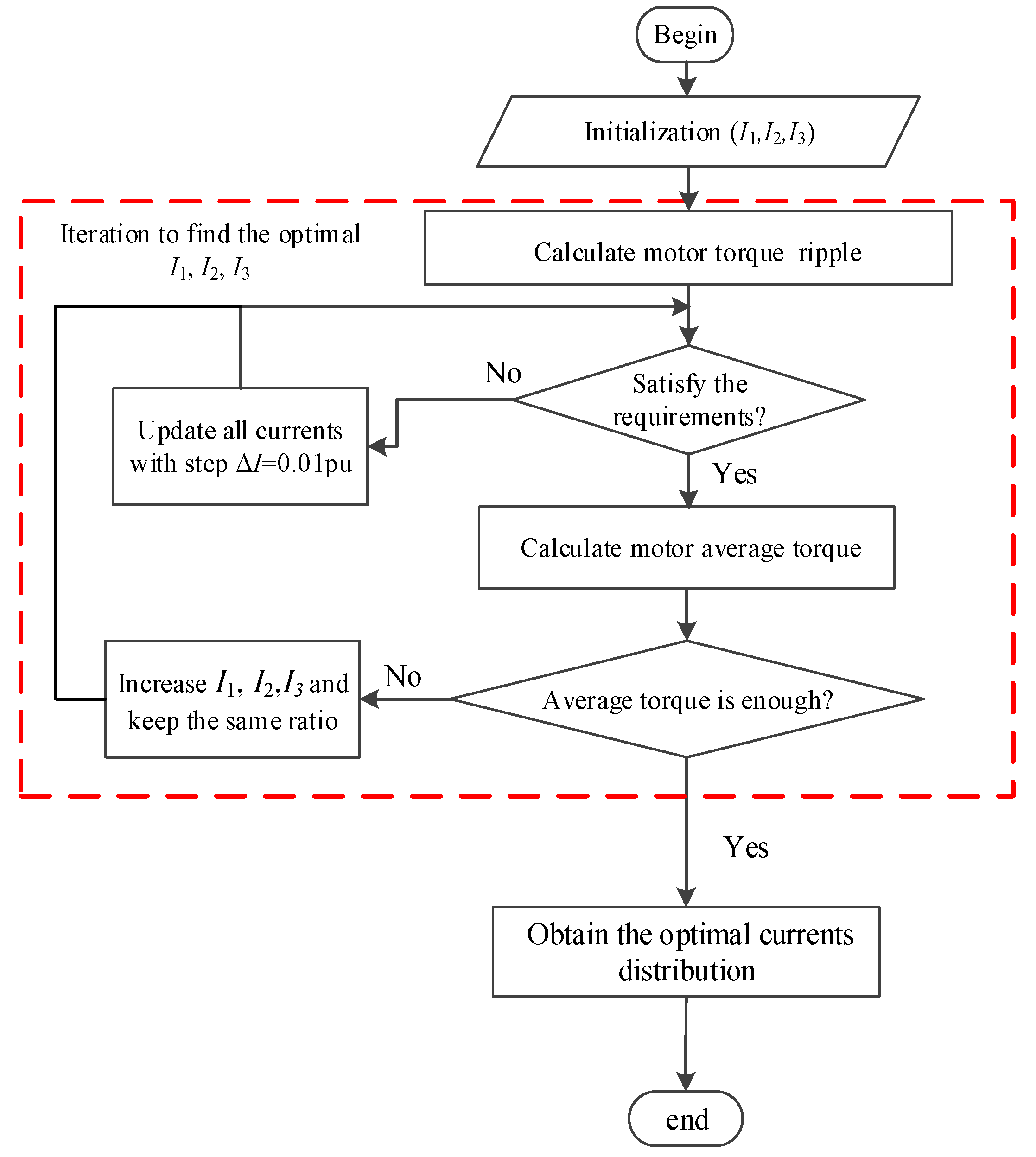
3. Efficiency Optimization Strategy of Asymmetric Winding
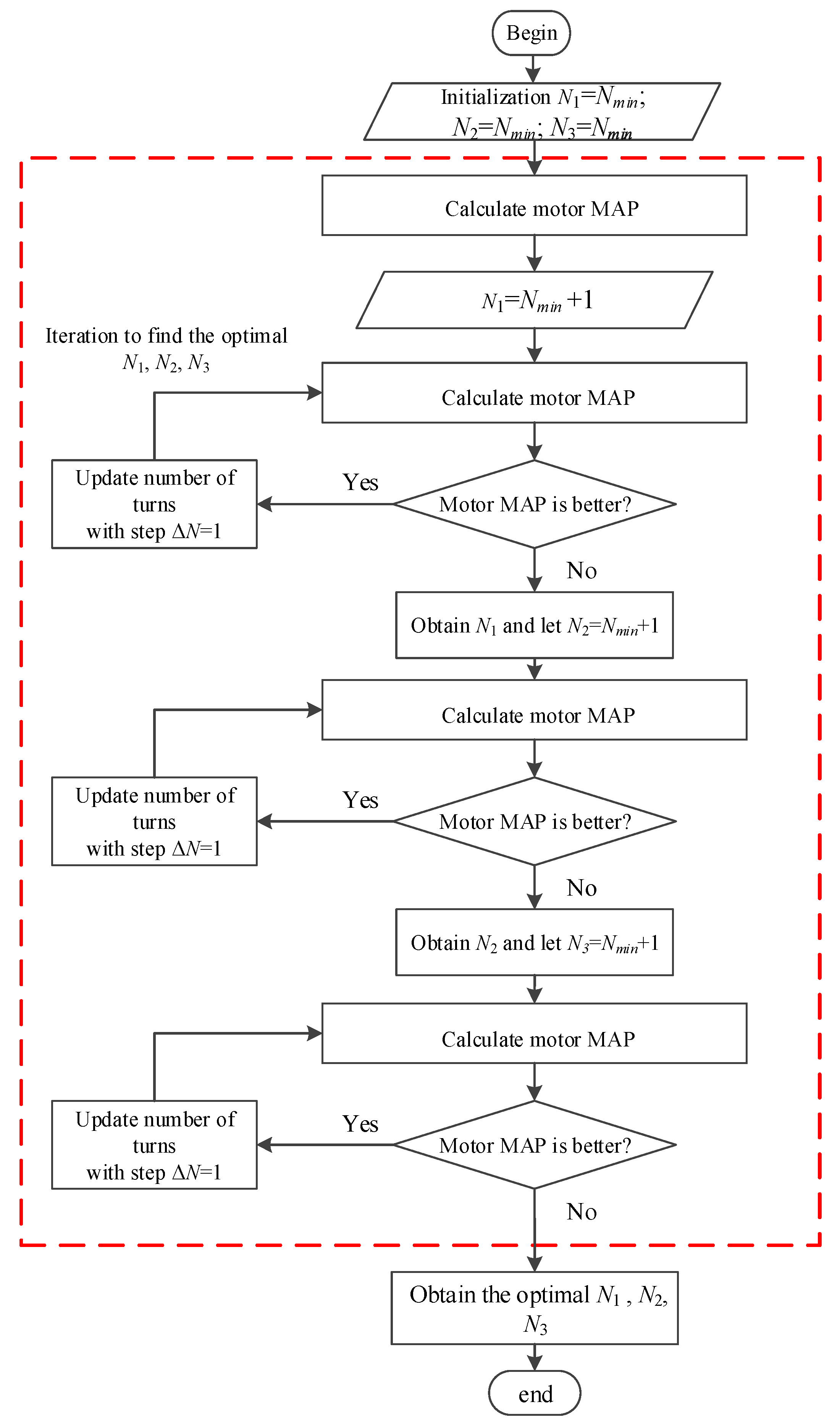
4. Matching of Winding Parameters
5. Simulation Analysis
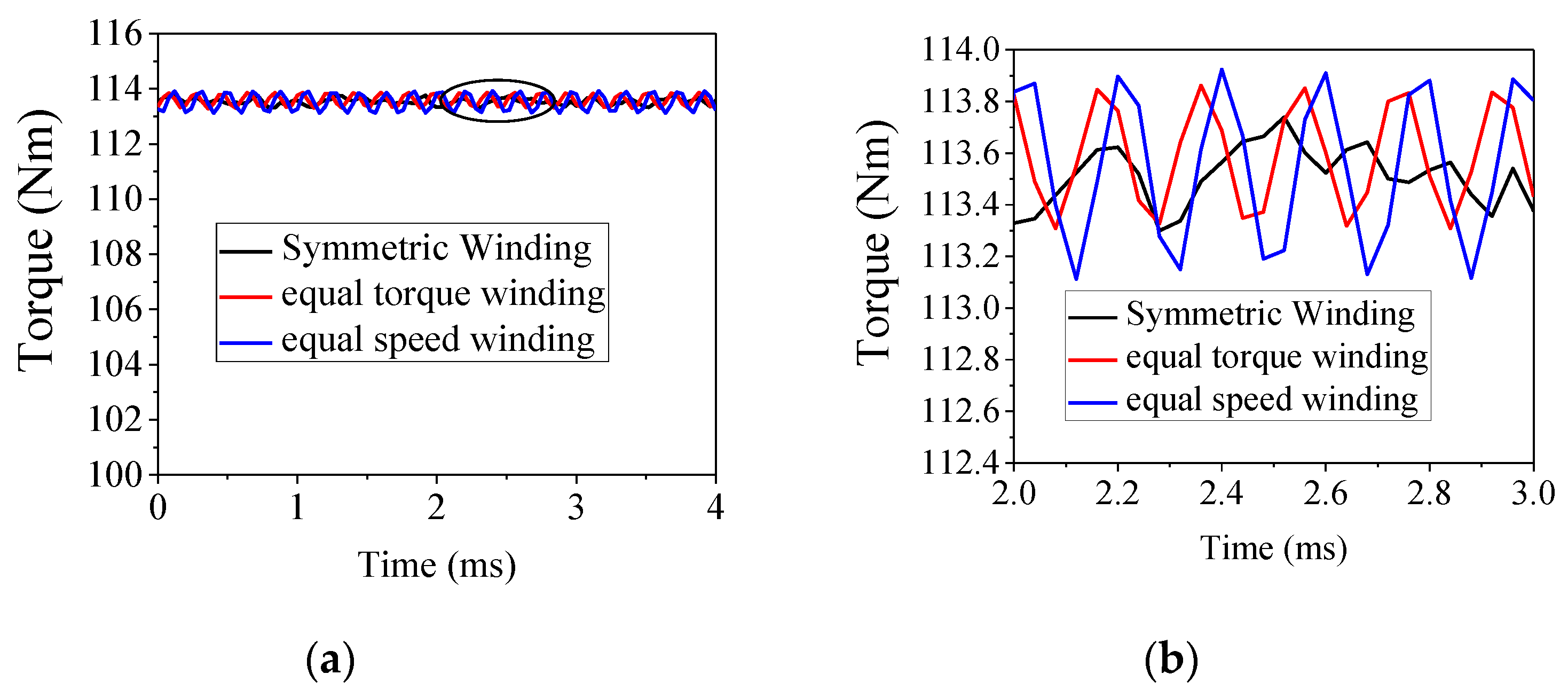
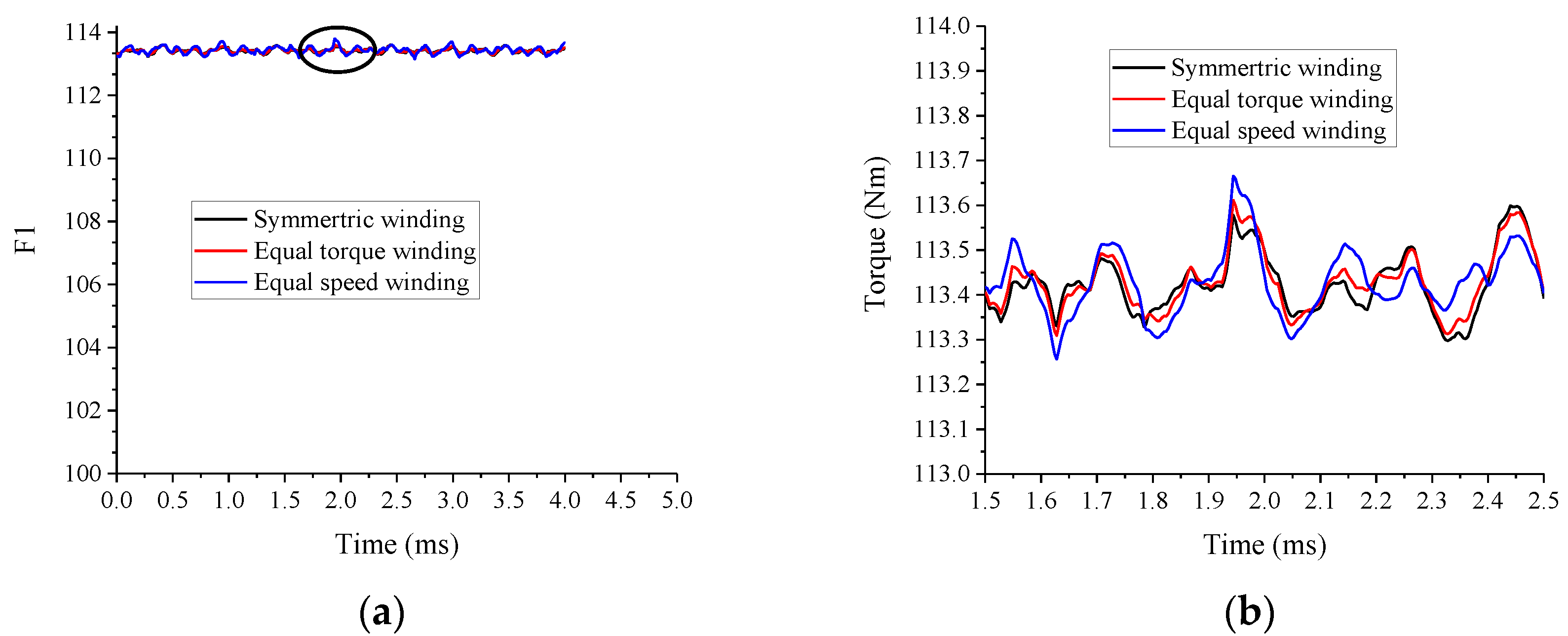
5.1. Motor Torque Characteristic Simulation
5.2. Optimization of Electromagnetic Design
5.3. Motor Efficiency Simulation
5.4. Size and Cost of the Motor System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kietley, J.L.; Banerjee, A.; Englebretson, S. Motors for Ship Propulsion. Proc. IEEE 2015, 103, 2320–2332. [Google Scholar] [CrossRef]
- Thongam, J.S.; Tarbouchi, M.; Okou, A.F.; Bouchard, D.; Beguenane, R. Trend in naval ship Propulsion drive motor technology. In Proceedings of the IEEE Electrical Power and Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–5. [Google Scholar]
- Soghomonian, Z.; Prousalidis, J.M.; Kanellos, F.; Dallas, S.E.; Spathis, D.; Kourmpelis, T.; Tsekouras, G. The role of efficiency of electric machinery on green shipping. In Proceedings of the International Conference on Electrical Machines, Lausanne, Switzerland, 4–7 September 2016; pp. 2968–3974. [Google Scholar]
- Wang, F.; Zhang, Z.; Ericsen, T.; Raju, R.; Burgos, R.; Boroyevich, D. Advances in Power Conversion and Drives for Shipboard Systems. Proc. IEEE 2015, 103, 2285–2311. [Google Scholar] [CrossRef]
- Park, S.J.; Song, J.H.; Choi, H.Y.; Lee, M.L.; Kong, Y.K.; Bin, J.G. A study on design of inverter for multi-phase brushless DC ship propulsion motor. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–5. [Google Scholar]
- Choi, H.Y.; Park, S.J.; Lee, M.L.; Kong, Y.K.; Bin, J.G. Efficiency compensation of multi-phase PM motor with redundant structure. In Proceedings of the XIX International Conference on Electrical Machines—ICEM, Rome, Italy, 6–8 September 2010; pp. 1–3. [Google Scholar]
- Moinoddin, S.; Iqbal, A.; Abu-Rub, H.; Khan, M.R.; Ahmed, S.M. Three-Phase to Seven-Phase Power Converting Transformer. IEEE Trans. Energy Convers. 2012, 27, 757–766. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, L.; Li, Y.; Zheng, Z. Vector control of fixed joint double fifteen-phase induction motors system with propeller load. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar]
- Choi, H.; Jasinski, M.; Liu, J. Novel permanent magnet systems for high efficiency electric ships. In Proceedings of the IEEE Electric Ship Technologies Symposium (ESTS), Alexandria, Egypt, 21–24 June 2015; pp. 219–223. [Google Scholar]
- Heising, C.; Staudt, V.; Steimel, A. Optimized energy-efficient drive system for ship propulsion. In Proceedings of the IEEE Electric Ship Technologies Symposium, Alexandria, Egypt, 10–13 April 2011; pp. 292–295. [Google Scholar]
- Frank, M.; van Habelt, P.; Kummeth, P.; Massek, P.; Nick, W.; Rothfischer, H.; Schmidt, H.; Wacker, B.; Neumuller, H.W.; Nerowski, G.; et al. High-Temperature Superconducting Rotating Machines for Ship Applications. IEEE Trans. Appl. Supercond. 2006, 16, 1465–1468. [Google Scholar] [CrossRef]
- Yanamoto, T.; Izumi, M.; Umemoto, K.; Oryu, T.; Murase, Y.; Kawamura, M. Load Test of 3-MW HTS Motor for Ship Propulsion. IEEE Trans. Appl. Supercond. 2017, 27, 5204305. [Google Scholar] [CrossRef]
- Baik, S.; Kwon, Y.; Park, S.; Kim, H. Performance Analysis of a Superconducting Motor for Higher Efficiency Design. IEEE Trans. Appl. Supercond. 2013, 23, 20–25. [Google Scholar]
- Park, S.W.; Park, H.S.; Moon, J.J. Maximum efficiency control method in 7-phase BLDC motor by changing the number of the excited phase windings. In Proceedings of the Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Debbou, M.; Damdoum, A.; Pietrzak-David, M. Optimal sliding mode control for DFIM electric marine thruster. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Bolvashenkov, I.; Herzog, H.G. Use of Stochastic Models for Operational Efficiency Analysis of Multi Power Source Traction Drives. In Proceedings of the Second International Symposium on Stochastic Models in Reliability Engineering, Life Science and Operations Management, Beer-Sheva, Israel, 15–18 February 2016; pp. 124–130. [Google Scholar]
- Romeo, G.; Moraglio, I.; Novarese, C. ENFICA-FC: Preliminary Survey & Design of 2-Seat Aircraft Powered by Fuel Cells Electric Propulsion. In Proceedings of the 7th AIAA Aviation Technology, Integration and Operations Conference, Belfast, UK, 18–20 September 2014; pp. 202–216. [Google Scholar]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J. Overview of Electric Motor Technologies Used for More Electric Aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar]
- Tomažič, T.; Plevnik, V.; Veble, G. Pipistrel Taurus G4: On Creation and Evolution of the Winning Aeroplane of NASA Green Flight Challenge 2011. Stroj. Vestn. J. Mech. Eng. 2011, 57, 869–878. [Google Scholar] [CrossRef] [Green Version]
- Sarlioglu, B.; Morris, C. More Electric Aircraft-Review, Challenges and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Yeoh, S.S.; Gao, F.; Bozhko, S.; Asher, G. Control Design for PMM-based Starter Generator System for More Electric Aircraft. In Proceedings of the 16th Conference on Power Electronics and Applications, EPE’14-ECCE Europe, Lappeenranta, Finland, 26–28 August 2014; pp. 1–10. [Google Scholar]
- Zhao, X.; Guerrero, J.M.; Wu, X. Review of Aircraft Electric Power Systems and Architectures. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 949–953. [Google Scholar]
- Zhao, T.; Wu, S.; Cui, S. Multiphase PMSM with Asymmetric Windings for More Electric Aircraft. IEEE Trans. Transp. Electrif. 2020. [Google Scholar] [CrossRef]



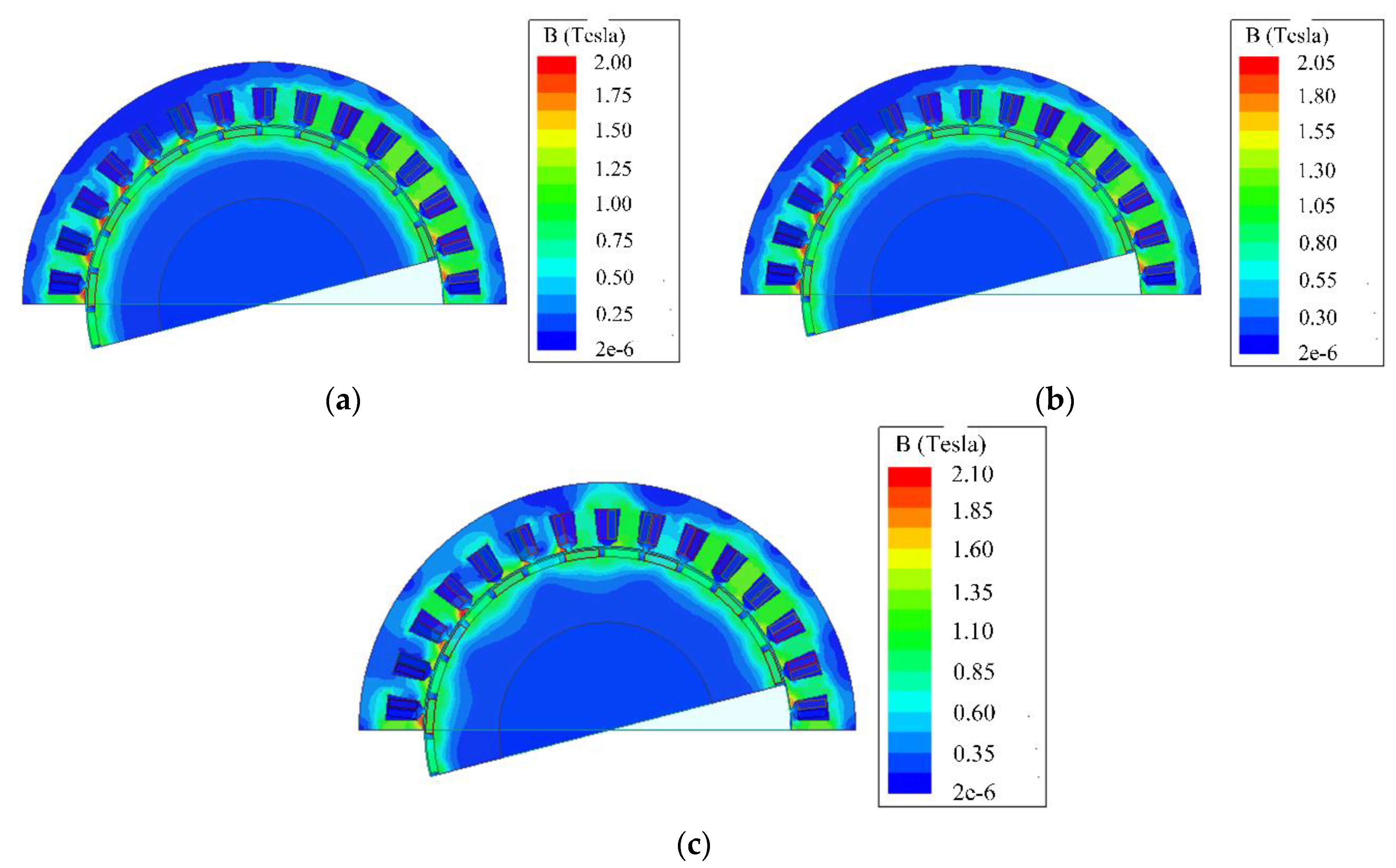

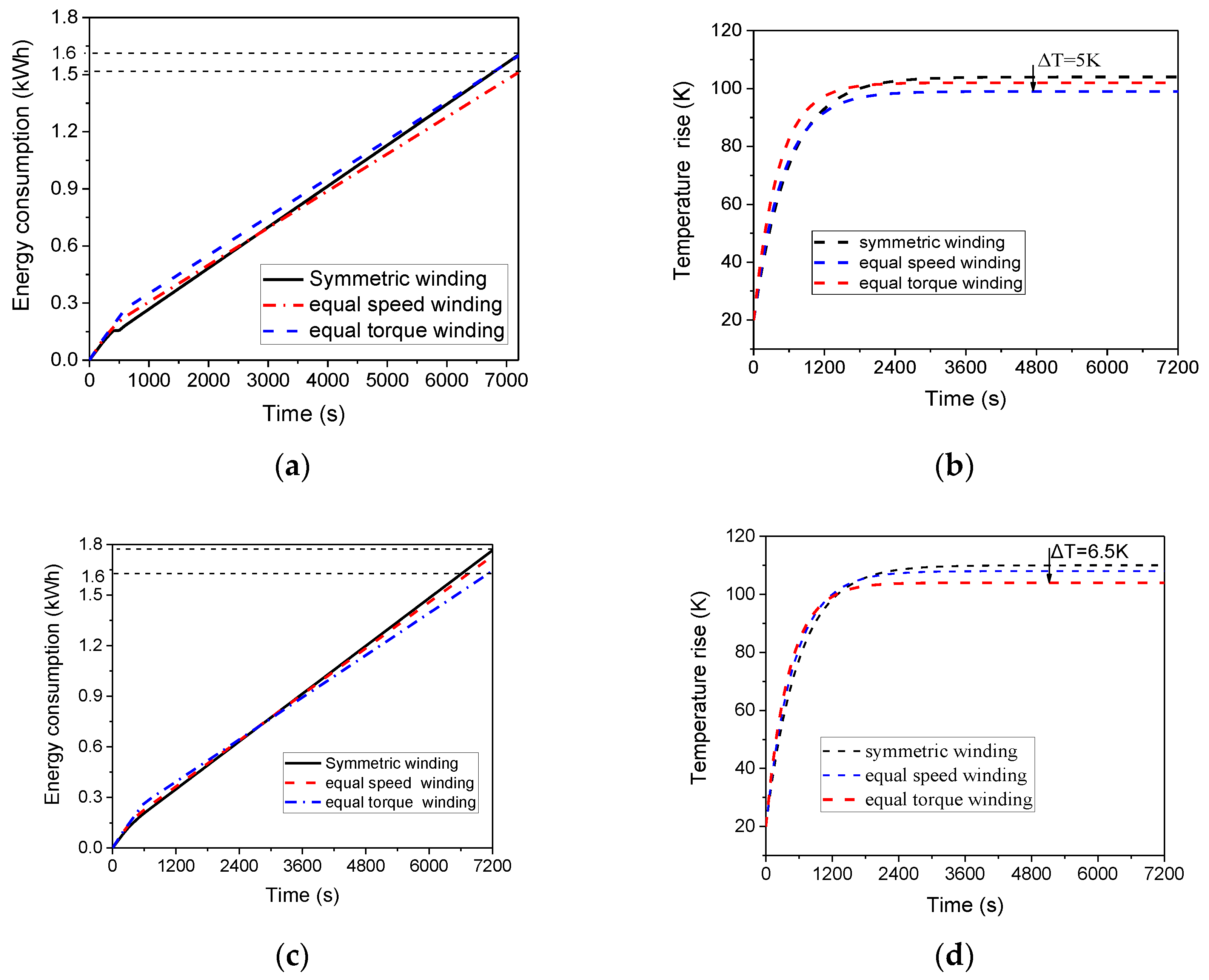
| Parameters | Equal Torque Winding | Equal Speed Winding | Symmetric Winding |
|---|---|---|---|
| DC voltage | 270 V | 270 V | 270 V |
| Rated speed | 1500/2000/2500 rpm | 2000 rpm | 2000 rpm |
| Rated torque | 120 Nm | 120 Nm | 120 Nm |
| Winding 1 | 24 turns, 20 A | 32 turns, 20 A | 32 turns, 15 A |
| Winding 2 | 32 turns, 15 A | 32 turns, 15 A | 32 turns, 15 A |
| Winding 3 | 40 turns, 12 A | 32 turns, 10 A | 32 turns, 15 A |
| Parameters | Equal Torque Winding | Equal Speed Winding |
|---|---|---|
| Rated speed | 1600/2000/2500 rpm | 2000 rpm |
| Rated torque | 120 Nm | 120 Nm |
| Winding 1 | 12 turns, 20.8 A | 16 turns, 18.3 A |
| Winding 2 | 16 turns, 14.7 A | 16 turns, 15.4 A |
| Winding3 | 20 turns, 11.8 A | 16 turns, 11.3 A |
| Motor | Power (kW) | Weight (kg) | Power Density (kw/kg) |
|---|---|---|---|
| Antares 20E | 42 | 29 | 1.45 |
| Rapid 200 | 46 | 38 | 1.21 |
| Diamond HK36 | 30 | 41 | 0.75 |
| Taurus Electro | 40 | 31 | 1.29 |
| Taurus G2 | 30 | 12.8 | 2.34 |
| E-Genius | 58 | 27 | 2.15 |
| Designed in this paper | 20 | 16.4 | 1.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Zhao, T.; Du, B.; Cheng, Y. Multiphase PMSM with Asymmetric Windings for Electric Drive. Energies 2020, 13, 3765. https://doi.org/10.3390/en13153765
Cui S, Zhao T, Du B, Cheng Y. Multiphase PMSM with Asymmetric Windings for Electric Drive. Energies. 2020; 13(15):3765. https://doi.org/10.3390/en13153765
Chicago/Turabian StyleCui, Shumei, Tianxu Zhao, Bochao Du, and Yuan Cheng. 2020. "Multiphase PMSM with Asymmetric Windings for Electric Drive" Energies 13, no. 15: 3765. https://doi.org/10.3390/en13153765






