Analysis and Design of a Double Fuzzy PI Controller of a Voltage Outer Loop in a Reversible Three-Phase PWM Converter
Abstract
1. Introduction
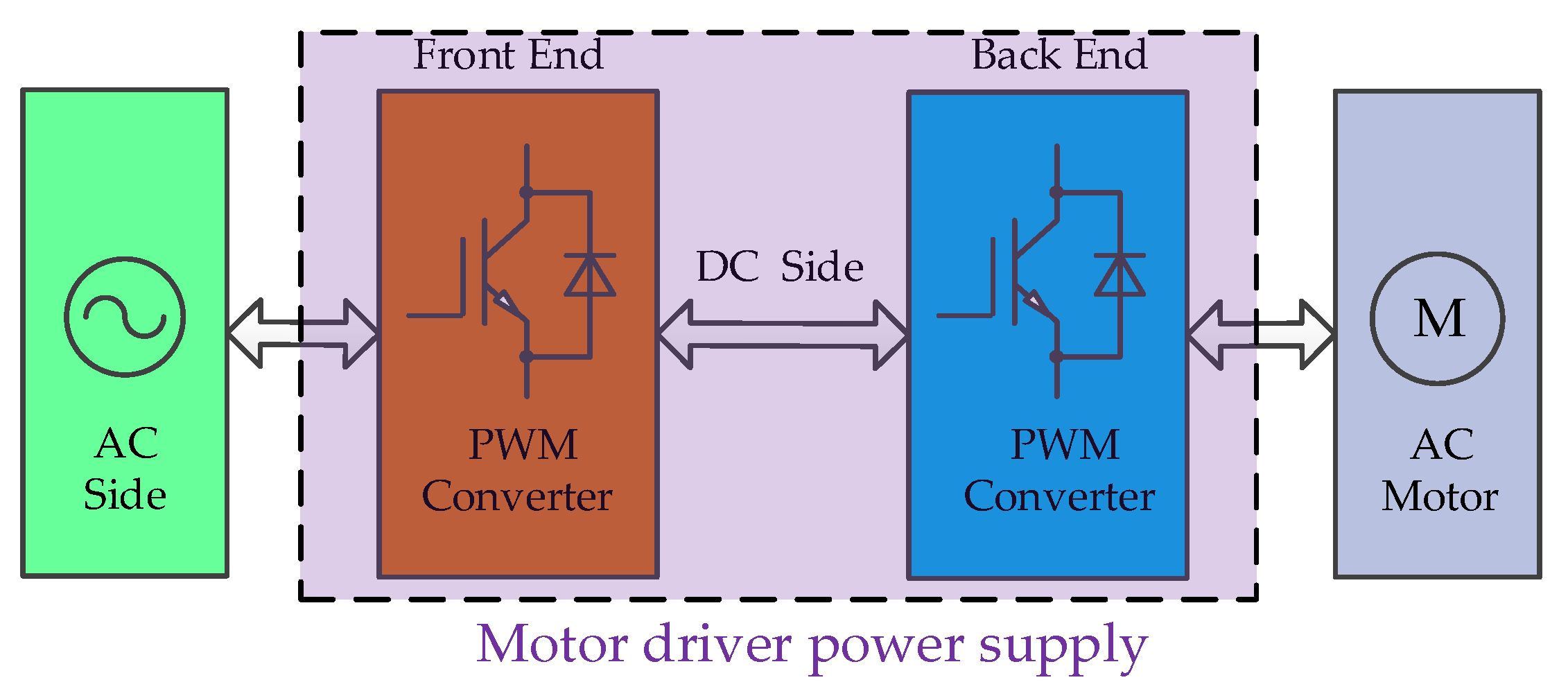
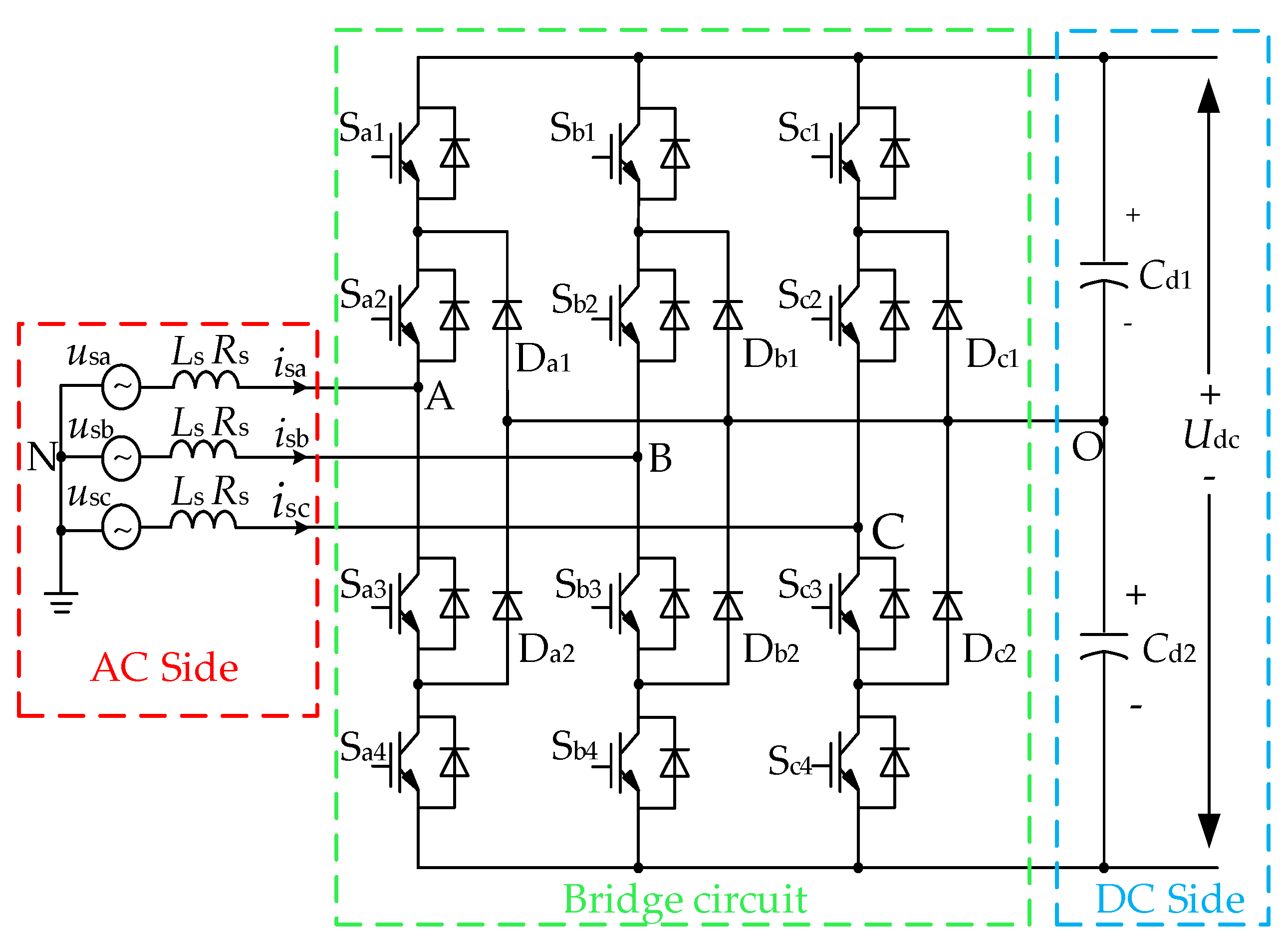
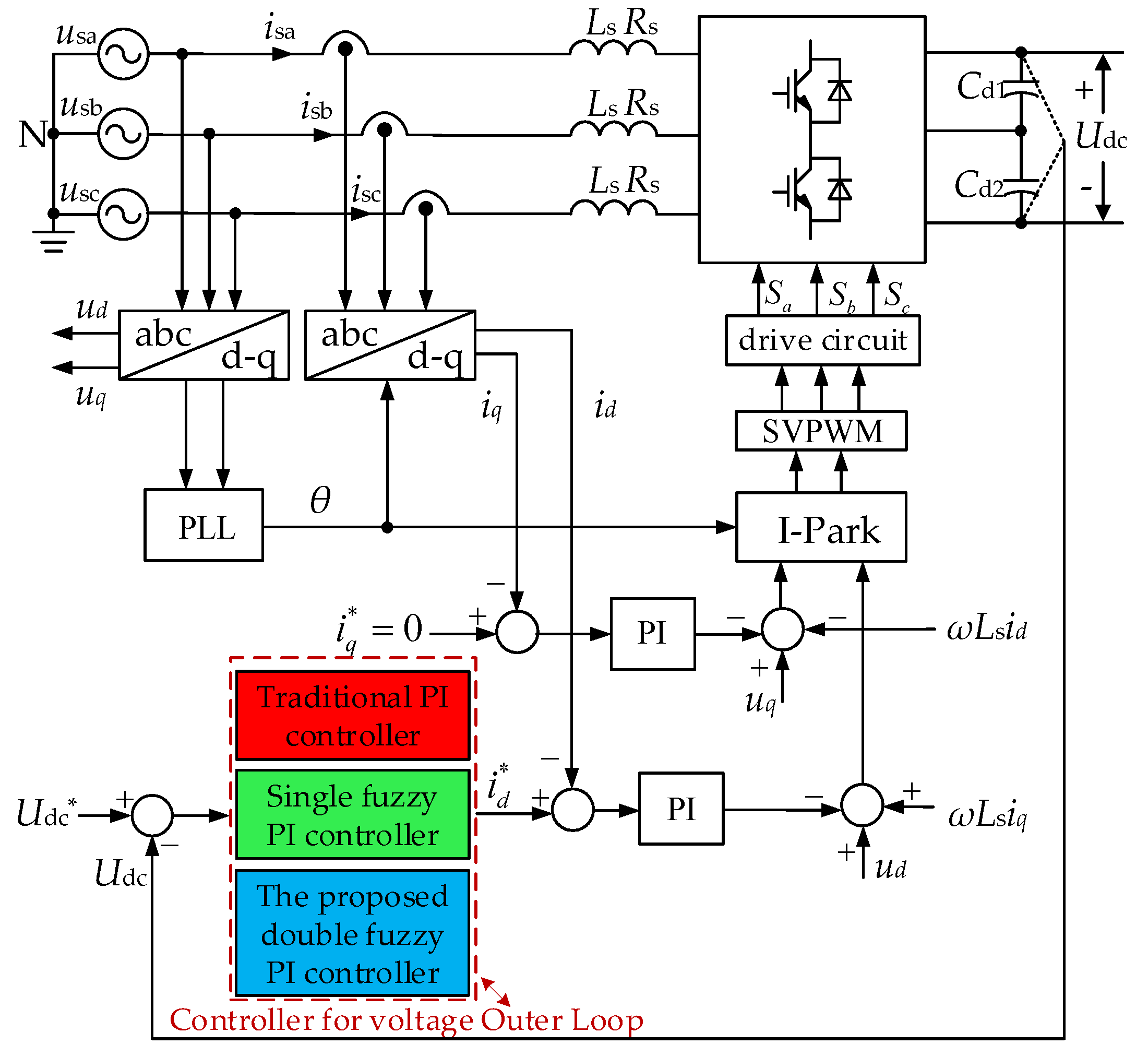
2. Circuit and Control Strategy of Reversible Three-Phase PWM Converter
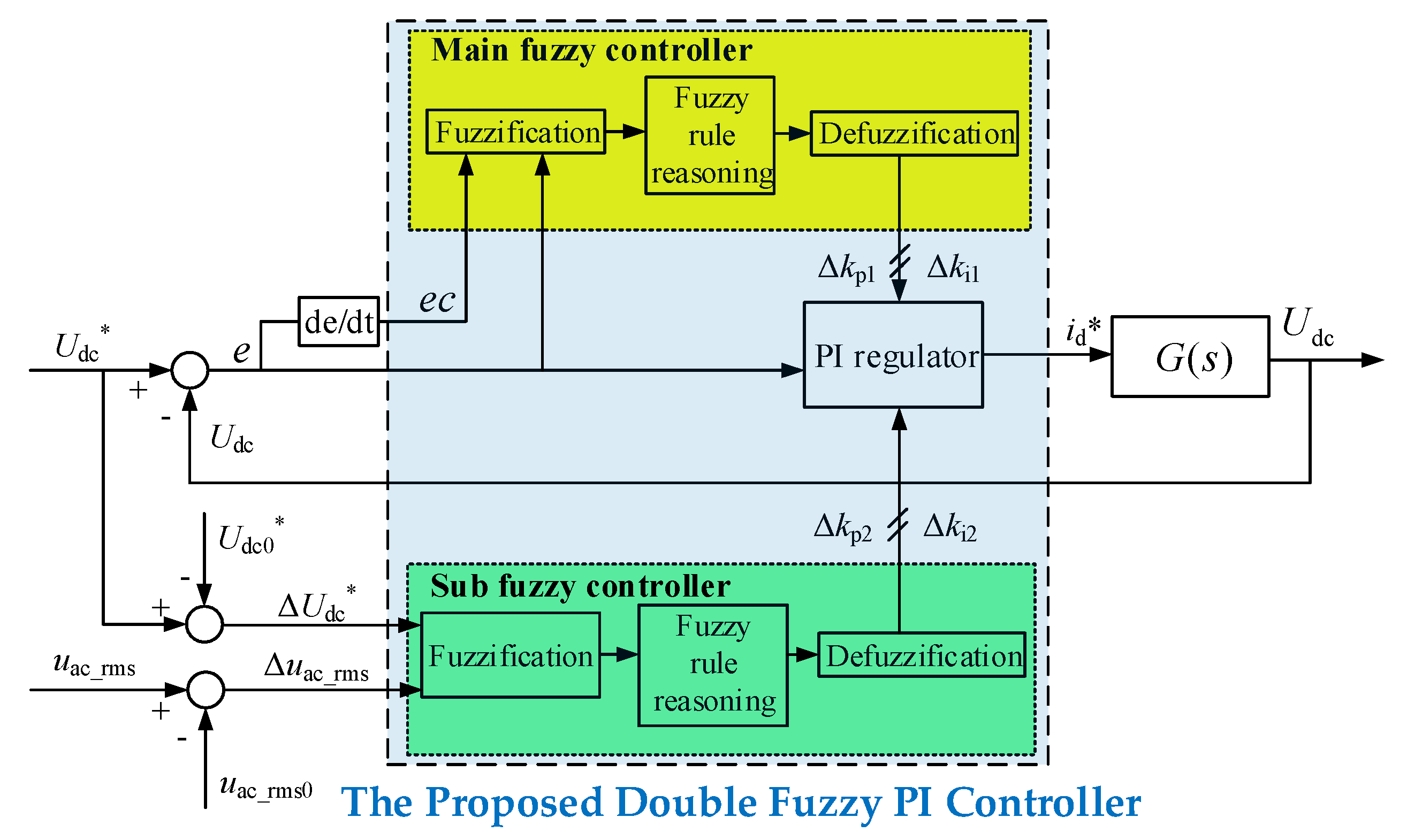
3. Analysis and Design Method of the Double Fuzzy PI Controller for Voltage Outer Loop
3.1. Design of Main Fuzzy Controller
3.1.1. Fuzzification
3.1.2. Fuzzy Rule Reasoning
- 1)
- Proportional coefficient kp—when kp is small, the response speed of the system is slow, the adjustment time is long, the regulation accuracy is low, and the dynamic and static performance of the system poor; with the increase of kp, the system response speed is accelerated, and the system regulation accuracy is increased, but when kp is too large, the system will produce large overshoot, and the oscillation times will increase, the adjustment time will become longer, and even leading to the system instability in serious cases.
- 2)
- Integral coefficient ki—when ki is small, the output static error of the system is difficult to eliminate, which leads to the low adjustment accuracy of the system; with the increase of ki, the elimination speed of static error of the system is accelerated, but if ki is too large, the system will produce integral saturation at the initial stage of response, causing large overshoot, and even leading to the system oscillating, which will affect the stability of the system [29].
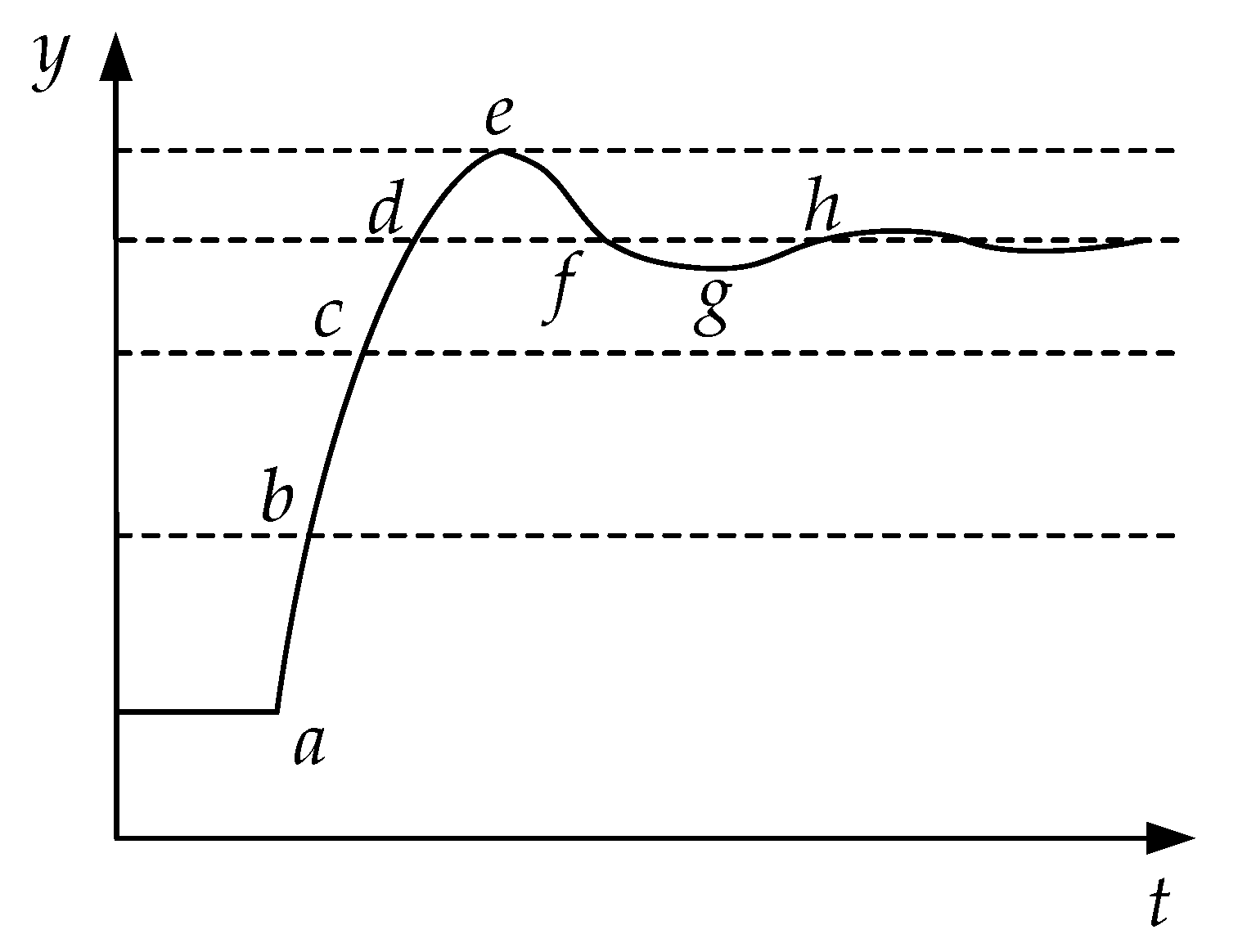
- 1)
- ab section—if e and ec are positive big then the larger kp and the smaller ki should be needed in order to achieve faster response speed and suppress occurrence of large overshoot;
- 2)
- bc section—if e is positive medium and ec is positive big, then larger kp, medium ki are selected in order to reach stable value as soon as possible;
- 3)
- cd section—if e changes from positive small value to 0 and ec is positive big, then the larger kp and ki should be selected in order to implement the stability of the system;
- 4)
- de section—if e changes from 0 to negative small value and ec changes from positive big value to 0, then larger kp and medium ki are needed in order to suppress the overshoot;
- 5)
- ef section—if e is from negative small (or negative middle) value to 0 and ec is from 0 to negative middle value, then the smaller kp should be chosen and ki gradually increases from positive middle value to positive big value in order to reduce or prevent secondary oscillation;
- 6)
- fg section—if e is from 0 to positive small (or positive middle) value and ec from negative big value to negative small value, then kp should be increased gradually and ki should be decreased gradually in order to speed up the system response and prevent overshoot;
- 7)
- gh section—if e decreases gradually from positive small (or positive middle) value to 0 and ec decreases slowly, then kp and ki should be increased gradually in order to make the system have good stability.
- 1)
- R1: if e is NB and ec is NB then Δkp1 is PB and Δki1 is NB
- 2)
- R2: if e is NB and ec is NM then Δkp1 is PB and Δki1 is NB
- 3)
- R3: if e is NB and ec is NS then Δkp1 is PB and Δki1 is NB
- 49)
- R49: if e is PB and ec is PB then Δkp1 is PB and Δki1 is NB
3.1.3. Defuzzification
3.2. Design of the Sub Fuzzy Controller
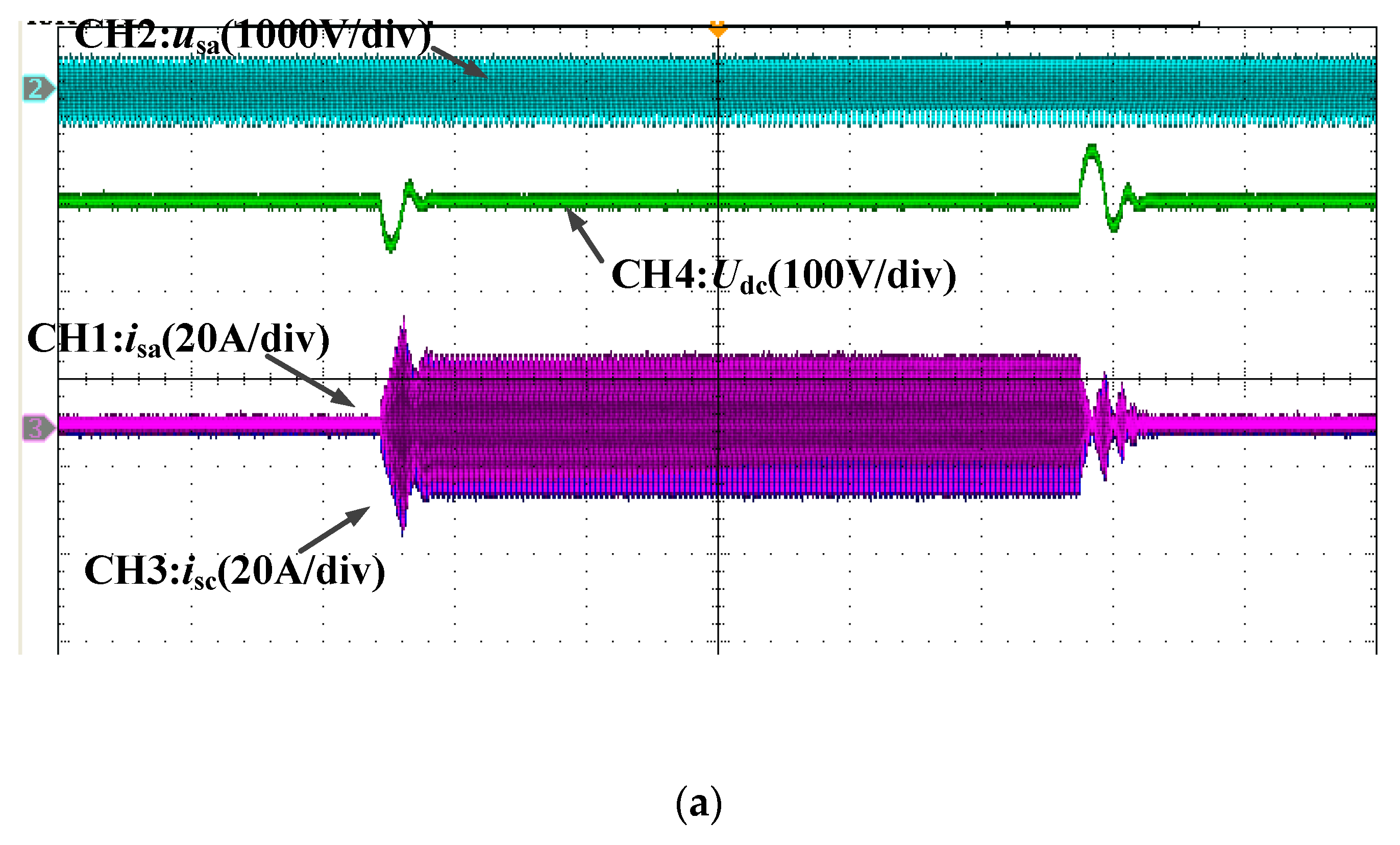
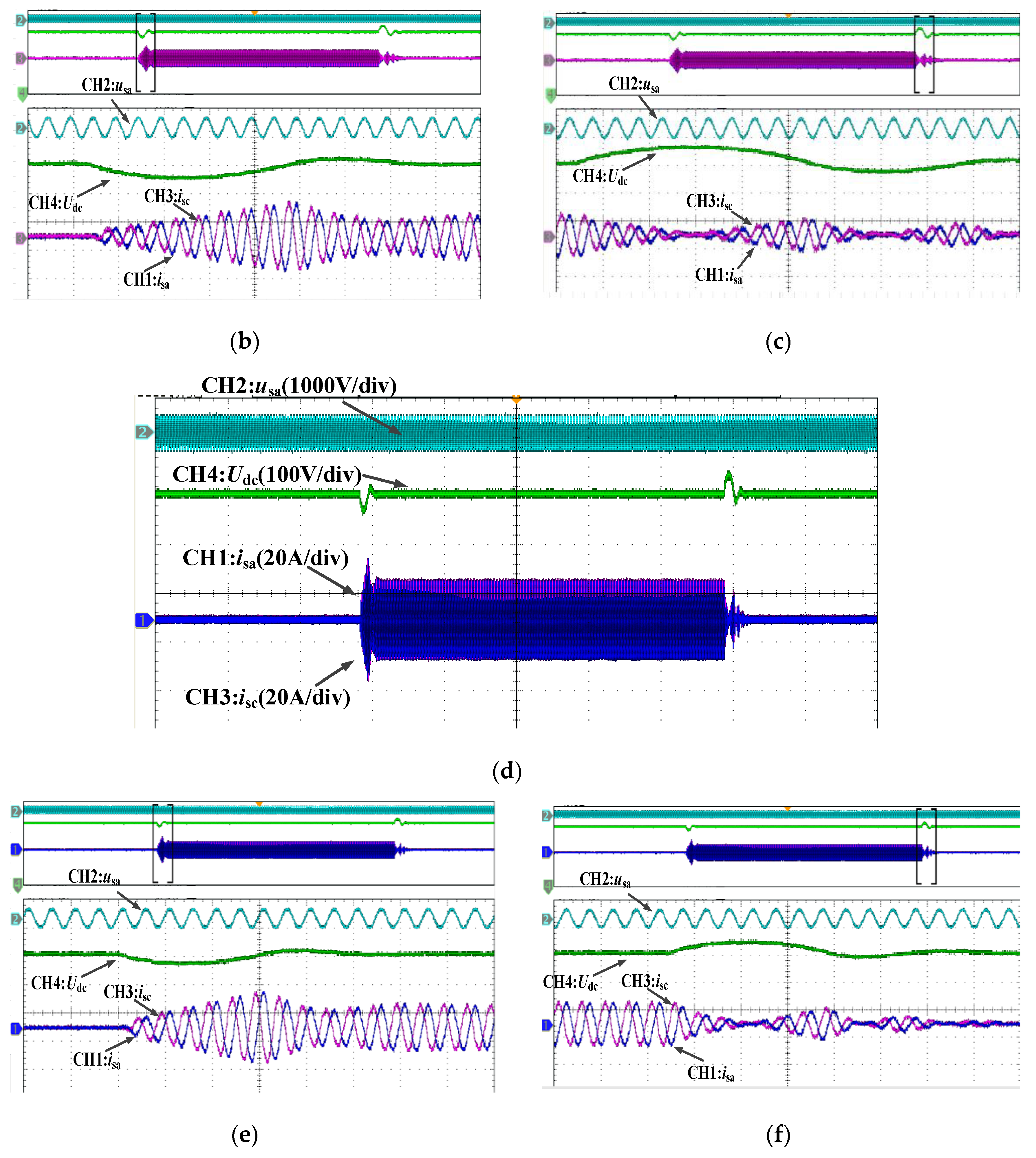
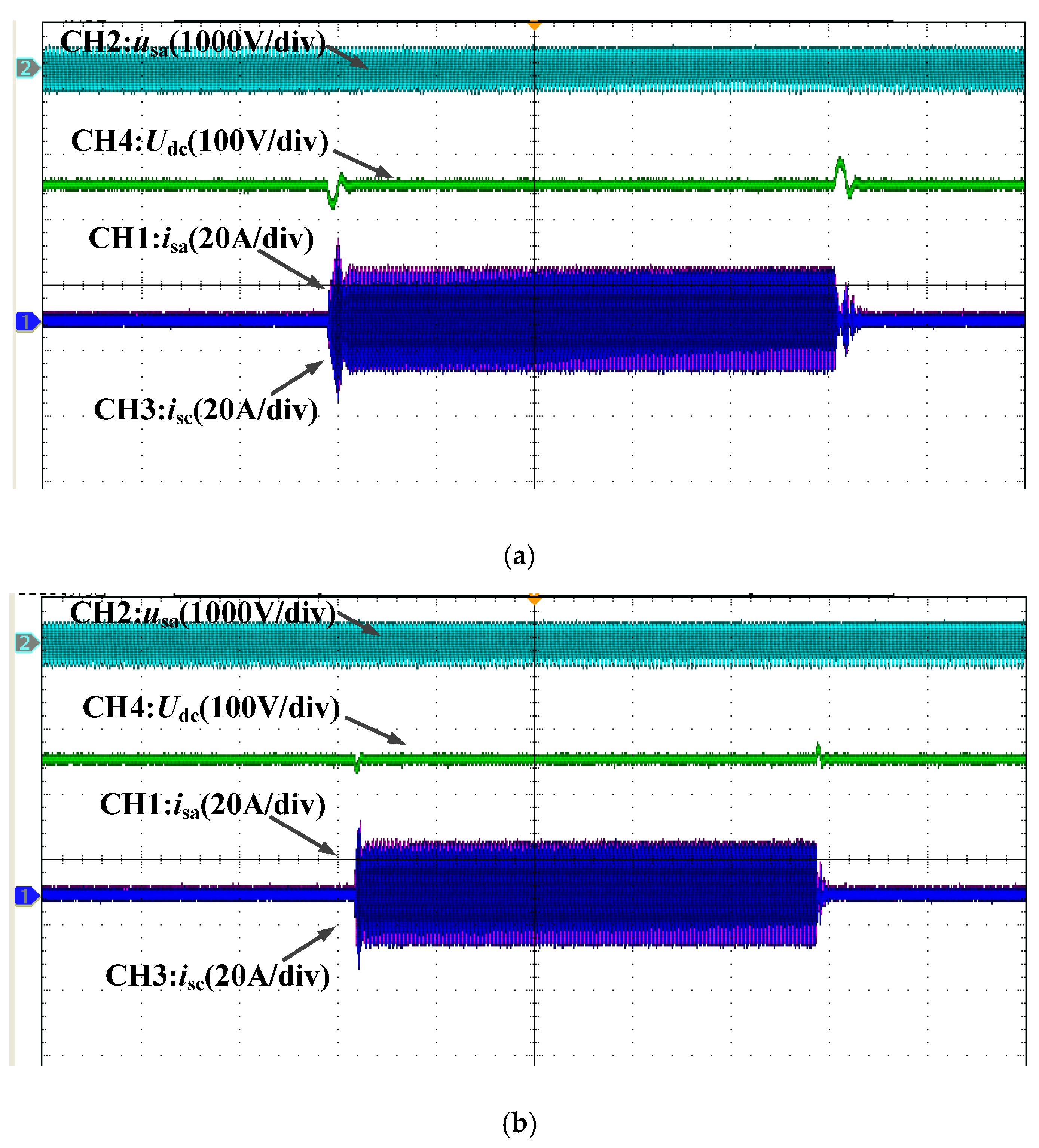
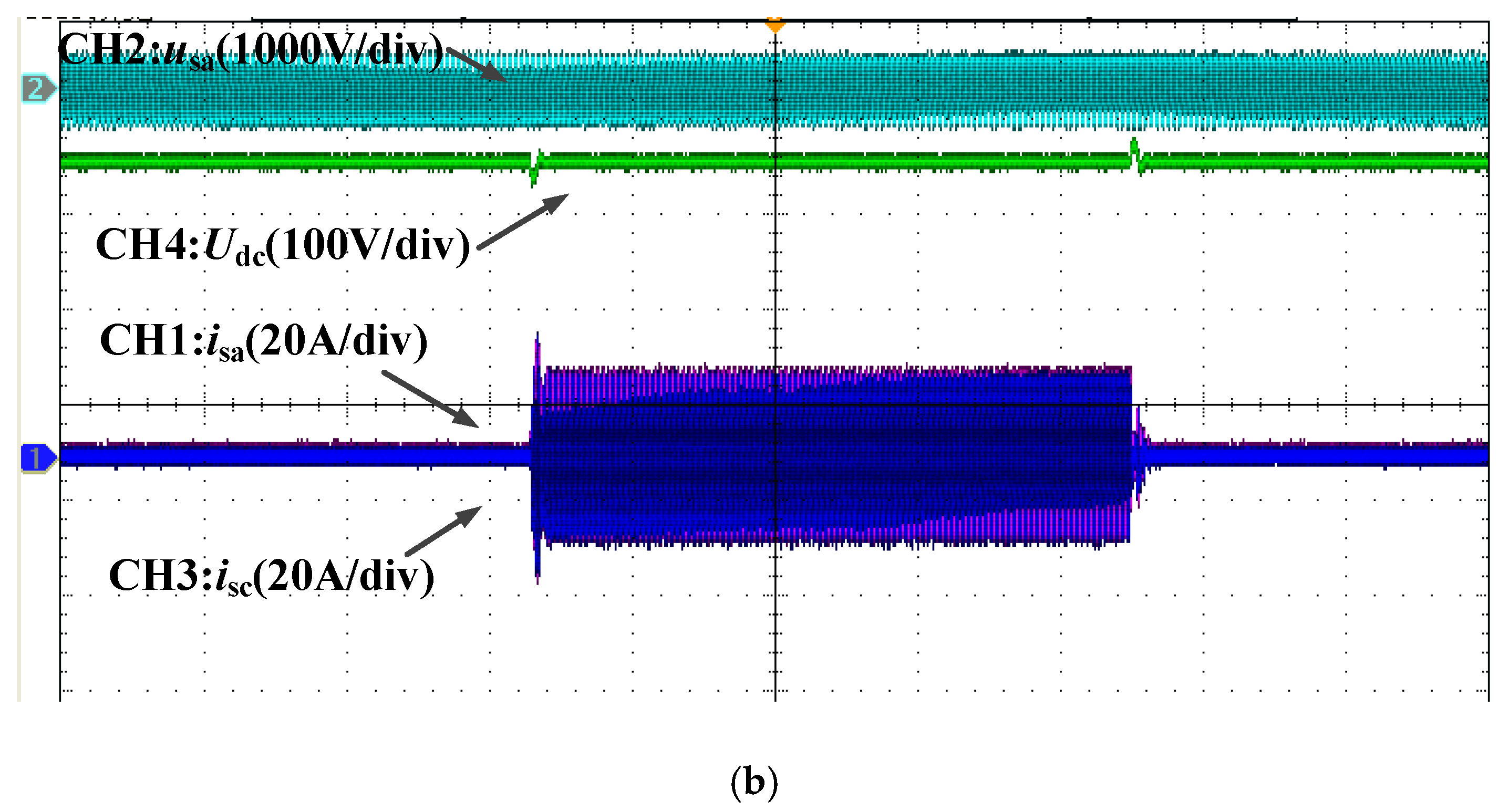
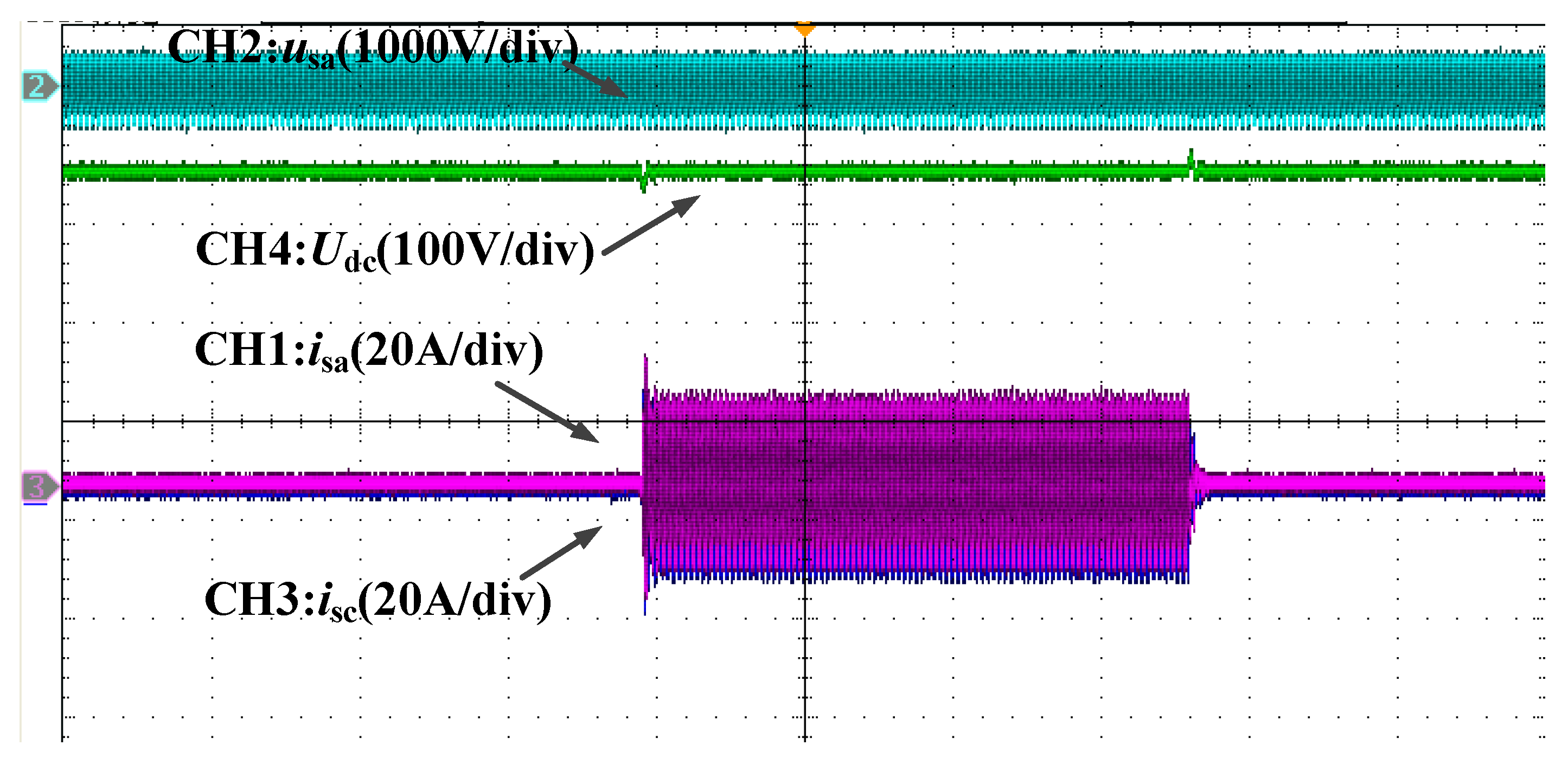
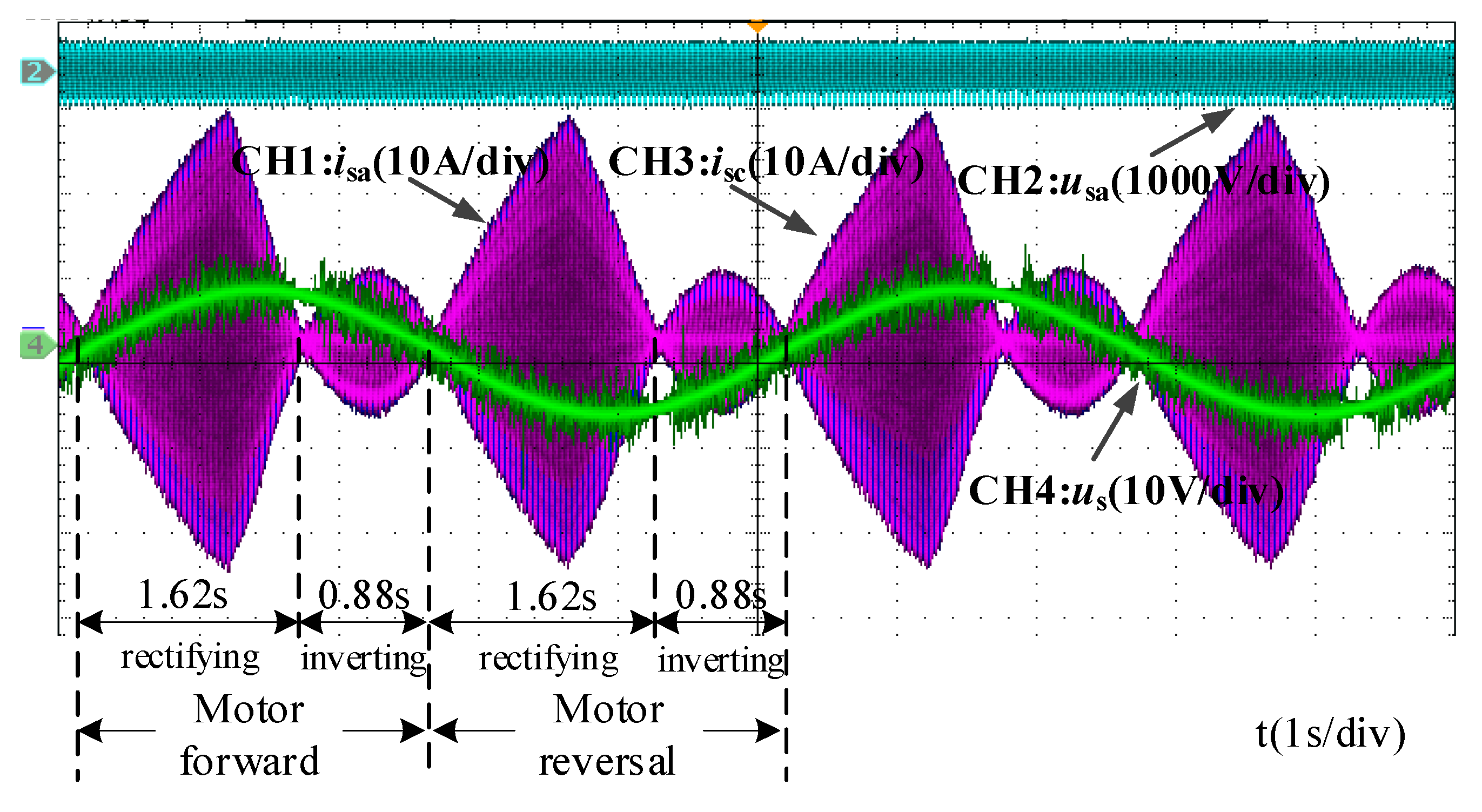
4. Analysis of Experimental Results
4.1. Experiment for Sudden Change of the Load
4.2. Practical Application of Double Fuzzy PI Controller
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PWM | Pulse Width Modulation |
| PI | Proportional Integral |
| IGBT | Insulated Gate Bipolar Transistor |
| NPC | Neutral Point Clamped |
| SVPWM | Space Vector Pulse Width Modulation |
| PLL | Phase-Locked Loop |
| I-Park | Inverse Park Transformation |
References
- Jung, J.; Ku, H.; Son, Y.; Kim, J. Open-switch fault diagnosis algorithm and tolerant control method of the three-phase three-level NPC active rectifier. Energies 2019, 12, 2495. [Google Scholar] [CrossRef]
- Lee, T.-S.; Kune-Shiang, T. Input-output linearizing control with load estimator for three-phase AC/DC voltage-source converters. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference, Cairns, Australia, 23–27 June 2002; pp. 791–795. [Google Scholar]
- Han, Z.; Wang, X.; Jiang, B.; Chen, J. A Control strategy for suppressing zero-sequence circulating current in paralleled three-phase voltage-source PWM converters. Appl. Sci. 2020, 10, 1703. [Google Scholar] [CrossRef]
- Vujacic, M.; Hammami, M.; Srndovic, M.; Grandi, G. Analysis of dc-link voltage switching ripple in three-phase PWM inverters. Energies 2018, 11, 471. [Google Scholar] [CrossRef]
- Li, Z.Q.; Cheng, W.Y.; Xiao, Q.H.; Liao, W.X. Deadbeat predictive power control with fuzzy PI compound controller and power predictive corrector for PWM rectifier under unbalanced grid conditions. Int. J. Fuzzy Syst. 2020, 22, 1277–1288. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, Y.; Wang, Q.; Tao, J.; Wang, X.; Zhao, H.; Li, G. A study on neutral-point potential in three-level NPC converters. Energies 2019, 12, 3367. [Google Scholar] [CrossRef]
- Wang, B.; Tang, Y.; Zhang, L. Research on voltage fuzzy adaptive control of PWM rectifier in synchronous coordinate. In Proceedings of the 3rd IEEE International Conference on Electronic Information Technology and Computer Engineering (EITCE), Xiamen, China, 18–20 October 2019; pp. 519–522. [Google Scholar]
- Lin, H.; Leon, J.I.; Luo, W.; Marquez, A.; Liu, J.; Vazquez, S.; Franquelo, L.G. Integral sliding-mode control-based direct power control for three-level NPC converters. Energies 2020, 13, 227. [Google Scholar] [CrossRef]
- Jamma, M.; Bennassar, A.; Akherraz, M.; Fahassa, C.; Barara, M.; Oproescu, M. Self-Tuning fuzzy PI dc-Bus voltage controller and fuzzy switching sequences selection for direct power control of PWM AC/DC converter. In Proceedings of the 9th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Targoviste, Romania, 29 June–1 July 2017; pp. 1–6. [Google Scholar]
- Hafsi, S.; Dhaoui, M.; Lassaad, S. Fuzzy logic control of grid-connected PWM rectifiers with LCL filters. In Proceedings of the 2017 IEEE International Conference on Green Energy and Conversion Systems, Hammamet, Tunisia, 23–25 March 2017. [Google Scholar]
- Juang, C.F.; Lu, C.F. Load-frequency control by hybrid evolutionary fuzzy PI controller. IET Gener. Transm. Distrib. 2006, 153, 196–204. [Google Scholar] [CrossRef]
- Yan, Q.Z.; Wu, X.J.; Yuan, X.B.; Geng, Y.W. An improved grid-voltage feedforward strategy for high-power three-phase grid-connected inverters based on the simplified repetitive predictor. IEEE Trans. Power Electron. 2016, 31, 3880–3897. [Google Scholar] [CrossRef]
- Lu, M.H.; Frede, B. Stability identification for grid-connected inverters with LCL filters considering grid-voltage feedforward regulator. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–5. [Google Scholar]
- Zhao, R.T.; Chang, Z.G.; Yuan, P.E.; Yang, L.Y.; Li, Z.X. A novel fuzzy logic and anti-windup PI controller for three-phase grid connected inverter. In Proceedings of the 2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 19–20 December 2009; pp. 442–446. [Google Scholar]
- Ahmed, K.Y.; Yahaya, N.Z.; Asirvadam, V.S.; Ramani, K.; Ibrahim, O. Comparison of fuzzy logic control and PI control for a three-level rectifier based on voltage oriented control. In Proceedings of the 6th IEEE International Conference on Power and Energy (PECON), Melaka, Malaysia, 28–29 November 2016; pp. 127–132. [Google Scholar]
- Zeb, K.; Islam, S.U.; Din, W.U.; Khan, I.; Ishfaq, M.; Busarello, T.D.C.; Ahmad, I.; Kim, H.J. Design of fuzzy-PI and fuzzy-sliding mode controllers for single-phase two-stages grid-connected transformerless photovoltaic inverter. Electronics 2019, 8, 520. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, B.; Singh, B.P. Fuzzy pre-compensated PI controller for PMBLDC motor drive. In Proceedings of the 2006 International Conference on Power Electronic, Drives and Energy Systems, New Delhi, India, 12–15 December 2006; pp. 1–5. [Google Scholar]
- Azli, N.A.; Wong, S.N. Development of a DSP-based fuzzy PI controller for an online optimal PWM control scheme for a multilevel inverter. In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; pp. 1457–1461. [Google Scholar]
- Lee, J.H. On methods for improving performance of PI-type fuzzy logic controllers. IEEE. Trans. Fuzzy Syst. 1993, 1, 298–301. [Google Scholar]
- Zheng, Z.; Tao, H.J. Research of three-phase PWM rectifier based on PI control with auto-tuning scaling factors. In Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 3844–3847. [Google Scholar]
- Liu, G.Q.; Li, L. Quantification factor self-tuning fuzzy PID controller research for a permanent magnet synchronous motor feeding system. In Proceedings of the 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 2510–2514. [Google Scholar]
- Singh, P.D.; Sharma, A.; Gao, S. PWM based AC-DC-AC converter for an Isolated hydro power generation with variable turbine input. In Proceedings of the 2018 2nd International Conference on Power, Energy and Environment (ICEPE), Shillong, India, 1–2 June 2018; pp. 1–6. [Google Scholar]
- Huang, J.; Yuan, X.M. Impact of the voltage feed-forward and current decoupling on VSC current control stability in weak grid based on complex variables. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6845–6852. [Google Scholar]
- Lakshmi, M.B.; Thangasankaran, R.; Gnanavadivel, J.; Christa, S.T.J. Performance evaluation of fuzzy controlled single phase PWM rectifier. In Proceedings of the 2nd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 1974–1979. [Google Scholar]
- Khairy, A.; Ibrahim, M.; Abdel-Rahim, N.; Elsherif, H. Comparing proportional-resonant and fuzzy-logic controllers for current controlled single-phase grid-connected PWM DC/AC inverters. In Proceedings of the IET Conference on Renewable Power Generation (RPG), Edinburgh, UK, 6–8 September 2011; pp. 1–6. [Google Scholar]
- Hoang, T.T.G.; Wang, X.H.; Zhou, X.Z.; Tian, L.F.; Chen, W.C. Fractional proportional integral controller applied into two parallel 3-phase PWM rectifiers. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 9–13. [Google Scholar]
- Han, Q.; Li, B.; Li, Z.; Ke, Q. Research of grid-connected photovoltaic inverter grid-connected system based on dual closed-loop of grid voltage vector orientation. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 5171–5176. [Google Scholar]
- Dyhia, K.; Hakim, D.; Lamine, H.M.; Arezki, F.; Nacereddine, B. Comparative study of PI and fuzzy logic controllers for three-phases parallel multi-cell converter. In Proceedings of the 2019 International Conference on Control, Automation and Diagnosis (ICCAD), Grenoble, France, 2–4 July 2019; pp. 1–5. [Google Scholar]
- Pivonka, P. Comparative analysis of fuzzy PI/PD/PID controller based on classical PID controller approach. In Proceedings of the 2002 IEEE World Congress on Computational Intelligence, Honolulu, HI, USA, 12–17 May 2002; pp. 541–546. [Google Scholar]
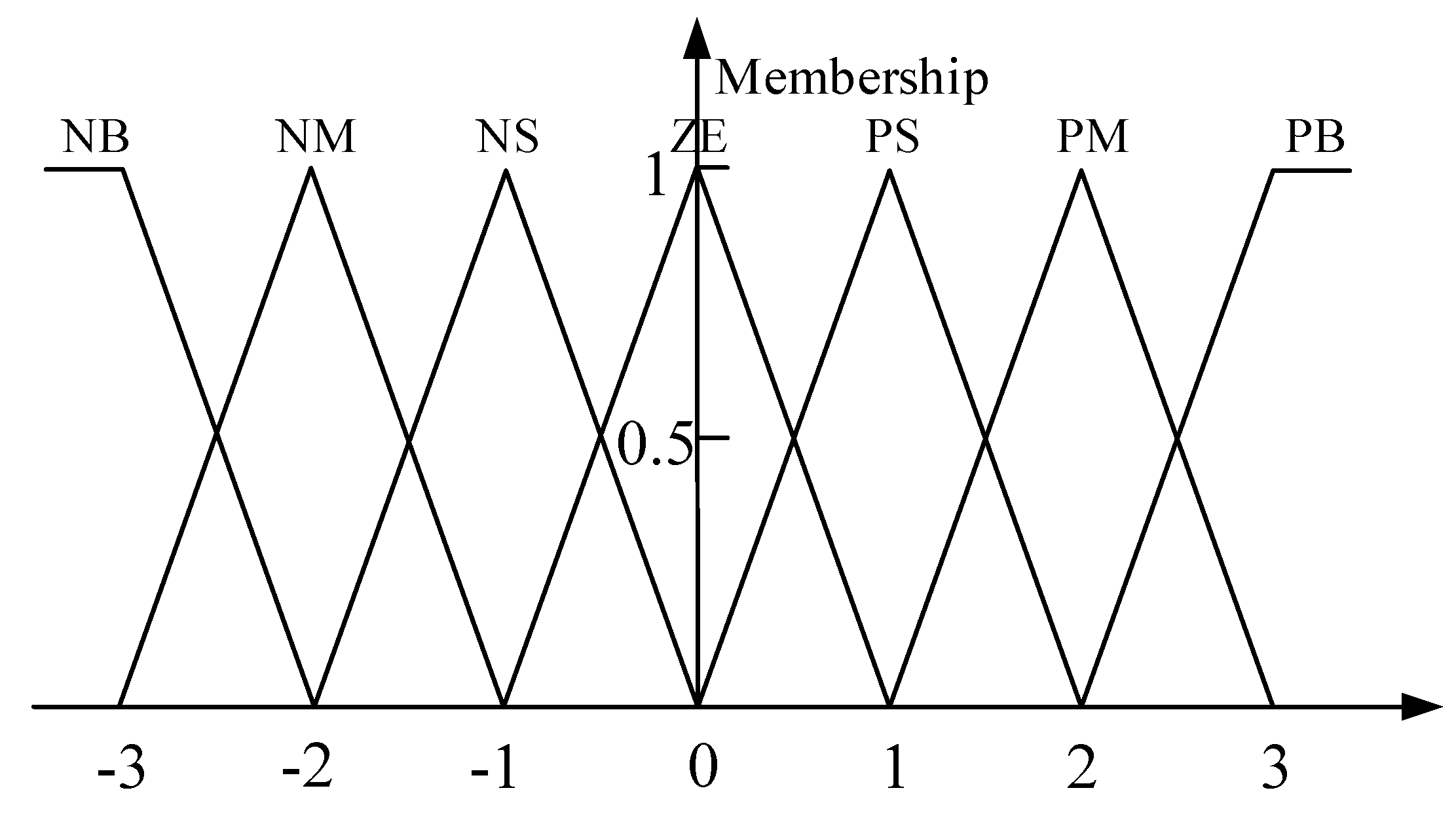



| ec | NB | NM | NS | ZE | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| e | |||||||
| NB | PB | PB | PB | PB | PS | ZE | NS |
| NM | PB | PM | PM | PM | ZE | NS | NM |
| NS | PM | PS | PM | PM | NS | ZE | NB |
| ZE | ZE | ZE | PS | PS | PS | ZE | ZE |
| PS | NB | NM | NS | PM | PM | PS | PM |
| PM | NM | NS | ZE | PM | PM | PM | PB |
| PB | NS | ZE | PS | PB | PB | PB | PB |
| ec | NB | NM | NS | ZE | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| e | |||||||
| NB | NB | NB | NB | PB | PM | PS | ZE |
| NM | NB | NB | NM | PB | PS | ZE | NS |
| NS | NB | NM | NM | PM | ZE | NS | NM |
| ZE | ZE | ZE | PS | ZE | NS | NM | NM |
| PS | NM | NS | ZE | NS | ZE | NM | NB |
| PM | NS | ZE | PS | NM | PS | NB | NB |
| PB | ZE | PS | PM | NM | PM | NB | NB |
| Udc* | 650 | 675 | 700 | 725 | 750 |
|---|---|---|---|---|---|
| Uac_rms | |||||
| 200 | 5.76 | 5.986 | 6.213 | 6.44 | 6.666 |
| 210 | 5.453 | 5.668 | 5.883 | 6.098 | 6.312 |
| 220 | 5.179 | 5.383 | 5.587 | 5.791 | 5.994 |
| 230 | 4.931 | 5.125 | 5.319 | 5.514 | 5.708 |
| 240 | 4.706 | 4.891 | 5.077 | 5.262 | 5.447 |
| Udc* | 650 | 675 | 700 | 725 | 750 |
|---|---|---|---|---|---|
| Uac_rms | |||||
| 200 | 0.05924 | 0.06143 | 0.06363 | 0.06583 | 0.06803 |
| 210 | 0.05698 | 0.05909 | 0.06121 | 0.06332 | 0.06544 |
| 220 | 0.05486 | 0.05689 | 0.05892 | 0.06096 | 0.063 |
| 230 | 0.05285 | 0.05481 | 0.05678 | 0.05874 | 0.06071 |
| 240 | 0.05097 | 0.05286 | 0.05475 | 0.05665 | 0.05855 |
| ΔUdc* | NB | NS | ZE | PS | PB |
|---|---|---|---|---|---|
| ΔUac_rms | |||||
| NB | ZE | PS | PB | PB | PB |
| NS | ZE | ZE | PS | PS | PB |
| ZE | NS | ZE | ZE | ZE | PS |
| PS | NS | NS | ZE | ZE | ZE |
| PB | NB | NB | NS | ZE | ZE |
| ΔUdc* | NB | NS | ZE | PS | PB |
|---|---|---|---|---|---|
| ΔUac_rms | |||||
| NB | ZE | ZE | PS | PB | PB |
| NS | ZE | ZE | PS | PS | PB |
| ZE | NS | ZE | ZE | PS | PB |
| PS | NB | NS | ZE | ZE | PS |
| PB | NB | NB | NS | ZE | ZE |
| AC 220 V, DC 700 V | Traditional PI Controller | Single Fuzzy PI Controller | |
|---|---|---|---|
| From null load to half load | Voltage drop | 32 V | 16 V |
| Adjustment time | 280 ms | 160 ms | |
| From half load to null load | Voltage overshoot | 30 V | 12 V |
| Adjustment time | 310 ms | 170 ms | |
| AC 200 V, DC 650 V | Traditional Single Fuzzy PI Controller | Double Fuzzy PI Controller | |
| From null load to half load | Voltage drop | 34 V | 20 V |
| Adjustment time | 240 ms | 100 ms | |
| From half load to null load | Voltage overshoot | 39 V | 19 V |
| Adjustment time | 210 ms | 110 ms | |
| AC 240 V, DC 750 V | Traditional Single Fuzzy PI Controller | Double Fuzzy PI Controller | |
| From null load to half load | Voltage drop | 48 V | 28 V |
| Adjustment time | 260 ms | 120 ms | |
| From half load to null load | Voltage overshoot | 33 V | 18 V |
| Adjustment time | 290 ms | 150 ms | |
| AC 240 V, DC 750 V | DC Side Capacitance | ||
|---|---|---|---|
| 2950 μF | 1600 μF | ||
| From null load to half load | Voltage drop | 28 V | 26 V |
| Adjustment time | 120 ms | 90 ms | |
| From half load to null load | Voltage overshoot | 18 V | 15 V |
| Adjustment time | 150 ms | 110 ms | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Fang, Y.; Ye, R.; Wang, Z. Analysis and Design of a Double Fuzzy PI Controller of a Voltage Outer Loop in a Reversible Three-Phase PWM Converter. Energies 2020, 13, 3778. https://doi.org/10.3390/en13153778
Zhang W, Fang Y, Ye R, Wang Z. Analysis and Design of a Double Fuzzy PI Controller of a Voltage Outer Loop in a Reversible Three-Phase PWM Converter. Energies. 2020; 13(15):3778. https://doi.org/10.3390/en13153778
Chicago/Turabian StyleZhang, Weixuan, Yu Fang, Rong Ye, and Zhengqun Wang. 2020. "Analysis and Design of a Double Fuzzy PI Controller of a Voltage Outer Loop in a Reversible Three-Phase PWM Converter" Energies 13, no. 15: 3778. https://doi.org/10.3390/en13153778
APA StyleZhang, W., Fang, Y., Ye, R., & Wang, Z. (2020). Analysis and Design of a Double Fuzzy PI Controller of a Voltage Outer Loop in a Reversible Three-Phase PWM Converter. Energies, 13(15), 3778. https://doi.org/10.3390/en13153778






