Fractional-Order Finite-Time, Fault-Tolerant Control of Nonlinear Hydraulic-Turbine-Governing Systems with an Actuator Fault
Abstract
:1. Introduction
2. Preliminaries and System Description
2.1. Definition of Fractional Calculus
2.2. Fractional-Order Finite-Time Stability
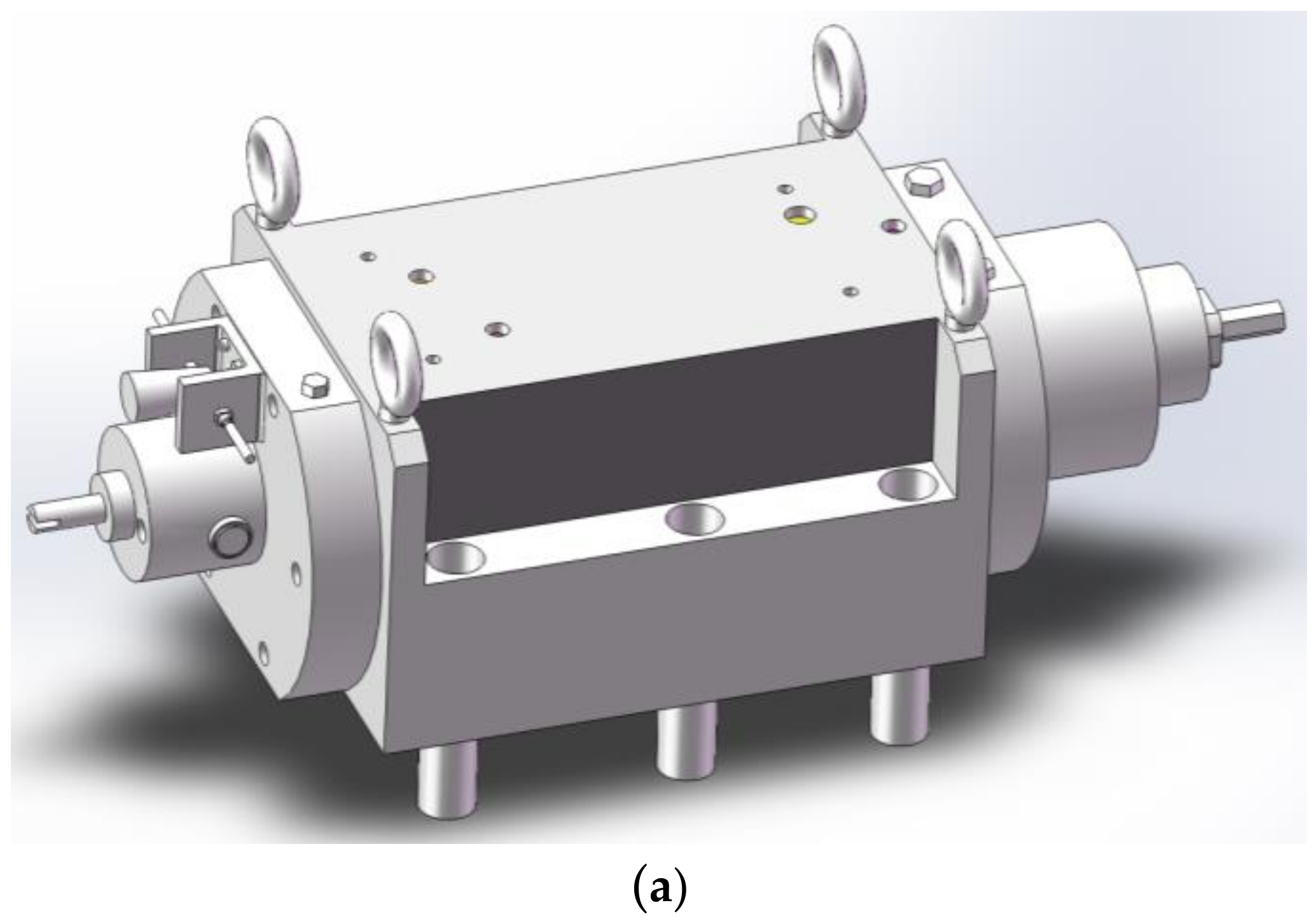
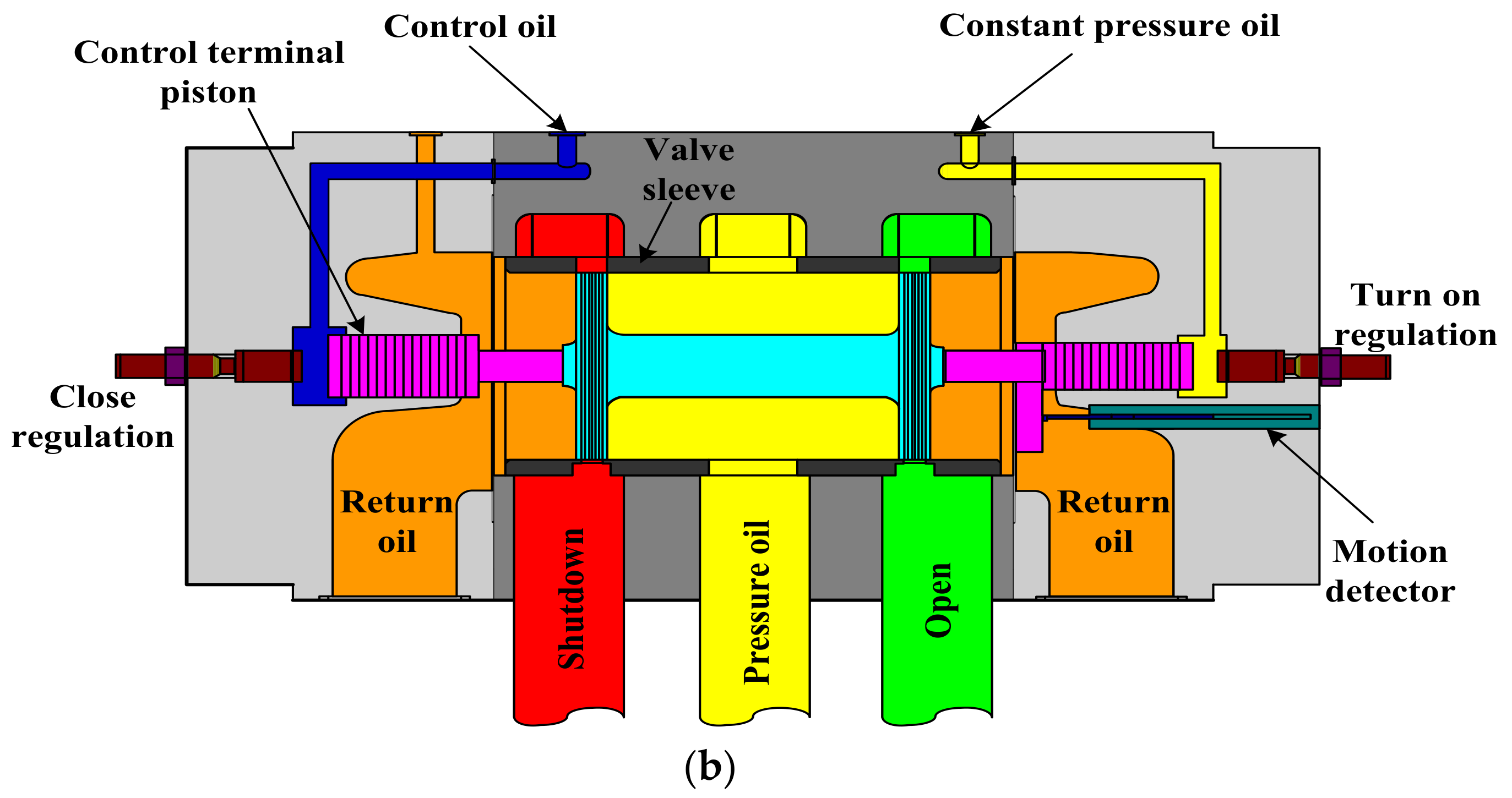
2.3. Non-Linear Model of an HTGS
3. Finite-Time, Fault-Tolerant Controller Design
3.1. Fault Estimator Design
3.2. Controller Design
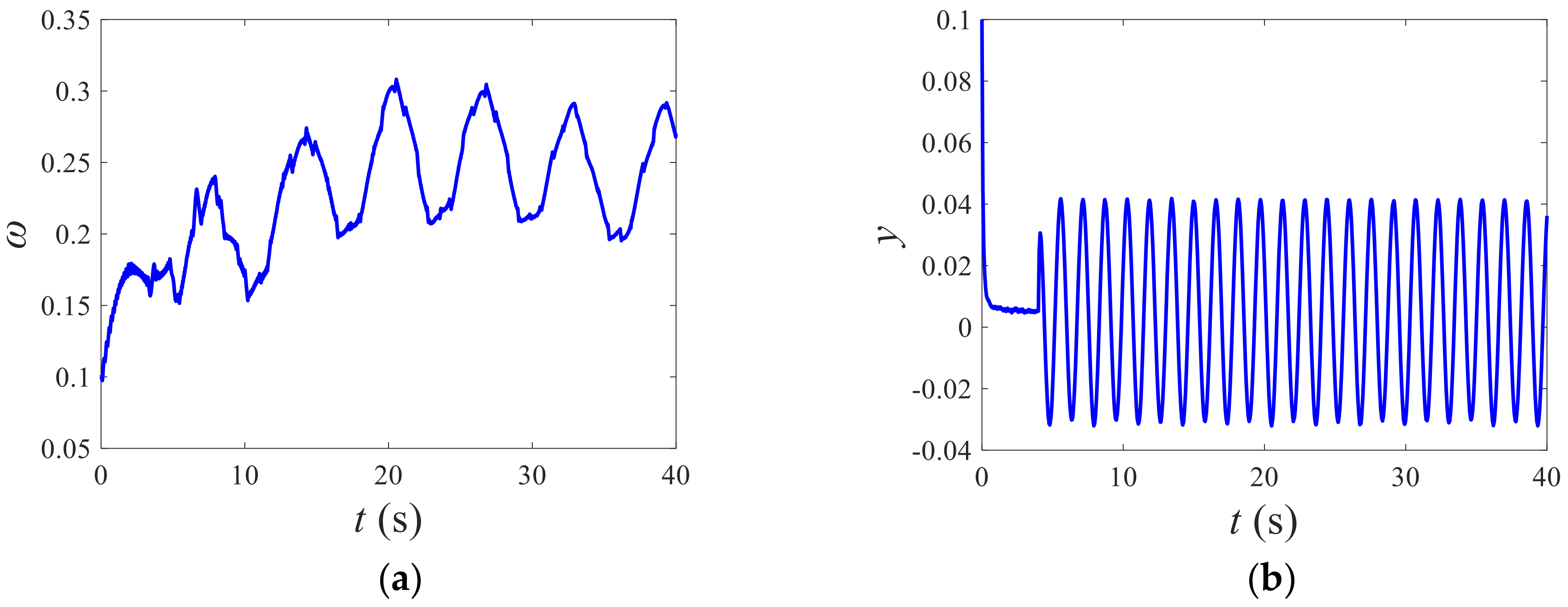
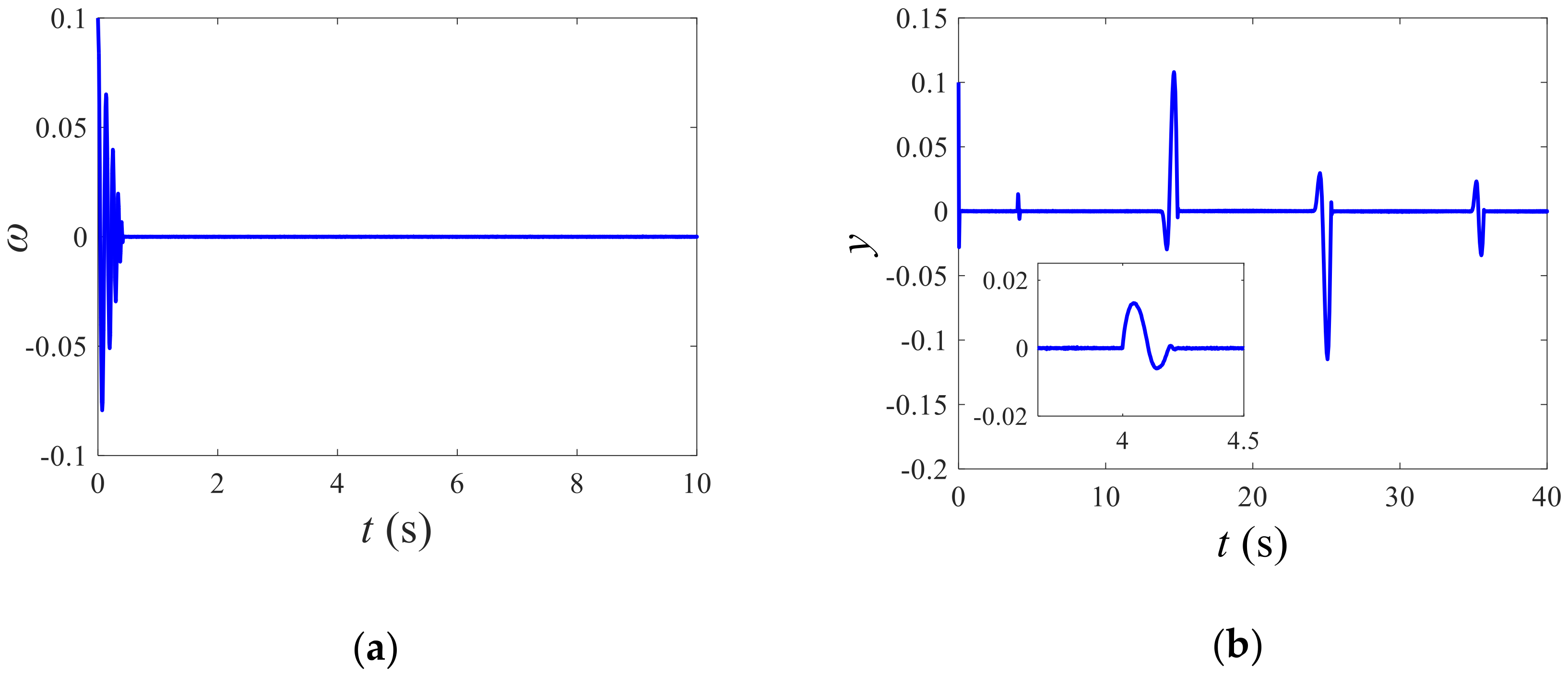
4. Numerical Experiments
- Case 1: Actuator Lock-in-Place Fault
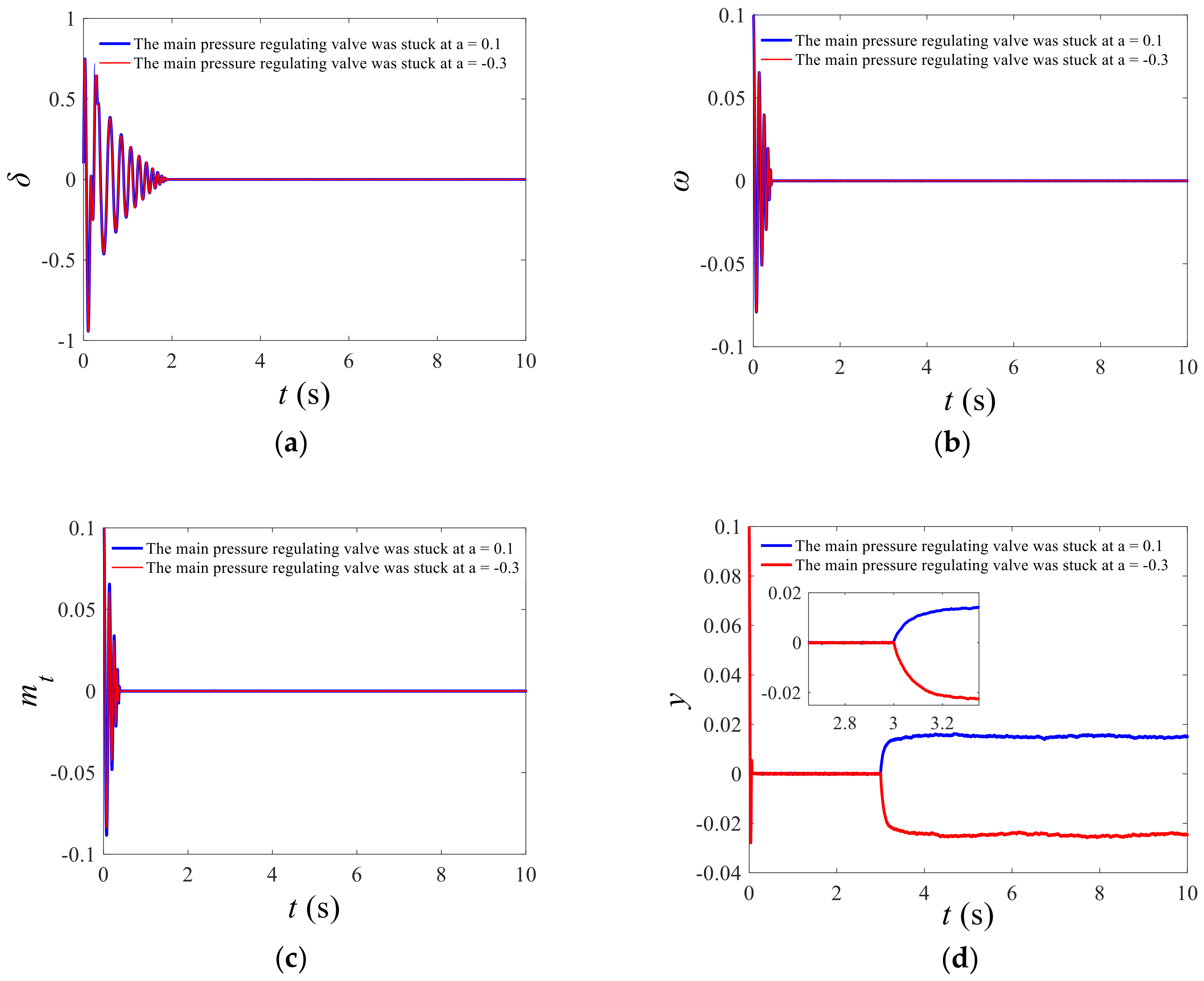
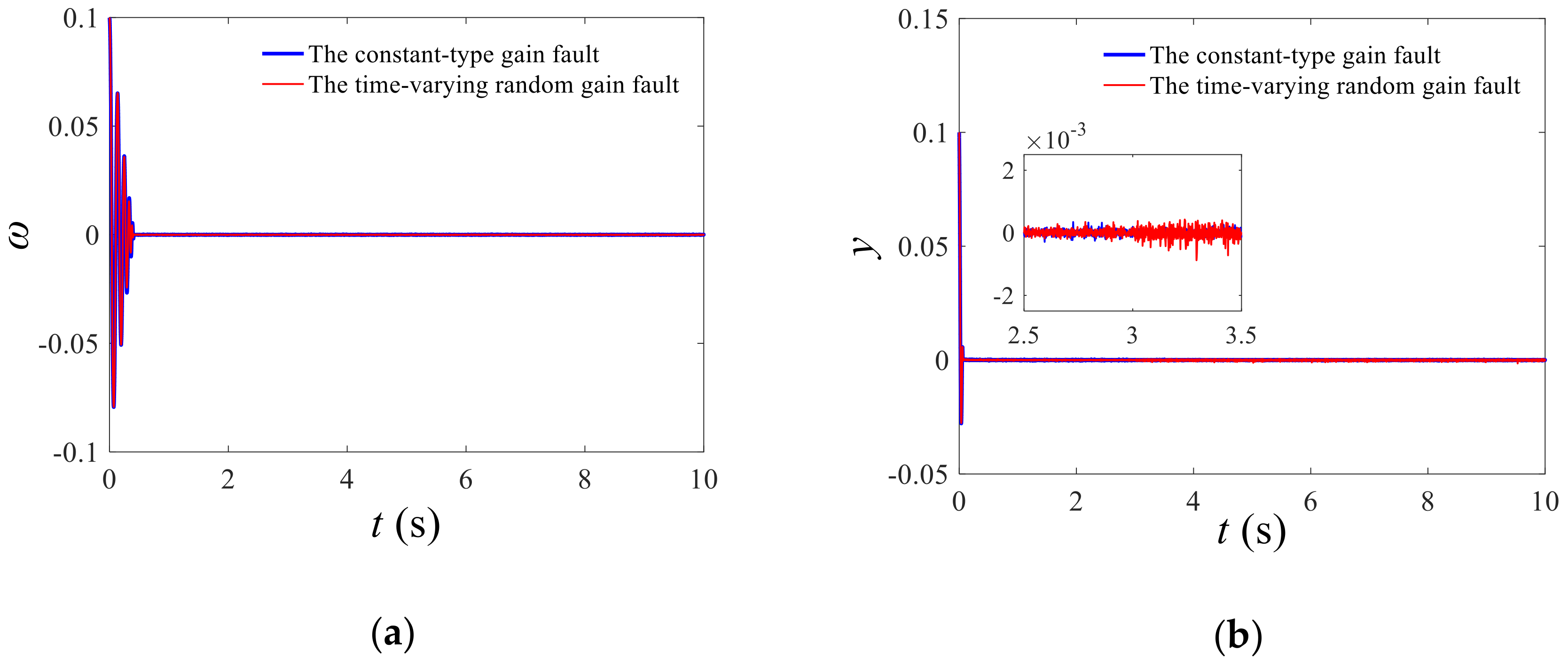
- Case 2: Actuator Constant-Gain Fault
- Case 3: Actuator Constant-Deviation Fault
- Case 4: Multiple Actuator Faults
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, X.L.; Liu, X.H.; Zhou, W. Hydropower in China at present and its further development. Energy 2010, 3, 4400–4406. [Google Scholar] [CrossRef]
- Shakya, S.R.; Shrestha, R.M. Transport sector electrification in a hydropower resource rich developing country: Energy security, environmental and climate change co-benefits. Energy Sustain. Dev. 2011, 15, 147–159. [Google Scholar] [CrossRef]
- Stenzel, P.; Linssen, J. Concept and potential of pumped hydro storage in federal waterways. Appl. Energy 2016, 162, 486–493. [Google Scholar] [CrossRef]
- Frey, G.W.; Linke, D.M. Hydropower as a renewable and sustainable energy resource meeting global energy challenges in a reasonable way. Energy Policy 2002, 30, 1261–1265. [Google Scholar] [CrossRef]
- Li, X.Z.; Chen, Z.J.; Fan, X.C.; Cheng, Z.J. Hydropower development situation and prospects in China. Renew. Sustain. Energy Rev. 2018, 82, 232–239. [Google Scholar] [CrossRef]
- Fu, W.L.; Wang, K.; Li, C.S.; Li, X.; Li, Y.H.; Zhong, H. Vibration trend measurement for a hydropower generator based on optimal variational mode decomposition and an LSSVM improved with chaotic sine cosine algorithm optimization. Meas. Sci. Technol. 2019, 30, 015012. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Chen, T.; Li, J.W.; Yu, J.X. Experimental study of load variations on pressure fluctuations in a prototype reversible pump turbine in generating mode. J. Fluids Eng. 2017, 139, 074501. [Google Scholar] [CrossRef]
- Xu, Y.H.; Li, C.S.; Wang, Z.B.; Zhang, N.; Peng, B. Load frequency control of a novel renewable energy integrated micro-grid containing pumped hydropower energy storage. IEEE Access 2018, 6, 29067–29077. [Google Scholar] [CrossRef]
- Guo, R.P.; Zhu, X.J.; Chen, B.; Yue, Y.L. Ecological network analysis of the virtual water network within China’s electric power system during 2007–2012. Appl. Energy 2016, 168, 110–121. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, X.L.; Alireza, R. Parametric uncertainty in affecting transient characteristics of multi-parallel hydropower systems in the successive load rejection. Int. J. Electr. Power 2019, 10, 444–454. [Google Scholar] [CrossRef]
- Riasi, A.; Tazraei, P. Numerical analysis of the hydraulic transient response in the presence of surge tanks and relief valves. Renew. Energy 2017, 107, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Kurzin, V.B.; Seleznev, V.S. Mechanism of emergence of intense vibrations of turbines on the Sayano-Shushensk hydro power plant. J. Appl. Mech. Tech. Phys. 2010, 51, 590–597. [Google Scholar] [CrossRef]
- Yu, X.D.; Zhang, J.; Fan, C.Y.; Chen, S. Stability analysis of governor-turbine-hydraulic system by state space method and graph theory. Energy 2016, 114, 613–622. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Zheng, X.H.; Li, J.W.; Du, X.Z. Experimental study on the vibrational performance and its physical origins of a prototype reversible pump turbine in the pumped hydro energy storage power station. Renew. Energy 2019, 130, 667–676. [Google Scholar] [CrossRef]
- Ren, H.P.; Fan, J.T.; Kaynak, O. Optimal design of a fractional-order proportional- integer-differential controller for a pneumatic position servo system. IEEE Trans. Ind. Electron. 2019, 66, 6220–6229. [Google Scholar] [CrossRef]
- Zerpa, J.M.; Canelas, A.; Sensale, B.; Santana, D.B.; Armentano, R.L. Modeling the arterial wall mechanics using a novel high-order viscoelastic fractional element. Appl. Math. Model. 2015, 39, 4767–4780. [Google Scholar] [CrossRef]
- Rasheed, A.; Anwar, M.S. Simulations of variable concentration aspects in a fractional nonlinear viscoelastic fluid flow. Commun. Nonlinear Sci. 2018, 65, 216–230. [Google Scholar] [CrossRef]
- Yu, W.; Luo, Y.; Pi, Y. Fractional order modeling and control for permanent magnet synchronous motor velocity servo system. Mechatronics 2013, 23, 813–820. [Google Scholar] [CrossRef]
- Gabano, J.D.; Poinot, T. Fractional modelling and identification of thermal systems. Signal. Process. 2011, 91, 531–541. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Biegler, L. Optimization of fractional order dynamic chemical processing systems. Ind. Eng. Chem. Res. 2014, 53, 5110–5127. [Google Scholar] [CrossRef]
- Wang, F.F.; Chen, D.Y.; Xu, B.B.; Zhang, H. Nonlinear dynamics of a novel fractional-order Francis hydro-turbine governing system with time delay. Chaos Solitons Fractals 2016, 91, 329–338. [Google Scholar] [CrossRef] [Green Version]
- Dounis, A.I.; Kofinas, P.; Alafodimos, C.; Tseles, D. Adaptive fuzzy gain scheduling PID controller for maximum power point tracking of photovoltaic system. Renew. Energy 2013, 60, 202–214. [Google Scholar] [CrossRef]
- Ge, M.; Chiu, M.S.; Wang, Q.G. Robust PID controller design via LMI approach. J. Process. Contr. 2002, 12, 3–13. [Google Scholar] [CrossRef]
- Chen, Z.H.; Yuan, X.H.; Tian, H.; Ji, B. Improved gravitational search algorithm for parameter identification of water turbine regulation system. Energy Convers. Manag. 2014, 78, 306–315. [Google Scholar] [CrossRef]
- Wang, B.; Xue, J.Y.; Wu, F.J.; Zhu, D.L. Robust Takagi-Sugeno fuzzy control for fractional order hydro-turbine governing system. ISA. Trans. 2016, 65, 72–80. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Yuan, X.H.; Yuan, Y.B.; Chen, Z.H. Nonlinear dynamic analysis and robust controller design for Francis hydraulic turbine regulating system with a straight-tube surge tank. Mech. Syst. Signal. Pr. 2017, 85, 927–946. [Google Scholar] [CrossRef]
- Mu, W.Y.; Wang, J.P.; Feng, W.W. Fault detection and fault-tolerant control of actuators and sensors in distributed parameter systems. J. Frankl. Inst. 2017, 354, 3341–3363. [Google Scholar] [CrossRef]
- Kavikumar, R.; Sakthivel, R.; Kaviarasan, B.; Kwon, O.M.; Anthoni, S.M. Non-fragile control design for interval-valued fuzzy systems against nonlinear actuator faults. Fuzzy Set. Syst. 2019, 365, 40–59. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, G.H. Adaptive asymptotic tracking control of uncertain non-linear systems with input quantization and actuator faults. Automatica 2016, 72, 177–185. [Google Scholar] [CrossRef]
- Joseph, A.; Chelliah, T.R.; Lee, K.B. Multi-channel VSI fed large variable speed asynchronous hydro-condenser: Fault analysis, fault diagnosis and fault tolerant control. IET. Renew. Power Gen. 2019, 13, 438–450. [Google Scholar] [CrossRef]
- Wang, J.H.; Gao, Y.B.; Qiu, J.B.; Ahn, C.K. Sliding mode control for non-linear systems by Takagi-Sugeno fuzzy model and delta operator approaches. IET. Control. Theory Appl. 2017, 11, 1205–1213. [Google Scholar] [CrossRef]
- Tin, Z.Y.; Luo, J.J.; Wei, C.S. Quasi fixed-time fault-tolerant control for nonlinear mechanical systems with enhanced performance. Appl. Math. Comput. 2019, 352, 157–173. [Google Scholar]
- Wang, B.; Xue, J.Y.; Wu, F.J.; Zhu, D.L. Finite time takagi-sugeno fuzzy control for hydro-turbine governing system. J. Vib. Control 2018, 24, 1001–1010. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Q.; Li, X.C. Finite-time convergent control of electrohydraulic velocity servo system under uncertain parameter and external load. IEEE Trans. Ind. Electron. 2019, 66, 4513–4523. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Sun, Y.M.; Lin, C. Finite time control of switched stochastic nonlinear systems. Fuzzy Set. Syst. 2019, 365, 140–152. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Samko, S.; Vakulov, B. Weighted Sobolev theorem with variable exponent for spatial and spherical potential operators. J. Math. Anal. Appl. 2005, 310, 229–246. [Google Scholar] [CrossRef] [Green Version]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Ling, D.J. Bifurcation and Chaos of Hydraulic Turbine Governor; Hohai University: Nanjing, China, 2007. [Google Scholar]
- Efe, M.O. Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm. IEEE Trans. Syst. Man Cybern. B 2008, 38, 1561–1570. [Google Scholar] [CrossRef]
- Peng, B. Fault Diagnosis of Hydroelectric Generating Units Based on Improved Support Vector Machine and Feature Information Fusion; Huazhong University of Science & Technology: Wuhan, China, 2008. [Google Scholar]
- Zhang, P. Research on Fault Detection and Diagnosis of Hydraulic Turbine Control System; Xi’an University of Technology: Xi’an, China, 2006. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wang, B.; Tian, Y.; Chen, P. Fractional-Order Finite-Time, Fault-Tolerant Control of Nonlinear Hydraulic-Turbine-Governing Systems with an Actuator Fault. Energies 2020, 13, 3812. https://doi.org/10.3390/en13153812
Yang Y, Wang B, Tian Y, Chen P. Fractional-Order Finite-Time, Fault-Tolerant Control of Nonlinear Hydraulic-Turbine-Governing Systems with an Actuator Fault. Energies. 2020; 13(15):3812. https://doi.org/10.3390/en13153812
Chicago/Turabian StyleYang, Ying, Bin Wang, Yuqiang Tian, and Peng Chen. 2020. "Fractional-Order Finite-Time, Fault-Tolerant Control of Nonlinear Hydraulic-Turbine-Governing Systems with an Actuator Fault" Energies 13, no. 15: 3812. https://doi.org/10.3390/en13153812




