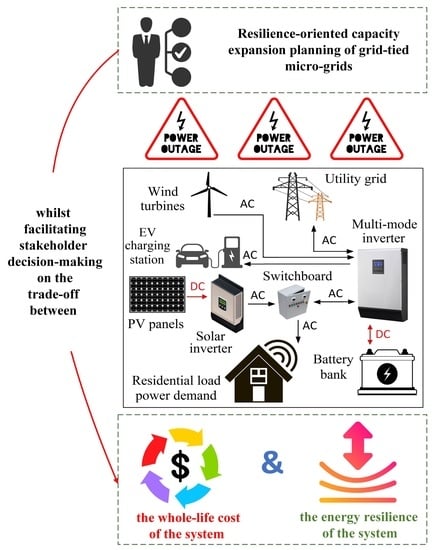
Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand
Abstract
:1. Introduction
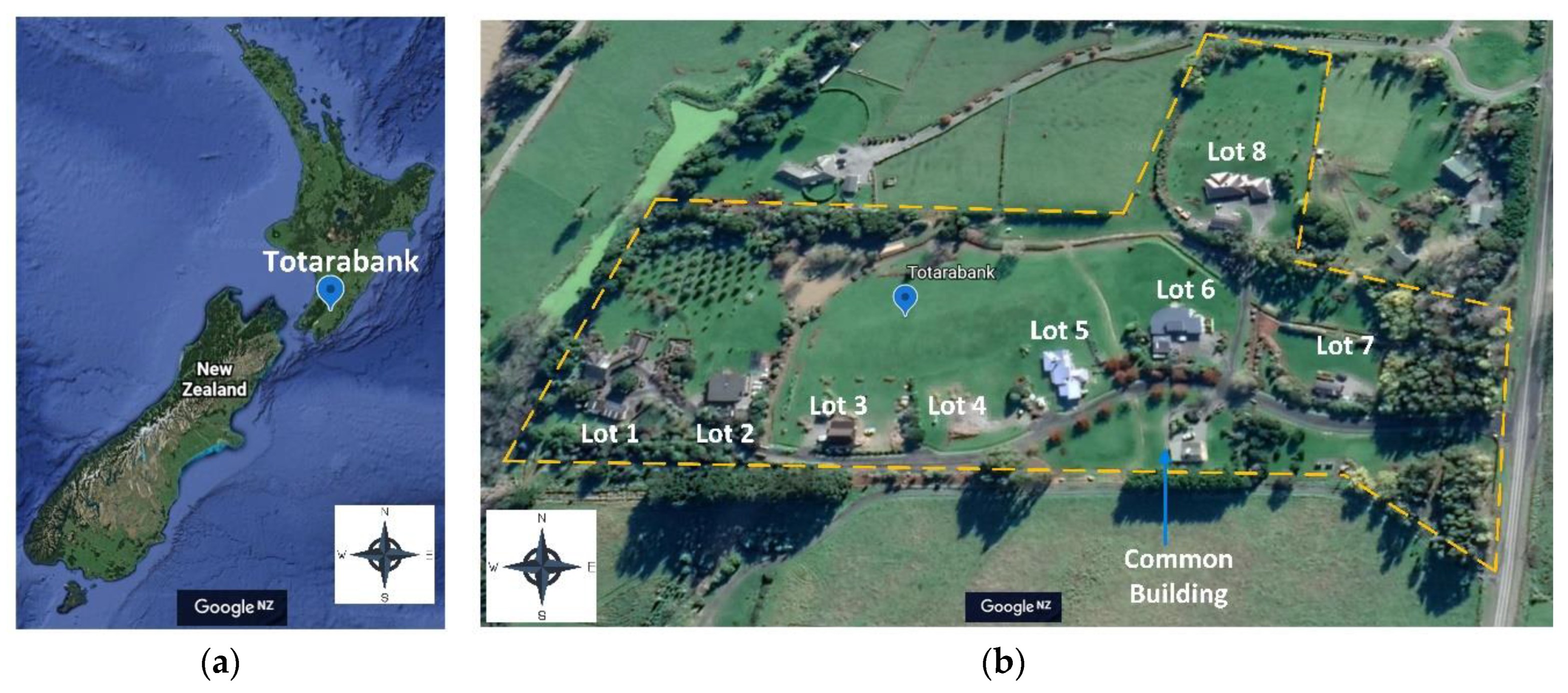
2. Test-Case System: Totarabank, New Zealand
2.1. Candidate Technologies
2.1.1. PV Modules
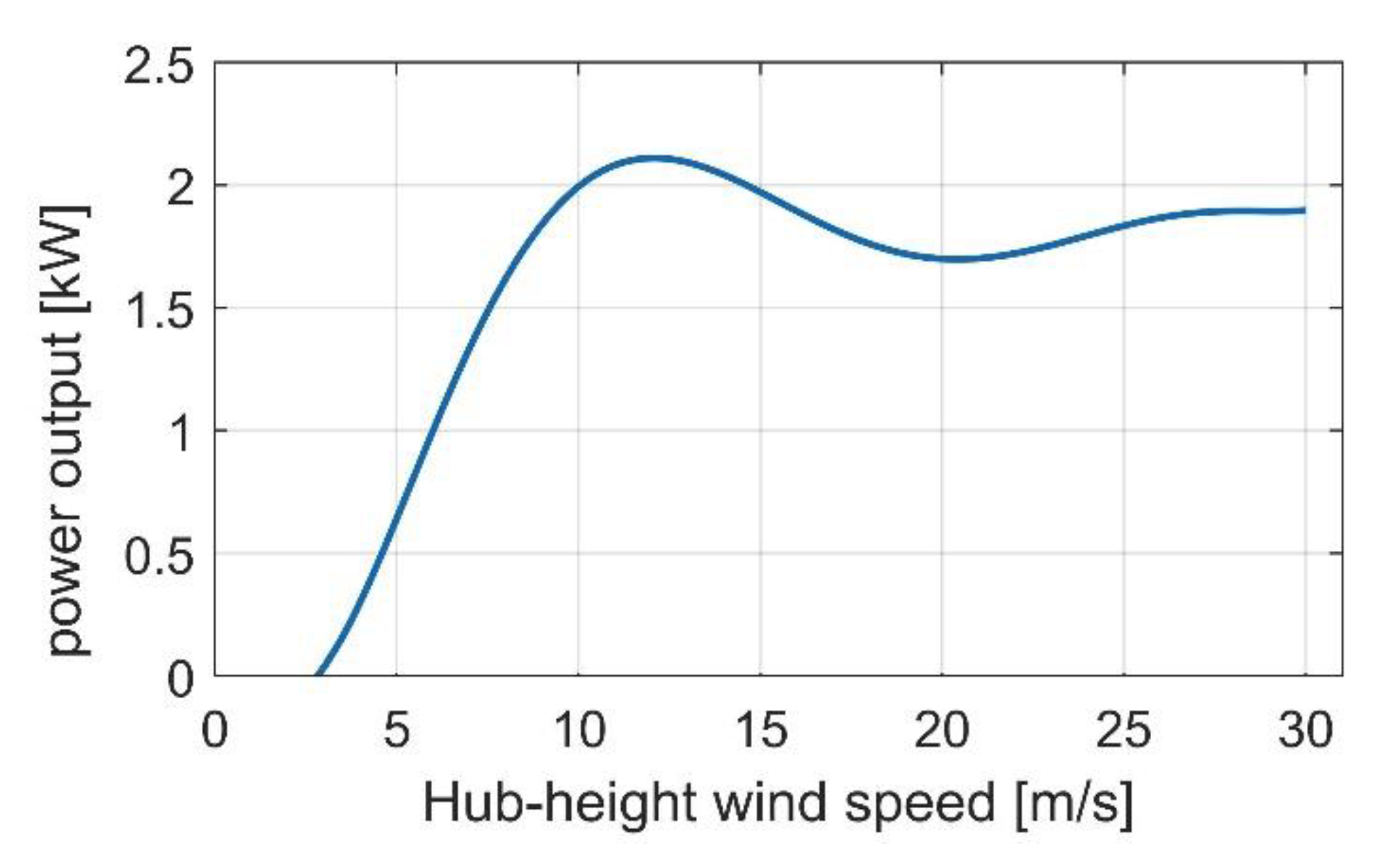
2.1.2. Wind Turbines
2.1.3. Battery Arrays
2.1.4. Hybrid Inverter
2.1.5. Utility Grid
2.1.6. Electric Vehicle Charging Station
2.2. Key Assumptions
- The MG capacity expansion planning was carried out from a macro (centralised) perspective. Accordingly, this study does not focus on how to optimally assign the equipment capacity to each lot.
- The costs associated with the replacement and operation and maintenance (O&M) of the existing installed solar inverters were not reflected in the model. The reason lies in the fact that these assets are privately owned, while the new capacity additions were assumed to be shared by the community. That is, accounting for the replacement and O&M costs of the currently privately held solar inverters will require more sophisticated market designs (such as peer-to-peer markets) for the intra-community electricity exchanges to establish a fair playing field—which are currently cleared under a pure flat-rate tariff structure. Note that the rationale behind making this assumption stems from the difference in the service life of PV panels and solar inverters.
- The energy stored in the stationary battery bank is not allowed to be used for electric vehicle (EV) charging purposes—allowed only for critical loads to address the resilience of the community and to improve the service life of the stationary battery bank.
- A cooperative energy scheduling strategy (for example the one proposed in [35]), to be materialised in the implementation phase, was assumed to be able to coordinate the flexible charging of EVs, such that the daily periods of time the EV charging infrastructure sits unused is minimised.
- Vehicle-to-grid (V2G) services [36], as well as the effect of load growth due to the eco-village’s population growth, were not taken into consideration. Rather, the system expansion is planned to meet the expectation of growing loads from the existing number of inhabitants.
- The product models were chosen, based on the authors’ judgement of both efficiency and cost-effectiveness, from the options available in the Australia and New Zealand renewable energy markets, while costs are always cited in New Zealand currency.
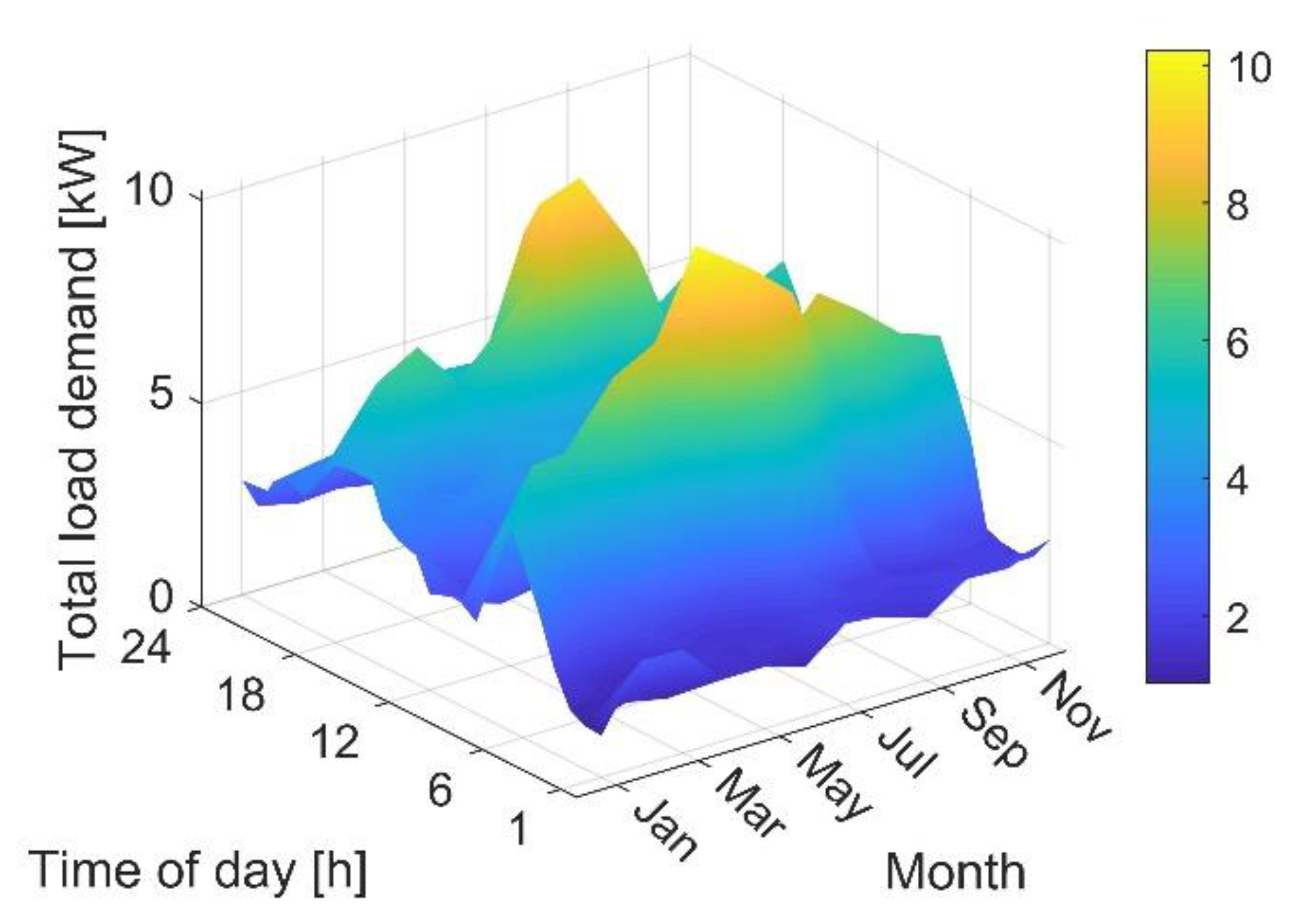
2.3. Data
3. Methodology
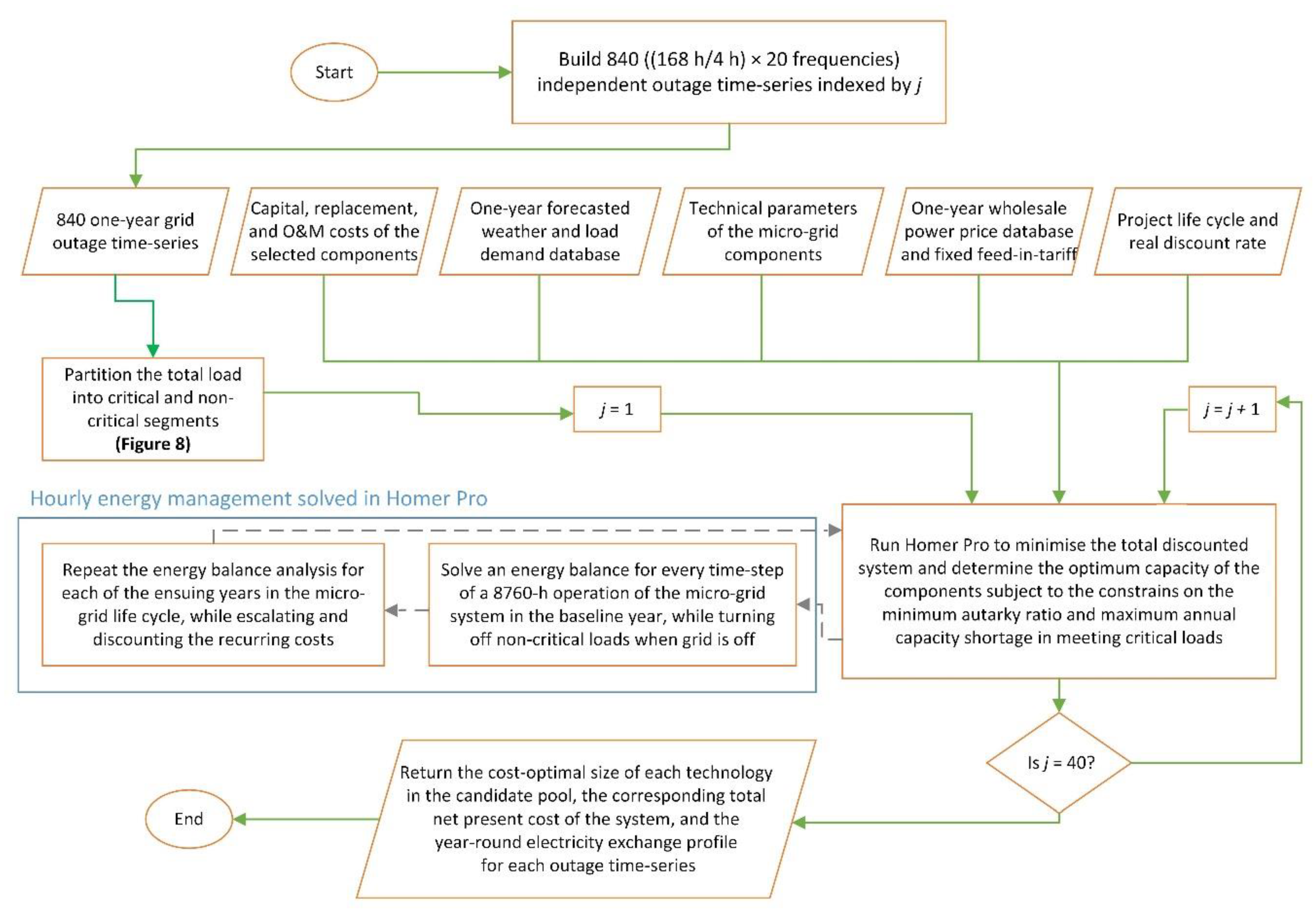
3.1. Modelling Approach
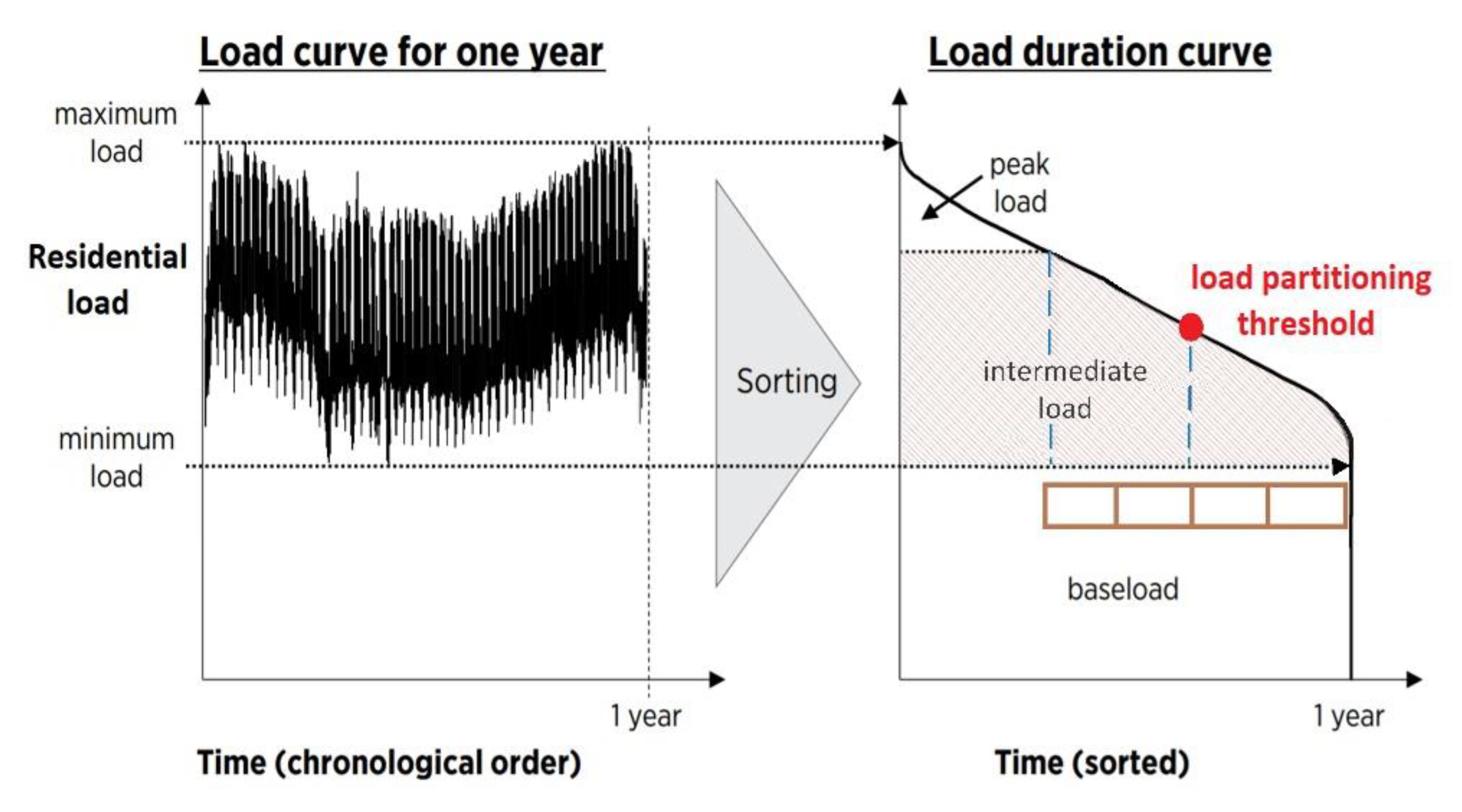
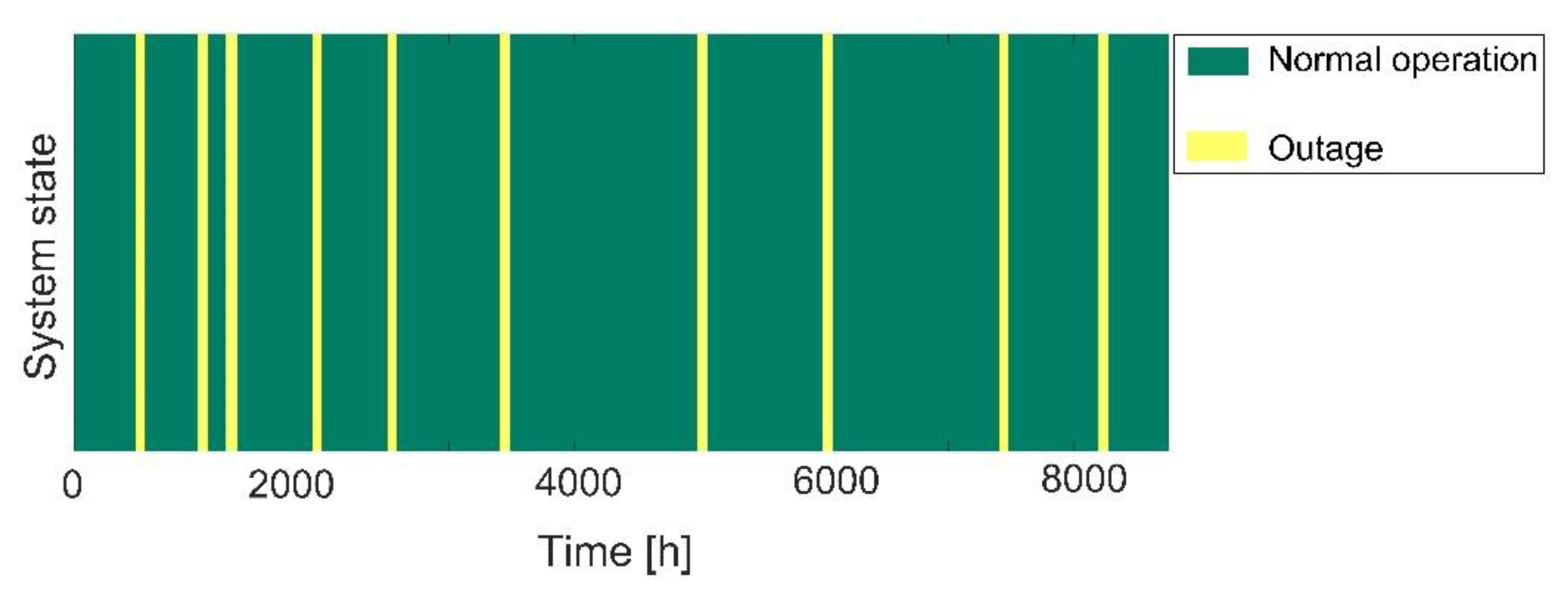
3.2. Characterisation of Energy Resilience
3.3. Model Assumptions and Design Standards
4. Results and Discussion
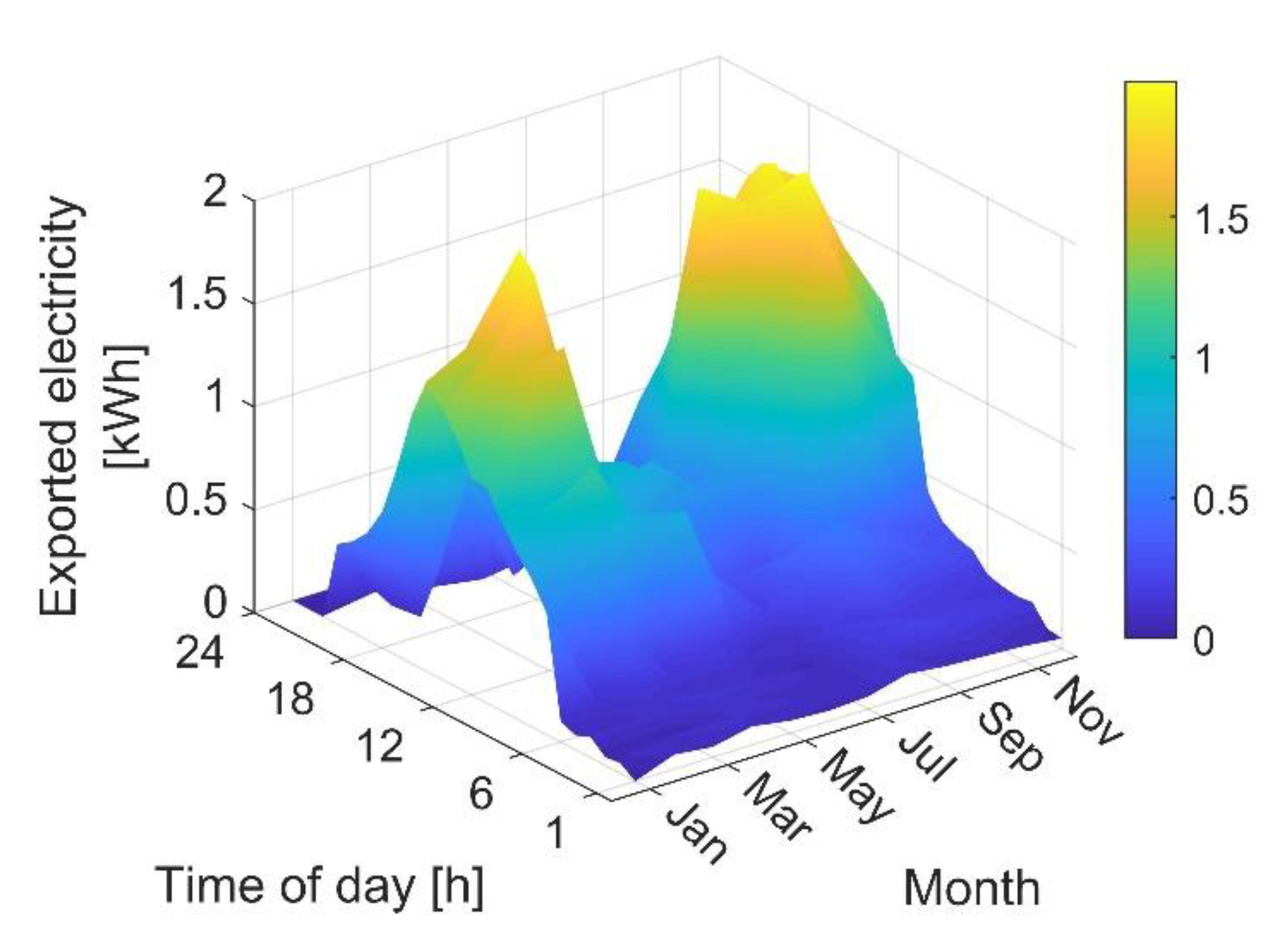
4.1. Feasibility and Optimal Capacity Configuration
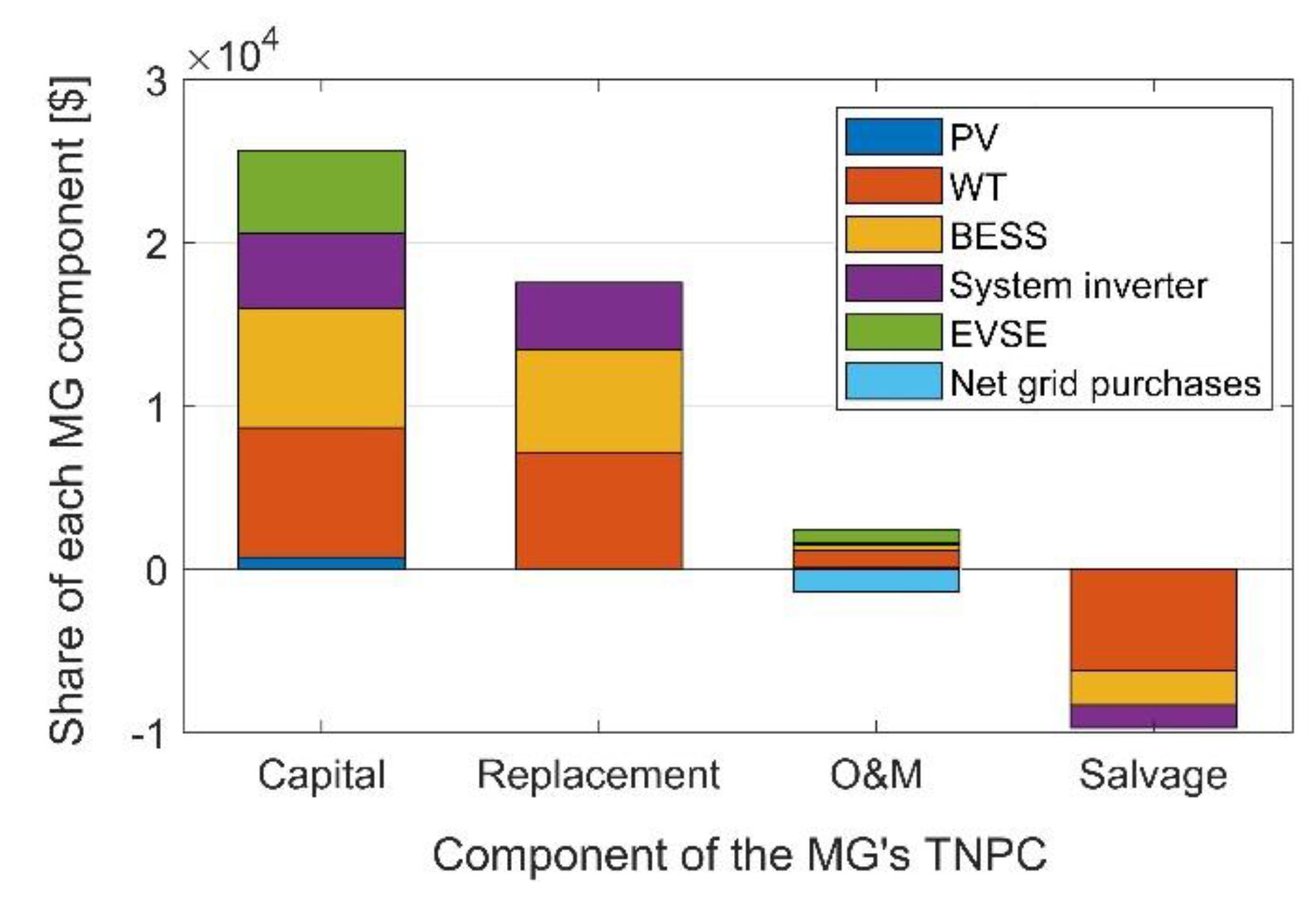
4.2. The Cost of Energy Resilience
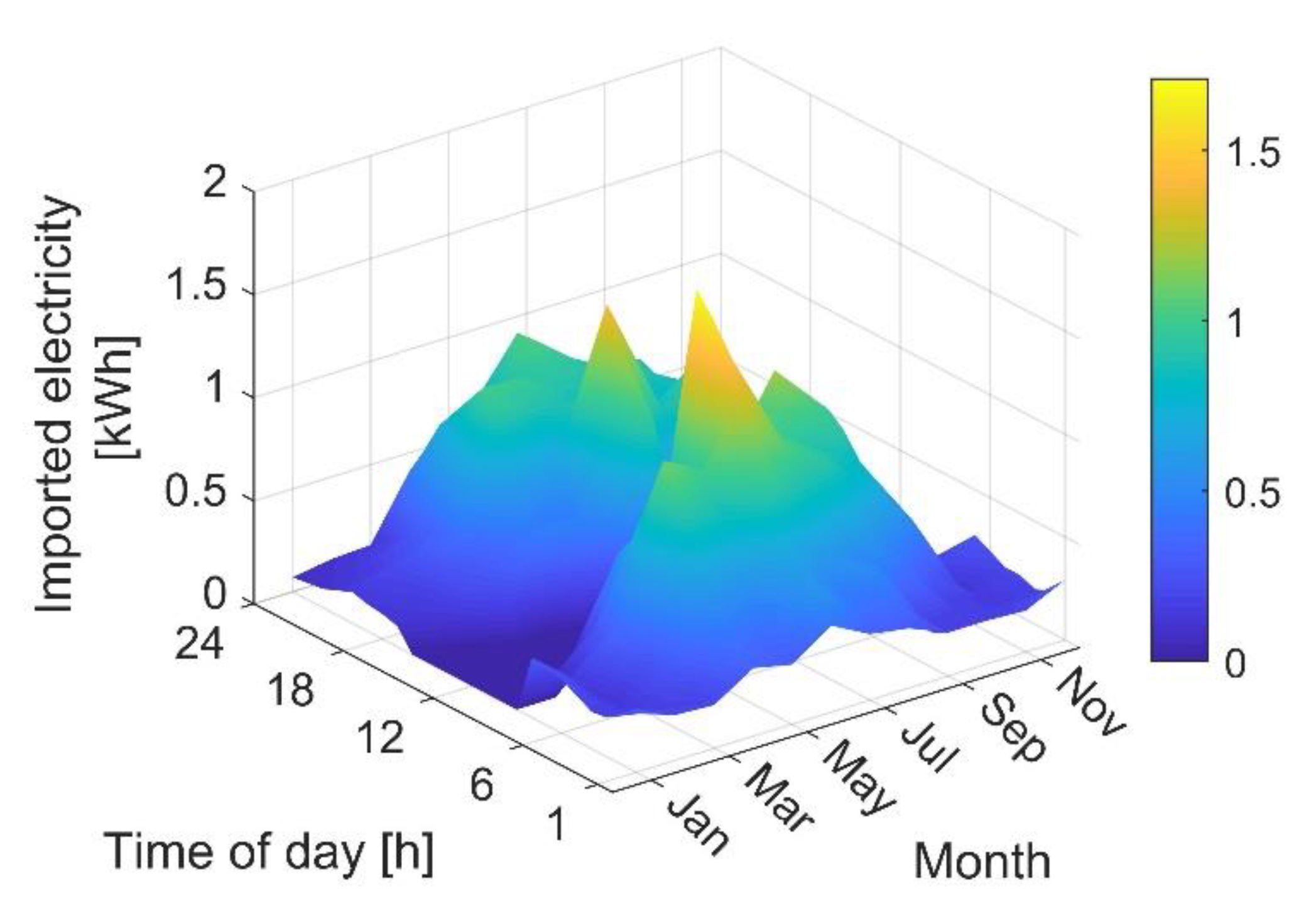
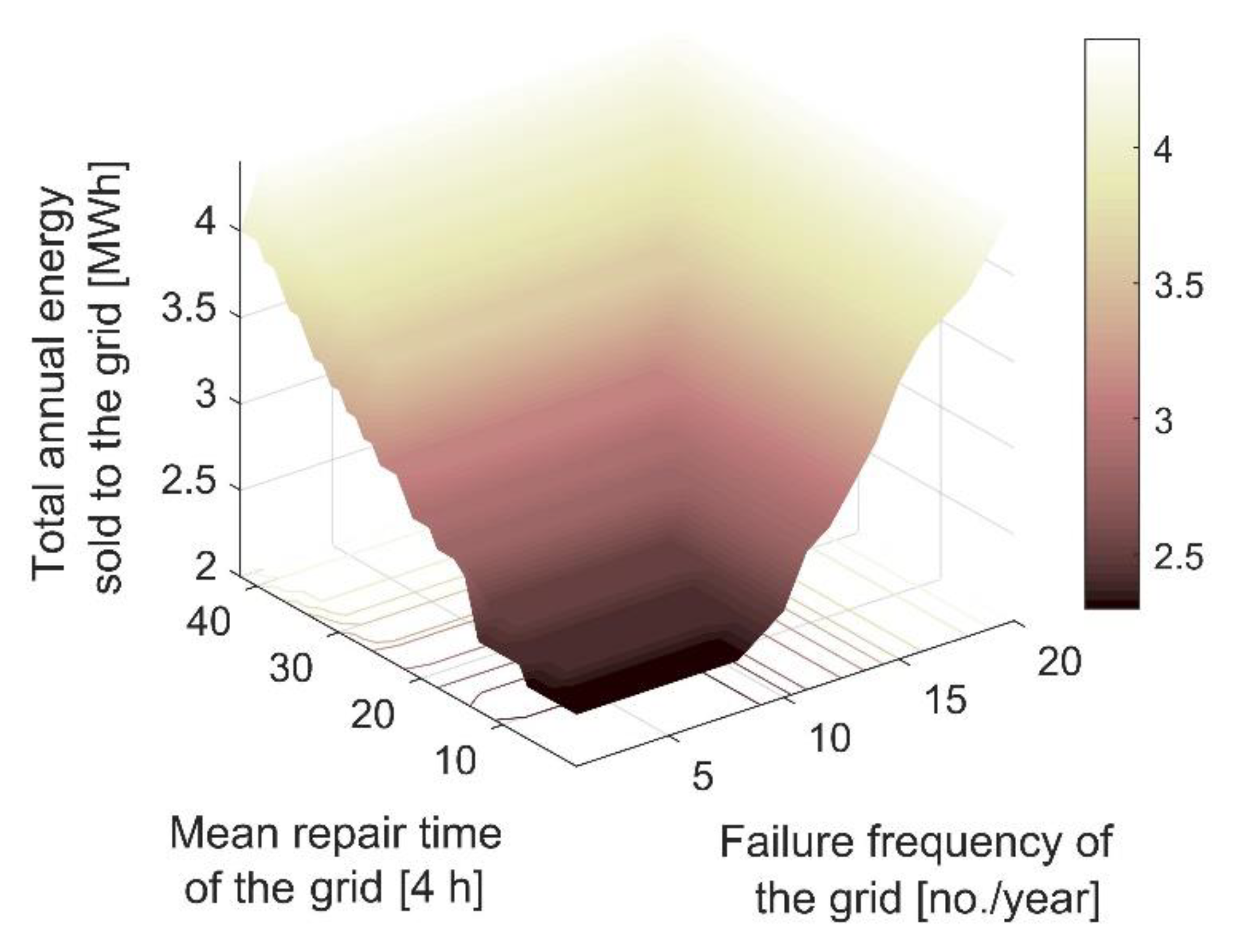
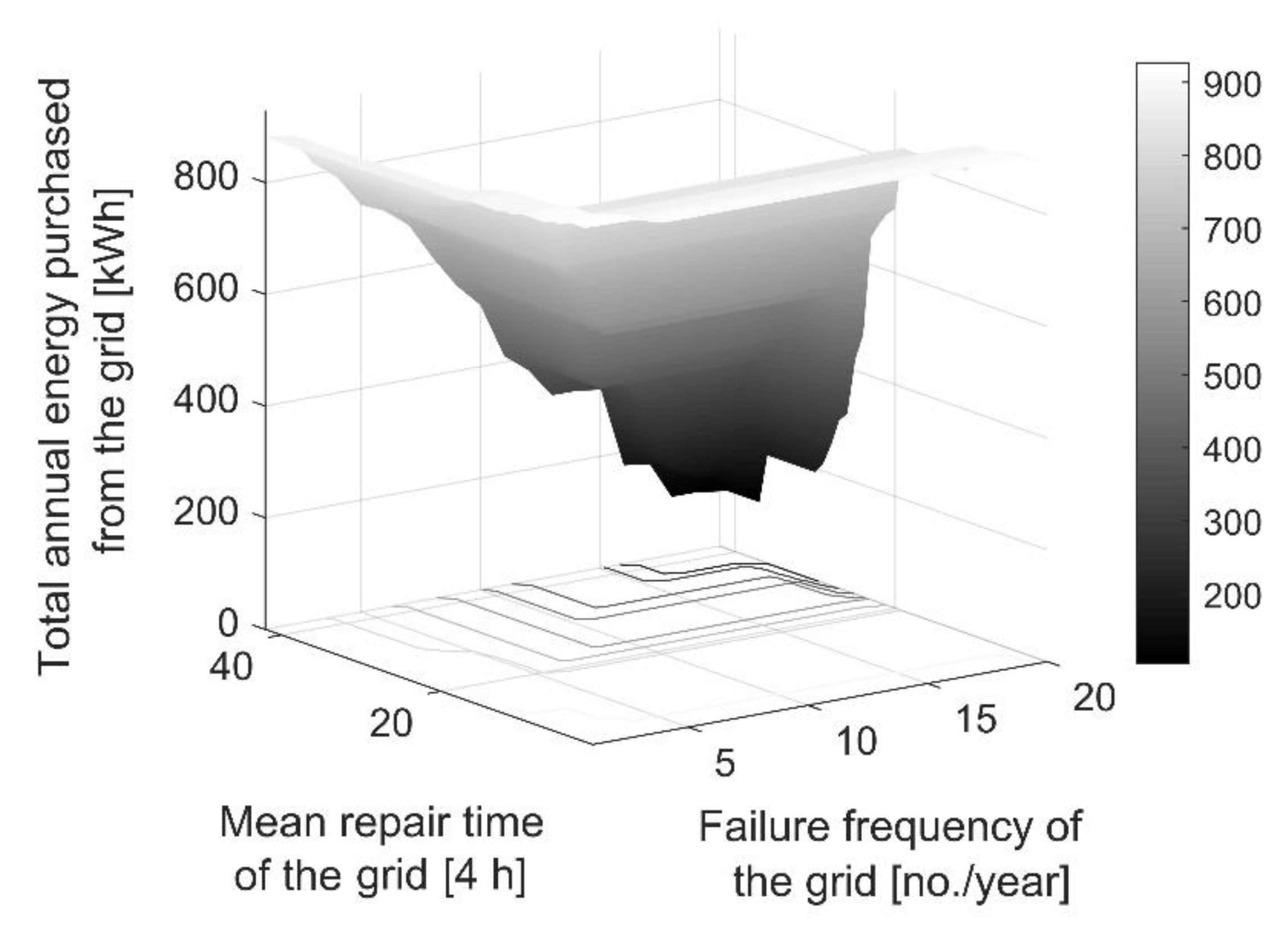
- The values of total annual energy imports and exports indicate that the MG’s net purchased electricity from the grid was approximately a monotonically decreasing function of the grid unreliability. That is, as the failure frequency of the grid and/or its mean repair time increased, the total power sold back to (purchased from) the grid increased (decreases) or remained constant. The underlying reason responsible for this model behaviour is the increase in the excess non-dispatchable power generation capacity of the MG during normal, grid-connected operations, as the grid reliability decreases. However, the increase in revenues generated from trading with the grid, as the MG’s resilience to grid outages improved, only partially offset the additional costs incurred. This emphasises the necessity to include a minimum acceptable limit for the target community’s energy resilience—to be derived from specifically-developed surveys to estimate the value of lost load—in the resilience-oriented MG capacity expansion planning processes to improve the accuracy of results.
- Non-surprisingly, increasing the unreliability level of the grid through dedicated parameters, increased the TNPC of the MG capacity expansion, which, in turn, increased the LCOE associated with the cost-minimal system.
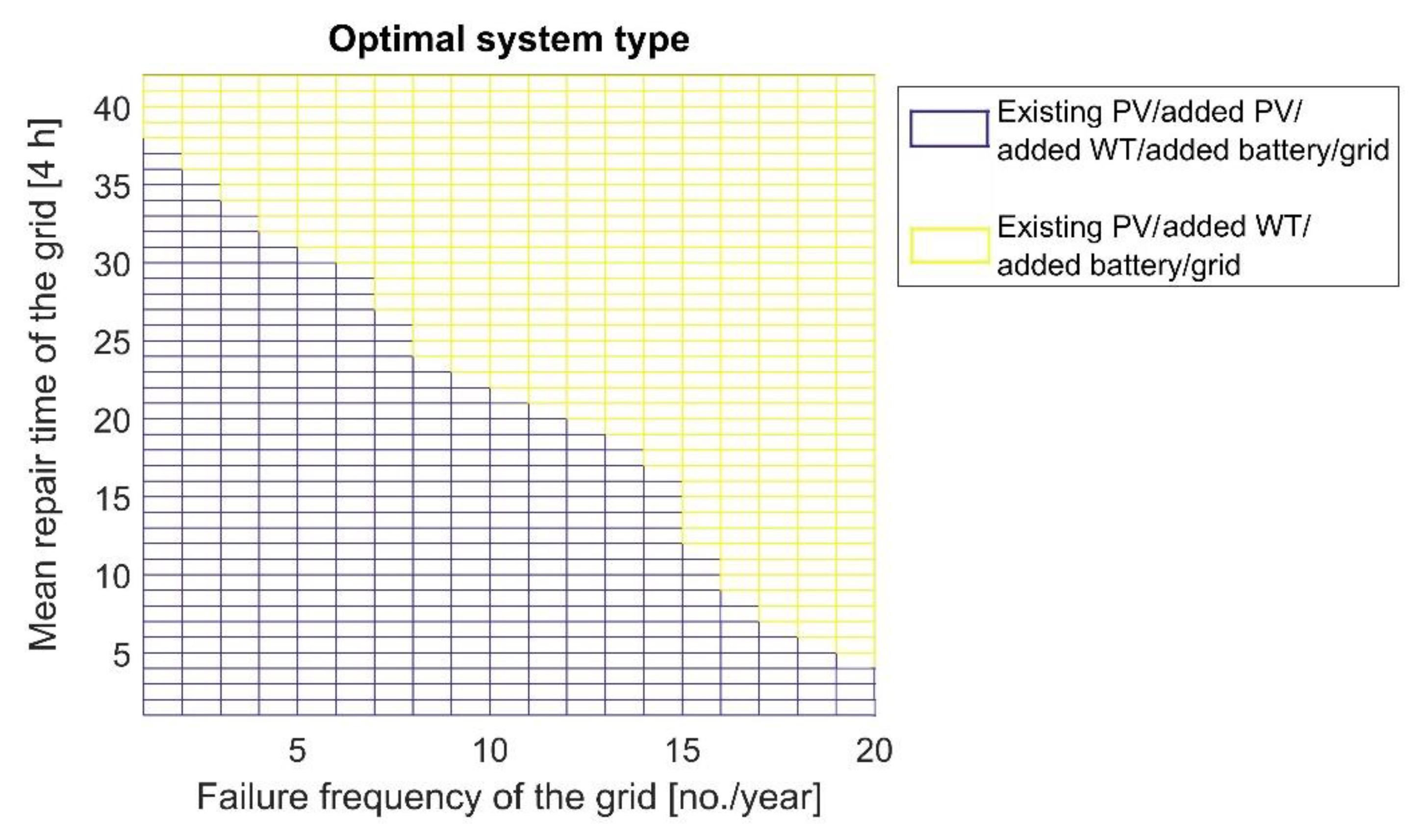
- The failure frequency of the grid and its mean repair time show almost the same degree of negative effect on the system’s life-cycle cost when normalised to the same scale (e.g., in the range of (0 to 1)). Additionally, there seems to exist a front of solutions with respect to the grid reliability parameters, beyond which the whole-life cost of the system grows exponentially. For example, in the middle case scenario, where the grid’s mean repair time and failure frequency were respectively considered to be 84 h and 10 per year, the system’s TNPC was increased only by about 48%. However, a further 10% increase of either of the above two parameters raised the MG’s TNPC by a further 26%. This observation can be rationalised by the change in the MG architecture when the grid unreliability level reaches a critical point, which is discussed in the next sub-section.
4.2.1. Optimal MG System Type
4.2.2. Indicative Resilient System Optimisation Analysis
4.3. Capital Budgeting Metrics
4.3.1. Return on Investment
4.3.2. Internal Rate of Return
4.3.3. Discounted Payback Period
4.3.4. Resulting Cash Flow Metrics
5. Conclusions
- Over the 25-year project life-cycle (planning horizon), the optimally expanded MG system can gain resilience against two outages per year, each up to four days in length, at relatively small discounted cost increases of 16% (equating to NZ$5892). This lends support to the idea that at current costs of renewable energy technologies, it is financially feasible for a community-level site to achieve a sufficient degree of survivability against sustained grid outages.
- The optimal architecture (component type combination), namely grid-connected existing PV/added PV/added WT/added BESS MG system, determined for the case with a 100% reliable grid, seems to be highly robust against a wide range of grid unreliability values. Much of the reason for this lies in the fact that solar resource tends to complement wind resource at the site. However, the evidence from this study shows that in high wind, low solar regions it is not cost-optimal to add PV capacity when the degree of grid unreliability passes certain limits. This can mainly be attributed to the lower capacity factor of the PV plant.
- With an IRR of about 55%, the initial investment required for the capacity expansion of the site’s energy infrastructure to meet the projected energy consumption growth (driven primarily by the decarbonisation of the transport), can be recouped in less than five years, while additionally ensuring backup power supply to critical loads for two outages per year, each up to four days in length. This, together with the capital affordability of the project, suggests that it can be financed completely by the local community. Moreover, given the demonstrated evidence of the cost-efficiency of such programmes, it is expected to be attractive to many third-party investors.
- All the estimates were based on defining energy resilience in terms of sustained grid outages. That is, the study has not accounted for the impact of extreme weather episodes on the operability of the considered site’s renewable energy generation assets.
- The proposed method does not account for the planned extended power outages related to grid capacity additions or equipment maintenance and repair.
- The study did not include any inputs from the site on the value the community places on the unserved energy during non-grid-connected operations. It is not implausible that the average annual loads that are deemed critical by end-consumers be different from the adjusted threshold criterion for load partitioning in this study.
- While the integration of unidirectional EV charging infrastructure is shown to be both technically feasible and economically viable, no attempt is made in this study to investigate the role that bidirectional charging (powered by V2G technology) can play in improving the profitability of the project.
Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | |
| BESS | Battery energy storage system |
| DPP | Discounted payback period |
| EV | Electric vehicle |
| EVSE | Electric vehicle supply equipment |
| HOMER | Hybrid Optimization of Multiple Energy Resources |
| IRR | Internal rate of return |
| LCOE | Levelised cost of energy |
| MG | Micro-grid |
| O&M | Operation and maintenance |
| PV | Photovoltaic |
| ROI | Return on investment |
| TNPC | Total net present cost |
| V2G | Vehicle-to-grid |
| WT | Wind turbine |
| Indices | |
| Index of year | |
| Scalars | |
| Length of time-step in hours | |
| PV module’s efficiency | |
| Wind shear exponent | |
| Real discount rate | |
| Depth of discharge | |
| Minimum/maximum usable capacity of each battery module | |
| PV module’s derating factor | |
| Solar irradiance at standard test conditions | |
| Hub height of the wind turbine | |
| Reference height of wind speed records | |
| PV module’s temperature coefficient | |
| Nominal operating cell temperature | |
| PV module’s rated power | |
| Project lifetime | |
| Cell temperature at standard test conditions | |
| Parameters | |
| Total load power demand on the micro-grid in time | |
| Power output from the PV system in time | |
| Power output from the wind turbine system in time | |
| Wholesale electricity price in time | |
| Feed-in-tariff | |
| PV module’s temperature in time | |
| Global horizontal irradiance in time | |
| Ambient temperature in time | |
| Hub-height wind speed in time | |
| Variables | |
| Cost of power exchange with the main grid | |
| Capital cost of the suggested micro-grid/reference system in year | |
| Energy content of the battery bank in time | |
| Net cash inflow sequence of the proposed micro-grid/baseline case in year | |
| Charging/discharging power of the battery bank in time | |
| Imported/exported power from/to the national grid in time | |
| Functions | |
| Present value function | |
References
- Warneryd, M.; Håkansson, M.; Karltorp, K. Unpacking the complexity of community microgrids: A review of institutions’ roles for development of microgrids. Renew. Sustain. Energy Rev. 2020, 121, 109690. [Google Scholar] [CrossRef]
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C. Smart Grid and Zero-Emissions Energy Systems: The Need for a Multi-Dimensional Investment Planning Perspective. IEEE Smart Grid eNewsl. 2018. Special Issue on the Paris Climate Agreement and the Role of the Smart Grid. [Google Scholar] [CrossRef]
- Achiluzzi, E.; Kobikrishna, K.; Sivabalan, A.; Sabillon, C.; Venkatesh, B. Optimal Asset Planning for Prosumers Considering Energy Storage and Photovoltaic (PV) Units: A Stochastic Approach. Energies 2020, 13, 1813. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Alsafasfeh, Q.; Pourbabak, H.; Su, W. The next-generation US retail electricity market with customers and prosumers—A bibliographical survey. Energies 2018, 11, 8. [Google Scholar] [CrossRef] [Green Version]
- Mohseni, S.; Brent, A.C.; Burmester, D. The Role of Artificial Intelligence in the Transition from Conventional Power Systems to Modernized Smart Grids. IEEE Smart Grid eNewsl. 2019. Special Issue on Grid Modernization. [Google Scholar] [CrossRef]
- Anderson, K.H.; DiOrio, N.A.; Cutler, D.S.; Butt, R.S. Increasing resiliency through renewable energy microgrids. J. Energy Manag. 2017, 2, 2. [Google Scholar]
- Eskandarpour, R.; Lotfi, H.; Khodaei, A. Optimal microgrid placement for enhancing power system resilience in response to weather events. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; pp. 1–6. [Google Scholar]
- Barnes, A.; Nagarajan, H.; Yamangil, E.; Bent, R.; Backhaus, S. Tools for improving resilience of electric distribution systems with networked microgrids. arXiv 2017, arXiv:1705.08229. [Google Scholar]
- Hussain, A.; Bui, V.-H.; Kim, H.-M. Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 2019, 240, 56–72. [Google Scholar] [CrossRef]
- Boloukat, M.H.S.; Foroud, A.A. Stochastic-based resource expansion planning for a grid-connected microgrid using interval linear programming. Energy 2016, 113, 776–787. [Google Scholar] [CrossRef]
- Waqar, A.; Wang, S.; Dawoud, S.M.; Tao, T.; Wang, Y. Optimal capacity expansion-planning of distributed generation in microgrids considering uncertainties. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 437–442. [Google Scholar]
- Motie, S.; Keynia, F.; Ranjbar, M.R.; Maleki, A. Generation expansion planning by considering energy-efficiency programs in a competitive environment. Int. J. Electr. Power Energy Syst. 2016, 80, 109–118. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H.; Siano, P. Coordinated short-term scheduling and long-term expansion planning in microgrids incorporating renewable energy resources and energy storage systems. Energy 2017, 134, 699–708. [Google Scholar] [CrossRef]
- He, Y.; Sharma, R. Microgrid generation expansion planning using agent-based simulation. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar]
- Salimi, M.; Nasr, M.-A.; Hosseinian, S.H.; Gharehpetian, G.B.; Shahidehpour, M. Information Gap Decision Theory-Based Active Distribution System Planning for Resilience Enhancement. IEEE Trans. Smart Grid 2020, (accepted; in press). [Google Scholar] [CrossRef]
- Ibanez, E.; Lavrenz, S.; Gkritza, K.; Mejía, D.; Krishnan, V.; McCalley, J.; Somani, A.K. Resilience and robustness in long-term planning of the national energy and transportation system. Int. J. Crit. Infrastruct. 2016, 12, 82. [Google Scholar] [CrossRef] [Green Version]
- Shao, C.; Shahidehpour, M.; Wang, X.; Wang, X.; Wang, B. Integrated planning of electricity and natural gas transportation systems for enhancing the power grid resilience. IEEE Trans. Power Syst. 2017, 32, 4418–4429. [Google Scholar] [CrossRef]
- Celtic Energy. Resilient Microgrids for Rhode Island Critical Services; Celtic Energy: Caerphilly, UK, 2017. [Google Scholar]
- Yuan, W.; Wang, J.; Qiu, F.; Chen, C.; Kang, C.; Zeng, B. Robust optimization-based resilient distribution network planning against natural disasters. IEEE Trans. Smart Grid 2016, 7, 2817–2826. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Ding, T.; Wang, X.; Li, Z.; Li, F. Microgrid planning considering the resilience against contingencies. IET Gener. Transm. Distrib. 2019, 13, 3534–3548. [Google Scholar] [CrossRef]
- Dong, J.; Zhu, L.; Su, Y.; Ma, Y.; Liu, Y.; Wang, F.; Tolbert, L.M.; Glass, J.; Bruce, L. Battery and backup generator sizing for a resilient microgrid under stochastic extreme events. IET Gener. Transm. Distrib. 2018, 12, 4443–4450. [Google Scholar] [CrossRef]
- Totarabank–Sustainable Rural Living. Available online: https://totarabank.weebly.com/ (accessed on 25 May 2020).
- Battery Systems. Available online: https://www.nexeon.co.uk/technology/ (accessed on 25 May 2020).
- Prasad, D.; Snow, M. Designing with Solar Power: A Source Book for Building Integrated Photovoltaics (BIPV); Routledge: Abingdon-on-Thames, UK, 2014; ISBN 1134032501. [Google Scholar]
- The X2000L Wind Turbine System. Available online: http://www.solazone.com.au/1kw-2kw-wind-turbines/ (accessed on 25 May 2020).
- Gipe, P. Wind power. Wind Eng. 2004, 28, 629–631. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.; Burmester, D.; Chatterjee, A. Optimal Sizing of an Islanded Micro-Grid Using Meta-Heuristic Optimization Algorithms Considering Demand-Side Management. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), 2018, Auckland, New Zealand, 27–30 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Jafari, M.; Mohseni, S.; Kelly, S. Optimal operation of an energy hub considering the uncertainty associated with the power consumption of plug-in hybrid electric vehicles using information gap decision theory. Int. J. Electr. Power Energy Syst. 2019, 112, 92–108. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Mohseni, S.; Karami, M.E.; Kelly, S. Optimal energy management of a grid-connected multiple energy carrier micro-grid. Appl. Therm. Eng. 2019, 152, 796–806. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2012, 28, 2151–2169. [Google Scholar] [CrossRef]
- 2014 Nissan Leaf. Available online: https://www.thecarconnection.com/overview/nissan_leaf_2014/ (accessed on 25 May 2020).
- Ode to the Nissan Leaf. Available online: http://evtalk.co.nz/ode-to-the-nissan-leaf/ (accessed on 25 May 2020).
- 2014 Nissan Leaf review: Electric car landmark. Available online: https://uk.motor1.com/reviews/139275/2014-nissan-leaf/ (accessed on 25 May 2020).
- Mohseni, S.; Moghaddas-Tafreshi, S.M. A multi-agent system for optimal sizing of a cooperative self-sustainable multi-carrier microgrid. Sustain. Cities Soc. 2018, 38, 452–465. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Trina Datasheet. Available online: https://static.trinasolar.com/sites/default/files/EN_TSM_PD05_datasheet_B_2017_web.pdf (accessed on 25 May 2020).
- Renew. Solar Panels. Available online: https://renew.org.au/wp-content/uploads/2019/12/150_solar_systems_guide_table.pdf (accessed on 25 May 2020).
- RESU: Residential Energy Storage Unit for Photovoltaic Systems. Available online: https://solarjuice.com.au/wp-content/uploads/2016/11/RESU-48V_installation_manual_R2_eng_2016-10-21-1.pdf (accessed on 25 May 2020).
- Change Your Energy Charge Your Life. Available online: https://solarjuice.com.au/wp-content/uploads/2016/10/160712_New-RESU-leaflet_Global-small.pdf (accessed on 25 May 2020).
- Battery Energy Storage Systems. Prices for the LG Chem RESU 3.3 kWh. Available online: http://www.batteryenergystoragesystems.com.au/ (accessed on 25 May 2020).
- SP PRO AU Series –Selectronic. Available online: http://www.selectronic.com.au/brochure/BR0007_09%20SP%20PRO%20Series%20II%20Data%20Sheet%20Web.pdf (accessed on 25 May 2020).
- Marshall Solar & Energy. Available online: https://marshallsolarandenergy.com.au/product/selectronic-sp-pro-inverter-charger-3-0-kw-24v-spmc240-au/ (accessed on 25 May 2020).
- Mohseni, S.; Brent, A.C.; Burmester, D. A demand response-centred approach to the long-term equipment capacity planning of grid-independent micro-grids optimized by the moth-flame optimization algorithm. Energy Convers. Manag. 2019, 200, 112105. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D. A comparison of metaheuristics for the optimal capacity planning of an isolated, battery-less, hydrogen-based micro-grid. Appl. Energy 2020, 259, 114224. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C. Economic viability assessment of sustainable hydrogen production, storage, and utilisation technologies integrated into on-and off-grid micro-grids: A performance comparison of different meta-heuristics. Int. J. Hydrogen Energy 2019, (accepted; in press). [Google Scholar] [CrossRef]
- Nikolaus, R.; Paul, T.J. Feasibility Study of Small and Micro Wind Turbines for Residential Use in New Zealand: An Analysis of Technical Implementation, Spatial Planning Processes and of Economic Viability of Small and Micro Scale Wind Energy Generation Systems for Residential Use in New Zealand. Available online: https://researcharchive.lincoln.ac.nz/handle/10182/4141 (accessed on 25 May 2020).
- Mohseni, S.; Brent, A.C.; Burmester, D. A Sustainable Energy Investment Planning Model Based on the Micro-Grid Concept Using Recent Metaheuristic Optimization Algorithms. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 219–226. [Google Scholar] [CrossRef]
- Chargers Direct. Delta Mini AC Electric Vehicle Charge Point-Networked 3G. Available online: https://www.chargersdirect.com.au/product/delta-ac-mini-plus/ (accessed on 25 May 2020).
- Delta AC Mini Plus EV Charger. Available online: https://yhipower.co.nz/catalog/ac-mini-plus-104892.htmx (accessed on 25 May 2020).
- Elkadeem, M.R.; Wang, S.; Azmy, A.M.; Atiya, E.G.; Ullah, Z.; Sharshir, S.W. A systematic decision-making approach for planning and assessment of hybrid renewable energy-based microgrid with techno-economic optimization: A case study on an urban community in Egypt. Sustain. Cities Soc. 2020, 54, 102013. [Google Scholar] [CrossRef]
- NASA Surface Meteorology and Solar Energy database. Available online: https://eosweb.larc.nasa.gov/ (accessed on 25 May 2020).
- Solar Power Buy-Back Rates. Available online: https://www.mysolarquotes.co.nz/about-solar-power/residential/solar-power-buy-back-rates-nz/ (accessed on 25 May 2020).
- Bücher, K. Site dependence of the energy collection of PV modules. Sol. Energy Mater. Sol. Cells 1997, 47, 85–94. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Chatterjee, A. Stochastic Optimal Sizing of Micro-Grids Using the Moth-Flame Optimization Algorithm. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wind Shear. Available online: https://www.engineeringtoolbox.com/wind-shear-d_1215.html/ (accessed on 25 May 2020).
- The Electricity Market Information: The New Zealand Electricity Authority’s Wholesale Database. Available online: https://www.emi.ea.govt.nz/Wholesale/Reports/ (accessed on 25 May 2020).
- Anderson, B.; Eyers, D.; Ford, R.; Ocampo, D.G.; Peniamina, R.; Stephenson, J.; Suomalainen, K.; Wilcocks, L.; Jack, M. New Zealand GREEN Grid Household Electricity Demand Study 2014–2018; UK Data Service: Colchester, UK, 2018. [Google Scholar] [CrossRef]
- Anderson, B. NZ GREEN Grid Household Electricity Demand Data: EECA Data Analysis (Part. C) Upscaling Advice Report v1.0; University of Otago: Dunedin, New Zealand, 2019. [Google Scholar]
- Twidell, J.; Weir, T. Renewable Energy Resources; Routledge: Abingdon-on-Thames, UK, 2015; ISBN 1317660374. [Google Scholar]
- HOMER Pro; HOMER Energy LLC: Boulder, CO, USA, 2020.
- Ueckerdt, F.; Kempener, R. From Baseload to Peak: Renewables Provide a Reliable Solution; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2015. [Google Scholar]
- Discount Rates and CPI Assumptions for Accounting Valuation Purposes. Available online: https://treasury.govt.nz/information-and-services/state-sector-leadership/guidance/financial-reporting-policies-and-guidance/discount-rates/discount-rates-and-cpi-assumptions-accounting-valuation-purposes/ (accessed on 25 May 2020).
- New Zealand Inflation Rate. Available online: https://tradingeconomics.com/new-zealand/inflation-cpi/ (accessed on 25 May 2020).
- New Zealand’s Energy Outlook: Electricity Insight. Available online: https://www.mbie.govt.nz/building-and-energy/energy-and-natural-resources/energy-statistics-and-modelling/energy-modelling/new-zealands-energy-outlook/new-zealands-energy-outlook-electricity-insight/ (accessed on 25 May 2020).
- Wanitschke, A.; Pieniak, N.; Schaller, F. Economic and environmental cost of self-sufficiency-analysis of an urban micro grid. Energy Procedia 2017, 135, 445–451. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D. A Reliability-Oriented Cost Optimisation Method for Capacity Planning of a Multi-Carrier Micro-Grid: A Case Study of Stewart Island, New Zealand. arXiv 2019, arXiv:1906.09544. [Google Scholar]
- Mohseni, S.; Moghaddas-Tafreshi, S.M. Development of a multi-agent system for optimal sizing of a commercial complex microgrid. arXiv 2018, arXiv:1811.12553. [Google Scholar]
- Mohseni, S.; Moghaddas-Tafreshi, S.M. A multi-agent approach to optimal sizing of a combined heating and power microgrid. arXiv 2018, arXiv:1812.11076. [Google Scholar]
- Electricity Cost and Price Monitoring. Available online: https://www.mbie.govt.nz/building-and-energy/energy-and-natural-resources/energy-statistics-and-modelling/energy-statistics/energy-prices/electricity-cost-and-price-monitoring/ (accessed on 25 May 2020).
- Seitz, N.; Ellison, M. Capital Budgeting and Long-Term Financing Decisions; Harcourt Brace College Publishers: New York, NY, USA, 1995; ISBN 0030754771. [Google Scholar]
- Compare Economics—HOMER Energy. Available online: https://www.homerenergy.com/products/pro/docs/latest/compare_economics.html/ (accessed on 25 May 2020).
- Return on Investment—HOMER Energy. Available online: https://www.homerenergy.com/products/pro/docs/latest/return_on_investment.html/ (accessed on 25 May 2020).
- Fisher, I. The theory of Interest, as Determined by Impatience to Spend Income and Opportunity to Invest It; Macmillan: New York, NY, USA, 1930. [Google Scholar]






| Ref. | Technologies Considered in the Candidate Pool | Optimisation Approach | Key Contribution(s) | Key Insight(s) from Case Study Analyses |
|---|---|---|---|---|
| [11] | Solar photovoltaic (PV), wind turbine, fuel cell, diesel generator, heat storage, and battery | Mixed-integer linear programming solved using the General Algebraic Modeling System (GAMS) |
|
|
| [12] | Solar PV, wind turbine, diesel generator, and battery | Scenario-based stochastic optimisation |
|
|
| [13] | Wind turbine, bi-directional electric vehicle charging infrastructure | Semi-dynamic, semi-static programming |
|
|
| [14] | Solar PV, wind turbine, diesel generator, battery, and utility line | Mixed-integer nonlinear programming solved using meta-heuristic optimisation algorithms |
|
|
| [15] | Solar PV and wind turbine | Multi-agent systems |
|
|
| Ref. | Technologies/Resources/Systems Considered in the Candidate Pool | Optimisation Approach | Key Contribution(s) | Key Insight(s) from Case Study Analyses |
|---|---|---|---|---|
| [16] | Unspecified distributed generation | Mixed-integer linear programming solved using GAMS |
|
|
| [17] | Hydro, wind, solar, geothermal, nuclear, coal, natural gas, and oil | Multi-objective optimisation of the national-level, energy infrastructure capacity expansion problem |
|
|
| [18] | Electric power system and natural gas system | Two-stage robust optimisation |
|
|
| [19] | Solar PV, battery, and combined heat and power | HOMER software |
|
|
| [20] | Unspecified distributed generation technologies | Two-stage robust optimisation |
|
|
| [21] | Solar PV, wind turbine, diesel generator, and battery | Two-stage robust optimisation |
|
|
| [22] | Battery and diesel generator | Mixed-integer linear programming solved using GAMS |
|
|
| Specification | Component | |||
|---|---|---|---|---|
| PV Modules 1 | Wind Turbines 2 | Battery Arrays | Converter | |
| Manufacturer part number | TSM-285 PD05, Trina Solar | X-2000L | RESU 3.3, LG Chem | SPMC240-AU, Selectronic |
| Rated capacity | 285 W | 2 kW | 3.3 kWh | 3 kW |
| Capital cost | $237/unit | $3967/unit | $3645/unit | $4600/unit |
| $832/kW | $1984/kW | $1105/kWh | $1533/kW | |
| Replacement cost 3 | $237/unit | $3229/unit | $3645/unit | $4600/unit |
| O&M cost 3 | $0.7/unit/year | $26.4/unit/year | $7.3/unit/year | $3.9/unit/year |
| Useful life | 25 years | 20 years 4 | 15 years | 15 years |
| Efficiency | 17.4% | N/A 5 | 95% 6 | 96% |
| Source | [37,38] | [26] | [39,40,41] | [42,43] |
| Scalar | Value | Source | Scalar | Value | Source |
|---|---|---|---|---|---|
| 88% | [51] | 7 m | (this paper) | ||
| −0.41%/°C | [37] | 50 m | [52] | ||
| 44 | [37] | $0.08/kWh | [53] | ||
| 1 kW/m2 | [54] | 1 h | [55] | ||
| 25 °C | [54] | 1 | 2.9 kWh | [40] | |
| 0.15 | [56] | 2 | 0.29 kWh | [40] |
| Parameter | Value | Source |
|---|---|---|
| Nominal discount rate | 4.5% | [63] |
| Expected inflation rate | 1.9% | [64] |
| Project lifetime | 25 years | (this paper) |
| Minimum autarky ratio 1 | 80% | (this paper) |
| Maximum annual capacity shortage in meeting critical loads | 0% | (this paper) |
| Load growth rate | 1.1% per annum | [65] |
| PV 1,2 [kW] | WT 1 [kW] | Battery 1 [kWh] | Inverter 1 [kW] | EVSE 1,3,4 [kW] | TNPC 5 [$] | LCOE [$/kWh] |
|---|---|---|---|---|---|---|
| 0.855 | 4 | 6.6 | 3 | 14.72 | 35,891 | 0.094 |
| PV (kW) | WT (kW) | Battery (kWh) | Inverter (kW) | EVSE (kW) | TNPC ($) | LCOE ($/kWh) |
|---|---|---|---|---|---|---|
| 0.855 | 4 | 9.9 | 3 | 14.72 | 41,783 | 0.109 |
| Metric | Return on Investment (%) | Internal Rate of Return (%) | Discounted Payback Period (Years) |
|---|---|---|---|
| Value | 47.63 | 54.51 | 4.74 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohseni, S.; Brent, A.C.; Burmester, D. Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand. Energies 2020, 13, 3970. https://doi.org/10.3390/en13153970
Mohseni S, Brent AC, Burmester D. Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand. Energies. 2020; 13(15):3970. https://doi.org/10.3390/en13153970
Chicago/Turabian StyleMohseni, Soheil, Alan C. Brent, and Daniel Burmester. 2020. "Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand" Energies 13, no. 15: 3970. https://doi.org/10.3390/en13153970
APA StyleMohseni, S., Brent, A. C., & Burmester, D. (2020). Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand. Energies, 13(15), 3970. https://doi.org/10.3390/en13153970