1. Introduction
Environmental concerns, inflating fossil fuel prices and the depletion of conventional energy resources, compel researchers to retain their efforts towards sustainable, reliable, and economical sources for electric power generation. In this aspect, renewable energy sources (RES) like biomass, solar, hydro, and wind are gaining the interest of researchers [
1,
2]. Among these RES, solar energy is a widely and freely available energy source, which can be easily captured directly through a photovoltaic (PV) system [
3,
4]. Some factors which emphasize the importance of solar energy are listed below:
Less operational cost (as no fuel is consumed) [
5];
Low maintenance (as it requires no lubrication as well as no dynamic part or machinery is involved) [
6];
Very little or no greenhouse gas emission results in reduced air pollution [
7].
A PV cell is a basic unit of a PV system, and various cells are combined in series and parallel configuration to form a PV module for generating electric power of a required level [
8]. The accurate electrical and mathematical modeling of PV cells/modules is a hot research topic nowadays, as it helps to understand the non-linear behavior of a PV system under certain atmospheric conditions, such as a partial shading condition or an abrupt change in temperature and irradiance levels [
9]. The most common approach to accurately model PV cells and module behavior is to utilize electrical equivalent models. Single and double-diode models are widely opted and utilized by various researchers for PV cell/module modeling [
10,
11,
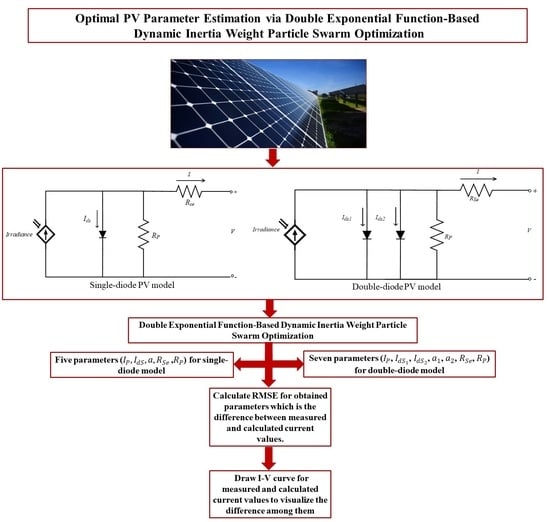
12]. The single-diode model presented in
Figure 1 has five associated parameters;
and
. The I–V characteristic defined by the Shockley diode equation is as follows in Equation (1) [
13]:
where,
are the photon current, diode saturation current, diode ideality factor, series resistance and the parallel resistance, respectively. These five parameters must be estimated for the modeling of single-diode solar cells and modules, while
represent the electron charge, Boltzmann constant, and temperature in Kelvin, respectively.
The second most utilized PV model is a double-diode model, presented in
Figure 2. The I–V characteristics of the double-diode model are depicted in Equation (2) [
14]:
where,
,
are the saturation currents of diode 1 and 2;
,
are the ideality factors of diode 1 and 2, respectively. The seven associated parameters
of the double-diode model must be estimated efficiently to accurately calculate the current from the double-diode cell or module [
15]. The double-diode model is more complex but offers more accuracy than a single-diode model [
16]. Five parameters for the single and seven parameters for the double-diode model must be estimated in such a way that the obtained model accurately emulates the I–V characteristics of the original model, such that the difference in the calculated and originally measured currents for the PV cell/module should be minimal [
17]. Therefore, this problem emerged as an optimization problem and is termed as the “parameter estimation of solar cells and modules”.
To solve this optimization problem, various methodologies have been utilized by researchers, which can be categorized into two broad term categories. Analytical approaches involve the formulation of functions based on the information obtained from the datasheet [
18,
19] and metaheuristic techniques which estimate PV parameters by converting them into an optimization problem. Analytical approaches require complex computational efforts and are not suitable for large or complex systems [
20]. However, metaheuristic approaches are artificially intelligent population-based techniques that aim to find a global best solution for any optimization problem [
1,
21] by updating the population in an iterative process and are mostly utilized for estimating the PV parameters of cells and modules [
22].
In [
23], a biogeography-based heterogeneous cuckoo search algorithm (BHCS) has been proposed, which combines the biogeography and cuckoo search algorithm. Two test systems, the RTC France solar cell and the STM6-40/36 module, were utilized for the validation of results. Data from [
24] were utilized for the parameter estimation of the PV cell and module, while the root mean square error (RMSE) was considered as an objective function as defined in Equation (3) [
25]:
where,
represents the measured current of the solar model obtained from [
24] ,
represents the calculated current and
is the number of I–V pairs.
In [
26], the artificial bee colony has been utilized for the parameter estimation of single- and double-diode RTC France solar cell considering varying temperature levels. A modified variant of artificial bee colony (ABC) has been proposed in [
27] for the parameter estimation of the single- and double-diode cell models. The RTC France solar cell with a 57 mm diameter was utilized for the validation of the proposed approach, and the obtained results were compared with various other algorithms. In [
28], a differential evaluation (DE) algorithm was utilized for the parameter estimation of solar cells, including thin-film, multi-crystalline, and mono-crystalline cells. A penalty function was introduced for constraint handling. An improved variant of DE was proposed in [
29] for the parameter estimation of the RTC France solar cell. An adoptive cross-over rate, a mutation strategy, and an adaptive scaling factor were introduced to improve the search ability of the conventional DE algorithm. In [
30], the cuckoo search (CS) algorithm was utilized for the parameter estimation of the RTC France solar cell, which represents high accuracy under various operating conditions. In [
31], a cat swarm optimization (CSO) has been presented for the parameter estimation of single- and double-diode cells and modules. The RTC France solar cell and PWP201 Photo-watt module have been considered for the validation of results.
Despite all the merits of metaheuristic approaches, they offer some limitations, such as the particle swarm optimization (PSO) which suffers from premature convergence problem, which implies that while searching for the global best solution, it can be easily trapped in local solution, hence providing non-optimal results. To solve this problem, the researchers proposed different improved variants of PSO. In [
32], a chaotic inertia weight PSO (CIWPSO) has been implemented for the parameter extraction of single- and double-diode solar cells. In this variant, the inertia weight follows a chaotic map logic to find an optimal solution while avoiding premature convergence. In [
33], time-varying acceleration coefficient PSO (TVACPSO) was proposed for the parameter estimation of single- and double-diode solar cells and modules. In this proposed variant, the personal acceleration coefficient was decreased, and the social acceleration coefficient was increased during the iterative process. In [
34], enhanced leader PSO (ELPSO) was proposed for the parameter estimation of single- and double-diode models. In this variant, the leader particle was enhanced by utilizing a five-staged mutation strategy. The results were compared with other available techniques. In [
35], another improved variant named guaranteed convergence PSO (GCPSO) was implemented for the parameter estimation of PV cells and modules. In this variant, the success and failure rate along with a scale factor were proposed, which guarantee the convergence of the algorithm towards an optimum solution.
The comprehensive evaluation of literature depicts that a lot of work has been presented in [
21,
22,
23,
24] to cope with the premature convergence problem of conventional PSO. However, the studies [
21,
22,
23] have not proven the strength of the proposed approaches on a real-time practical system, that undergoes variation in irradiance and temperature levels, hence increasing the computational burden. There is thus a need to present a dynamic strategy that can effectively deal with the issues of conventional PSO in real-time scenarios. This paper proposes a double exponential dynamic inertia weight PSO (DEDIWPSO) for the parameter estimation of single- and double-diode cells and modules. This inertia weight strategy was inspired by decreasing the rate of an exponential function. The fast growing nature of the exponential function improves the speed of convergence by maintaining a balance between the global and local search. The notable contributions of this paper are mentioned below:
A dynamic and efficient strategy—DEDIWPSO—was proposed to solve the premature convergence problem of conventional PSO, hence providing optimal, efficient, and accurate solutions for the parameter estimation problem;
A Newton–Raphson method (NRM)-based computational intelligent (CI) approach was implemented to accurately estimate the current for each set of optimal parameters;
Three case studies, (1) the RTC France solar cell, (2) the PWP201 Photo-watt module, and a practical test system JKM330P-72 (310 W) polycrystalline module under real environmental conditions were considered for the validation of the proposed approach;
The obtained optimal results and statistical analysis were compared with other techniques available in the literature to present the effectiveness of the proposed approach.
The remainder of this paper is arranged as follows:
Section 2 formulates the PV parameter estimation as an optimization problem,
Section 3 presents the proposed methodology to solve this optimization problem,
Section 4 discusses the obtained results from the proposed technique, and finally
Section 5 concludes the whole paper.
3. Proposed Methodology
Particle swarm optimization (PSO) is a population-based metaheuristic technique inspired by the swarming behavior of birds and fishes they present while moving from one place to another in search of food. A population consists of
number of particles, and these individuals (particles) explore search space to find a globally optimum solution. Equation (9) presents the position of the
particle in the multidimensional search space:
where
represents the number of decision variables (dimensions). At first, the
number of particles were initialized randomly in a confined search space. Then, the personal best
and global best
are calculated and updated by evaluating the objective function. Personal best position of a particle is considered as
and the best value among all particles is considered as
The position and velocity of each particle are updated in every iteration using the following Equations (10) and (11):
where
,
represent the velocity and position of the
particle, respectively.
are the personal and social acceleration coefficients, respectively.
is the inertia weight coefficient and
are random numbers between 0 and 1. After updating
and
, the personal best
and global best
are updated, and this procedure continues until the stopping criteria is achieved.
PSO is simple and widely utilized by researchers for solving various optimization problems [
36] but like other metaheuristic techniques, it has a tendency to become stuck in local minima due to the “stagnation of particles” that leads to non-optimal solutions and the premature convergence problem. To improve the search capability of PSO, many variants have been proposed in which different strategies have been employed to tune its controlling parameters. Inertia weight (
is an important parameter of PSO, responsible for an appropriate tradeoff between the global and local search. An efficient mechanism of inertia weight can solve the premature convergence problem of conventional PSO [
37]. This study presents double exponential function-based dynamic inertia weight PSO (DEDIWPSO), intended to improve the search capability of conventional PSO by solving the premature convergence problem. DEDIW is inspired by the rapid growing nature of the exponential function and incorporate the “Gompertzian function” which is a dying double exponential function as Equations (12) and (13) below:
where
and
is the performance index, which is calculated for each particle at every iteration. This dynamic inertia weight decreases with increasing iterations. At first,
is set to 0.8 [
37] then calculated using Equations (12) and (13). In early iterations, the particles are away from the global best solution, and the proposed strategy provides a greater rate of exploration so that the particles can explore more search space to find the best optimum solution. Later, a relatively smaller value of
is provided to guarantee precision in the exploration phase. The fast-growing nature of exponential function improves the speed of convergence, and hence provides optimal, efficient, and accurate solutions for the parameter estimation problem. The flow chart of the proposed methodology is presented in
Figure 5.