Hybrid Multi-Criteria Method of Analyzing the Location of Distributed Renewable Energy Sources

Abstract

This paper presents the development and the application of a hybrid multi-criteria method, the combination of the Analytic Hierarchy Process (AHP), and numerical taxonomy (NT), to support the decision making on the location of distributed renewable energy sources meeting various types of assessment criteria. Finding criteria weights, using the AHP method, eliminates the disadvantage of NT—which, in current form, is defined by its extreme values. The NT method is less mathematically complicated than the AHP method, and thus, less time-consuming. The combination of methods was used to investigate: (1) Which location among these analyzed has the best chance of implementation considering the author’s set of criteria to describe the proposed locations in detail; and (2) which detailed criterion has the greatest impact on achieving the main goal. The proposed universal set of criteria consists of five main criteria (technical, economic, social, environmental, and legal), under which twenty-eight detailed criteria are listed. The hybrid multi-criteria methodology was used to rank the proposed set of four wind farm locations in terms of chances for investment implementation in the shortest possible time. The ranking of the location obtained with this method should be treated as an element supporting the decision-maker. The location for wind power plant with installed capacity 40 MW was found to be the most suitable, and the results showed that the main contributing factors are carbon avoidance rate and the impact of the investment on environmentally protected areas.

1. Introduction

One of the hallmarks of a growing society is the ability to ensure a reliable electricity supply meeting a wide range of needs and requirements in all sectors of the economy. Reliability and security of electricity supply is the reason why power system planning is an issue, and solutions to related problems have been taken on for years [1,2,3]. The research aimed at ensuring the security of electricity supply includes the development of indicators, methodologies, databases, tools and decision-making support. The literature review presented in this work discusses the importance of this topic.

Technological development, political conditions and the need to diversify electricity sources have changed the approach to power system development planning. Growing concerns about the impact of the power system on the environment and depletion of non-renewable energy resources, as well as the growing public interest in the energy sector in general, have resulted in the inclusion of ecological and social aspects in the power system development planning. Considerations on the impact of energy fuels on the environment are currently being undertaken in the scientific literature [4].

The process of planning the development of the power transmission and distribution grids, as well as searching for the location of the construction of generating sources, is one of the most important undertakings for both generators and power system operators.

To ensure the country’s long-term electricity security is the main goal of planning [5]. Due to the lack of sufficient computing power, the development of energy systems was based for a long time on the function of minimizing costs, the so-called classical method. However, this method does not take into account all the requirements that should be met by the considered locations of the elements of the energy system. There are studies available in the literature describing, for example, health costs of greenhouse gas emissions to the atmosphere [6], health costs of wind turbine noise, and global warming [7]. Despite this, social acceptance aspects and costs of obtaining all necessary decisions and permits are not included.

Multi-criteria methods have been used in solving development problems of both the electricity generation sector, and transmission and distribution systems thanks to a comprehensive approach to the problem. These methods consist of arranging objects and checking whether those in higher rankings meet the assumed goal.

The methods used in multi-criteria analyzes can also include outranking methods and interactive methods. Classification methods rely on building a classification relationship, representing decision-maker preferences, which is then used to support the decision-making process. Interactive methods rely on alternating computational and dialogue steps, which effectively provide a more consensual and preference-indicating solution [8].

Multi-criteria decision analysis methods are widely applied in the energy sector and transportation because they help decision-makers consider and weigh diverse criteria that include economic, environmental, social and technological aspects [9].

Decision options are a solution to the decision problem, which is determined by a set of factors—criteria that influence the decision-making by the decision-maker. The criteria are a measure of the assessment of individual decision options [10]. In the decision-making process, the decision-maker faces the necessity of choosing one of at least two decision variants that can be described by one or more criteria. In this way, a hierarchical structure of criteria is created.

The main purpose of the multi-criteria analysis is the priority value for which the analysis is performed, e.g., the selection of the location of the energy source. In pursuit of the main goal of multi-criteria analysis, a decision option should not be inferior compared to other options [11].

Decision options, or alternatives, are potential solutions to the decision problem [12]. There are cases in which individual decision options are mutually exclusive. To compare decision options, the optimization criteria by which they are compared should be set [13].

The multitude of advantages of multi-criteria methods, such as the possibility of integrating qualitative and quantitative criteria, objectivity, and merging of various entities participating in the decision-making process, has resulted in their extensive development and application in many areas. The wide use of multi-criteria methods described in the literature has been observed. There are studies in which multi-criteria methods are used for location analysis of generating sources.

The most commonly used multi-criteria method is the Analytic Hierarchy Process (AHP) method. Despite the necessity of multiple pair-vice comparisons of criteria and time-consuming calculations, researchers often use the AHP method in various fields of science. Tegou et al. proposes to carry out an analysis of the selection of a wind power plant location, using an AHP method [14]. The selection of criteria was based on a literature review, experience and expert knowledge. The result of the analysis is the indication of the wind energy potential and the roughness of the terrain as the most important criteria determining the location of the wind farm. The least important criterion turned out to be the economic one. It should be noted that the article does not consider social criteria, except the impact on the landscape. Cebi et al. used the following methods: AHP, a model described on a set of fuzzy numbers, a preference aggregation method and an axiomatic method to determine the location of a biomass power plant [15]. As a result, the most important evaluation criteria for biomass power plant location selection as the calorific value of biomass source, the quantity of biomass source, the unit cost of biomass were indicated, respectively.

The combination of AHP and ANP (Analytic Network Process) methods was used in to determine the location of the solar power plant [16]. In this case, the ANP method was used to determine the criteria that interact with each other. Sánchez-Lozano et al. [17] used a combination of GIS (Geographic Information System), AHP and TOPSIS (Technique for Order Preference using Similarity to Ideal Solution) methods to determine the location of a photovoltaic power plant. The AHP method was used to determine the weights of individual criteria and the TOPSIS method to estimate alternative solutions to the problem. The authors note that the choice of methodology was made due to the lack of the need for an expert to evaluate individual alternatives and the impact of criteria on individual solutions. This assessment can be made based on data provided by the GIS geoinformation system.

The selection of the type of renewable energy source and its location is presented in ref. [18], where the VIKOR-AHP method was used. In addition to technical, economic and social criteria, criteria related to the emission of greenhouse gases into the atmosphere were distinguished.

A combination of multi-criteria methods and the creation of the so-called hybrid methods or the use of fuzzy forms of previously created methods are also often found in the literature. For example, the use of GIS software includes maps for specific locations and reduces the need for expert participation due to information on GIS maps, such as insolation, land use, and transmissions lines [19]. It has also been observed in the literature, that multi-criteria location analysis of distributed generation is rare. However, in the studies found, the AHP method is the most common [15]. The use of a specific method to solve a decision problem in the literature is usually not explained. The authors present the assumptions for the methods and tools they use, without commenting on why they use them. There was also a lack of consistency in the selection of criteria [20]. The criterion is a measure of the assessment of individual decision options [11]. Choosing the location of the source of electricity generation is a complex issue and requires the development of a method that will allow its universal application regardless of the nature of the source.

Renewable power plants limit environmental degradation, which is why this method of generating electricity is preferred and promoted in the European Union. Due to the great interest in renewable energy sources, this article focuses on the location of sources of generating electricity produced by renewable sources with installed capacity 50–150 MW classified as distributed generation [21].

The reasons for the need to develop a power system described above and the legitimacy of using multi-criteria methods for this purpose have become the basis for the implementation of this work. The work contributes to the development of research on multi-criteria methods and also comprehensively captures activities aimed at building new sources of electricity production.

The main objective of this article is to describe the proposed method, which includes elements of the method of Analytic Hierarchy Process (AHP) and numerical taxonomy (NT). This combination has not been used so far in location analyzes of the energy sector and can significantly systematize, and thus, shorten the duration of the investment process in new generation sources.

The article also presents a case study in which location of distributed power generation sources among the analyzed has the best chance of implementation, taking into account various types of optimization criteria and location barriers that were indicated. The determination of global weights of detailed criteria was introduced into the method, which was then taken into account when determining the location ranking coefficient, which was not previously discussed in the literature.

Therefore, a methodology and example are shown that the proposed method can be applied in any country by using a universal set of criteria. The set of criteria can also be used to compare the profitability of construction of various generation sources with each other.

2. Materials and Methods

2.1. Multi-Criteria Method

The multi-criteria method of searching for the best location of a distributed electricity generation installation, proposed and developed in this article, should be understood as an algorithm of conduct that finds the best solution among the available location variants, taking into account the relationships between the parameters of the criteria for assessing variants. The ranking of the location obtained thanks to the method should be treated as an element supporting the decision-maker and not making the final decision for them. As mentioned earlier, there are many methods of multi-criteria analysis, the selection of which depends on the knowledge and preferences of the decision-maker. There is currently no single method in place that should be used to address location issues in the energy sector.

According to the methodology for solving problems of the development of the energy sector, the analysis should start with determining the types of generating sources. The proposed method allows the ranking of locations of electricity generating sources, such as photovoltaic and wind farms, biogas plants, and biomass power plants. With the use of the presented method, it is possible to perform a ranking of the different types of sources of electricity.

2.1.1. The General Algorithm of the Method

This section provides an overview of the method. Based on an analysis of the study’s background, motivation, and objective, and during the author’s cooperation with experts from a local energy company, and a review of the related literature, I constructed a general algorithm of the method.

First of all, it is necessary to determine the type of distributed electricity generation sources. Identifying locations and assessment criteria should be understood as determining the specific parameters of each of the compared locations so that they can be compared against selected criteria. The set of location assessment criteria proposed by the author, among which the selection criteria used for the comparative location analysis is presented in

Table 1. A universal set of criteria used to assess the location of electricity generation sources.

Symbol	Specification of Criteria
$X_1$	Technical criteria
	$X_{1,1}$	availability of primary raw materials
	$X_{1,2}$	time of installed power utilization
	$X_{1,3}$	distance from the power system
	$X_{1,4}$	distance from the district heating network
	$X_{1,5}$	short-circuit power on the medium voltage (MV) side
	$X_{1,6}$	static voltage change
	$X_{1,7}$	dynamic voltage change
	$X_{1,8}$	permissible load of power system components
	$X_{1,9}$	system efficiency
$X_2$	Economic criteria
	$X_{2,1}$	investment expenditures
	$X_{2,2}$	the cost of producing energy in the life cycle analysis
	$X_{2,3}$	net present value (NPV)
	$X_{2,4}$	internal rate of return (IRR)
$X_3$	Social criteria
	$X_{3,1}$	public support for investment
	$X_{3,2}$	favor of local authorities for investments
	$X_{3,3}$	investment compliance with local policies
$X_4$	Environmental criteria
	$X_{4,1}$	carbon avoidance rate
	$X_{4,2}$	noise emission
	$X_{4,3}$	impact on animal population
	$X_{4,4}$	impact of the investment on the landscape
	$X_{4,5}$	impact of the investment on nature protected areas
	$X_{4,6}$	land surface indicator
	$X_{4,7}$	location of the area for post-fermentation waste management
$X_5$	Legal criteria
	$X_{5,1}$	planning documents for the power line
	$X_{5,2}$	planning documents for the investment area
	$X_{5,3}$	the environmental decision for the power line
	$X_{5,4}$	the environmental decision for the investment area

. The author proposes to use the advantage of the AHP method, which is weight determination by pair-vice comparison of criteria and a problem presentation in a hierarchical structure. When using the AHP method, weights should be determined for all main and specific criteria. A method of choosing decision criteria adapted to the specific decision situation has been proposed. This process is objective thanks to the AHP method.

The AHP method is used to choose from a general, universal set of criteria relevant for the assessment of the currently analyzed decision case. To be able to compare locations, one must compare criteria and select those that have the greatest impact on the desired location ranking. The author proposes to use the AHP method to determine the weight of the main and specific criteria by pair-vice matching relevant criteria.

If there is a need to reduce large data sets describing generating sources or gathering all the necessary information is not feasible the author proposes that the set of criteria adopted for further analysis should consider the eliminated and reduced criteria. After determining the set of criteria adopted for the analysis, the reference and anti-reference values should be determined using the NT method. Then, the authors propose to determine of metric distances of individual locations from the reference and anti-reference values. Using the NT method, the locations are organized due to the increasing values of the ranking coefficient, and the ranking is presented.

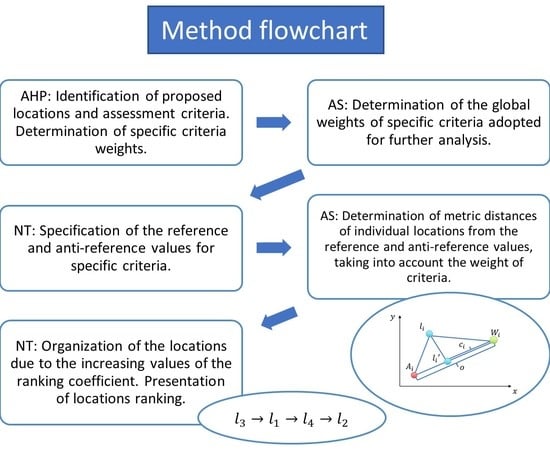
The general algorithm of the method is shown in Figure 1. The diagram indicates the areas of application of the AHP method, numerical taxonomy (NT), and the author’s suggestions (AS).

2.1.2. Analytic Hierarchy Process

The AHP method is a hierarchical structure method, which is why the criteria are divided into main criteria, which directly affect the implementation of the investment and detailed criteria having an indirect impact on the implementation of the investment. Figure 2. Depicts the hierarchical structure of the location problem in the power system.

The assumption of the AHP method is to compare pairs of criteria by creating a diagonal matrix of comparisons by $\mathit{X}$ pairs of size ($nxn$) (Equation (1)), where $n$ is the number of criteria. The AHP method is a method based on a hierarchical structure, shown in Figure 2. The main criteria for the assessment $X_I$, which directly affect the result of the main analysis goal, are defined by specific criteria $X_{\mathrm{i}.\mathrm{s}}$. To determine the impact of the main criteria on the achievement of the analysis objective, they should be compared pair-vice according to the scale of comparisons presented in ref. [22].

The specific criteria are compared in pairs with respect to the main criteria which they specify, so their impact on the achievement of the main objective is indirect [23]. Individual preferences correspond to specific numbers of T. Saat’’s scale of comparisons [22]. Giving relative preference is an important advantage of the method because the assessments are subjective and depend on expert judgment, which further increases the substantive correctness of the results. An expert is a person who has the knowledge and experience in a given field. In the case of multi-criteria issues, it is necessary to cooperate with experts from various fields, e.g., in the assessment of technological investment possibilities, taking into account its environmental impact [12].

The impact of the criterion in the i-th row on the criterion from the j-th column $\left(x_{i,j}\right)$, is presented in a diagonal matrix of pair-vice comparisons of main criteria X, as it is shown below:

$$\mathit{X}=\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_n\end{array}\begin{array}{c}\begin{array}{cccc}{X}_1& X_2& \cdots & X_n\end{array}\\ \left[\begin{array}{cccc}1& x_{1,2}& \cdots & x_{1,n}\\ \frac{1}{x_{1,2}}& 1& \cdots & x_{2,n}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{1}{x_{1,n}}& \frac{1}{x_{2,n}}& \cdots & 1\end{array}\right]\end{array}$$

(1)

If it has been determined that the criterion in the i-th row is $x_{i,j}$ more important than the criterion in the j-th column, then the influence of the criterion in the j-th column on the criterion from the i-th row is equal to:

$$x_{j,i}=\frac{1}{x_{i,j}}$$

(2)

In case the compared criteria have the same impact, the product of the criteria equals one [22]. For a diagonal matrix of pairs comparison of main criteria $\mathit{X}$ a normalized inverse matrix $\overline{\mathit{X}}$ is determined, whose elements ${\overline{x}}_{i,j}$ arise by dividing each element of the matrix $x_{i,j}$ by the sum of grades in a given column, according to the Equation:

$${\overline{x}}_{i,j}=\frac{x_{i,j}}{{{\displaystyle \sum }}_{j=1}^n{x}_{i,j}}$$

(3)

Elements of the priority vector of individual main criteria due to the implementation of the main analysis goal $w_i$ are determined by dividing the sums of individual rows of the normalized inverse matrix $\overline{\mathit{X}}$ by the number of criteria n.

$$w_i=\frac{{{\displaystyle \sum }}_{i=1}^n{\overline{x}}_{i,j}}{n}$$

(4)

The values of the elements of the priority vector $w_i$ indicate the place of the i-th main criterion in the criteria ranking. The higher it is, the higher its ranking position and the greater its impact on achieving the analysis goal.

The priority vector $\mathit{w}$, consisting of the elements of the priority vector $\mathit{I}$ is a column vector according to the notation:

$$\mathit{w}={\left[w_i\right]}_n=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\end{array}\right]$$

(5)

Due to the inverse of pair-vice comparisons, the i-th row is the inverse of the i-th column of matrix X, so there is equality [23]:

$$\mathit{X}\mathit{w}=\left[\begin{array}{cccc}1& x_{1,2}& \cdots & x_{1,n}\\ \frac{1}{x_{1,2}}& 1& \cdots & x_{2,n}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{1}{x_{1,n}}& \frac{1}{x_{2,n}}& \cdots & 1\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\end{array}\right]=n\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\end{array}\right]=n$$

(6)

The above Equation means that the X-pair comparison matrix multiplied by the priority vector of individual criteria w satisfies the linear matrix equation, in which n is the eigenvalue of the X. This enables the use of the matrix equations and the calculation of the inverse matrix, which reduces the level of sophistication of mathematical methods. The priority vector $\mathit{w}$ is determined by solving the Equation:

$$\left(\mathit{X}-n\mathit{I}\right)\mathit{w}=0$$

(7)

where $\mathit{I}$ is the unit matrix.

Since matrices X and I are known, the above Equation (7) is solvable and has non-zero solutions when n is the eigenvalue of the matrix X [24]. Even though the method is simple to use due to the linear matrix equation, it can be time-consuming for a large number of criteria [25].

As mentioned above, the expert making a pairwise linguistic comparison determines the advantage of one criterion over another, then writes their judgment in numerical form, according to [24]. Because of the specific value of pairwise comparison $\mathit{I}$ it is not directly quantified. The expert assessments may contain errors of erroneous assessments or logical errors. The AHP method allows slight deficiencies as a consequence of assessing criteria, which result in small changes in the coefficients of the pairwise comparison matrix and changes in the value of the priority vector $\mathit{w}$.

It has been proven that when the largest eigenvalue of the matrix ${\lambda }_{\max }$ is equal to or close to the number of n criteria being compared the expert comparisons are coherent and consistent [22]. Pairwise comparisons are consistent if the largest eigenvalue of the matrix ${\lambda }_{\max }$ is close to n [26].

A small, but acceptable, pairwise compared inconsistency $x_{i,j}$ causes a slight change in the largest eigenvalue of the matrix ${\lambda }_{\max }$ and represents a deviation from pairwise comparisons of the coherence factor expressed Consistency index (CI).

The determined inconsistencies factor CI compared with the Random Index (RI) allows the determination of the Consistency Ratio (CR), which determines the extent to which comparisons of the validity of criteria are incompatible with each other. RI values, which are presented in the study [27].

The CR is easier to interpret than the CI because it is expressed as a percentage. The value of CR for the matrix (3 × 3) should not exceed 5%, for the matrix (4 × 4) it should be less than 8%, and for larger matrices, it should not exceed 10% [28], so that pairwise comparisons can be considered consistent (compatible).

Priority vectors for the specific criteria ${\mathit{w}}_{\mathit{i},\mathit{s}}$ (Equation (13)) are also determined by using the AHP method.

Assuming that Si is the number of detailed criteria in a given group (i-th main criterion), the following procedure is performed for each set of detailed criteria. Pairwise comparison of specific criteria is made according to their respective main criteria, as shown by the matrix of pairwise comparison of specific criteria:

$${\mathit{X}}_{\mathit{i},\mathit{s}}=\begin{array}{c}{X}_{i,1}\\ X_{i,2}\\ ⋮\\ X_{i,Si}\end{array}\begin{array}{c}\begin{array}{cccc}{X}_{i,1}& X_{i,2}& \cdots & X_{i,Si}\end{array}\\ \left[\begin{array}{cccc}1& x_{i,1,2}& \cdots & x_{i,1,S\mathrm{i}}\\ \frac{1}{x_{i,2,1}}& 1& \cdots & x_{i,2,Si}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{1}{x_{i,Si,1}}& \frac{1}{x_{i,Si,2}}& \cdots & 1\end{array}\right]\end{array}$$

(8)

Matrix of pairwise comparison of specific criteria multiplied by the priority vector of particular criteria ${\mathit{w}}_{\mathit{i},\mathit{s}}$ satisfies the linear matrix Equation $\mathit{s}\mathit{w}$. Therefore, the following Equations (7) and (8), it is possible to determine the priority vector of pairwise comparison of specific criteria ${\mathit{w}}_{\mathit{i},\mathit{s}}$. According to the AHP method, CI and CR should also be determined.

It should be emphasized that priority vectors of specific criteria are determined only in relation to the main criteria, which specify, i.e., the impact of the criterion specifying the main criterion $X_1$ on another main criterion, for example $X_2$ is not tested.

The vector of global weights of the sub-criteria ${\mathit{w}}_{\mathit{i},\mathit{s}}^{\mathit{g}}$ is determined by multiplying the individual priority vectors of pairwise comparison of detailed criteria ${\mathit{w}}_{\mathit{i},\mathit{s}}$ by the corresponding elements of the priority vector of the pairwise comparison of the main criteria ${\left[w_i\right]}_n$, receiving the column vector as written:

$${\mathit{w}}_{\mathit{i},\mathit{s}}^{\mathit{g}}={\mathit{w}}_{\mathit{i},\mathit{s}}·{\left[w_i\right]}_n=\left[\begin{array}{c}{w}_{1,1}^g\\ w_{1,2}^g\\ ⋮\\ w_{i,s}^g\end{array}\right]$$

(9)

The vector of global weights of sub-criteria presents the impact of each detailed criterion on the investment implementation.

2.1.3. Elimination of Redundant Criteria and Calculation of the Global Specific Criteria Weights

Due to the special nature of the issue, which is the choice of the location of the distributed generation energy source, the author proposes that the location analysis should be carried out for a set of sub-criteria.

The $X_i$ criteria weights selected in the pairwise comparison process (Equation (6)) determine the position in the ranking of all criteria derived from the universal set of location assessment criteria proposed by the author. The criteria that do not describe a given generation source are also taken into account when determining the weighting of the criteria. Their weight is then zero. This is the case when comparing different types of generation sources, for example, a wind farm and a photovoltaic power plant [29].

In addition, the expert can specify the impact threshold for specific criteria below which criteria are not taken into account for further calculations. Therefore, the author of this article proposes that the set of criteria adopted for further analysis should be determined to take into account the eliminated and reduced criteria.

The need to reduce the criteria for assessing the location of a power source can be explained by two reasons. The first reason concerns the need to use large data sets describing generating sources. Often, gathering all the necessary information is not feasible. The second reason is the so-called economic demand, which assumes that the minimum number of variables explains as many phenomena as possible.

The method of functional reduction of criteria occurs when there is a similarity between the criteria that allows a reduction in the number of calculations [30]. Numeric reduction of criteria consists of combining criteria with the same impact, i.e., those with equal weights.

The reduction of the number of criteria significant for the analyzed location comparison, proposed by the author and described by the Equation (10), aims to reduce the number of necessary calculations to a minimum and to indicate and eliminate criteria with a negligible impact on the implementation of the investment and can be done by determining the acceptable threshold of weights of the specific criteria—K. If the criterion weight is below the acceptable criterion threshold then it is not taken into account in further analyses and must meet the minimum value of the K threshold, as stated in:

$$w_{i,s}^g>K$$

(10)

In the case of criteria whose impact on investment implementation is close to or equal to zero, or the expert has determined that the impact of a given criterion is acceptable, in order to be omitted in further analyzes, the weights for the criteria adopted for analysis should be re-determined.

If for criterion $X_{i,s}$ the weight is lower than the acceptable threshold of weights of detailed criteria $(w_{i,s}^g>K)$ then this criterion is included in the criteria adopted for further analysis (whose number is marked as $S_i^{\prime }$) according to the Equation:

$$S_i^{\prime }\le S_i$$

(11)

where $S_i$ is the original number of detailed criteria under the i-th main criterion, and $S_i^{\prime }$ is the number of detailed criteria under the i-th main criterion after reduction according to the condition (100).

The number of criteria included in the analysis $c$ is determined as the sum of the number of detailed criteria assigned to specific main criteria $S{\prime }_i$ and is determined from the Equation:

$$c={\displaystyle \sum }_{i=1}^{n}S{\prime }_i$$

(12)

For a changed number of criteria adopted for further analysis c, due to the removal of some elements of the global specific criteria weights vector $w_{i,s}^g$, the global specific criteria weights should be re-designated, marked as $w{\prime }_{i,s}^g$.

$$w{\prime }_{i,s}^g=\frac{w_{i,s}^g}{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{s=1}^{S{\prime }_i}{w}_{i,s}^g}$$

(13)

The purpose of determining the global specific criteria weights is to meet the condition that the sum of the weights should be one, as described:

$${{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{s=1}^{S{\prime }_i}w{\prime }_{i,s}^g=1$$

(14)

Determining the global specific criteria weights that are eligible for further analysis ends the use of the AHP method.

2.1.4. Numerical Taxonomy

The disadvantage of numerical taxonomy in its current form, known in the literature, is that the criteria are defined as maximum or minimum values among the values describing the criteria. By using the AHP method to determine the weight of criteria, this disadvantage has been eliminated.

Based on the numerical taxonomy method, reference and anti-reference values should be selected for each detailed criterion. The numerical taxonomy method compares locations relative to their metric distance from reference and anti-reference values, which results in the possibility of examining the problem more thoroughly, but it is necessary, to determine reference and anti-reference values.

The advantage of determining a location using a large number of criteria is the ability to examine it in detail and using a large number of parameters. Unlike other methods, numerical taxonomy can include technical criteria, which are most often omitted in location analyzes, due to the difficulty in making a comparative assessment. A large number of criteria and their diverse nature makes it difficult to compare them because they are defined in different ways and have different units. To ensure comparability of criteria, those that are destimulants should be converted to stimulants and normalized. Then the measures of the location distance from the reference values for each criterion describing the locations should be determined.

Determining metric distances from reference and anti-reference locations creates a location ranking. The location which is first in the ranking has the best chances of implementation.

The measure of the location distance from the reference values of the assessment meter, determined as the sum of the distance of Euclidean locations from the reference and anti-reference value in relation to each detailed criterion, is additionally multiplied by the weight of the criterion. As a result, the locations being at a large distance from the standard values for the criteria low weight are not placed at last places in the ranking of locations.

The measure of the distance of individual locations from the standard values is used to determine the final ranking coefficient whose values determine the position of a given location in the ranking.

The next step towards determining the ranking of locations is to determine reference and anti-reference values for specific criteria. A location for which all criteria are close to reference values can be defined as a reference location. The reference and anti-reference set out for individual criteria are determined using elements of the numerical taxonomy method.

The reference location is the one whose chances of success are maximal, in contrast to an anti-reference location that has no chance of implementation. It should be emphasized that fictitious reference and anti-reference locations are not included in the ranking, although this is not unacceptable.

The reference $W_i$ and anti-reference $A_i$ indicate location points in the space of the Cartesian system (x,y) (Figure 3). Locations marked as points $l_i$ are ranked relative to the distance $c_i$ orthogonal projections of individual locations $l_i^{\prime }$ from the reference location $W_i$ [31].

The length of the section $c_i$ can be determined using Carnot’s theore’ [31], according to the Equation:

$$c_i=d\left(l_i^{\prime },W\right)=\frac{{\left|l_i,W_i\right|}^2+{\left|A_i,W_i\right|}^2-{\left|l_i,A_i\right|}^2}{2\left|A_i,W_i\right|}$$

(15)

The reference $W_i$ and anti-reference $A_i$ can be determined in two ways:

Method 1: Determining the reference as a function of maximum and anti-reference as a function of minimum from among the criterion values for compared locations. For this case, all criteria must be designated as stimulants.

Method 2: Determination of the reference and anti-reference value by the experts.

The predominance of the expert method of determining the reference and anti-reference value in relation to defining it as a MIN / MAX function from the values given is the reduction of the weight of locations that have the highest value relative to the given criterion $X_i$ which is sufficient for it and may not guarantee success in the implementation of the investment.

In the case where the reference and anti-reference value is not specified as the MIN or MAX function or when the reference and anti-reference value are specified by an expert, the objects may be better or worse than the reference and anti-reference value. The advantage of considering better or worse values than the reference value is the freedom to choose and control over the set points of the reference and anti-reference value.

The method of determining the location ranking was based on the numerical taxonomy. The method’s assump’ion is the classification, ordering and analysis of multi-feature energy sources location.

For the set of energy sources locations $L=\left\{l_1,l_2,\dots ,l_k\right\}$ a matrix of location values A should be determined in relation to particular detailed criteria.

$$\mathit{A}=\begin{array}{c}\begin{array}{c}\begin{array}{c}{X}_{1,1}{X}_{1,2}\cdots X_{n,s}\\ \left[\begin{array}{cccc}{a}_{1,1,1}& a_{1,1,2}& \cdots & a_{1,n,s}\\ a_{2,1,1}& a_{2,1,2}& \cdots & a_{2,n,s}\\ ⋮& ⋮& ⋮& ⋮\\ a_{k,1,1}& a_{k,1,2}& \cdots & a_{k,n,s}\end{array}\right]\begin{array}{c}{l}_1\\ l_2\\ ⋮\\ l_k\end{array}\end{array}\end{array}\end{array}$$

(16)

To determine the location ranking, Euclidean distances of orthogonal projections $c_i=d\left(l_i^{\prime },W_i\right)$ of individual locations from the reference value $W_i$should be determined. Due to the different values describing individual criteria (e.g., the cost criterion value is given in monetary units and the social one is determined by a five-point scale), it is not possible to compare them with each other without prior normalization.

Increasing or decreasing the weight value of the criterion before normalization may result in the loss of standard deviation. Therefore, the determination of weights in the numerical taxonomy method follows normalization. The proposed method assumes the determination of criteria weights using the AHP method—thus, weights will not be determined by the numerical taxonomy method.

The object rank method based on the numerical taxonomy method requires that all criteria be stimulants. If the value of the i-th detailed criterion $X_{i.s}$, specified for each location as $a_{k,n,s}$ is a destimulant, it should be changed to the stimulant $Z_{i,s}$ by transforming $a_{k,n,s}\to z_{k,n,s}$ according to the Equation:

$$z_{k,n,s}=2\overline{a_{k,n,s}}-a_{k,n,s}$$

(17)

Thanks to this transformation, the criterion value maintains the standard deviation and the arithmetic mean.

To compare the criteria of different sizes and units, normalization should be done. With normalization, it is possible to describe the criteria for using different scales (numerical rates) and compare them with each other. The normalized value for each location $a{\prime }_{k,n,s}$ is determined by the Equation:

$$a{\prime }_{k,n,s}=\frac{a_{k,n,s}-\overline{a_{k,n,s}}}{{\delta }_{k,n,s}}$$

(18)

Location ranking consists of ordering them according to distance measurement values $m_i$ which are normalized values of the distance of their orthogonal projections $c_i$ from the reference location $W_i$. The values of the distance measure $m_i$ are in the range 0–1. The distance measure is determined from the Equation:

$$m_i=1-\frac{c_i}{o}$$

(19)

where $o=d\left(W_i,A_i\right)$ is the Euclidean distance of the reference $W_i$ and anti-reference value $A_i$.

2.1.5. Determination of Metric Distances of Individual Locations from the Reference and Anti-Reference Values

The author proposes to determine the sum of the distance of Euclidean locations from the reference and anti-reference location (additionally multiplied by the weight of criteria) and to reduce the value to relative units, which determines the ranking of locations.

The sum of the measures of the distance of individual locations from the reference and anti-reference locations $m_i$ multiplied by the weights of the detailed criteria adopted for the ranking of locations $w{\prime }_{i,s}^g$ can be determined by the Equation:

$$r_i={\displaystyle \sum }_{i=1}^k{m}_i·w{\prime }_{i,s}^g$$

(20)

In this way, the sum of measures of the distance of the location from the reference and anti-reference location increased by the weight of detailed criteria determines the sum of measures of all locations from the reference and anti-reference location $r_k$ according to the Equation:

$$r_k={\displaystyle \sum }_{i=1}^k{r}_i$$

(21)

2.1.6. A Ranking Coefficient

Location ranking $R_i$ is determined by the ranking values comprising in the range 0–1 the sum of which is equal to 1 and are defined by the Equation:

$$R_i=\frac{{{\displaystyle \sum }}_{i=1}^k{r}_i}{r_k}$$

(22)

The best location will be the one with the highest value of the ranking coefficient $R_i$ and analogously, the location with the least chance of investment implementation will be with the smallest value of the ranking coefficient $R_i$.

It should be noted that locations that have similarly high chances or similarly low chances for investment implementation can be selected for analysis. Placing the location highest in the ranking does not guarantee that it will be accomplished. A similar situation applies to the lowest place in the ranking. If the other locations were slightly better, the last place in the location ranking does not mean that the investment is impossible. The decision on the selection of a given location and analysis of the resulting ranking of locations should be made by an expert.

2.2. A Universal Set of Criteria for Optimizing the Location of Renewable Energy Sources

The set of criteria for the location of generating sources proposed by the author based on a literature review and cooperation with experts from the local energy company. The set of criteria can be regarded as universal, because it can be tailored to the analyzed types of generating sources and takes into account issues that are often introduced only as limitations, for example in the linear-programming-based optimization [29].

The main assumption of the proposed method is its universality in terms of the nature of the given distributed generation source. Therefore, a set of criteria has been specified that can be regarded as universal. Five groups of main criteria $\left(X_i\right)$ are specified: technical $\left(X_1\right)$, economic $\left(X_2\right)$, social$\left(X_3\right)$, environmental $\left(X_4\right)$, and legal $\left(X_5\right)$.

Within each main criterion detailed criteria $X_{i.s}$ were developed and presented in Table 1.

For the set of criteria to be treated as universal, scales of individual, specific criteria depending on their nature and type of production source were introduced. By using standardization, the criteria evaluation scales can be expressed in numbers, percentages or other convenient ways for the user. Proposals for the scale of assessment of selected detailed criteria are presented below.

For technical criteria $\left(X_1\right)$ the scale was chosen using the method based on expert knowledge and literature analysis. Scale values should be considered as stimulants. The parameter ranges and the corresponding scale are shown in

Table 2. Scale for the detailed criterion $X_{1,1}$—the availability of primary raw materials.

Type of Electricity Generating Source	Parameter	Unit	Scale of Assessment
			1	2	3	4	5
Wind power plant	Wind class		V—extremely unfavorable	IV—unfavorable	III—quite favorable	II—favorable	I—very favorable
Solar power plant	Insolation	kWh/m2	<1000	1000–1050	1051–1150	1151–1250	1250<
Biomass power plant	Raw material availability	km	>20	10–20	5–10	<5	available on site
Biogas plant	Substrate availability	%	<50	50–59	60–79	80–99	100

. Depending on the type of distributed energy generation source analyzed, the criterion $X_{1,1}$ has different units.

Two social criteria $\left(X_3\right)$: $X_{3,1}$ (the public support for investment) and $X_{3,2}$ (the support from local authorities for investments) are rated by a numerical scale in the range of 1–5, which has no linguistic equivalent. The appropriate value in the range should be selected by an expert method.

Criterion $X_{3,3}$ is the investment compliance with local policies, and uses a numerical scale corresponding to the linguistic assessment of the detailed criterion. The scale was developed based on ref. [32] and extended by the author

Table 3. The numerical scale of assessment of detailed criterion $X_{3,3}$—the investment compliance with local policies.

Name	Scale
Incompatible	1
Partially compliant	2
Mostly compatible	3
Compatible	4

.

For the environmental detailed criterion $X_{4,3}$ (the impact on animal population), the percentage scale of assessment are presented in

Table 4. Percentage scale of assessment of detailed criterion $X_{4,3}$—impact on animal population

Name	Scale
The animal population makes it impossible to build a power plant	100%
Not tested	100%
In the course of monitoring	30%
No impact on animal populations	0%

. It should be highlighted that this criterion is described as a destimulant—therefore, the desired value is the minimum value.

Detailed criterion $X_{4,4}$ determining the impact of the investment on the landscape was determined by a percentage scale in the range of 0–100%. As this criterion is a destimulant, the minimum value is the desired value. Due to the subjectivity of the assessment of this criterion, it is the expert’s respon’ibility to determine the level of investment impact on the landscape.

For the detailed legal criteria with the symbols $X_{5,1}{–X}_{5,4}$ it is proposed to adopt a percentage scale of assessment which shows the degree of progress of the process aimed at obtaining a building permit. The scale by which it is proposed to assess the criteria described above was developed with the help of specialists involved in the implementation of investments in the energy sector. For the detailed criteria $X_{5,1}$ (planning documents for the power line) and $X_{5,2}$ (planning documents for the investment area), the percentage scale of the advancement of the process of including the power line in the local spatial development plan is presented in

Table 5. Percentage scale of the advancement of the process of including the power plant and the power line in the local spatial development plan.

Name		Scale
The Procedure for Adopting the Study of Spatial Development Conditions and Directions
	No action is taken	0%
	Resolution to proceed to adoption	10%
	Project arrangements	50%
	Providing public access to the project	65%
	Resolution of the study of spatial development conditions and directions	70%
The Procedure for Adopting the Local Spatial Development Plan
	No action is taken	70%
	Resolution to proceed to adoption	75%
	Project arrangements	80%
	Making the project available to the public	85%
	Adoption of the Local Plan	100%

.

If the construction of a power line or reconstruction of an existing one belongs to a public-purpose investment, a decision should be made to determine the site location of a public-purpose line-investment project. The percentage scale of the process of obtaining a decision on the site location of a public-purpose line-investment project is presented in

Table 6. The percentage scale of the process of obtaining a decision on the site location of a public-purpose line-investment project.

Name	Scale
No action is taken	0%
Application for a decision	70%
Obtaining a decision	100%

.

For the criteria $X_{\mathit{5},\mathit{3}}$ (the environmental decision for the power line) and $X_{\mathit{5},\mathit{4}}$ (the environmental decision for the investment area) we propose to use the scale, shown in

Table 7. Percentage scale of progress assessment in the procedure of obtaining a decision on the environmental conditions for consent to implement the project.

Name	Scale
No action is taken	0%
Application for a decision	5%
Application for issuing an environmental decision	15%
Natural studies (monitoring chiropterological, ornithological, habitat inventory)	20–45%
Not required	45%
Agreements / opinions Regional Directorate for Environmental Protection	60%
Arrangements/opinions of the Chief Sanitary Inspectorate	70%
Not required/set of documents	100%

.

3. Case Study: A Selection of Location for Four Potential Wind Power Plants Locations

3.1. Location Identification in Relation to Optimization Criteria

The calculation example is intended to illustrate the use of the method, and thanks to the universal set of optimization criteria, can be mapped anywhere. Location identification was made on the basis of real planned investments implemented by the polish energy company. To perform the location ranking, four potential wind power plants locations were identified, designated $l_1$, $l_2$, $l_3$ and $l_4$, respectively. Despite the fact that work is underway in all locations, the company must decide which will be its priority in terms of the time of implementation and allocation of funds. Therefore, the main goal of optimization is to indicate which location has the best chance of implementation with the shortest time to obtain building permits.

The locations, shown in Figure 4, differ in the possibilities of constructing wind farms with different installed capacities and different properties of the resulting power plants, which were described by location assessment criteria.

The largest installed capacity may have a wind farm at the location $l_4$ (40 MW) and the smallest at the location $l_1$ (20 MW). The locations of individual wind farms are placed in zones with different wind classes. Due to the different types of turbines and different windiness classes, the annual usage time of installed power is also different for each location. The amount of investment outlays is related to the power of the wind farm and the required surface area, which is why the highest investment outlays index was determined for the location $l_3$. Correspondingly higher installed power, combined with a high windiness class, for location $l_3$ results in the lowest cost of generating energy over the life cycle of the power plant. The progress of administrative and legal works, for all locations, is at a similar level, except for the location $l_4$ where the progress of works related to obtaining the environmental decision and building permit is the lowest. In the presented case study, the local energy company provided data on the location of the power plant. As a result of discussions with specialists from project groups, the maximum and minimum values were determined for the standard and anti-standard values. These specialists were project managers, people involved in obtaining legal, environmental, construction and connection permits, and people analyzing the results of wind measurements, 20 experts in total.

The values of detailed criteria for the analyzed locations are summarized in

Table 8. The assumptions for the comparative analysis of the location of wind power plants.

Symbol/Name		Unit	S/D	Symbol of the Location of the Wind Power Plants				Reference	Anti-Reference
				${\mathit{l}}_1$	${\mathit{l}}_2$	${\mathit{l}}_3$	${\mathit{l}}_4$
$X_{\mathbf{1}}$—Technical criteria
$X_{\mathbf{1},\mathbf{1}}$	availability of primary raw materials	class	S	3	2	4	3	5	1
$X_{1,2}$	time of installed power utilization	h/a	S	2453	2190	2540	2365	2579	1250
$X_{1,3}$	distance from the power system	km	D	6	10	5	25	30	0
$X_{1,4}$	distance from the district heating network	km	D	0	0	0	0	0	0
$X_{1,5}$	short-circuit power on the medium voltage (MV) side	MVA	S	250	250	60	60	250	60
$X_{1,6}$	static voltage change	%	S	9	11,6	10	11	<10%	>10%
$X_{1,7}$	dynamic voltage change	%	S	2	2,5	3,5	4	<3%	>3%
$X_{1,8}$	permissible load of power system components	MVA	S	25	25	6	6	25	6
$X_{1,9}$	system efficiency	%	S	0.4	0.3	0.39	0.35	0.45	0.3
$X_2$—Economic criteria
$X_{2,1}$	investment outlays	106 PLN	D	84	126	168	126	10	120
$X_{2,2}$	the cost of producing energy in the life cycle analysis	PLN/MWh	D	314	341	307	322	200	440
$X_{2,3}$	net present value (NPV)	106 PLN2017	S	86.1	102.2	184.2	120.2	max	min
$X_{2,4}$	Internal rate of return (IRR)	%	S	8.2	6.7	8.7	7.7	max	min
$X_3$—Social criteria
$X_{3,1}$	public support for investment	−	S	3	5	5	3	5	0
$X_{3,2}$	favor of local authorities for investments	−	S	4	3	2	3	5	0
$X_{3,3}$	investment compliance with local policies	−	S	3	2	1	3	4	1
$X_4$—Environmental criteria
$X_{4,1}$	carbon avoidance rate	${10}^6$kg CO2/a	S	40.2	53.9	83.3	58.2	max	min
$X_{4,2}$	noise emission	dB	D	34.1	37.5	35.0	40.0	20.0	40.0
$X_{4,3}$	impact on animal population	%	D	100	100	30	30	100	0
$X_{4,4}$	impact of the investment on the landscape	%	D	30	40	50	70	100	0
$X_{4,5}$	impact of the investment on nature protected areas	km	D	20	30	20	25	50	0
$X_{4,6}$	land surface indicator	km2/MW	D	0.150	0.083	0.098	0.120	min	max
$X_{4,7}$	location of the area for post-fermentation waste management	km	D	0	0	0	0	min	max
$X_5$—Legal criteria
$X_{5,1}$	planning documents for the power line	−	S	70	80	85	50	100	0
$X_{5,2}$	planning documents for the investment area	−	S	70	70	70	50	100	0
$X_{5,3}$	environmental decision for the power line	−	S	45	25	60	60	100	0
$X_{5,4}$	environmental decision for the investment area	−	S	60	15	70	45	100	0

Legend: S, stimulant, D, destimulant.

.

3.2. Application of the Method

Following the methodology for determining the location ranking, described in Section 3, at the beginning of the location analysis, pairwise comparison of main criteria were based on the cooperation with a group of specialists investigated: (1) Which of the criteria is more important to the implementation of the construction of the power plant in a given location; or (2) how much more important are the detailed criteria at the same level in the structure of the decision-making process on the given scale (from an absolute advantage (9 points) to the balance of both comparable elements (1 point)); and (3) based on studies [33,34]. Then the specialists’ respons’s were aggregated using the simple geometric mean (SGM) method and the results of the pairwise comparison of main criteria are presented in

Table 9. Pairwise comparison of main criteria $X_{\mathrm{i}}.$

Diagonal Matrix of Main Criteria
	$X_1$	$X_2$	$X_3$	$X_4$	$X_5$
$X_1$	1.00	0.50	2.00	0.33	0.50
$X_2$	2.00	1.00	2.00	0.33	0.33
$X_3$	0.50	0.50	1.00	0.50	0.50
$X_4$	3.00	3.00	2.00	1.00	2.00
$X_5$	2.00	3.00	2.00	0.50	1.00
Σ	8.50	8.00	9.00	2.67	4.33

.

Pairwise comparison of main criteria creates a diagonal matrix X from which the normalized inverse matrix $\overline{\mathbf{X}}$ is then determined. Based on the matrix $\overline{\mathit{X}}$, the values of the priority vector $w_{\mathrm{i}}$ are determined (Equation (5)). According to the description of the methodology, the determined values of the priority vector $w_{\mathrm{i}}$ indicate the weight of individual criteria in relation to the implementation of the goal, which is the successful implementation of the investment in a given location.

Table 10. Priority vector values and calculation correctness indicators for pair-vice comparison of main criteria.

Normalized Values of Pairwise Comparison of Main Criteria						Priority Vector Values	Eigenvalue of the Matrix
	$X_1$	$X_2$	$X_3$	$X_4$	$X_5$	$w_{\mathrm{i}}$	$\lambda$
$X_1$	0.12	0.06	0.22	0.13	0.12	0.13	1.09
$X_2$	0.24	0.13	0.22	0.13	0.08	0.16	1.26
$X_3$	0.06	0.06	0.11	0.19	0.12	0.11	0.96
$X_4$	0.35	0.38	0.22	0.38	0.46	0.36	0.95
$X_5$	0.24	0.38	0.22	0.19	0.23	0.25	1.08
Σ	1.00	1.00	1.00	1.00	1.00	1.00	5.35

λ_max = 5.35, CI = 0.09, RI = 1.12, CR = 0.08.

presents the results of the pair-vice comparison of the main criteria.

According to the pairwise comparison of main criteria concerning wind farm construction, criterion $X_4$ (the environmental criterion) has the highest impact. This is due to the impact of the wind farm on the environment and the need to meet numerous environmental criteria, such as distance from residential areas, distance from protected areas, or land surface index.

The criterion $X_3$ (the social criterion) received the lowest weight of impact on the construction of the wind farm. Carrying out promotional and information campaigns related to the construction of new generating sources increases the possibility of convincing the public and local authorities to support investments in a given area.

According to the methodology, global weights of specific criteria were determined. As can be seen (

Table 11. Global weights of specific criteria.

Criterion Symbol	Weight	Criterion Symbol	Weight	Criterion Symbol	Weight	Criterion Symbol	Weight
$X_{1,1}$	0.009	$X_{1,8}$	0.037	$X_{3,2}$	0.068	$X_{4,6}$	0.029
$X_{1,2}$	0.016	$X_{1,9}$	0.026	$X_{3,3}$	0.011	$X_{4,7}$	0.000
$X_{1,3}$	0.011	$X_{2,1}$	0.011	$X_{4,1}$	0.166	$X_{5,1}$	0.036
$X_{1,4}$	0.000	$X_{2,2}$	0.025	$X_{4,2}$	0.087	$X_{5,2}$	0.105
$X_{1,5}$	0.023	$X_{2,3}$	0.065	$X_{4,3}$	0.020	$X_{5,3}$	0.013
$X_{1,6}$	0.004	$X_{2,4}$	0.056	$X_{4,4}$	0.010	$X_{5,4}$	0.097
$X_{1,7}$	0.003	$X_{3,1}$	0.028	$X_{4,5}$	0.044	−	−

) the criterion $X_{4,1}$ (carbon avoidance rate) has the highest global weight among the detailed criteria.

For the analyzed case, both the reference and anti-reference values were determined using method 2: Determination of the reference and anti-reference value by the experts.

If it is not possible to determine the reference and anti-reference values by the expert method, maximum or minimum values may be determined from among the available values. The adopted values of the reference and anti-reference values are presented in Table 8. It should be highlighted that for criteria that are destimulants for the needs of calculations, standard values were entered in the table as stimulants.

3.3. Wind Power Plants Location Ranking

The author proposes that the determined measure of the location distance from the reference value for individual criteria should be multiplied by their weight in order to increase the significance of the location distance from the reference for criteria of particular importance, i.e., those whose weight is high. As a result, a location with a significant distance from the reference, for a criterion of negligible importance, will not be placed at the end of the ranking.

Table 12. Calculated values of distance measure and ranking coefficient values.

Symbol of Location	Presents the Selected Values of a Measure Distance from the Reference Value Multiplied by the Global Weights for Individual Criteria								Distance Measure	Ranking Coefficient	Place in the Ranking
	$X_{1,1}$	$X_{1,2}$	$\cdots$	$X_{4,1}$	$X_{4,2}$	$\cdots$	$X_{5,3}$	$X_{5,4}$	−	−	−
$l_1$	0.004	0.014	$\cdots$	0.000	0.003	$\cdots$	0.006	0.058	0.479	0.243	2
$l_2$	0.002	0.011	$\cdots$	0.053	0.018	$\cdots$	0.003	0.015	0.403	0.204	4
$l_3$	0.006	0.015	$\cdots$	0.166	0.007	$\cdots$	0.008	0.068	0.651	0.331	1
$l_4$	0.004	0.013	$\cdots$	0.069	0.029	$\cdots$	0.008	0.044	0.437	0.222	3

presents the values of a measure distance from the reference value $m_i$ multiplied by the global weights of the detailed criteria $w_{i,s}^{g^{\prime }}$, according to the Equation (20), their sum $r_i$ and normalized values of the ranking $R_i$, determined according to the Equation (22).

The ranking coefficients $R_i$ determine the position of individual locations in the location ranking. According to the Equation (22), ranking values always fall within range 0–1, and their sum equals one. Due to the scale used, the difference between individual ranking values for different locations is used to determine the position of a given location in the ranking. The higher the $R_i$ value, the higher the location is in the ranking and the greater the chances of implementation. As can be seen in Table 12, the location $l_3$ with installed capacity 40 MW was found to be most suitable and have the greatest chances of implementation in the shortest possible time. The main contributing factors are carbon avoidance rate, the impact of the investment on nature protected areas, state of advancement in collecting planning documents for the power line. Therefore, it is advisable to locate funds and expenditure of work in this location.

It should be noted that the location ranking shown should be treated as an aid in the decisions making process. The last place in the ranking does not mean that the investment has no chance of success in a given location.

4. Discussion

The combination of the AHP method and the numerical taxonomy allowed to present a new approach to the analysis of distributed generation source location.

Both the proposed hybrid multi-criteria method and universal set of criteria can serve as a source of inspiration for future research, for example, for analyzing localization of non-renewable power plants or to compare different energy sources. A universal set of criteria is presented, developed based on literature analysis, which can be applied to various types of production sources. The limitation of the method in its current form is the requirement to have complete knowledge of the power plant construction process in a given location. Future research should focus on cases of incomplete knowledge of the process. The obtained ranking of wind farm locations indicates where financial resources should be allocated to keep the construction time as short as possible. The obtained results will be presented to the energy company so that it can implement processes aimed at validating the ranking results.

5. Conclusions and Recommendations

The main purpose of this article was to present a developed hybrid method which includes elements of the Analytic Hierarchy Process and numerical taxonomy. Then, an example of the ranking of wind power plant localizations using the aforementioned multi-criteria method was presented.

The determination of global weights of detailed criteria was introduced into the method, which was then taken into account when determining the location ranking coefficient, which was not previously discussed in the literature. During the work, it was necessary to develop a universal set of criteria for the assessment of distributed generation sources, such as wind, solar, biomass, and biogas power plants—which take into account all the requirements for locations, because the available literature adopts different criteria and lacks consistency in studies.

The advantage of the proposed method is to reduce the time-consuming calculations and simplify mathematical calculations in relation to the multi-criteria methods used so far. Location assessment using the proposed set of assessment criteria allows for detailed location recognition and facilitates the implementation of individual stages of the investment process. The use of multi-criteria analysis method to determine the ranking of locations of generating sources and includes assessment criteria—which in the single-criteria approach are omitted.

To indicate the correctness of the proposed method, a case study was conducted. Within the study, an example of generation sources location ranking was presented. Among the four analyzed locations of wind farms, the highest-ranked was the location $l_3$ with installed capacity 40 MW. From all detailed criteria, the carbon avoidance rate was the greatest impact on investment implementation. In the author’s opinion, the proposed method is a practical tool for determining the location of sources of distributed electricity generation and can be used in commercial applications.

In the light of the research results presented above, the proposed multi-criteria method of analyzing the location of distributed generation sources, the proposed method, unlike the methods analyzed in the literature, takes into account the weights determined by the AHP method in determining the ranking factor.

The article also demonstrates the legitimacy of the expert’s participation in determining the reference and anti-reference values in relation to the currently used method of selecting maximum or minimum values from those that describe locations.

It is advisable to communicate the results of the case study to an energy company for the purpose of capital relocation so that a wind farm is built in the indicated location in the shortest possible time.