A Real Options Approach to Valuate Solar Energy Investment with Public Authority Incentives: The Italian Case
Abstract
:1. Introduction
2. Basic Model
The Real Options Approach for the Valuation of a Solar Investment Project
- The closed-form approach, which is suitable for a European option, which can be only exercised at maturity. The most important model is, for instance, that of Black and Scholes (1973) [26].
- The open-form method, including the lattice approach, which provides a straightforward way to analyze and value of more general types of options.
3. Case Study
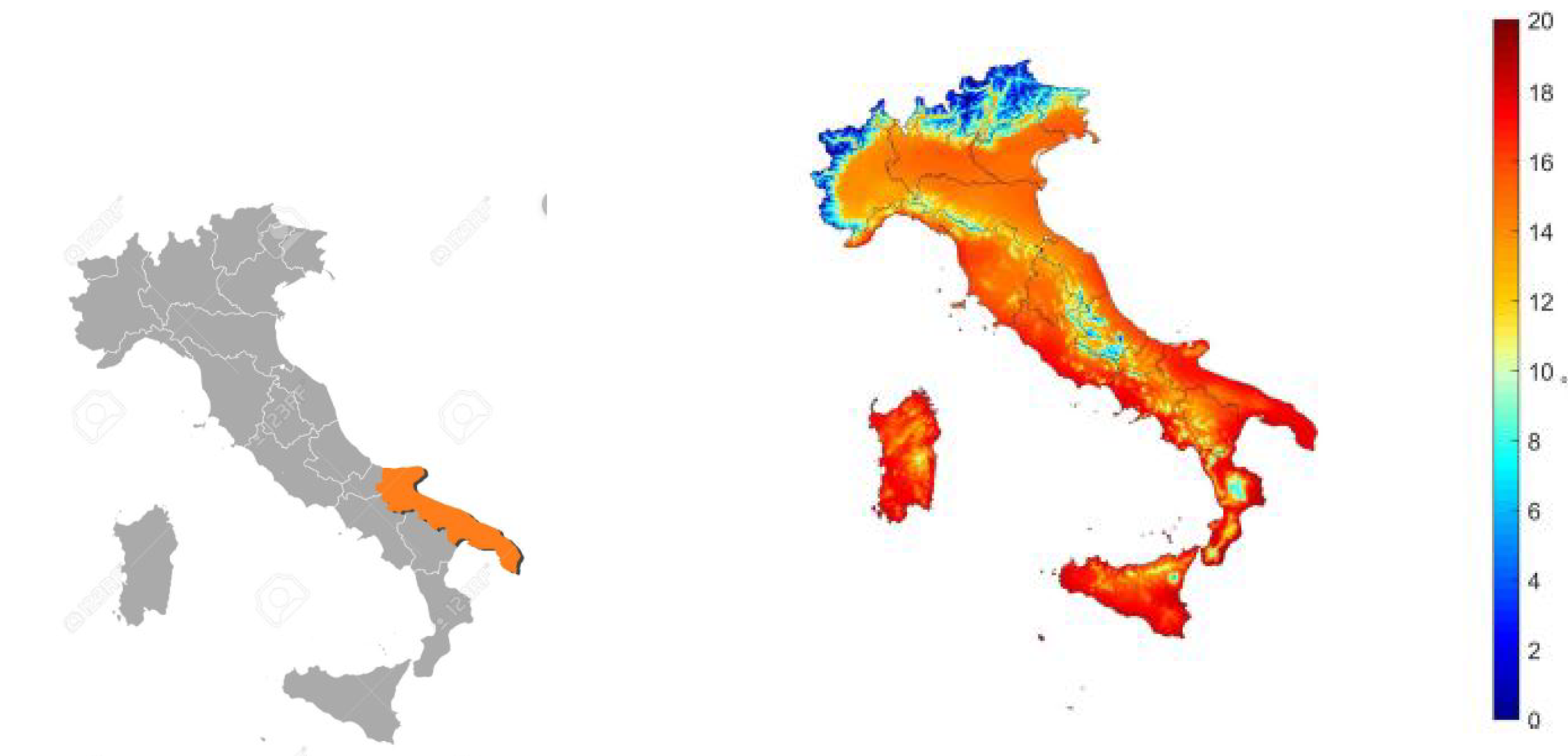
3.1. Analysis of Meteorological and Geographical Conditions
3.2. Economic and Financial Analysis of a Solar Energy Investment
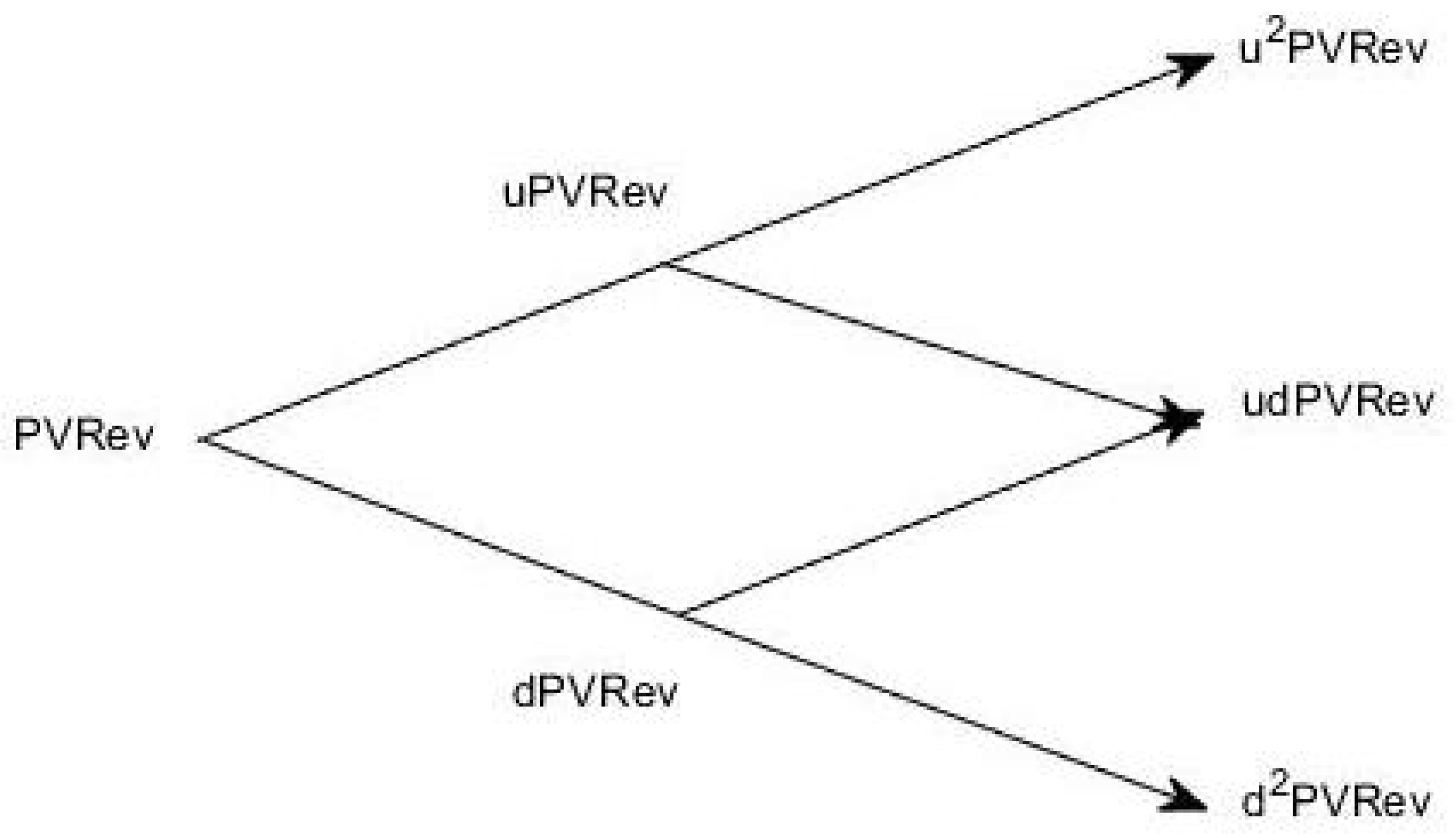
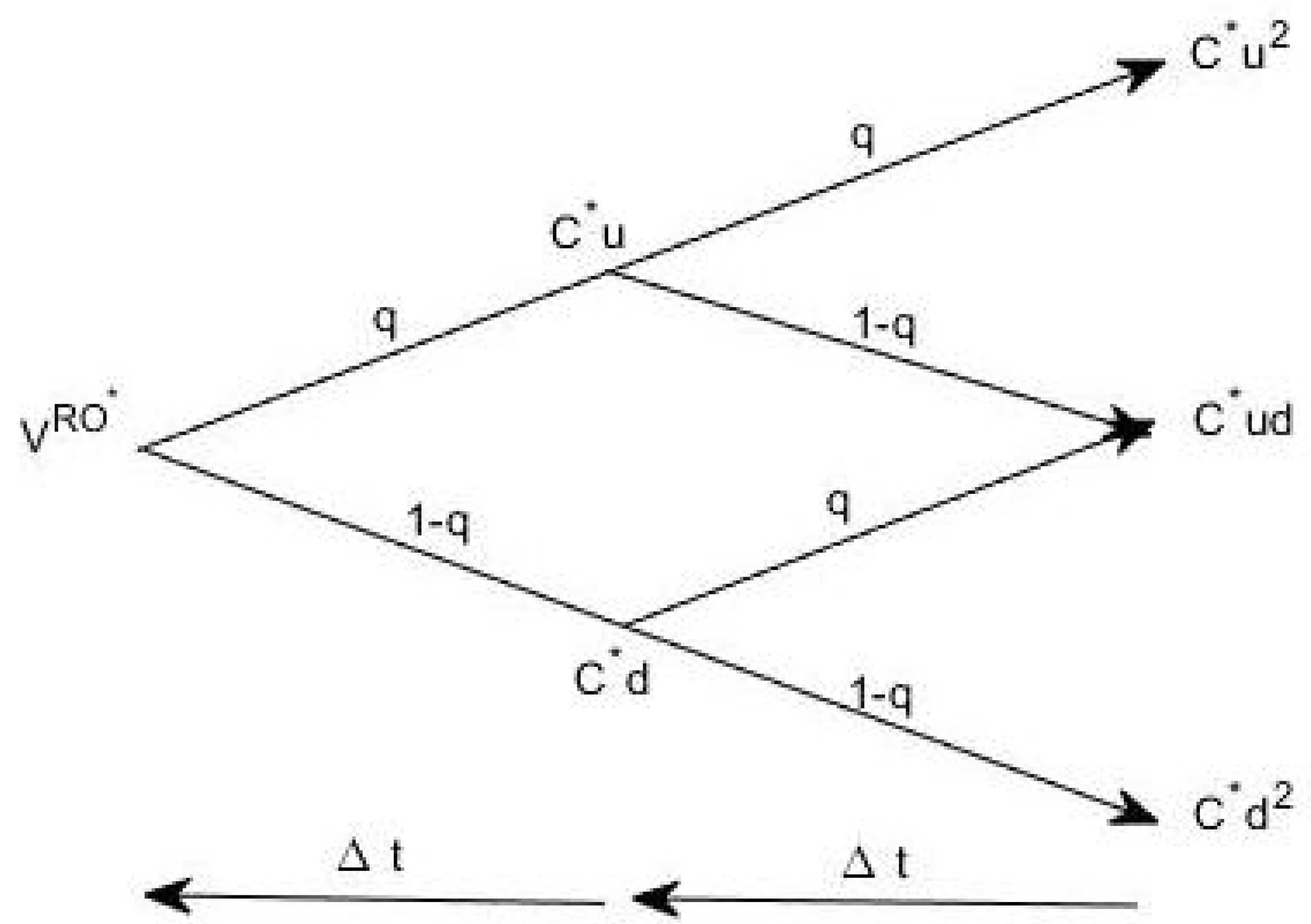
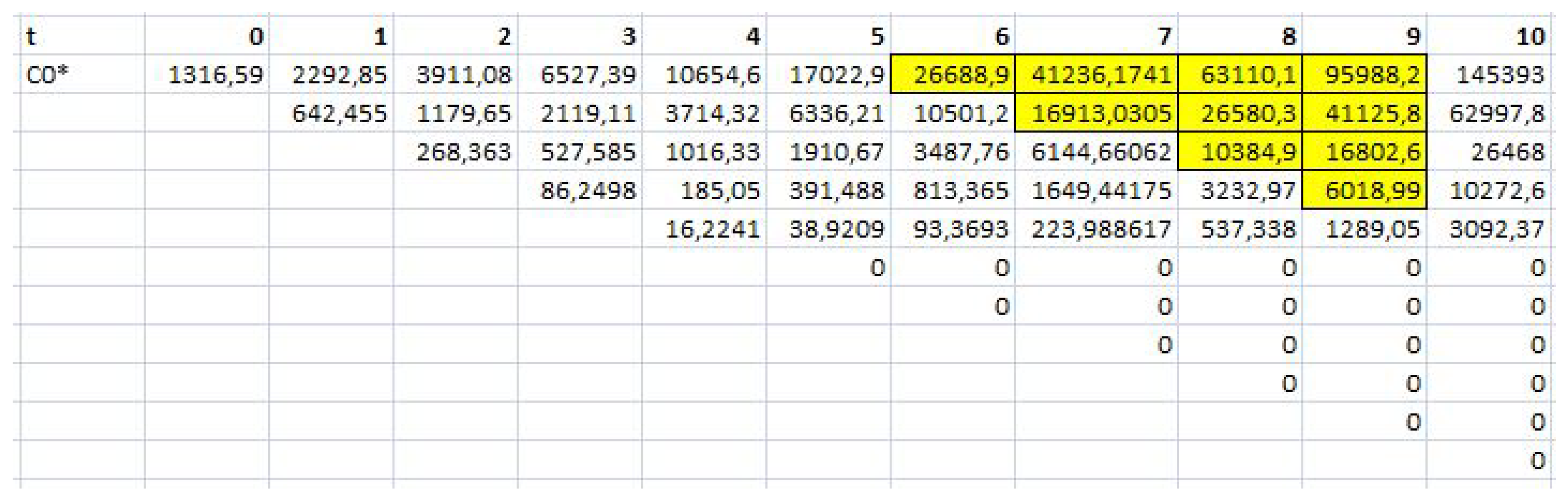
3.3. Real Options Approach for the Valuation of PV Investment
4. Conclusions
Funding
Conflicts of Interest
References
- Li, X.; Ramshani, M.; Khoj, I.A.; Omitaomu, O.; Hathaway, J.M. An agent based model for joint placement of PV panels and green roofs. In Proceedings of the Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 1133–1144. [Google Scholar]
- Cui, Y.; Yao, H.; Hong, L.; Zhang, T.; Xu, Y.; Xian, K.; Hou, J. Achieving over 15% efficiency in organic photovoltaic cells via copolymer design. Adv Mater. 2019, 31, 1808356. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.K.H.; Barbé, J.; Meroni, S.M.; Du, T.; Lin, C.T.; Pockett, A.; Carnie, M.J. Outstanding indoor performance of perovskite photovoltaic cells-effect of device architectures and interlayers. Sol. RRL 2019, 3, 1800207. [Google Scholar] [CrossRef] [Green Version]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Tran, H.V. Determination of optimal location and sizing of solar photovoltaic distribution generation units in radial distribution systems. Energies 2019, 12, 74. [Google Scholar] [CrossRef] [Green Version]
- Abdul Kadir, A.F.; Khatib, T.; Lii, L.S.; Hassan, E.E. Optimal placement and sizing of photovoltaic based distributed generation considering costs of operation planning of monocrystalline and thin-film technologies. J. Sol. Energy Eng. 2019, 141, 011017. [Google Scholar] [CrossRef]
- Premalatha, L.; Rahim, N.A. The Effect of Dynamic Weather Conditions on Three Types of PV Cell Technologies—A Comparative Analysis. Energy Procedia 2017, 117, 275–282. [Google Scholar] [CrossRef]
- Castaneda, M.; Zapata, S.; Cherni, J.; Aristizabal, A.J.; Dyner, I. The long-term effects of cautious feed-in tariff reductions on photovoltaic generation in the UK residential sector. Renew. Energy 2020, 155, 1432–1443. [Google Scholar] [CrossRef]
- Zander, K.K.; Simpson, G.; Mathew, S.; Nepal, R.; Garnett, S.T. Preferences for and potential impacts of financial incentives to install residential rooftop solar photovoltaic systems in Australia. J. Clean. Prod. 2019, 230, 328–338. [Google Scholar] [CrossRef]
- Zhang, M.M.; Zhou, D.Q.; Zhou, P.; Liu, G.Q. Optimal feed-in tariff for solar photovoltaic power generation in China: A real options analysis. Energy Policy 2016, 97, 181–192. [Google Scholar] [CrossRef]
- Durica, M.; Guttenova, D.; Pinda, L.; Svabova, L. Sustainable Value of Investment in Real Estate: Real Options Approach. Sustainability 2018, 10, 4665. [Google Scholar] [CrossRef] [Green Version]
- Trigeorgis, L. Real Options and Interactions with Financial Flexibility. Financ. Manag. 1993, 22, 202–224. [Google Scholar] [CrossRef]
- Villani, G. Valuation of R&D Investment Opportunities with the Threat of Competitors Entry in Real Option Analysi. Comput. Econ. 2012, 43, 331–355. [Google Scholar]
- Yeo, K.T.; Qiu, F. The value of management flexibility—A real option approach to investment evaluation. Int. J. Proj. Manag. 2003, 21, 243–250. [Google Scholar] [CrossRef]
- Kellogg, D.; Charnes, J.M. Real-Options Valuation for a Biotchnology Company. Financ. Anal. J. 2000, 56, 76–84. [Google Scholar] [CrossRef]
- Bastian, H.; Daniel, R. Modeling sequential R&D investment: A binomial compound option approach. Bus. Res. 2015, 8, 39–59. [Google Scholar]
- Panayi, S.; Trigeorgis, L. Multi-stage Real Options: The Cases of Information Technology Infrastructure and International Bank Expansion. Q. Rev. Econ. Financ. 1998, 38, 675–692. [Google Scholar] [CrossRef]
- Santos, L.I.; Mendes, S.C.; Ferreira, P. Real Options versus Traditional Methods to assess Renewable Energy Projects. Renew. Energy 2014, 68, 588–594. [Google Scholar] [CrossRef]
- Ghazi, S.; Ip, K. The effect of weather conditions on the efficiency of PV panels in the southeast of UK. Renew. Energy 2014, 69, 50–59. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. Six-years-long effects of the Italian policies for photovoltaics on the pay-back period of grid-connected PV systems installed in urban contexts. Energy 2017, 122, 458–470. [Google Scholar] [CrossRef]
- Fernandes, B.; Cunha, J.; Ferreira, P. The use of real options approach in energy sector investments. Renew. Sustain. Energy Rev. 2011, 15, 4491–4497. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Park, H.; Kim, H. Real options analysis for renewable energy investment decsions in developing countries. Renew. Sustain. Energy Rev. 2017, 75, 918–926. [Google Scholar] [CrossRef]
- Madlener, R.; Stoverink, S. Power plant investments in the Turkish electricity sector: A real options approach taking into account market liberalization. Appl. Energy 2012, 97, 124–134. [Google Scholar] [CrossRef]
- Oliva, S.H.; Passey, R.; Abdullah, A.M. A semi-empirical financial assessment of combining residential photovoltaics, energy efficiency and battery storage systems. Renew. Sustain. Energy Rev. 2019, 105, 206–214. [Google Scholar] [CrossRef]
- Agaton, C.B.; Karl, H. A real options approach to the renewable electricity generation in the Philippines. Energy Sustain. Soc. 2018, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Mun, J. Real Options Analysis: Tools and Techniques for Valuing Strategic Investments and Decisions with Integrated Risk Management Advanced Quantitative Decision Analytics, 3rd ed.; Thomson-Shore: Dexter, MI, USA; ROV Press: San Diego, CA, USA, 2016. [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Decreto Legge 83 del 22.6.2012—Misure Urgenti per la Crescita del Paese, con l’art. 11 “Detrazioni per Interventi di Ristrutturazione e di Efficientamento Energetico. Available online: https://www.gazzettaufficiale.it/eli/id/2012/08/11/12A08941/sg (accessed on 22 June 2012).
- Decreto Legge 63 del 4.6.2013—Disposizioni Urgenti per il Recepimento Della Direttiva 2010/31/UE del Parlamento Europeo e del Consiglio del 19 Maggio 2010, sulla Prestazione Energetica Nell’edilizia per la Definizione delle Procedure D’infrazione Avviate dalla Commisssione Europea, Nonchè altre Disposizioni in Materia di Coesione Sociale. Available online: https://www.gazzettaufficiale.it/eli/id/2013/06/05/13G00107/sg (accessed on 4 June 2013).
- Legge 147 del 27.12.2013—Disposizioni per la Formazione del Bilancio Annuale e Pluriennale dello Stato (Legge di Stabilità 2014). Available online: https://www.gazzettaufficiale.it/eli/id/2013/12/27/13G00191/sg (accessed on 27 December 2013).
- Malvoni, M.; Leggieri, A.; Maggiotto, G.; Congedo, P.M.; De Giorgi, M.G. Long term performance, losses and efficiency analysis of a 960 KWp photovoltaic system in the Mediterranean climate. Energy Convers. Manag. 2017, 145, 169–181. [Google Scholar] [CrossRef]


| Provided Inputs | Simulation Outputs | ||
|---|---|---|---|
| Location (lat;long) | 41,126; 16,862 | Slope angle (°) | 35 |
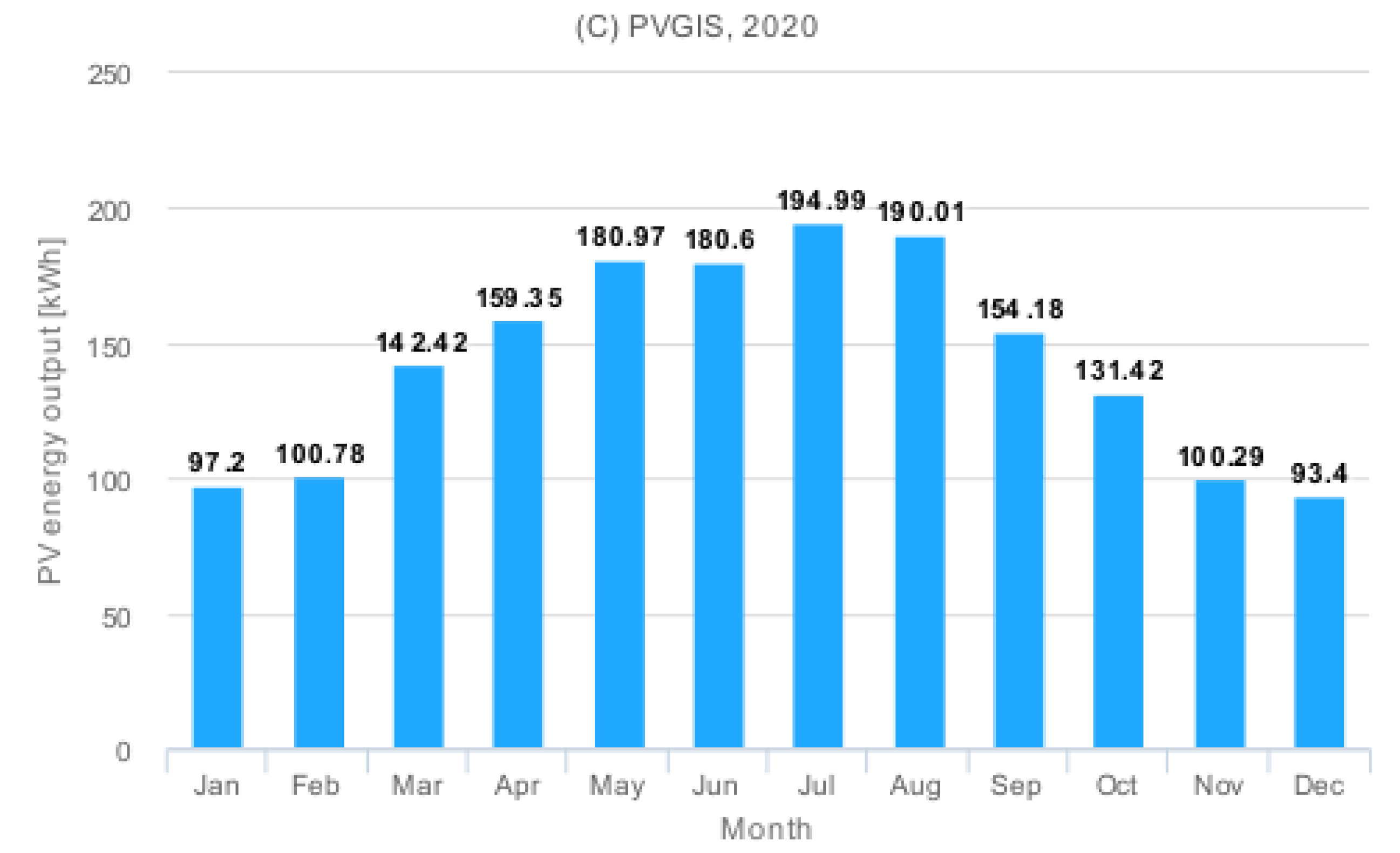
| Database used | PVGIS-SARAH | Yearly PV energy production (kWh) | 1725.61 |
| PV technology | Crystalline silicon | Yearly in-plane irradiation (kWh/m2) | 1895.4 |
| PV installed (kWp) | 1 | Year-to-year variability (kWh) | 68.83 |
| PV electricity cost (per kWh) | 0.154 |
| Year | Production (kWh) | Revenues | Maintenance Costs | Tax Benefits |
|---|---|---|---|---|
| 0 | 1725.61 | |||
| 1 | 1700.07 | 391.19 | 200 | 0.50 |
| 2 | 1674.91 | 385.40 | 200 | 0.50 |
| 3 | 1650.12 | 379.69 | 200 | 0.50 |
| 4 | 1625.70 | 374.07 | 200 | 0.50 |
| 5 | 1601.64 | 368.54 | 200 | 0.50 |
| 6 | 1577.94 | 363.08 | 200 | 0.50 |
| 7 | 1554.58 | 357.71 | 200 | 0.50 |
| 8 | 1531.57 | 352.41 | 200 | 0.50 |
| 9 | 1508.91 | 347.20 | 200 | 0.50 |
| 10 | 1486.58 | 342.06 | 200 | 0.50 |
| Regional Capitals | Yearly Production (kWh) | NPV | ENPV | |
|---|---|---|---|---|
| Aosta | 1380.44 | −658.18 | 963.25 | +305.05 |
| Trieste | 1491.39 | −495.16 | 1076.81 | +581.65 |
| Trento | 1495.01 | −489.84 | 1080.52 | +590.68 |
| Milano | 1524.98 | −445.81 | 1111.2 | +665.39 |
| Ancona | 1530.45 | −437.77 | 1116.8 | +679.03 |
| Bologna | 1547.18 | −413.19 | 1133.93 | +720.74 |
| Venezia | 1560.34 | −393.86 | 1147.4 | +753.54 |
| Firenze | 1570.58 | −378.81 | 1157.88 | +779.07 |
| Potenza | 1574.14 | −373.58 | 1161.53 | +787.95 |
| Perugia | 1577.20 | −369.09 | 1164.66 | +795.57 |
| Genova | 1579.72 | −365.38 | 1167.24 | +801.86 |
| Torino | 1588.38 | −352.66 | 1176.1 | +823.44 |
| Campobasso | 1594.87 | −343.12 | 1182.75 | +839.63 |
| Catanzaro | 1678.48 | −220.28 | 1268.34 | +1048.06 |
| L’Aquila | 1688.73 | −205.22 | 1278.83 | +1073.61 |
| Bari | 1725.61 | −151.03 | 1316.59 | +1165.56 |
| Napoli | 1735.40 | −136.65 | 1326.61 | +1189.96 |
| Roma | 1755.47 | −107.16 | 1347.16 | +1240.00 |
| Palermo | 1770.96 | −84.40 | 1363.01 | +1278.61 |
| Cagliari | 1843.47 | +22.14 | 1451.98 | +1474.12 |
| p | TB | p | TB | ||
|---|---|---|---|---|---|
| 0.975 | 0.36 | 1315.85 | 0.85 | 0.36 | 1308.71 |
| 0.40 | 1316.92 | 0.40 | 1308.98 | ||
| 0.50 | 1319.58 | 0.50 | 1309.68 | ||
| 0.95 | 0.36 | 1313.66 | 0.825 | 0.36 | 1308.08 |
| 0.40 | 1314.48 | 0.40 | 1308.28 | ||
| 0.50 | 1316.59 | 0.50 | 1308.79 | ||
| 0.925 | 0.36 | 1311.93 | 0.80 | 0.36 | 1307.60 |
| 0.40 | 1312.56 | 0.40 | 1307.75 | ||
| 0.50 | 1314.26 | 0.50 | 1308.12 | ||
| 0.90 | 0.36 | 1310.58 | 0.775 | 0.36 | 1307.24 |
| 0.40 | 1311.06 | 0.40 | 1307.35 | ||
| 0.50 | 1312.38 | 0.50 | 1307.62 | ||
| 0.875 | 0.36 | 1309.52 | 0.75 | 0.36 | 1306.97 |
| 0.40 | 1309.88 | 0.40 | 1307.05 | ||
| 0.50 | 1310.86 | 0.50 | 1307.24 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Bari, A. A Real Options Approach to Valuate Solar Energy Investment with Public Authority Incentives: The Italian Case. Energies 2020, 13, 4181. https://doi.org/10.3390/en13164181
Di Bari A. A Real Options Approach to Valuate Solar Energy Investment with Public Authority Incentives: The Italian Case. Energies. 2020; 13(16):4181. https://doi.org/10.3390/en13164181
Chicago/Turabian StyleDi Bari, Antonio. 2020. "A Real Options Approach to Valuate Solar Energy Investment with Public Authority Incentives: The Italian Case" Energies 13, no. 16: 4181. https://doi.org/10.3390/en13164181
APA StyleDi Bari, A. (2020). A Real Options Approach to Valuate Solar Energy Investment with Public Authority Incentives: The Italian Case. Energies, 13(16), 4181. https://doi.org/10.3390/en13164181




