Managing Wind Power Generation via Indexed Semi-Markov Model and Copula
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Model
2.2.1. The Indexed Semi-Markov Chain
2.2.2. From Univariate to Multivariate Models: The Copula Function Approach
3. Results of Modeling
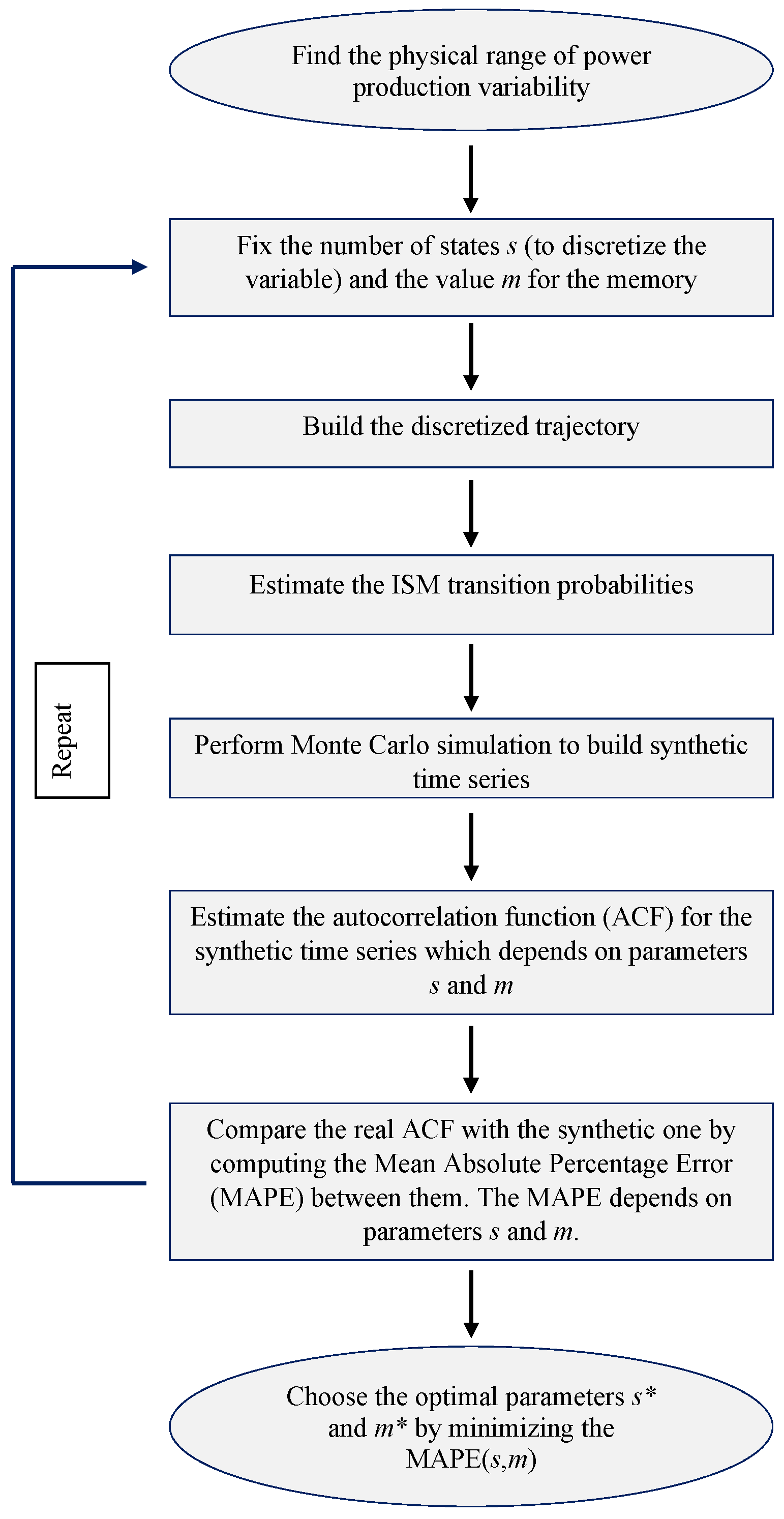
3.1. Parameter Optimization
3.2. Estimation of Reliability Indices
3.2.1. Loss of Load Hours
- Fix the length of the period H;
- By means of a Monte Carlo algorithm, generate N trajectories of the power produced by the wind farm according to the multivariate ISMC model with the same initial conditions. More specifically, the data can be described in the form of an array:where is the energy produced by the wind farm (generating capacity) at time j in the simulation. We introduce the notation with and observe that the are N independent realizations of the same stochastic process.
- Convert the array in a 0–1 array according to whether the system’s demand at the time j, exceeds the generating capacity in the considered simulation. This can be expressed as follows:
- Let denote the number of hours in which the demand is not supplied. The sequence is a random sample of size N because the random variables are mutually independent and identically distributed according to the simulation scheme in step 2. Estimate the LOLH using the sample mean; i.e.,and denote bythe sample variance. From basic statistical inference, we know that estimates (8) and (9) are unbiased, and for large N, due to the central limit theorem, we can construct confidence intervals for the LOLH at a given significance level :where are the critical values at the level of a normal standard distribution.
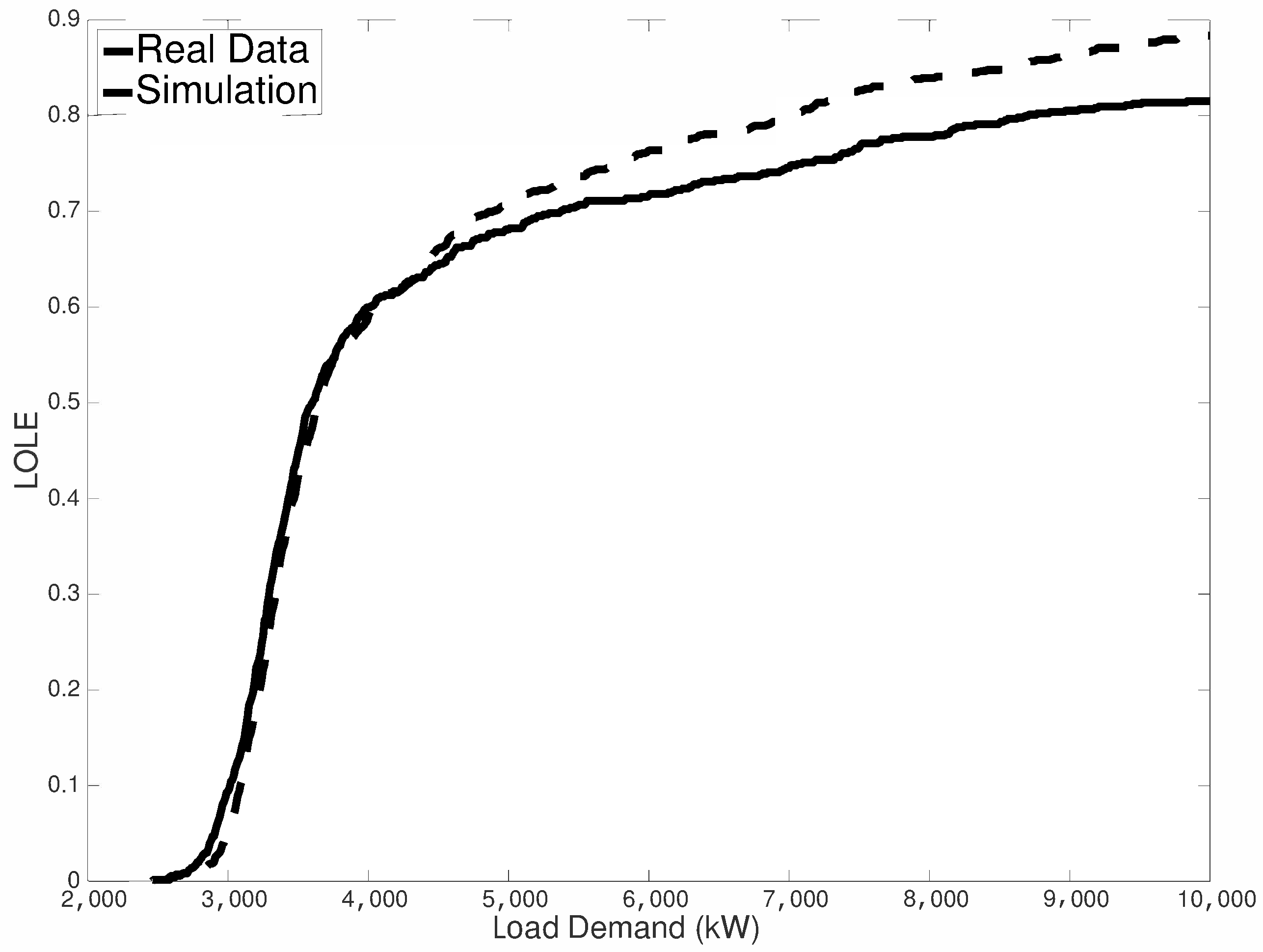
3.2.2. Loss of Load Expectation
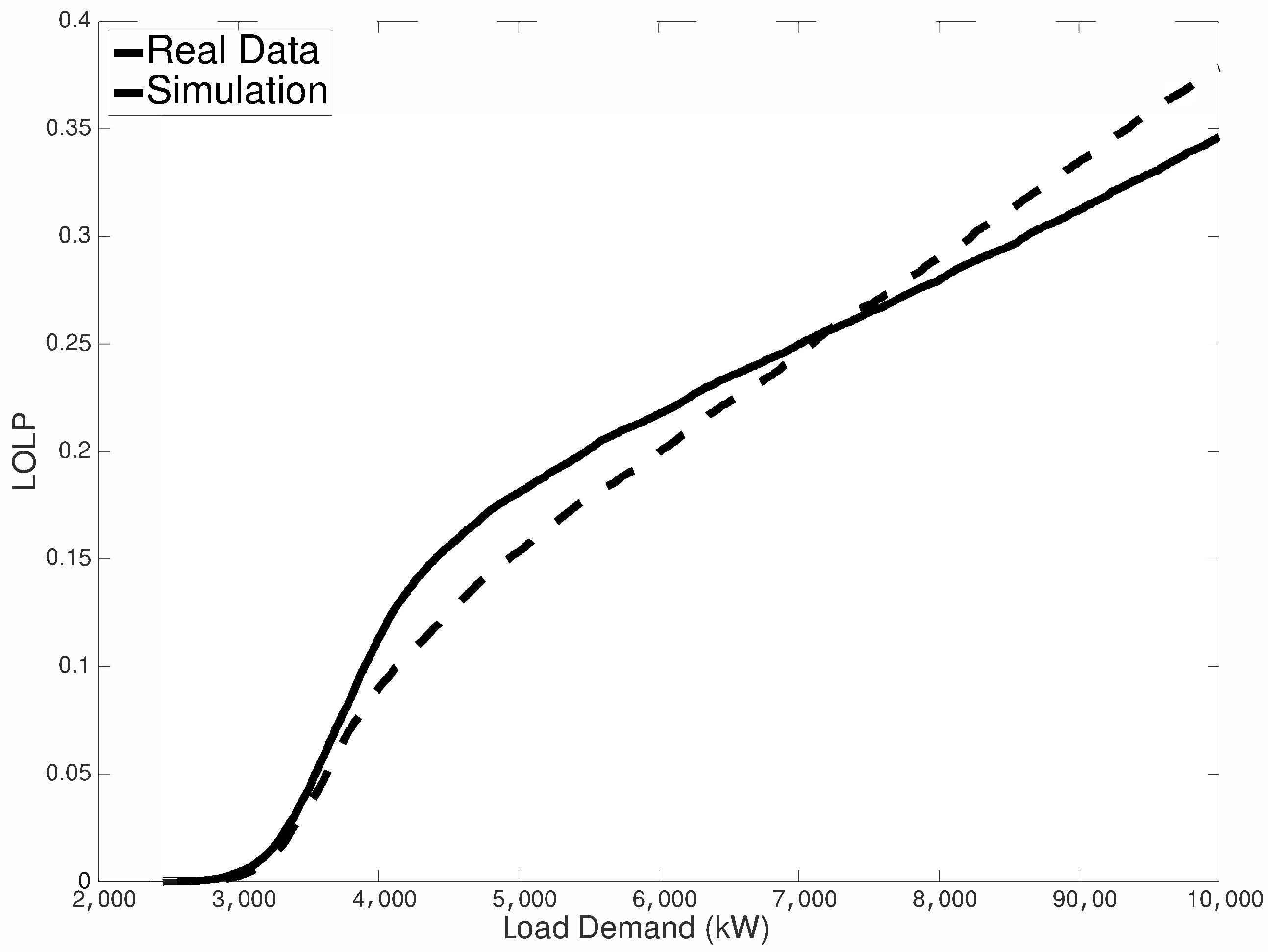
3.2.3. Loss of Load Probability
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Choi, S.; Kim, S. An investigation of operating behavior characteristics of a wind power system using a fuzzy clustering method. Expert Syst. Appl. 2017, 81, 244–250. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Kurowicka, D. Using copulas for modeling stochastic dependence in power system uncertainty analysis. IEEE Trans. Power Syst. 2008, 24, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Geng, X.; Kusiak, A.; Xu, C. Mining markov chain transition matrix from wind speed time series data. Expert Syst. Appl. 2011, 38, 10229–10239. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Ortiz-Garcı, E.G.; Pérez-Bellido, Á.M.; Portilla-Figueras, A.; Prieto, L. Short term wind speed prediction based on evolutionary support vector regression algorithms. Expert. Appl. 2011, 38, 4052–4057. [Google Scholar] [CrossRef]
- Chang, T.P. Estimation of wind energy potential using different probability density functions. Appl. Energy 2011, 88, 1848–1856. [Google Scholar] [CrossRef]
- Chang, T.P. Performance comparison of six numerical methods in estimating weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. Economic performance indicators of wind energy based on wind speed stochastic modeling. Appl. Energy 2015, 154, 290–297. [Google Scholar] [CrossRef]
- Danao, L.A.; Eboibi, O.; Howell, R. An experimental investigation into the influence of unsteady wind on the performance of a vertical axis wind turbine. Appl. Energy 2013, 107, 403–411. [Google Scholar] [CrossRef]
- Nagai, B.M.; Ameku, K.; Roy, J.N. Performance of a 3kw wind turbine generator with variable pitch control system. Appl. Energy 2009, 86, 1774–1782. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A.; Pazos, J.L. Simulation of correlated wind speed data for economic dispatch evaluation. IEEE Trans. Sustain. Energy 2012, 3, 142–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Ambach, D. Short-term wind speed forecasting in germany. J. Appl. Stat. 2016, 43, 351–369. [Google Scholar] [CrossRef] [Green Version]
- Iman, R.L.; Conover, W.J. A distribution-free approach to inducing rank correlation among input variables. Commun. Stat. Simul. Comput. 1982, 11, 311–334. [Google Scholar] [CrossRef]
- Morales, J.M.; Mínguez, R.; Conejo, A.J. A methodology to generate statistically dependent wind speed scenarios. Appl. Energy 2010, 87, 843–855. [Google Scholar] [CrossRef]
- Yunus, K.; Chen, P.; Thiringer, T. Modelling spatially and temporally correlated wind speed time series over a large geographical area using varma. IET Renew. Power Gener. 2017, 11, 132–142. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. Wind speed prediction for wind farm applications by extreme value theory and copulas. J. Wind Eng. Ind. Aerodyn. 2015, 145, 229–236. [Google Scholar] [CrossRef]
- Hu, W.; Min, Y.; Zhou, Y.; Lu, Q. Wind power forecasting errors modelling approach considering temporal and spatial dependence. J. Mod. Power Syst. Clean Energy 2017, 5, 489–498. [Google Scholar] [CrossRef] [Green Version]
- Votsi, I.; Brouste, A. Confidence interval for the mean time to failure in semi-markov models: An application to wind energy production. J. Appl. Stat. 2019, 46, 1756–1773. [Google Scholar] [CrossRef]
- Danisman, O.; Uzunoglu Kocer, U. Construction of a semimarkov model for the performance of a football team in the presence of missing data. J. Appl. Stat. 2019, 46, 559–576. [Google Scholar] [CrossRef]
- Barbu, V.; Limnios, N. Semi-Markov Chains and Hidden Semi-Markov Models toward Applications: Their Use in Reliability and DNA Analysis; Lecture Notes in Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Votsi, I.; Limnios, N.; Papadimitriou, E.; Tsaklidis, G. Earthquake Statistical Analysis through Multi-State Modeling; Wiley-ISTE: London, UK, 2019. [Google Scholar]
- D’Amico, G. Age-usage semi-markov models. Appl. Math. Model. 2011, 35, 4354–4366. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F. A semi-markov model with memory for price changes. J. Stat. Mech. Theory Exp. 2011, 2011, P12009. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, G.; Petroni, F. Weighted-indexed semi-markov models for modeling financial returns. J. Stat. Mech. Theory Exp. 2012, 2012, P07015. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, G.; Petroni, F.; Prattico, F. Reliability measures of second-order semi-markov chain applied to wind energy production. J. Renew. Energy 2013, 2013, 368940. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. Wind speed modeled as an indexed semi-markov process. Environmetrics 2013, 24, 367–376. [Google Scholar] [CrossRef] [Green Version]
- Abolude, A.T.; Zhou, W. Assessment and performance evaluation of a wind turbine power output. Energies 2018, 11, 1992. [Google Scholar] [CrossRef] [Green Version]
- Abolude, A.T.; Zhou, W. A Comparative Computational Fluid Dynamic Study on the Effects of Terrain Type on Hub-Height Wind Aerodynamic Properties. Energies 2019, 12, 83. [Google Scholar] [CrossRef] [Green Version]
- Yunus, K.; Chen, P.; Thiringer, T. Modelling and simulating the spatio-temporal correlations of clustered wind power using copula. J. Electr. Eng. Technol. 2013, 8, 1615–1625. [Google Scholar]
- Grothe, O.; Schnieders, J. Spatial dependence in wind and optimal wind power allocation: A copula-based analysis. Energy Policy 2011, 39, 4742–4754. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, G.; Petroni, F. Copula based multivariate semi-markov models with applications in high-frequency finance. Eur. J. Oper. 2018, 267, 765–777. [Google Scholar] [CrossRef]
- Luickx, P.; Vandamme, W.; Pérez, P.S.; Driesen, J.; D’haeseleer, W. Applying Markov chains for the determination of the capacity credit of wind power. In Proceedings of the 6th International Conference on the European Energy Market, Leuven, Belgium, 27–29 May 2009. [Google Scholar]
- D’Amico, G.; Lika, A.; Petroni, F. Change point dynamics for financial data: An indexed markov chain approach. Ann. Financ. 2019, 15, 247–266. [Google Scholar] [CrossRef]
- Durante, F.; Sempi, C. Principles of Copula Theory; CRC/Chapman & Hall: Boca Raton, FL, USA, 2016. [Google Scholar]
- Sklar, A. Fonction de Répartition à n Dimensions et Leurs Marges. Publ. Inst. Statist. Univ. 1959, 8, 229–231. [Google Scholar]
- Genest, C.; Nešlehová, J.; Ziegel, J. Inference in multivariate archimedean copula models. Test 2011, 20, 223. [Google Scholar] [CrossRef]
- NERC. Probabilistic Adequacy and Measures: Technical Reference Report. July 2018. Available online: https://www.nerc.com/comm/PC/Probabilistic%20Assessment%20Working%20Group%20PAWG%20%20Relat/Probabilistic%20Adequacy%20and%20Measures%20Report.pdf (accessed on 15 July 2020).
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Advanced Series; Duxbury: Pacific Grove, CA, USA, 2002. [Google Scholar]
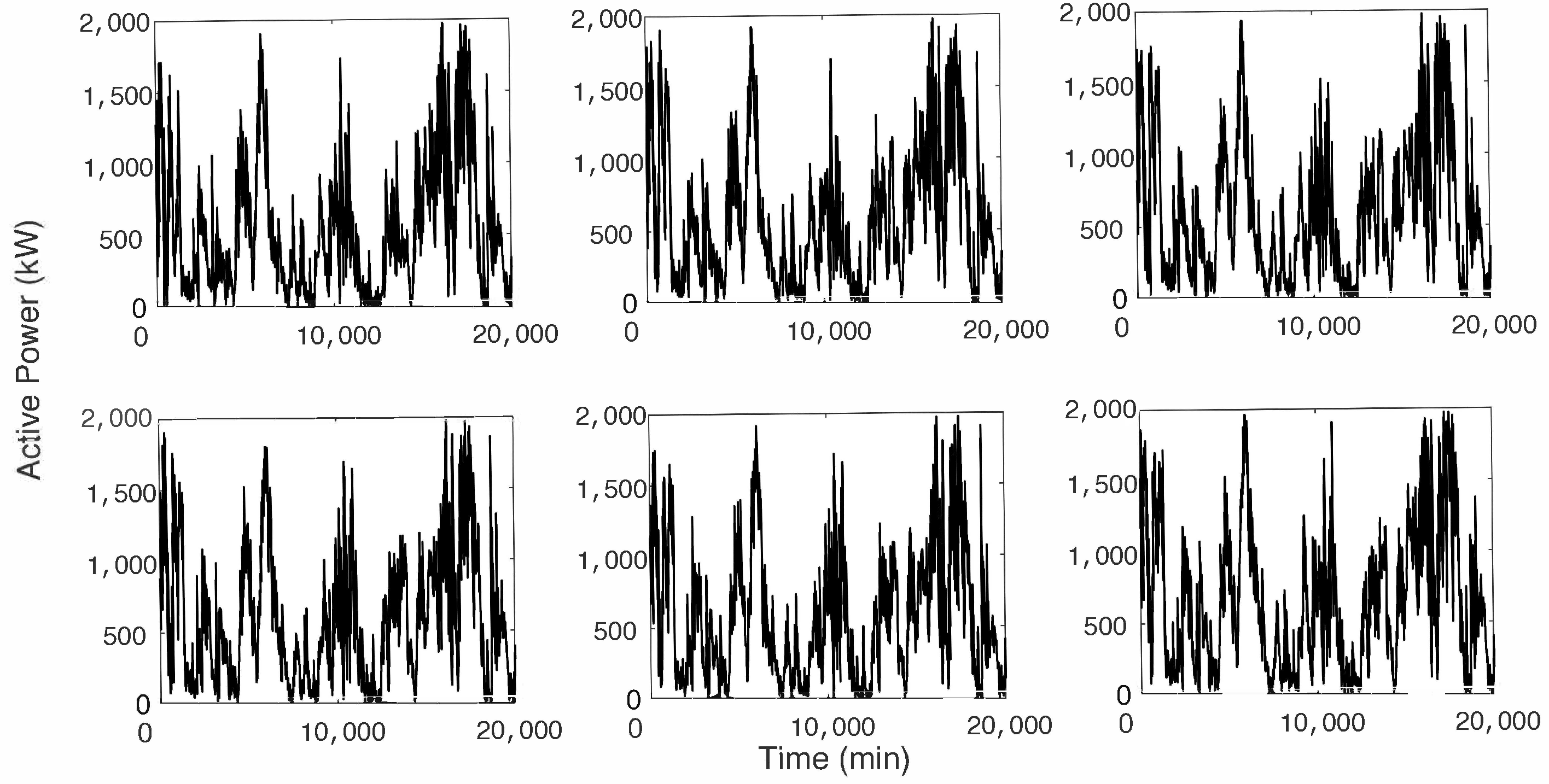
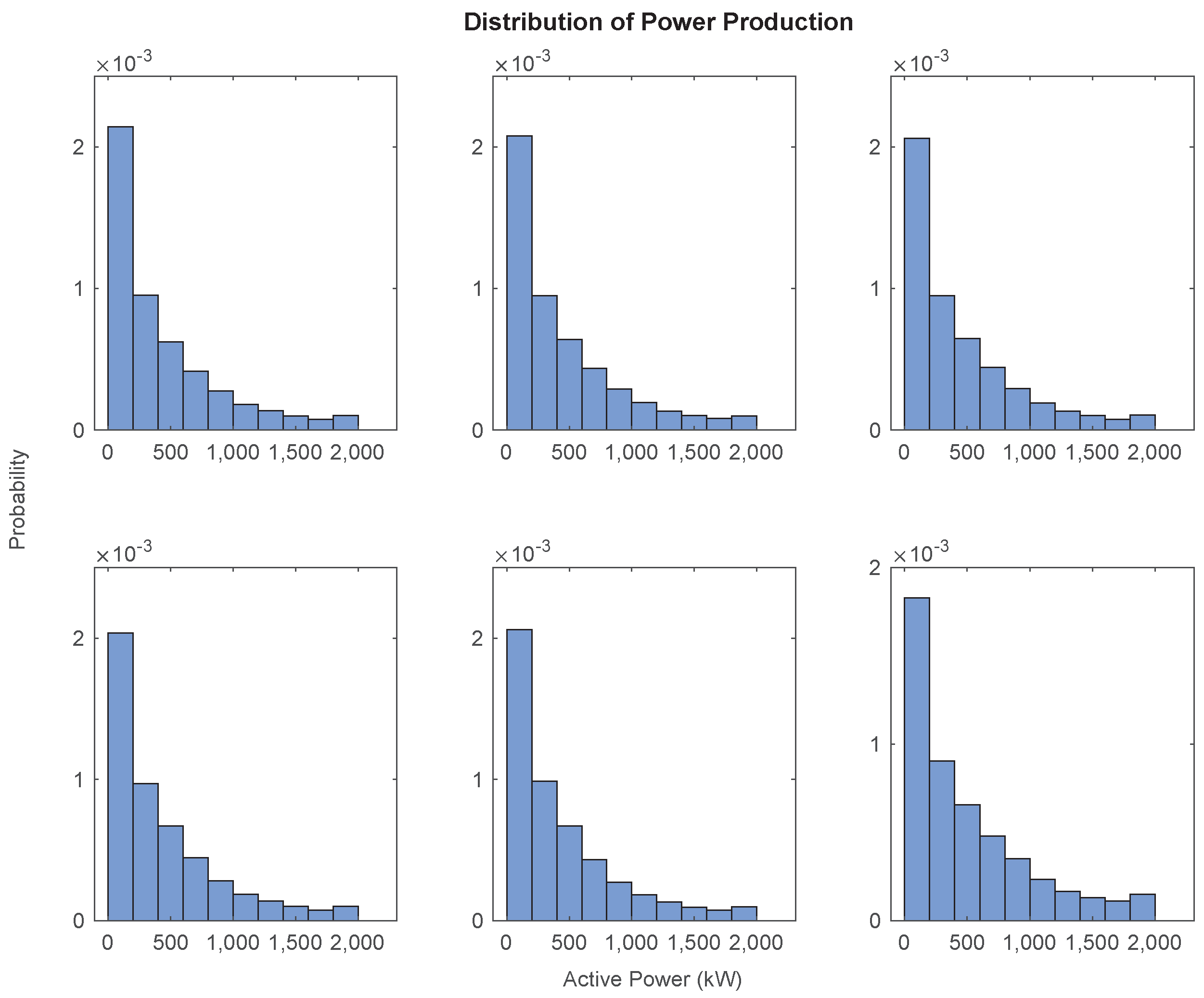
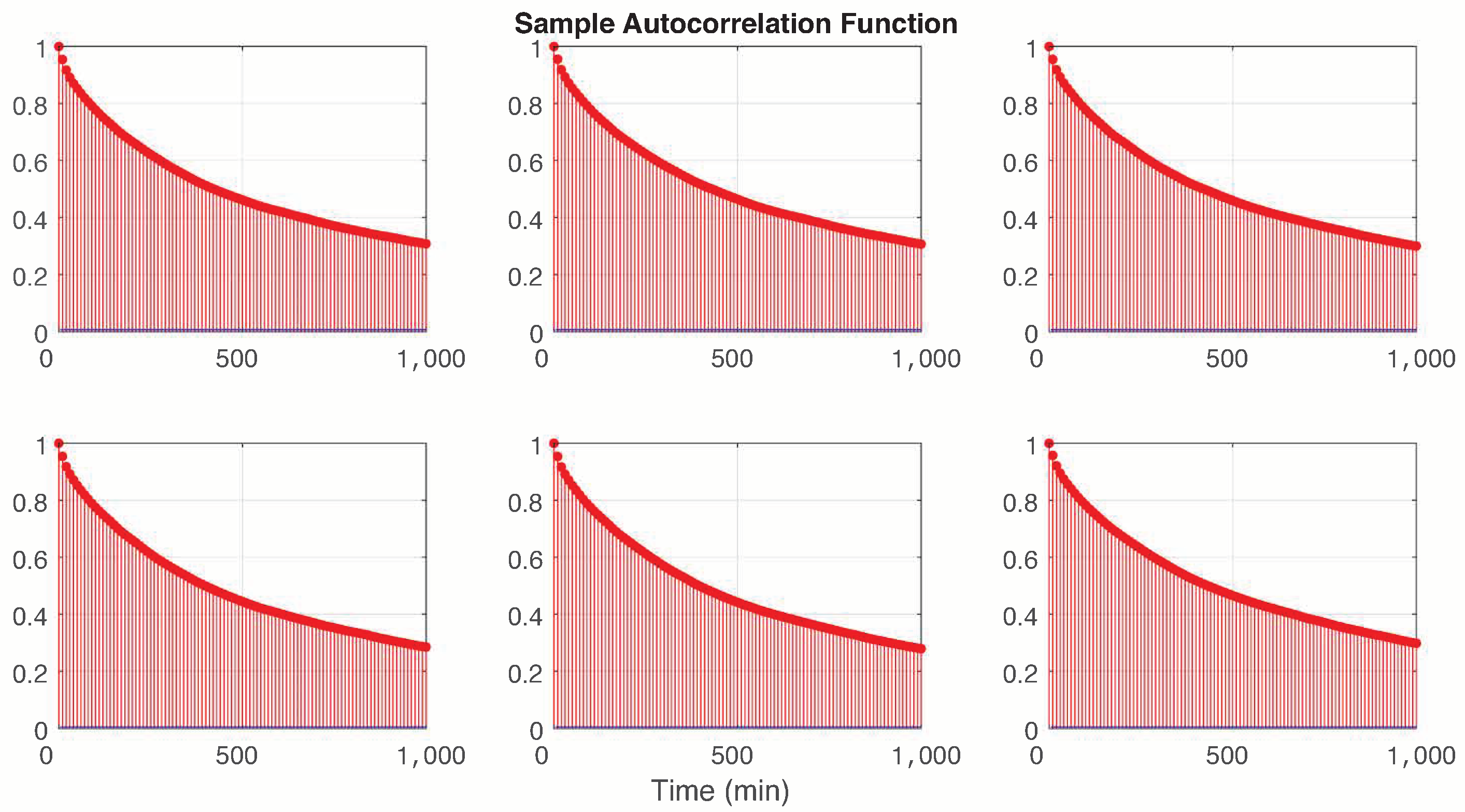

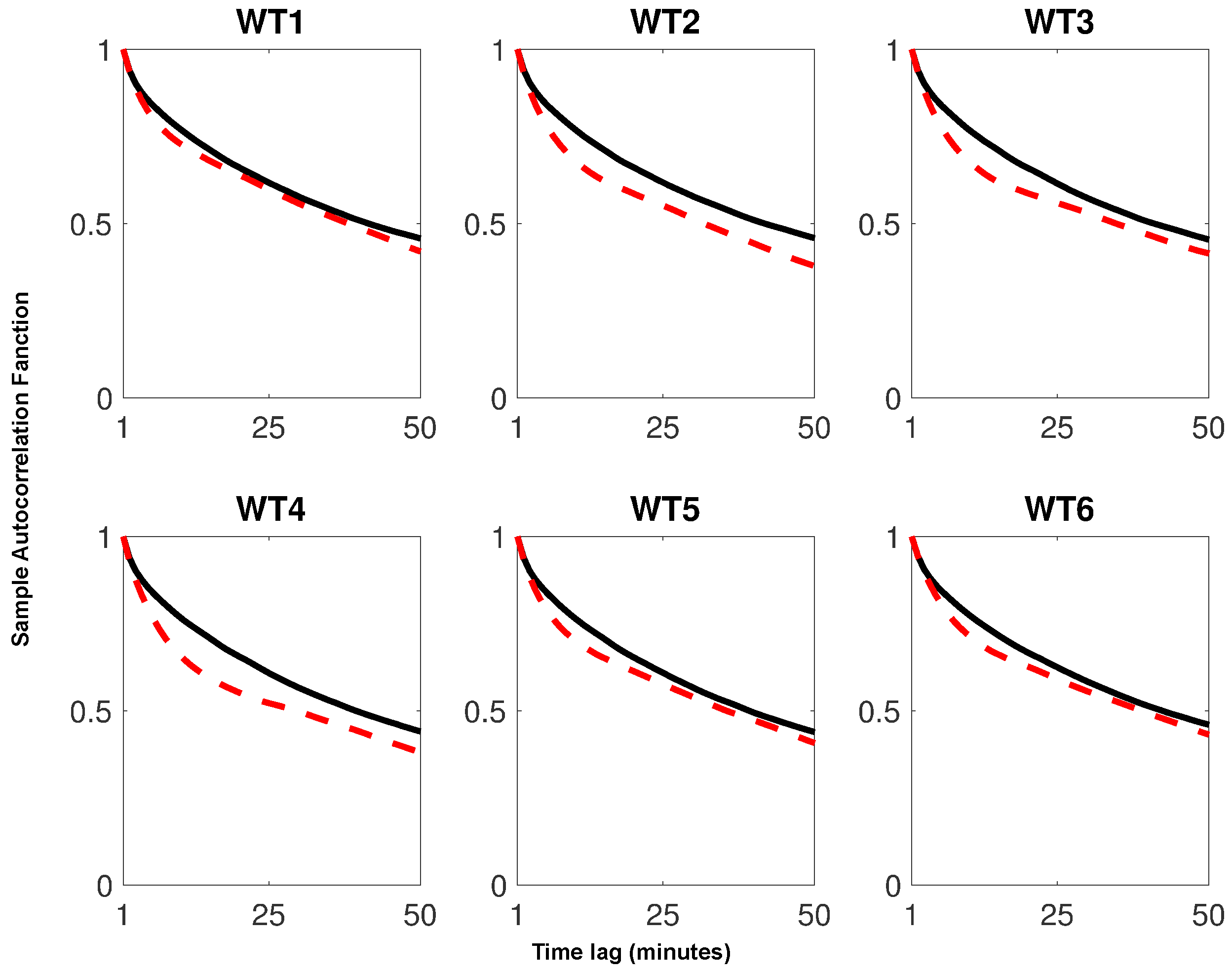

| Indicator | Turbine WT1 | Turbine WT2 | Turbine WT3 | Turbine WT4 | Turbine WT5 | Turbine WT6 |
|---|---|---|---|---|---|---|
| Mean | 507.80 | 519.55 | 523.89 | 521.89 | 512.35 | 601.90 |
| Std. dev. | 457.99 | 458.16 | 458.71 | 453.02 | 449.83 | 490.90 |
| Skewness | 1.3339 | 1.2875 | 1.2910 | 1.3068 | 1.3531 | 1.0880 |
| Kurtosis | 4.2468 | 4.1213 | 4.1436 | 4.2147 | 4.3758 | 3.4454 |
| Min. | 0.10 | 0.07 | 0.05 | 0.10 | 0.10 | 0.10 |
| Max. | 1997.3 | 1997.1 | 1999.1 | 1998.8 | 1998.6 | 1998.8 |
| Number of observations | 1.0088 × 10 | 1.0088 × 10 | 1.0088 × 10 | 1.0088 × 10 | 1.0088 × 10 | 1.0088 × 10 |
| State | Wind Power Range kW |
|---|---|
| 1 | 0–200 |
| 2 | 201–400 |
| 3 | 401–600 |
| 4 | 601–800 |
| 5 | 801–1000 |
| 6 | 1001–1200 |
| 7 | 1201–1400 |
| 8 | 1401–1600 |
| 9 | 1601–max |
| State | Range MW |
|---|---|
| 1 | 0–2 |
| 2 | 2–3 |
| 3 | 3–4 |
| 4 | 4–5 |
| 5 | 5–7 |
| 6 | >7 |
| Indicator | Gumbel | t2-St. | t6-St. | t8-St. | t10-St. | t20-St. | Gaussian | VAR |
|---|---|---|---|---|---|---|---|---|
| LOLE | 5.95% | 9.11% | 12.34% | 8.25% | 4.88% | 8.38% | 6.71% | 24.14% |
| LOLH | 9.54% | 19.16% | 22.74% | 24.22% | 8.32% | 14.71% | 10.78% | 76.47% |
| LOLP | 8.63% | 14.09% | 21.08% | 13.43% | 7.23% | 12.04% | 9.15% | 126.81% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Amico, G.; Masala, G.; Petroni, F.; Sobolewski, R.A. Managing Wind Power Generation via Indexed Semi-Markov Model and Copula. Energies 2020, 13, 4246. https://doi.org/10.3390/en13164246
D’Amico G, Masala G, Petroni F, Sobolewski RA. Managing Wind Power Generation via Indexed Semi-Markov Model and Copula. Energies. 2020; 13(16):4246. https://doi.org/10.3390/en13164246
Chicago/Turabian StyleD’Amico, Guglielmo, Giovanni Masala, Filippo Petroni, and Robert Adam Sobolewski. 2020. "Managing Wind Power Generation via Indexed Semi-Markov Model and Copula" Energies 13, no. 16: 4246. https://doi.org/10.3390/en13164246





