Single Column Model Simulations of Icing Conditions in Northern Sweden: Sensitivity to Surface Model Land Use Representation
Abstract
:1. Introduction
2. Method
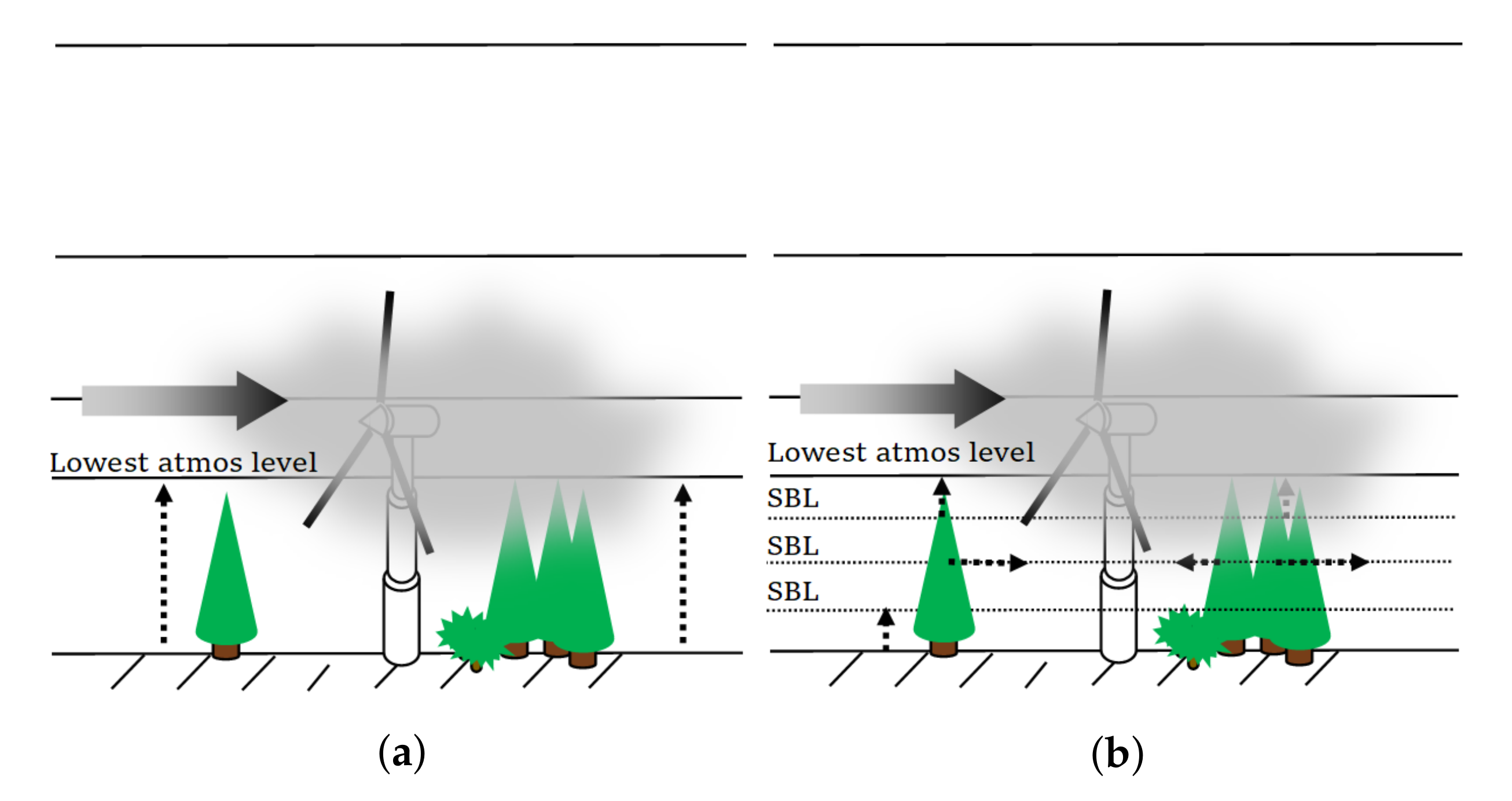
2.1. Surface Model
2.2. Icing Model
2.3. Experimental Setup
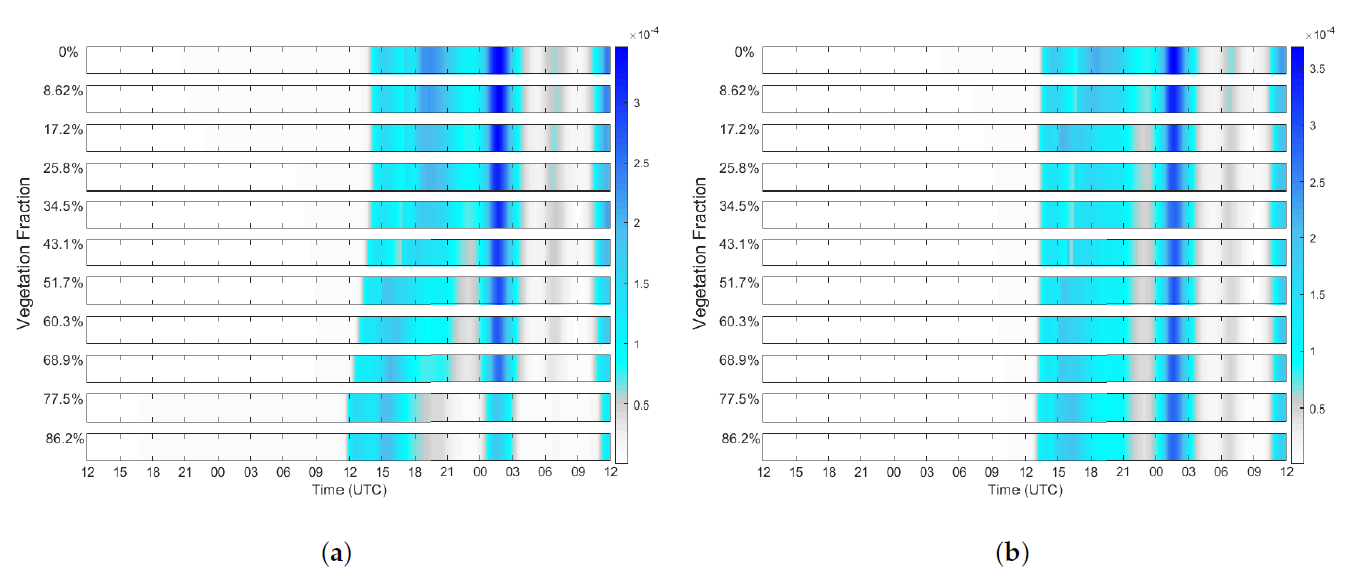
3. Results
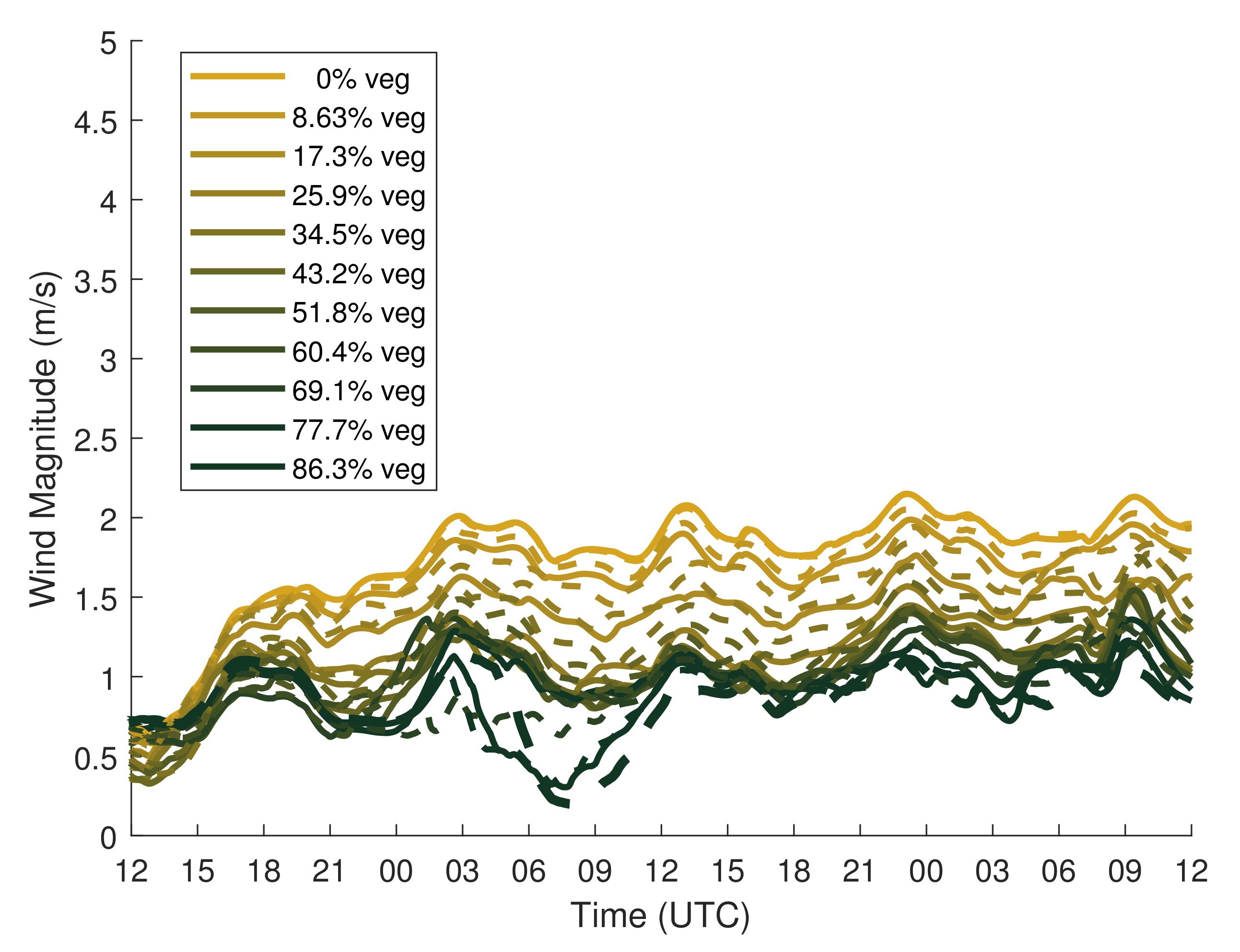
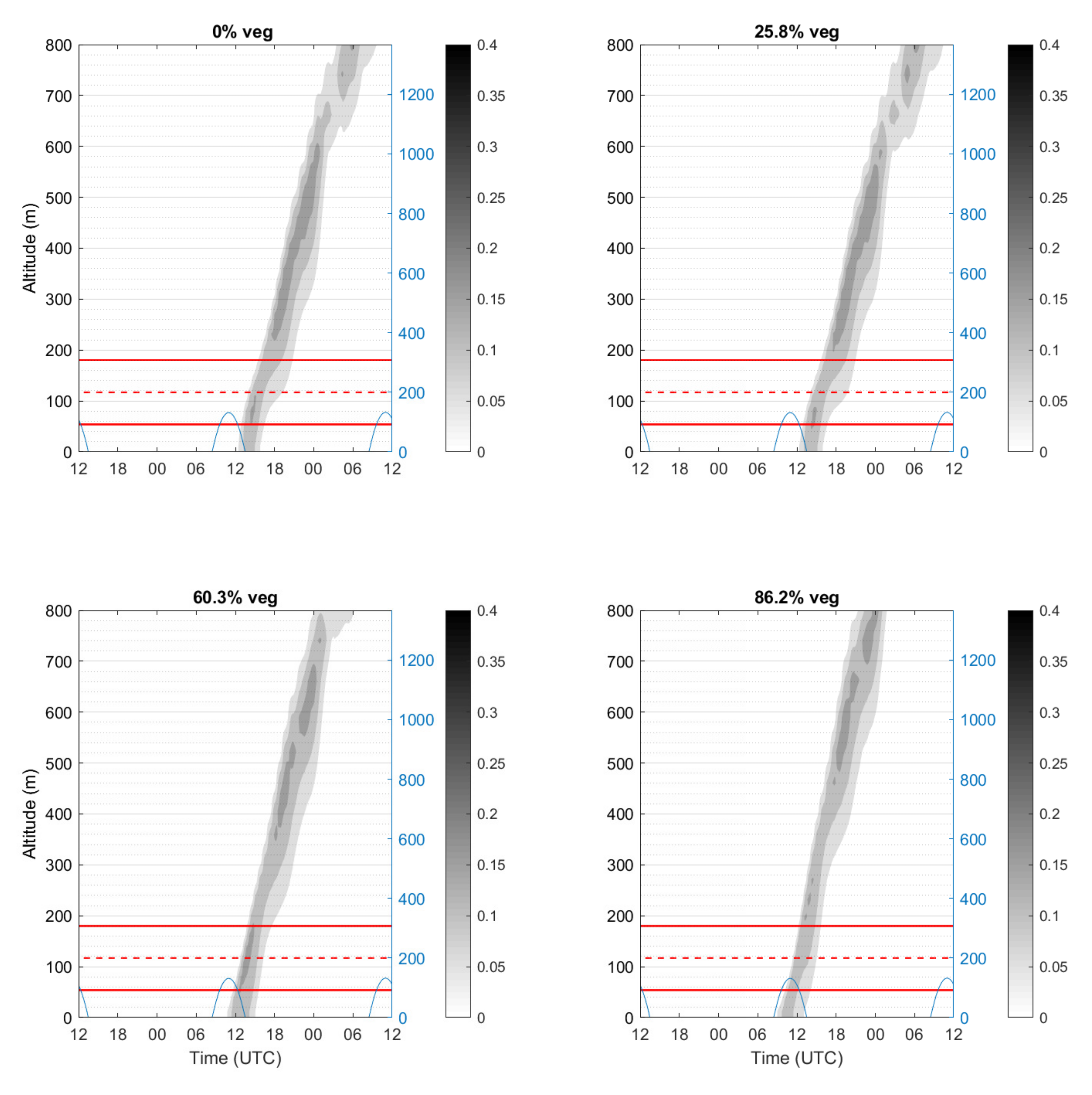
3.1. Impacts on Icing Forecast
3.2. Assessment of Icing Model Input Variables
3.3. Cases
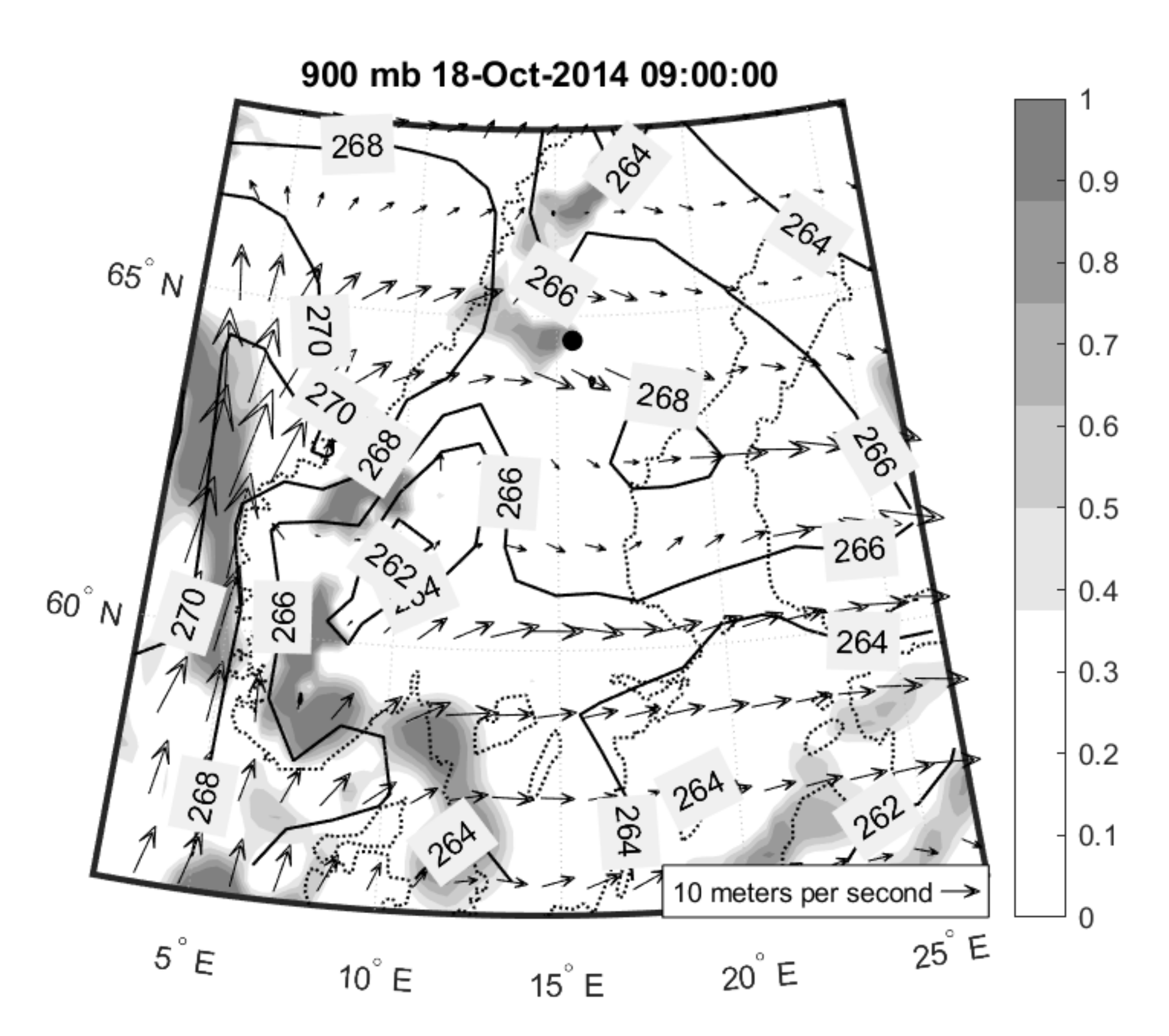
3.3.1. 18 October 2014 Case
3.3.2. 24 December 2013 Case
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IEA. Wind Energy in Cold Climates Available Technologies—Report; IEA: Paris, France, 2016; pp. 1–119. [Google Scholar]
- Battisti, L. Wind Turbines in Cold Climates: Icing Impacts and Mitigation Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 10–12. [Google Scholar] [CrossRef]
- Davis, N.; Hahmann, A.N.; Clausen, N.E.; Žagar, M. Forecast of icing events at a wind farm in Sweden. J. Appl. Meteorol. Climatol. 2014, 53, 262–281. [Google Scholar] [CrossRef] [Green Version]
- Hämäläinen, K.; Niemelä, S. Production of a Numerical Icing Atlas for Finland. Wind Energy 2017, 20, 171–189. [Google Scholar] [CrossRef]
- Molinder, J.P.; Körnich, H.; Olsson, E.; Bergström, H.; Sjöblom, A. Probabilistic forecasting of wind power production losses in cold climates: A case study. Wind Energy Sci. Discuss. 2017, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Makkonen, L. Models for the growth of rime, glaze, icicles and wet snow on structures. Philos. Trans. R. Soc. London Ser. Math. Phys. Eng. Sci. 2000, 358, 2913–2939. [Google Scholar] [CrossRef]
- Betts, A.K.; Ball, J.H. Albedo over the boreal forest. J. Geophys. Res. Atmos. 1997, 102, 28901–28909. [Google Scholar] [CrossRef] [Green Version]
- Bergot, T.; Escobar, J.; Masson, V. Effect of small-scale surface heterogeneities and buildings on radiation fog: Large-eddy simulation study at Paris-Charles de Gaulle Airport. Q. J. R. Meteorol. Soc. 2015, 141, 285–298. [Google Scholar] [CrossRef]
- Wetzel, J.; Argentini, S. Role of land surface in controlling daytime cloud amount: Two case studies are modeled using. J. Geophys. Res. 1996, 101, 7359–7370. [Google Scholar] [CrossRef]
- Nakanishi, M. Large-eddy simulation of radiation fog. Bound. Layer Meteorol. 2000, 94, 461–493. [Google Scholar] [CrossRef]
- Malardel, S.; Bruijn, C.D.; Rooy, W.D. A Single Column Model of HARMONIE in KNMI Parametrization Testbed (CY33T1 Version). 2010. Available online: http://netfam.fmi.fi/muscwd11/docCY33.knmi.pdf (accessed on 5 May 2020).
- Bengtsson, L.; Andrae, U.; Aspelien, T.; Batrak, Y.; Calvo, J.; de Rooy, W.; Gleeson, E.; Hansen-Sass, B.; Homleid, M.; Hortal, M.; et al. The HARMONIE–AROME Model Configuration in the ALADIN–HIRLAM NWP System. Mon. Weather Rev. 2017, 145, 1919–1935. [Google Scholar] [CrossRef]
- Pinty, J.P.; Jabouille, P. A mixed-phase cloud parameterization for use in a mesoscale non-hydrostatic model: Simulations of a squall line and of orographic precipitation. In Proceedings of the 14th Conference on Planned and Inadvertent Weather Modification, Everett, WA, USA, 17–21 August 1998. [Google Scholar]
- Lascaux, F.; Richard, E.; Pinty, J.P. Numerical simulations of three different MAP IOPs and the associated microphysical processes. Q. J. R. Meteorol. Soc. 2006, 132, 1907–1926. [Google Scholar] [CrossRef]
- Müller, M.; Homleid, M.; Ivarsson, K.I.; Køltzow, M.A.; Lindskog, M.; Midtbø, K.H.; Andrae, U.; Aspelien, T.; Berggren, L.; Bjørge, D.; et al. AROME-MetCoOp: A nordic convective-scale operational weather prediction model. Weather Forecast. 2017, 32, 609–627. [Google Scholar] [CrossRef]
- Bergot, T. Large-eddy simulation study of the dissipation of radiation fog. Q. J. R. Meteorol. Soc. 2016, 142, 1029–1040. [Google Scholar] [CrossRef]
- Le Moigne, P.; Boone, A.; Calvet, J.C.; Decharme, B.; Faroux, S. SURFEX scientific documentation. In Note de Centre (CNRM/GMME); Météo-France: Toulouse, France, 2018; p. 268. [Google Scholar]
- Faroux, S.; Masson, V.; Roujean, J.L. ECOCLIMAP-II: A climatologic global data base of ecosystems and land surface parameters at 1 km based on the analysis of time series of VEGETATION data. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 1008–1011. [Google Scholar] [CrossRef]
- Masson, V.; Seity, Y. Including atmospheric layers in vegetation and urban offline surface schemes. J. Appl. Meteorol. Climatol. 2009, 48, 1377–1397. [Google Scholar] [CrossRef]
- Bergström, H.; Olsson, E.; Söderberg, S.; Thorsson, P.; Unden, P.; Undén, P. Wind Power in Cold Climates: Ice Mapping Methods; Technical Report March; Elforsk: Stockholm, Sweden, 2013. [Google Scholar]
- Finstad, K.J.; Lozowski, E.P.; Makkonen, L. On the Median Volume Diameter Approximation for Droplet Collision Efficiency. J. Atmos. Sci. 1988, 45, 4008–4012. [Google Scholar] [CrossRef] [Green Version]
- Kringlebotn Nygaard, B.E.; Ágústsson, H.; Somfalvi-Tóth, K. Modeling Wet Snow Accretion on Power Lines: Improvements to Previous Methods Using 50 Years of Observations. J. Appl. Meteorol. Climatol. 2013, 52, 2189–2203. [Google Scholar] [CrossRef]
- Mazin, I.P.; Korolev, A.V.; Heymsfield, A.; Isaac, G.A.; Cober, S.G. Thermodynamics of icing cylinder for measurements of liquid water content in supercooled clouds. J. Atmos. Ocean. Technol. 2001, 18, 543–558. [Google Scholar] [CrossRef]
- Molinder, J.; Körnich, H.; Olsson, E.; Hessling, P. The use of uncertainty quantification for the empirical modeling of wind turbine icing. J. Appl. Meteorol. Climatol. 2019, 58, 2019–2032. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Jackson, P.S. On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 1981, 111, 15. [Google Scholar] [CrossRef]
- Brousseau, P.; Seity, Y.; Ricard, D.; Léger, J. Improvement of the forecast of convective activity from the AROME-France system. Q. J. R. Meteorol. Soc. 2016, 142, 2231–2243. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.L.; Masson, V.; Martin, E.; Le Moigne, P. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.Y.; Margulis, S.A. Impact of soil moisture heterogeneity length scale and gradients on daytime coupled land-cloudy boundary layer interactions. Hydrol. Process. 2013, 27, 1988–2003. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, S.; Schween, J.H.; Crewell, S. Large-Eddy Atmosphere-Land-Surface Modelling over Heterogeneous Surfaces: Model Development and Comparison with Measurements. Bound. Layer Meteorol. 2013, 148, 333–356. [Google Scholar] [CrossRef]
- Mazoyer, M.; Lac, C.; Thouron, O.; Bergot, T.; Masson, V.; Musson-Genon, L. Large eddy simulation of radiation fog: Impact of dynamics on the fog life cycle. Atmos. Chem. Phys. 2017, 17, 13017–13035. [Google Scholar] [CrossRef] [Green Version]
- Floors, R.; Enevoldsen, P.; Davis, N.; Arnqvist, J.; Dellwik, E. From lidar scans to roughness maps for wind resource modelling in forested areas. Wind Energy Sci. 2018, 3, 353–370. [Google Scholar] [CrossRef] [Green Version]
- Arnqvist, J.; Olivares-Espinosa, H.; Ivanell, S. Investigation of Turbulence Accuracy When Modeling Wind in Realistic Forests Using LES; Springer: Berlin/Heidelberg, Germany, 2019; pp. 291–296. [Google Scholar] [CrossRef]













| 3D Model Date | MUSC Init Hour | Event Type | Snow Cover | Max TOA SW Down | Initial Wind Speed at 117 m | Initial Temperature at 117 m |
|---|---|---|---|---|---|---|
| 24 December 2013 0600 | 0900 | Lifting fog | Yes | 132.5 W/m | 13.7 m/s | 266 K |
| 5 January 2014 0600 | 0900 | Lifting fog | Yes | 157.1 W/m | 4.7 m/s | 270 K |
| 5 January 2014 1800 | 2100 | Lifting fog | Yes | 157.1 W/m | 5.7 m/s | 269 K |
| 18 October 2014 0600 | 0900 | Elevated cloud/Lifting fog | Yes | 449.6 W/m | 1.2 m/s | 268 K |
| 22 October 2014 0600 | 0900 | Elevated cloud/Lifting fog | Yes | 417.9 W/m | 9.9 m/s | 267 K |
| 23 October 2014 0600 | 0900 | Elevated cloud/Lifting fog | Yes | 410.0 W/m | 13.9 m/s | 269 K |
| COVER 301 (Tundra) | COVER 302 (Broadleaf Forest) | COVER 310 (Boreal Forest) | BARE GROUND |
|---|---|---|---|
| 0% | 0% | 0% | 100% |
| 2% | 2% | 7% | 90% |
| 3% | 3% | 13% | 80% |
| 5% | 5% | 20% | 70% |
| 7% | 7% | 27% | 60% |
| 8% | 8% | 33% | 50% |
| 10% | 10% | 40% | 40% |
| 12% | 12% | 47% | 30% |
| 13% | 13% | 53% | 20% |
| 15% | 15% | 60% | 10% |
| 17% | 17% | 67% | 0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janzon, E.; Körnich, H.; Arnqvist, J.; Rutgersson, A. Single Column Model Simulations of Icing Conditions in Northern Sweden: Sensitivity to Surface Model Land Use Representation. Energies 2020, 13, 4258. https://doi.org/10.3390/en13164258
Janzon E, Körnich H, Arnqvist J, Rutgersson A. Single Column Model Simulations of Icing Conditions in Northern Sweden: Sensitivity to Surface Model Land Use Representation. Energies. 2020; 13(16):4258. https://doi.org/10.3390/en13164258
Chicago/Turabian StyleJanzon, Erik, Heiner Körnich, Johan Arnqvist, and Anna Rutgersson. 2020. "Single Column Model Simulations of Icing Conditions in Northern Sweden: Sensitivity to Surface Model Land Use Representation" Energies 13, no. 16: 4258. https://doi.org/10.3390/en13164258
APA StyleJanzon, E., Körnich, H., Arnqvist, J., & Rutgersson, A. (2020). Single Column Model Simulations of Icing Conditions in Northern Sweden: Sensitivity to Surface Model Land Use Representation. Energies, 13(16), 4258. https://doi.org/10.3390/en13164258





