Numerical Analysis and Preliminary Experiment of a Solar Assisted Heat Pump Drying System for Chinese Wolfberry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lab Experiment and Kinetic Model
2.1.1. Lab Experiment
2.1.2. Kinetic Model
2.2. Description of the SAHP Drying System
3. Drying System Model
4. Results and Discussion
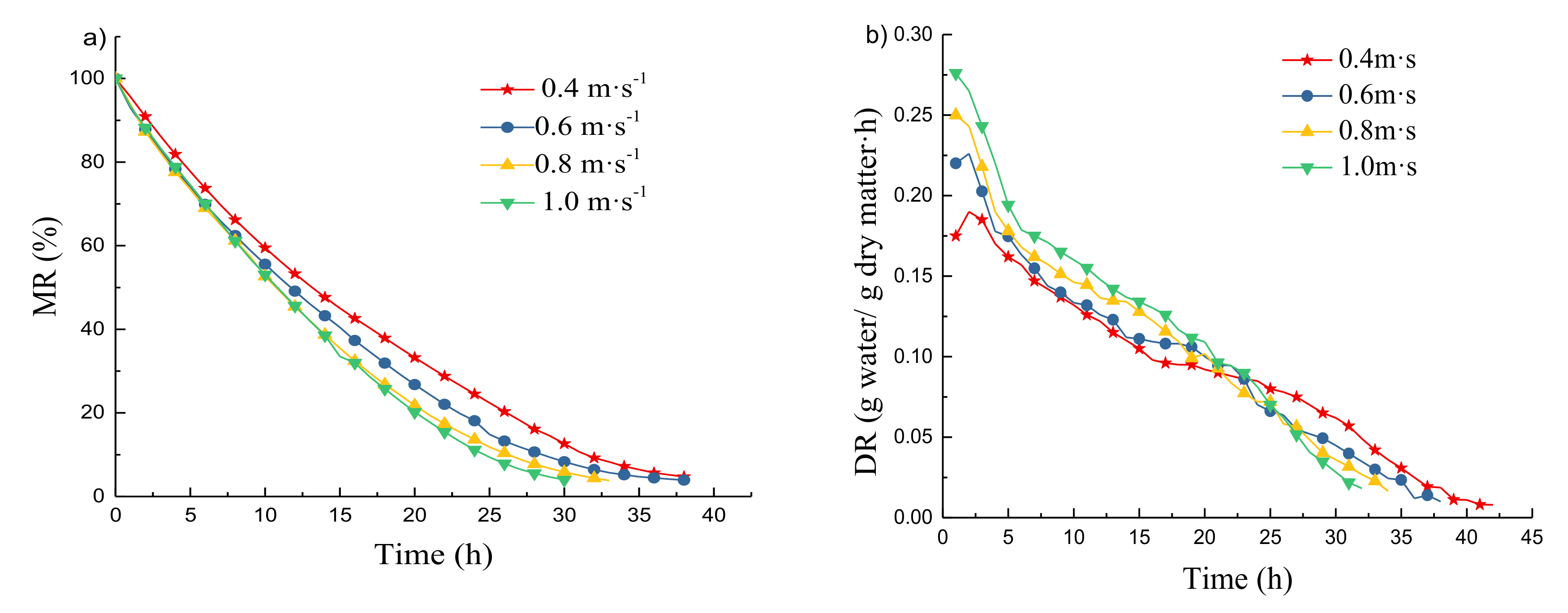
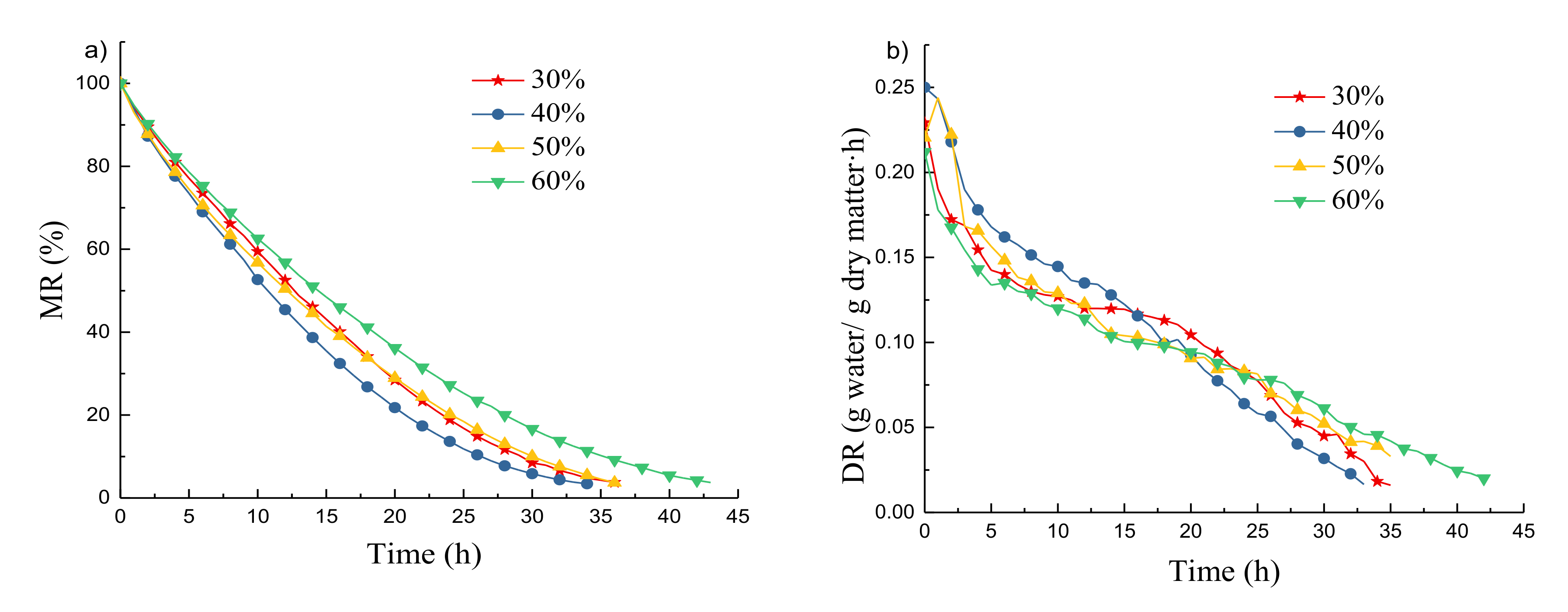
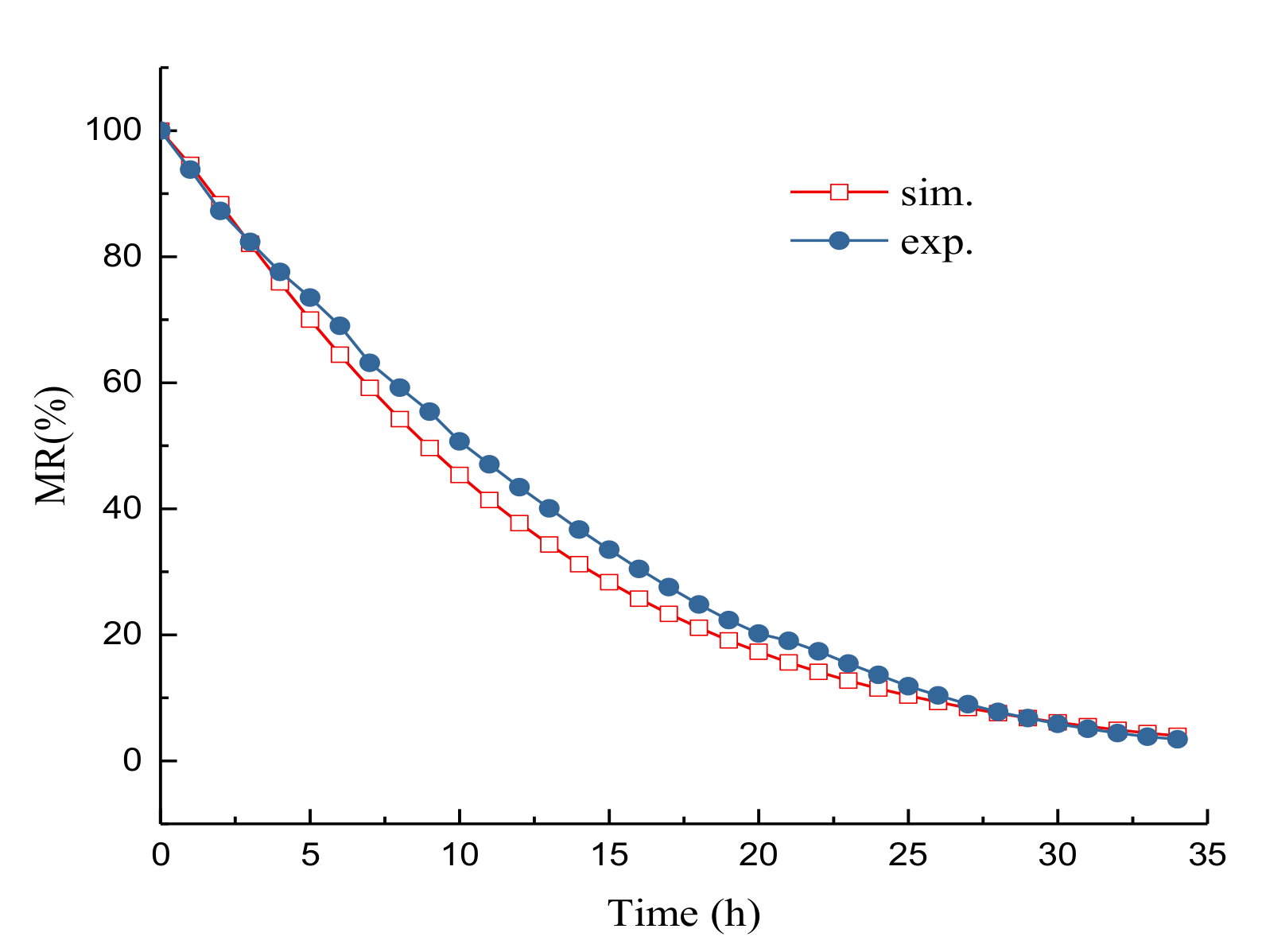
4.1. Drying Kinetic Characteristics
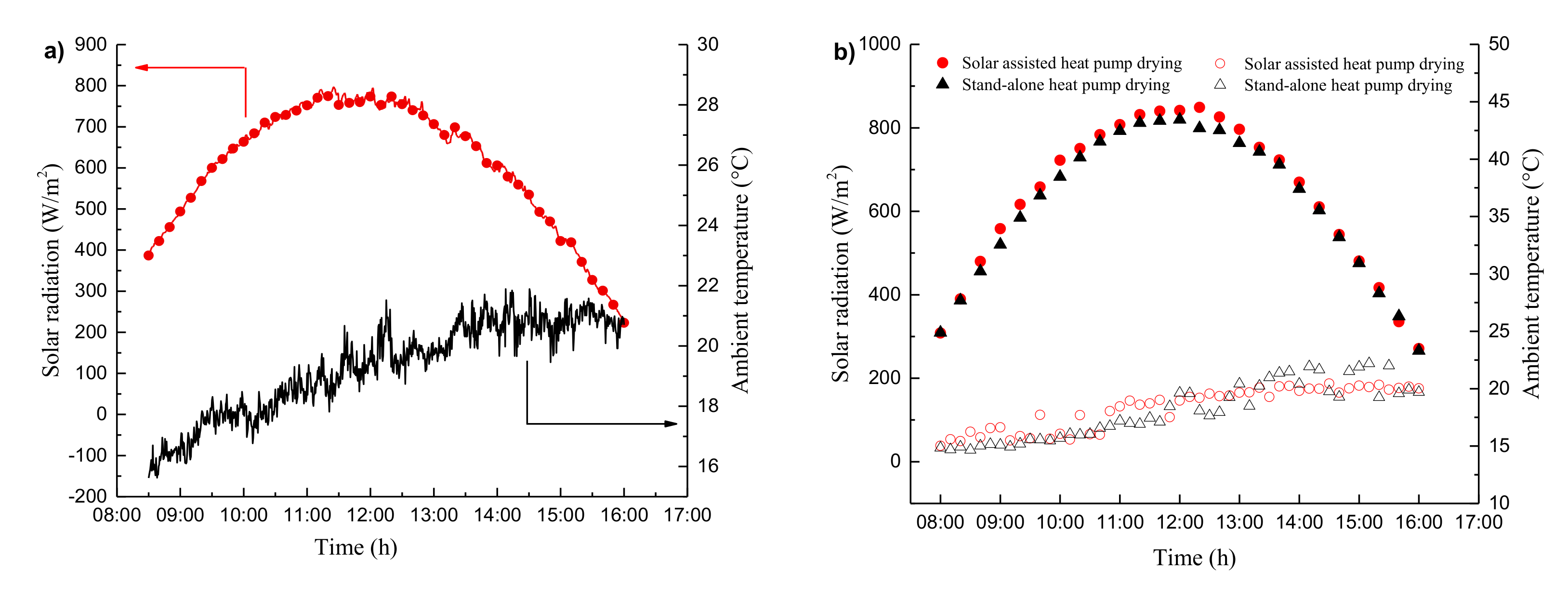
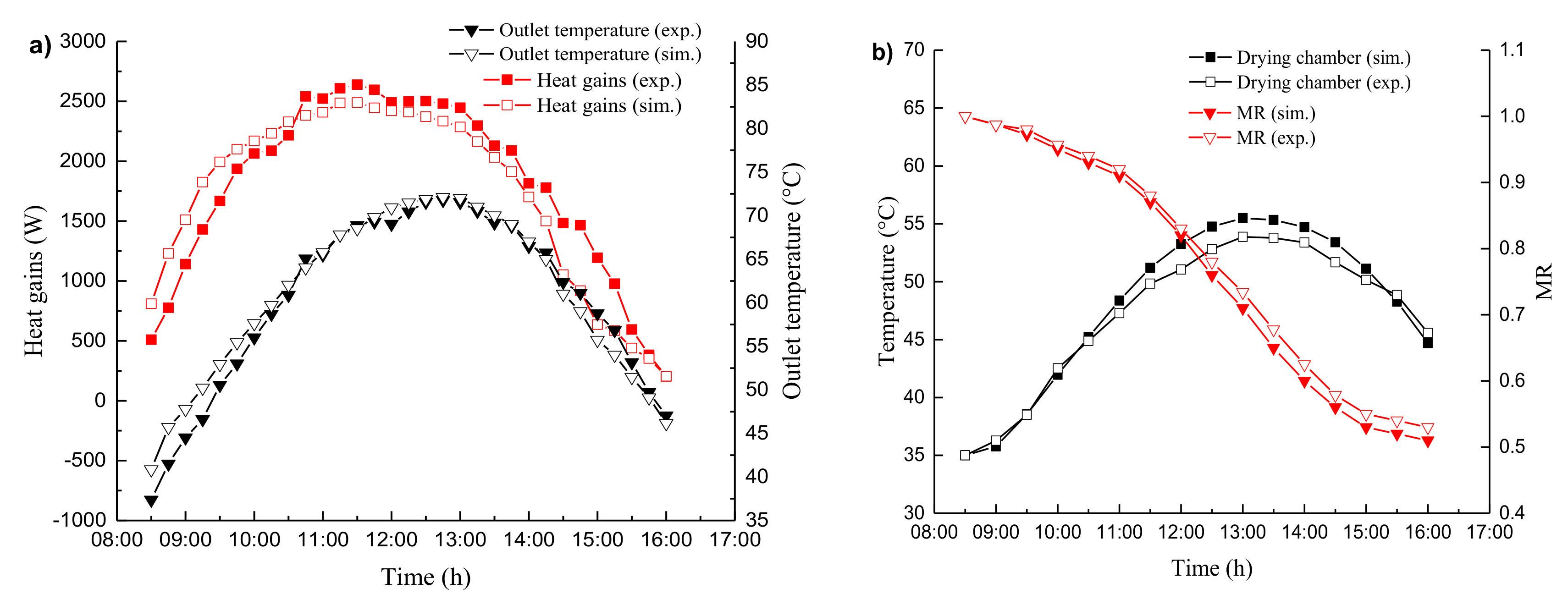
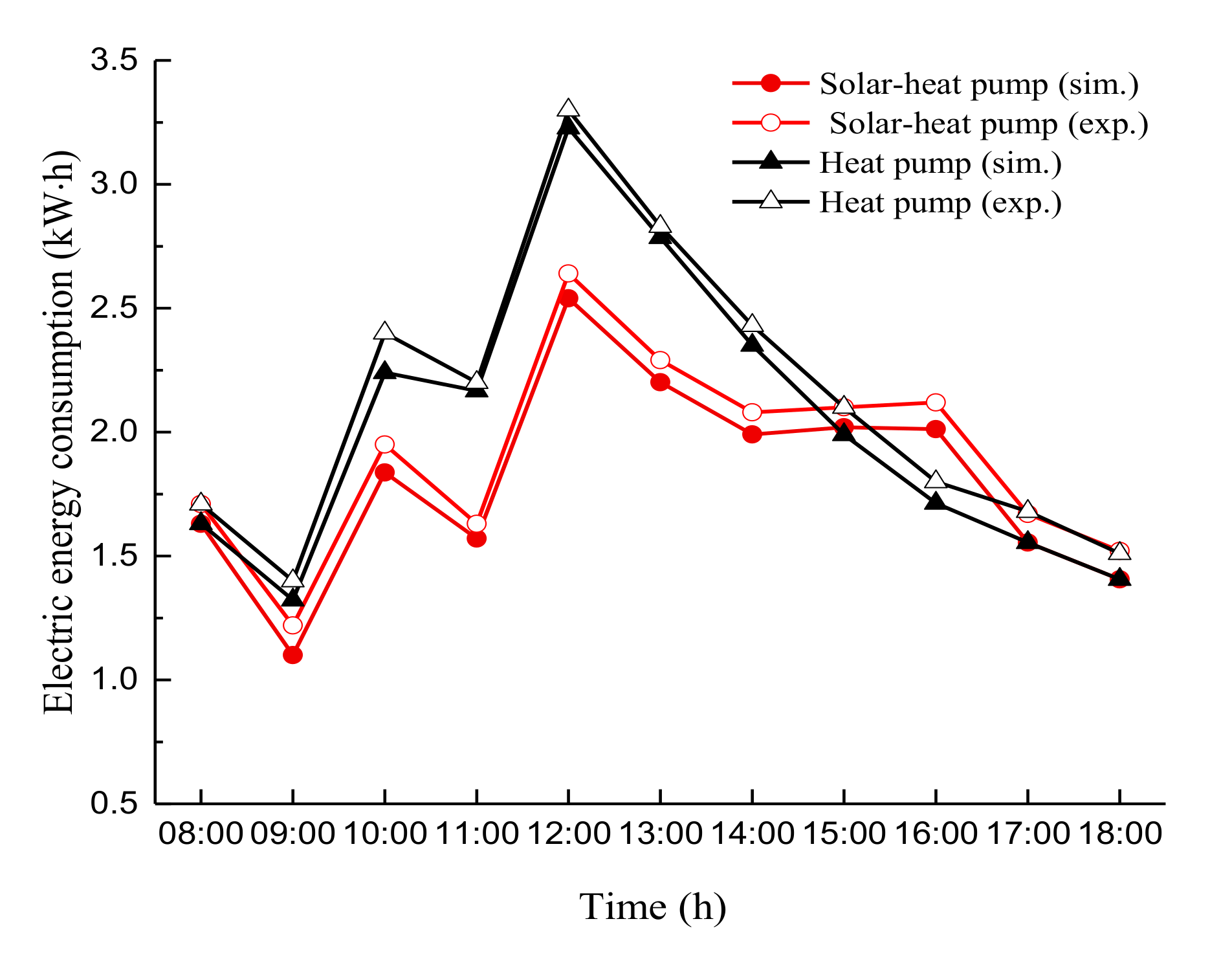
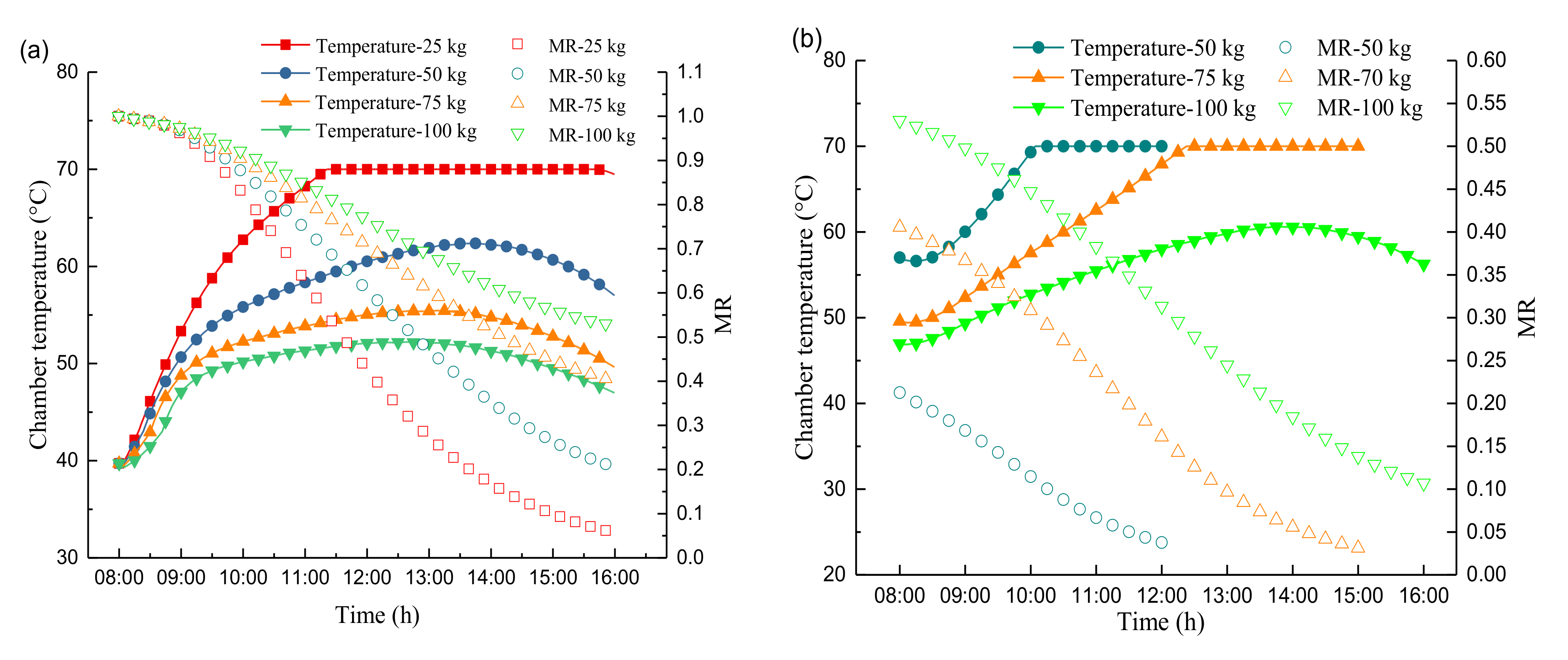
4.2. Validation of Drying System Model
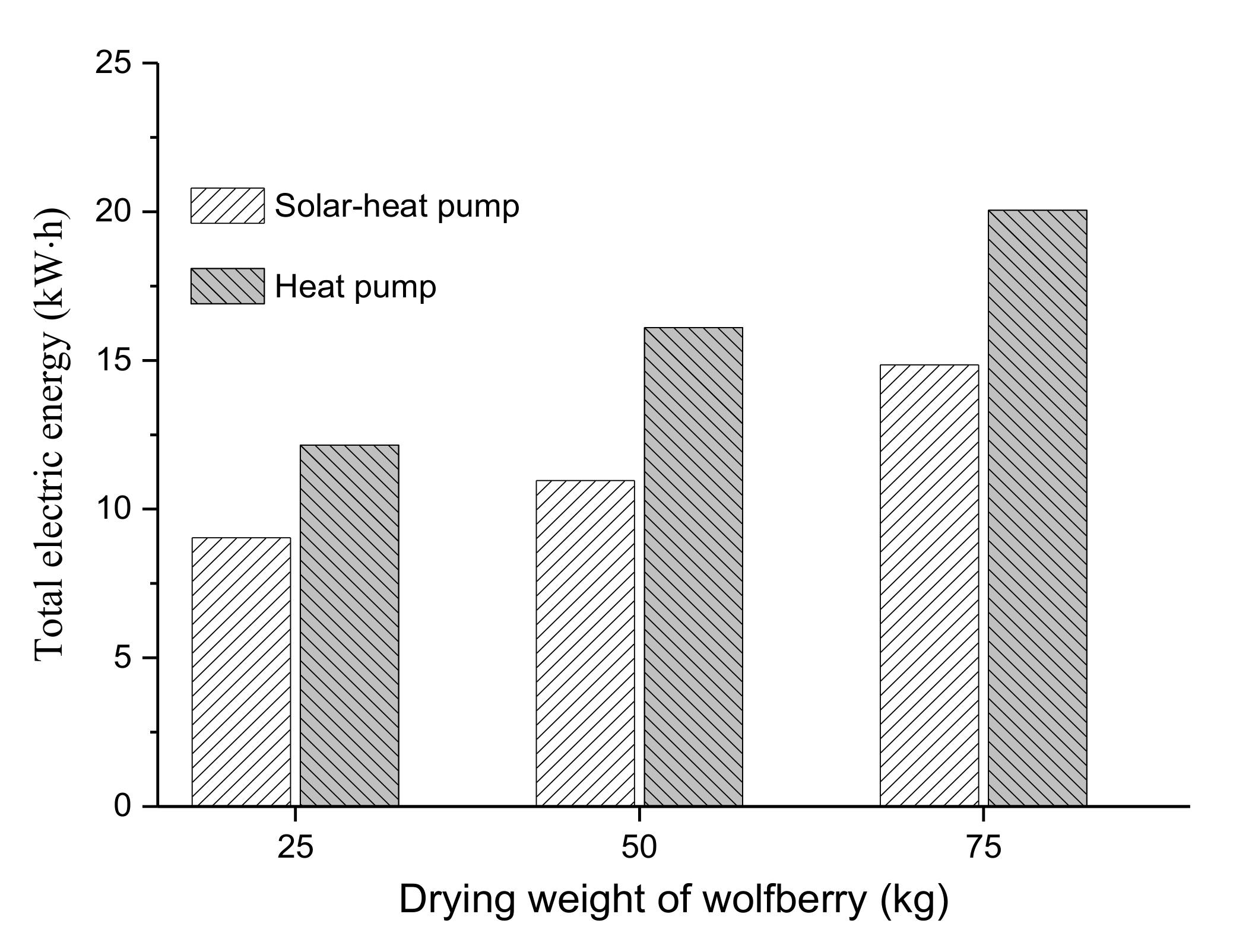
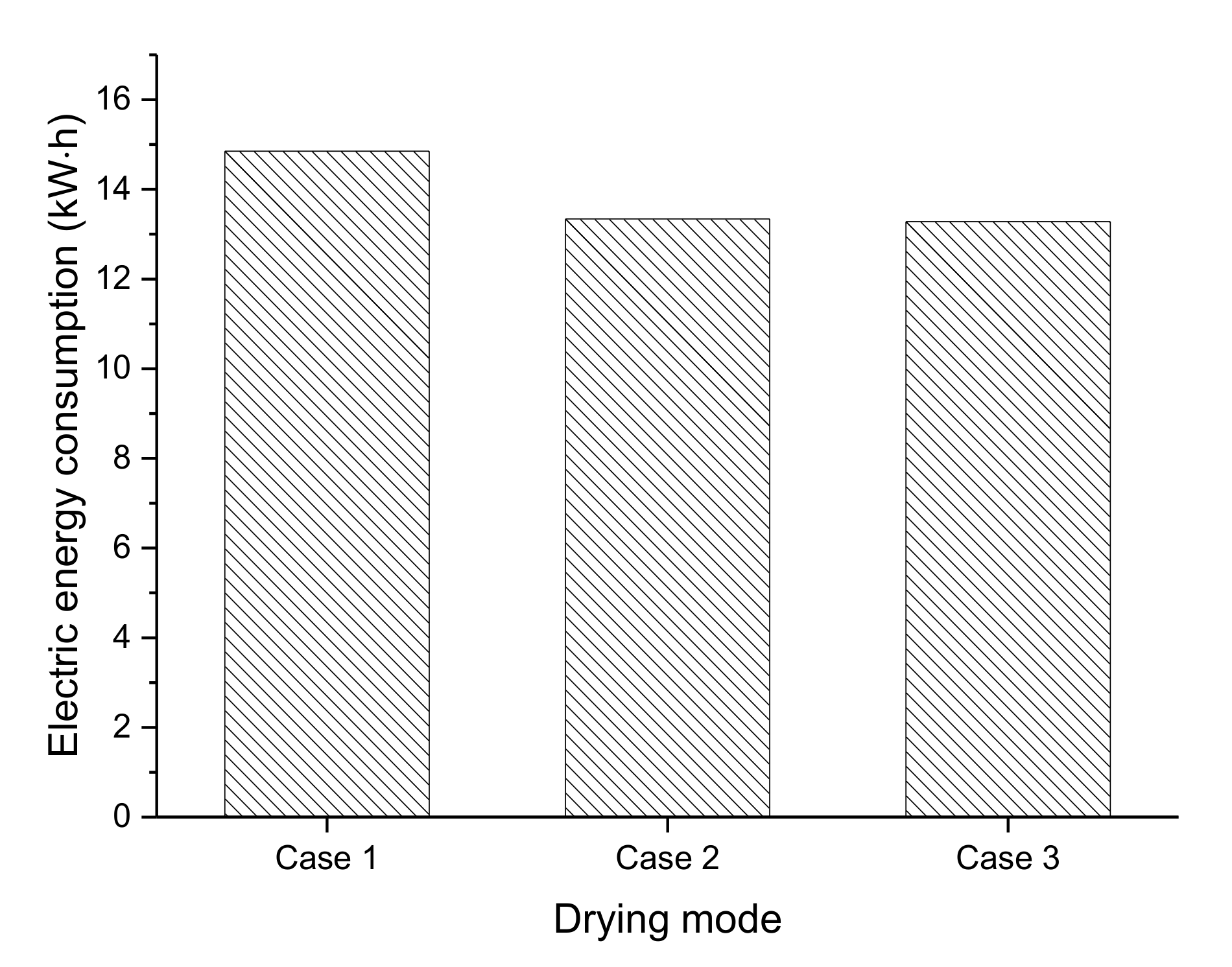
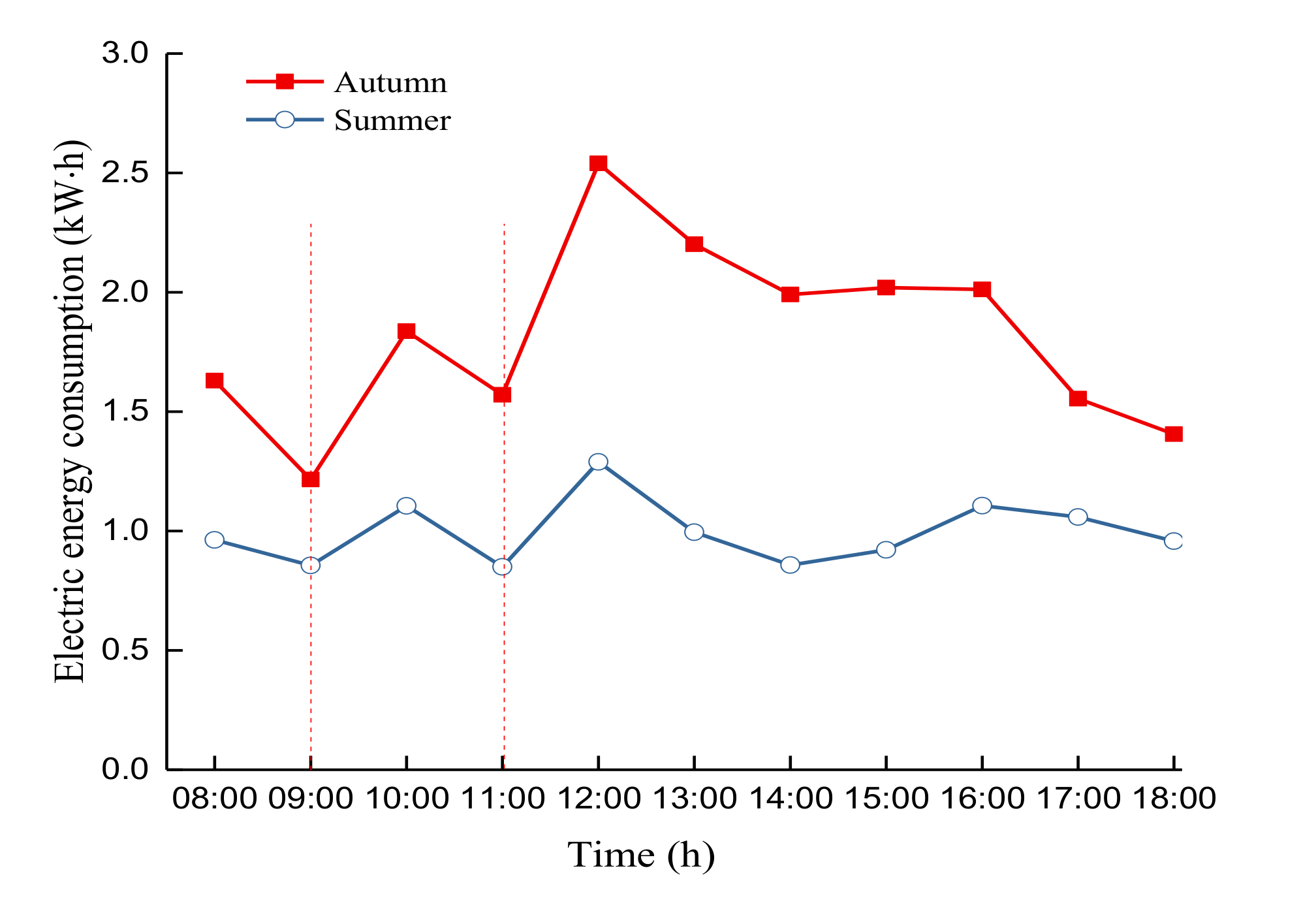
4.3. Parametric Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Morad, M.M.; El-Shazly, M.A.; Wasfy, K.I.; El-Maghawry, H.A.M. Thermal analysis and performance evaluation of a solar tunnel greenhouse dryer for drying peppermint plants. Renew. Energy 2017, 101, 992–1004. [Google Scholar] [CrossRef]
- Montero, I.; Teresa Miranda, M.; Jose Sepulveda, F.; Ignacio Arranz, J.; Victoria Rojas, C.; Nogales, S. Solar dryer application for olive oil mill wastes. Energies 2015, 8, 14049–14063. [Google Scholar] [CrossRef] [Green Version]
- Lingayat, A.B.; Chandramohan, V.P.; Raju, V.R.K.; Meda, V. A review on indirect type solar dryers for agricultural crops—Dryer setup, its performance, energy storage and important highlights. Appl. Energy 2020, 258, 114005. [Google Scholar] [CrossRef]
- Chaouch, W.B.; Khellaf, A.; Mediani, A.; Slimani, M.E.A.; Loumani, A.; Hamid, A. Experimental investigation of an active direct and indirect solar dryer with sensible heat storage for camel meat drying in Saharan environment. Solar Energy 2018, 174, 328–341. [Google Scholar] [CrossRef]
- Azouma, Y.O.; Drigalski, L.; Jegla, Z.; Reppich, M.; Turek, V.; Weiss, M. Indirect convective solar drying process of pineapples as part of circular economy strategy. Energies 2019, 12, 2841. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.B.; Manikandan, G.; Kanna, P.R.; Taler, D.; Taler, J.; Nowak-Oclon, M.; Mzyk, K.; Toh, H.T. A performance evaluation of a solar air heater using different shaped ribs mounted on the absorber plate—A review. Energies 2018, 11, 3104. [Google Scholar] [CrossRef] [Green Version]
- Satcunanathan, S.; Deonarine, S. A two-pass solar air heater. Solar Energy 1973, 15, 41–49. [Google Scholar] [CrossRef]
- Fudholi, A.; Ruslan, M.H.; Othman, M.Y.; Azmi, M.S.M.; Zaharim, A.; Sopian, K. Drying of palm oil fronds in solar dryer with finned double-pass solar collectors. WSEAS Trans. Heat. Mass. Transf. 2012, 4, 105–114. [Google Scholar]
- Ruslan, M.H.; Fudholi, A.; Othman, M.Y.; Azmi, M.S.M.; Yahya, M.; Zaharim, A.; Sopian, K. The double-pass solar dryer for drying palm oil fronds. In Proceedings of the 10th WSEAS International Conference on System Science and Simulation in Engineering (ICOSSSE’11), Stevens Point, WI, USA; 2011; pp. 143–149. [Google Scholar]
- Fudholi, A.; Sopian, K.; Yazdi, M.H.; Ruslan, M.H.; Gabbasa, M.; Kazem, H.A. Performance analysis of solar drying system for red chili. Solar Energy 2014, 99, 47–54. [Google Scholar] [CrossRef]
- Yahya, M.; Ruslan, M.H.; Othman, M.Y.; Yatim, B.; Sulaiman, M.; Mat, S.; Lim, C.H.; Alghoul, M.; Zaharim, A.; Sopian, K. Evaluation of energy requirement for drying of green tea using a solar assisted drying system (V-groove solar collector). In Proceedings of the 3rd WSEAS International Conference on Renewable Energy Sources, Kuala Lumpur, Malaysia, 2–4 April 2013; pp. 298–303. [Google Scholar]
- Raj, A.K.; Srinivas, M.; Jayaraj, S. A cost-effective method to improve the performance of solar air heaters using discrete macro-encapsulated PCM capsules for drying applications. Appl. Therm. Eng. 2019, 146, 910–920. [Google Scholar] [CrossRef]
- Atalay, H. Performance analysis of a solar dryer integrated with the packed bed thermal energy storage (TES) system. Energy 2019, 172, 1037–1052. [Google Scholar] [CrossRef]
- Pal, U.S.; Khan, M.K. Calculation steps for the design of different components of heat pump dryers under constant drying rate condition. Dry. Technol. 2008, 26, 864–872. [Google Scholar] [CrossRef]
- Fudholi, A.; Sopian, K. A review of solar air flat plate collector for drying application. Renew. Sustain. Energy Rev. 2019, 102, 333–345. [Google Scholar] [CrossRef]
- Daghigh, R.; Ruslan, M.H.; Sulaiman, M.Y.; Sopian, K. Review of solar assisted heat pump drying systems for agricultural and marine products. Renew. Sustain. Energy Rev. 2010, 14, 2564–2579. [Google Scholar] [CrossRef]
- Sopian, K.; Supranto; Othman, M.; Daud, W.; Yatim, B. Double-pass solar collectors with porous media suitable for higher-temperature solar-assisted drying systems. J. Energy Eng. 2007, 133, 13–18. [Google Scholar] [CrossRef]
- Mohanraj, M. Performance of a solar-ambient hybrid source heat pump drier for copra drying under hot-humid weather conditions. Energy Sustain. Develop. 2014, 23, 165–169. [Google Scholar] [CrossRef]
- Hawlader, M.N.A.; Jahangeer, K.A. Solar heat pump drying and water heating in the tropics. Solar Energy 2006, 80, 492–499. [Google Scholar] [CrossRef]
- Hawlader, M.N.A.; Chou, S.K.; Jahangeer, K.A.; Rahman, S.M.A.; Eugene Lau, K.W. Solar-assisted heat-pump dryer and water heater. Appl. Energy 2003, 74, 185–193. [Google Scholar] [CrossRef]
- Aktaş, M.; Ceylan, İ.; Yilmaz, S. Determination of drying characteristics of apples in a heat pump and solar dryer. Desalination 2009, 239, 266–275. [Google Scholar] [CrossRef]
- Saensabai, P.; Prasertsan, S. Effects of component arrangement and ambient and drying conditions on the performance of heat pump dryers. Dry. Technol. 2003, 21, 103–127. [Google Scholar] [CrossRef]
- Saensabai, P.; Prasertsan, S. Condenser coil optimization and component matching of heat pump dryer. Dry. Technol. 2007, 25, 1571–1580. [Google Scholar] [CrossRef]
- Bi, Y.; Guo, T.; Zhang, L.; Chen, L. Solar and ground source heat-pump system. Appl. Energy 2004, 78, 231–245. [Google Scholar] [CrossRef]
- Chauhan, P.S.; Kumar, A.; Nuntadusit, C. Heat transfer analysis of PV integrated modified greenhouse dryer. Renew. Energy 2018, 121, 53–65. [Google Scholar] [CrossRef]
- Tiwari, S.; Agrawal, S.; Tiwari, G.N. PVT air collector integrated greenhouse dryers. Renew. Sustain. Energy Rev. 2018, 90, 142–159. [Google Scholar] [CrossRef]
- Maurer, C.; Mueller, J. Drying characteristics of biogas digestate in a hybrid waste-heat/solar dryer. Energies 2019, 12, 1294. [Google Scholar] [CrossRef] [Green Version]
- Chandramohan, V.P.; Talukdar, P. Estimation of Equilibrium Moisture Content and Drying Time of Potato Through Hot Air Drying; Springer India: New Delhi, India, 2017; pp. 205–213. [Google Scholar]
- Diamante, L.M.; Munro, P.A. Mathematical modeling of hot air drying of sweet potato slices. Int. J. Food Sci. Technol. 2007, 26, 99–109. [Google Scholar] [CrossRef]
- Akpinar, E.; Midilli, A.; Bicer, Y. Single layer drying behaviour of potato slices in a convective cyclone dryer and mathematical modeling. Energy Convers. Manag. 2003, 44, 1689–1705. [Google Scholar] [CrossRef]
- Diamante, L.M.; Munro, P.A. Mathematical modelling of the thin layer solar drying of sweet potato slices. Solar Energy 1993, 51, 271–276. [Google Scholar] [CrossRef]
- Asiru, W.B.; Raji, A.O.; Igbeka, J.C.; Elemo, G.N. Mathematical modelling of thin layer dried cashew kernels. Nigerian Food J. 2013, 31, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Li, M.; Hassanien, R.H.E.; Wang, Y.; Yang, L. Thermal performance of indirect forced convection solar dryer and kinetics analysis of mango. Appl. Therm. Eng. 2018, 134, 310–321. [Google Scholar] [CrossRef]
- Guo, C.; Ji, J.; Sun, W.; Ma, J.; He, W.; Wang, Y. Numerical simulation and experimental validation of tri-functional photovoltaic/thermal solar collector. Energy 2015, 87, 470–480. [Google Scholar] [CrossRef]


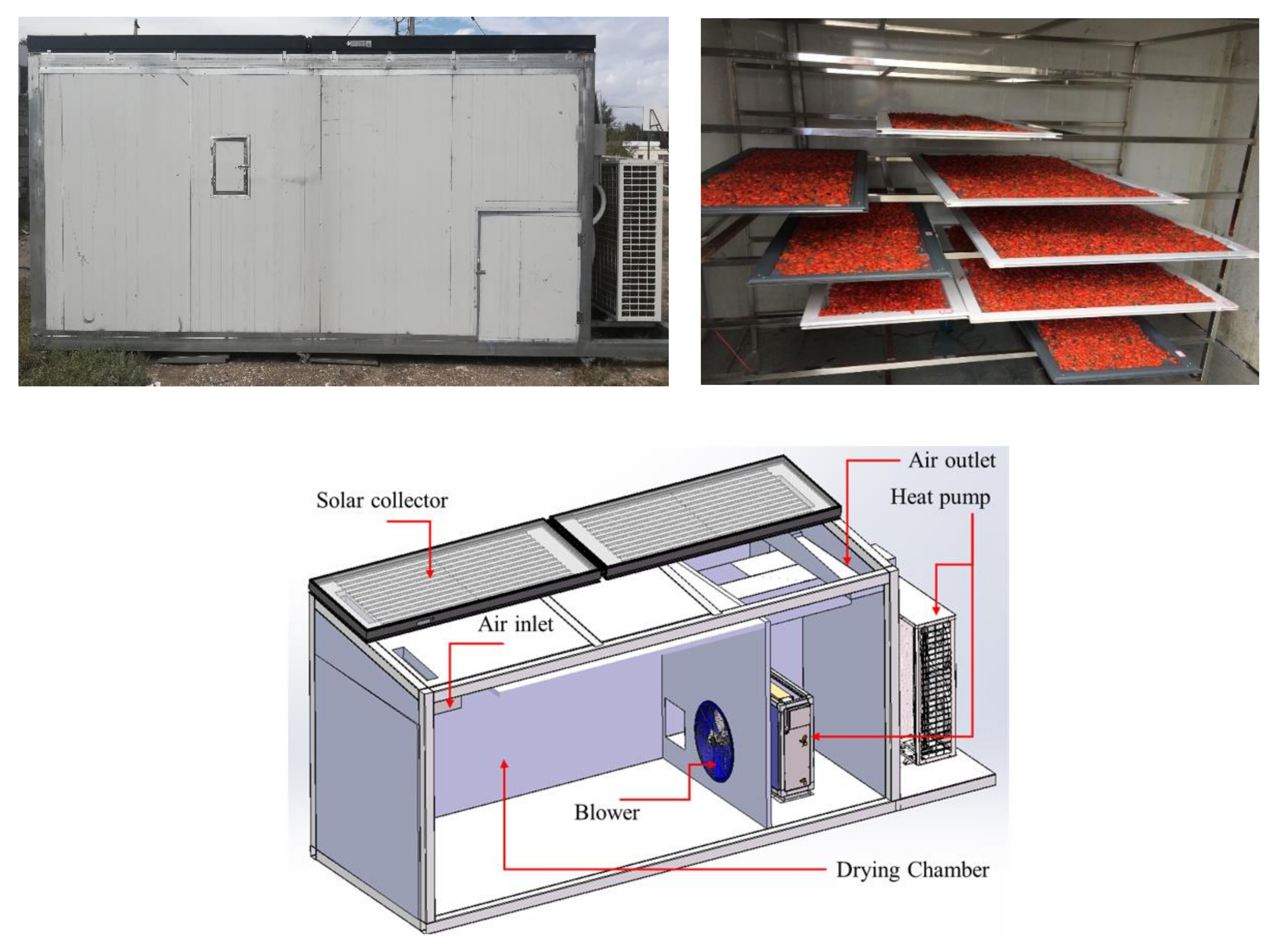
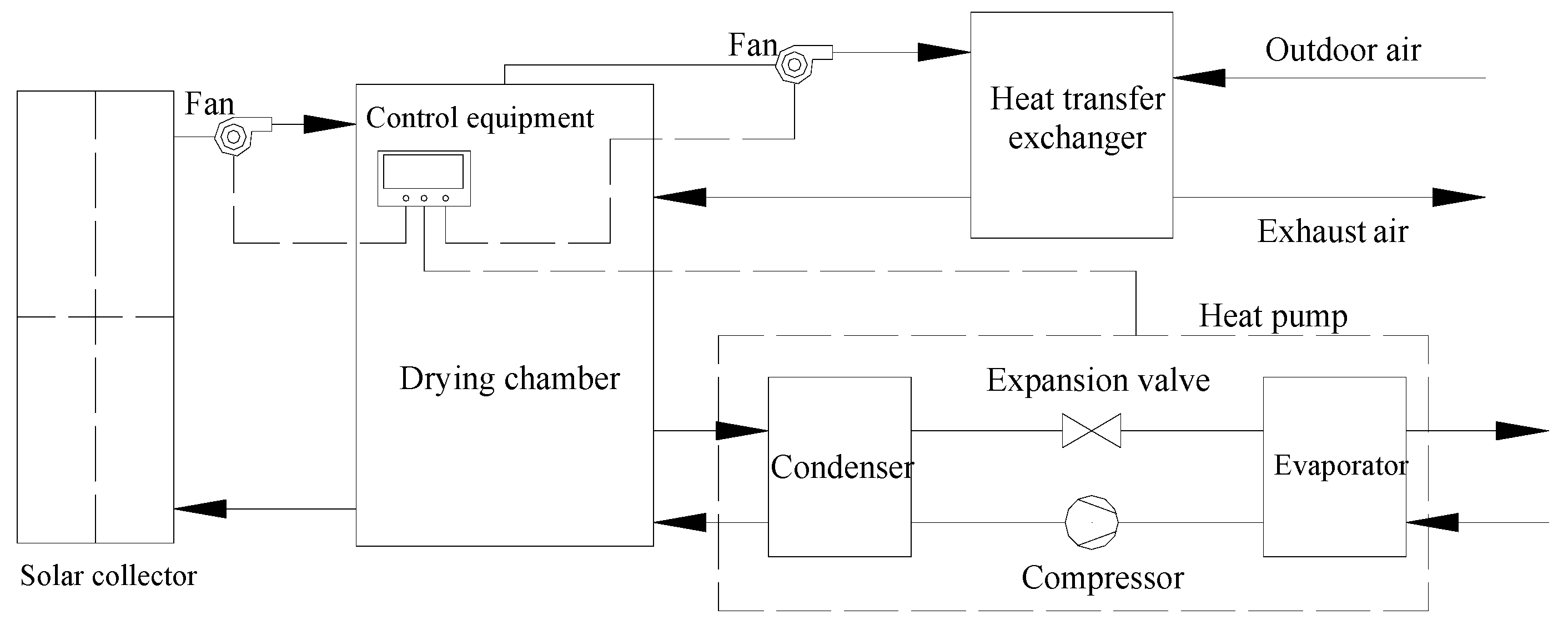

| Parameter | Values | Specifications | |||
|---|---|---|---|---|---|
| Drying temperature (T), °C | 40 | 50 | 60 | 70 | RH = 40%, v = 0.8 m/s |
| Relative humidity (RH), % | 30 | 40 | 50 | 60 | RH = 40%, T = 50 °C |
| Air velocity (V), m/s | 0.4 | 0.6 | 0.8 | 1.0 | T = 50 °C, v = 0.8 m/s |
| Instrument | Type | Accuracy |
|---|---|---|
| Drying oven | DNF-300 A | ± 2% (RH), ± 2 °C (T) |
| Digital balance | JA2002 | ± 0.01 g |
| Hot-wire anemometer | KANOMAX | ± 0.01 ms−1 |
| Thermocouple | T | ±0.5 °C |
| Model | Equation | Ref. |
|---|---|---|
| Newton | [30] | |
| Page | [31] | |
| Henderson and Pabis | [32] |
| Cases | ||||||||
|---|---|---|---|---|---|---|---|---|
| k | R2 | a | k | R2 | k | m | R2 | |
| 40 ℃, 0.8 ms-1, 40% | 0.0478 | 0.9464 | 1.354 | 0.0553 | 0.97 | 0.0345 | 1.0763 | 0.987 |
| 50 ℃, 0.8 ms-1, 40% | 0.0832 | 0.9422 | 1.458 | 0.0992 | 0.9753 | 0.0511 | 1.148 | 0.989 |
| 60 ℃, 0.8 ms-1, 40% | 0.2077 | 0.8849 | 1.896 | 0.2739 | 0.9569 | 0.1162 | 1.2766 | 0.9832 |
| 70 ℃, 0.8 ms-1, 40% | 0.3888 | 0.8700 | 2.427 | 0.5452 | 0.9707 | 0.2405 | 1.3889 | 0.9934 |
| 50 ℃, 0.4 ms-1, 40% | 0.0687 | 0.9360 | 1.466 | 0.0819 | 0.9691 | 0.0372 | 1.1727 | 0.9903 |
| 50 ℃, 0.6 ms-1, 40% | 0.0791 | 0.9570 | 1.299 | 0.0896 | 0.9749 | 0.0523 | 1.1052 | 0.9846 |
| 50 ℃, 1.0 ms-1, 40% | 0.0869 | 0.9164 | 1.388 | 0.107 | 0.9607 | 0.0479 | 1.1822 | 0.9828 |
| 50 ℃, 0.8 ms-1, 30% | 0.0747 | 0.9213 | 1.527 | 0.0992 | 0.9628 | 0.0408 | 1.1717 | 0.9823 |
| 50 ℃, 0.8 ms-1, 50% | 0.0712 | 0.9302 | 1.389 | 0.0844 | 0.9608 | 0.0535 | 1.0781 | 0.9822 |
| 50 ℃, 0.8 ms-1, 60% | 0.0638 | 0.9814 | 1.302 | 0.0729 | 0.9664 | 0.0399 | 1.1161 | 0.9858 |
| Operating Mode | Parameter | RMSD |
|---|---|---|
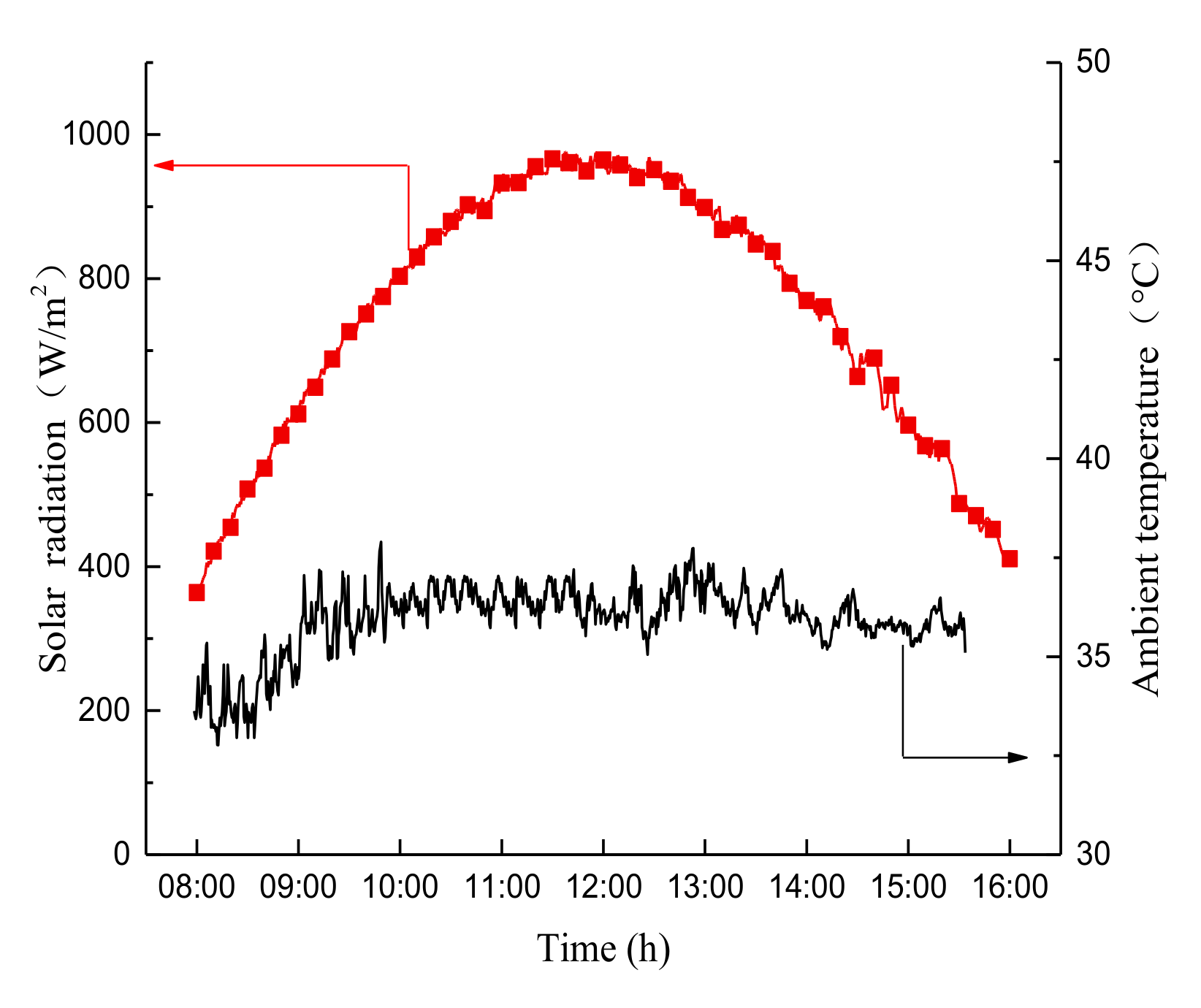
| Stand-alone solar drying (Figure 10) | Outlet temperature | 16.5% |
| Heat gains | 4.6% | |
| Chamber temperature | 2.4% | |
| Moisture ratio | 3.5% | |
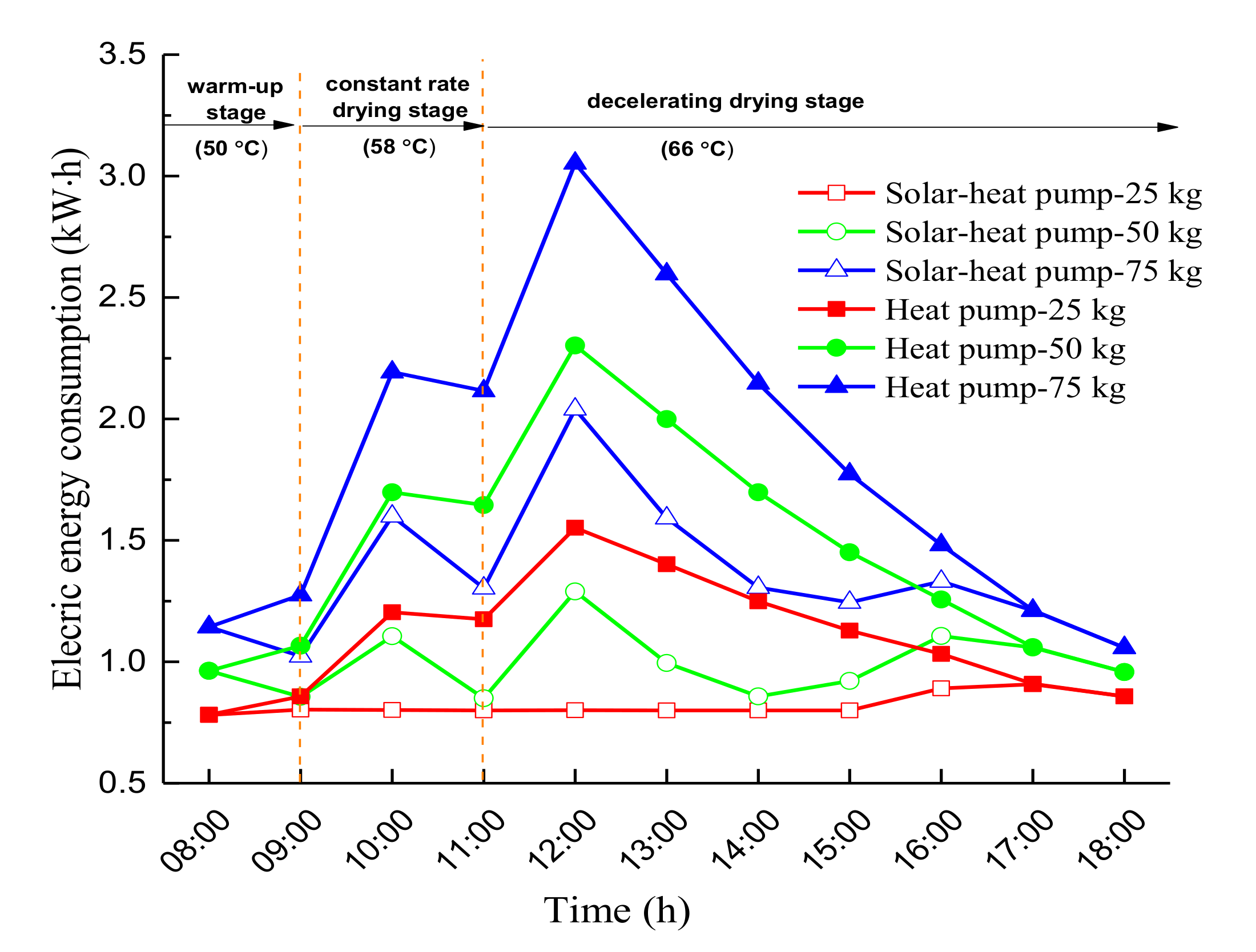
| Stand-alone heat pump drying (Figure 11) | Electric energy consumption | 4.9% |
| Solar assisted heat pump drying (Figure 11) | Electric energy consumption | 6.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Zhang, S.; Chu, W.; He, W.; Yu, C.; Yu, H. Numerical Analysis and Preliminary Experiment of a Solar Assisted Heat Pump Drying System for Chinese Wolfberry. Energies 2020, 13, 4306. https://doi.org/10.3390/en13174306
Hu Z, Zhang S, Chu W, He W, Yu C, Yu H. Numerical Analysis and Preliminary Experiment of a Solar Assisted Heat Pump Drying System for Chinese Wolfberry. Energies. 2020; 13(17):4306. https://doi.org/10.3390/en13174306
Chicago/Turabian StyleHu, Zhongting, Sheng Zhang, Wenfeng Chu, Wei He, Cairui Yu, and Hancheng Yu. 2020. "Numerical Analysis and Preliminary Experiment of a Solar Assisted Heat Pump Drying System for Chinese Wolfberry" Energies 13, no. 17: 4306. https://doi.org/10.3390/en13174306




