Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation
Abstract
:1. Introduction
2. Modeling and Analysis of Dead-Time Effect on Three-Level SHE-PWM Modulation
2.1. Modulation Principles of the Ideal Three-Level SHE-PWM
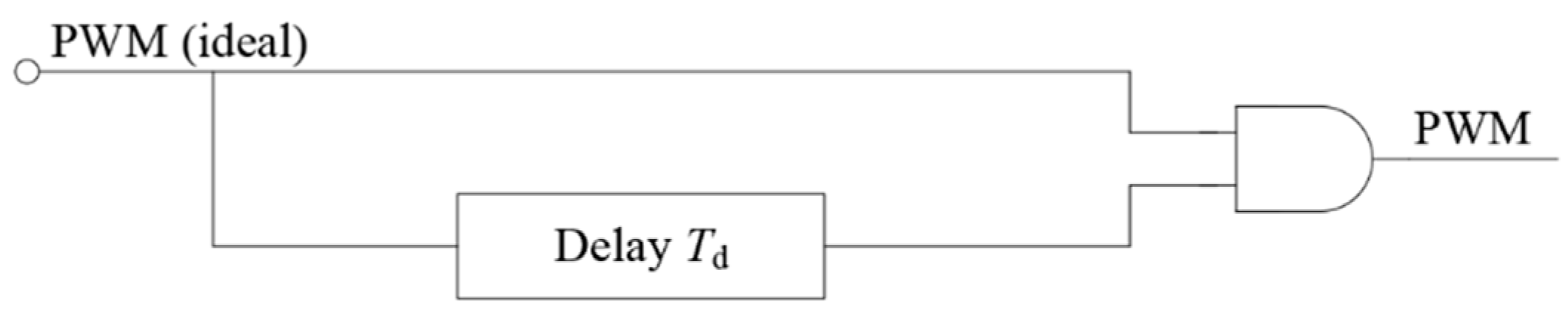
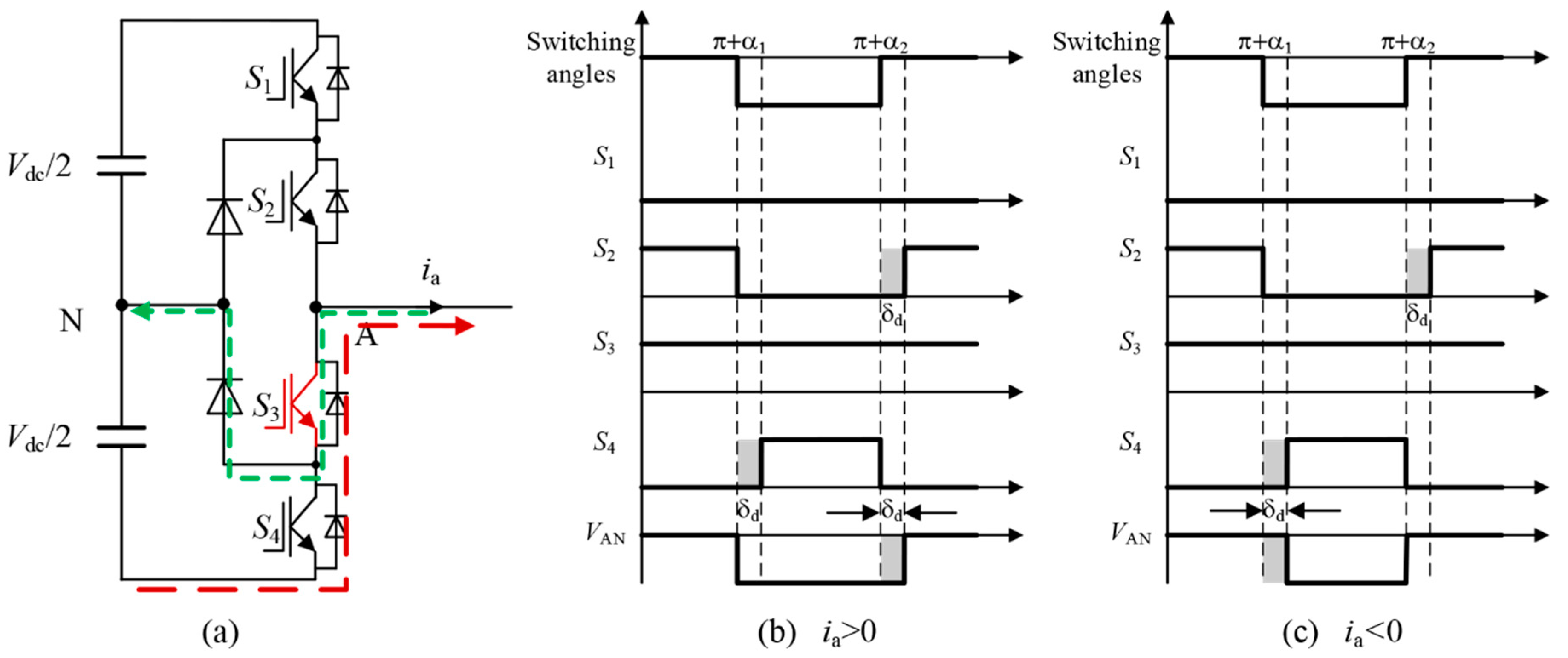
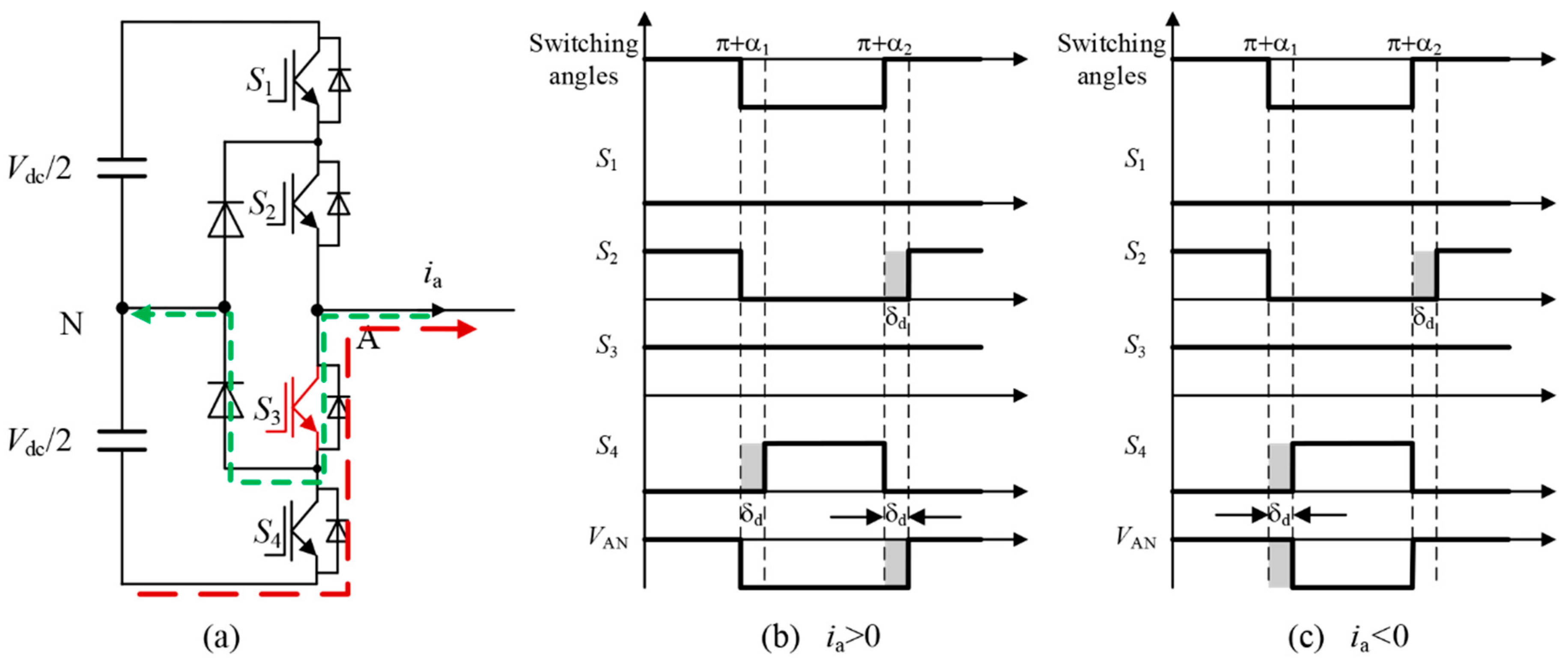
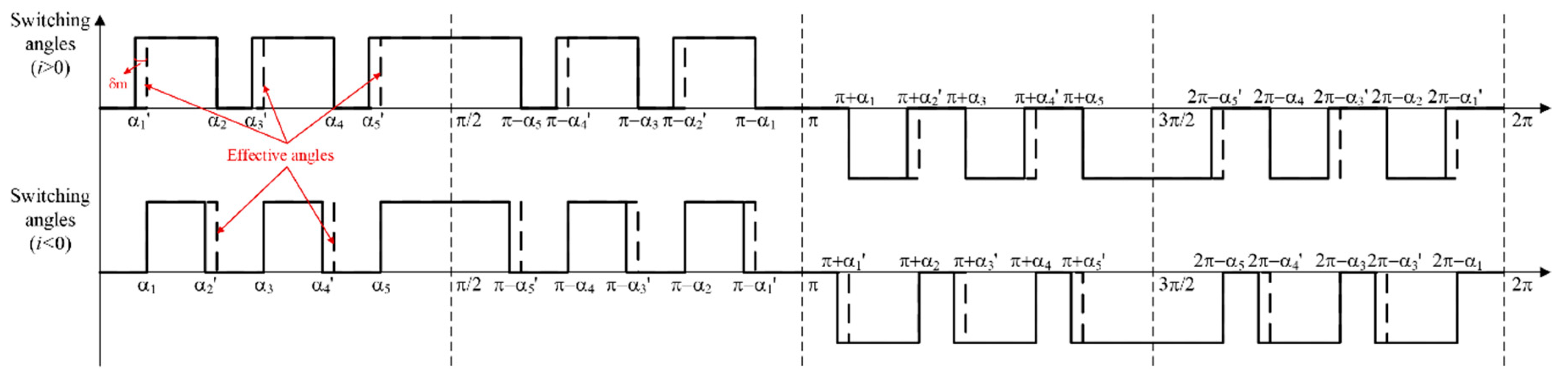
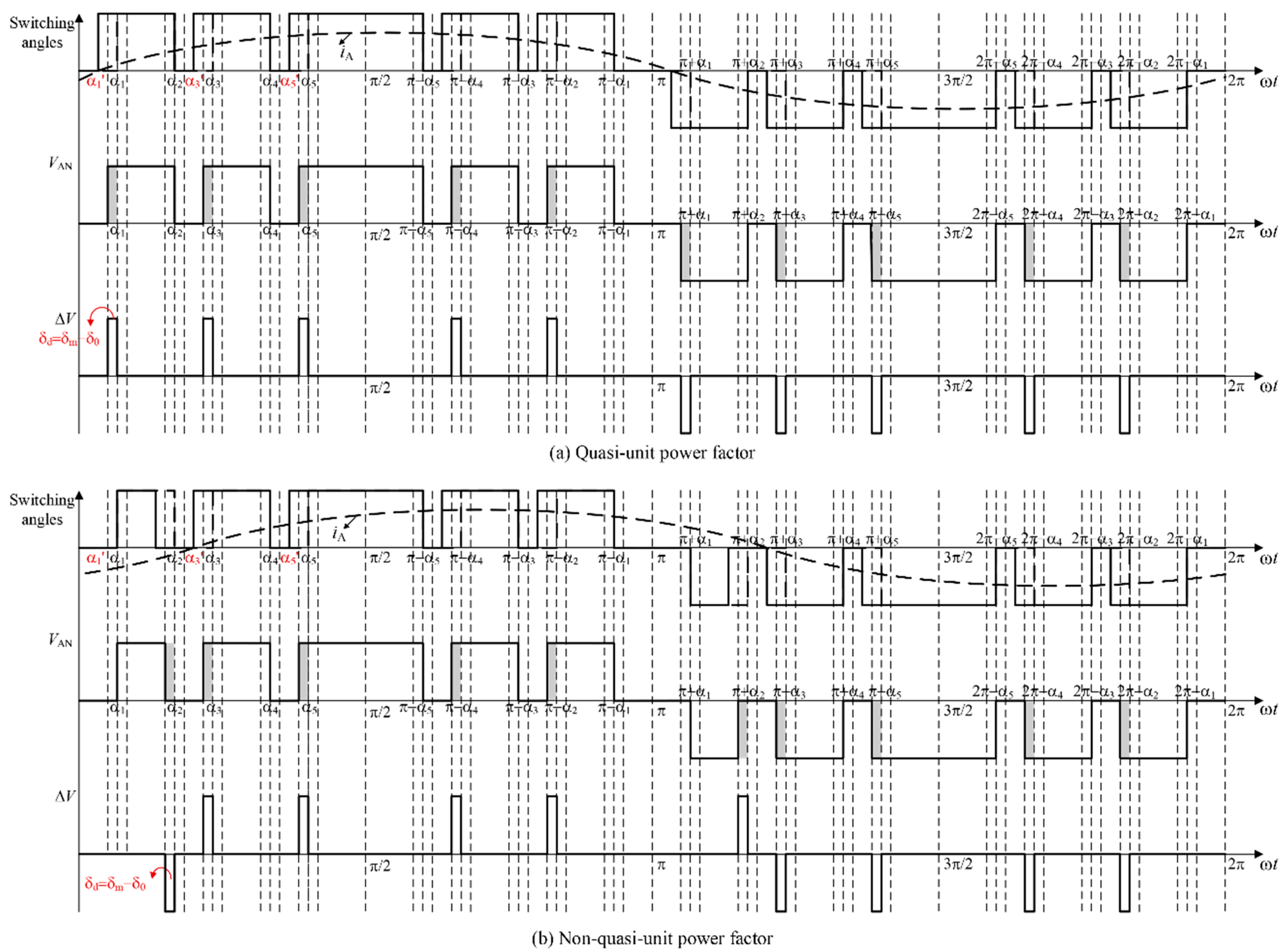
2.2. Circuit State Analysis during Dead Time
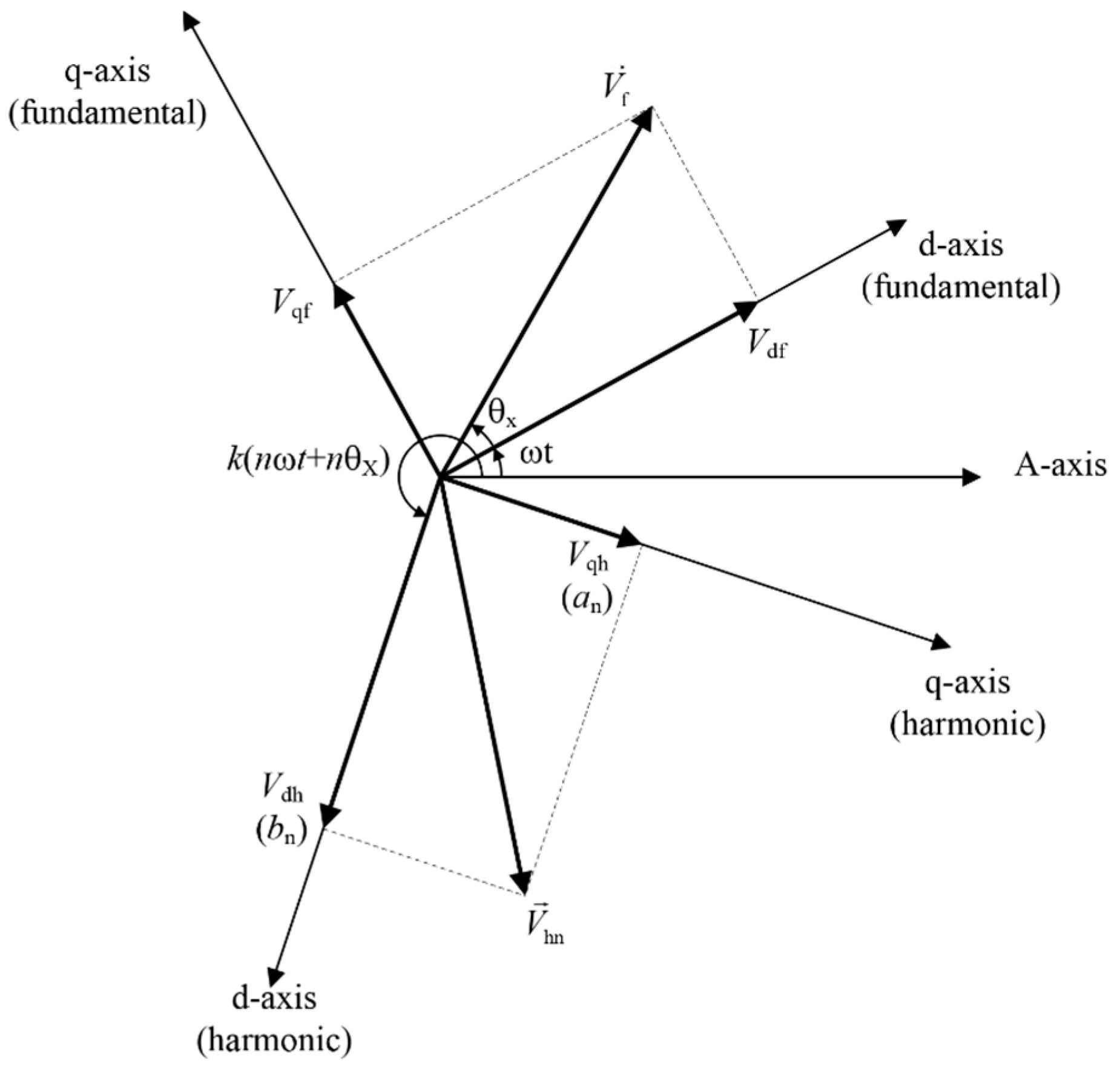
2.3. Modeling of Dead-Time Effect
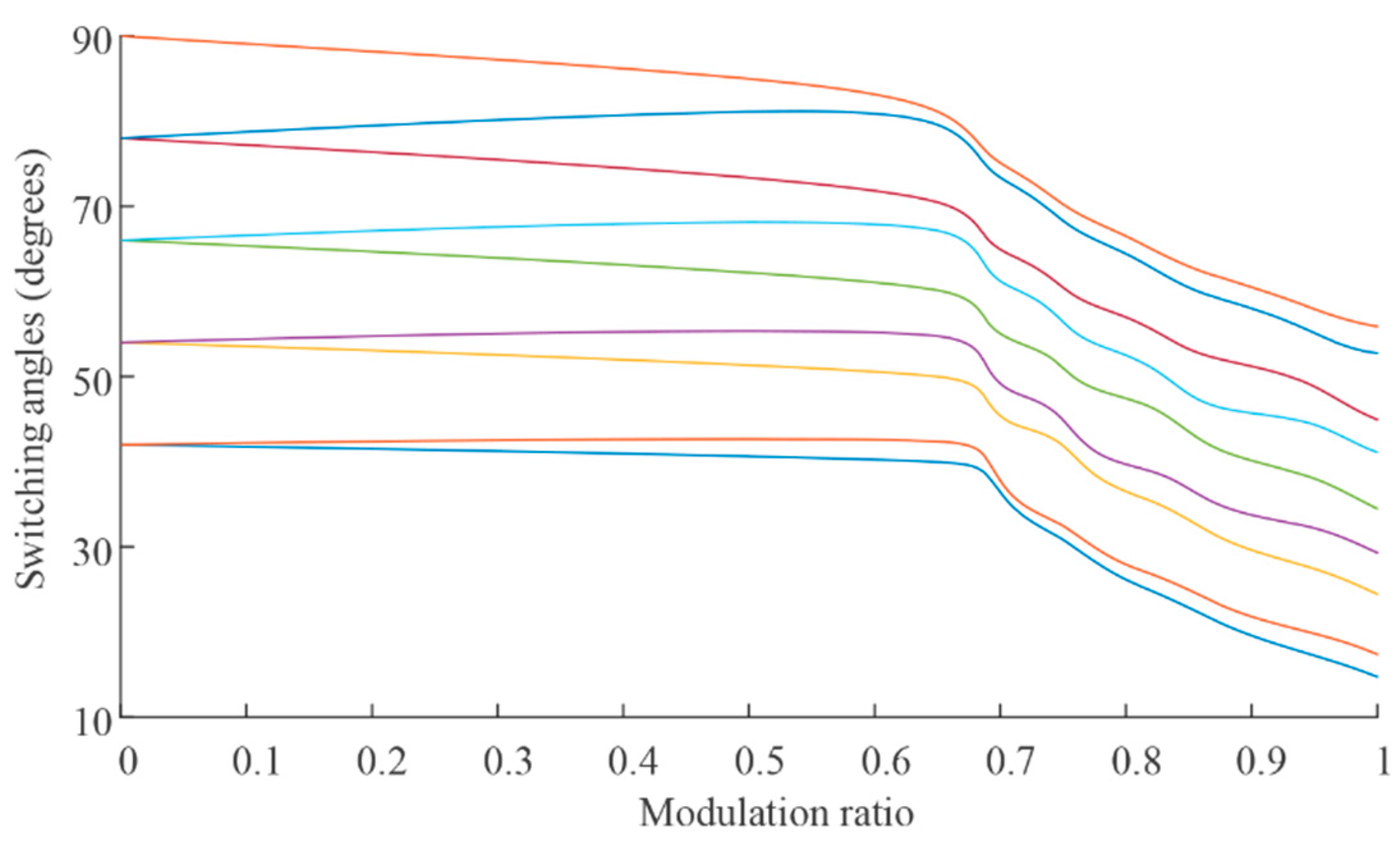
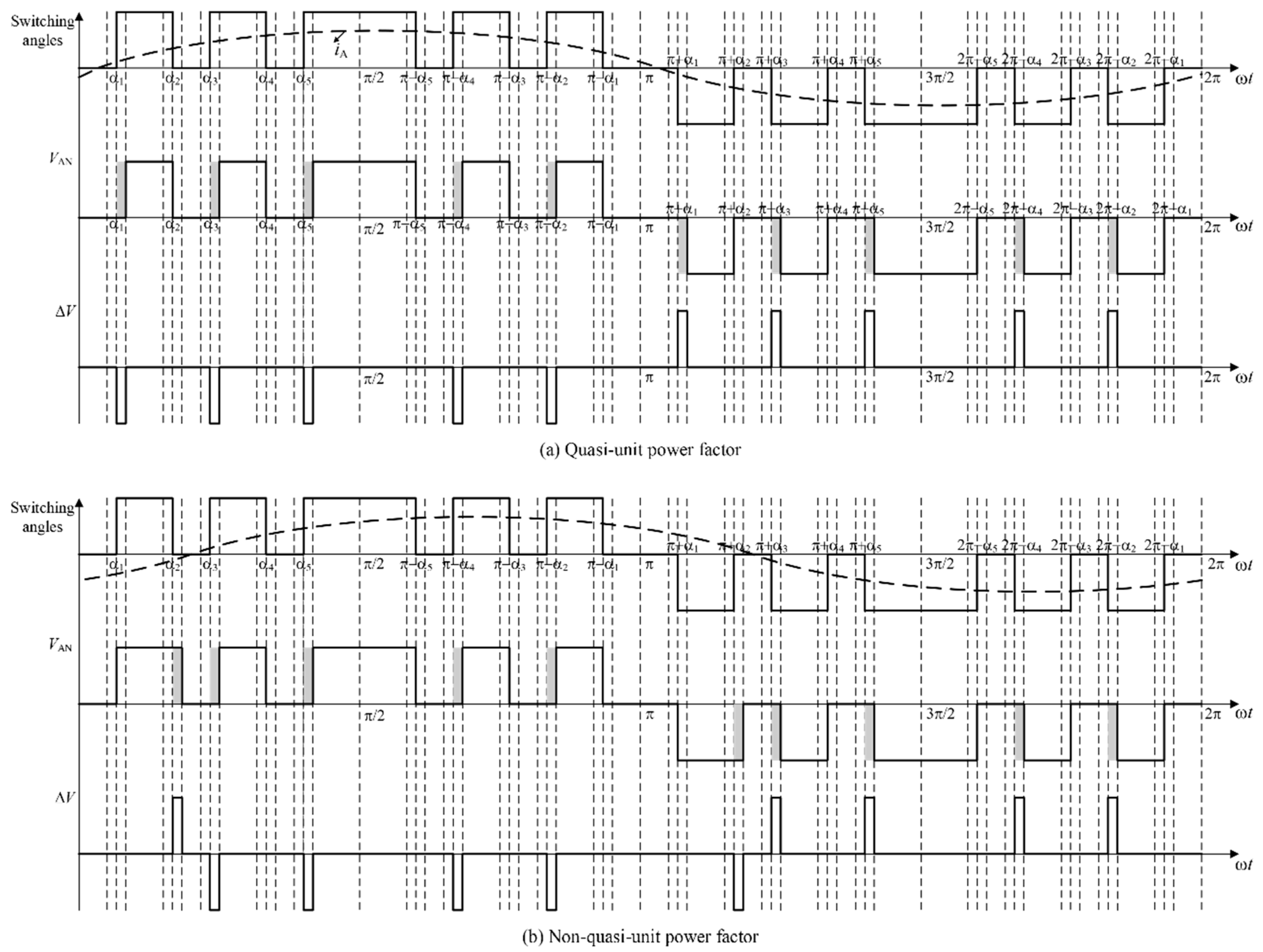
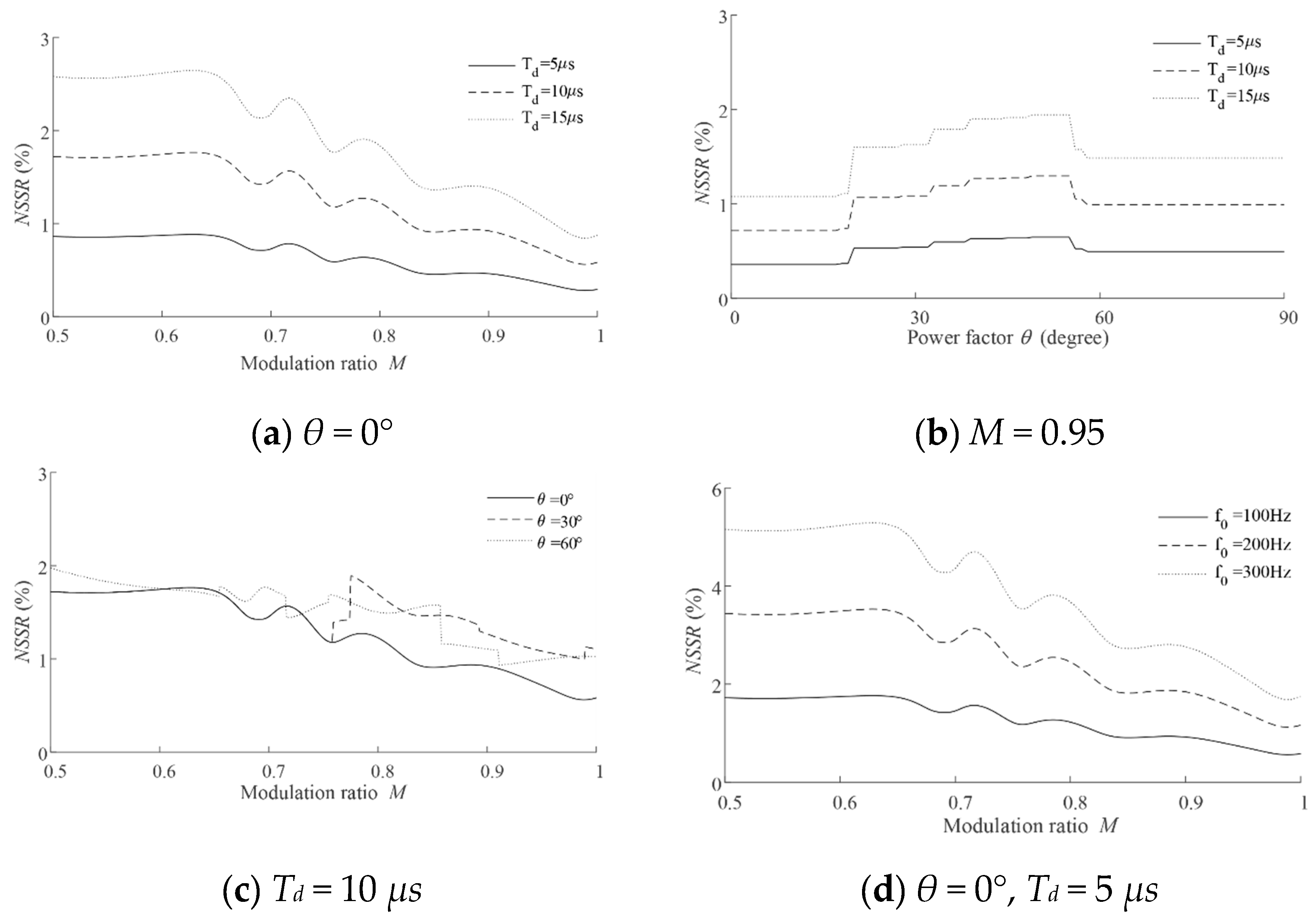
2.4. Dead-Time Effect under Different Operation Conditions
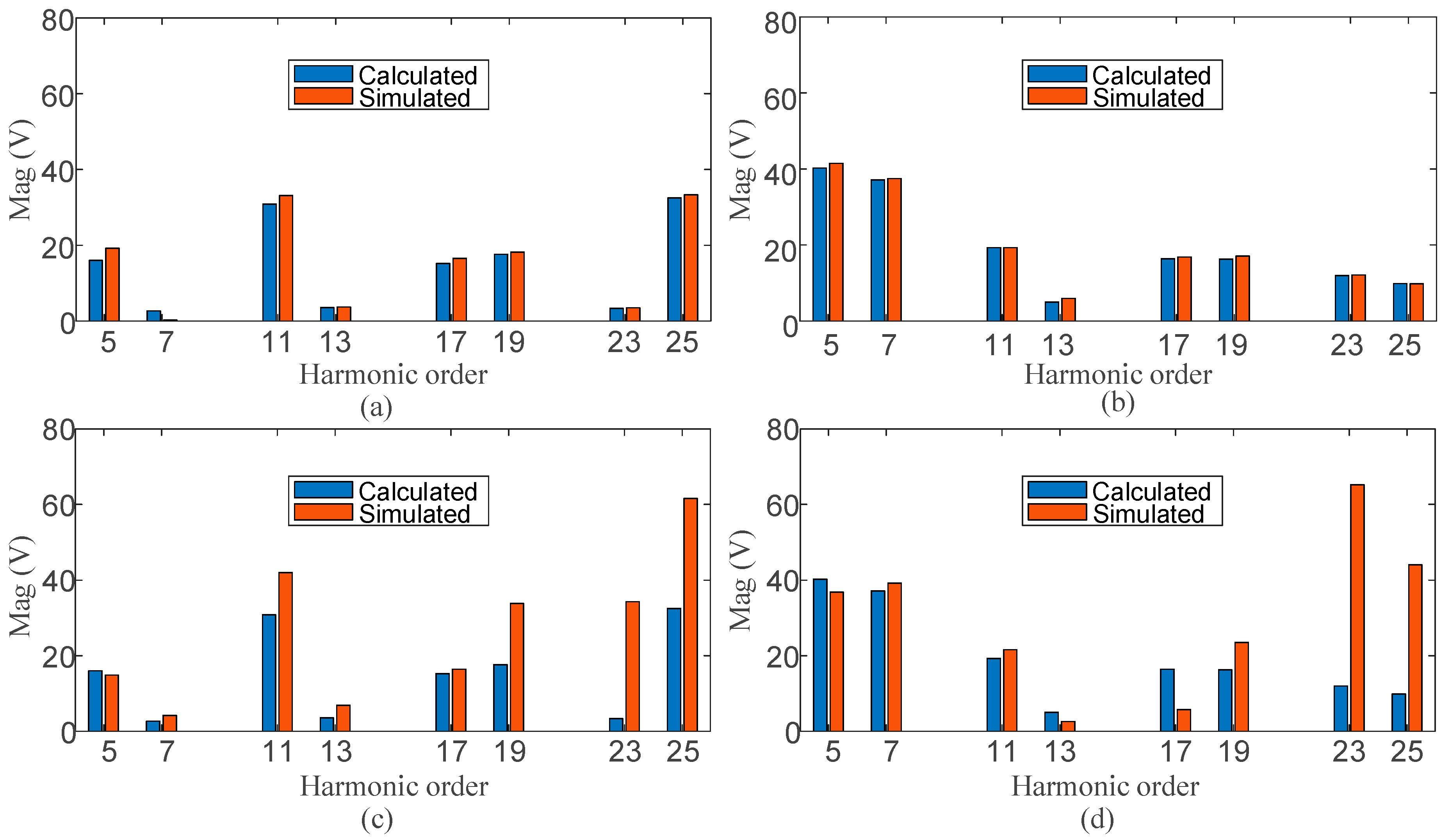
- The longer the dead time, the severer the dead-time effect, at any power factor angle or modulation ratio, as shown in Figure 10a,b.
- Dead-time effect is nonlinearly distributed over the entire modulation ratio range, but decreases overall as the modulation ratio increases as shown in Figure 10a,c.
- The power factor angle has a large impact on dead-time effect. And the dead-time effect is basically lighter at quasi-unit power factor, as shown in Figure 10b,c.
- The dead-time effect remains the same when the power factor angle varies between two adjacent angles, as shown in Figure 10b.
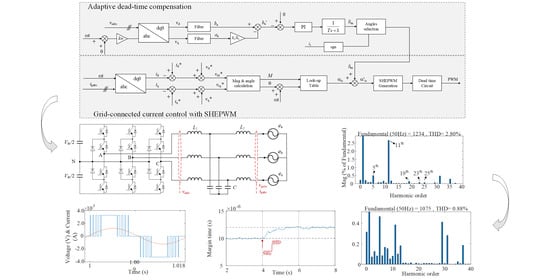
3. Dead-Time Compensation Method
3.1. Open-Loop Dead-Time Compensation Method
3.2. Closed-Loop Dead-Time Compensation Method
3.3. Convergence Analysis on Closed-Loop Control
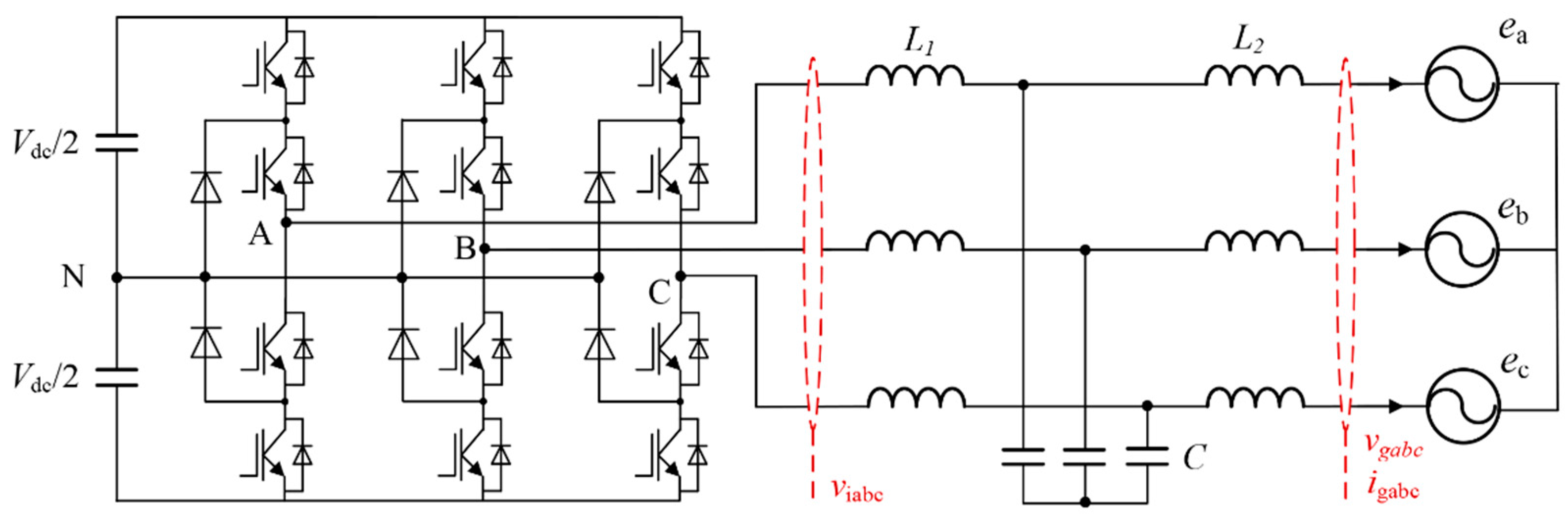
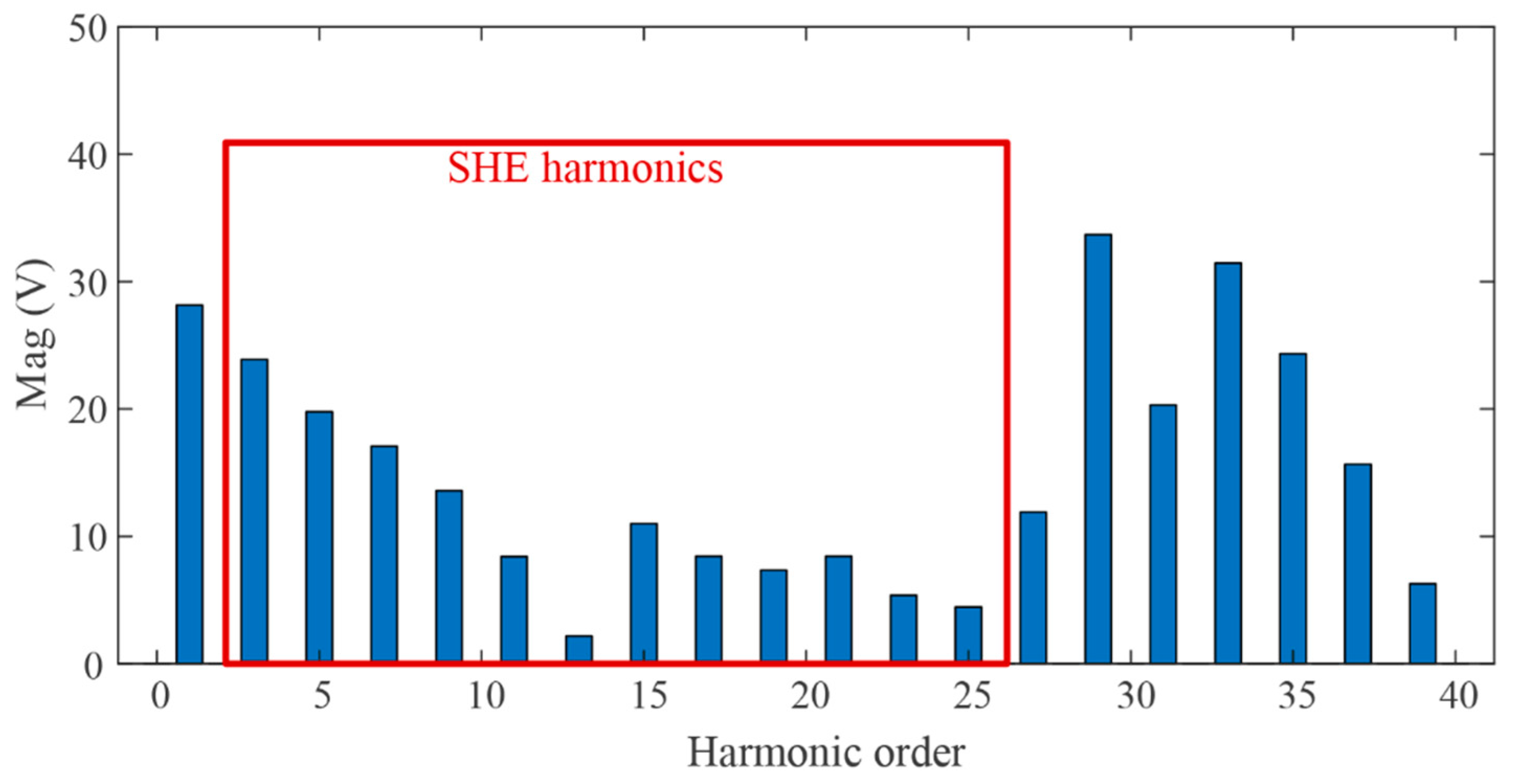
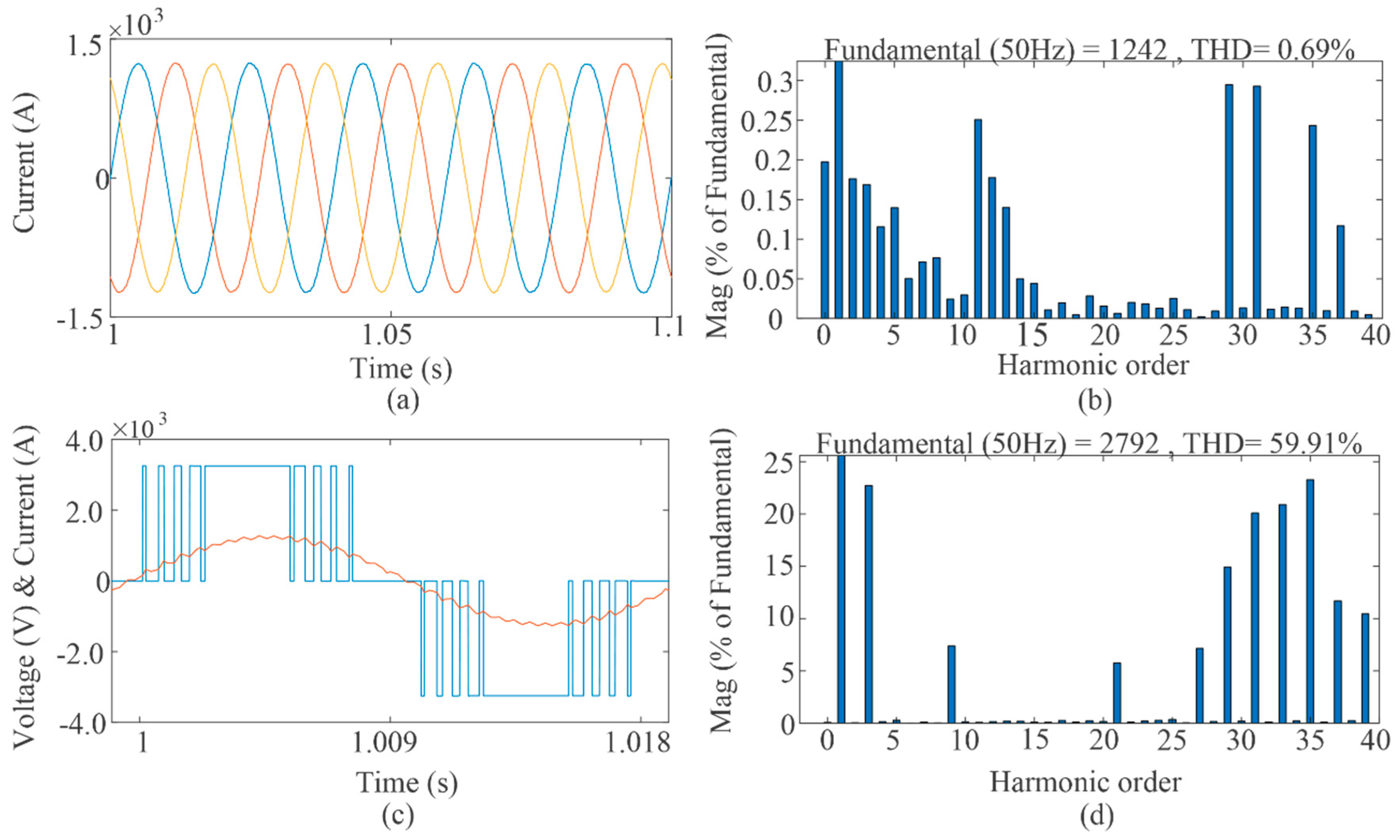
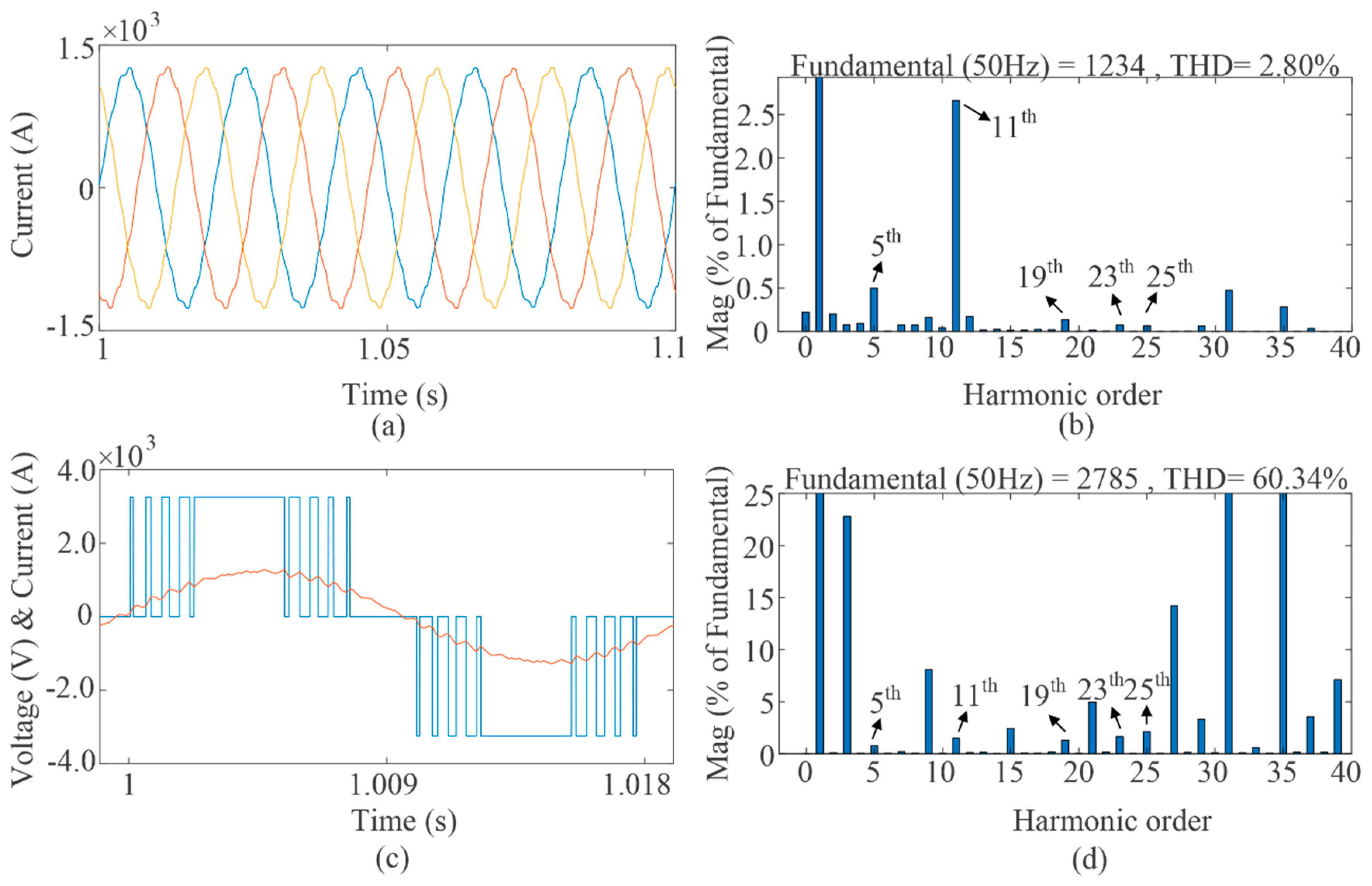
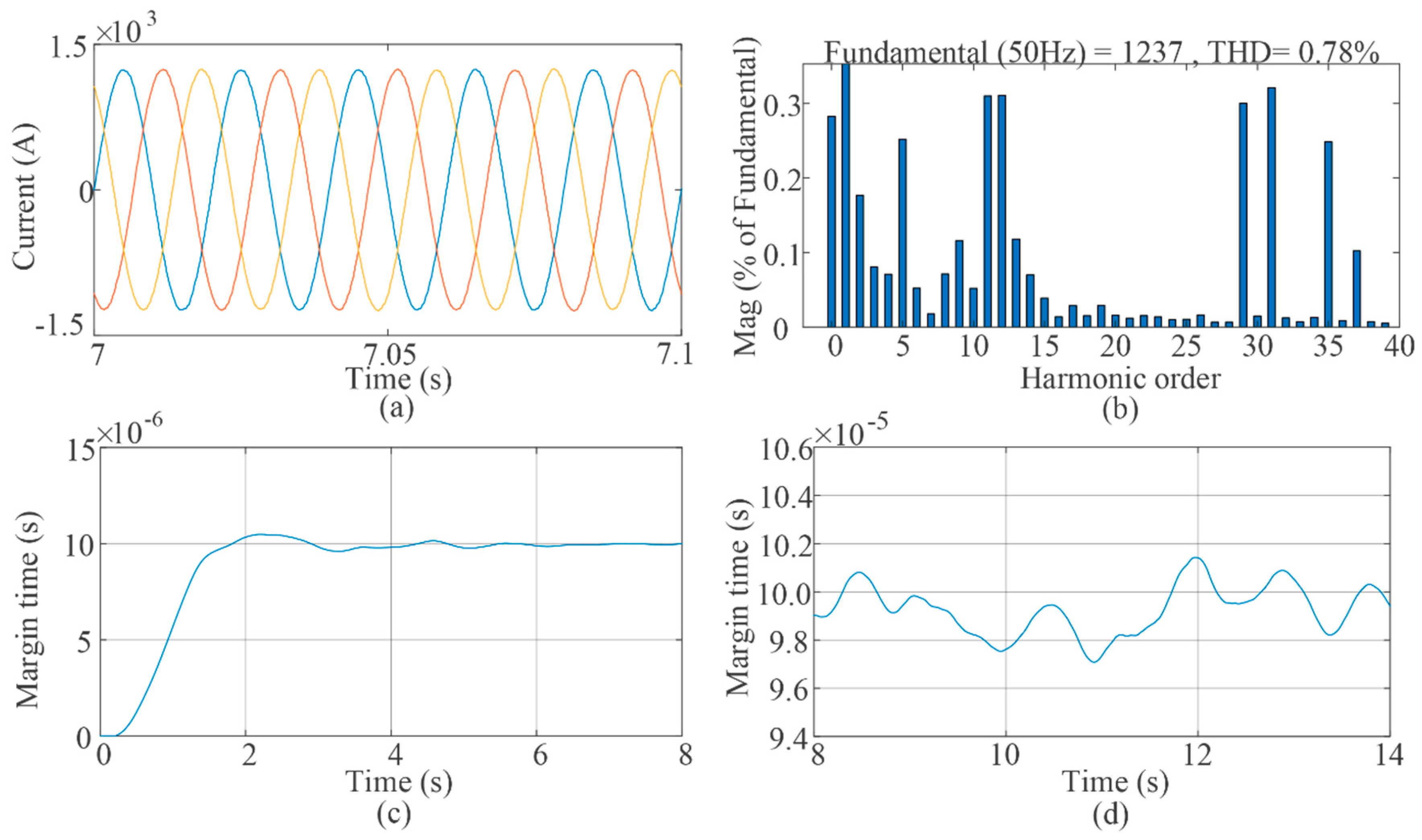
4. Simulation Results
- The resonant frequency should be lower than half of the lowest harmonic frequency, which will provide a sufficient attenuation to filter out the harmonics. For a 9-pulse SHE modulation, the lowest harmonic frequency locates at (3N + 2) f0 = (3 × 9 + 2) × 50 = 1450 Hz. As a result, the filter resonant frequency used in the simulation was designed as 580 Hz.
- The damping ratio needs to be set reasonably to reduce the risk of system oscillations. At the same time, the power loss of the damping resistor should be limited.
- The reactive power capacity of the filter needs to be limited.
- The performance and the size of the filter should be compromised.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Turnbull, F.G. Selected Harmonic Reduction in Static D-C—A-C Inverters. IEEE Trans. Commun. Electron. 1964, 83, 374–378. [Google Scholar] [CrossRef]
- Patel, H.S.; Hoft, R.G. Generalized Techniques of Harmonic Elimination and Voltage Control in Thyristor Inverters: Part I—Harmonic Elimination. IEEE Trans. Ind. Appl. 1973, IA-9, 310–317. [Google Scholar] [CrossRef]
- Patel, H.S.; Hoft, R.G. Generalized Techniques of Harmonic Elimination and Voltage Control in Thyristor Inverters: Part II — Voltage Control Techniques. IEEE Trans. Ind. Appl. 1974, IA-10, 666–673. [Google Scholar] [CrossRef]
- Konstantinou, G.; Agelidis, V.G.; Pou, J. Theoretical Considerations for Single-Phase Interleaved Converters Operated with SHE-PWM. IEEE Trans. Power Electron. 2014, 29, 5124–5128. [Google Scholar] [CrossRef]
- Pérez-Basante, A.; Ceballos, S.; Konstantinou, G.; Pou, J.; Kortabarria, I.; de Alegría, I.M. A Universal Formulation for Multilevel Selective-Harmonic-Eliminated PWM with Half-Wave Symmetry. IEEE Trans. Power Electron. 2019, 34, 943–957. [Google Scholar] [CrossRef]
- Dahidah, M.S.A.; Konstantinou, G.; Agelidis, V.G. A Review of Multilevel Selective Harmonic Elimination PWM: Formulations, Solving Algorithms, Implementation and Applications. IEEE Trans. Power Electron. 2015, 30, 4091–4106. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Zhu, J. A Hybrid PWM Applied to High-Power Three-Level Inverter-Fed Induction-Motor Drives. IEEE Trans. Ind. Electron. 2011, 58, 3409–3420. [Google Scholar] [CrossRef]
- Liu, W.; Song, Q.; Xie, X.; Chen, Y.; Yan, G. 6 kV/1800 kVA Medium Voltage Drive with Three-Level NPC Inverter Using IGCTs. In Proceedings of the Eighteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2003. APEC ’03, Miami Beach, FL, USA, 9–13 February 2003; pp. 223–227. [Google Scholar]
- Wang, Y.; Wen, X.; Zhao, F.; Guo, X. Selective Harmonic Elimination PWM Technology Applied in PMSMs. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 92–97. [Google Scholar]
- Haw, L.K.; Dahidah, M.S.A.; Almurib, H.A.F. SHE–PWM Cascaded Multilevel Inverter with Adjustable DC Voltage Levels Control for STATCOM Applications. IEEE Trans. Power Electron. 2014, 29, 6433–6444. [Google Scholar] [CrossRef]
- He, J.; Li, Q.; Zhang, C.; Han, J.; Wang, C. Quasi-Selective Harmonic Elimination (Q-SHE) Modulation-Based DC Current Balancing Method for Parallel Current Source Converters. IEEE Trans. Power Electron. 2019, 34, 7422–7436. [Google Scholar] [CrossRef]
- Kamani, P.L.; Mulla, M.A. Middle-Level SHE Pulse-Amplitude Modulation for Cascaded Multilevel Inverters. IEEE Trans. Ind. Electron. 2018, 65, 2828–2833. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Vahedi, H.; Portillo, R.; Franquelo, L.G.; Al-Haddad, K. Selective Harmonic Mitigation Based Self-Elimination of Triplen Harmonics for Single-Phase Five-Level Inverters. IEEE Trans. Power Electron. 2019, 34, 86–96. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, S.; Moeini, A. Critical Parameter Design for a Cascaded H-Bridge with Selective Harmonic Elimination/Compensation Based on Harmonic Envelope Analysis for Single-Phase Systems. IEEE Trans. Ind. Electron. 2019, 66, 2914–2925. [Google Scholar] [CrossRef]
- Liu, Y.; Hong, H.; Huang, A.Q. Real-Time Calculation of Switching Angles Minimizing THD for Multilevel Inverters with Step Modulation. IEEE Trans. Ind. Electron. 2009, 56, 285–293. [Google Scholar] [CrossRef]
- Filho, F.; Tolbert, L.M.; Cao, Y.; Ozpineci, B. Real-Time Selective Harmonic Minimization for Multilevel Inverters Connected to Solar Panels Using Artificial Neural Network Angle Generation. IEEE Trans. Ind. Appl. 2011, 47, 2117–2124. [Google Scholar] [CrossRef]
- Wang, J.; Ahmadi, D. A Precise and Practical Harmonic Elimination Method for Multilevel Inverters. IEEE Trans. Ind. Appl. 2010, 46, 857–865. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, D.; Hu, Y.; Chen, G. An improved SHE algorithm and Filter Design Method for High Power Grid-Connected Converter under Unbalanced and Harmonic Distorted Grid. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 594–599. [Google Scholar]
- Ghoreishy, H.; Varjani, A.Y.; Farhangi, S.; Mohamadian, M. Hybrid Cascaded H-bridge Inverter with Even Power Distribution and Improved Total Harmonic Distortion: Analysis and Experimental Validation. IET Power Electron. 2012, 5, 1245–1253. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, R.; Yuan, X.; Ma, W.; He, J. A DSOGI-FLL-Based Dead-Time Elimination PWM for Three-Phase Power Converters. IEEE Trans. Power Electron. 2019, 34, 2805–2818. [Google Scholar] [CrossRef]
- Oliveira, A.C.; Jacobina, C.B.; Lima, A.M.N. Improved Dead-Time Compensation for Sinusoidal PWM Inverters Operating at High Switching Frequencies. IEEE Trans. Ind. Electron. 2007, 54, 2295–2304. [Google Scholar] [CrossRef]
- Townsend, C.D.; Mirzaeva, G.; Goodwin, G.C. Deadtime Compensation for Model Predictive Control of Power Inverters. IEEE Trans. Power Electron. 2017, 32, 7325–7337. [Google Scholar] [CrossRef]
- Mannen, T.; Fujita, H. Dead-Time Compensation Method Based on Current Ripple Estimation. IEEE Trans. Power Electron. 2015, 30, 4016–4024. [Google Scholar] [CrossRef]
- Abronzini, U.; Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Tomasso, G. Steady-State Dead-Time Compensation in VSI. IEEE Trans. Ind. Electron. 2016, 63, 5858–5866. [Google Scholar] [CrossRef]
- Mora, A.; Juliet, J.; Santander, A.; Lezana, P. Dead-Time and Semiconductor Voltage Drop Compensation for Cascaded H-Bridge Converters. IEEE Trans. Ind. Electron. 2016, 63, 7833–7842. [Google Scholar] [CrossRef]
- Li, X.; Akin, B.; Rajashekara, K. Vector-Based Dead-Time Compensation for Three-Level T-Type Converters. IEEE Trans. Ind. Appl. 2016, 52, 1597–1607. [Google Scholar] [CrossRef]
- Lee, D.; Ahn, J. A Simple and Direct Dead-Time Effect Compensation Scheme in PWM-VSI. IEEE Trans. Ind. Appl. 2014, 50, 3017–3025. [Google Scholar] [CrossRef]
- Qiu, T.; Wen, X.; Zhao, F. Adaptive-Linear-Neuron-Based Dead-Time Effects Compensation Scheme for PMSM Drives. IEEE Trans. Power Electron. 2016, 31, 2530–2538. [Google Scholar] [CrossRef]
- Herran, M.A.; Fischer, J.R.; Gonzalez, S.A.; Judewicz, M.G.; Carrica, D.O. Adaptive Dead-Time Compensation for Grid-Connected PWM Inverters of Single-Stage PV Systems. IEEE Trans. Power Electron. 2013, 28, 2816–2825. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Q.; Cai, X. Mixed PWM for Dead-Time Elimination and Compensation in a Grid-Tied Inverter. IEEE Trans. Ind. Electron. 2011, 58, 4797–4803. [Google Scholar] [CrossRef]
- Kim, S.; Lee, W.; Rho, M.; Park, S. Effective Dead-Time Compensation Using a Simple Vectorial Disturbance Estimator in PMSM Drives. IEEE Trans. Ind. Electron. 2010, 57, 1609–1614. [Google Scholar] [CrossRef]
- Blasko, V. A Novel Method for Selective Harmonic Elimination in Power Electronic Equipment. IEEE Trans. Power Electron. 2007, 22, 223–228. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Ge, Q. Dead-Time Compensation of 3-level NPC Inverter for Medium Voltage IGCT Drive System. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 3524–3528. [Google Scholar]
- Tang, F.; Liang, J.; Jiang, J.; Xin, Z.; Huang, S.; Loh, P.C. Review and Re-Evaluation of Modulation Techniques for Neutral-Point-Clamped Inverters with High-Order Filters. IET Power Electron. 2019, 12, 1307–1320. [Google Scholar] [CrossRef]
- Giri, S.K.; Banerjee, S.; Chakraborty, C. An Improved Modulation Strategy for Fast Capacitor Voltage Balancing of Three-Level NPC Inverters. IEEE Trans. Ind. Electron. 2019, 66, 7498–7509. [Google Scholar] [CrossRef]
- Mukherjee, S.; Kumar Giri, S.; Kundu, S.; Banerjee, S. A Generalized Discontinuous PWM Scheme for Three-Level NPC Traction Inverter with Minimum Switching Loss for Electric Vehicles. IEEE Trans. Ind. Appl. 2019, 55, 516–528. [Google Scholar] [CrossRef]


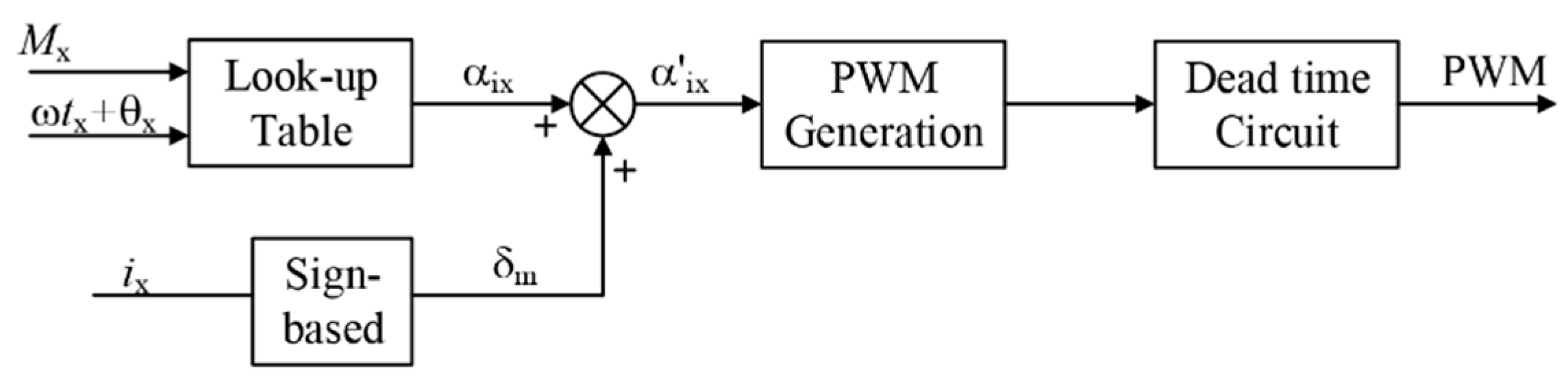




| Phase Range | Current Polarity | Adjustment Implementation |
|---|---|---|
| 0 ~ π | ||
| π/2 ~ π | ||
| π ~ 3π/2 | ||
| 3π/2 ~ 2 π | ||
| Rated power | kW |
| rated voltage | kV |
| Switching angle number | = 9 |
| harmonic feedback | = 11 |
| Dead time size | μs |
| LCL filter | mH, mH, |
| mF, | |
| Sample time | Simulation step = μs, |
| Control step = μs, | |
| Modulation step = μs |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Chen, D.; Chen, G. Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation. Energies 2020, 13, 4348. https://doi.org/10.3390/en13174348
Cheng J, Chen D, Chen G. Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation. Energies. 2020; 13(17):4348. https://doi.org/10.3390/en13174348
Chicago/Turabian StyleCheng, Jingling, Dongdong Chen, and Guozhu Chen. 2020. "Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation" Energies 13, no. 17: 4348. https://doi.org/10.3390/en13174348
APA StyleCheng, J., Chen, D., & Chen, G. (2020). Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation. Energies, 13(17), 4348. https://doi.org/10.3390/en13174348