An Integration Optimization Strategy of Line Voltage Cascaded Quasi-Z-Source Inverter Parameters Based on GRA-FA
Abstract
:1. Introduction
- (1)
- In the LVC-qZSI system, there are complex coupling relations between DC voltage and current vectors, AC voltage and current vectors, total output voltage and current vectors after cascading, etc. Therefore, it is not feasible to establish a mathematical model to determine the reasonable range of LVC-qZSI parameters;
- (2)
- LVC-qZSI is a complex dynamic system composed of a quasi-Z network, three three-phase inverter bridges, and a LVC network. There are many circuit parameters in the system, and most of the parameter design methods rely on repeated tests. Under different experimental conditions, it is time-consuming and laborious to determine multiple LVC-qZSI parameters and circuit performance evaluation indexes;
- (3)
- The influence of circuit parameters on LVC-qZSI performance indexes is nonlinear and antagonistic. For example, increasing the quasi-Z network inductance and capacitance can effectively reduce the double frequency ripple, but it will increase the power loss. Therefore, there are contradictions in the selection of parameters. The trial and error method based on previous experience is not easy to find the optimal parameters.
- (1)
- In this paper, a single module model of qZSI and a cascaded network coupling model of LVC-qZSI are established. According to the analysis of LVC-qZSI, three optimization objective functions including double frequency voltage ripples ratios and power loss ratio are listed;
- (2)
- In GRA, six parameters in LVC-qZSI that affect the optimization objective functions are summarized and sorted in descending order of correlation degrees, then three main parameters are selected to construct the FA solution vector based on the introduction of preference coefficient;
- (3)
- The paper adopts the information entropy weighting method to establish a multi-objective optimization model of LVC-qZSI parameters, and uses penalty factors to modify the model;
- (4)
- The paper establishes GRA-FA to simplify the multi-objective optimization model, and proposes an integration optimization strategy of LVC-qZSI parameters based on GRA-FA;
- (5)
- The effectiveness of the proposed integration optimization strategy is verified by simulation experiments. The experimental results show that the double frequency voltage ripples ratios are reduced by 87.48% and 87.57%, and the power loss ratio is reduced by 82.78%.
2. Establishment and Analysis of LVC-qZSI Model
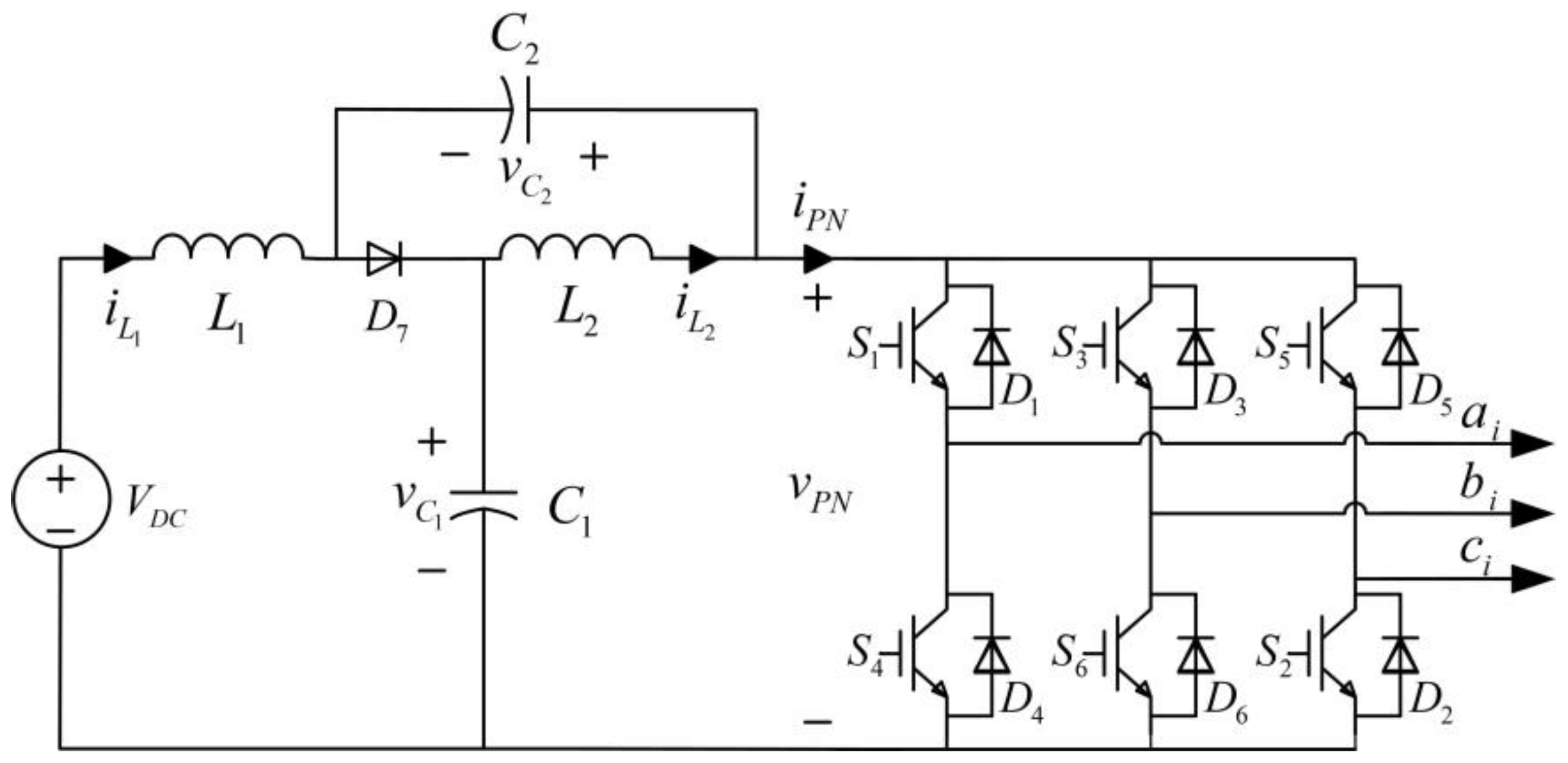
2.1. LVC-qZSI
2.2. Performance Index
2.2.1. Double Frequency Voltage Ripple Ratio
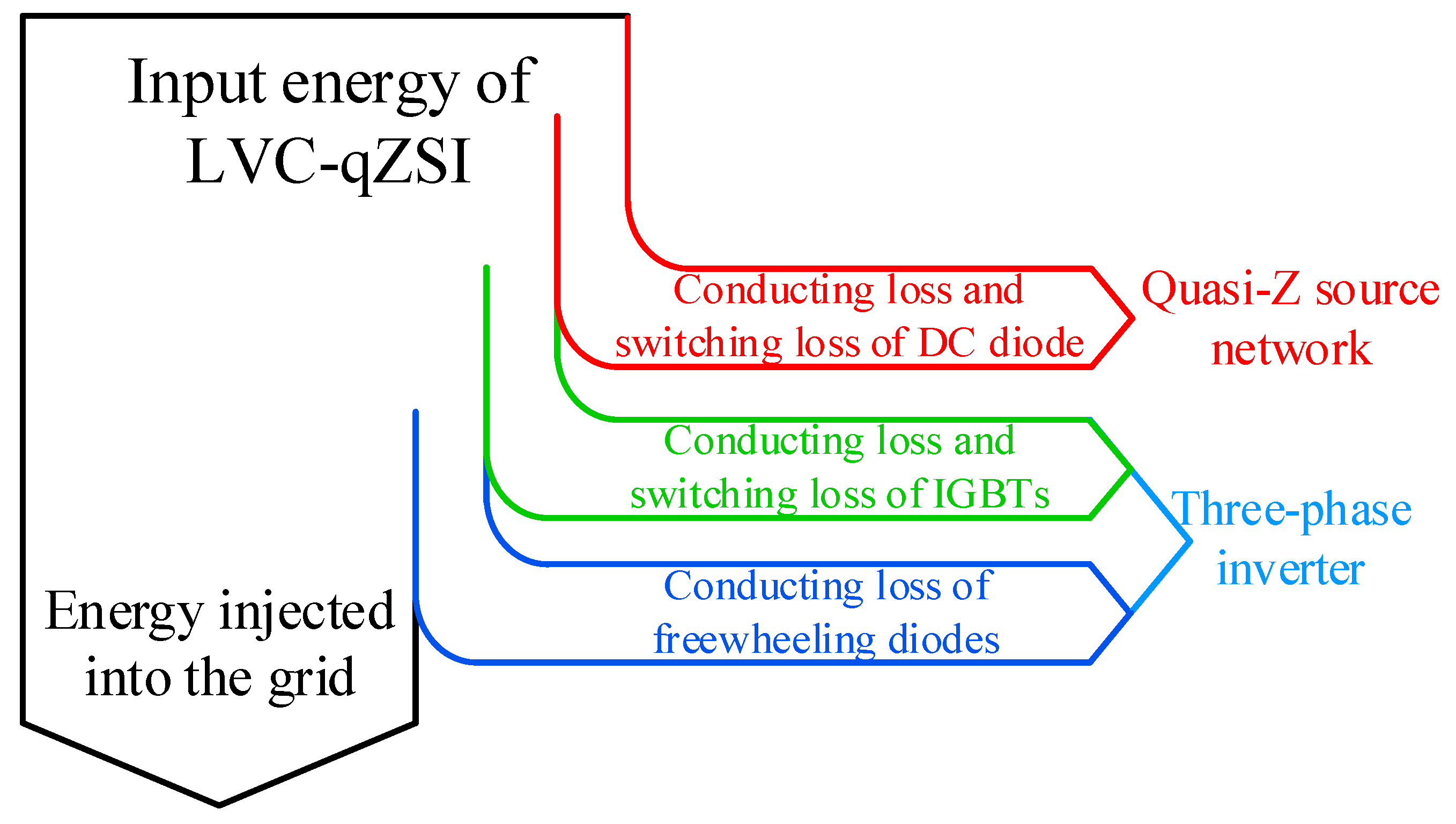
2.2.2. Power Loss Ratio
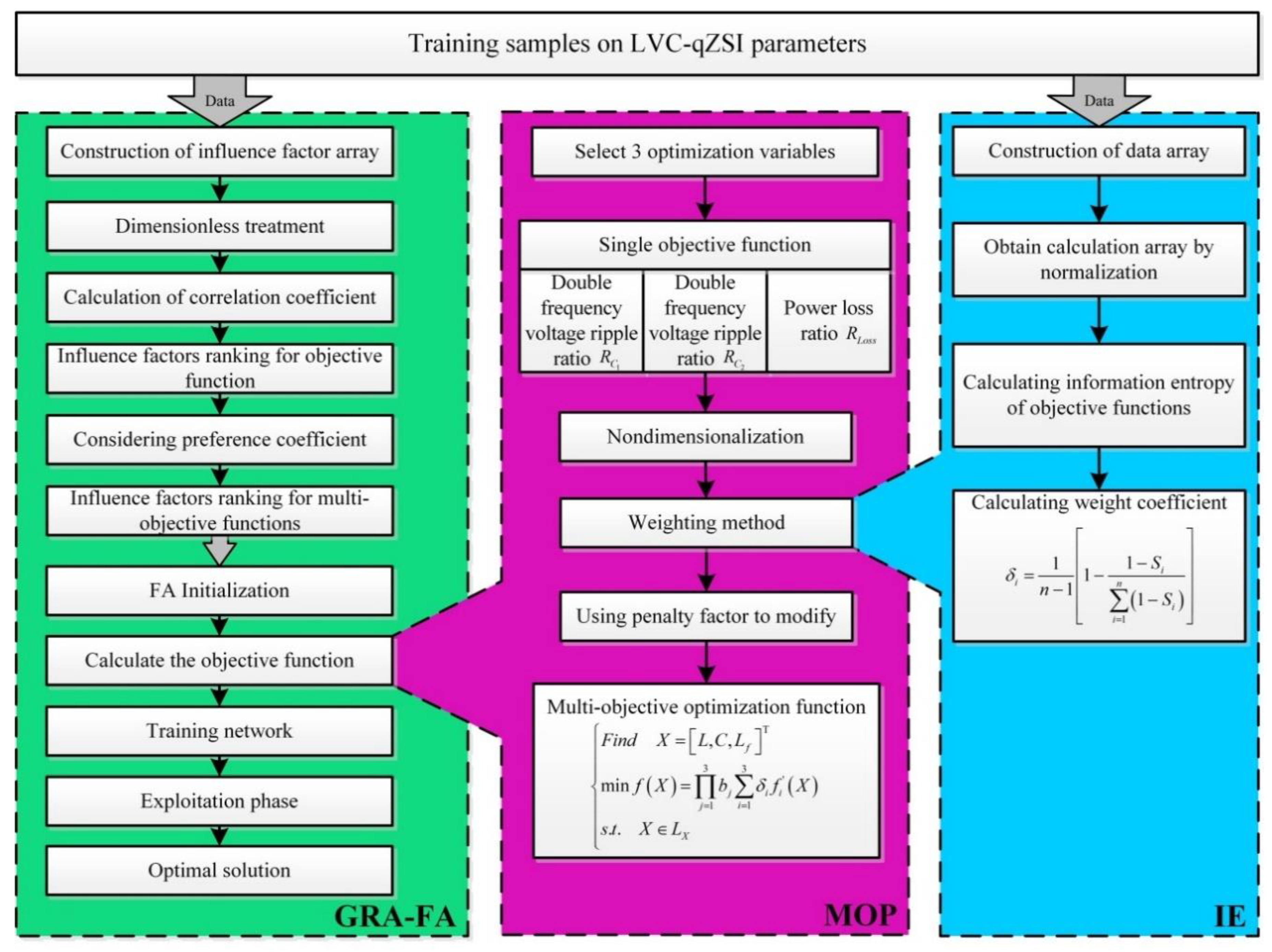
3. GRA of LVC-qZSI Parameters
3.1. Description
3.2. Sorting of LVC-qZSI Parameters Based on GRA
- (1)
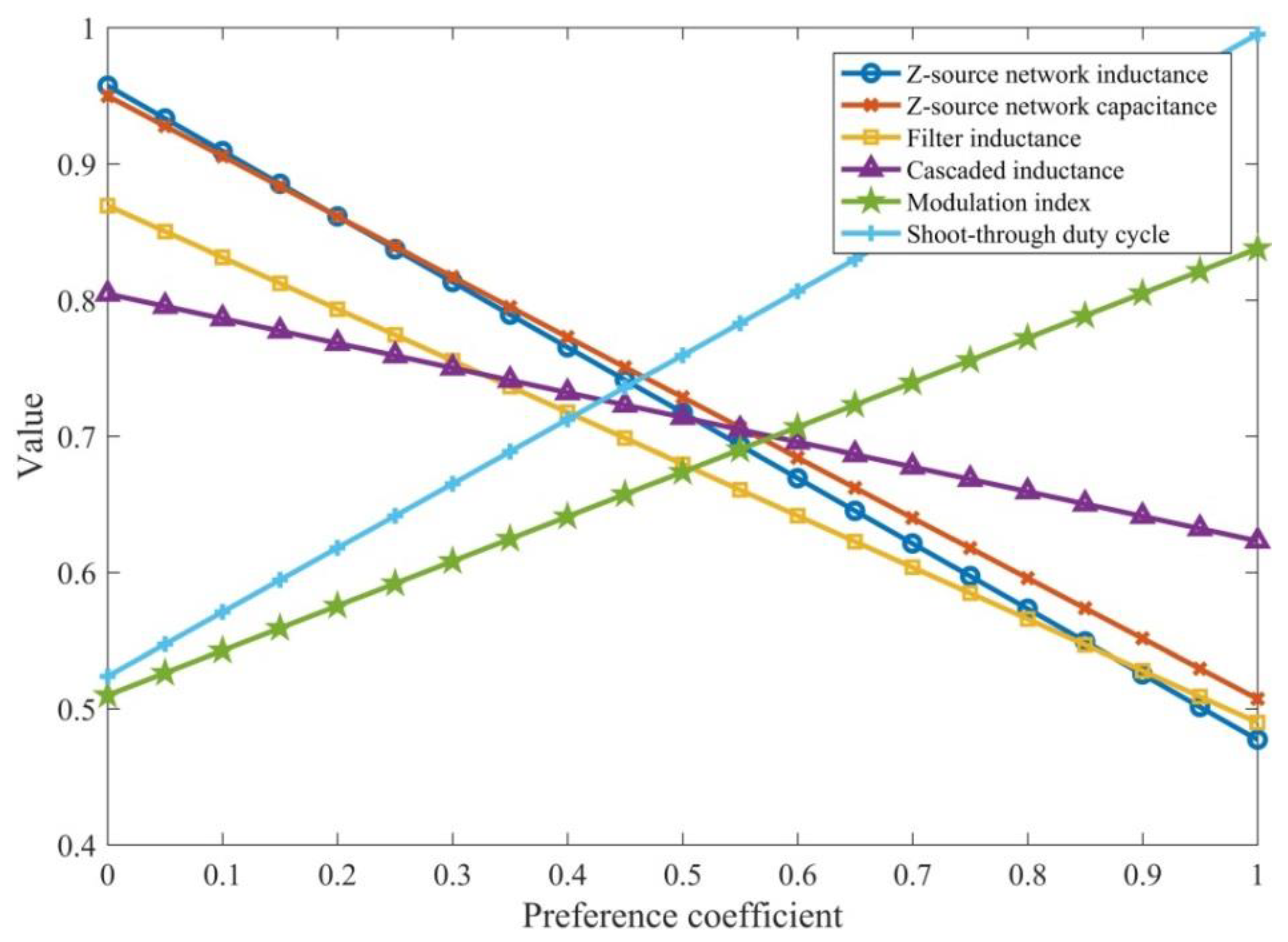
- For the value range of preference coefficient , with the increase of , the main influence factors are constantly changing. When , Z-source network inductance, Z-source network capacitance, and filter inductance have the greatest influence on objective functions; when , Z-source network inductance, Z-source network capacitance, and cascaded inductance are selected as main influence factors; when , the results of influence factors are complex and confusing, which need to be analyzed according to the specific situation; when , shoot-through duty cycle, modulation index, and cascaded inductance have the greatest influence;
- (2)
- For the trend, the correlation degrees of Z-source network inductance, Z-source network capacitance, filter inductance, and cascaded inductance are negatively correlated with preference coefficient ; the correlation degrees of modulation index and shoot-through duty cycle are positively correlated with preference coefficient ;
- (3)
- When the power loss is not considered, the influence of circuit device parameters (including Z-source network inductance, Z-source network capacitance, filter inductance, and cascaded inductance) on the comprehensive correlation degrees is obvious; when the power loss is considered, the influence of circuit control parameters (including shoot-through duty cycle and modulation index) is obvious.
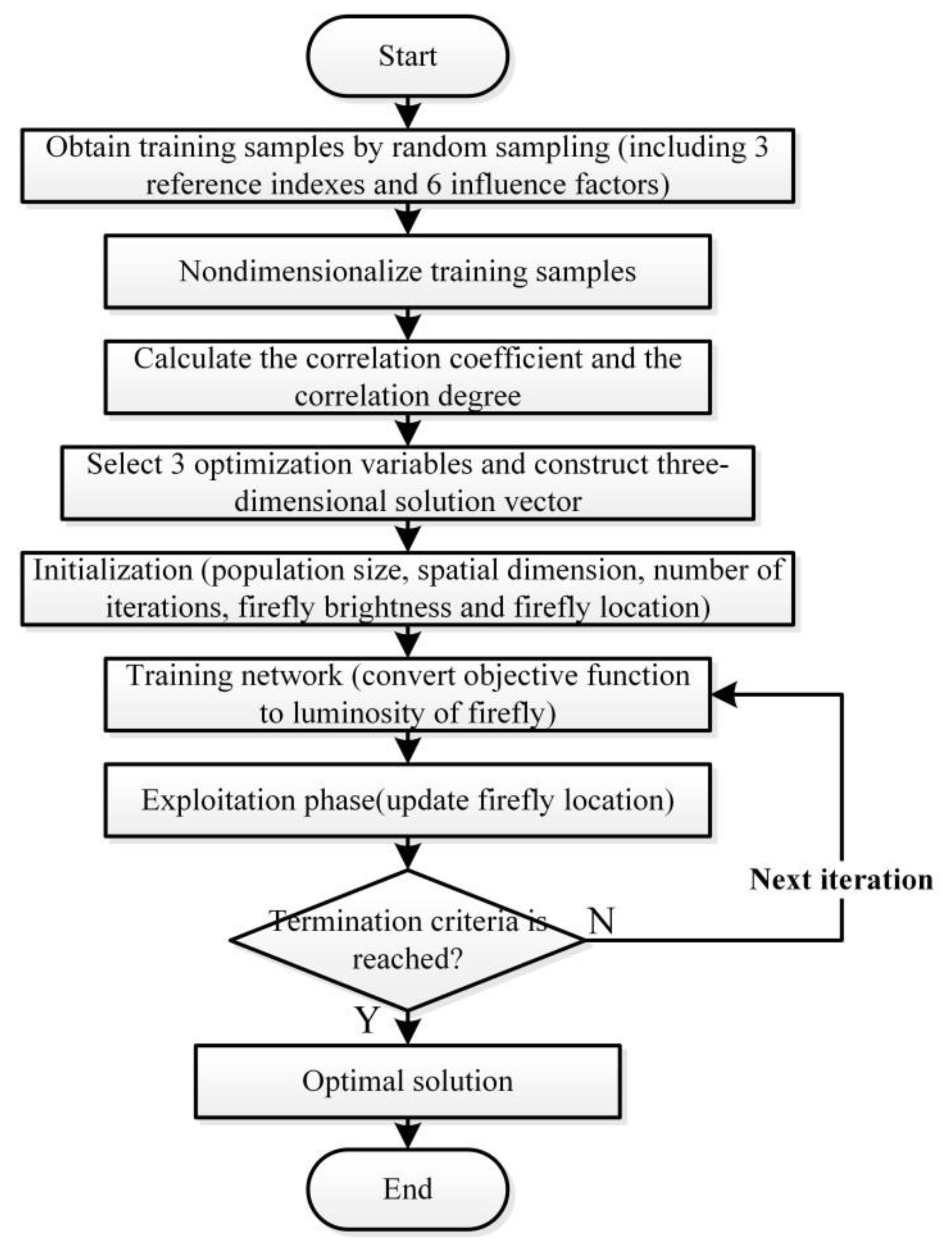
4. Integration Optimization Strategy of LVC-qZSI Parameters Based on GRA-FA
4.1. GRA-FA
- Set the sample size to 30 and randomly adjust the values of six circuit parameters in LVC-qZSI to obtain training samples (including three reference indexes and six influence factors);
- Nondimensionalize the training samples;
- Calculate the correlation degrees between three reference indexes and six influence factors;
- By introducing the preference coefficient, three main influence factors are selected as optimization variables, and the three-dimensional solution vector is constructed;
- Set the population size, the total number of iterations, and the spatial dimension, then randomly initialize the individual position and the fluorescence brightness of the fireflies;
- Train the network and transform the objective functions into the fluorescence brightness of fireflies;
- Exploitation phase (update fireflies locations);
- Judge whether the number of iterations reaches the upper limit. If the upper limit is reached, the optimal solution will be output; otherwise, return to step f for the next iteration.
4.2. Multi-Objective Optimization
4.2.1. Optimization Variables
4.2.2. Objective Functions
4.2.3. Constraints
5. Experiment and Analysis
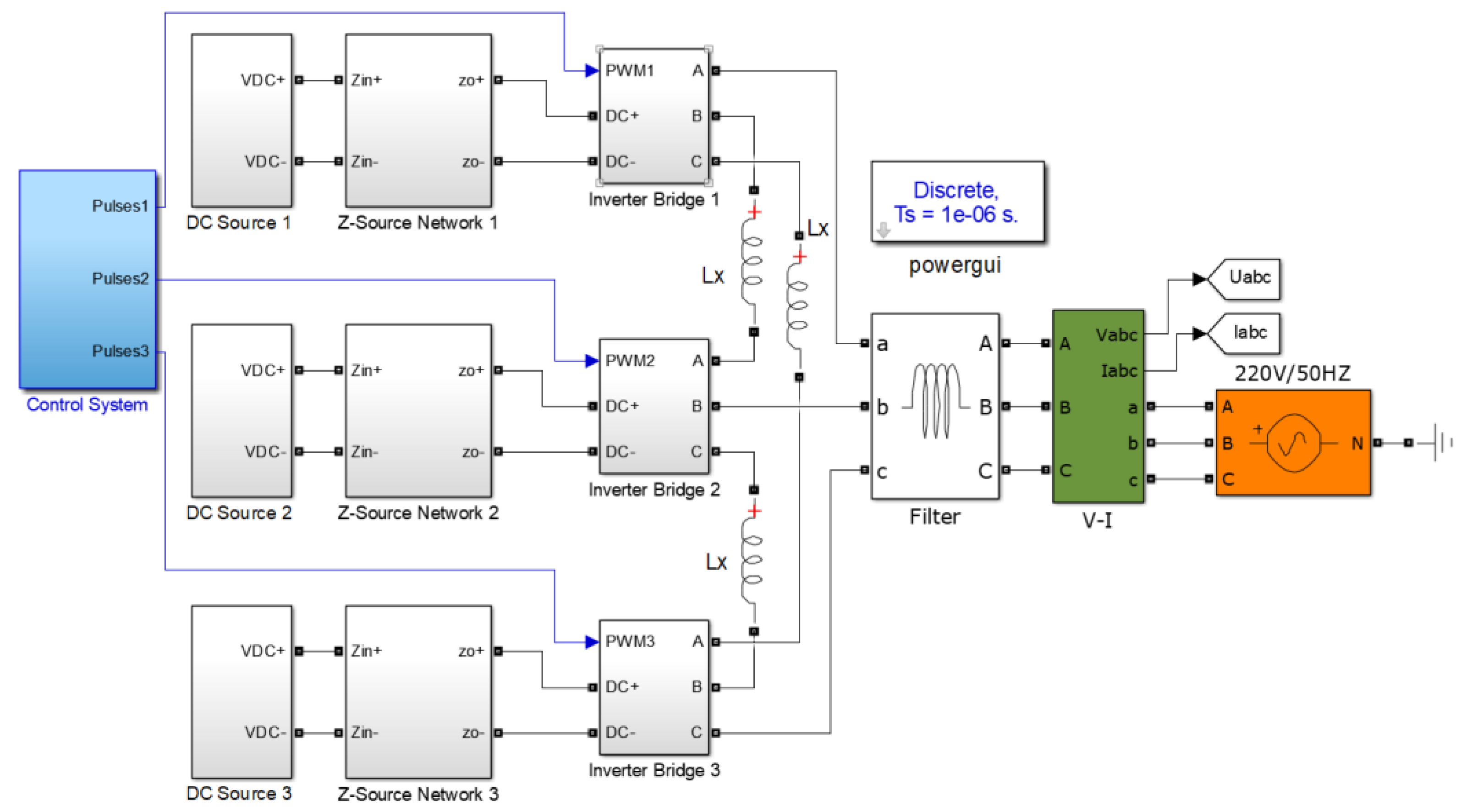
5.1. Experimental Setup
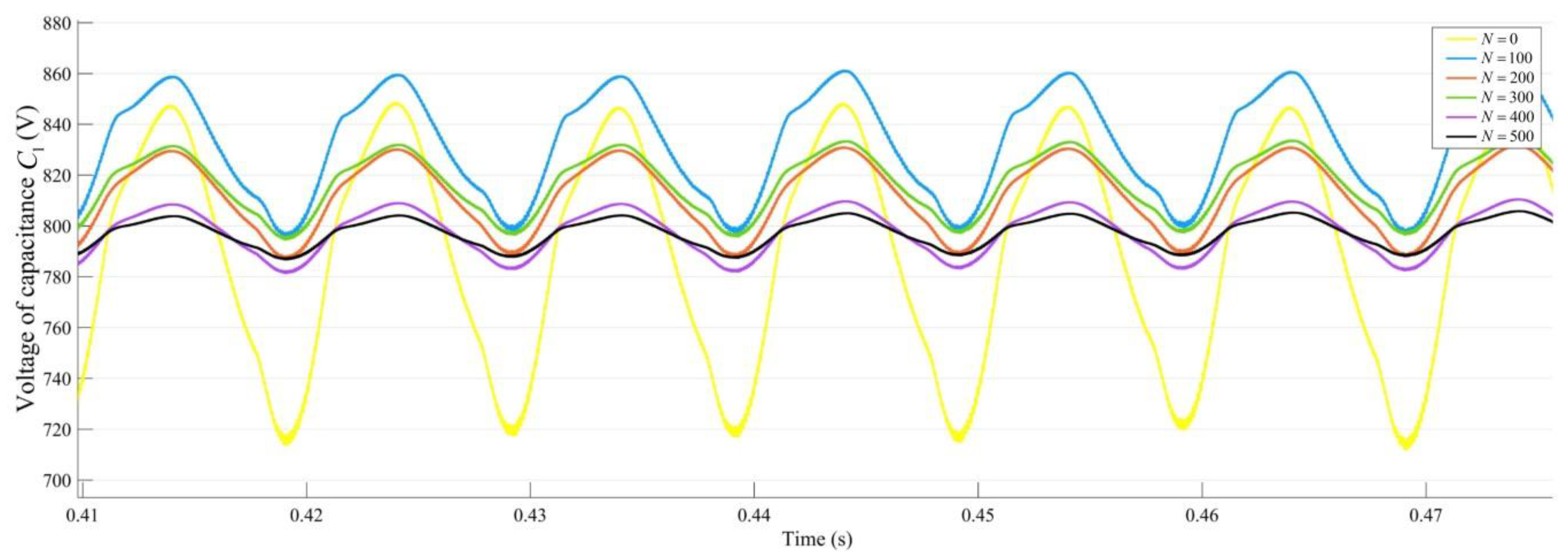
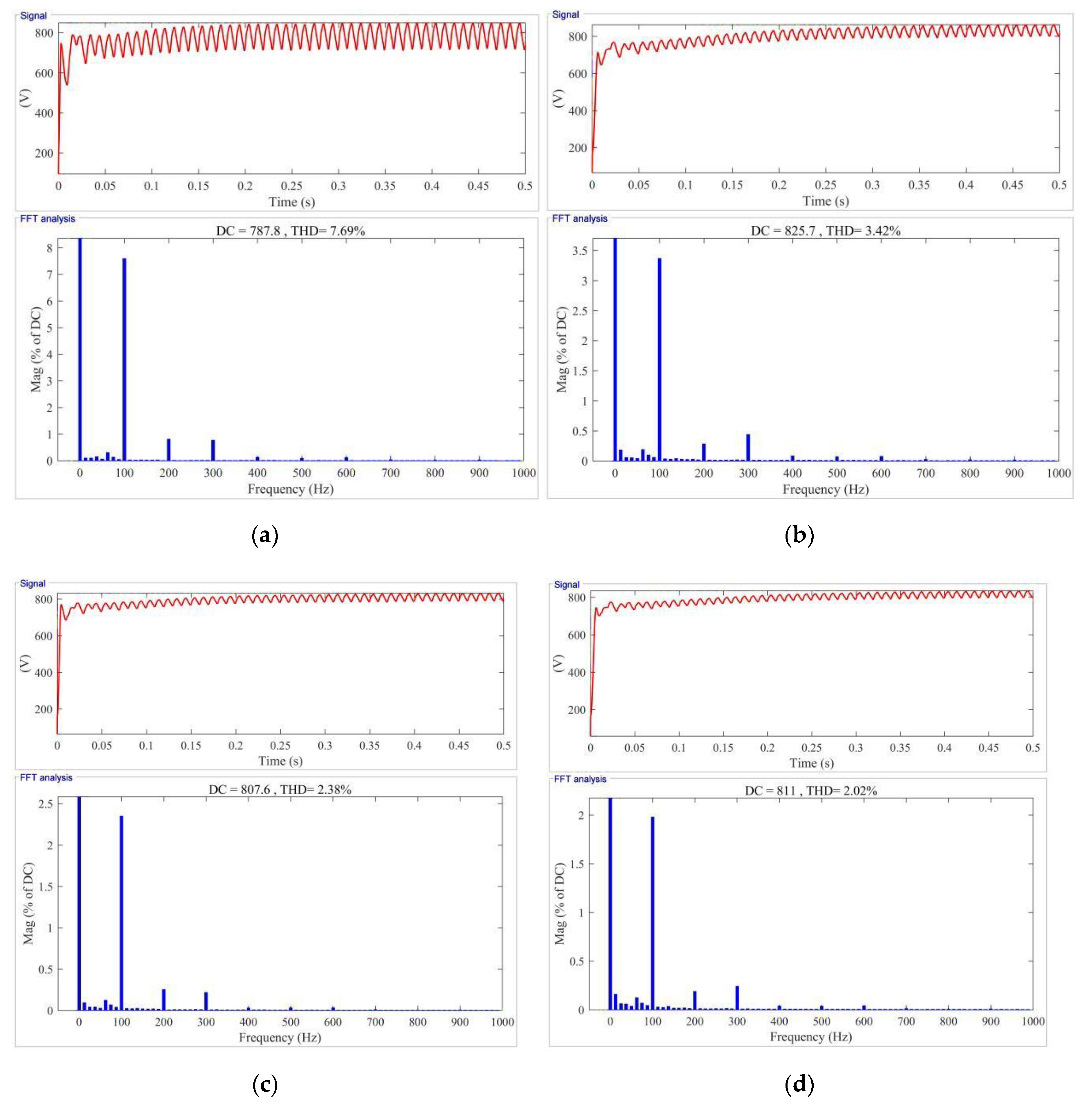
5.2. Numerical Results
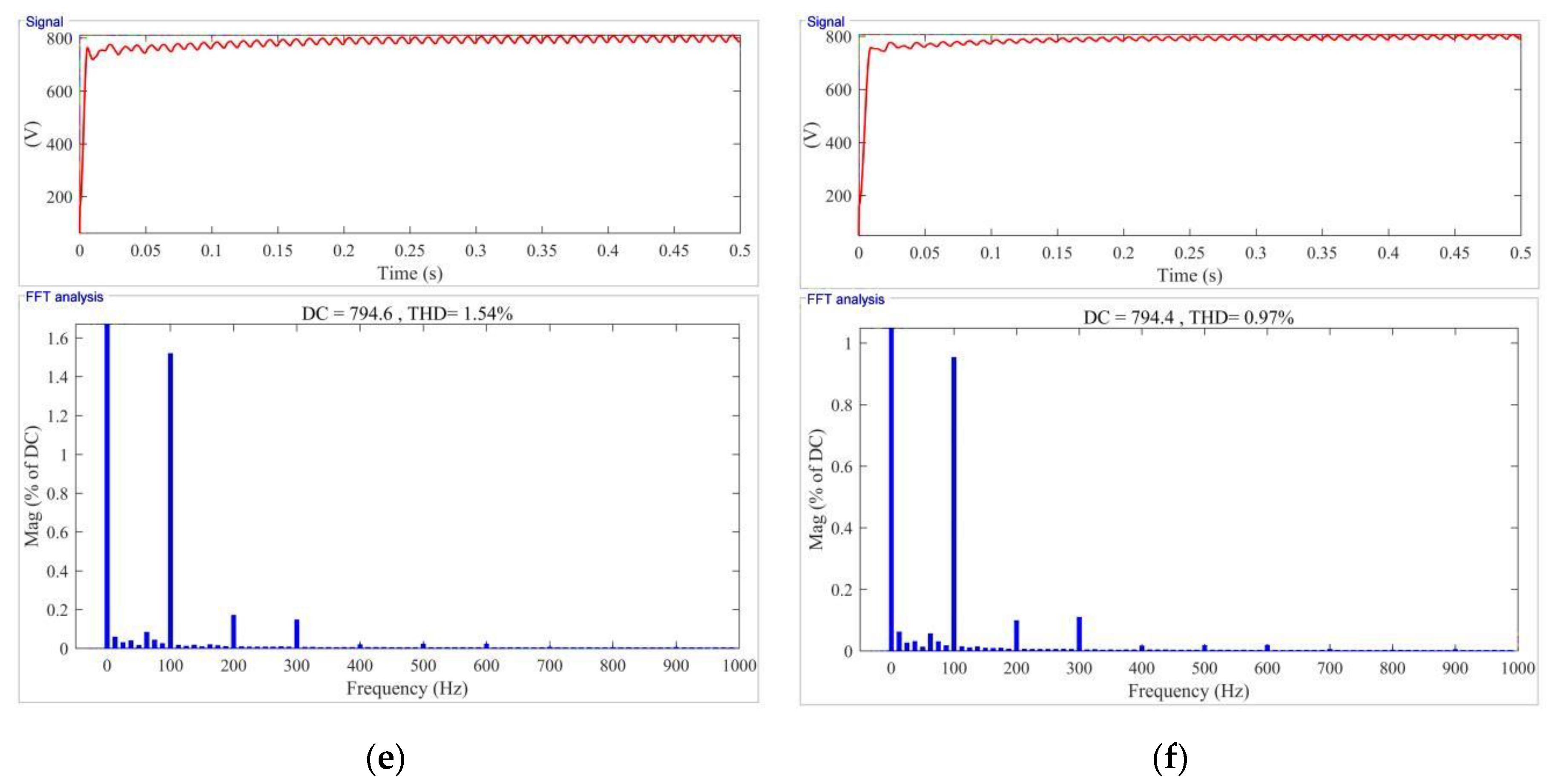
5.3. Results Assessment and Comparison
6. Conclusions
- (1)
- Establish a small signal model of LVC-qZSI, and calculate the double frequency voltage ripples ratios and power loss ratio;
- (2)
- Summarize the six LVC-qZSI parameters and use GRA to sort them in descending order, then select three main influence factors as optimization variables based on the introduction of preference coefficient;
- (3)
- Use the information entropy method to assign weights to three objective functions, and construct a multi-objective optimization model of LVC-qZSI parameters;
- (4)
- Use GRA to improve FA and propose an integration optimization strategy of LVC-qZSI parameters based on GRA-FA;
- (5)
- After the iterative calculation of GRA-FA, the values of , , and are 0.95%, 1.59%, and 1.25%, which are reduced by 87.48%, 87.57%, and 82.78%, respectively. The results indicate that the proposed strategy has excellent optimization ability.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Li, H. A single-phase PV quasi-Z-source inverter with reduced capacitance using modified modulation and double-frequency ripple suppression control. IEEE Trans. Power Electron. 2016, 31, 2166–2173. [Google Scholar] [CrossRef]
- Khajesalehi, J.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. Modeling and control of quasi Z-source inverters for parallel operation of battery energy storage systems: Application to microgrids. Electr. Power Syst. Res. 2015, 125, 164–173. [Google Scholar] [CrossRef]
- Belila, A.; Berkouk, E.M.; Benbouzid, M.; Amirat, Y.; Tabbache, B.; Mamoune, A. Control methodology and implementation of a Z-source inverter for a stand-alone photovoltaic-diesel generator-energy storage system microgrid. Electr. Power Syst. Res. 2020, 185, 1–16. [Google Scholar] [CrossRef]
- Khajesalehi, J.; Sheshyekani, K.; Hamzeh, M.; Afjei, E. High-performance hybrid photovoltaic-battery system based on quasi-Z-source inverter: Application in microgrids. IET Gener. Transm. Distrib. 2015, 9, 895–902. [Google Scholar] [CrossRef]
- Battiston, A.; Miliani, E.-H.; Pierfederici, S.; Meibody-Tabar, F. Efficiency improvement of a quasi-Z-source inverter-fed permanent-magnet synchronous machine-based electric vehicle. IEEE Trans. Transp. Electrif. 2016, 2, 14–23. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, W.; Zheng, Y.; He, G. EMI suppression of high-frequency isolated quasi Z-source inverter based on multi-scroll chaotic PWM modulation. IEEE Access 2019, 7, 146198–146208. [Google Scholar] [CrossRef]
- Guisso, R.A.; Andrade, A.M.S.S.; Hey, H.L.; Martins, M.L.d.S. Grid-tied single source quasi-Z-source cascaded multilevel inverter for PV applications. Electron. Lett. 2019, 55, 342–343. [Google Scholar] [CrossRef]
- Hu, S.; Liang, Z.; Fan, D.; He, X. Hybrid ultracapacitor-battery energy storage system based on quasi-Z-source topology and enhanced frequency dividing coordinated control for EV. IEEE Trans. Power Electron. 2016, 31, 7598–7610. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.; Zhang, W.; Tang, Y.; Chen, Y. Cascaded three-phase quasi-Z source photovoltaic inverter. In Proceedings of the 2018 8th International Conference on Power and Energy Systems (ICPES), IEEE, Colombo, Sri Lanka, 21–22 December 2018; pp. 6–10. [Google Scholar]
- Steinbring, M.; Pacas, M. Increasing the efficiency of a single phase Z-source inverter by utilizing SiC-MOSFETS. In Proceedings of the PCIM Europe 2014; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, VDE, Nuremberg, Germany, 20–22 May 2014; pp. 1–7. [Google Scholar]
- Ozpineci, B.; Tolbert, L.M.; Islam, S.K. Silicon carbide power device characterization for HEVs. In Proceedings of the Power Electronics in Transportation, Auburn Hills, MI, USA, 24–25 October 2002; pp. 93–97. [Google Scholar]
- Rabkowski, J. Improvement of Z-source inverter properties using advanced PWM methods. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1893–1901. [Google Scholar]
- Sun, D.; Ge, B.; Yan, X.; Abu-Rub, H.; Bi, D.; Peng, F.Z. Impedance design of quasi-Z source network to limit double fundamental frequency voltage and current ripples in single-phase quasi-Z source inverter. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 2745–2750. [Google Scholar]
- Pu, S.; Li, Z.; Chen, Y.; Tang, Y.; Wei, R. A novel ripple self-injection APF for quasi-Z-source inverter. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, Australia, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Hosseini, S.M.; Beromi, Y.A. A multi-objective optimization for performance improvement of the Z-source active power filter. J. Electr. Eng. 2016, 67, 358–364. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Li, Z.; Chen, Y.; Wei, R. Ripple vector cancellation modulation strategy for single-phase quasi-Z-source inverter. Energies 2019, 12, 3344. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.; Hongpeng, L.; Jiawan, Z.; Dianguo, X. Analysis of power losses in Z-source PV grid-connected inverter. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 2588–2592. [Google Scholar]
- Franke, W.; Mohr, M.; Fuchs, F.W. Comparison of a Z-source inverter and a voltage-source inverter linked with a DC/DC-boost-converter for wind turbines concerning their efficiency and installed semiconductor power. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference (PESC), Rhodes, Greece, 15–19 June 2008; pp. 1814–1820. [Google Scholar]
- Kumar, A.; Singh, R.K. Power loss calculation of diode assisted cascaded quasi-Z-source converter with CCM and DCM operation. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Wang, H.; Wang, W.; Cui, L.; Sun, H.; Zhao, J.; Wang, Y.; Xue, Y. A hybrid multi-objective firefly algorithm for big data optimization. Appl. Soft. Comput. 2018, 69, 806–815. [Google Scholar] [CrossRef]
- Dac-Khuong, B.; Tuan Ngoc, N.; Tuan Duc, N.; Nguyen-Xuan, H. An artificial neural network (ANN) expert system enhanced with the electromagnetism-based firefly algorithm (EFA) for predicting the energy consumption in buildings. Energy 2020, 190, 1306–1317. [Google Scholar]
- Bramerdorfer, G.; Zăvoianu, A. Surrogate-based multi-objective optimization of electrical machine designs facilitating tolerance analysis. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
- Zeng, X.; Wu, J.; Wang, D.; Zhu, X.; Long, Y. Assessing Bayesian model averaging uncertainty of groundwater modeling based on information entropy method. J. Hydrol. 2016, 538, 689–704. [Google Scholar] [CrossRef]



| Symbol | Definition | Value Range | Unit |
|---|---|---|---|
| Z-source network inductance | 450–2000 | ||
| Z-source network capacitance | 300–1500 | ||
| Filter inductance | 0.50–20 | ||
| Cascaded inductance | 0.50–20 | ||
| Modulation index | 0.50–1.00 | ||
| Shoot-through duty cycle | 0.05–0.40 |
| LVC-qZSI Parameters | ||||||
|---|---|---|---|---|---|---|
| 7.17 | 200 | 200 | 12 | 10 | 0.69 | 0.16 |
| 13.33 | 300 | 250 | 6 | 16 | 0.52 | 0.37 |
| 0.88 | 400 | 300 | 5 | 7 | 0.75 | 0.09 |
| 0.59 | 420 | 300 | 2 | 3 | 0.90 | 0.14 |
| 9.77 | 500 | 400 | 10 | 9 | 0.70 | 0.33 |
| 12.73 | 550 | 500 | 5 | 11 | 0.72 | 0.30 |
| 3.39 | 600 | 1300 | 4 | 14 | 0.82 | 0.19 |
| 0.12 | 640 | 850 | 3 | 5 | 0.55 | 0.15 |
| 2.23 | 680 | 700 | 12 | 9 | 0.67 | 0.22 |
| 4.34 | 700 | 600 | 15 | 12 | 0.77 | 0.25 |
| 2.06 | 750 | 1300 | 7 | 6 | 0.61 | 0.27 |
| 5.06 | 800 | 700 | 13 | 10 | 0.75 | 0.30 |
| 11.89 | 830 | 300 | 10 | 8 | 0.82 | 0.35 |
| 10.40 | 880 | 500 | 8 | 10 | 0.71 | 0.32 |
| 1.79 | 920 | 1070 | 16 | 7 | 0.74 | 0.22 |
| 1.70 | 960 | 950 | 12 | 11 | 0.66 | 0.24 |
| 5.05 | 1000 | 800 | 8 | 15 | 0.65 | 0.35 |
| 8.99 | 1080 | 400 | 6 | 9 | 0.59 | 0.31 |
| 4.86 | 1150 | 760 | 10 | 6 | 0.56 | 0.38 |
| 3.90 | 1200 | 900 | 12 | 13 | 0.60 | 0.40 |
| 1.97 | 1260 | 1000 | 6 | 10 | 0.64 | 0.23 |
| 1.82 | 1300 | 1100 | 17 | 8 | 0.80 | 0.20 |
| 3.85 | 1350 | 1000 | 10 | 4 | 0.78 | 0.22 |
| 11.59 | 1470 | 400 | 5 | 9 | 0.55 | 0.36 |
| 2.23 | 1500 | 1200 | 11 | 5 | 0.85 | 0.15 |
| 2.02 | 1550 | 800 | 13 | 8 | 0.63 | 0.26 |
| 0.92 | 1600 | 1400 | 9 | 11 | 0.55 | 0.28 |
| 5.26 | 1640 | 900 | 10 | 16 | 0.83 | 0.35 |
| 5.03 | 1750 | 1050 | 8 | 4 | 0.88 | 0.18 |
| 0.03 | 1800 | 1500 | 6 | 7 | 0.57 | 0.10 |
| LVC-qZSI Parameters | ||||||
|---|---|---|---|---|---|---|
| 1.4838 | 0.2015 | 0.2561 | 1.3284 | 1.0989 | 0.9923 | 0.6258 |
| 2.7585 | 0.3022 | 0.3201 | 0.6642 | 1.7582 | 0.7478 | 1.4472 |
| 0.1821 | 0.4030 | 0.3841 | 0.5535 | 0.7692 | 1.0786 | 0.3520 |
| 0.1221 | 0.4231 | 0.3841 | 0.2214 | 0.3297 | 1.2943 | 0.5476 |
| 2.0218 | 0.5037 | 0.5122 | 1.1070 | 0.9890 | 1.0067 | 1.2907 |
| 2.6343 | 0.5541 | 0.6402 | 0.5535 | 1.2088 | 1.0355 | 1.1734 |
| 0.7015 | 0.6044 | 1.6645 | 0.4428 | 1.5385 | 1.1793 | 0.7432 |
| 0.0248 | 0.6447 | 1.0883 | 0.3321 | 0.5495 | 0.7910 | 0.5867 |
| 0.4615 | 0.6850 | 0.8963 | 1.3284 | 0.9890 | 0.9636 | 0.8605 |
| 0.8981 | 0.7052 | 0.7682 | 1.6605 | 1.3187 | 1.1074 | 0.9778 |
| 0.4263 | 0.7555 | 1.6645 | 0.7749 | 0.6593 | 0.8773 | 1.0561 |
| 1.0471 | 0.8059 | 0.8963 | 1.4391 | 1.0989 | 1.0786 | 1.1734 |
| 2.4605 | 0.8361 | 0.3841 | 1.1070 | 0.8791 | 1.1793 | 1.3690 |
| 2.1522 | 0.8865 | 0.6402 | 0.8856 | 1.0989 | 1.0211 | 1.2516 |
| 0.3704 | 0.9268 | 1.3700 | 1.7712 | 0.7692 | 1.0642 | 0.8605 |
| 0.3518 | 0.9671 | 1.2164 | 1.3284 | 1.2088 | 0.9492 | 0.9387 |
| 1.0450 | 1.0074 | 1.0243 | 0.8856 | 1.6484 | 0.9348 | 1.3690 |
| 1.8604 | 1.0880 | 0.5122 | 0.6642 | 0.9890 | 0.8485 | 1.2125 |
| 1.0057 | 1.1585 | 0.9731 | 1.1070 | 0.6593 | 0.8054 | 1.4863 |
| 0.8071 | 1.2089 | 1.1524 | 1.3284 | 1.4286 | 0.8629 | 1.5645 |
| 0.4077 | 1.2693 | 1.2804 | 0.6642 | 1.0989 | 0.9204 | 0.8996 |
| 0.3766 | 1.3096 | 1.4085 | 1.8819 | 0.8791 | 1.1505 | 0.7823 |
| 0.7967 | 1.3600 | 1.2804 | 1.1070 | 0.4396 | 1.1218 | 0.8605 |
| 2.3984 | 1.4809 | 0.5122 | 0.5535 | 0.9890 | 0.7910 | 1.4081 |
| 0.4615 | 1.5111 | 1.5365 | 1.2177 | 0.5495 | 1.2224 | 0.5867 |
| 0.4180 | 1.5615 | 1.0243 | 1.4391 | 0.8791 | 0.9060 | 1.0169 |
| 0.1904 | 1.6118 | 1.7926 | 0.9963 | 1.2088 | 0.7910 | 1.0952 |
| 1.0885 | 1.6521 | 1.1524 | 1.1070 | 1.7582 | 1.1937 | 1.3690 |
| 1.0409 | 1.7629 | 1.3444 | 0.8856 | 0.4396 | 1.2656 | 0.7040 |
| 0.0062 | 1.8133 | 1.9206 | 0.6642 | 0.7692 | 0.8198 | 0.3911 |
| 0.4966 | 0.5076 | 0.9011 | 0.7729 | 0.7250 | 0.5976 |
| 0.3384 | 0.3400 | 0.3752 | 0.5594 | 0.3849 | 0.4909 |
| 0.8604 | 0.8717 | 0.7794 | 0.6868 | 0.5868 | 0.8917 |
| 0.8153 | 0.8366 | 0.9391 | 0.8683 | 0.5194 | 0.7539 |
| 0.4539 | 0.4554 | 0.5818 | 0.5514 | 0.5557 | 0.6363 |
| 0.3768 | 0.3869 | 0.3767 | 0.4698 | 0.4410 | 0.4636 |
| 0.9407 | 0.5689 | 0.8384 | 0.6037 | 0.7308 | 0.9818 |
| 0.6746 | 0.5440 | 0.8119 | 0.7113 | 0.6251 | 0.6964 |
| 0.8588 | 0.7497 | 0.5950 | 0.7101 | 0.7205 | 0.7662 |
| 0.8773 | 0.9180 | 0.6263 | 0.7561 | 0.8673 | 0.9532 |
| 0.8005 | 0.5055 | 0.7906 | 0.8532 | 0.7424 | 0.6710 |
| 0.8484 | 0.9040 | 0.7695 | 0.9740 | 0.9897 | 0.9204 |
| 0.4370 | 0.3773 | 0.4829 | 0.4437 | 0.4968 | 0.5374 |
| 0.4999 | 0.4550 | 0.4997 | 0.5464 | 0.5284 | 0.5856 |
| 0.6986 | 0.5596 | 0.4742 | 0.7663 | 0.6486 | 0.7256 |
| 0.6763 | 0.5957 | 0.5654 | 0.5979 | 0.6829 | 0.6868 |
| 0.9849 | 0.9982 | 0.8984 | 0.6807 | 0.9315 | 0.8032 |
| 0.6232 | 0.4839 | 0.5142 | 0.5938 | 0.5565 | 0.6645 |
| 0.9028 | 0.9888 | 0.9377 | 0.7918 | 0.8727 | 0.7296 |
| 0.7648 | 0.7923 | 0.7126 | 0.6740 | 0.9709 | 0.6278 |
| 0.5965 | 0.5934 | 0.8397 | 0.6495 | 0.7161 | 0.7248 |
| 0.5769 | 0.5516 | 0.4561 | 0.7203 | 0.6227 | 0.7630 |
| 0.6959 | 0.7283 | 0.8103 | 0.7864 | 0.8026 | 0.9650 |
| 0.5810 | 0.4003 | 0.4057 | 0.4727 | 0.4396 | 0.5619 |
| 0.5473 | 0.5413 | 0.6282 | 0.9472 | 0.6267 | 0.9211 |
| 0.5257 | 0.6796 | 0.5543 | 0.7380 | 0.7264 | 0.6823 |
| 0.4705 | 0.4405 | 0.6129 | 0.5549 | 0.6817 | 0.5845 |
| 0.6958 | 0.9649 | 1.0000 | 0.6569 | 0.9350 | 0.8264 |
| 0.6393 | 0.8139 | 0.9011 | 0.6814 | 0.8581 | 0.7966 |
| 0.4107 | 0.3967 | 0.6610 | 0.6261 | 0.6106 | 0.7728 |
| Reference Index | Influence Factors | |||||
|---|---|---|---|---|---|---|
| 0.6556 | 0.6316 | 0.6780 | 0.6815 | 0.6866 | 0.7261 | |
| 0.7789 | 0.8254 | 0.6811 | 0.7461 | 0.6609 | 0.7926 | |
| 0.9573 | 0.9498 | 0.8692 | 0.8045 | 0.5098 | 0.5237 | |
| Definition | Value |
|---|---|
| Z-source network inductance | 500 |
| Z-source network capacitance | 400 |
| Filter inductance | 4.00 |
| Cascaded inductance | 4.00 |
| Voltage of DC source | 320 |
| Modulation index | 0.60 |
| Shoot-through duty cycle | 0.25 |
| Output frequency | 50 |
| Carrier frequency | 10 |
| Iterations | Optimization Variables | Value |
|---|---|---|
| (%) | (%) | (%) | |
|---|---|---|---|
| Before optimization | 7.59 | 12.79 | 7.26 |
| After optimization | 0.95 | 1.59 | 1.25 |
| Optimization Strategy | (%) | (%) | (%) |
|---|---|---|---|
| RVCMS | 2.53 | 7.75 | 8.17 |
| APF | 0.89 | 1.34 | 9.32 |
| MOGA | 1.27 | 1.78 | 2.41 |
| Proposed | 0.95 | 1.59 | 1.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Pu, S.; Chen, Y.; Wei, R. An Integration Optimization Strategy of Line Voltage Cascaded Quasi-Z-Source Inverter Parameters Based on GRA-FA. Energies 2020, 13, 4391. https://doi.org/10.3390/en13174391
Li Z, Pu S, Chen Y, Wei R. An Integration Optimization Strategy of Line Voltage Cascaded Quasi-Z-Source Inverter Parameters Based on GRA-FA. Energies. 2020; 13(17):4391. https://doi.org/10.3390/en13174391
Chicago/Turabian StyleLi, Zhiyong, Shiping Pu, Yougen Chen, and Renyong Wei. 2020. "An Integration Optimization Strategy of Line Voltage Cascaded Quasi-Z-Source Inverter Parameters Based on GRA-FA" Energies 13, no. 17: 4391. https://doi.org/10.3390/en13174391





