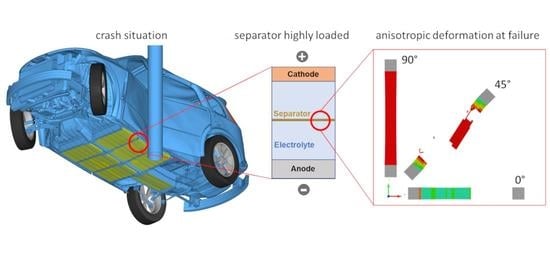
An Experimental and Computational Study on the Orthotropic Failure of Separators for Lithium-Ion Batteries

Abstract

In the present study, the mechanical properties of a dry-processed polyethylene (PE) separator are investigated in terms of deformation and failure limits. The focus is set on the anisotropic mechanical behavior of this material. A deeper understanding of the damage mechanism is important for further safety and crashworthiness investigations and predictions of damage before failure. It has been found that separator integrity is one of the crucial parts in preventing internal short circuit and thermal runaway in lithium-ion (Li-ion) batteries. Based on uniaxial tensile tests with local strain measurement, a novel failure criterion for finite element analysis (FEA), using the explicit FEA solver Altair Radioss, has been developed to predict the effect of high mechanical loads with respect to triaxiality, large plastic strain and orthotropy. Finally, a simulation model of a PE separator was developed combining the novel failure criterion with Hill’s yield surface and a Swift–Voce hardening rule. The model succeeded in predicting the anisotropic response of the PE separator due to deformation and failure. The proposed failure model can also be combined with other constitutive material laws.

1. Introduction

In recent years, the automotive market has been pushed to reduce CO₂ emissions significantly and to ramp up their efforts to develop and produce electric-powered drivetrains. Currently the best industrial energy storage method is the lithium-ion (Li-ion) battery, which is already widely used in the consumer electronic industry (e.g., cellphones and computer laptops). There are also other electric storage batteries (e.g., solid-state batteries [1]), but these are not yet commercially viable options and will not be the topic of this work. The Li-ion cell is seen as the most promising energy storage source currently commercially available [2]. Electronic consumer goods and vehicles go through various crash and misuse scenarios under different load cases. With the increasing use of batteries in those devices and vehicles, safety has become an issue due to inadvertent failures. Finite element modeling (FEM) has been used extensively for many years to study the crashworthiness of vehicles, resulting in the development of many concepts for damage and failure criteria.

The need to shorten development times and global competition has led to an increased use of virtual analysis for different load scenarios a vehicle is subjected to. A very well-known example of a reduction in development time is the next generation Volkswagen Golf. The development period between the Golf I and II model generations was eight years. The development phase between the Volkswagen Golf III the VI was completed in only four years [3]. Increased use of nonlinear FEM also reduces the number of prototypes and tests required for evaluating misuse (failure) conditions. A reduction of real tests ultimately reduces the overall costs in the development process. One of the best known all-electric vehicles is the Tesla Model S. In 2013, two fires caused by traffic accidents involving this model brought the safety of electric vehicles to the attention of the public and government [4]. This led to the realization that sufficient knowledge of the behavior of Li-ion batteries and their internal components is essential to developing effective countermeasures to improve the crash safety of electric vehicles and consumer goods.

Most failure criteria are based on varying the failure strain as a function of the state of stress, strain rate and temperature [5]. A comparison between these failure models was provided by Wierzbicki et al. [6]. The increased computational power of new generations of computers and workstations has allowed the development of more advanced material and failure models. In particular, anisotropic effects have to be taken into account due to the layered structure and manufacturing processes of the inner components of a battery cell.

Inside a Li-Ion battery, the separator has the task of preventing contact between the anode and cathode. A failure in the separator can lead to a short circuit and possible thermal runaway. A common material used as the separator in commercially available batteries is a micro-porous polymeric film made of polyethylene or polypropylene, or a combination of the two. A ceramic coating is commonly added to such layers for further enhancement of their properties. A dry-processed polyethylene (PE) film is usually manufactured using a blown film process. The orientation in machine direction (MD) and transverse direction (TD), as well as the diameter of the bubble and film thickness, are determined simultaneously.

Many experimental and computational studies have been conducted to investigate the structural behavior of lithium-ion battery cells under different loading and boundary conditions [7,8,9]. Also, an experimental and computational study on failure behavior of a vehicle battery module was performed. Corresponding numerical simulations and real test results have been reported [10]. The increased computational power of commercially available clusters, along with new numerical methods, such as the multi-domain approach, allows the utilization of finer discretization and more detailed numerical investigations of the misuse of Li-ion batteries, and provides a deeper understanding of their internal failure mechanisms. This has led to the characterization and modeling of subcomponents of battery cells such as electrodes and separators in recent literature. Many recent investigations have focused on orthotropy and visco-elasticity of separators, but only in small strain regions where failure did not occur [11,12,13]. Wierzbicki et al. conducted recent research into the failure strain of lithium-ion batteries treated as a discrete layered structure [14]. Within this study, a smeared approach for coated materials and isotropic failure criteria was used. For a deeper understanding of the failure phenomena in Li-ion batteries, it is necessary to understand and model the behavior of their individual layers. The failure of the separator under high mechanical load, followed by a short and possible thermal runaway, remains a phenomenon that is not well understood, and that requires further investigation and research. There are well-developed damage and failure criteria for layered structures, which are widely used (e.g., for damage and failure prediction of fiber reinforced plastics), but these cannot be applied in this specific case, due to the different elasto-plastic behavior of the individual layers. Most of the available failure criteria for composite materials are stress based, such as Puck or Hashin and other existing models [15]. Using them for predicting failure of the PE separator, however, would lead to a much-too-conservative, underestimated numerical failure treatment. In addition to that, the isolator material behavior is extremely ductile at a constant stress level, but only in one of the orthotropic directions. This behavior can be explained by the induced pre-stretching during the manufacturing process [16].

With increased usage of Li-ion batteries (mobile phones, e-mobility, etc.), the demand for higher safety in devices is also increasing. Regarding e-mobility, a rapidly increasing number of electrically powered vehicles is expected in the coming years. In connection with this, the number of electrically driven vehicles involved in traffic accidents will also increase significantly. This requires an improved predictability and calculability of the risk of short circuits, and thus thermal run-away, due to the failure of the isolator layer in case of large deformations. Figure 1 shows a possible final application for the crashworthiness of a full electric vehicle. It shows the FE model of a Toyota Venza from National Highway Traffic Safety Administration (NHTSA) [17]. The model was modified by adding a generic battery package in the lower area. The load case is the European side impact where the car impacts a pole with an initial velocity of 8.9 m/s.

So far, no failure models for separators have been found in the literature. Therefore, a new failure model is developed herein to consider the observed mechanical and physical behavior, revealing large orthotropic plasticity and different fracture limits in different loading directions as well as a high strain-rate dependency for the failure strain. Based on the idea of the modified rate-dependent Hosford-Coulomb model [18] and the BiQuad failure criterion [19], the effects of different states of stress, orthotropies and strain limits were developed and validated with the tested PE separator.

2. Materials and Methods

Two types of commercial polymeric separators were provided to us from a battery manufacturing company: MTI Corporation (860 S. 19th Street, Richmond, CA 94804-3809, USA). The exact chemical composition of the materials used in these samples was not clear. The separators were purchased from MTI Corporation with a specified porosity of 36–46%. Figure 2 shows the results of a differential scanning calorimetry (DSC) analysis that was performed with the specimen material.

The results show a crystallization temperature of around 134 °C, which indicates a standard PE material. No anomalies were found within this analysis. In this study, mechanical properties of the specimen were studied by conducting tensile tests on small strips cut out in two perpendicular spatial directions corresponding to the MD and TD of the separator samples. Figure 3 shows the experimental setup used for performing the tensile tests. Each specimen with dimensions of 12 × 60 × 0.025 mm was glued at each end to metal specimen holders that led to a free test length of 36 mm. A gray pattern was spread on each specimen to allow digital image correlation (DIC), and the 3D ARAMIS system from GOM GmbH (Schmitzstrasse 2, 38122 Braunschweig, Germany) was used for analysis of the strain field. For each of the PE materials provided, three different tension velocities were used for testing: 0.1, 1 and 10 mm s⁻¹. To ensure repeatability, each test was repeated five times.

Figure 4 shows one set of the prepared specimens used for testing. In addition to the DIC measurement, the machine displacement and force were tracked to correlate the results. Due to very large deformation in the 0° direction, compared to the 90° test direction, the capability of the DIC measurements were at their limit; so, for these results, the force displacement curves were used. The tracking frequency for the force and displacement measurements were at 2 Hz for the slowest tension velocity to 40 Hz for the fastest one.

The results of all tests will be discussed individually as well as the preparation and selection for the numerical simulations. The fracture location in almost all the samples started close to their fixation points. This indicates the need of a triaxiality-based differentiation of the failure strain, because in this region, close to the fixations, the assumption of pure uniaxial tension is no longer valid. The elongation measured was in the range of 12–19 mm, which is 33–53% total strain at quasi-static tension velocity. At higher velocities, the specimen failure occurred at significantly lower total strain values. After failure, the specimen retained almost all its extension, which indicates that the relaxation was very low. This leads to the conclusion of high plasticity and low elasticity behavior. Compared to the load applied in MD, the tested samples show completely different behavior in this direction. Localization occurs close to the center and proceeds to one of the fixed ends. The results of the tests can be divided in two main groups. The first group of tested samples shows lower ductility with a higher force level. The second group of test samples shows high ductility at a much lower force level. The maximum peak force is approximately 40 N. The displacement varies in a huge range and depends on the orientation of the specimen as well as the test velocity.

To illustrate the anisotropic (orthotropic) behavior of the investigated materials, four representative examples in which the localization occurred at different locations and propagated differently to the tested samples are shown in Figure 5. This behavior was also observed by Sahraei [20] where the failure mode in MD was different compared to the failure mode in TD. The results in 45° to MD, which is referred to as diagonal direction (DD), also showed different deformation patterns until failure. The tested specimens showed a very high scatter in fracture strains, but were in the same qualitative range.

Figure 6 shows representative true stress vs. true strain curves for the specimens in two directions for three velocities of testing. The fracture strain in the MD direction is lower than the failure strain in the TD direction, whereas the stress level in the MD direction is always higher than the stress in the TD direction. One feature observed in both testing directions is that the failure strain decreases with increasing testing velocity.

3. Modeling and Results

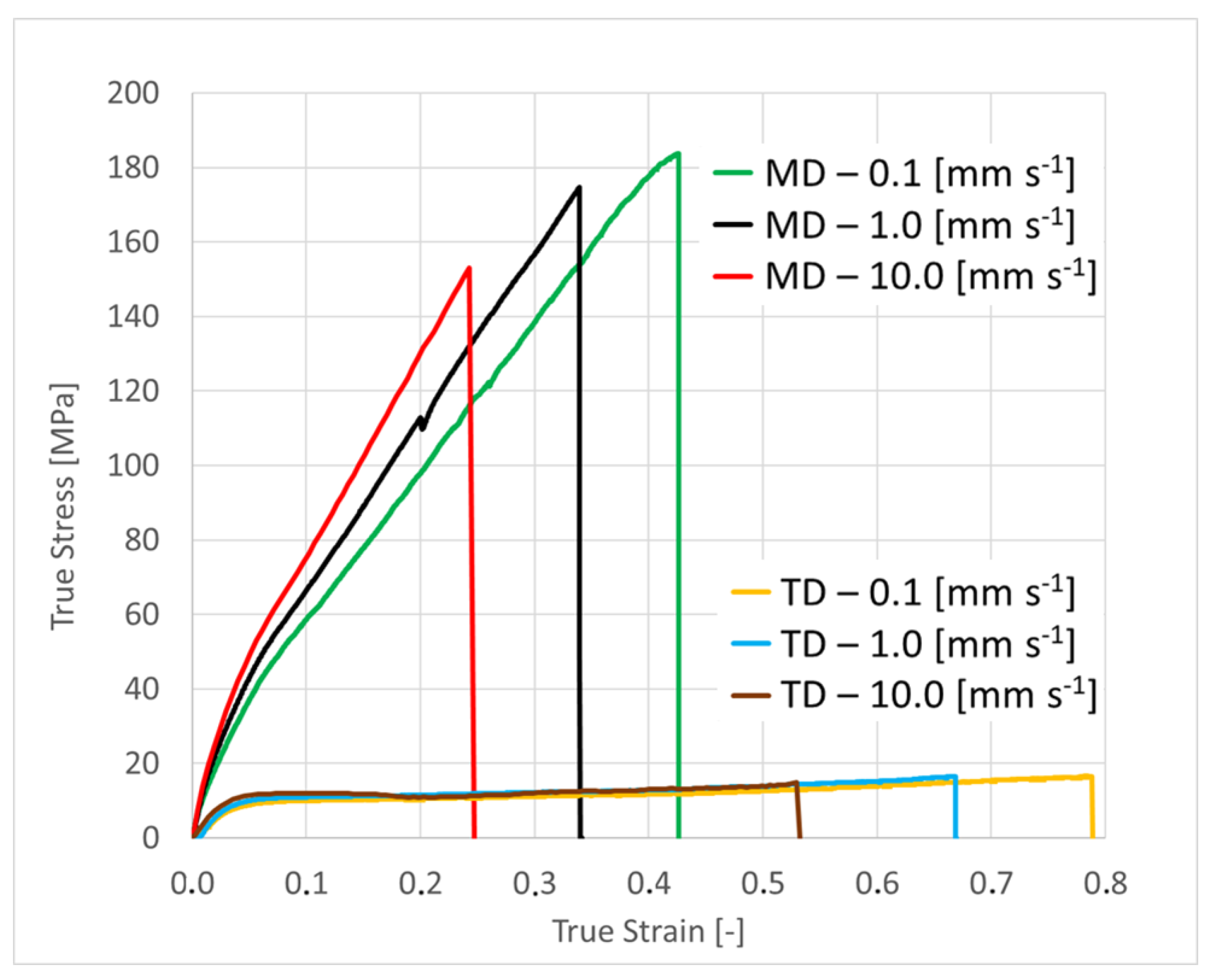
3.1. Material Modeling

Based on the test results, an associated elasto-plastic material law was used to model the material behavior. In crashworthiness simulation, a von Mises yield surface was used due to its stability, robustness and performance in full vehicle applications. The most common materials in crash applications, where high mechanical loads and fractures can occur, were modeled using elasto-plastic material laws. Within this work, an orthotropic model with a Hill’s yield surface [15] is used, since orthotropy in the material stiffness was observed. Hill’s model describes an anisotropic yield behavior and can be considered a generalization of von Mises’s yield criterion for anisotropic yield behavior. The input parameters for these types of material, besides the basic values like density, Young’s modulus and so on, are the hardening functions that describe the material hardening in the plastic region. The Hill constants are obtained by material tests under different orientations. The stress components are expressed in the Cartesian reference system, parallel to the three planes of orthotropy. In a general case, the loading direction is not the orthotropic direction. In each plane, the orthotropy is characterized by different strengths in different directions. The commercial crash solvers require the input of true plastic strain vs. true stress curves to describe this nonlinear stiffness during plastification. In this study, both DIC and the classic force-displacement measurement was performed. Figure 7 shows the comparison of both methods, where one can verify whether the output from the measurement device is in a valid and reliable range.

Wherever possible, the curves obtained by the DIC measurement were used for further material parameter identification. For the measurements in the TD direction, the deformation of the specimen ultimately reached a non-measurable level where it was no longer possible to track the speckles using the optical measurement method. For these samples, where the DIC measurement was not successful, the classic force vs. displacement approach was used to compute the true-stress vs. true-plastic-strain curves.

The process to calculate the material data is split into five steps:

1.

The resultant force vs. displacement curves are recalculated to engineering stress vs. strain curves. The engineering stress ${\sigma }_{eng}$ is defined as

$${\sigma }_{eng}=\frac{F}{S_0}$$

(1)

where

${\sigma }_{eng}$ = engineering stress (MPa),

$F$ = measured force (N),

$S_0$ = initial cross section (mm²).

2.

In the next step, it is necessary to calculate the true strain ${\epsilon }_{true}$ from the engineering strain ${\epsilon }_{eng}$ within the parallel length of the test specimen

$${\epsilon }_{eng}=\frac{\Delta L}{L_0}$$

(2)

$${\epsilon }_{true}={{\displaystyle \int }}_{L_0}^{L_1}\frac{dL}{L}=\ln \frac{L_1}{L_0}=\ln \frac{L_0+\Delta L}{L_0}=\ln \left(1+\frac{\Delta L}{L_0}\right)=\ln \left(1+{\epsilon }_{eng}\right)$$

(3)

where

${\epsilon }_{eng}$ = engineering strain (-),

${\epsilon }_{true}$ = true strain (-),

$L_0$ = initial length (mm),

$L_1$ = final length(mm),

$\Delta L$ = relative displacement (mm) of the parallel length.

3.

With the assumption of constant volume (i.e., isochoric deformation), the true stress is the ratio of the measured force F and the actual cross section S:

$${\sigma }_{true}=\frac{F}{S}=\frac{F·L}{S·L}=\frac{F·L}{S_0·L_0}={\sigma }_{eng}·e^{{\epsilon }_{true}}={\sigma }_{eng}·\left(1+{\epsilon }_{eng}\right)$$

(4)

where

${\sigma }_{true}$ = true stress (MPa),

$S$ = actual cross section (mm²) of the parallel length.

4.

For use in FEM applications, where the total true stain is the sum of the plastic strain and the elastic strain, the true plastic strain

$${\epsilon }_{true,plastic}={\epsilon }_{true}-{\epsilon }_{true,elastic}$$

(5)

is needed with

$${\sigma }_{true}={\epsilon }_{true,elastic}·E$$

(6)

$${\epsilon }_{true,plastic}={\epsilon }_{true}-\frac{{\sigma }_{true}}{E}$$

(7)

where

${\epsilon }_{eng,plastic}$ = engineering plastic strain (-),

${\epsilon }_{eng,elastic}$ = engineering elastic strain (-),

${\sigma }_{true}$ = true stress (MPa),

$E$ = Young’s modulus (MPa).

5.

As the measured data are coming from a tensile test, it shows softening after reaching the maximum stress, where the slope of the stress-strain curve becomes zero or negative. This is often referred to as the necking or instability point. In more complex load scenarios, other load-states can occur, like shear or compression, and the obtained curve can go beyond that point. In the present work, the extrapolation based on the combined equations from Swift and Voce [18] is found as a suitable extrapolation approach for the measured true stress vs. true strain curves:

$${\sigma }_{yiel{d}_{Swift}}=A{\left({\overline{\epsilon }}_{pl.}·{\epsilon }_0\right)}^n$$

(8)

$${\sigma }_{yiel{d}_{Voce}}=k_0+Q·\left(1-\exp \left(-B·{\overline{\epsilon }}_{pl.}\right)\right)$$

(9)

where

${\sigma }_{yiel{d}_{Swift}}$ = yield stress, based on Swift (MPa),

${\sigma }_{yiel{d}_{Voce}}$ = yield stress, based on Voce (MPa),

${\overline{\epsilon }}_{pl.}$ = equivalent plastic strain (-),

$A$ = Swift hardening coefficient (MPa),

${\epsilon }_0$ = Swift hardening parameter (-),

$n$ = Swift hardening exponent (-),

$k_0$ = Voce hardening parameter (MPa),

$Q$ = Voce hardening coefficient (MPa),

$B$ = Voce plastic strain coefficient (-).

Using the coupling parameter α together with Equations (8) and (9), one obtains the interpolation function for stress-strain hardening as

$${\sigma }_{yield}=\alpha ·{\sigma }_{yiel{d}_{Swift}}+\left(1-\alpha \right)·{\sigma }_{yiel{d}_{Voce}}$$

(10)

where

$\alpha$ = yield weighting coefficient

Figure 8 demonstrates the individual steps needed to get from the obtained test curve to the final hardening curve needed by FE solvers. For this coupling, the parameter for the Swift function and the Voce functions must be fitted separately based on the measured curves.

The parameter identification was performed using Microsoft Excel (Office 365, Microsoft corporation, Redmond, Washington, USA) but could also be automated using optimization algorithms. After the individual parameter identification for the Swift and Voce functions, the coupling term $\alpha$ is used to extrapolate the hardening curve after the necking point. Figure 9 demonstrates the influence of α on the final hardening curve.

A value of $\alpha$ = 0 leads to a pure Voce curve, which mostly underestimates the material stiffness, while $\alpha$ = 1 leads to a pure Swift hardening curve, which mostly overestimates the material stiffness. In the present investigation, an alpha value of 0.5 was chosen, which gave an intermediate interpolation function.

Table 1. Parameters obtained for the hardening curve.

Swift: A (MPa)	Swift: eps0 (-)	Swift: n (-)	Voce: k0 (MPa)	Voce: Q (MPa)	Voce: B (-)
429.255	5.32 × 10−3	0.7071	14.544	303.095	2.741

shows the parameter list for the calculation of the hardening curve.

3.2. Failure Criterion Modeling

Since the failure of the specimen occurs near to the tensile test crossheads, a high dependency on the state of stress (triaxiality) is assumed. Therefore, a triaxiality-based failure model was used to model the fracture observed in the tests. This is a well-known approach that is also used to model fractures for metals in commercial crash solvers. The thickness of the separator was very small (0.025 mm) compared to the other two dimensions. For that reason, membrane theory was applied, and the Lode angle was not considered. In membranes, the triaxiality value clearly determines the state of stress. For bulky structures, the Lode angle is needed for a clear identification of the state of stress. Inspired by the approach of Johnson–Cook [21], the state of stress of the load case was calculated using the triaxiality value $\eta$ for plane stress:

$$\eta =\frac{{\sigma }_1+{\sigma }_2}{3·\sqrt{0.5·\left[{\sigma }_1^2+{\sigma }_2^2+{\left({\sigma }_1-{\sigma }_2\right)}^2\right]}}$$

(11)

where

$\eta$ = triaxiality (-)

${\sigma }_1,{\sigma }_2$ = principal stresses (MPa).

One can see in the equation by Johnson-Cook (Equation (12)) that the failure strain monotonically decreases with a negative $D_3$ value, or monotonically increases if $D_3$ > 0:

$${\epsilon }_{failure}=\left[D_1+D_2·\exp (D_3·\eta )\right]·[1+D_4·\ln (\dot{{\epsilon }^{*}})]$$

(12)

where

$D_1,D_2,D_3,D_4$ = Johnson–Cook failure parameter (-),

$\dot{{\epsilon }^{*}}$ = strain rate (1/s).

The assumption from Johnson and Cook can be easily fit in the compression and shear stress as well as for the equi-biaxial tension condition at a triaxiality of 2/3. In-between, however, it is not possible to match the often-observed local maximum around uniaxial tension (triaxiality = 1/3). This can be easily improved using a more advanced failure criterion. A new approach using two parabolic equations with an intersection at triaxiality point η = 1/3 (Equation (13)) was implemented in the Altair Radioss software (Altair Inc., 1820 E. Big Beaver Rd., Troy, MI 48083, USA), and is already in industrial use in crashworthiness applications.

$${\epsilon }_{failure}=\{\begin{array}{c}a·{\eta }^2+b·\eta +c\eta \le \frac{1}{3}\\ d·{\eta }^2+e·\eta +f\eta >\frac{1}{3}\end{array}$$

(13)

Two other types of failure models, Modified Hosford-Coulomb and BiQuad were also considered and compared in this study. Figure 10 shows a comparison of the failure curves of the three investigated failure models. Only the Hosford-Coulomb and the BiQuad failure criteria show an increase in the failure strain close to the uniaxial state of stress.

By considering the orthotropic behavior of the test material, the simulation results can be significantly improved. This new development makes it possible to individually adjust the failure limits in the three directions, MD, TD, and DD. The input for the failure strains is obtained directly from the individual tests and applied separately for two (0° and 90°) or three (0°, 45° and 90°) values, depending on the existing test results. The interpolation between orthotropic failure curves is performed using the trigonometric cosine-function between 0 and $\pi$:

$${\epsilon }_{fail\left(\widehat{\alpha }\right)}={\epsilon }_0·\frac{1+\cos \left(\pi \ast \widehat{\alpha }\right)}{2}+{\epsilon }_1·\left(1-\frac{\left(1+\cos \left(\pi \ast \widehat{\alpha }\right)\right)}{2}\right)$$

(14)

where

${\epsilon }_{fail\left(\widehat{\alpha }\right)}$ = interpolated failure strain (-),

${\epsilon }_0$ = lower orthotropy angle, failure strain (-),

${\epsilon }_1$ = higher orthotropy angle, failure strain (-),

$\widehat{\alpha }$ = projected in-between orthotropy angle (-).

$\widehat{\alpha }$ as an actual orthotropic angle projected to a numerical range between 0 and 1. The advantage of using a trigonometric cosine-function in the range between 0 and $\pi$ is in its slope (see Equation (15), which is the derivative of Equation (14)). The derivate proves that we obtain a zero slope at the beginning and end of this function ($\widehat{\alpha }$ = 0 and $\widehat{\alpha }$ = 1) [22]. This corresponds to the three orthotropic angles defined by the user.

$$\epsilon {\prime }_{fail\left(\widehat{\alpha }\right)}=\frac{1}{2}·{\epsilon }_1·\pi ·\sin \left(\pi ·\widehat{\alpha }\right)-\frac{1}{2}·{\epsilon }_0·\pi ·\sin \left(\pi ·\widehat{\alpha }\right)$$

(15)

Figure 11 compared the linear interpolation method and the trigonometric interpolation method for the failure limits of a pure uniaxial tension case depending on the individual orthotropy directions. The sinus-based interpolation leads to a smoother transition between the three measured fracture limits (MD, DD, TD). This can provide higher numerical stability during the detection of failure and deletion of the corresponding elements. The first derivative of this function did not show any sudden jumps and remained zero at the user-defined values, leading to smooth damage accumulation by changing the orthotropy during the loading phase to a plastic strain increment with a non-zero value.

Figure 12 demonstrates the resultant failure curves vs. triaxiality for the three user-input orthotropy angles. The individual failure curves were calibrated using the failure strain from the tensile tests at the triaxiality value of 1/3 (-).

Table 2. Parameters for the failure criteria model.

Orientation (degree)	Uniaxial Compression (-)	Pure Shear (-)	Uniaxial Tension (-)	Plain Strain Tension (-)	Equi-Biaxial Tension (-)
0	1.0	0.75	0.53	0.50	0.7
45	2.5	1.35	0.95	0.60	0.8
90	4.0	1.85	1.20	0.70	0.9

shows the list of failure parameter used in the calibrated FE model. The values for uniaxial tension failure strain are obtained directly from the test results. The other values are estimated based on experience obtained from the characterization of other plastic materials.

3.3. FE-Model

As a first step, a FEM model was created using the newly developed failure criterion. For the validation simulation, the failure strain was derived from the measured test results in 0° and 90° orientations, where the failure values were highest. This served to test the numerical stability due to these high values (compared to metals). The failure strain, as well as the stress-strain values for the material stiffness, were obtained from Sahraei [20] for the DD (45°) direction:

• 0° with failure strain = 53%;
• 45° with failure strain = 95%;
• 90° with failure strain = 120%.

The first test model, using the single-element-test where all elements used the same material and failure criterion, showed that the failure sequence occurred as expected and in perfect correlation with the input failure strain in uniaxial tension for each of the individual directions. In larger models that consist of more than one element, the material properties and boundary conditions playing a more important role. As material instability occurs in elements, that reach this strain, the deformation begins to localize and deformation remains in these elements, while other elements start to relax. In the beginning, the total deformation is distributed uniformly over many elements. When plasticity begins, the element length effect starts to have a bigger influence on the results of the fracture. High necking leads to numerical problems, as the element theory can reach its limit. It can be seen that the smaller elements localize first. This is a typically observed behavior in all elasto-plastic material models. Therefore, the strain-based failure criterion must be adjusted to the specific element size used with the material. Other methods also exist to overcome this issue. One is a user-defined function scaling the fracture strain depending on the characteristic element length. This procedure is the so-called “regularization”. In the present study, this method for scaling the failure strain using a user defined table was applied. It considered scaling factors vs. the characteristic element length. This will be investigated further in future studies.

The simulations were conducted with the explicit FEA solver Radioss (version 2020) by Altair Engineering Inc. (1820 E. Big Beaver Rd., Troy MI 48083, USA), on a Windows computer with four Intel i7–6820 CPUs at 2.70 GHz with 32 GB RAM. The failure criterion was developed in FORTRAN as a dynamically linked library (dll) using the freeware MinGW-W64 project with a gcc 7.2.0 compiler [23]. The dll was loaded into RADIOSS during the runtime. The user-failure criterion was used with an existing elasto-plastic, isotropic material law, with a von Mises yield surface, using a tabulated hardening function. The calculation time for the 2160 4-node 1 × 1 mm shell elements was around 355.18 s, taking 192,771 cycles for a 110-ms simulation time with a minimum timestep of 0.555 × 10⁻³ ms and zero mass scaling, which ensured the high-quality results.

Figure 12 (left) shows the final FE model setup using the specimen geometry as used in the real tests. The thickness of the shell elements was defined as 0.025 mm, using the Radioss QEPH (orthotropic, quadrilateral-elasto-plastic element with physical hourglass stabilization) element formulation and one integration point through thickness. The thickness change of elements during the simulation was considered. On the right side of Figure 13, one can see the FE results at a 40-mm displacement, which is just before final fracture of the TD specimen.

Table 3. Failure displacement results in test and simulation.

Orientation (degree)	Displacement at Failure in Test (mm)	Displacement at Failure in Simulation (mm)
0	19.1	18.9
45	34.2	33.5
90	43.2	44.2

shows the displacements at the failure for all three specimens.

Figure 14 shows the correlation of the tested force vs. displacement results (upper) compared to the FEM result curves (lower) for the three material directions using the same failure criterion card.

Table 3 shows the sequence of failures in the model depending on the orthotropy orientation of the material specimen compared to the results obtained by the real tests.

4. Discussion

The objective of the presented study was the development of a numerical method for predicting the mechanical deformation and failure behavior of Li-ion PE separators. Particularly in crash simulations, highly non-linear and orthotropic behavior must be considered. For this purpose, quasi-static and dynamic tests were performed using a typical Li-ion, one-layered separator material. Different orientations of a given material sample were tested using local strain measurements via DIC. For material modeling, an elasto-plastic-associated constitutive law with Hill’s yield surface was used and calibrated separately in the plastic region. Based on the tested failure deflections, a new user-defined failure criterion was developed to simulate the physical effect of orthotropy on the strain at failure. In order to consider load path dependency, a linear damage accumulation rule is implemented. The failure limit of the individual integration points is detected when the damage reaches 1 (=100% damage). If all integration points reach the failure limit, the element will be deleted from the simulation, and its stiffness is set to zero.

In future work, further enhancements in the failure model will be added to simulate dynamic influence on the failure strain, as well as the scatter of the observed results. In addition, an automated or semi-automated regularization method for element length influence will be introduced. Within this work, Hill’s orthotropic yield surface was used. An investigation into a more flexible yield surface according to Pfeiffer [24] will be performed as a next step. Also, experiments under different loading conditions and triaxialities are topics for further investigations.

5. Conclusions and Outlook

The modeling method introduced in this work accurately predicted the stiffness of the tested PE separator. The proposed new failure criterion predicted the failure strain for all three directions within a range of 3% and was in a very good agreement with the performed tests. Some small differences appeared due to the simplified boundary conditions as well as the influence of element length. However, it is noted that the real tests had scatter in a much larger range. The quantitative comparison was made in terms of failure strain response from the three differently oriented cut-out specimens (MD, DD, TD). The present failure criterion and the detailed computational method should be useful in the battery design process and will serve as an important new computational tool for assessing the safety of lithium-ion batteries against high mechanical loading and crashworthiness. The failure model will be implemented in the commercial FE solver Altair Radioss and will thus be available for practical application in e-mobility simulations in the near future.