Optimized Layouts of Borehole Thermal Energy Storage Systems in 4th Generation Grids
Abstract
1. Introduction
2. Case Study Setup
3. System Design Scenarios
3.1. Cooling Operation
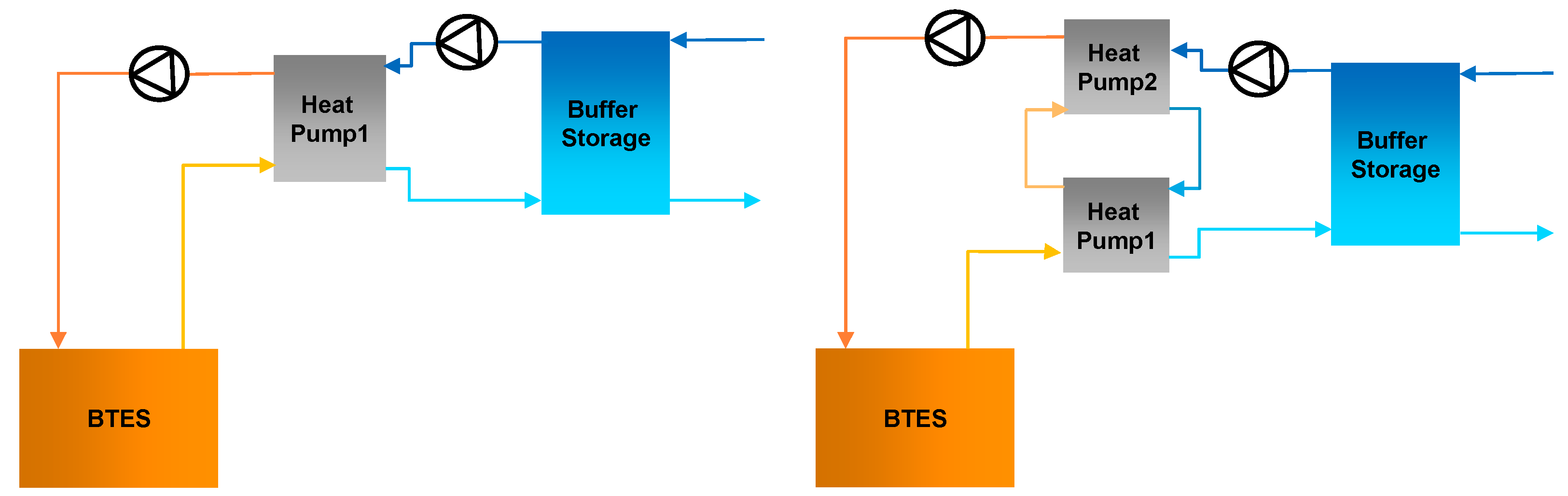
- Active Cooling (Scenarios ActSer and ActPar): The total cooling load is supplied actively by heat pumps, which use the BTES as their heat sink (Figure 2) and
- Passive Cooling (Scenarios PasSer and PasPar): The total cooling load is supplied passively by the BTES using heat exchangers (HEX), which separate load and sink side (Figure 3).
3.2. Heating Operation
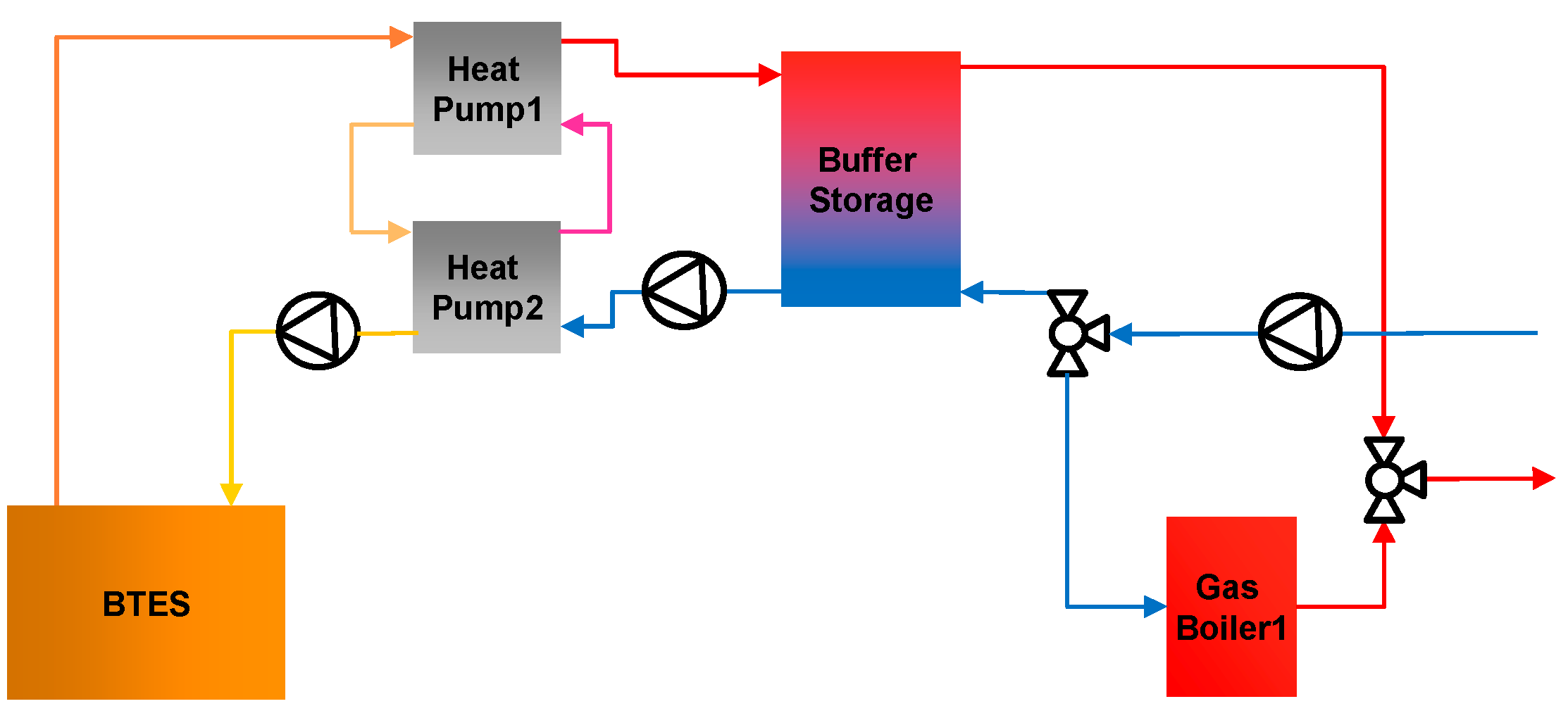
3.2.1. Serial Scenarios
3.2.2. Parallel Scenarios
4. Evaluation Criterion
4.1. Exergy Analysis
4.2. Economic Analysis
4.3. Exergoeconomic Analysis
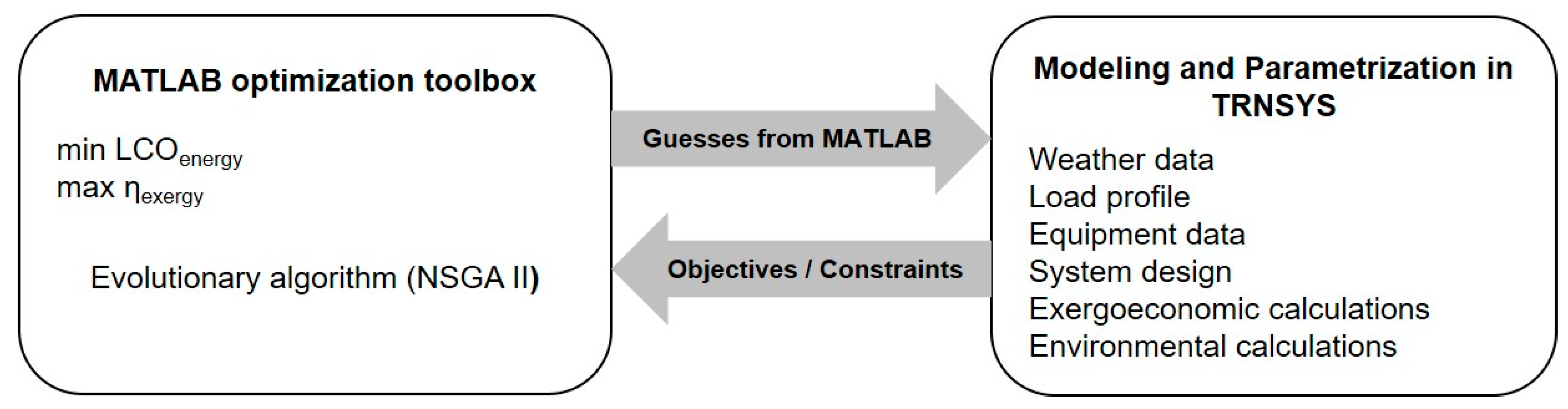
5. Computational Model
5.1. Multi-Objective Optimization
5.2. System Simulation
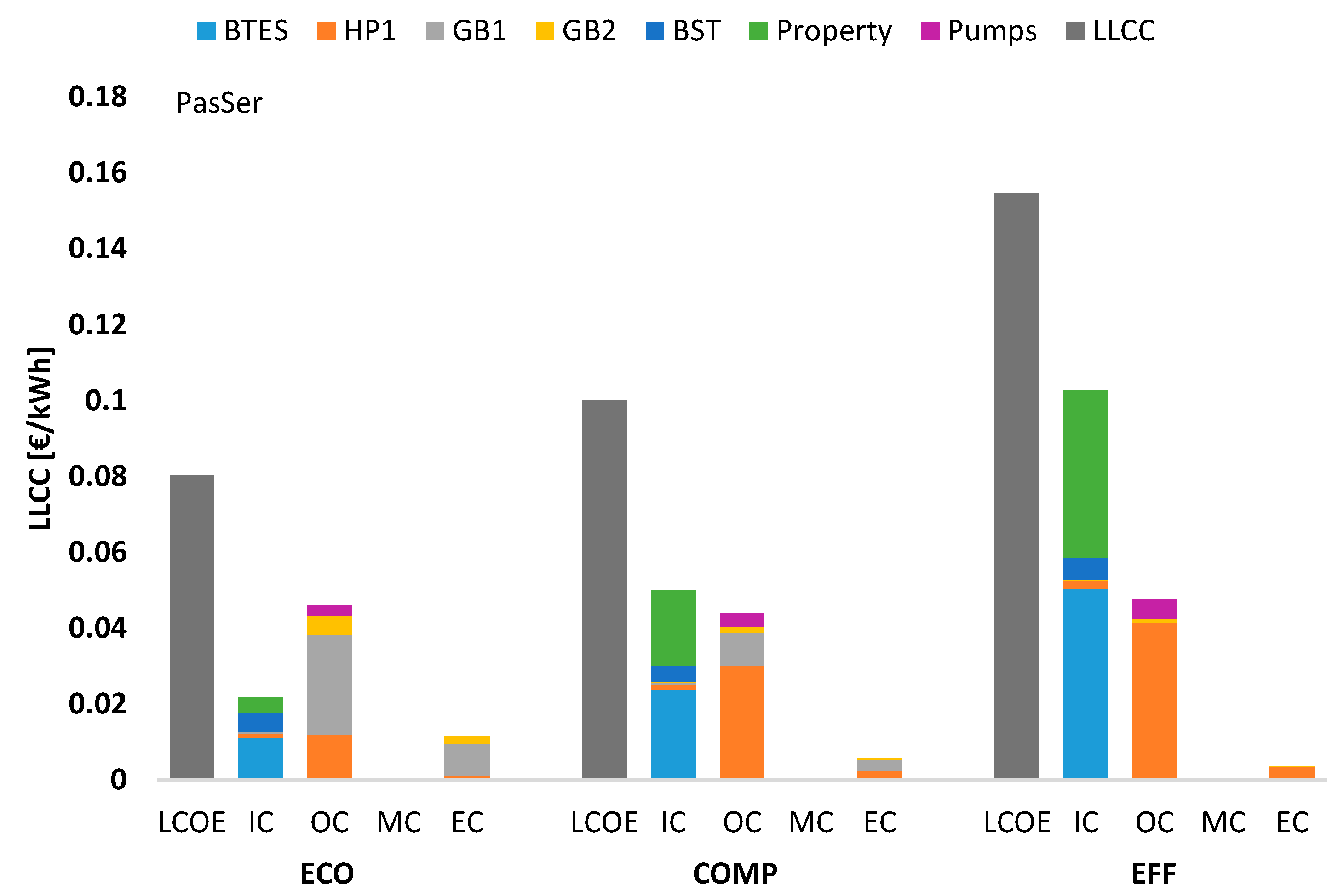
6. Results
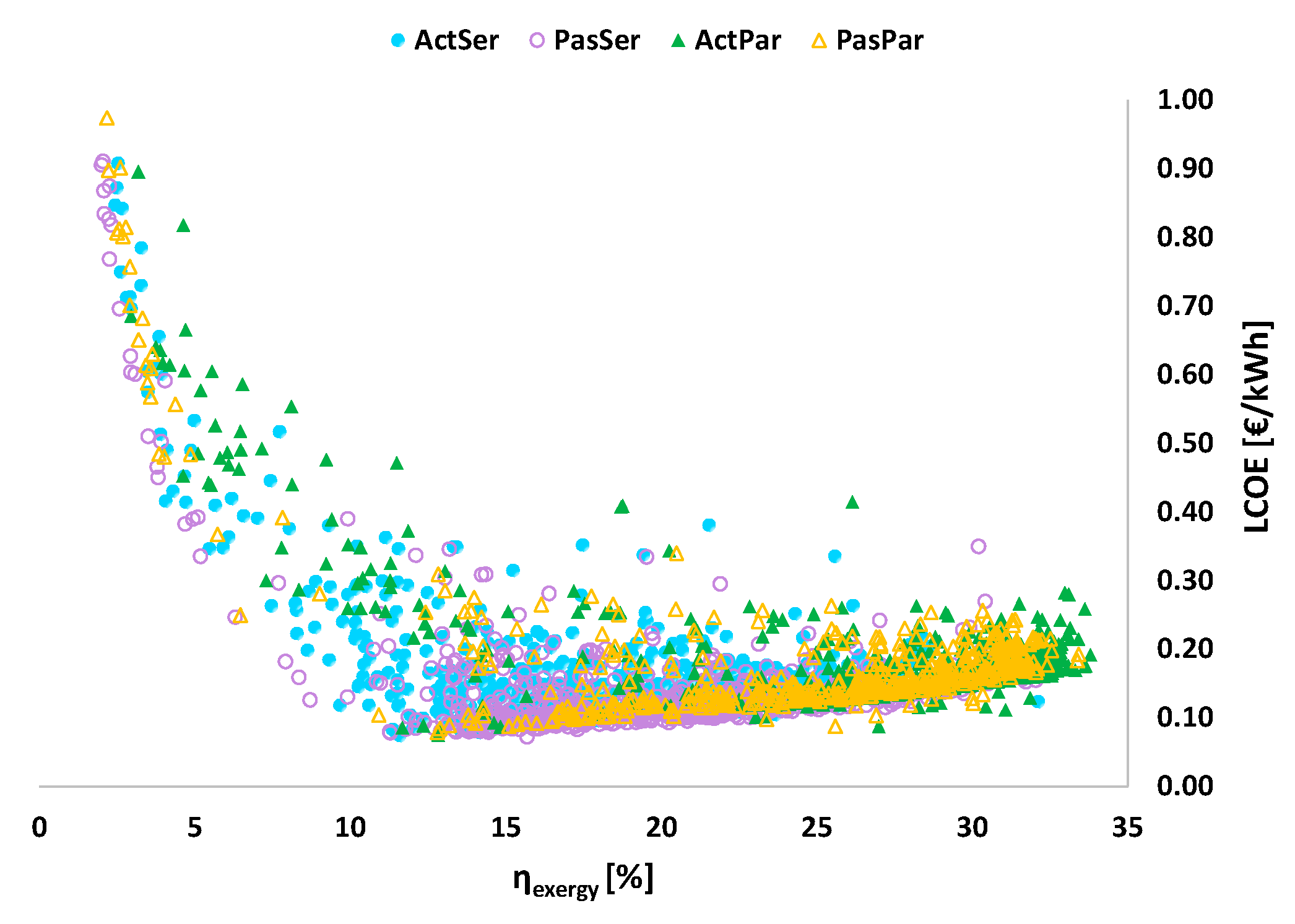
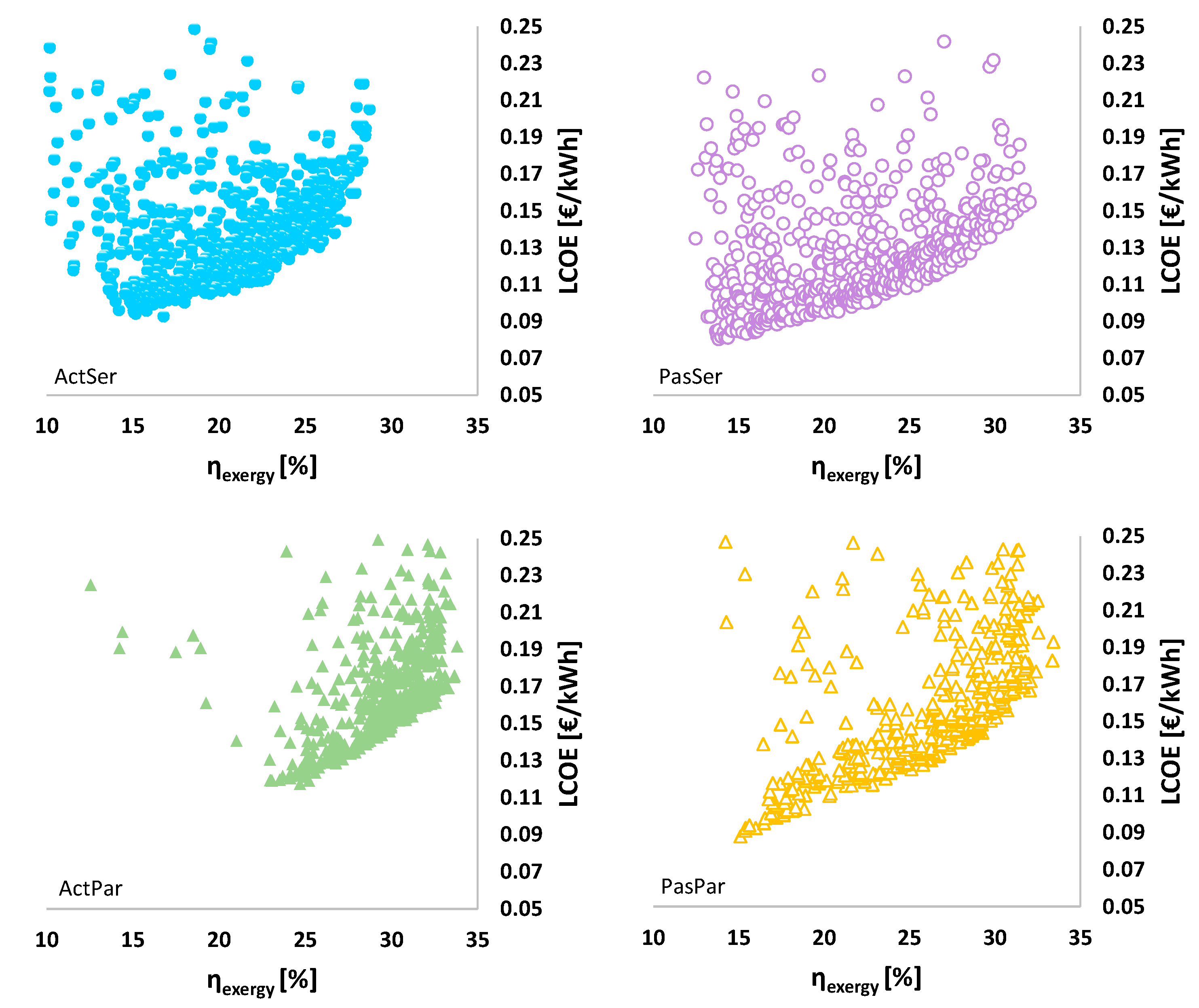
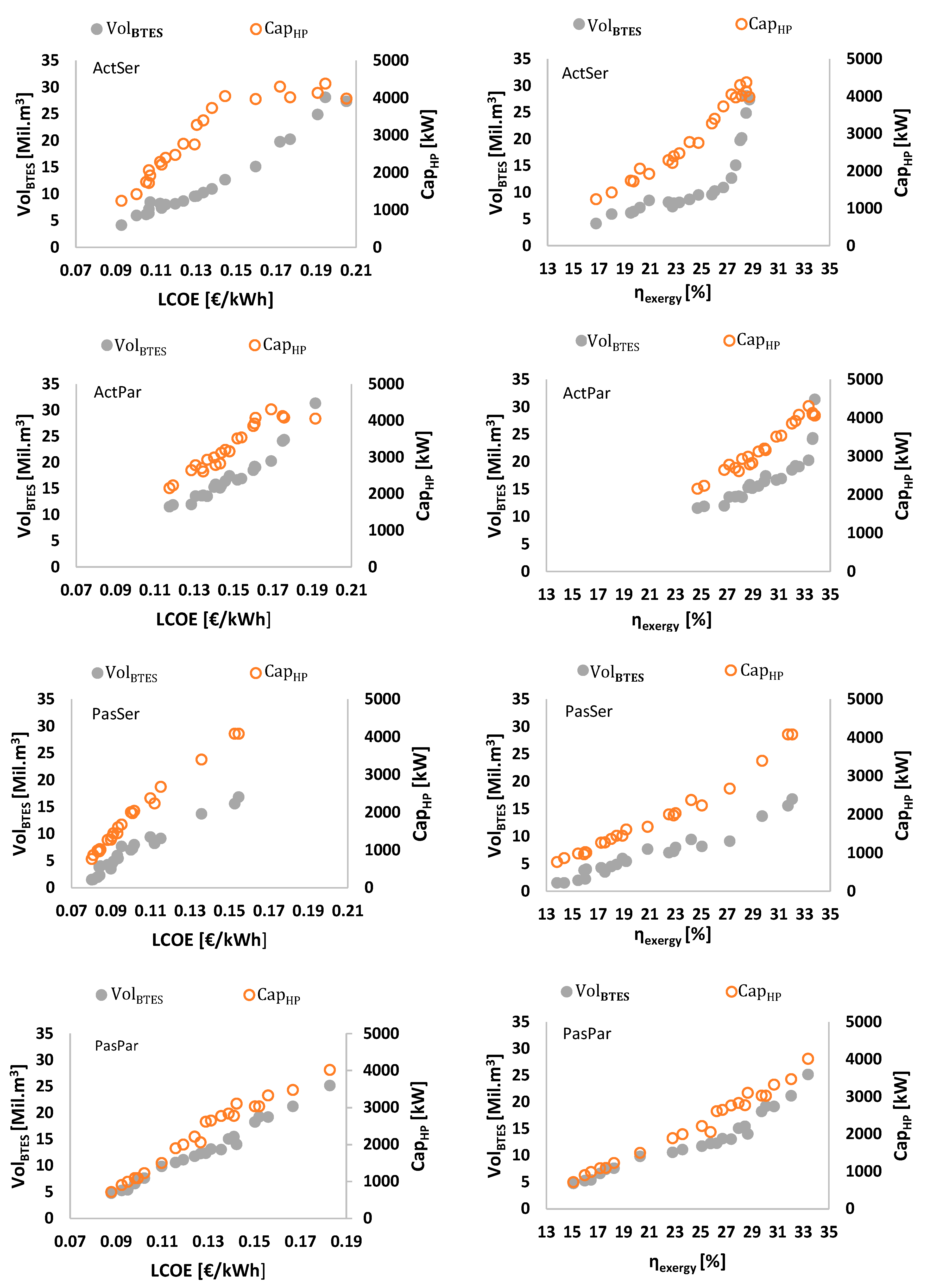
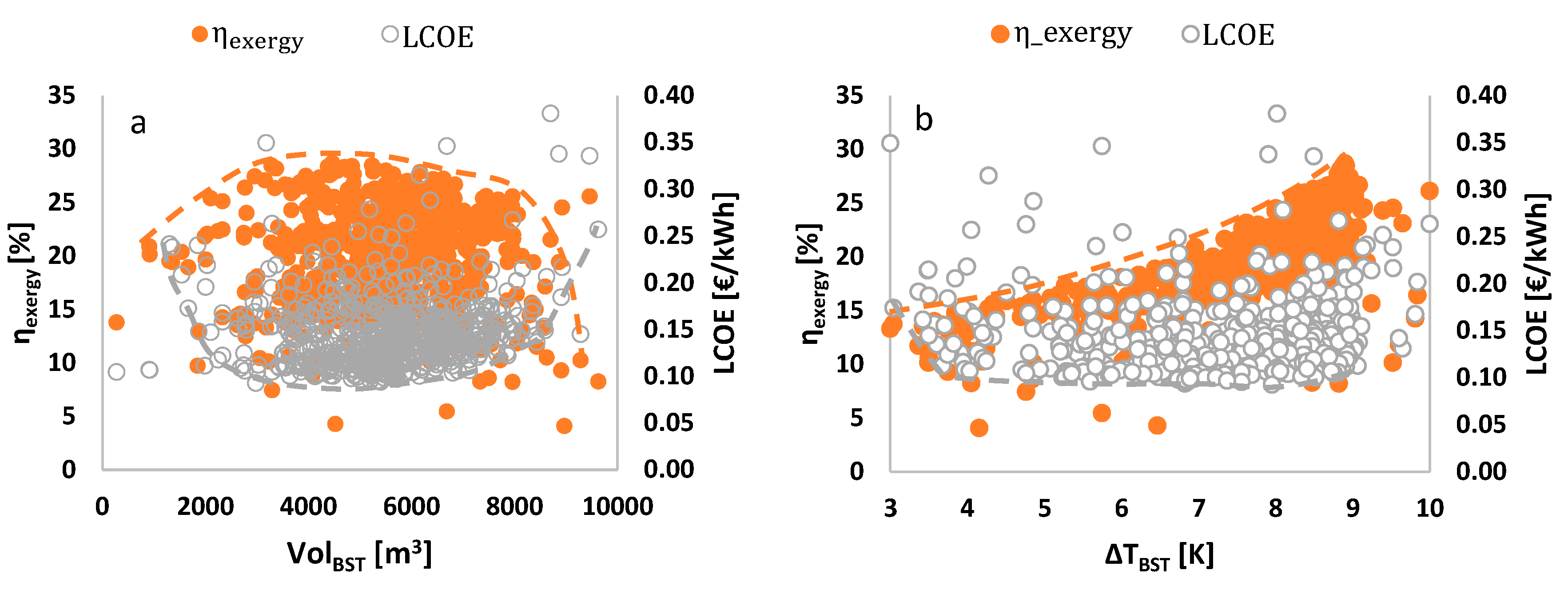
6.1. Pareto Efficient Solutions
6.2. Scenario Analysis
6.2.1. Reference Case
6.2.2. ActSer–Active Cooling and Serial Heating
6.2.3. ActPar–Active Cooling and Parallel Heating
6.2.4. PasSer–Passive Cooling and Serial Heating
6.2.5. PasPar–Passive Cooling and Parallel Heating
6.3. Sensitivity Analysis
6.3.1. Variation of Initial Costs and Energy Costs
6.3.2. Changing Heat Pump Type
6.4. Exergy and Global Warming Potential
7. Discussion
7.1. Limitations
- Load scenarios were calculated based on German standards for renovated buildings. Results of this study can provide design guidelines for buildings with different performances as long as they have the same temperature ranges and similar functionalities. The definition of the DHC grid temperature levels were based on the target return temperatures of low-temperature grids. However, due to simplification, the DHC grid configuration and the associated costs and exergy destruction rates are not considered in this study. Future studies, which assess different building types and grid configurations, and consider DHC pipes and circulation pumps as main components of BTES-assisted DHC grids are required for more comprehensive analysis.
- To set up an optimization algorithm according to real HP data within a wide range, it is assumed that the selected HP consists of a number of HP modules with similar performances. However, there is a maximum limit for the number of HP modules to avoid technical issues in practice. Moreover, according to an inquiry from a HP manufacturer, large-scale HPs can be ordered with desired technical specifications which are easily compatible with part-load applications.
- It is assumed that GBs cover the load which cannot be supplied by the ground loop, without considering the effect of part-load ratio on its performance. However, modulating GBs mainly have a minimum turn-down ratio, which specifies the minimum acceptable part-load ratio. For a more detailed assessment the boiler and the combustion efficiencies need to be provided as a function of entering liquid temperature and device part-load ratio.
- The selected BST volume by the optimization algorithm is allocated to one tank with an aspect ratio (the ratio of height to diameter) of 2.5, according to an estimation regarding an efficient design as well as the maximum acceptable tank height for large-scale applications. Splitting the selected volume into multiple tank units with different aspect ratios can be considered as a future study.
- The project lifetime is considered to be 30 years. Approx. 2000 evaluations, each taking around 20 min, were required for the initial convergence of the optimization algorithm. Consequently, a time step of one hour was considered for the simulations. However, a more detailed assessment required shorter time steps down to a few minutes, which also enables an application of more exact control strategies. The optimization always results in better solutions with shorter time steps and a larger number of evaluations.
- The heat transfer mechanism of the BTES is considered to be conductive. It is also assumed that BTES is installed in the ground with a uniform thermal conductivity and heat capacity. However, in real geothermal applications convective heat transfer might exist and ground thermal characteristics might not be uniform. Moreover, there are always regional limitations for the implementation of large-scale geothermal projects, e.g., unfavorable subsurface conditions or restrictions due to groundwater protection.
- The IC functions (Table 2) are based on the available literature, which are mainly defined by having data from real projects in a specific range. However, due to the large ranges of the optimization boundaries, it is assumed that extrapolation is acceptable. Regarding OCs (Table 3), energy cost functions are specified by the predicted costs from the economic studies for the years 2030 and 2050 and assuming a linear interpolation between the available data points. Similar assumptions have been made for the environmental emissions and the associated costs. Consequently, cost functions are subject to large uncertainties and the sensitivity analysis was done with the purpose of lowering these uncertainties.
7.2. Discussion of Results
8. Conclusions
- In cooling mode, passive strategy yields to a high share of the optimized designs from the most economical up to highly efficient ones. Active cooling with serially-connected heat pumps results in a small share of the optimized designs, which are the most efficient but the most expensive ones.
- In heating mode, maximizing the heating temperature shift by single HPs and supplying the remaining shift up to the grid supply temperature by serially-connected GBs yields to a high percentage of the optimized designs. However, in the most economical design, the maximum 40% of the overall heating share are supplied by this configuration and the rest is met by parallel-operating GBs. The share increases up to 100% for more efficient designs.
- The most efficient but most expensive designs are resulted from covering nearly the overall heating demand on the grid temperature shift by serially-connected HPs and supplying only the peak loads by GBs.
- Larger BTES volumes and corresponding HP capacities mainly result in more efficient designs with higher costs. However, less efficient and more economical designs have higher capacities of GBs. The highest share of exergy destruction comes from HPs for the most efficient and from GBs for the least efficient designs. BTES, BST and HEX have the lowest exergy destruction for all Pareto efficient layouts.
- For the most efficient designs ICs significantly exceed OCs. While the largest share of ICs arises either from the BTES itself or from the property, which is used for building it, the highest share in OCs originates from the HPs. Nevertheless, for the most economical designs, OCs usually exceed ICs. For all layouts, ECs decrease from the most economical to the most efficient designs while MCs increase.
- GWPs decrease with increasing exergetic efficiency and their relation can be expressed with a function. Therefore, by conducting exergoeconomic analysis, thermodynamic inefficiencies as well as environmental impacts are improved. By considering GWPs and as objective functions and comparing the results with the optimized results of this study, further relations between LCA and exergoeconomic analysis and their application for optimization problems can be specified.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ActSet | active serial | |
| ActPar | active parallel | |
| BHE | borehole heat exchanger | |
| BST | buffer storage tank | |
| BTES | borehole thermal energy storage | |
| COMP | compromise | |
| DC | district cooling | |
| DH | district heating | |
| DHC | district heating and cooling | |
| ECO | economical | |
| EFF | efficient | |
| GB | gas boiler | |
| HP | heat pump | |
| NSGA | non-dominated sorting genetic algorithm | |
| PasSer | passive serial | |
| PasPar | passive parallel | |
| Symbols | ||
| A | area | m2 |
| c | specific heat capacity | kJ/(kg K) |
| c | specific cost | €/tCO2, €/kWh |
| Ċ | cost rate | €/yr. |
| Cap | capacity | kW |
| EC | emission cost | €/kWh |
| Ė | thermal exergy rate | kW |
| GWP | global warming potential | CO2/kWh |
| i | discount rate | % |
| IC | initial cost | €/kWh |
| L | length | m |
| LHV | lower heating value | kW |
| LCOE | levelized cost of energy | €/kWh |
| ṁ | flow rate | kg/s |
| MC | maintenance cost | €/kWh |
| OC | operational cost | €/kWh |
| n | year | |
| N | number | |
| Rey | Reynolds number | |
| S | spacing | m |
| T | temperature | °C |
| Vol | Volume | m3 |
| f | fuel consumption | kWh |
| Q̇ | heat flux | kW |
| η | efficiency | % |
| Subscripts | ||
| BHE | borehole heat exchanger | |
| BST | buffer storage tank | |
| BTES | borehole thermal energy storage | |
| CL | cooling load | |
| elec | electricity | |
| env | environmental | |
| f | fuel | |
| HL | heating load | |
| IC | initial cost | |
| MC | maintenance cost | |
| prod | production | |
| ret | return | |
| sup | supply | |
| 0 | reference | |
| b | boundary | |
References
- Fleiter, T.; Steinbach, J.; Ragwitz, M.; Dengler, J.; Köhler, B.; Reitze, F.; Tuille, F.; Hartner, M.; Kranzl, L.; Forthuber, S. Mapping and Analyses of the Current and Future (2020–2030) Heating/Cooling Fuel Deployment (Fossil/Renewables); European Commission, Directorate-General for Energy: Brussel, Belgium, 2016. [Google Scholar]
- Werner, S. European space cooling demands. Energy 2016, 110, 148–156. [Google Scholar] [CrossRef]
- United Nations Department of Economics and Social Affairs, Population Division. World Urbanization Prospects: The 2014 Revision; United Nations Department of Economics and Social Affairs, Population Division: New York, NY, USA, 2015; p. 41. [Google Scholar]
- Rezaie, B.; Rosen, M.A. District heating and cooling: Review of technology and potential enhancements. Appl. Energy 2012, 93, 2–10. [Google Scholar] [CrossRef]
- Werner, S. International review of district heating and cooling. Energy 2017, 137, 617–631. [Google Scholar] [CrossRef]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Schulte, D.O.; Rühaak, W.; Oladyshkin, S.; Welsch, B.; Sass, I. Optimization of medium-deep borehole thermal energy storage systems. Energy Technol. 2016, 4, 104–113. [Google Scholar] [CrossRef]
- Skarphagen, H.; Banks, D.; Frengstad, B.S.; Gether, H. Design considerations for Borehole Thermal Energy Storage (BTES): A review with emphasis on convective heat transfer. Geofluids 2019, 2019, 4961781. [Google Scholar] [CrossRef]
- Welsch, B.; Ruehaak, W.; Schulte, D.O.; Baer, K.; Sass, I. Characteristics of medium deep borehole thermal energy storage. Int. J. Energy Res. 2016, 40, 1855–1868. [Google Scholar] [CrossRef]
- Schulte, D.O.; Welsch, B.; Boockmeyer, A.; Rühaak, W.; Bär, K.; Bauer, S.; Sass, I. Modeling insulated borehole heat exchangers. Environ. Earth Sci. 2016, 75, 910. [Google Scholar] [CrossRef]
- Bär, K.; Rühaak, W.; Welsch, B.; Schulte, D.; Homuth, S.; Sass, I. Seasonal high temperature heat storage with medium deep borehole heat exchangers. Energy Procedia 2015, 76, 351–360. [Google Scholar] [CrossRef]
- Sibbitt, B.; McClenahan, D.; Djebbar, R.; Thornton, J.; Wong, B.; Carriere, J.; Kokko, J. The performance of a high solar fraction seasonal storage district heating system–five years of operation. Energy Procedia 2012, 30, 856–865. [Google Scholar] [CrossRef]
- Bauer, D.; Marx, R.; Nußbicker-Lux, J.; Ochs, F.; Heidemann, W.; Müller-Steinhagen, H. German central solar heating plants with seasonal heat storage. Sol. Energy 2010, 84, 612–623. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M. A unique borehole thermal storage system at University of Ontario Institute of Technology. In Thermal Energy Storage for Sustainable Energy Consumption; Springer: Dordrecht, The Netherlands, 2007; pp. 221–228. [Google Scholar]
- Lanahan, M.; Tabares-Velasco, P.C. Seasonal thermal-energy storage: A critical review on BTES systems, modeling, and system design for higher system efficiency. Energies 2017, 10, 743. [Google Scholar] [CrossRef]
- Formhals, J.; Hemmatabady, H.; Welsch, B.; Schulte, D.O.; Sass, I. A modelica toolbox for the simulation of borehole thermal energy storage systems. Energies 2020, 13, 2327. [Google Scholar] [CrossRef]
- Welsch, B.; Rühaak, W.; Schulte, D.O.; Formhals, J.; Bär, K.; Sass, I. Co-simulation of geothermal applications and HVAC systems. Energy Procedia 2017, 125, 345–352. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Nuss, P. Life Cycle Assessment Handbook: A Guide for Environmentally Sustainable Products; Curran, A.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA; Scrivener Publishing LLC: Salem, MA, USA, 2015. [Google Scholar]
- Welsch, B.; Göllner-Völker, L.; Schulte, D.O.; Bär, K.; Sass, I.; Schebek, L. Environmental and economic assessment of borehole thermal energy storage in district heating systems. Appl. Energy 2018, 216, 73–90. [Google Scholar] [CrossRef]
- Karasu, H.; Dincer, I. Life cycle assessment of integrated thermal energy storage systems in buildings: A case study in Canada. Energy Build. 2020, 217, 109940. [Google Scholar] [CrossRef]
- Kizilkan, O.; Dincer, I. Borehole thermal energy storage system for heating applications: Thermodynamic performance assessment. Energy Convers. Manag. 2015, 90, 53–61. [Google Scholar] [CrossRef]
- Kizilkan, O.; Dincer, I. Exergy analysis of borehole thermal energy storage system for building cooling applications. Energy Build. 2012, 49, 568–574. [Google Scholar] [CrossRef]
- Sayadi, S.; Tsatsaronis, G.; Morosuk, T. Dynamic exergetic assessment of heating and cooling systems in a complex building. Energy Convers. Manag. 2019, 183, 561–576. [Google Scholar] [CrossRef]
- Klein, S.; Beckman, W.; Mitchell, J.; Duffie, J.; Duffie, N.; Freeman, T.; Mitchell, J.; Braun, J.; Evans, B.; Kummer, J. Trnsys 18—Volume 6 Multizone Building Modeling with Type 56 and Trnbuild; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2017; p. 199. [Google Scholar]
- DIN4108. Thermal Protection and Energy Economy in Buildings-Part 2: Minimum Requirements to Thermal Insulation; Beuth Verlag: Berlin, Germany, 2013. [Google Scholar]
- Merkblatt, S. Raumnutzungsdaten für die Energie-und Gebäudetechnik; SIA: Zürich, Switzerland, 2015. [Google Scholar]
- Meteotest. Meteonorm: Irradiation Data for Every Place on Earth. Available online: http://www.meteonorm.com/ (accessed on 12 August 2020).
- Nussbaumer, T. Planungshandbuch Fernwärme; EnergieSchweiz, Bundesamt für Energie: Bern, Switzerland, 2017. [Google Scholar]
- Viessmann GmbH. Available online: www.viessmann.de (accessed on 12 August 2020).
- Gautschi, T. Anergienetze in Betrieb; Städtische Wärmewende: Wien, Austria, 2015. [Google Scholar]
- Waterfurnace Co. Available online: https://www.waterfurnace.com/commercial/products/water-source-geothermal-heat-pumps/ (accessed on 12 August 2020).
- Karim, A.; Burnett, A.; Fawzia, S. Investigation of stratified thermal storage tank performance for heating and cooling applications. Energies 2018, 11, 1049. [Google Scholar] [CrossRef]
- Viessmann GmbH. Available online: https://www.viessmann.de/de/wohngebaeude/gasheizung/vitocrossal.html (accessed on 12 August 2020).
- Viessmann GmbH. Available online: https://www.viessmann.de/de/wohngebaeude/hybridheizung/gas-hybridgeraete/vitocal-250-s.html (accessed on 12 August 2020).
- Sayadi, S.; Tsatsaronisb, G.; Morosuk, T. A New Approach for Applying Dynamic Exergy Analysis and Exergoeconomics to a Building Envelope. Available online: https://pdfs.semanticscholar.org/e5d6/e5929d68b7d153f590d8d8e113ee1e86993b.pdf (accessed on 24 August 2020).
- Bargel, S. Entwicklung eines exergiebasierten Analysemodells zum umfassenden Technologievergleich von Wärmeversorgungssystemen unter Berücksichtigung des Einflusses einer veränderlichen Außentemperatur. Ph.D. Thesis, Ruhr-Universität Bochum, Universitätsbibliothek, Bochum, Germany, 2011. [Google Scholar]
- Short, W.; Packey, D.J.; Holt, T. A Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies; National Renewable Energy Lab.: Golden, CO, USA, 1995. [Google Scholar]
- Luo, J.; Rohn, J.; Bayer, M.; Priess, A. Thermal performance and economic evaluation of double U-tube borehole heat exchanger with three different borehole diameters. Energy Build. 2013, 67, 217–224. [Google Scholar] [CrossRef]
- Statistisches Bundesamt. Available online: https://www.destatis.de/DE/Home/_inhalt.html (accessed on 12 August 2020).
- Croteau, R.; Gosselin, L. Correlations for cost of ground-source heat pumps and for the effect of temperature on their performance. Int. J. Energy Res. 2015, 39, 433–438. [Google Scholar] [CrossRef]
- Mauthner, F.; Herkel, S. Technology and Demonstrators-Technical Report Subtask C–Part C1-C1: Classification and Benchmarking of Solar Thermal Systems in Urban Environments. Available online: http://task52.iea-shc.org/data/sites/1/publications/IEA-SHC-Task52-STC1-Classification-and-benchmarking-Report-2016-03-31.pdf (accessed on 24 August 2020).
- Gebhardt, M.; Kohl, H.; Steinrötter, T. Preisatlas, Ableitung von Kostenfunktionen für Komponenten der rationellen Energienutzung; Institut für Energie und Umwelttechnik eV (IUTA): Duisburg-Rheinhausen, Germany, 2002; pp. 1–356. [Google Scholar]
- Bundesamt, S. Preise–Daten zur Energiepreisentwicklung. Available online: https://www.destatis.de/DE/Themen/Wirtschaft/Preise/Publikationen/Energiepreise/energiepreisentwicklung-pdf-5619001.pdf?__blob=publicationFile (accessed on 24 August 2020).
- Schlesinger, M.; Hofer, P.; Kemmler, A.; Kirchner, A.; Koziel, S.; Ley, A.; Piégsa, A.; Seefeldt, F.; Straßburg, S.; Weinert, K. Entwicklung der Energiemarkte-Energiereferenzprognose: Studie im Auftrag des Bundesministeriums für Wirtschaft und Technologie. Available online: https://www.bmwi.de/Redaktion/DE/Publikationen/Studien/entwicklung-der-energiemaerkte-energiereferenzprognose-endbericht.html (accessed on 24 August 2020).
- German Federal Government. German Federal Government (2019): Climate Action Programme 2030; German Federal Government: Berlin, Germany, 2019.
- Fritsche, U.R.; Greß, H.-W. Der nicht erneuerbare kumulierte Energieverbrauch und THG-Emissionen des deutschen Strommix im Jahr 2016 sowie Ausblicke auf 2020 bis 2050; Internationales Institut für Nachhaltigkeitsanalysen und-strategien GmbH (IINAS): Darmstadt, Germany, 2018. [Google Scholar]
- IINAS (2017): GEMIS-Globales Emissions-Modell Integrierter Systeme-Model and Database; International Institute for Sustainability Analysis and Strategy: Darmstadt, Germany, 2017.
- VDI. VDI 4640 Thermal Use of the Underground. VDI-Gessellschaft Energie und Umwelt (GEU); Beuth Verlag: Berlin, Germany, 2019. [Google Scholar]
- Klein, S.; Beckman, W.; Mitchell, J.; Duffie, J.; Duffie, N.; Freeman, T.; Mitchell, J.; Braun, J.; Evans, B.; Kummer, J. TRNSYS 18–A TRaNsient System Simulation Program, User Manual; Solar Energy Laboratory, University of Wisconsin-Madison: Madison, WI, USA, 2017. [Google Scholar]
- MATLAB. 9.2.0.556344 (R2017a), The MathWorks Inc.: Natick, MA, USA, 2017.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hellstrom, G. Ground Heat Storage: Thermal Analyses of Duct Storage Systems. Ph.D. Thesis, Lund University, Lund, Sweden, 1991. [Google Scholar]
- Mesquita, L.; McClenahan, D.; Thornton, J.; Carriere, J.; Wong, B. Drake Landing Solar Community: 10 Years of Operation. In Proceedings of the ISES Conference Proceedings, Abu Dhabi, UAE, 11 February 2017; pp. 1–12. [Google Scholar]
- Bär, K.; Arndt, D.; Fritsche, J.-G.; Götz, A.E.; Kracht, M.; Hoppe, A.; Sass, I. 3D-Modellierung der tiefengeothermischen Potenziale von Hessen–Eingangsdaten und Potenzialausweisung [3D modelling of the deep geothermal potential of the Federal State of Hesse (Germany)–input data and identifi cation of potential. Z. Dtsch. Ges. Geowiss. 2011, 162, 371–388. [Google Scholar]
- Renaldi, R.; Friedrich, D. Techno-economic analysis of a solar district heating system with seasonal thermal storage in the UK. Appl. Energy 2019, 236, 388–400. [Google Scholar] [CrossRef]
- Allard, Y.; Kummert, M.; Bernier, M.; Moreau, A. Intermodel comparison and experimental validation of electrical water heater models in TRNSYS. In Proceedings of the Building Simulation, Sydney, Australia, 14 November 2011; pp. 688–695. [Google Scholar]
- Baldwin, C.; Cruickshank, C.A. Using TRNSYS types 4, 60, and 534 to model residential cold thermal storage using water and water/glycol solutions. In Proceedings of the IBPSA-Canada’s eSim Conference, Hamilton, ON, Canada, 3–6 May 2016; pp. 335–348. [Google Scholar]
- LIPP GmbH. Available online: https://www.lipp-system.de/tanks/thermal-storage-tanks (accessed on 12 August 2020).
- Trane Co. Available online: https://www.trane.com/commercial/north-america/us/en/products-systems/equipment/unitary/water-source-heat-pumps.html (accessed on 12 August 2020).
- Viessmann GmbH. Available online: https://www.viessmann.de/de/wohngebaeude/waermepumpe/sole-wasser-waermepumpen/vitocal-350-g.html (accessed on 12 August 2020).
- Ökobaudat–Sustainable Construction Information Portal. Available online: https://www.oekobaudat.de/OEKOBAU.DAT/ (accessed on 12 August 2020).
- Miedaner, O.; Mangold, D.; Sørensen, P.A. Borehole thermal energy storage systems in Germany and Denmark-Construction and operation experiences. In Proceedings of the 13th International Conference on Energy Storage, Beijing, China, 19–21 May 2015; pp. 1–8. [Google Scholar]
- BMWi-This Is How Germans Heat Their Homes. Available online: https://www.bmwi-energiewende.de/EWD/Redaktion/EN/Newsletter/2015/09/Meldung/infografik-heizsysteme.html (accessed on 12 August 2020).




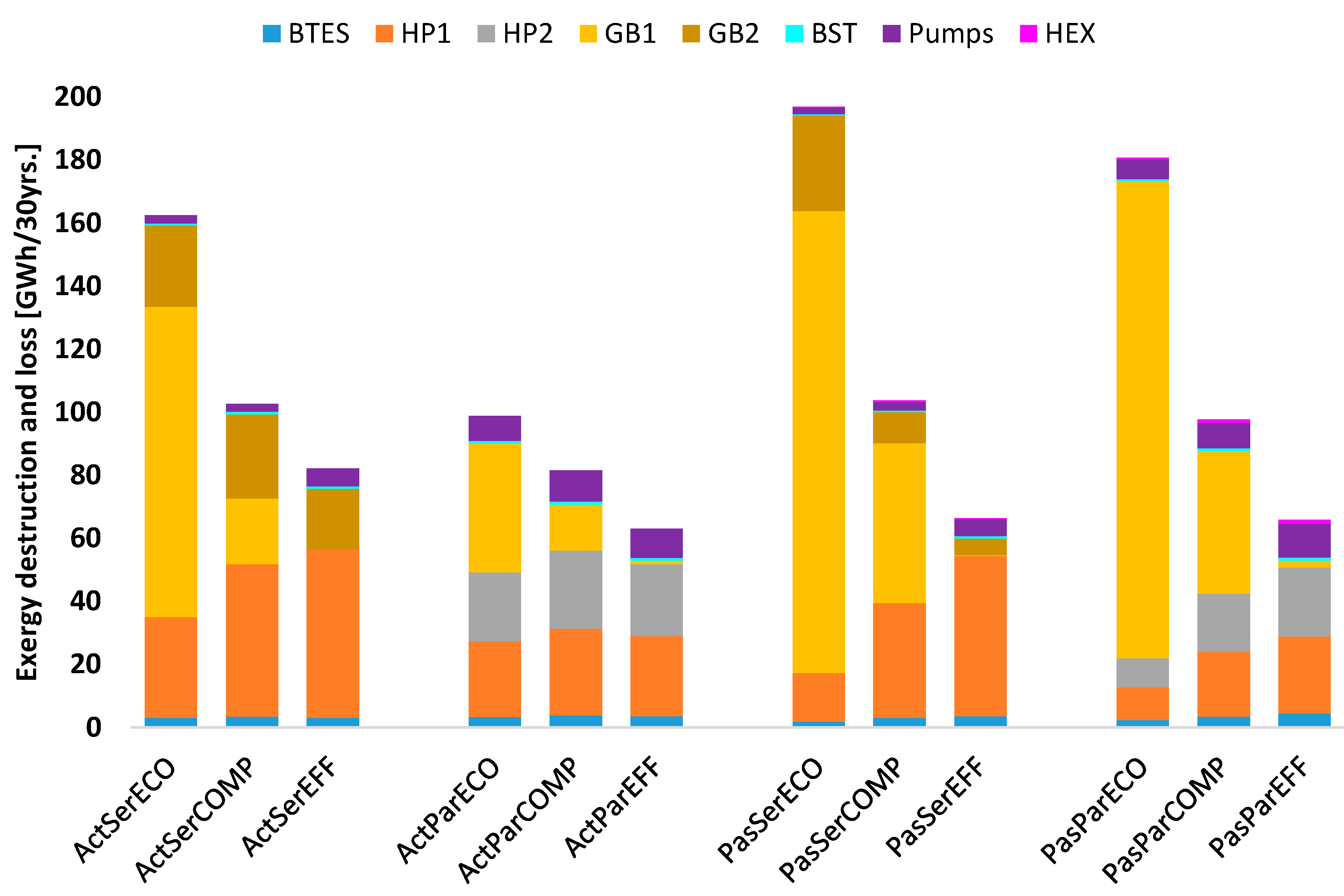






| Scenario | Cooling | GB | HPs | BST |
|---|---|---|---|---|
| ActSer | Active | Serial | Single stage | Cooling/Heating |
| ActPar | Active | Parallel | Double stage | Cooling/Heating |
| PasSer | Passive | Serial | Single stage | Cooling/Heating |
| PasPar | Passive | Parallel | Double stage | Cooling/Heating |
| Component | Investment Cost Function (€) | Maintenance (€/yr.) | Reference |
|---|---|---|---|
| BTES | 65 × LBHE | - | [39] |
| Property | 75.05 × AProperty | - | [40] |
| HP | (2053.8·CapHP−0.348) × CapHP | 0.0075 × CIC | [41] |
| BST | (130 + 11,680·VolBST−0.5545) × VolBST | - | [42] |
| GB | (11,418.60 + 64.6115·CapGB0.7978) × fGB a | 0.02 × CIC | [43] |
| Parameter | Cost Function 2020–2030 | Cost Function 2030–2050 | Reference |
|---|---|---|---|
| Celec,n(€/kWh) | 0.002364n + 0.131 | −0.0005n + 0.1625 | [44,45] |
| Cgas,n(€/kWh) | 0.00216n + 0.0268 | 0.00321n + 0.04702 | [44,45] |
| cCO2,n(€/tCO2) | −0.2083n2 + 9.072n + 5.553 | 80 | [46] |
| GWPelec,n(tCO2/kWh) | (−20.99n + 423.89) × 10−6 | (−8.595n + 287.55) × 10−6 | [47] |
| GWPgas,n(tCO2/kWh) | 250 × 10−6 | 250 × 10−6 | [48] |
| Subject to | Reason |
|---|---|
| 30 m ≤ LBHE ≤ 400 m | Length range of shallow BHEs [49] |
| 30 ≤ NBHE ≤ 1200 | Heat transfer range of BHEs (W/m), corresponds to LBHE |
| 2 m ≤ SBHE ≤ 25 m | Maximum available surface area |
| 50 kW ≤ CapHP ≤ 8150 kW | Minimum capacity of each HP module/Maximum heating load |
| 25 m3 ≤ VolBST ≤ 10,000 m3 | HP min. running time/continuous HP operation in peak load |
| 3 K ≤ ΔTBST b ≤ 10 K | Minimum temperature shift of HPs/Grid temperature shift |
| Constraints | Reason |
| ReyBHE ≥ 2300 | Minimum Reynolds number for turbulent flow in BHEs |
| TBHE,in ≥ −5 °C | Minimum peak load BHE inlet temperature [49] |
| Component | Parameter | Value | Component | Parameter | Value |
|---|---|---|---|---|---|
| BTES | BHE type | 2U | HP | 1st stage cooling capacity | 102.9 kW |
| Type 557 | Boreholes in series | 6 | Type 1221 c | 2nd stage cooling capacity | 56.1 kW |
| Borehole radius | 0.065 m | 1st stage cooling power | 22.9 kW | ||
| Pipe outer/inner radius | 0.016/0.0131 m | 2nd stage cooling power | 10.2 kW | ||
| Pipe thermal conductivity | 0.38 W/m.K | 1st stage heating capacity | 86.9 kW | ||
| BTES thermal conductivity | 2.6 W/m.K | 2nd stage heating capacity | 49.8 kW | ||
| BTES heat capacity | 2080 kJ/m3.K | 1st stage heating power | 28.9 kW | ||
| Grout thermal conductivity | 2 W/m.K | 2nd stage heating power | 15.1 kW | ||
| Fluid specific heat (EG 25%) | 3.811 kJ/kg.K | ||||
| BST | Number of tank nodes | 30 | HP | Cooling capacity | 59.8 kW |
| Type 534 | Number of ports | 4 | Type 927 c | Cooling power | 13 kW |
| Aspect ratio | 2.5 | Heating capacity | 50.6 kW | ||
| Loss Coefficient | 0.15 W/m2.K | Heating power | 18 kW | ||
| Pump | Total pump efficiency | 60% | Boiler | Efficiency | 95% |
| Type 110 | Type 700 | ||||
| Thermostat | Dead band temperature | 0.5 K | HEX | Effectiveness | 0.895 |
| 106, 113 | Type 91 |
| Scenario | LBHE [m] | NBHE | SBHE [m] | CapHP [kW] | VolBST [m3] | ΔTBST [K] |
|---|---|---|---|---|---|---|
| ActSer | 95–155 | 294–1194 | 10.7–15.1 | 1264–4400 | 917–6847 | 7.9–9.1 |
| ActPar | 156–200 | 426–924 | 11.4–15 | 2175–4349 | 1260–5630 | - |
| PasSer | 143–169 | 222–1026 | 7.3–11.6 | 809–4097 | 795–6356 | 6.7–9.8 |
| PasPar | 159–224 | 174–1008 | 11.3–14 | 759–4046 | 1459–7045 | - |
| Scenario | LCOE [ct/kWh] | ηexergy [%] | LBHE [m] | NBHE | SBHE [m] | CapHP [kW] | VolBST [m3] | ΔTBST [K] | |
|---|---|---|---|---|---|---|---|---|---|
| ActSer | Economical | 9.27 | 16.77 | 112 | 294 | 12.0 | 1264 | 2989 | 7.95 |
| Compromise | 12.37 | 24.05 | 116 | 702 | 11.0 | 2782 | 4646 | 8.59 | |
| Most efficient | 19.45 | 28.49 | 136 | 1036 | 15.1 | 4400 | 3281 | 8.91 | |
| ActPar | Economical | 11.73 | 24.69 | 190 | 426 | 12.8 | 2175 | 1260 | - |
| Compromise | 14.37 | 29.42 | 170 | 660 | 12.6 | 3136 | 5420 | - | |
| Most efficient | 19.16 | 33.80 | 175 | 918 | 15.0 | 4097 | 4307 | - | |
| PasSer | Economical | 8.02 | 13.81 | 145 | 222 | 7.4 | 809 | 3556 | 6.68 |
| Compromise | 10.00 | 22.47 | 143 | 480 | 10.9 | 2007 | 3008 | 9.50 | |
| Most efficient | 15.47 | 32.04 | 153 | 942 | 11.6 | 4097 | 4658 | 9.65 | |
| PasPar | Economical | 8.79 | 15.10 | 185 | 174 | 12.9 | 758 | 4186 | - |
| Compromise | 12.66 | 25.78 | 164 | 636 | 11.6 | 2073 | 4007 | - | |
| Most efficient | 18.29 | 33.38 | 162 | 1008 | 13.3 | 4046 | 5128 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hemmatabady, H.; Formhals, J.; Welsch, B.; Schulte, D.O.; Sass, I. Optimized Layouts of Borehole Thermal Energy Storage Systems in 4th Generation Grids. Energies 2020, 13, 4405. https://doi.org/10.3390/en13174405
Hemmatabady H, Formhals J, Welsch B, Schulte DO, Sass I. Optimized Layouts of Borehole Thermal Energy Storage Systems in 4th Generation Grids. Energies. 2020; 13(17):4405. https://doi.org/10.3390/en13174405
Chicago/Turabian StyleHemmatabady, Hoofar, Julian Formhals, Bastian Welsch, Daniel Otto Schulte, and Ingo Sass. 2020. "Optimized Layouts of Borehole Thermal Energy Storage Systems in 4th Generation Grids" Energies 13, no. 17: 4405. https://doi.org/10.3390/en13174405
APA StyleHemmatabady, H., Formhals, J., Welsch, B., Schulte, D. O., & Sass, I. (2020). Optimized Layouts of Borehole Thermal Energy Storage Systems in 4th Generation Grids. Energies, 13(17), 4405. https://doi.org/10.3390/en13174405







