Thermal Bridge Modeling and a Dynamic Analysis Method Using the Analogy of a Steady-State Thermal Bridge Analysis and System Identification Process for Building Energy Simulation: Methodology and Validation
Abstract
:1. Introduction
2. Thermal Bridge Modeling and Analysis Methods
3. Methodology
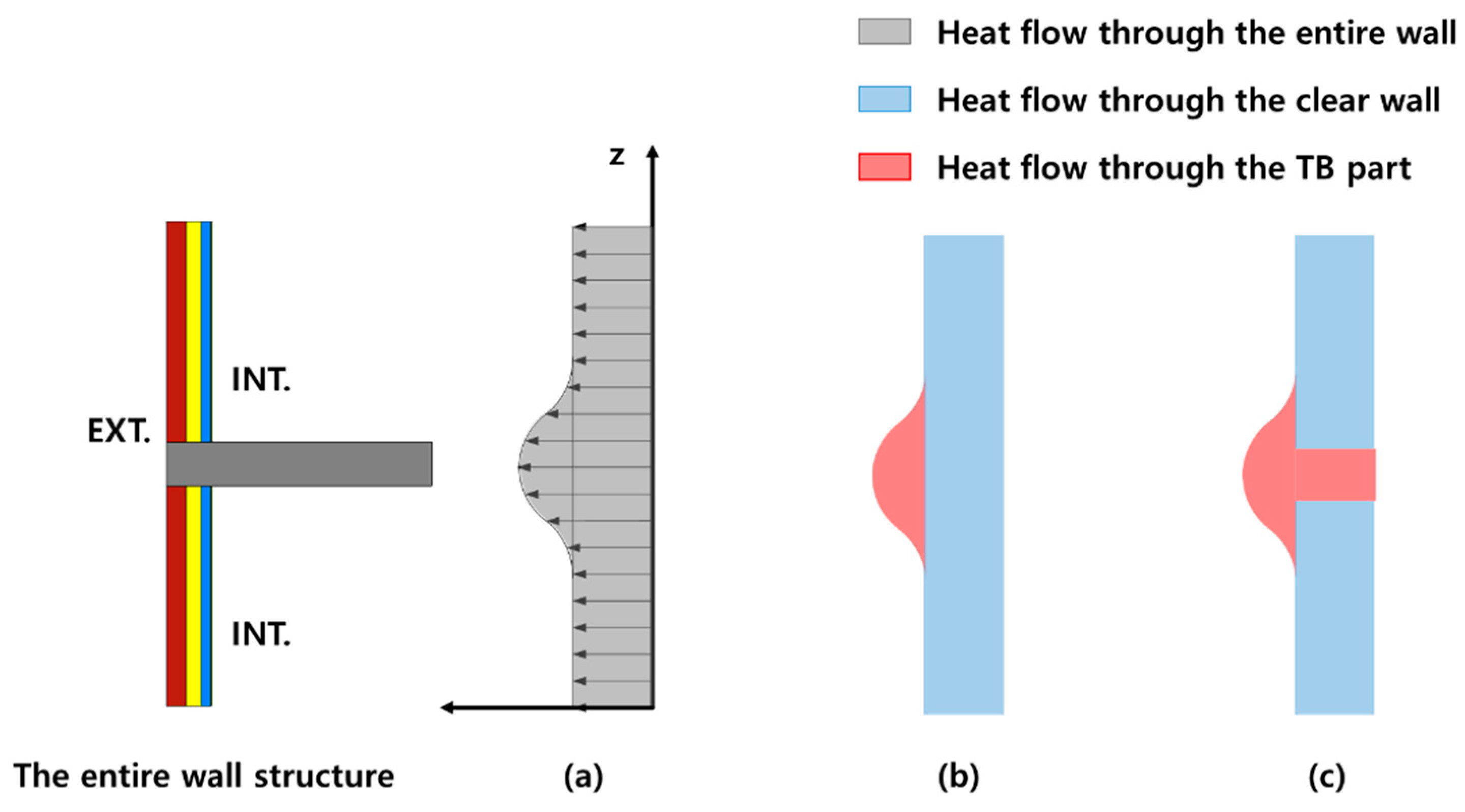
3.1. Analogy of Steady-State Thermal Bridge Analysis
3.2. Linear Time Invariant System for the Thermal Bridge Part and System Order
3.3. Thermal Bridge Transfer Function and System Identification
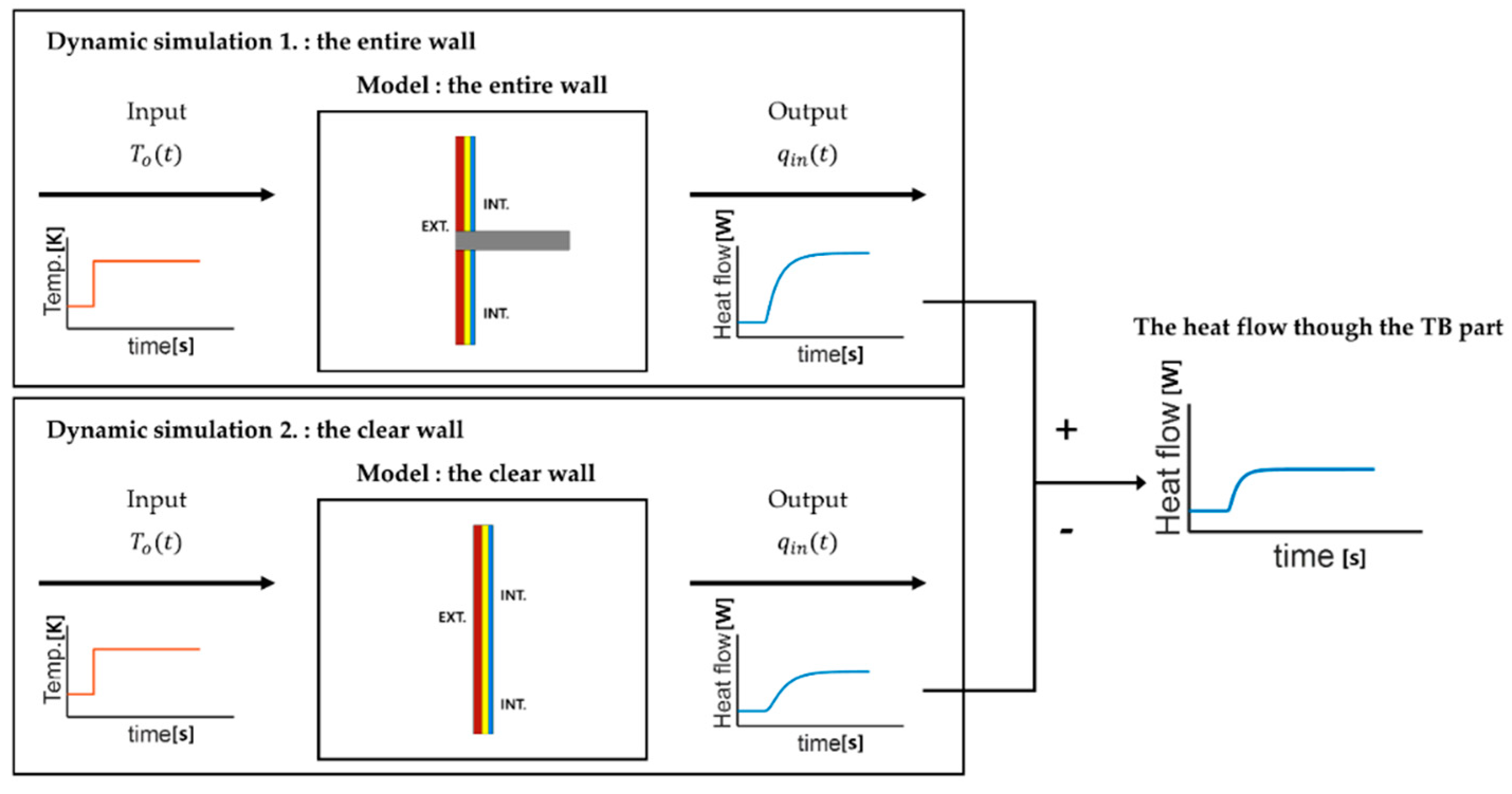
3.4. Procedure
- Step 1: Disaggregation stageDetermine the dimensional system.
- Step 2: Dynamic simulation stagePerform the dynamic simulation of the entire wall and the clear wall.
- Step 3: Model construction stageChoose the LTI system order of the TB part and construct the TBTF.
- Step 4: System identification stageObtain the parameter of TBTF using the system identification process.
4. Explanatory Example
4.1. Disaggregation Stage: Step 1
4.2. Dynamic Simulation for System Identification: Step 2
4.3. Model Construction and Transfer Function: Step 3
4.4. System Identification: Step 4
5. Results and Validation
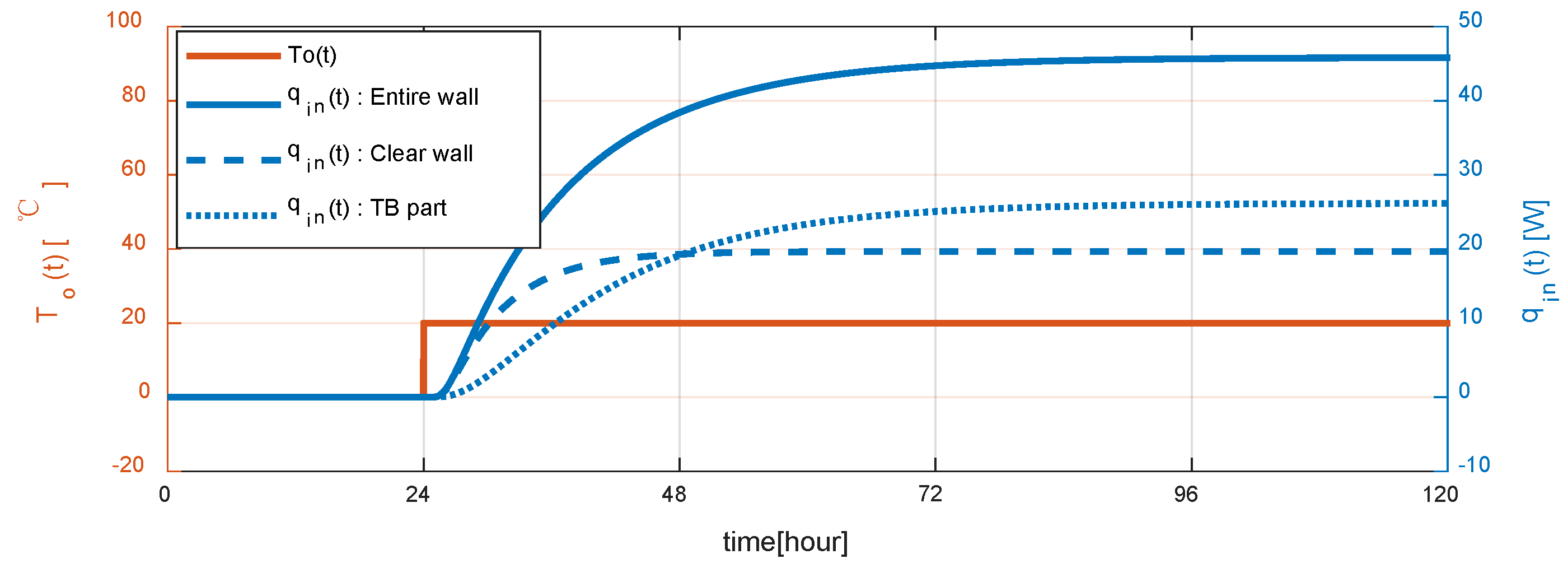
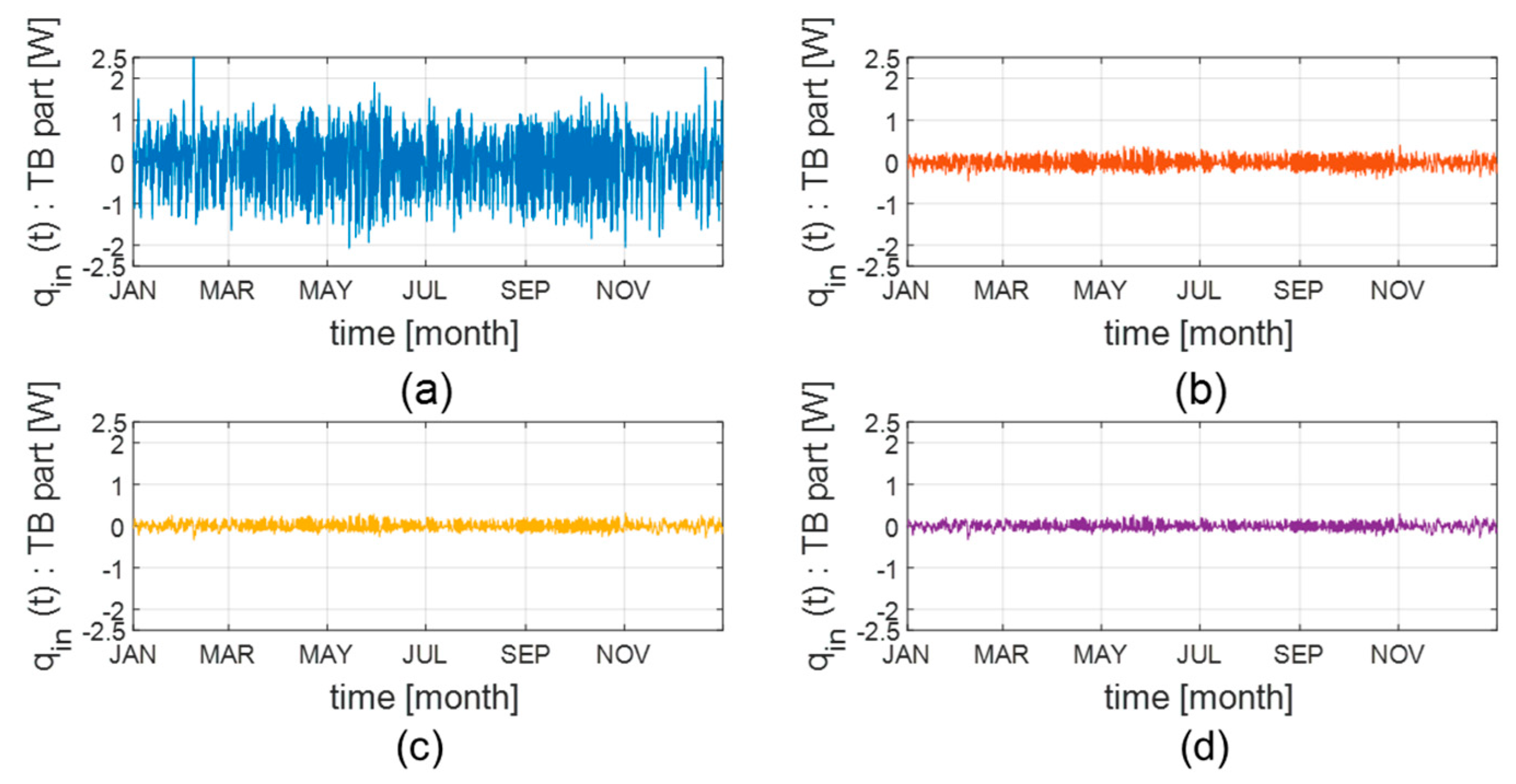
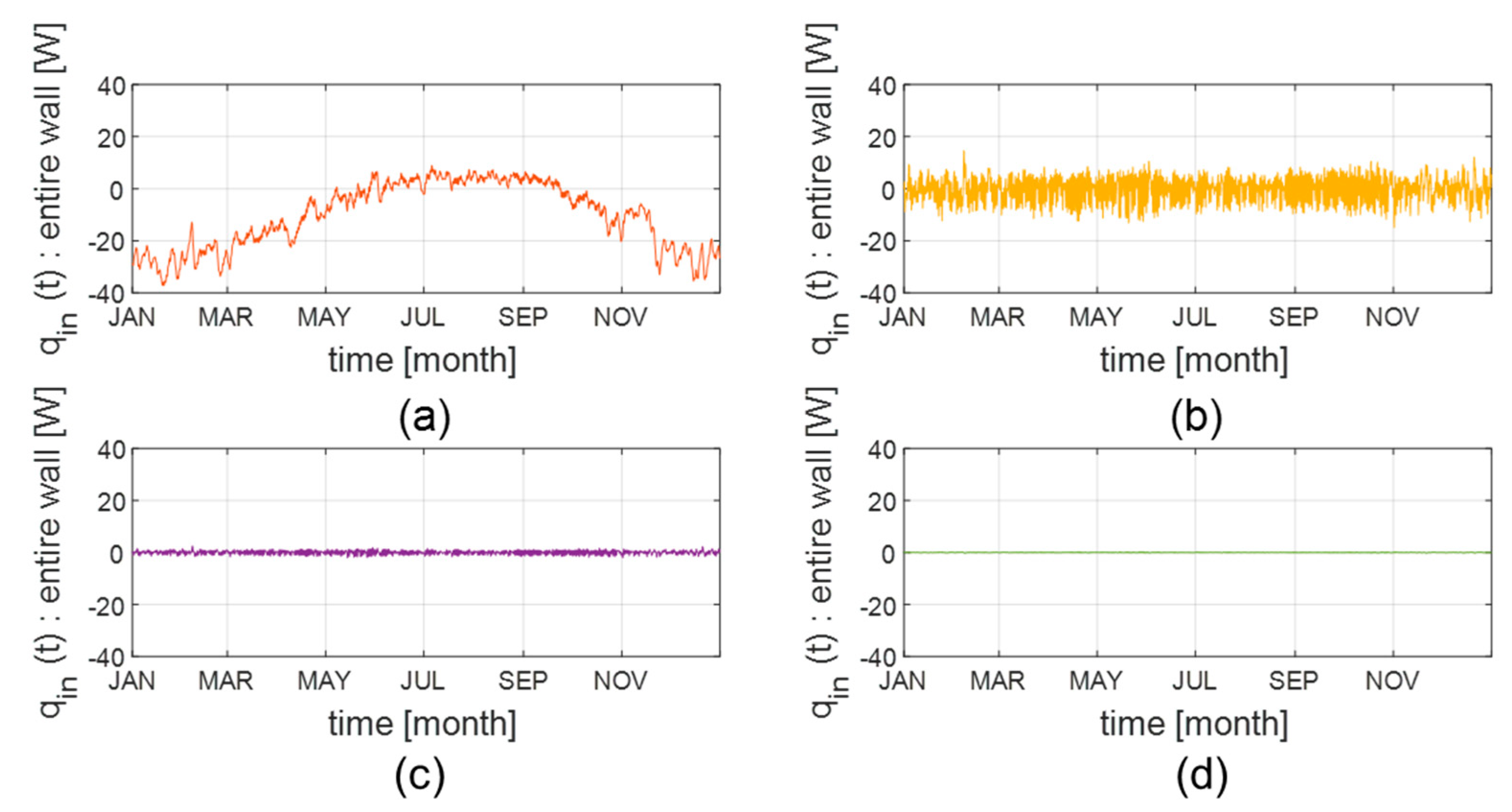
5.1. Dynamic Simulation Results and System Identification Results
5.2. Validation of the System Identification
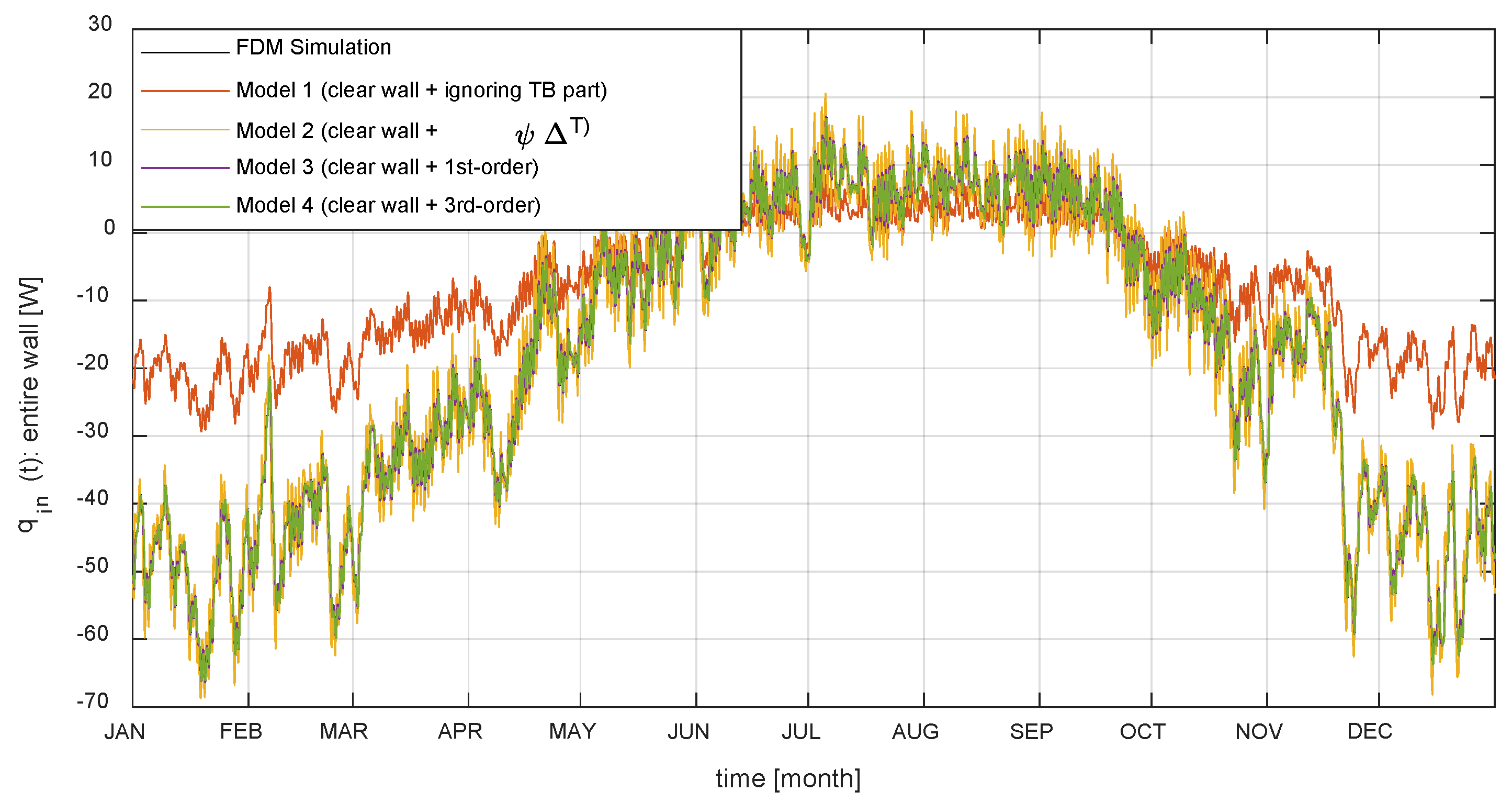
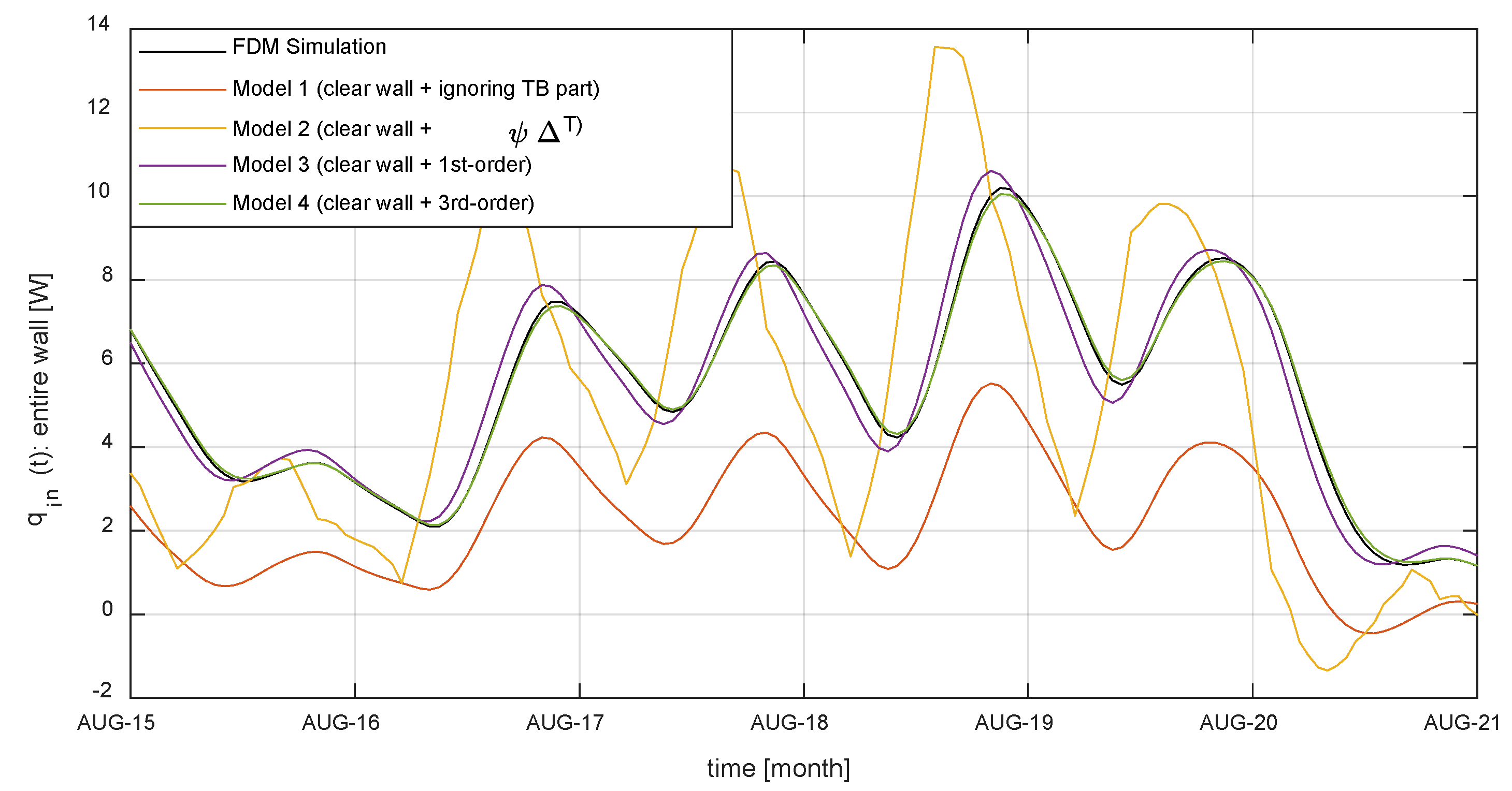
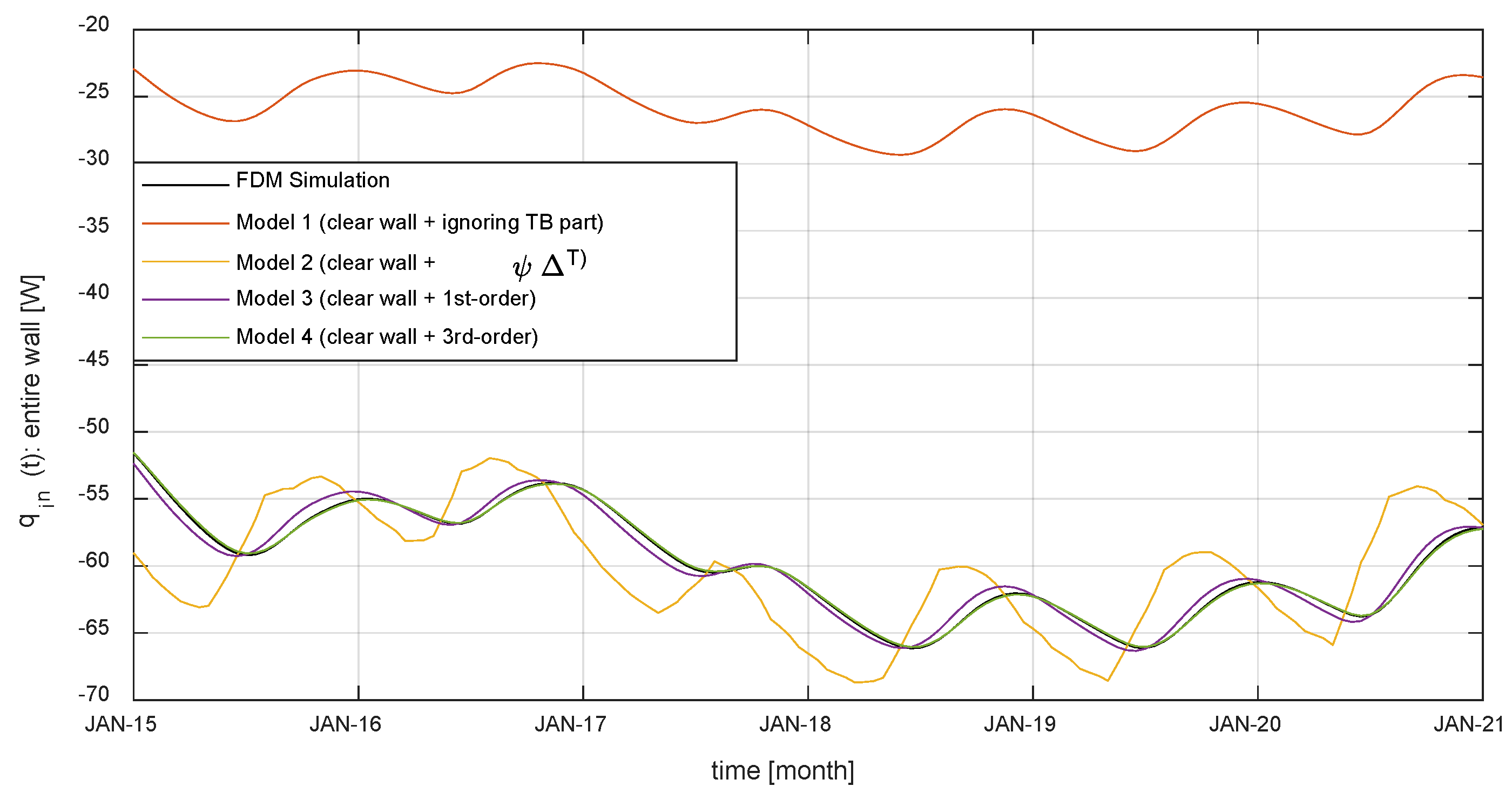
6. Comparison and Discussion
- FDM simulation: A model defined as a true value in this comparison simulated by the FDM method;
- Model 1: A model that ignores TB and analyzes only the clear wall (clear wall + ignored TB part);
- Model 2: A model that simply analyzes a TB part in a steady-state condition (clear wall + );
- Model 3: A model that proposes the TB part as a first-order system (clear wall + 1st-order);
- Model 4: A model that proposes the TB part as a third-order system (clear wall + 3rd-order).
7. Conclusions
- The proposed TB model is simple because it can be expressed with several parameters according to the system order as a transfer function. When the TB is modeled with a third-order system, the TB model can be expressed with only four parameters (one parameter for the numerator and three parameters for the denominator).
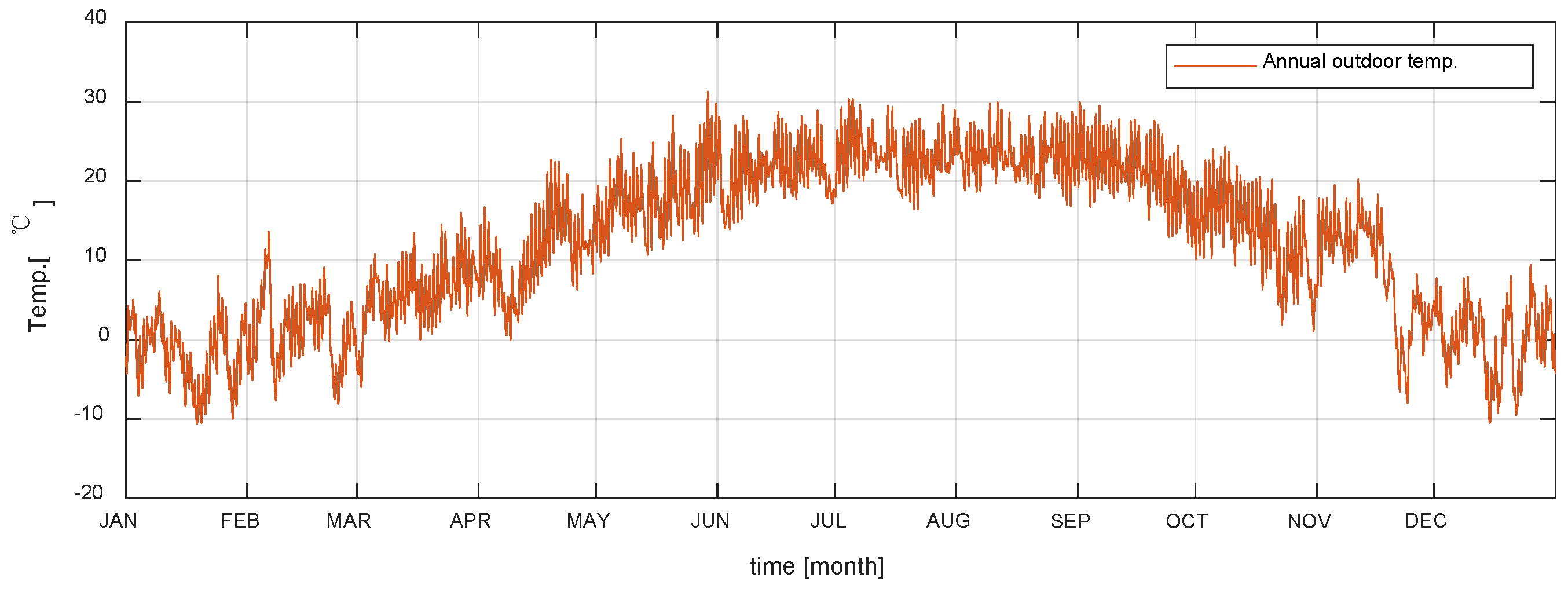
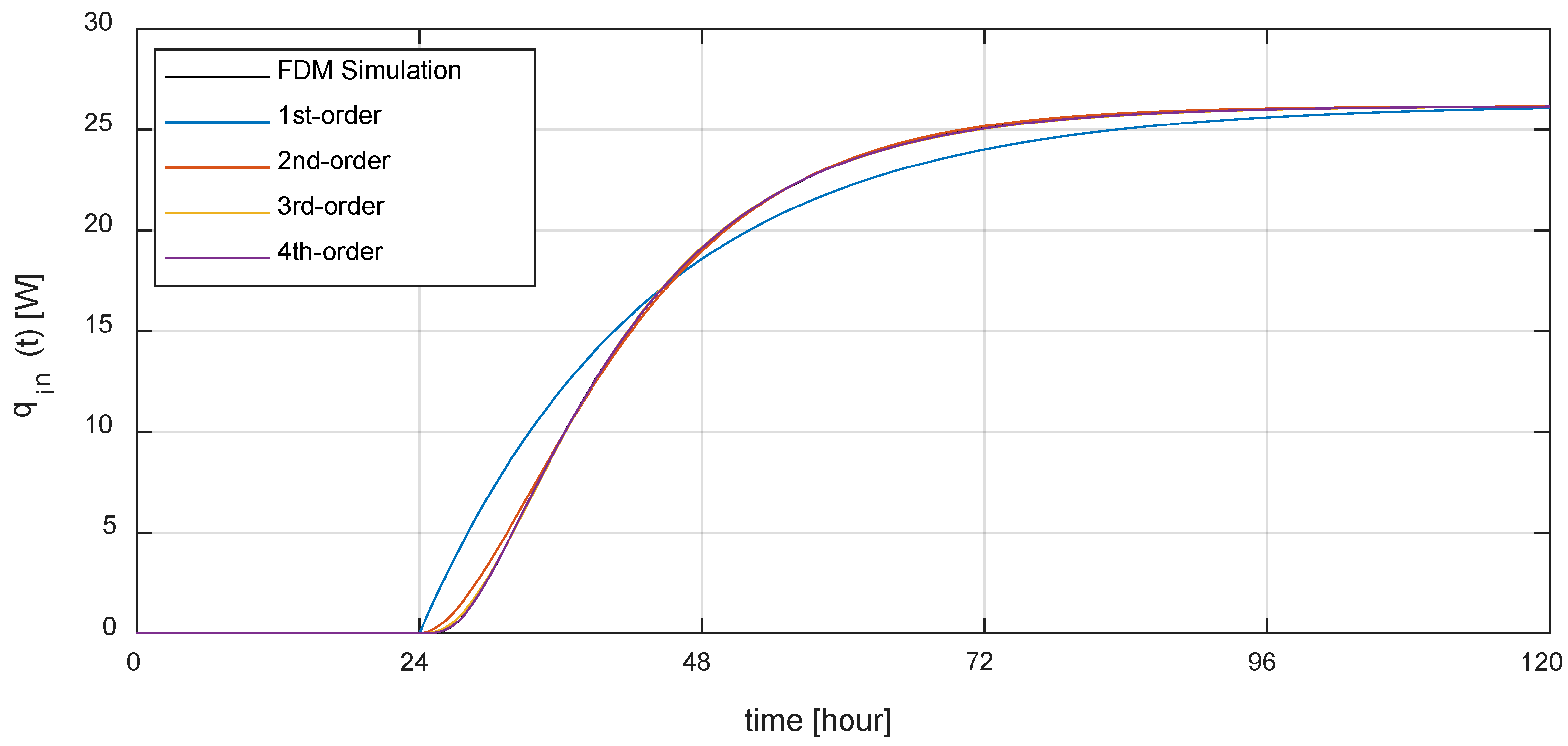
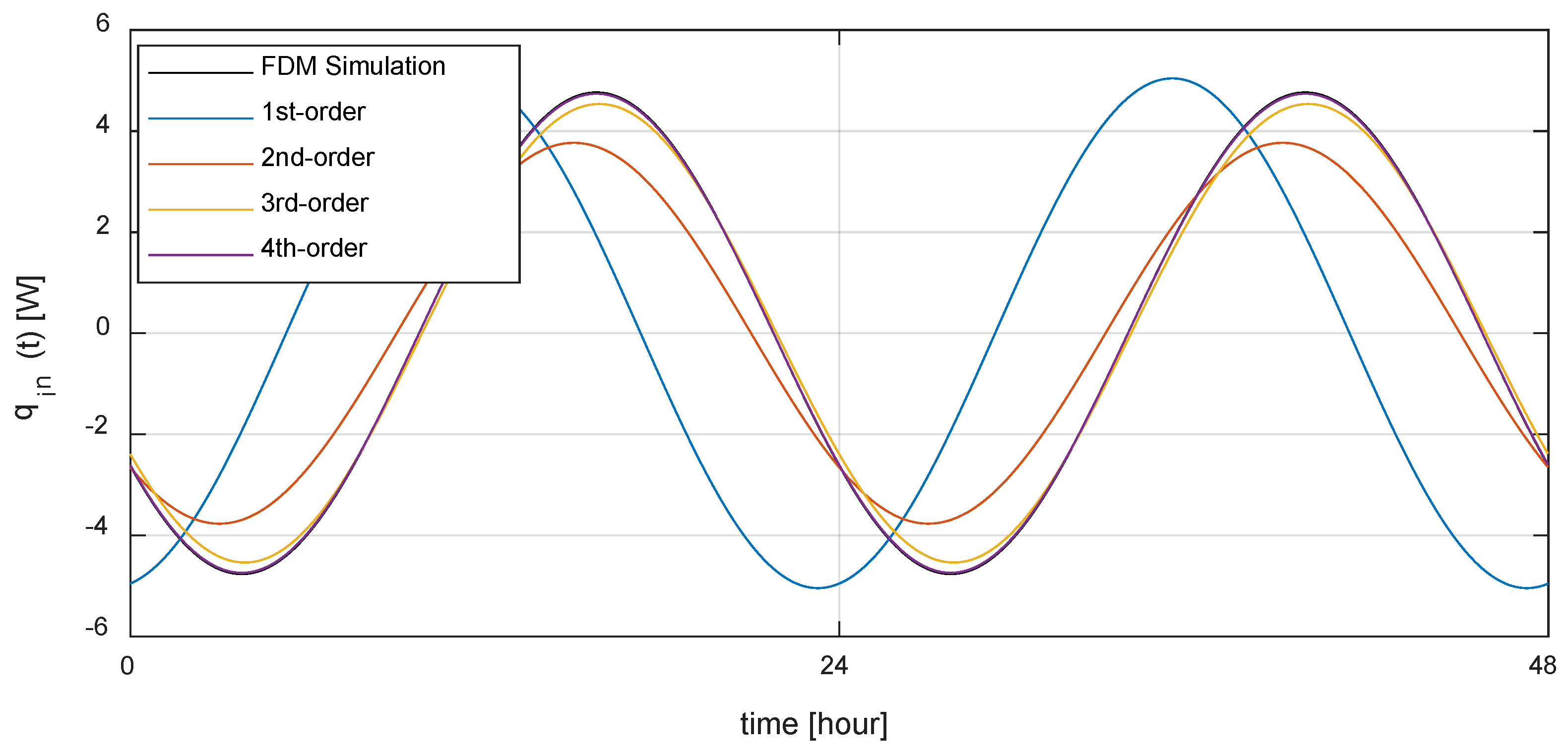
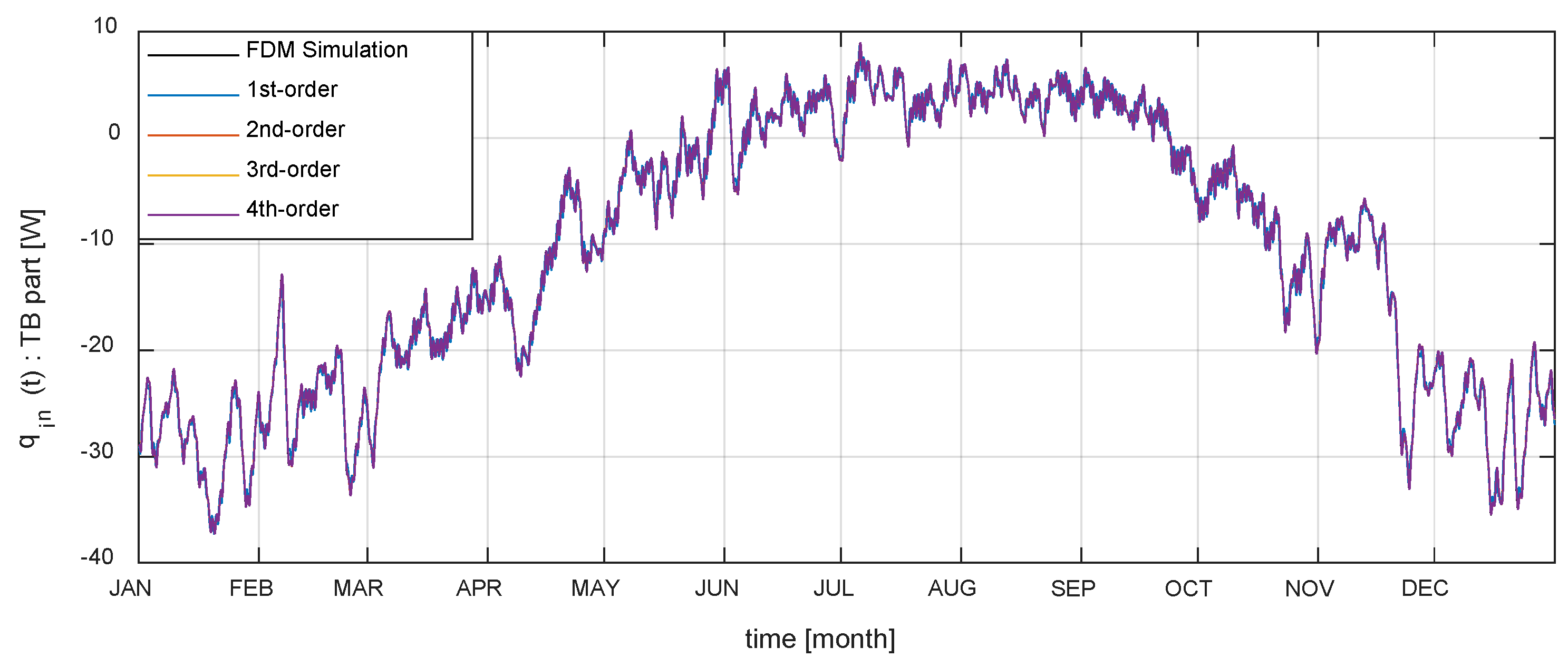
- The accuracy of the proposed TB model depends on the system order, but the normalized root mean square error of the step response is more than 99% (99.76% for the third-order system and 99.97% for the fourth-order system). The amplitude error of the sinusoidal response is −4.78% for the third-order system and −0.52% for the fourth-order system, and the time shift error is 360 s for the third-order system and 0 s for the fourth-order system. In addition, since the RMSE is 0.1 W in the system response of annual outdoor temperature, it can be said that the proposed TB model has sufficient accuracy.
- In the method of this study, thermal fields calculation software capable of 3D dynamic analysis is needed to obtain input/output data required for the system identification process, which is a step to estimate the parameter of TBTF. In the explanatory example, since the steady state is reached in a simulation period of about 5 days, a simulation of about 10 days can sufficiently implement the proposed method. Thereafter, using the estimated TBTF, the simulation time for one year is only a few seconds. Therefore, the computer memory and time-consuming problems are alleviated rather than directly performing 3D thermal fields calculation for one year.
- The proposed method is a method that calculates only the heat flow that additionally enters through the TB, excluding the heat flow through the clear wall that can be analyzed in BES. In terms of heat flow, since the heat flow through the entire wall is separated into heat flow through the clear wall and heat flow through the TB part and linearly combined, the heat flow through the entire wall can be calculated separately and simply added. Therefore, BES program code can be used as it is to calculate the heat flow through the clear wall, and dynamic analysis of TB is possible by adding additional program code for calculating TBTF to BES program. There is an efficiency applicable to BES in that it simply adds a program code that calculates TBTF while continuing to use the existing code of the BES program that analyzes the clear wall.
- The accuracy of the proposed models is significantly higher than that of other models. The RMSE of the model that ignored the TB is 16 W, and the RMSE of the model that analyzes the TB in steady-state is 4.3 W, whereas the RMSE of the proposed model is 0.69 W for the first-order system model and 0.1 W for the third-order system model.
- Among the proposed models, the first-order system model is more inaccurate than the third-order system model, but it is clearly more accurate than other models.
- The accuracy of the dynamic analysis of TB is lower in winter than in summer. The temperature difference between indoor and outdoor is larger in winter than in summer, so the amount of heat flow through the TB is increased, which reduces the accuracy of the models.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Thermal Network Model and the LTI System

- 2R1C model

- 3R2C model
References
- Crawley, D.B.; Hand, J.W.; Kummert, M.; Griffith, B.T. Contrasting the capabilities of building energy performance simulation programs. Build. Environ. 2008, 43, 661–673. [Google Scholar] [CrossRef] [Green Version]
- Harish, V.; Kumar, A. A review on modeling and simulation of building energy systems. Renew. Sustain. Energy Rev. 2016, 56, 1272–1292. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef] [Green Version]
- Balaji, N.; Mani, M.; Reddy, B.V. Dynamic thermal performance of conventional and alternative building wall envelopes. J. Build. Eng. 2019, 21, 373–395. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Zhai, Z.J. Modeling phase change materials embedded in building enclosure: A review. Renew. Sustain. Energy Rev. 2013, 21, 659–673. [Google Scholar] [CrossRef]
- Li, Q.; Rao, J.; Fazio, P. Development of HAM tool for building envelope analysis. Build. Environ. 2009, 44, 1065–1073. [Google Scholar] [CrossRef]
- Wang, H.; Zhai, Z.J. Advances in building simulation and computational techniques: A review between 1987 and 2014. Energy Build. 2016, 128, 319–335. [Google Scholar] [CrossRef]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hobokene, NJ, USA, 2011. [Google Scholar]
- Quinten, J.; Feldheim, V. Dynamic modelling of multidimensional thermal bridges in building envelopes: Review of existing methods, application and new mixed method. Energy Build. 2016, 110, 284–293. [Google Scholar] [CrossRef]
- ISO. 10211: 2017 Thermal Bridges in Building Construction–Heat Flows and Surface Temperatures–Detailed Calculations; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Kosny, J.; Desjarlais, A. Influence of architectural details on the overall thermal performance of residential wall systems. J. Therm. Insul. Build. Envel. 1994, 18, 53–69. [Google Scholar] [CrossRef]
- Ge, H.; Baba, F. Effect of dynamic modeling of thermal bridges on the energy performance of residential buildings with high thermal mass for cold climates. Sustain. Cities Soc. 2017, 34, 250–263. [Google Scholar] [CrossRef]
- Martin, K.; Erkoreka, A.; Flores, I.; Odriozola, M.; Sala, J. Problems in the calculation of thermal bridges in dynamic conditions. Energy Build. 2011, 43, 529–535. [Google Scholar] [CrossRef]
- Kośny, J.; Kossecka, E. Multi-dimensional heat transfer through complex building envelope assemblies in hourly energy simulation programs. Energy Build. 2002, 34, 445–454. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Pedersen, C.O.; Winkelmann, F.C. Energy plus: Energy simulation program. Ashrae J. 2000, 42, 49–56. [Google Scholar]
- Fiksel, A.; Thornton, J.; Klein, S.; Beckman, W. Developments to the TRNSYS simulation program. J. Sol. Energy Eng. 1995, 117, 2. [Google Scholar] [CrossRef]
- Mitchell, R.; Kohler, C.; Curcija, D.; Zhu, L.; Vidanovic, S.; Czarnecki, S.; Arasteh, D.; Carmody, J.; Huizenga, C. THERM 7/WINDOW 7 NFRC Simulation Manual; Lawrence Berkeley National Lab.(LBNL): Berkeley, CA, USA, 2017. [Google Scholar]
- Standaert, P. PHYSIBEL Software Pilot Book; PHYSIBEL: Gent, Belgium, 2010. [Google Scholar]
- Zirkelbach, D.; Schmidt, T.; Kehrer, M.; Künzel, H. Wufi® Plus–Manual; Fraunhofer-Gesellschaft: Munchen, Germany, 2007. [Google Scholar]
- TRISCO v11.0w Manual; PHYSIBEL: Gent, Belgium, 2005.
- VOLTRA v6.0w Manual; PHYSIBEL: Gent, Belgium, 2006.
- Kossecka, E.; Kosny, J. Equivalent wall as a dynamic model of a complex thermal structure. J. Therm. Insul. Build. Envel. 1997, 20, 249–268. [Google Scholar] [CrossRef]
- Nagata, A. A simple method to incorporate thermal bridge effects into dynamic heat load calculation programs. In Proceedings of the International IBPSA Conference, Montreal, QC, Canada, 15–18 August 2005; pp. 817–822. [Google Scholar]
- Xiaona, X.; Yi, J. Equivalent slabs approach to simulate the thermal performance of thermal bridges in building constructions. IbpsaProc. Build. Simul. 2007, 10, 287–293. [Google Scholar]
- Martin, K.; Escudero, C.; Erkoreka, A.; Flores, I.; Sala, J. Equivalent wall method for dynamic characterisation of thermal bridges. Energy Build. 2012, 55, 704–714. [Google Scholar] [CrossRef]
- Alhawari, A.; Mukhopadhyaya, P. Thermal bridges in building envelopes–An overview of impacts and solutions. Int. Rev. Appl. Sci. Eng. 2018, 9, 31–40. [Google Scholar] [CrossRef]
- Simões, N.; Prata, J.; Tadeu, A. 3D Dynamic Simulation of Heat Conduction through a Building Corner Using a BEM Model in the Frequency Domain. Energies 2019, 12, 4595. [Google Scholar] [CrossRef] [Green Version]
- Baba, F. Dynamic Effect of Thermal Bridges on the Energy Performance of Residential Buildings. Master Thesis, Concordia University, Montreal, QC, Canada, 2015. [Google Scholar]
- Iodice, P.; Massarotti, N.; Mauro, A. Effects of inhomogeneities on heat and mass transport phenomena in thermal bridges. Energies 2016, 9, 126. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Quiñones, J.A.F.; Moyano, J.; Rodríguez-Jiménez, C.E. Patents analysis of thermal bridges in slab fronts and their effect on energy demand. Energies 2018, 11, 2222. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Roux, J.; Zhao, L.; Jiang, Y. Dynamical building simulation: A low order model for thermal bridges losses. Energy Build. 2008, 40, 2236–2243. [Google Scholar] [CrossRef]
- DOE. EnergyPlus Version 9.0.1 Documentation: EnergyPlus Engineering Reference; US Department of Energy: Washington, DC, USA, 2016.
- ISO. 14683: 2017 Thermal Bridges in Building Construction-Linear Thermal Tansmittance-Simplified Methods and Default Values; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Ogata, K. System Dynamics; Pearson/Prentice Hall Englewood Cliffs: Upper Saddle River, NJ, USA, 2004; Volume 13. [Google Scholar]
- Li, X.Q.; Chen, Y.; Spitler, J.; Fisher, D. Applicability of calculation methods for conduction transfer function of building constructions. Int. J. Therm. Sci. 2009, 48, 1441–1451. [Google Scholar] [CrossRef]
- Tangirala, A.K. Principles of System Identification: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Martinez, R.G.; Riverola, A.; Chemisana, D. Disaggregation process for dynamic multidimensional heat flux in building simulation. Energy Build. 2017, 148, 298–310. [Google Scholar] [CrossRef]
- Matlab, M. MATLAB R2018b; Mathworks: Natick, MA, USA, 2018. [Google Scholar]


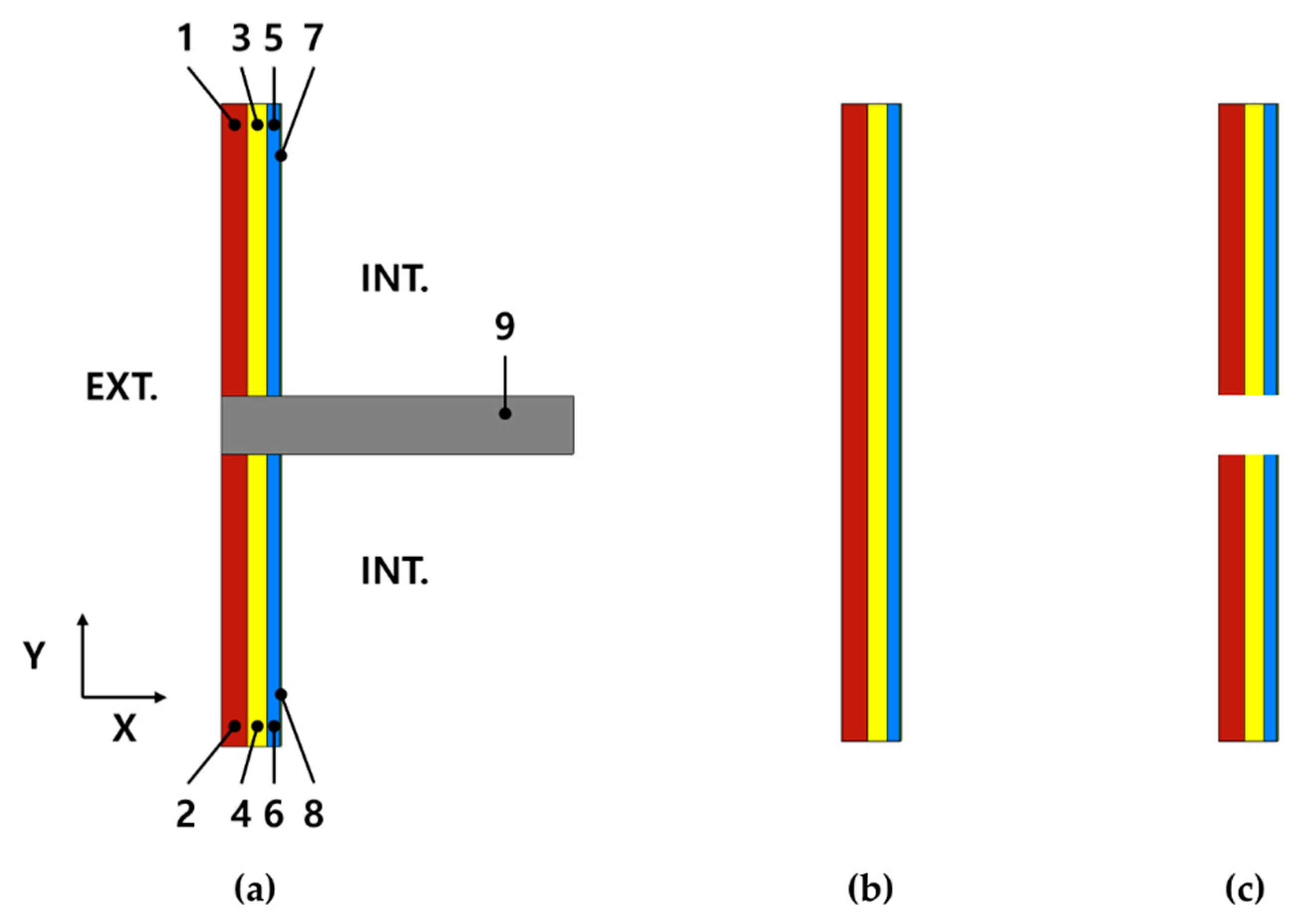

| # | Material | Lx (mm) | Ly (mm) | (W/mK) | (kg/m3) | (J/kgK) |
|---|---|---|---|---|---|---|
| 1 | Brick | 135 | 1500 | 0.700 | 1600.0 | 850.0 |
| 2 | 135 | 1500 | 0.700 | 1600.0 | 850.0 | |
| 3 | Extruded polystyrene | 100 | 1500 | 0.035 | 25.0 | 1470.0 |
| 4 | 100 | 1500 | 0.035 | 25.0 | 1470.0 | |
| 5 | Air gap | 65 | 1500 | 0.560 | 1.185 | 1004.4 |
| 6 | 65 | 1500 | 0.560 | 1.185 | 1004.4 | |
| 7 | Plasterboard | 10 | 1500 | 0.500 | 1300.0 | 840.0 |
| 8 | 10 | 1500 | 0.500 | 1300.0 | 840.0 | |
| 9 | Concrete | 1810 | 300 | 2.600 | 2300.0 | 930.0 |
| Dimensional System | Thermal Transmittance | |||||
|---|---|---|---|---|---|---|
| Entire Wall (W/m2K) | Clear Wall (W/m2K) | TB Part (W/mK) | Entire Wall (W) | Clear Wall (W) | TB Part (W) | |
| External | 0.6945 | 0.2980 | 1.3086 | 45.8376 | 19.6657 | 26.1719 |
| Time Step | Duration | Initial Condition | Boundary Condition |
|---|---|---|---|
| 1,728,000 s (20 days) | All structures and | 86,400 s 86,400 s |
| Entire Wall | Clear Wall | TB Part | |
|---|---|---|---|
| (1,728,000 s) | 45.8468 W | 19.6659 W | 26.1717 W |
| steady-state Error | 0.0000% | −0.0010% | 0.0008% |
| the time to reach 99.99% of the steady-state value | 427,380 s (4 d 22 h 43 m 00 s) | 193,740 s (2 d 05 h 49 m 00 s) | 90,240 s (1 d 01 h 04 m 00 s) |
| System Order | First-Order | Second-Order | Third-Order | Forth-Order |
|---|---|---|---|---|
| Transfer Function | ||||
| # of Poles | 1 | 2 | 3 | 4 |
| # of Zeros | 0 | 0 | 0 | 0 |
| 1.4223 × 10−5 | 8.9437 × 10−10 | 1.9993 × 10−13 | 7.4085 × 10−17 | |
| - | 6.0387 × 10−5 | 1.3706 × 10−8 | 5.0793 × 10−12 | |
| - | - | 2.2273 × 10−4 | 8.3760 × 10−8 | |
| - | - | - | 3.7200 × 10−4 | |
| 1.8679 × 10−5 | 1.1700 × 10−9 | 2.6164 × 10−13 | 9.6947 × 10−17 | |
| Fit to the estimation data 1 | 90.86% | 98.73% | 99.76% | 99.97% |
| FPE 2 | 0.3833 | 0.0074 | 0.0003 | 0.0000 |
| MSE 3 | 0.3832 | 0.0074 | 0.0003 | 0.0000 |
| Step Input | Sinusoidal Input | Annual Outdoor Temperature Input |
|---|---|---|
| 86,400 s 86,400 s | Figure 7 |
| System Model | FDM Model | First-Order | Second-Order | Third-Order | Fourth-Order |
|---|---|---|---|---|---|
| Amplitude (W) | 4.7632 | 2.1169 | 3.7667 | 4.5354 | 4.7385 |
| Amplitude error (basis on FDM model) (%) | - | +5.85% | −20.92% | −4.78% | −0.52% |
| Time shift error (basis on FDM model) | - | −16,200 s (−4 h 30 min) | −2700 s (−45 min) | 360 s (6 min) | 0 s |
| Model | First-Order | Second-Order | Third-Order | Fourth-Order |
|---|---|---|---|---|
| RMSE | 0.6920 | 0.1366 | 0.1007 | 0.0895 |
| Model | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| TB part analysis | Ignored | first-order | third-order | |
| Year | 16.2445 | 4.3467 | 0.6920 | 0.1007 |
| Summer (JUL, AUG, SEP) | 4.1399 | 3.9504 | 0.6371 | 0.0917 |
| Winter (JAN, FEB, DEC) | 27.0304 | 4.3264 | 0.6771 | 0.1001 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Yeo, M. Thermal Bridge Modeling and a Dynamic Analysis Method Using the Analogy of a Steady-State Thermal Bridge Analysis and System Identification Process for Building Energy Simulation: Methodology and Validation. Energies 2020, 13, 4422. https://doi.org/10.3390/en13174422
Kim H, Yeo M. Thermal Bridge Modeling and a Dynamic Analysis Method Using the Analogy of a Steady-State Thermal Bridge Analysis and System Identification Process for Building Energy Simulation: Methodology and Validation. Energies. 2020; 13(17):4422. https://doi.org/10.3390/en13174422
Chicago/Turabian StyleKim, Heegang, and Myoungsouk Yeo. 2020. "Thermal Bridge Modeling and a Dynamic Analysis Method Using the Analogy of a Steady-State Thermal Bridge Analysis and System Identification Process for Building Energy Simulation: Methodology and Validation" Energies 13, no. 17: 4422. https://doi.org/10.3390/en13174422
APA StyleKim, H., & Yeo, M. (2020). Thermal Bridge Modeling and a Dynamic Analysis Method Using the Analogy of a Steady-State Thermal Bridge Analysis and System Identification Process for Building Energy Simulation: Methodology and Validation. Energies, 13(17), 4422. https://doi.org/10.3390/en13174422







