Study on Fast Cold Start-Up Method of Proton Exchange Membrane Fuel Cell Based on Electric Heating Technology
Abstract
:1. Introduction
2. Model
2.1. Model Equation
- (1)
- The energy conservation equation in the solid region (such as end plates and gas flow channel) within the PEMFC stack is expressed bywhere are the density, enthalpy, thermal conductivity, and temperature of the solid region material, respectively.
- (2)
- The two liquid/solid phases in the fluid may coexist. Therefore, the volume of fluid (VOF) model as well as the solidification and melting model are used to observe the water/ice boundary and control the melting process.
- (3)
- The energy equation of the porous media (such as gas diffusion layer, proton exchange membrane, and electrothermal membrane) in a PEMFC stack is as followswhere the total energy of the fluid is defined as , the total energy of the solid medium is defined as , is the porosity of the porous medium, is the temperature of the porous medium region, is the source term, is the effective thermal conductivity of the medium, is the thermal conductivity of the liquid phase and is the thermal conductivity of the solid phase.
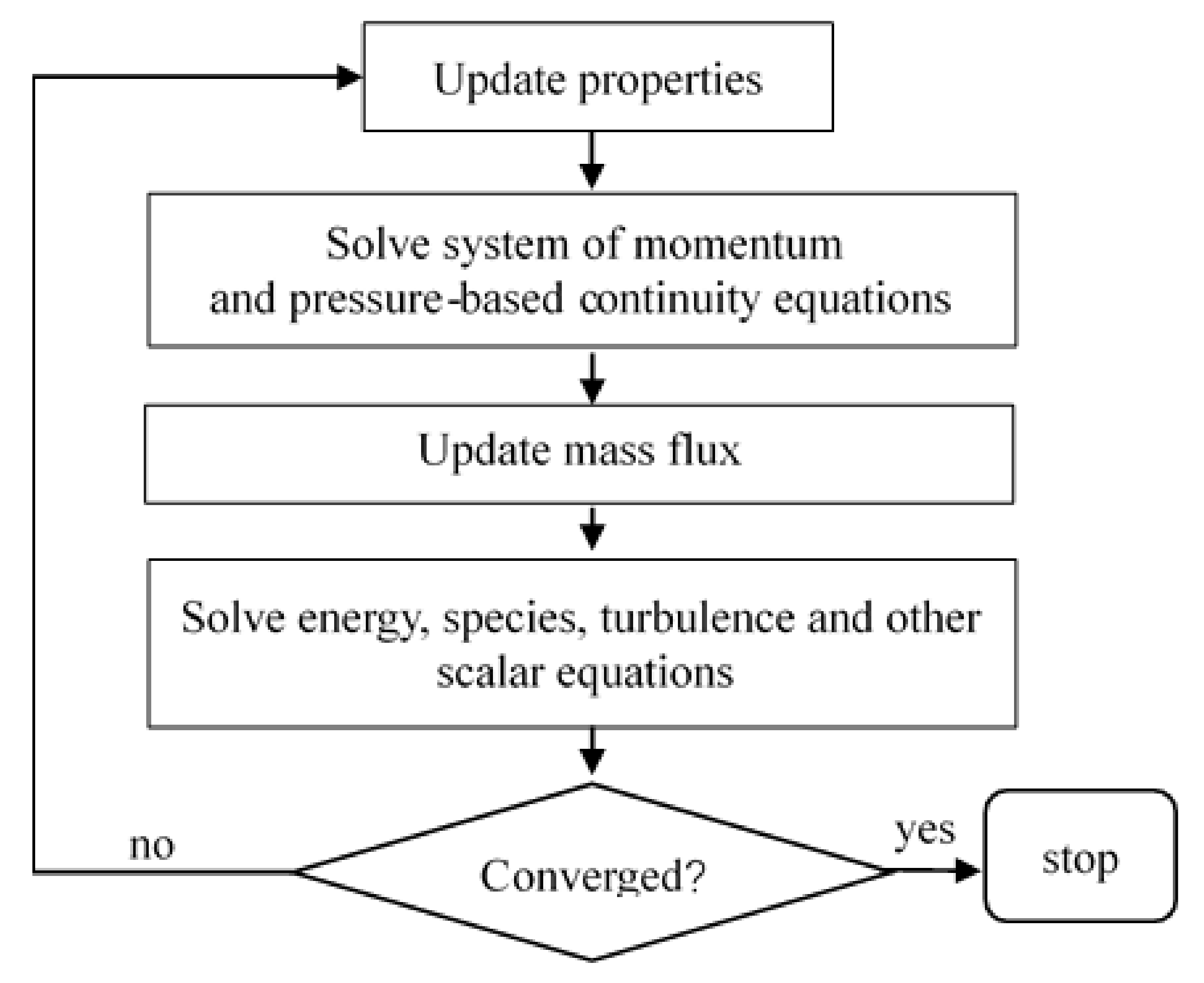
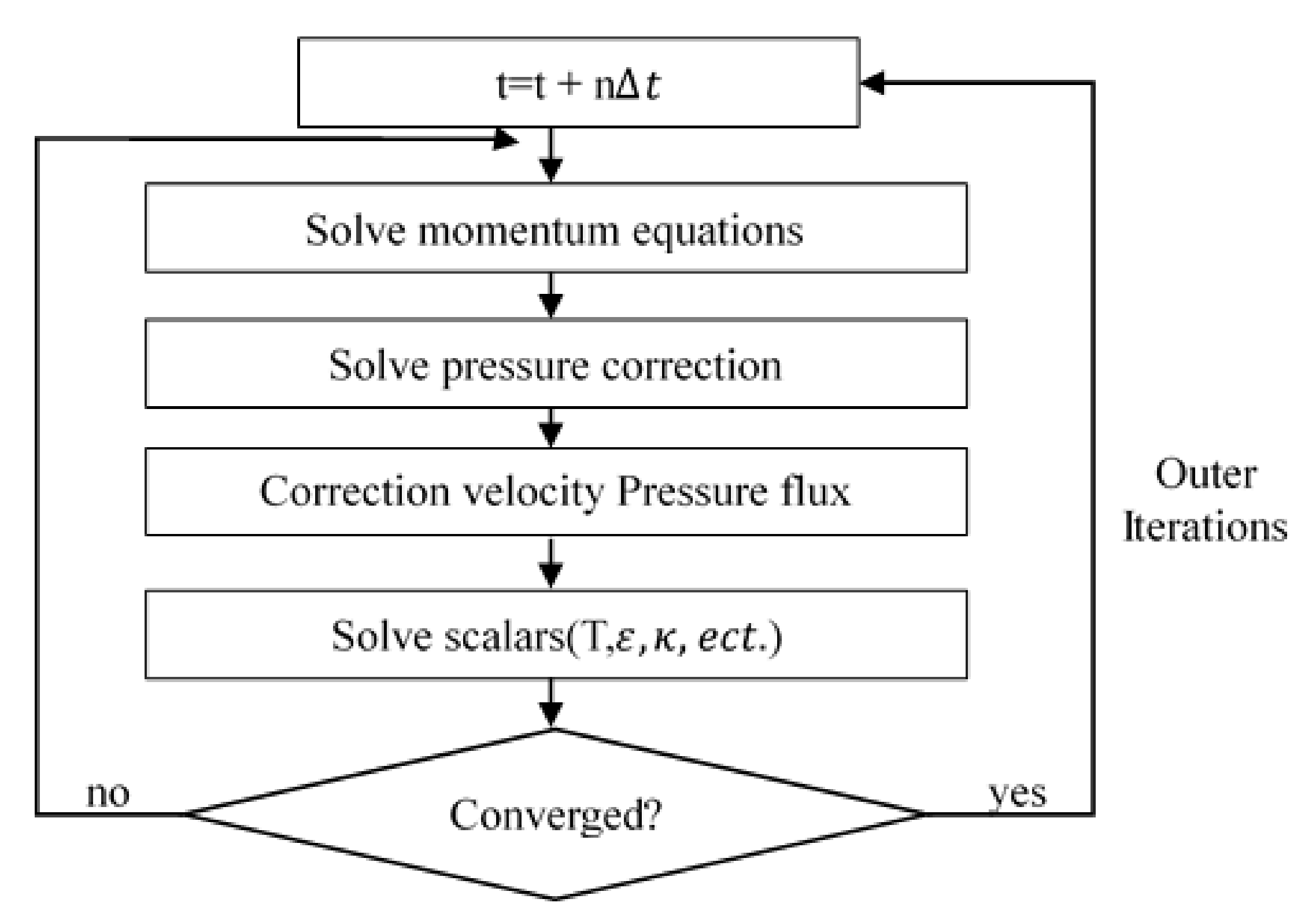
2.2. Numerical Implementations
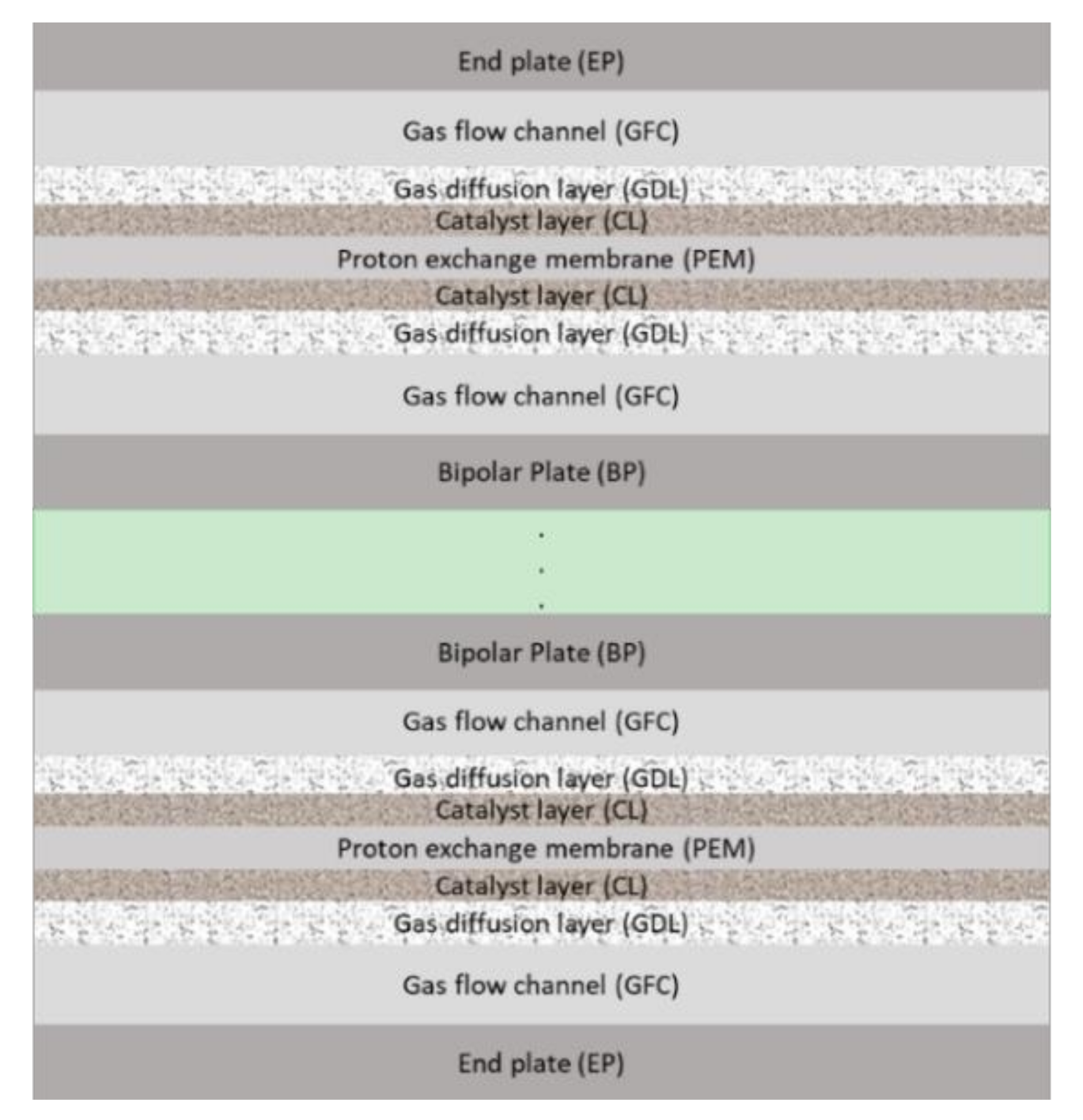
2.2.1. PEMFC Stack Geometries and Properties
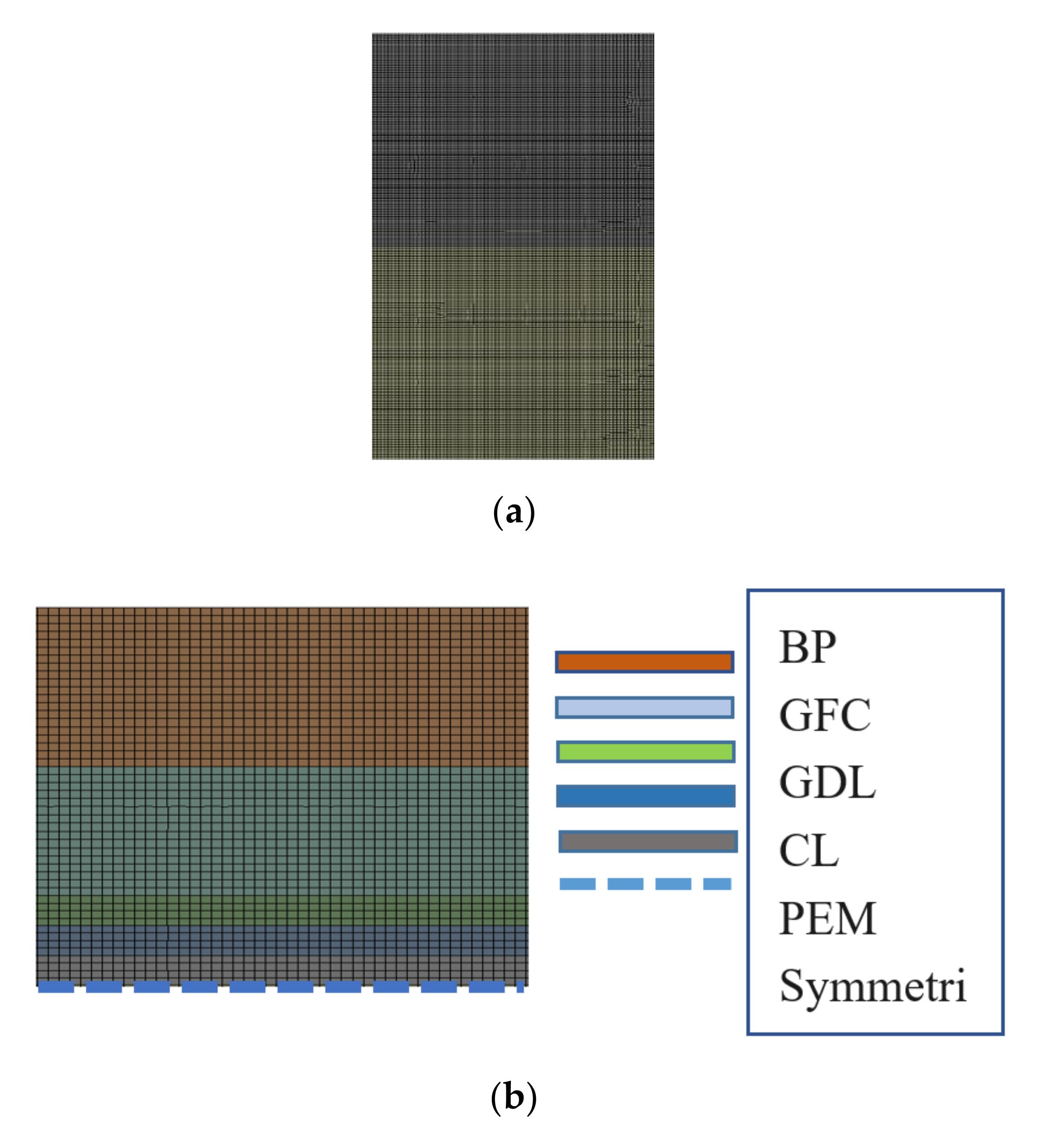
2.2.2. Meshing and Boundary
3. Results and Discussions
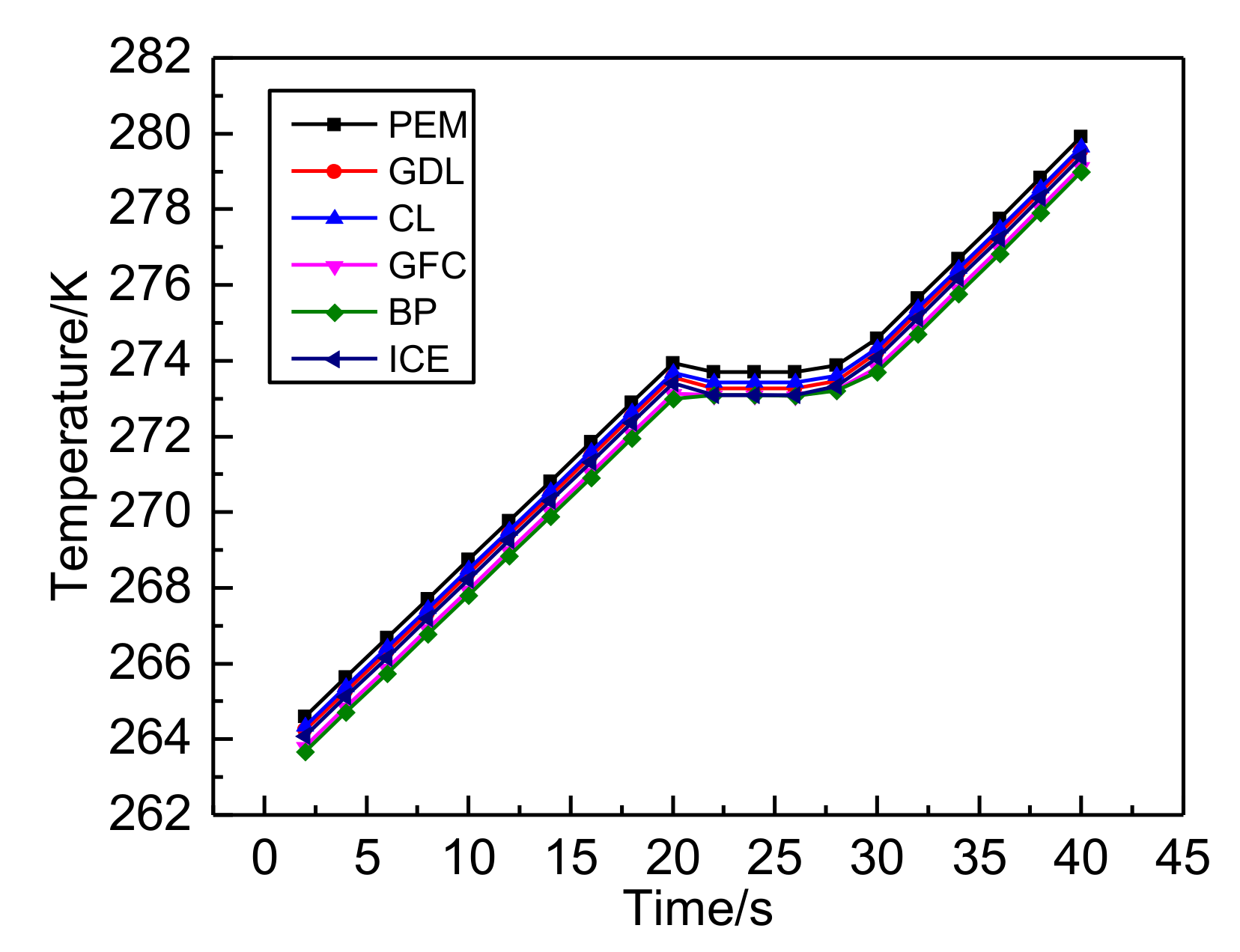
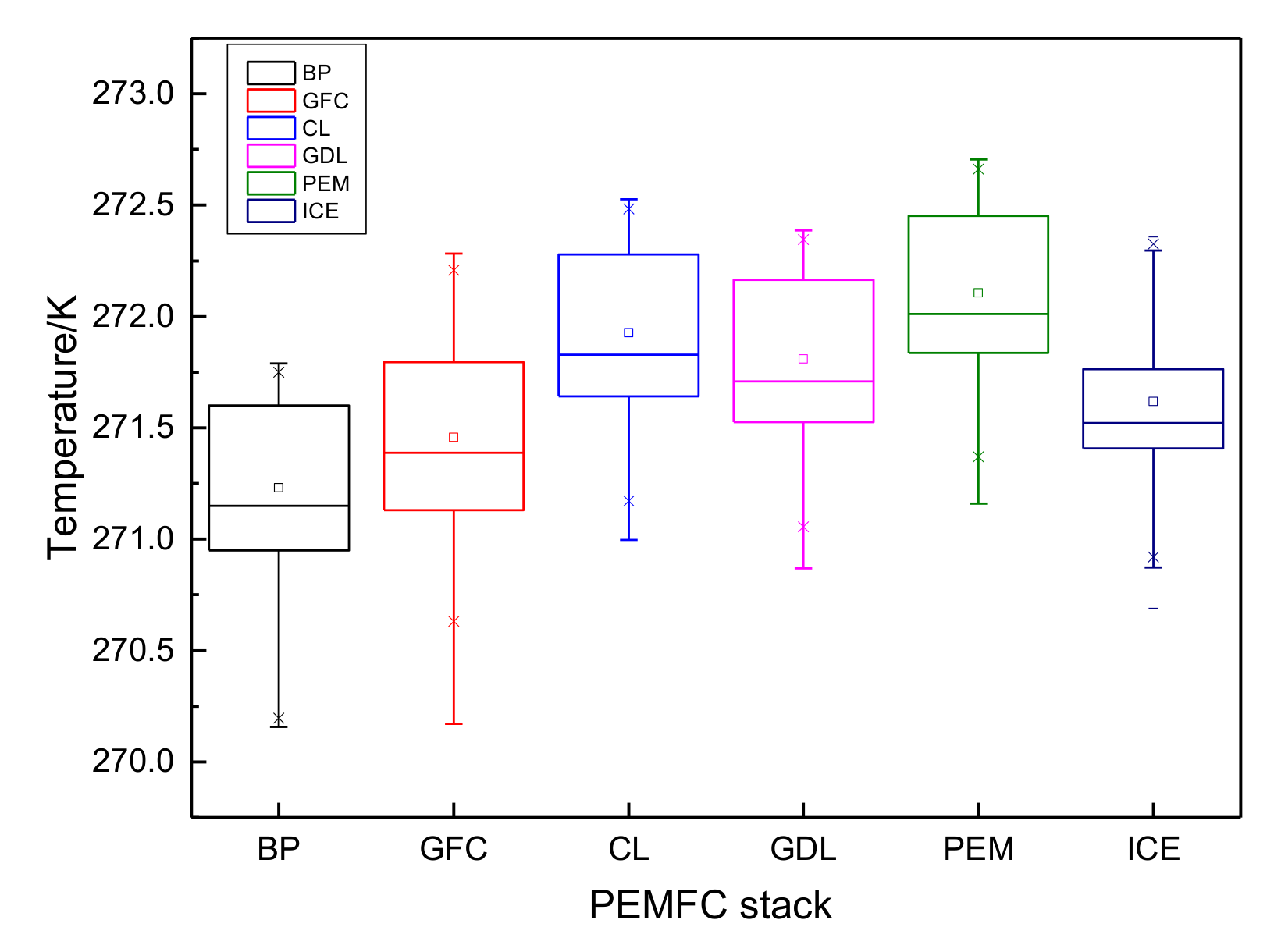
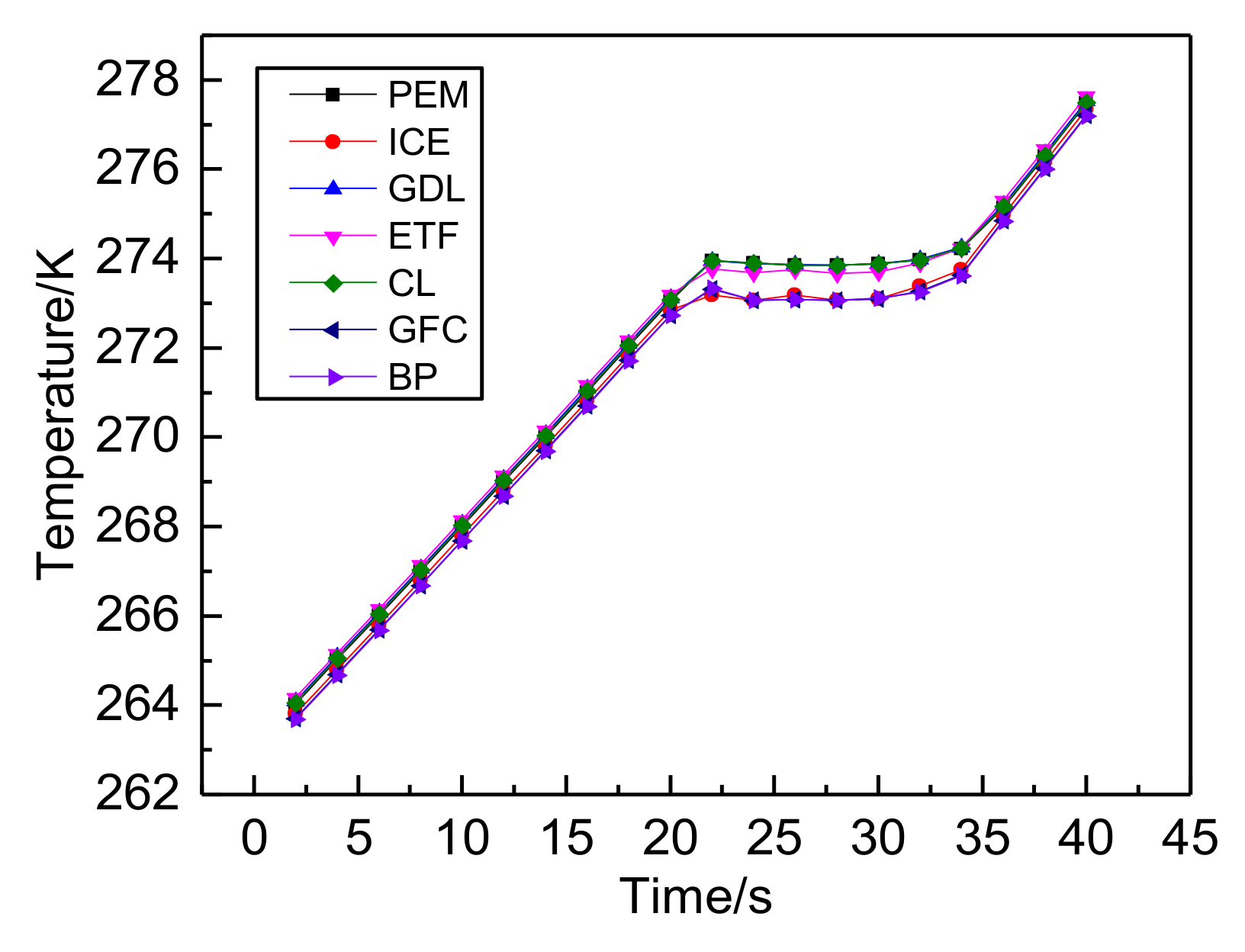
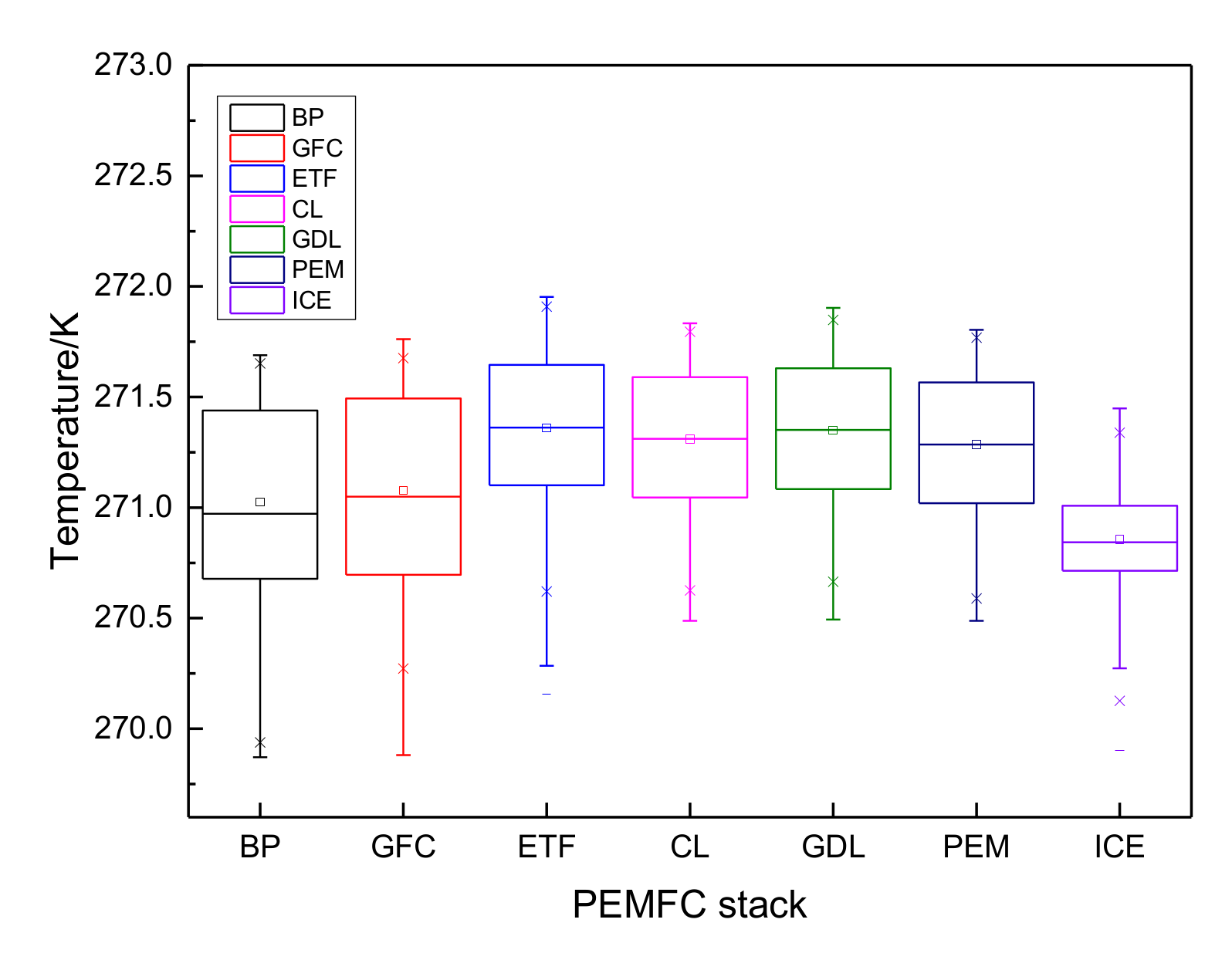
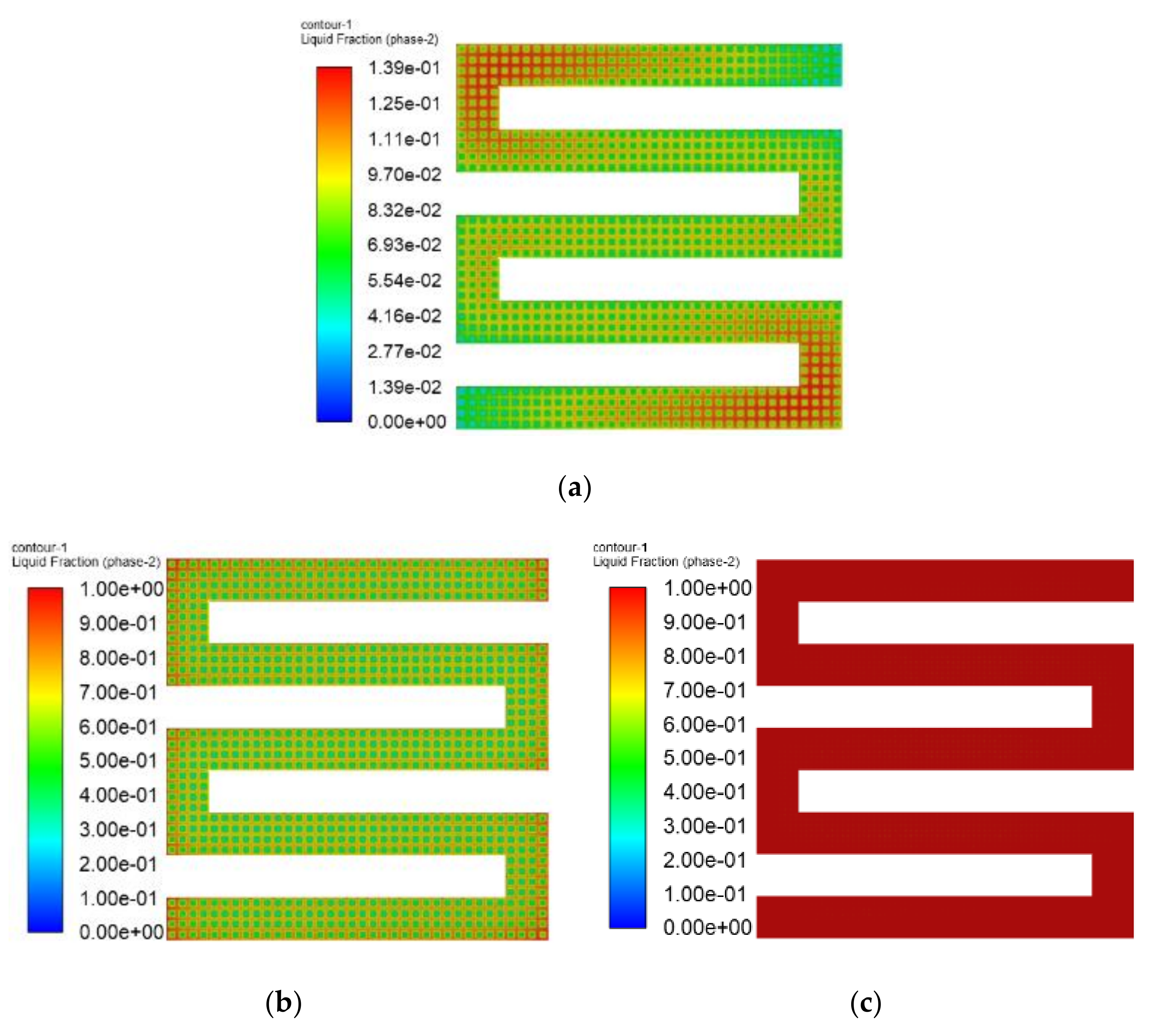
3.1. The Results of PEMFC Stack Heating with Proton Exchange Membrane
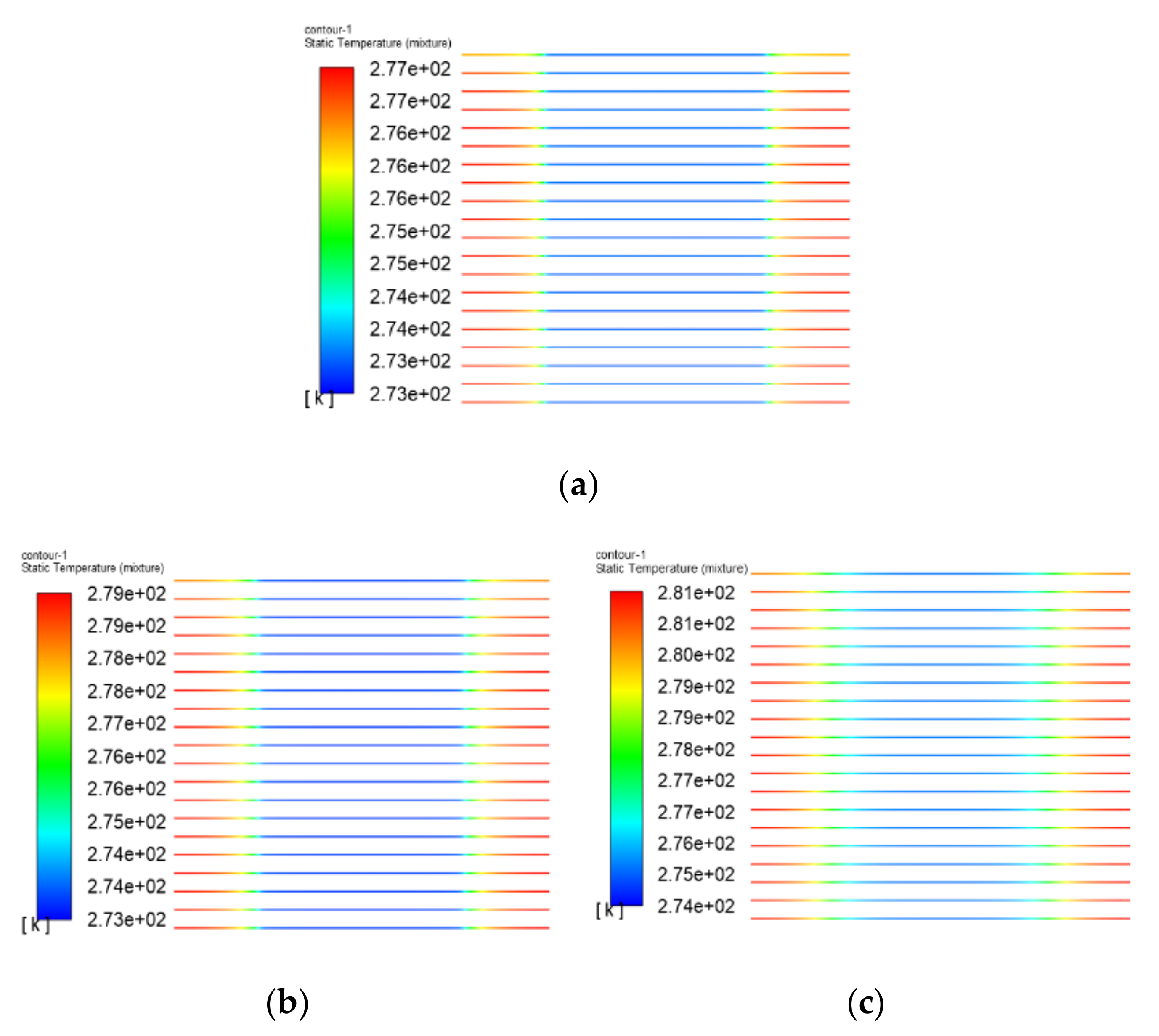
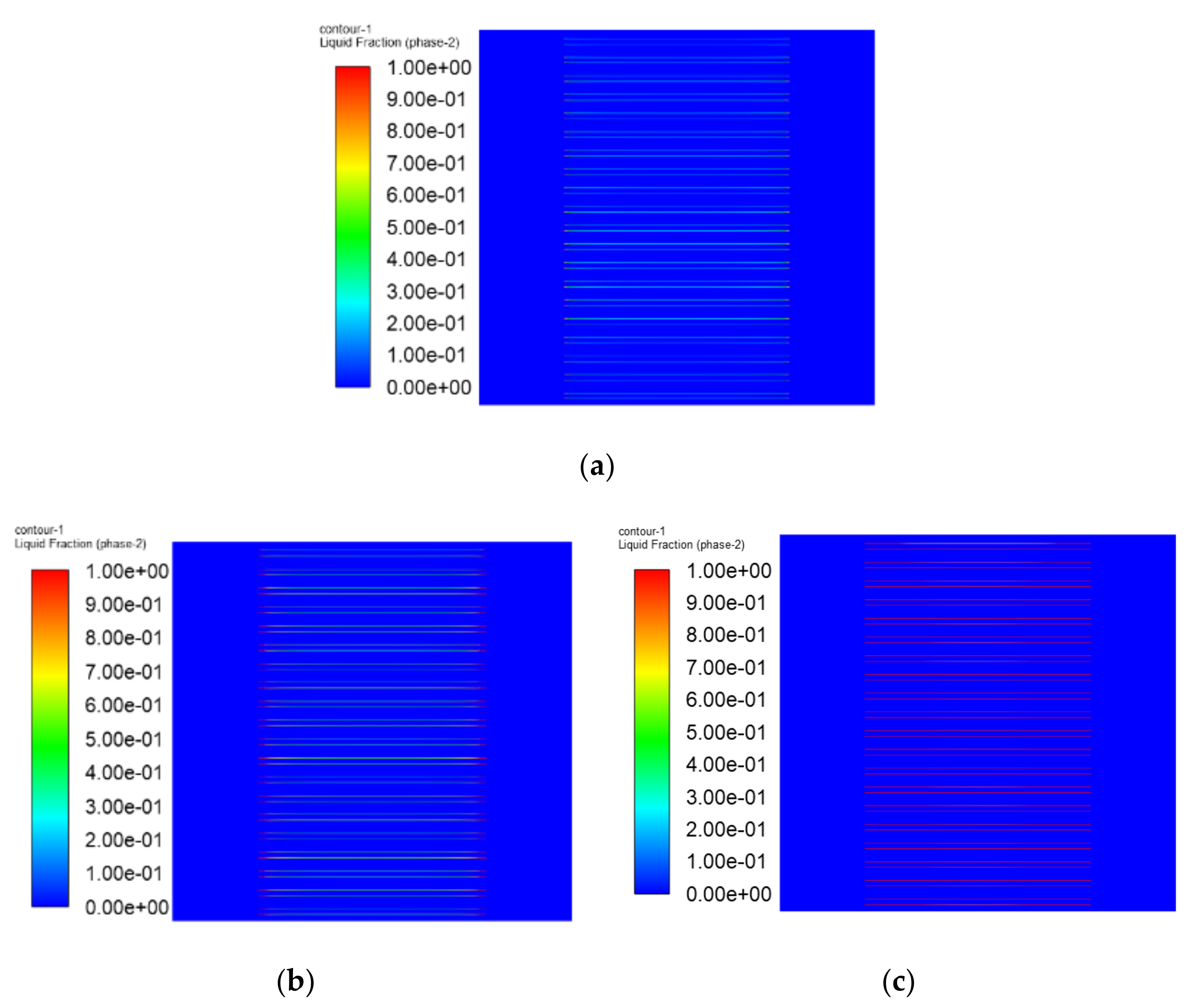
3.2. The Results of PEMFC Stack Heating with Electrothermal Film
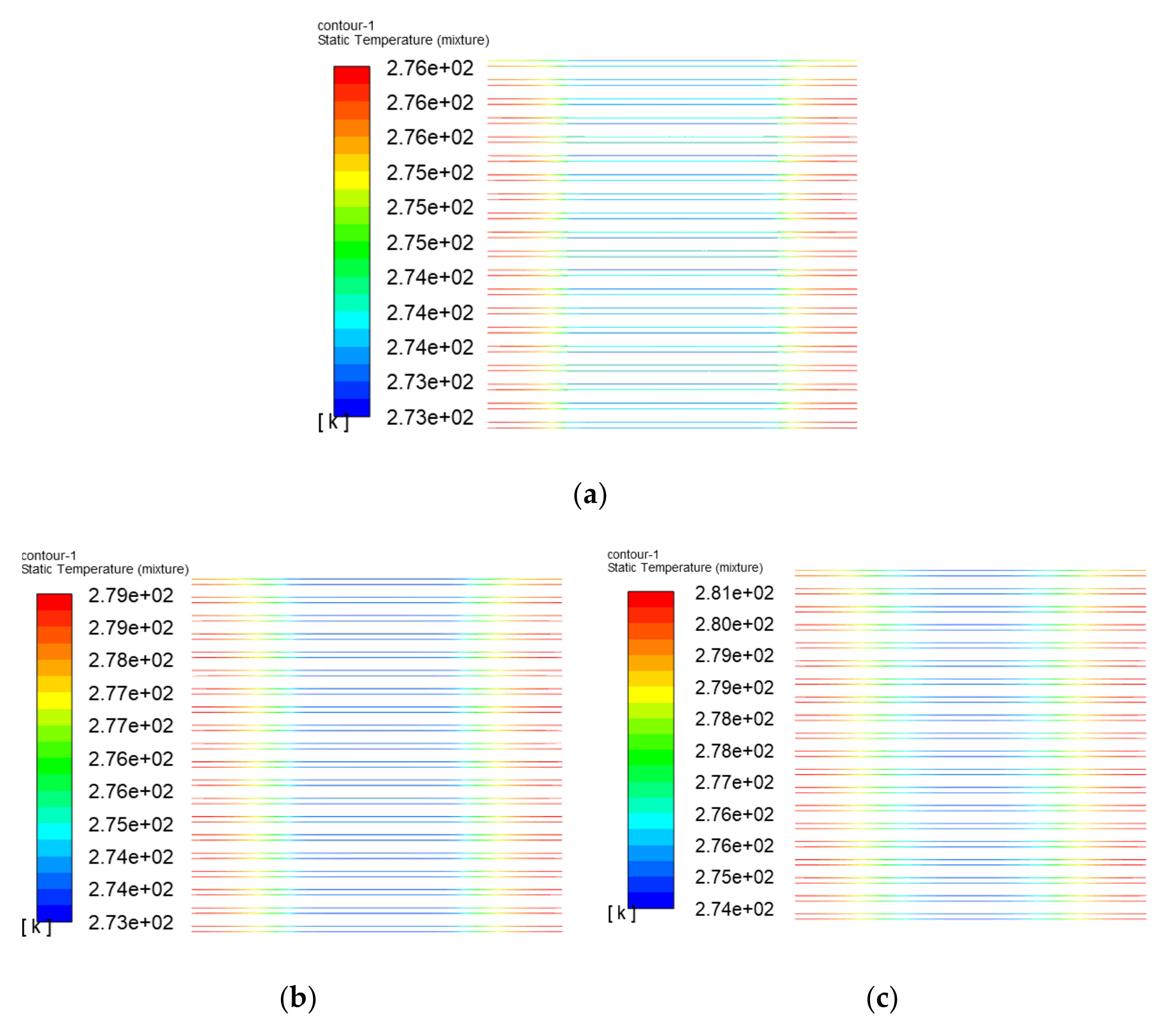
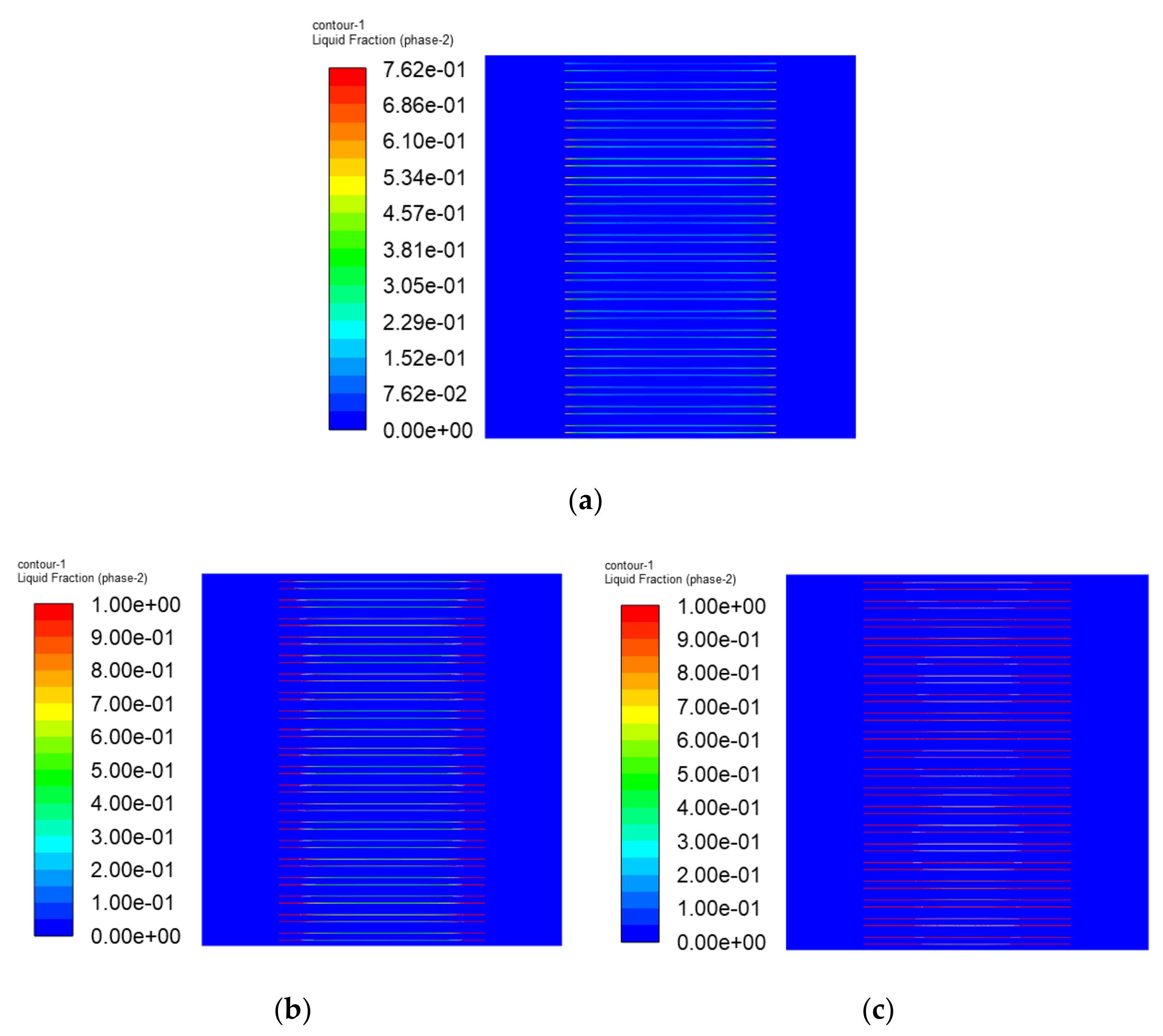
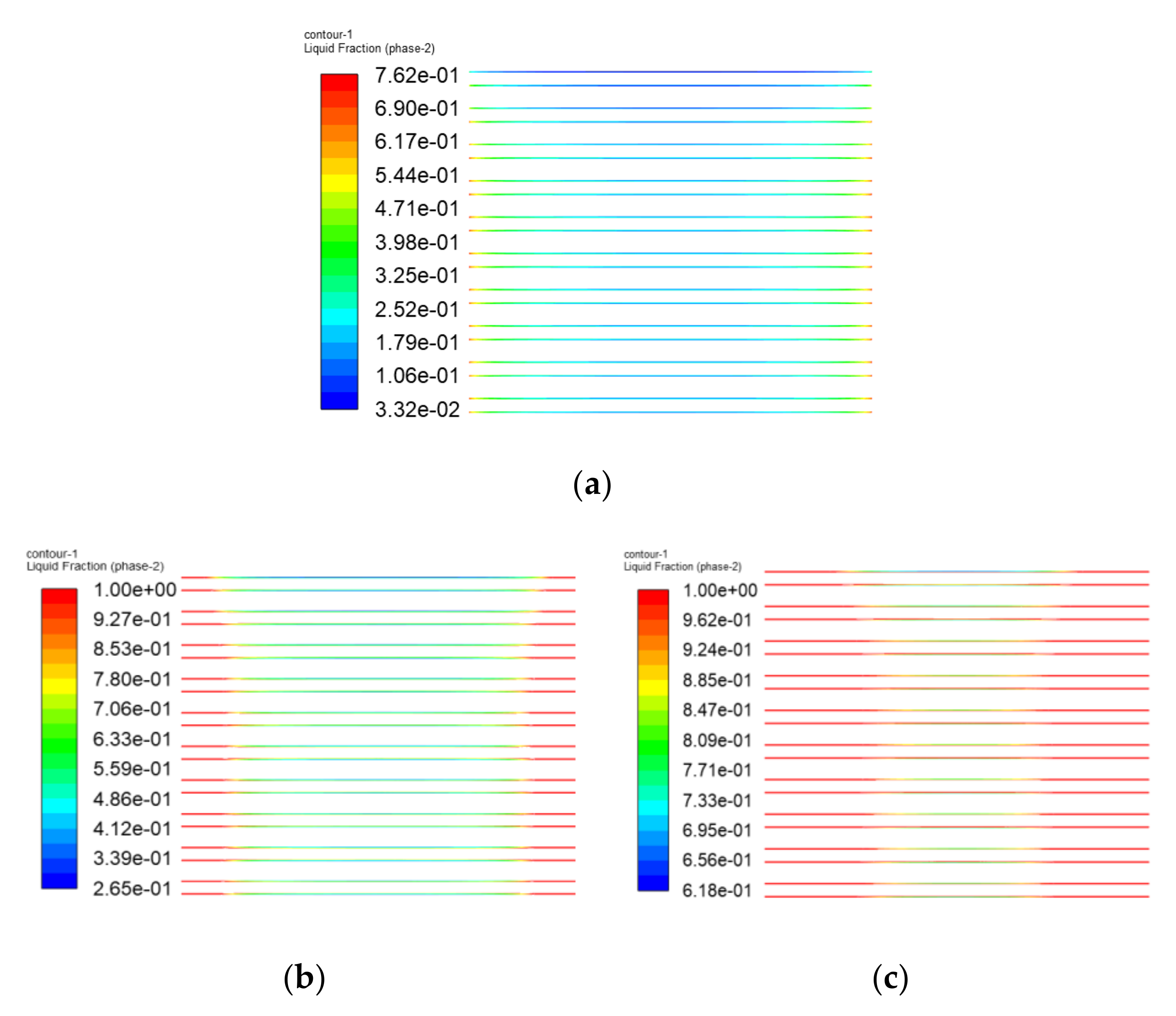
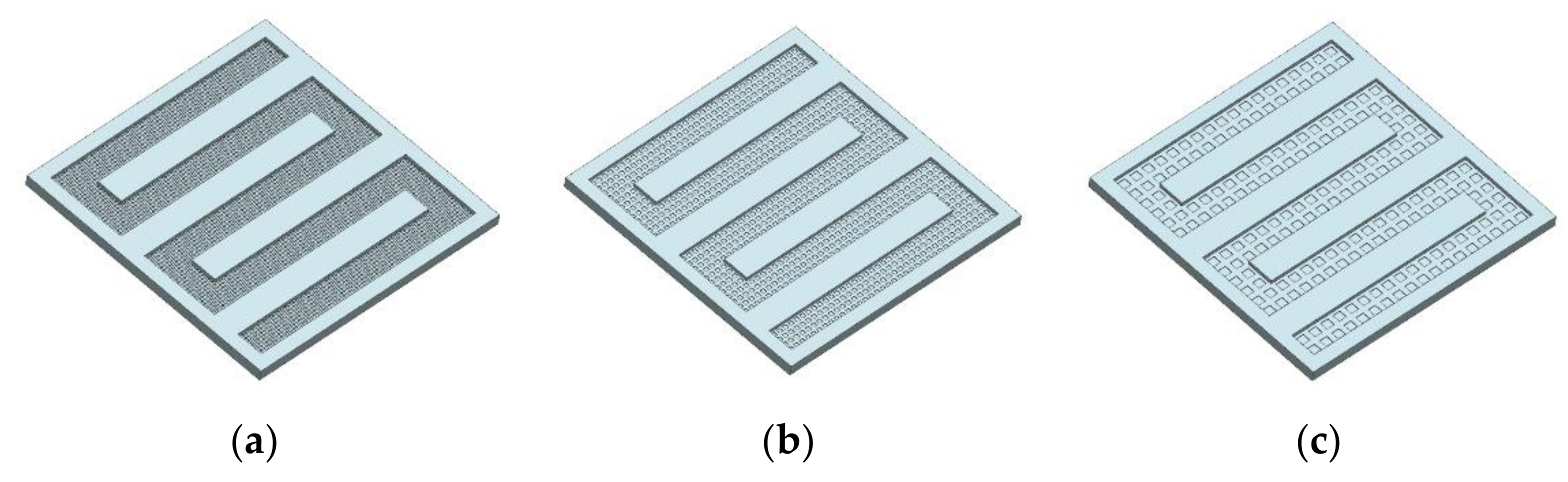
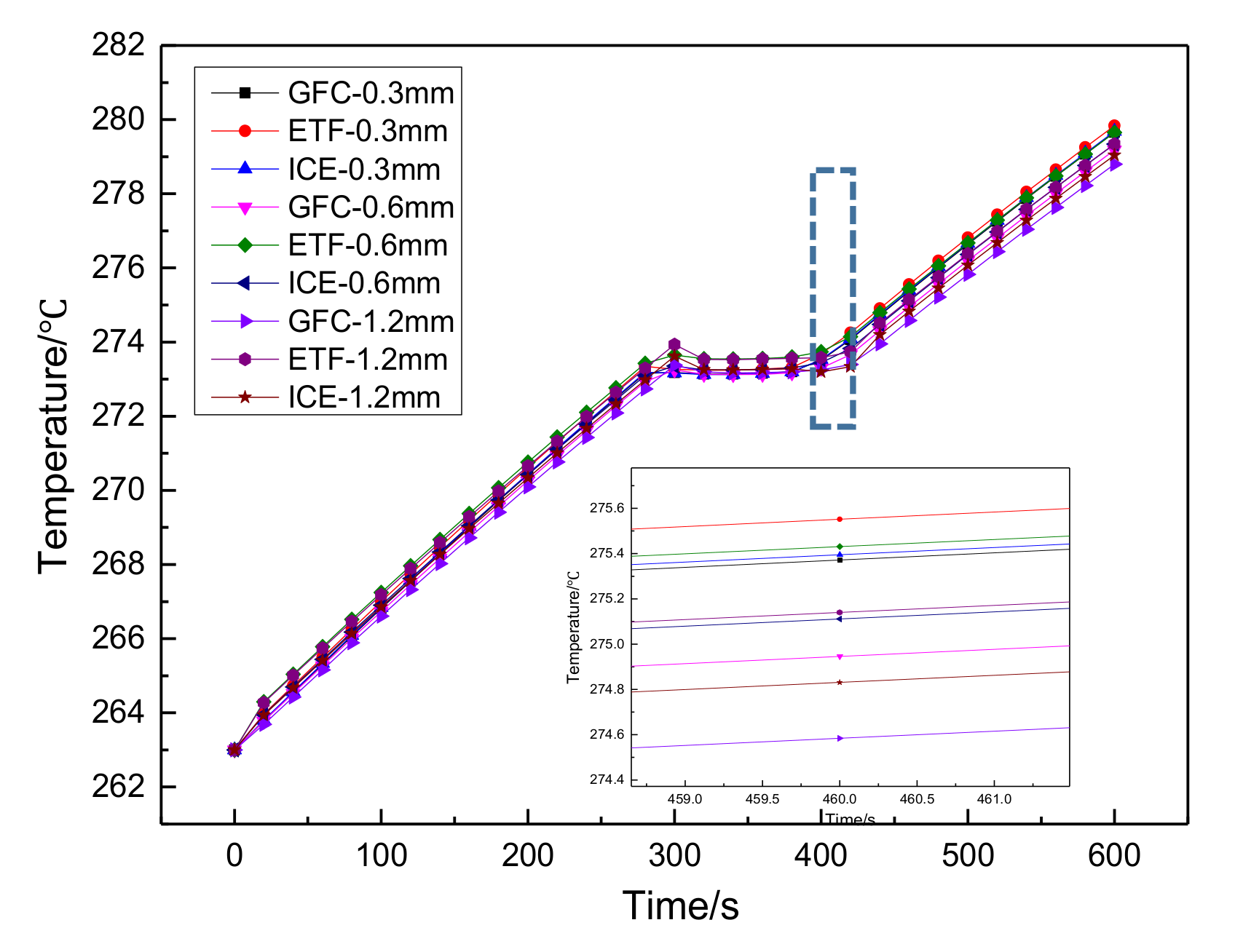
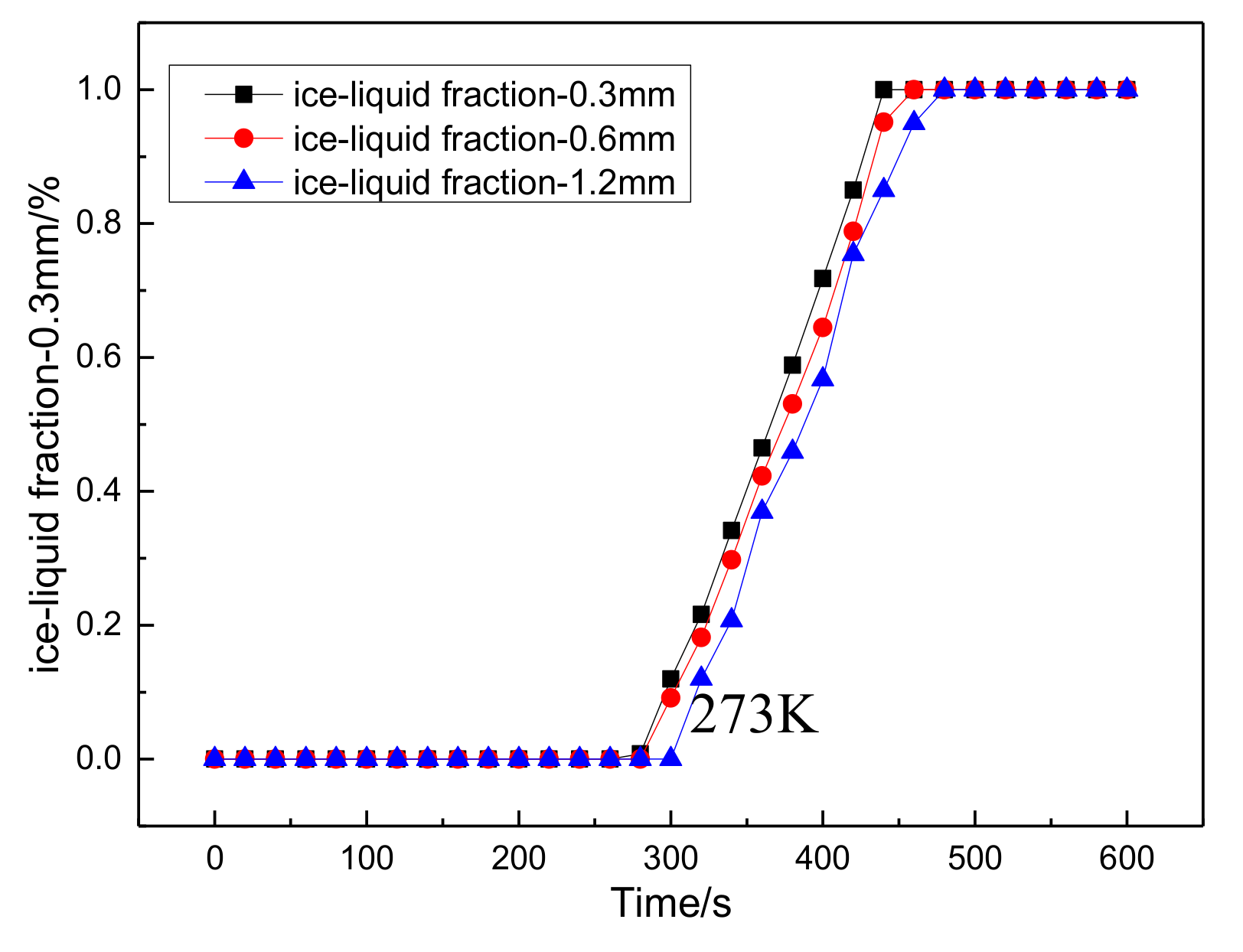
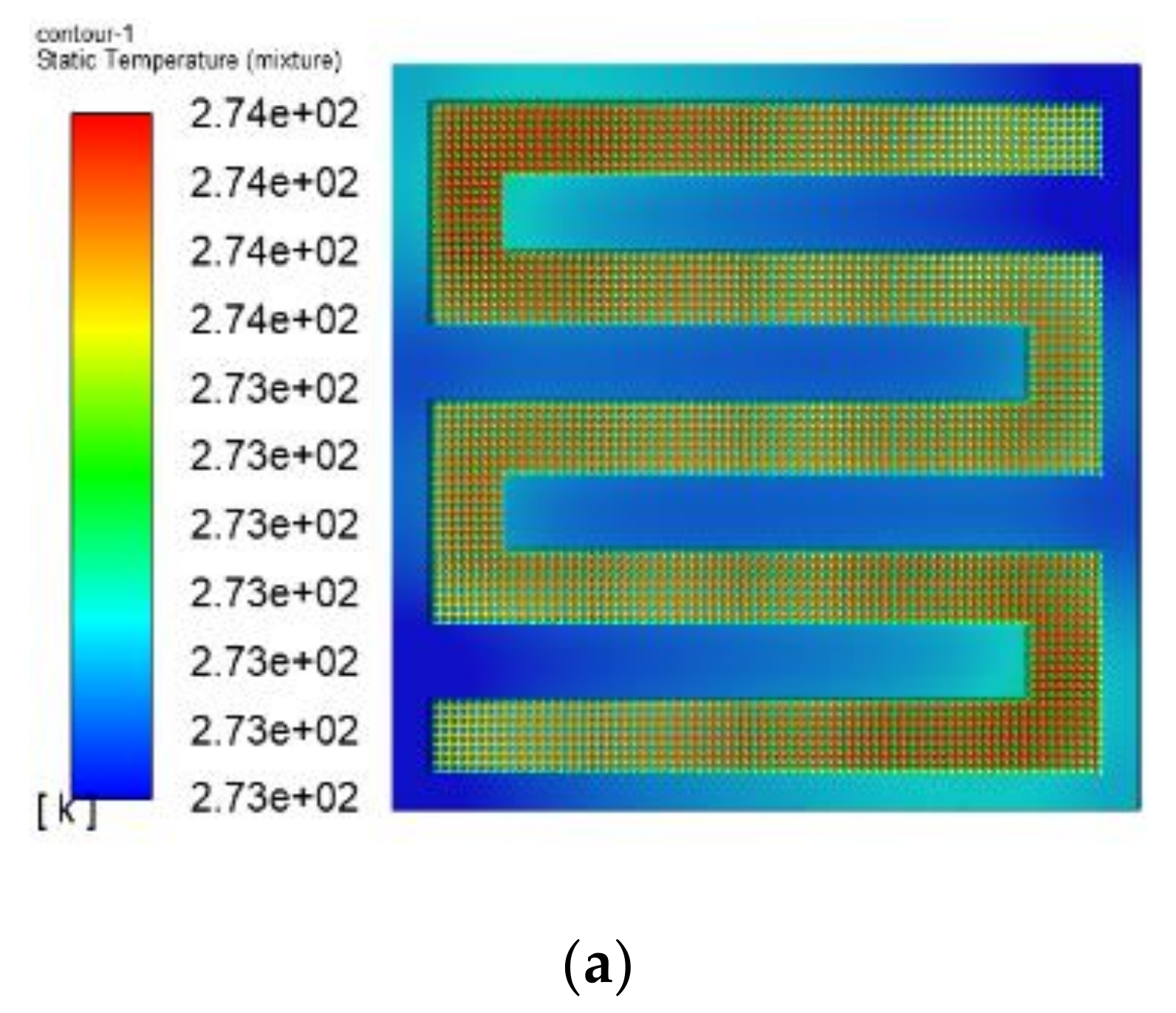
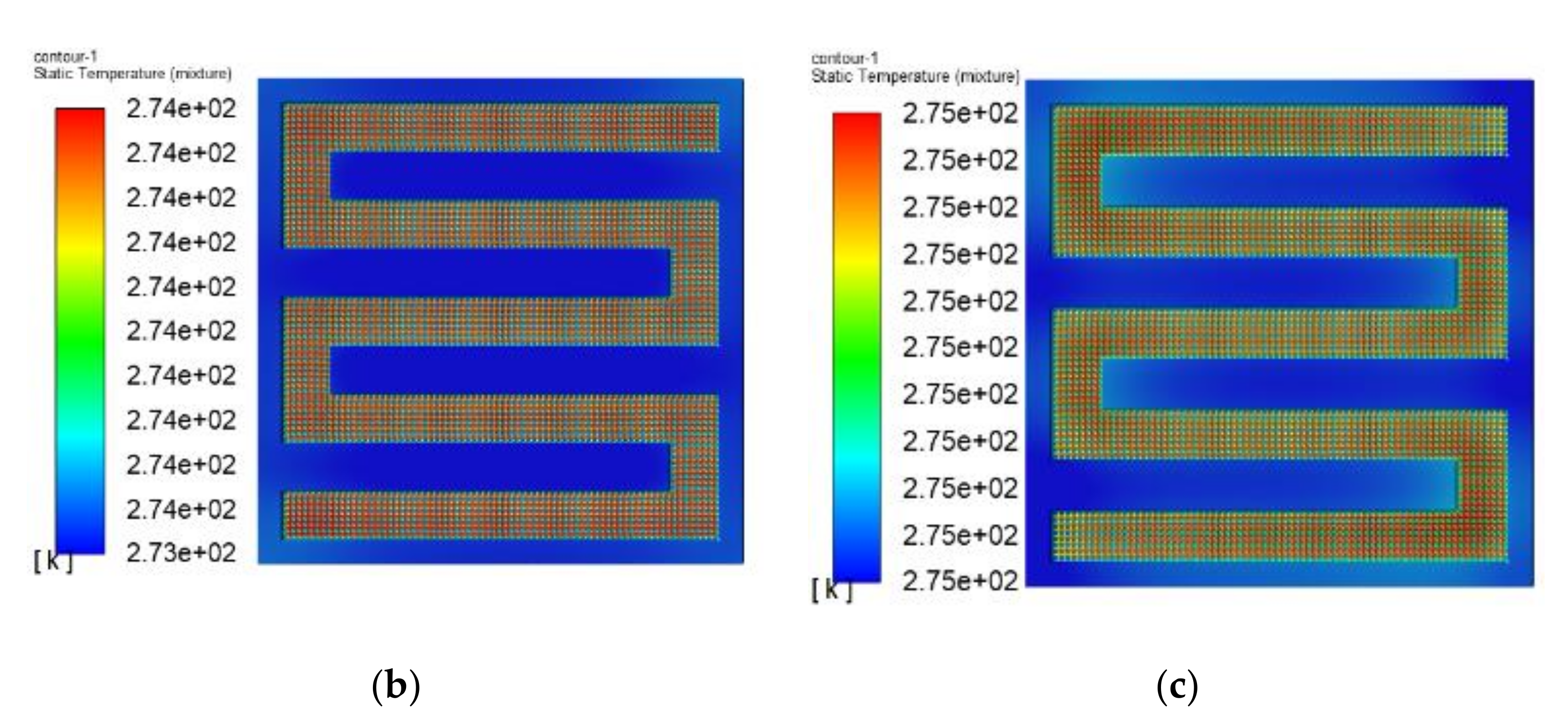
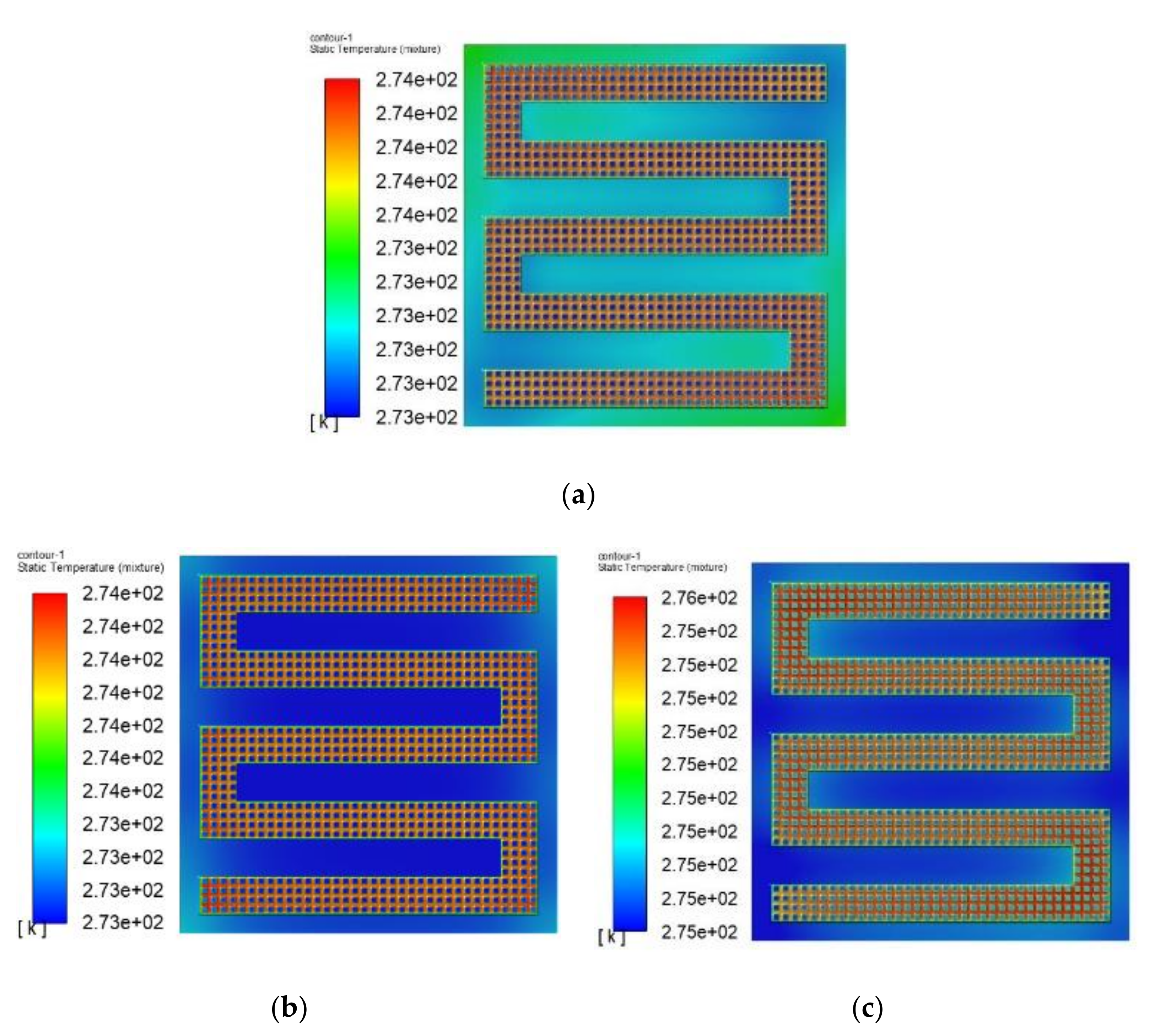
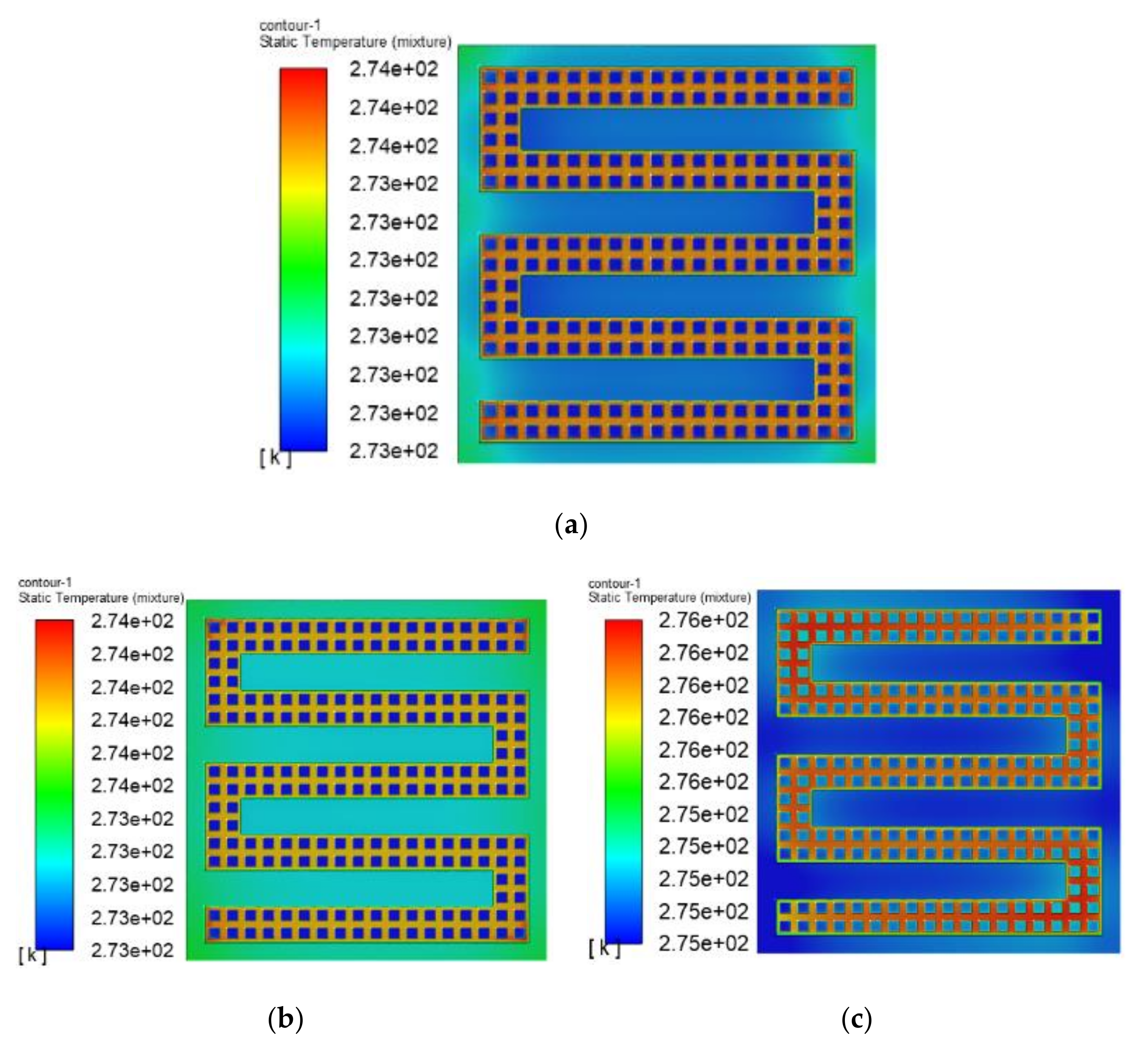
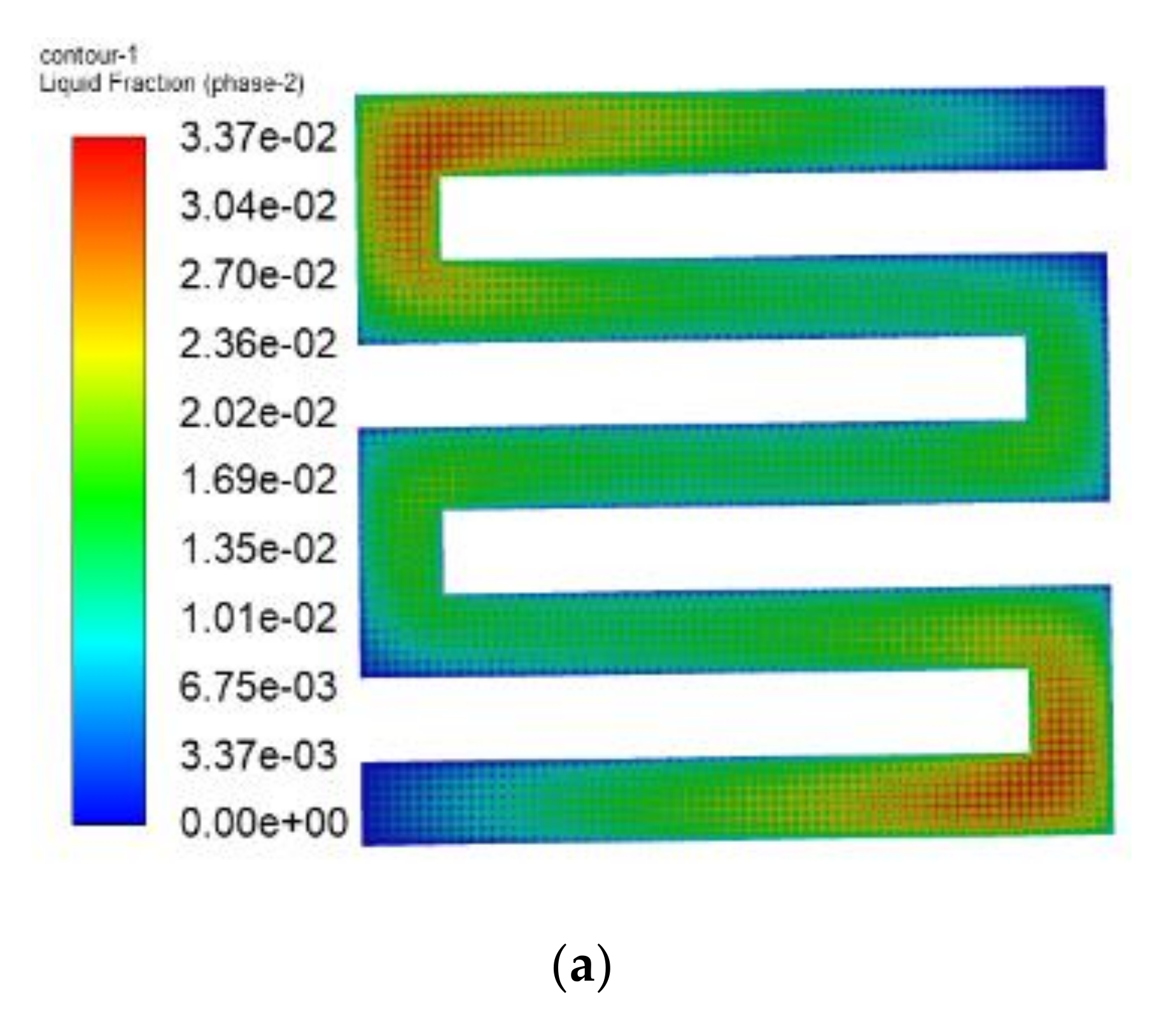
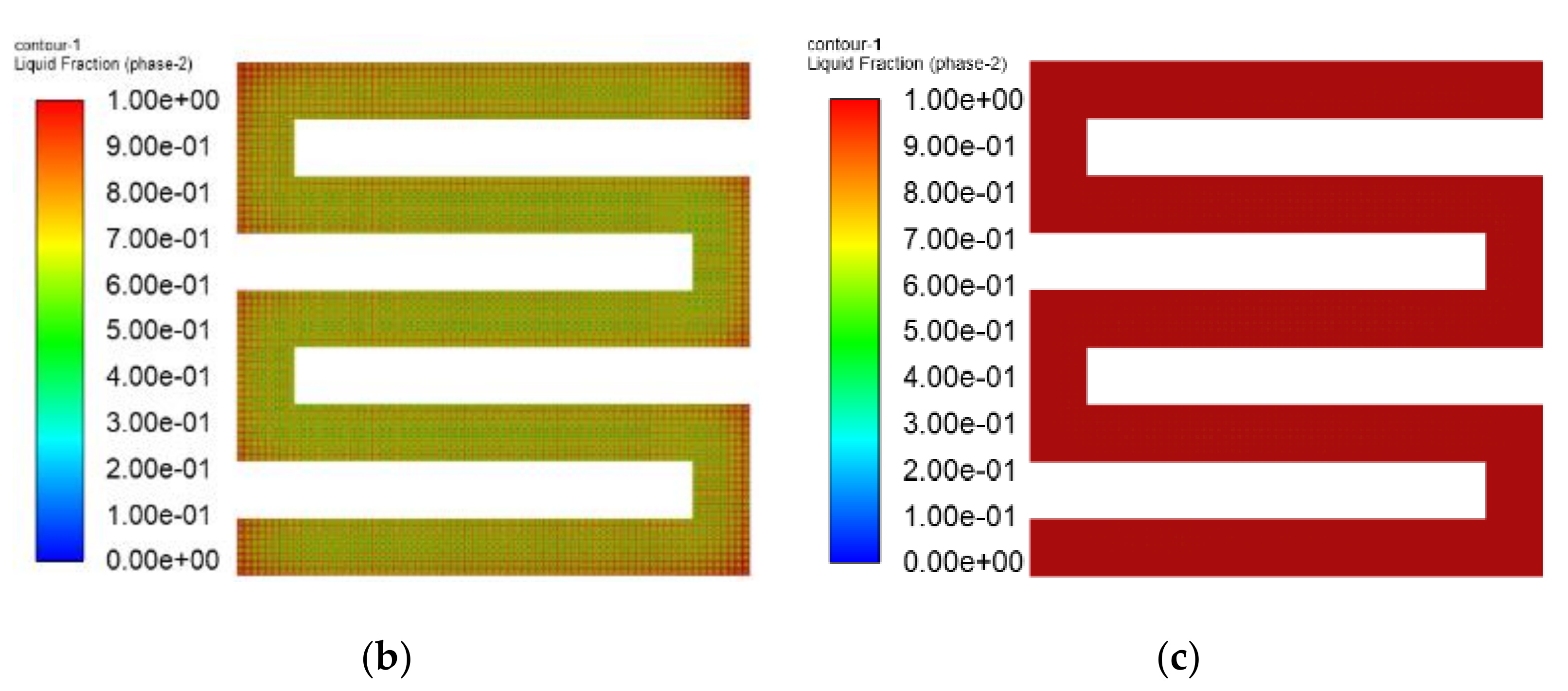
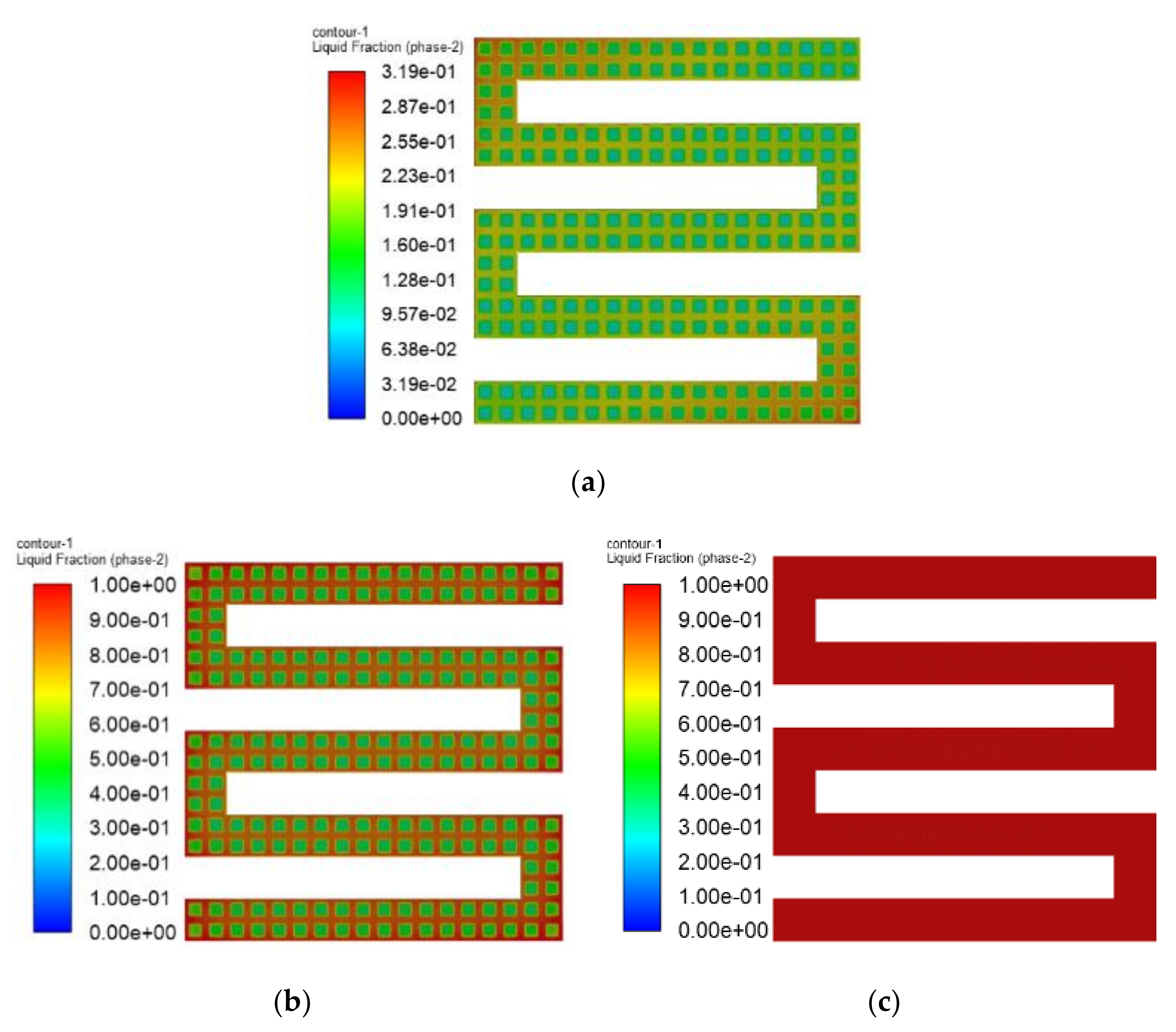
3.3. The Simulation Results of Different Electrothermal Film Structure
3.3.1. The Three-Dimensional Structure Design of Electrothermal Film
3.3.2. Simulation Results
4. Conclusions
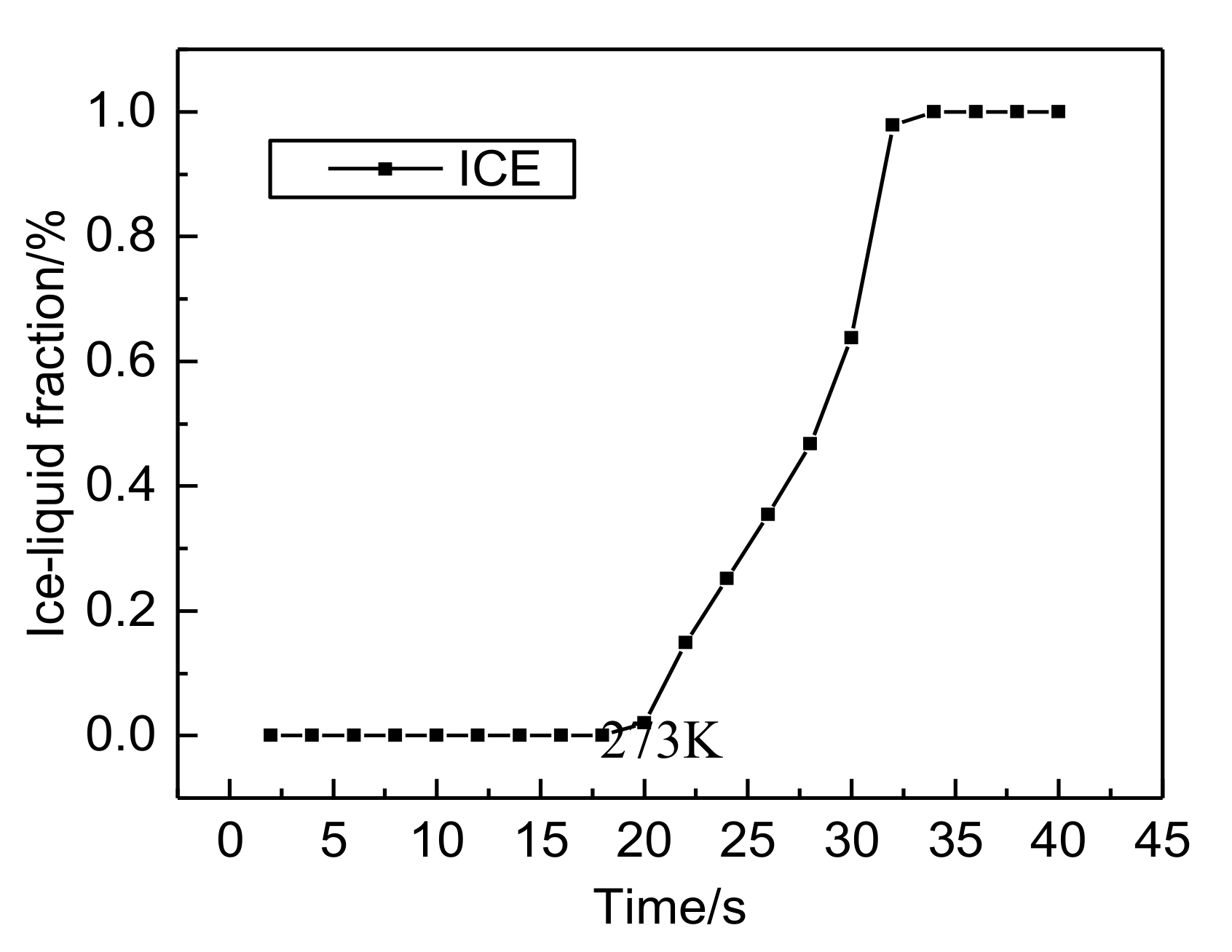
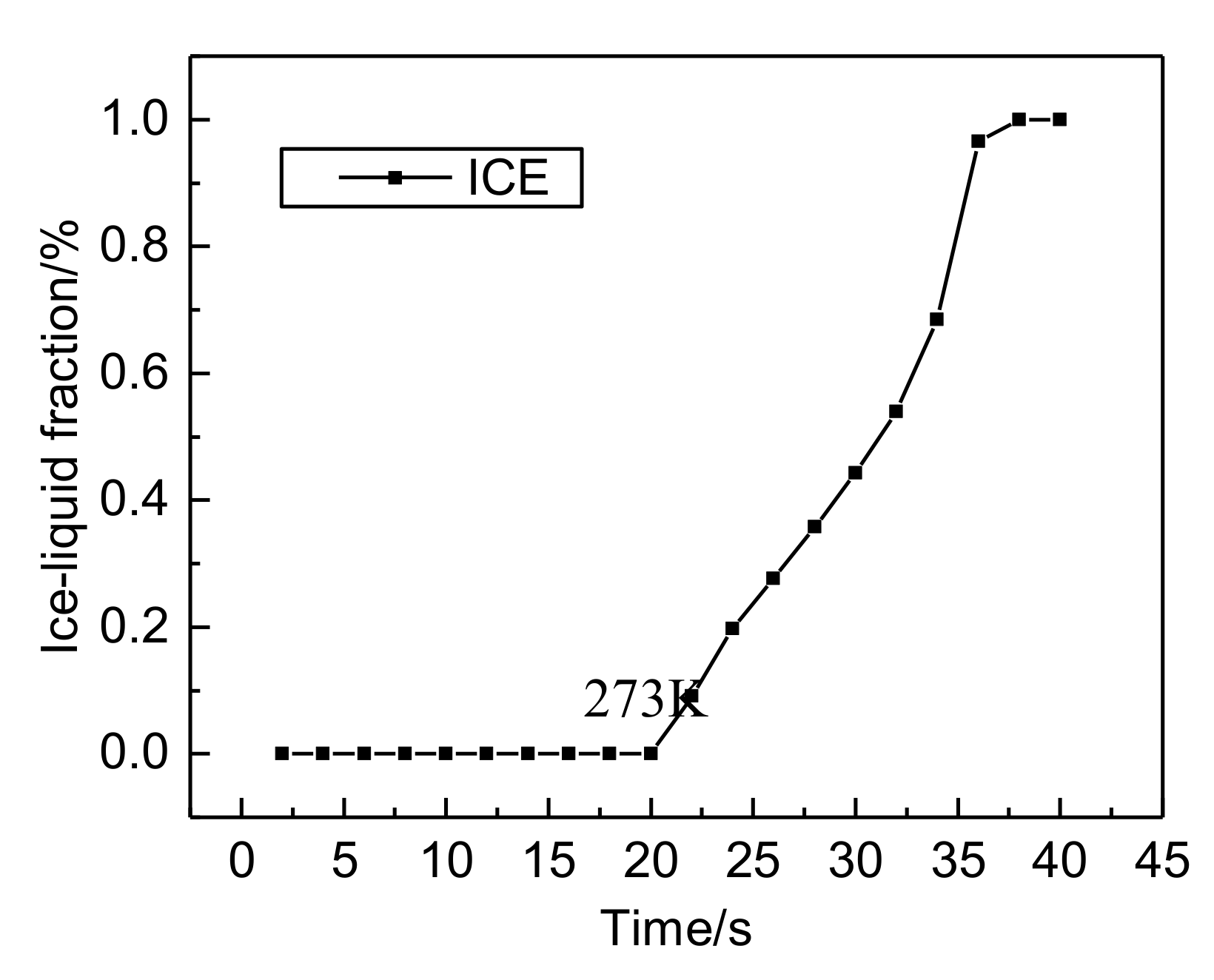
- Both the PEM electric heating method and the electrothermal film heating method were able to achieve rapid cold start-up. The ice inside the PEMFC stack melted first, and the first and 40th pieces melted afterwards. The ice melting time of the PEMFC stack of the two methods was 32.5 s and 36.5 s, respectively.
- In order to study the effect of different electrothermal film (ETF) structures on cold start-up performance, ETFs with pore diameters of 0.3 mm, 0.6 mm, and 0.9 mm were established. It was found that the pore size of 0.3 mm melts first, followed by 0.6 mm, and then 1.2 mm. When the pore sizes of the ETF were 0.3 mm, 0.6 mm and 1.2 mm, the ice initial melting times were 28 s, 30 s and 32 s, respectively, and the corresponding final melting times were 44 s, 46 s and 48 s, respectively.
Author Contributions
Funding
Conflicts of Interest
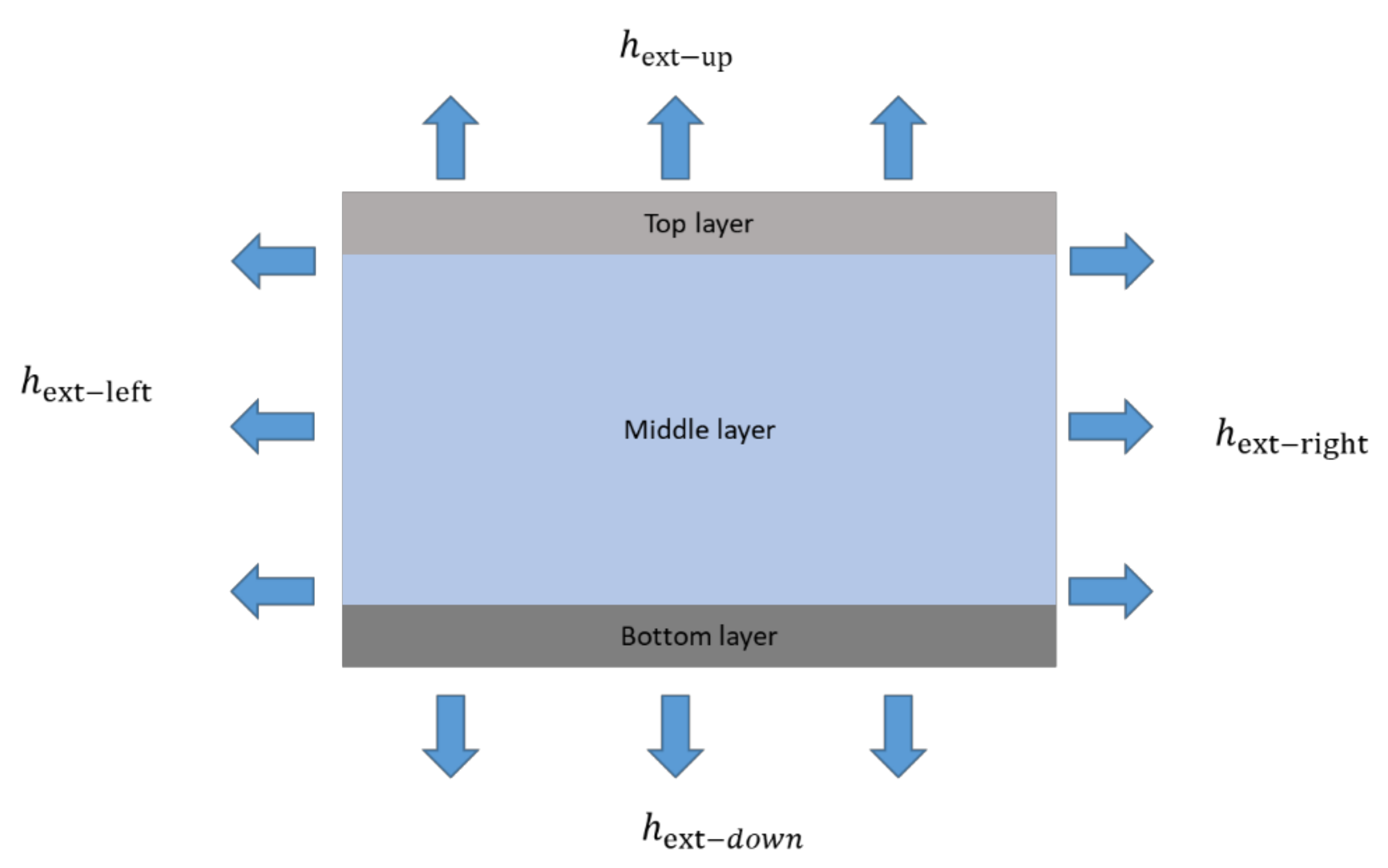
Appendix A. Determination of the Heat Transfer Coefficient hext
- When = 1.22, = 0.35, represents the vertical surface convection heat transfer coefficient, P = H;
- When = 1.0, = 0.33, represents the convection heat transfer coefficient of horizontal top surface, ;
- When = 0.5, = 0.33, represents the convection heat transfer coefficient of horizontal bottom surface;
- Where L is the length of the horizontal plane, W is the width of the horizontal plane, and H is the vertical height.
Appendix B. Determination of Thermal Conductivity and Volume Power Density of the ETF
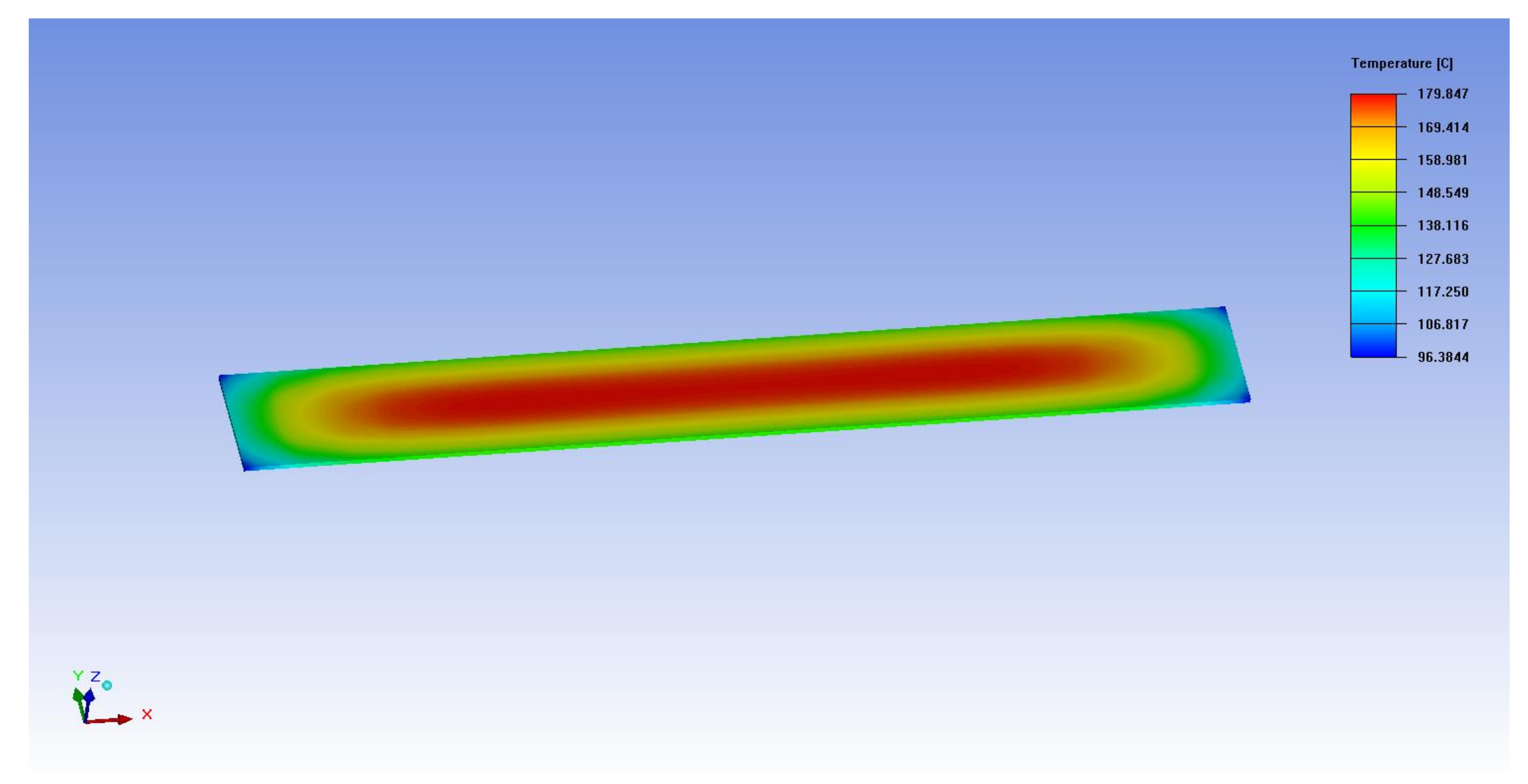
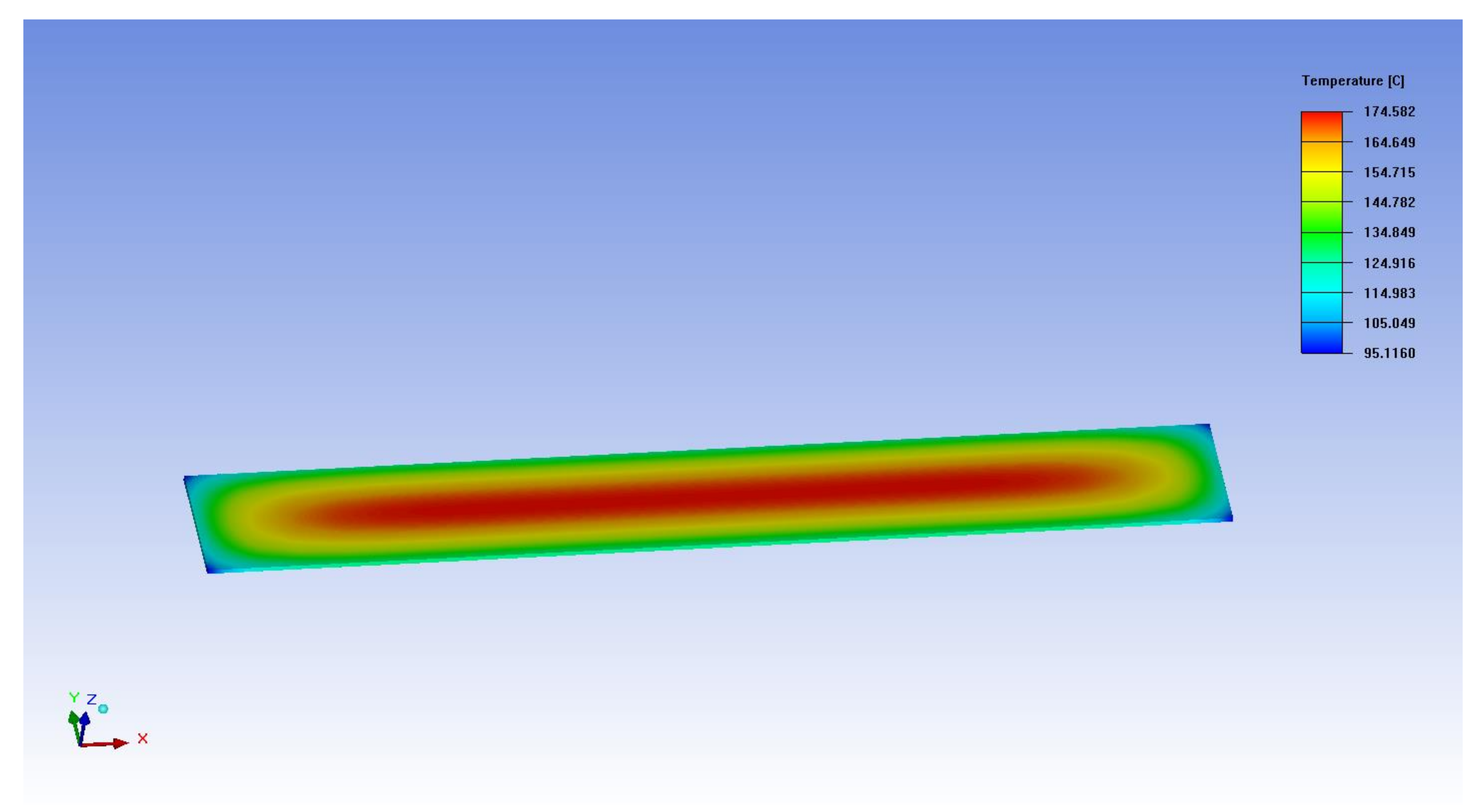
Appendix C. The Units of Variables
| Symbol | Variable | Units |
| density of solid | kg m−3 | |
| density of fluid | ||
| density of fulid | ||
| density | ||
| thermal conductivity of the solid phase. | W m−1 K−1 | |
| thermal conductivity of the liquid phase | ||
| effective thermal conductivity of the medium | ||
| the fluid’s volume fraction | ||
| velocity of fluid | m.s−1 | |
| velocity vector | ||
| source term | W.m−3 | |
| source term | ||
| the mass transfer from phase q to phase p | kg | |
| the mass transfer from phase p to phase q | ||
| enthalpy | kJ/kg | |
| enthalpy of fluid | ||
| enthalpy variation | ||
| reference enthalpy | ||
| specific heat | J.kg−1. K−1 | |
| volume fraction of the liquid | ||
| latent heat of liquid water | J.kg−1 | |
| temperature of q-phase | K | |
| temperature of the porous medium region | ||
| outer surface temperature of the material | ||
| external ambient temperature | ||
| temperature of water starts to freeze | ||
| temperature of liquid begins to melt | ||
| porosity of the porous medium | ||
| energy of fluid | J | |
| total energy of the fluid | J | |
| total energy of the solid medium | J | |
| convective heat transfer coefficient | W/(m2 °C) |
References
- Cano, Z.P.; Banham, D.; Ye, S.; Hintennach, A.; Lu, J.; Fowler, M.; Chen, Z. Batteries and fuel cells for emerging electric vehicle markets. Nat. Energy 2018, 3, 279–289. [Google Scholar] [CrossRef]
- Knorr, F.; Sanchez, D.G.; Schirmer, J.; Gazdzicki, P.; Friedrich, K.A. Methanol as antifreeze agent for cold start of automotive polymer electrolyte membrane fuel cells. Appl. Energy 2019, 238, 1–10. [Google Scholar] [CrossRef]
- Li, L.; Wang, S.; Yue, L.; Wang, G. Cold-start icing characteristics of proton-exchange membrane fuel cells. Int. J. Hydrogen Energy 2019, 44, 12033–12042. [Google Scholar] [CrossRef]
- Hou, J.; Yu, H.; Zhang, S.; Sun, S.; Wang, H.; Yi, B.; Ming, P. Analysis of PEMFC freeze degradation at −20 °C after gas purging. J. Power Sources 2006, 162, 513–520. [Google Scholar] [CrossRef]
- Huo, S.; Jiao, K.; Park, J.W. On the water transport behavior and phase transition mechanisms in cold start operation of PEM fuel cell. Appl. Energy 2019, 233–234, 776–788. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Three-dimensional multiphase modeling of cold start processes in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6876–6891. [Google Scholar] [CrossRef]
- Jean, B.S.; Marcelo, D.V. Global Change, Energy Issues and Regulation Policies; Integrated Science and Technology Program; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Jiao, K.; Alaefour, I.E.; Karimi, G.; Li, X. Simultaneous measurement of current and temperature distributions in a proton exchange membrane fuel cell during cold start processes. Electrochim. Acta 2011, 56, 2967–2982. [Google Scholar] [CrossRef]
- Du, Q.; Jia, B.; Luo, Y.Q.; Chen, J.; Zhou, Y.; Jiao, K. Maximum power cold start mode of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2014, 39, 8390–8400. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, N.W.; Kim, Y.S.; Kim, M.S. Effective purge method with addition of hydrogen on the cathode side for cold start in PEM fuel cell. Int. J. Hydrogen Energy 2013, 38, 11357–11369. [Google Scholar] [CrossRef]
- Guo, Q.; Luo, Y.Q.; Jiao, K. Modeling of assisted cold start processes with anode catalytic hydrogen–oxygen reaction in proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 1004–1015. [Google Scholar] [CrossRef]
- Zhan, Z.; Yuan, C.; Hu, Z.; Wang, H.; Sui, P.C.; Djilali, N.; Pan, M. Experimental study on different preheating methods for the cold-start of PEMFC stacks. Energy 2018, 162, 1029–1040. [Google Scholar] [CrossRef]
- Jeong, Y.G.; Jeon, G.W. Microstructure and performance of multiwalled carbon nanotube/m-aramid composite films as electric heating elements. ACS Appl. Mater. Interfaces 2013, 5, 6527–6534. [Google Scholar] [CrossRef] [PubMed]
- Janas, D.; Koziol, K.K. Rapid electrothermal response of high-temperature carbon nanotube film heaters. Carbon 2013, 59, 457–463. [Google Scholar] [CrossRef]
- Biercuk, M.J.; Llaguno, M.C.; Radosavljevic, M.; Hyun, J.K.; Johnson, A.T.; Fischer, J.E. Carbon nanotube composites for thermal management. Appl. Phys. Lett. 2002, 80, 2767–2769. [Google Scholar] [CrossRef]
- Jang, H.-S.; Jeon, S.K.; Nahm, S.H. The manufacture of a transparent film heater by spinning multi-walled carbon nanotubes. Carbon 2011, 49, 111–116. [Google Scholar] [CrossRef]
- Yan, J.; Jeong, Y.G. Multiwalled carbon nanotube/polydimethylsiloxane composite films as high performance flexible electric heating elements. Appl. Phys. Lett. 2014, 105, 051907. [Google Scholar] [CrossRef]
- Xiao, Z.; Sheng, C.; Xia, Y.; Yu, X.; Liang, C.; Huang, H.; Gan, Y.; Zhang, J.; Zhang, W. Electrical heating behavior of flexible thermoplastic polyurethane/Super-P nanoparticle composite films for advanced wearable heaters. J. Ind. Eng. Chem. 2019, 71, 293–300. [Google Scholar] [CrossRef]
- Bai, B.C.; Kang, S.C.; Im, J.S.; Lee, S.H.; Lee, Y.-S. Effect of oxyfluorinated multi-walled carbon nanotube additives on positive temperature coefficient/negative temperature coefficient behavior in high-density polyethylene polymeric switches. Mater. Res. Bull. 2011, 46, 1391–1397. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Zhao, H.M.; Wang, D.Y.; Wang, Q.; Pang, Y.; Deng, N.Q.; Cao, H.-W.; Yang, Y.; Ren, T.-L. A super flexible and custom-shaped graphene heater. Nanoscale 2017, 9, 14357–14363. [Google Scholar] [CrossRef]
- Tan, L.; Zeng, M.; Wu, Q.; Chen, L.; Wang, J.; Zhang, T.; Eckert, J.; Rümmeli, M.H.; Fu, L. Direct growth of ultrafast transparent single-layer graphene defoggers. Small 2015, 11, 1840–1846. [Google Scholar] [CrossRef]
- Sui, D.; Huang, Y.; Huang, L.; Liang, J.; Ma, Y.; Chen, Y. Flexible and transparent electrothermal film heaters based on graphene materials. Small 2011, 7, 3186–3192. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Yang, J.; Yang, C.; Hao, S. Compression and reduction of graphene oxide aerogels into flexible, porous and functional graphene films. J. Mater. Sci. 2019, 54, 13147–13156. [Google Scholar] [CrossRef]
- An, J.-E.; Jeong, Y.G. Structure and electric heating performance of graphene/epoxy composite films. Eur. Polym. J. 2013, 49, 1322–1330. [Google Scholar] [CrossRef]
- Bae, J.J.; Lim, S.C.; Han, G.H.; Jo, Y.W.; Doung, D.L.; Kim, E.S.; Chae, S.J.; Huy, T.Q.; Van Luan, N.; Lee, Y.H. Heat Dissipation of Transparent Graphene Defoggers. Adv. Funct. Mater. 2012, 22, 4819–4826. [Google Scholar] [CrossRef]
- Shin, K.-Y.; Hong, J.-Y.; Lee, S.; Jang, J. High electrothermal performance of expanded graphite nanoplatelet-based patch heater. J. Mater. Chem. 2012, 22, 23404–23410. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Kang, J.; Kim, H.; Kim, K.S.; Lee, S.K.; Bae, S.; Ahn, J.H.; Kim, Y.-J.; Choi, J.-B.; Hong, B.H. High-performance graphene-based transparent flexible heaters. Nano Lett. 2011, 11, 5154–5158. [Google Scholar] [CrossRef]
- Li, C.; Xu, Y.-T.; Zhao, B.; Jiang, L.; Chen, S.-G.; Xu, J.-B.; Fu, X.-Z.; Sun, R.; Wong, C.-P. Flexible graphene electrothermal films made from electrochemically exfoliated graphite. J. Mater. Sci. 2015, 51, 1043–1051. [Google Scholar] [CrossRef]
- Luo, J.; Lu, H.; Zhang, Q.; Yao, Y.; Chen, M.; Li, Q. Flexible carbon nanotube/polyurethane electrothermal films. Carbon 2016, 110, 343–349. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Li, H.; Lai, X.; Yang, Z.; Chen, Z.; Wu, W.; Zeng, X. Vacuum-assisted layer-by-layer superhydrophobic carbon nanotube films with electrothermal and photothermal effects for deicing and controllable manipulation. J. Mater. Chem. A 2018, 6, 16910–16919. [Google Scholar] [CrossRef]
- Sun, H.; Chen, D.; Ye, C.; Li, X.; Dai, D.; Yuan, Q.; Chee, K.W.A.; Zhao, P.; Jiang, N.; Lin, C.-T. Large-area self-assembled reduced graphene oxide/electrochemically exfoliated graphene hybrid films for transparent electrothermal heaters. Appl. Surf. Sci. 2018, 435, 809–814. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of navier-stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Ko, J.; Kim, W.-G.; Lim, Y.-D.; Ju, H. Improving the cold-start capability of polymer electrolyte fuel cells (PEFCs) by using a dual-function micro-porous layer (MPL): Numerical simulations. Int. J. Hydrogen Energy 2013, 38, 652–659. [Google Scholar] [CrossRef]

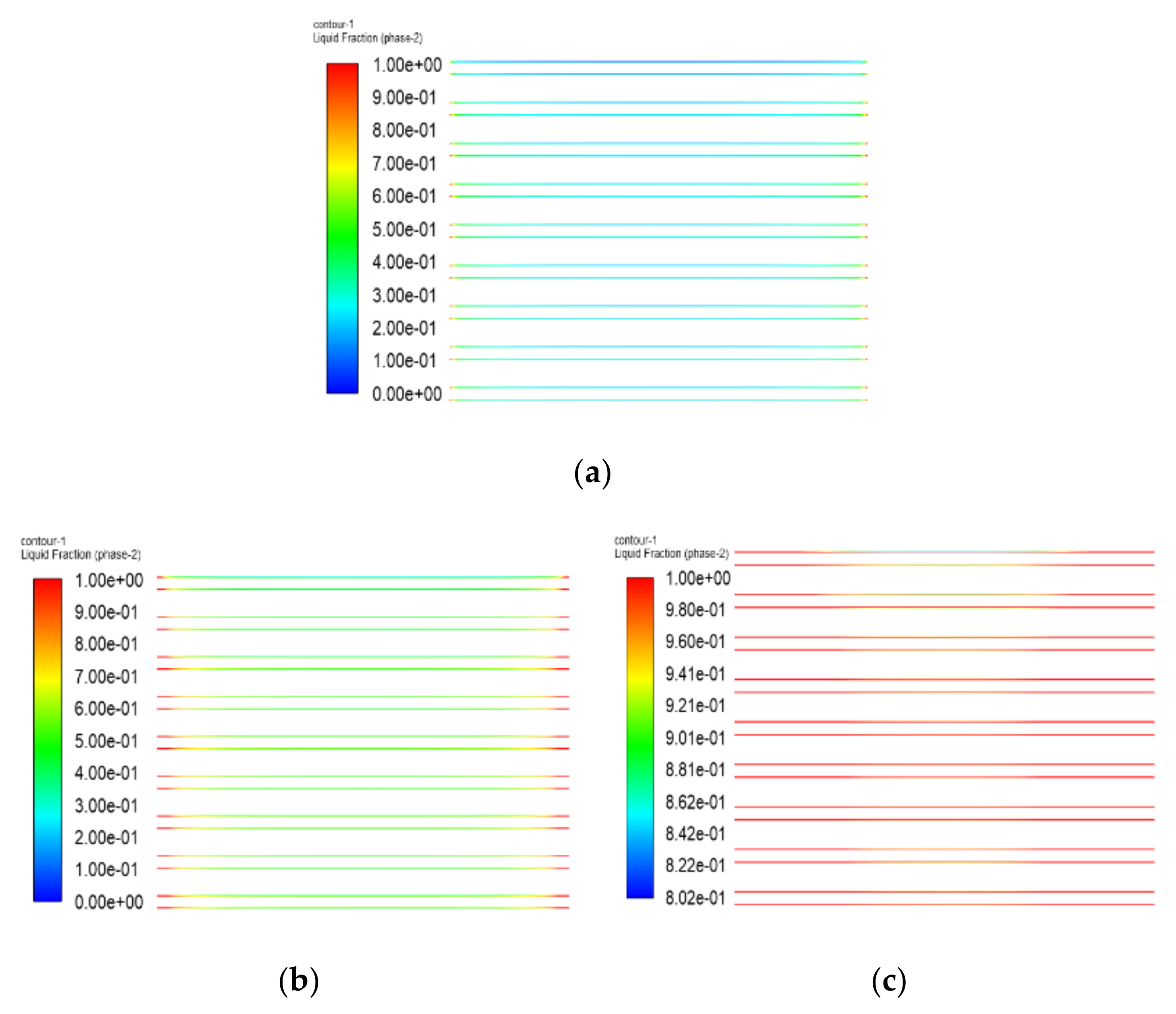



| Material | Parameters | Material | Parameters |
|---|---|---|---|
| Density of GDL/(kg. m−3) | 2200 | Density of PEM/(kg. m−3) | 1980 |
| Specific heat capacity of GDL/(J.kg−1. K−1) | 1050 | Specific heat capacity of PEM/(J.kg−1. K−1) | 1050 |
| Thermal conductivity of GDL/(W.m−1. K−1) | 1.5 | Thermal conductivity of PEM/(W.m−1. K−1) | 1.5/0.95 |
| Porosity of GDL | 0.5 | Porosity of PEM | 0.1 |
| Densities of BP, GFC/(kg. m−3) | 1900 | Density of CL/(kg. m−3) | 2000 |
| Specific heat capacities of BP, GFC/(J.kg−1. K−1) | 710 | Specific heat capacity of CL/(J.kg−1. K−1) | 833 |
| Thermal conductivities of BP, GFC/(W.m−1. K−1) | 20 | Thermal conductivity of CL/(W.m−1. K−1) | 1.2 |
| Density of water/(kg. m−3) | 998.2 | Reference temperature of liquid water/K | 298 |
| Specific heat capacity of liquid water/(J.kg−1. K−1) | 4182 | Reference enthalpy of liquid water/(J. kg−1. mol−1) | −2.858 × 108 |
| Thermal conductivity of liquid water/(W.m−1. K−1) | 0.6 | Melting heat/(J.kg−1) | 334,000 |
| Solidus of liquid water/K | 273.15 | Liquidus of liquid water/K | 273.15 |
| Material | Dimension | Material | Dimension |
| GDL (mm × mm) | 70 × 0.15 | PEM (mm × mm) | 70 × 0.3 |
| BP,GFC (mm × mm) | 70 × 0.8 | CL (mm × mm) | 70 × 0.15 |
| ICE (mm × mm) | 50 × 0.1 | ETF (mm × mm) | 70 × 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Song, K.; Zheng, B.; Xu, Y.; Fang, R. Study on Fast Cold Start-Up Method of Proton Exchange Membrane Fuel Cell Based on Electric Heating Technology. Energies 2020, 13, 4456. https://doi.org/10.3390/en13174456
Jiang W, Song K, Zheng B, Xu Y, Fang R. Study on Fast Cold Start-Up Method of Proton Exchange Membrane Fuel Cell Based on Electric Heating Technology. Energies. 2020; 13(17):4456. https://doi.org/10.3390/en13174456
Chicago/Turabian StyleJiang, Wei, Ke Song, Bailin Zheng, Yongchuan Xu, and Ruoshi Fang. 2020. "Study on Fast Cold Start-Up Method of Proton Exchange Membrane Fuel Cell Based on Electric Heating Technology" Energies 13, no. 17: 4456. https://doi.org/10.3390/en13174456
APA StyleJiang, W., Song, K., Zheng, B., Xu, Y., & Fang, R. (2020). Study on Fast Cold Start-Up Method of Proton Exchange Membrane Fuel Cell Based on Electric Heating Technology. Energies, 13(17), 4456. https://doi.org/10.3390/en13174456




